Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60807,8 pages
10.4236/jamp.2015.310162
Structure of Schrödinger’s Nucleon: Elastic Form-Factors and Radii
Gintautas P. Kamuntavičius
Vytautas Magnus University, Kaunas, Lithuania
Email: g.kamuntavicius@gmf.vdu.lt
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 September 2015; accepted 27 October 2015; published 30 October 2015
ABSTRACT
The Galilei invariant model of the nucleon as a system of three point particles, whose dynamics is governed by Schrödinger equation, after six Hamiltonian parameters fitting, predicts magnetic momenta, masses and charge radii of the proton and neutron with experimental precision. Now this model is applied in order to investigate nucleon charge, mass and magnetism distributions. The obtained electric and magnetic form factors at low values of momentum transfer are in satisfactory agreement with experimental information. The model predicts that neutron is a more compact system than proton.
Keywords:
Solutions of Wave Equations (Bound States), Potential Models, Proton and Neutron

1. Introduction
Different and significant changes of quantum systems, composing more complex structures (for example, atoms forming molecules or solid state) are obvious. The well-known experiments of atomic nuclei structure also indicate that a nucleon embedded in a nucleus is slightly modified in comparison with a free one [1] -[3] . Therefore, for the investigation of this effect, the simple model is necessary, which is compatible with the technique of atomic nuclei description and is able to predict the changes of nucleon structure once it appears in vicinity of other nucleons.
The Schrödinger’s model of nucleon [4] is introduced namely for the solution of this problem. The model considers proton and neutron as different systems of three point particles (PP) in correspondence with the Standard Model recommendations: proton as the system of two up (uPP) and one down (dPP) particle, while neutron ―as a system of one uPP and two dPP particles. These particles should not be identified with the quarks of the Standard Model because only their spins , charges (+2e/3 and −e/3) and baryon numbers (1/3) match the respective quarks quantum numbers. Both PP of our model are different; thus isospin quantum number is not necessary. Therefore, the color quantum number, which is used in the Standard Model to antisymmetrize the wave function, is also unnecessary. In our model antisymmetry is ensured with a smaller number of wave-func- tion’s degrees of freedom. Baryon number is necessary to prevent the possibility of system excitation when one or two PP escapes to continuous spectrum. The PPs, composing the nucleon, allow defining the magnetic momenta of structureless particles in Dirac’s way. The interactions of different pairs of PP (uu, ud and dd) contain the Coulomb and three-dimensional harmonic oscillator (spring) potentials, having four free parameters. Together with PP masses the model Hamiltonian has six free parameters. The conditions for this model are as follows. Firstly, it has to be Galilei invariant. Secondly, finite ranges of potential wells are applied in order to avoid the appearance of nonexistent bound excited states of the nucleon. Finally, the number of parameters of nucleon Hamiltonian has to be equal with the number of nucleon characteristics, applied for fitting. These are the best known characteristics of the proton and neutron―masses, magnetic momenta and charge distribution radii. The values of experimental results, given in Particle Data Group 2014 report [5] and corresponding model results are presented in Table 1. It is shown that six parameters of model Hamiltonian can be chosen so that the mentioned characteristics of nucleon could be predicted with experimental precision.
, charges (+2e/3 and −e/3) and baryon numbers (1/3) match the respective quarks quantum numbers. Both PP of our model are different; thus isospin quantum number is not necessary. Therefore, the color quantum number, which is used in the Standard Model to antisymmetrize the wave function, is also unnecessary. In our model antisymmetry is ensured with a smaller number of wave-func- tion’s degrees of freedom. Baryon number is necessary to prevent the possibility of system excitation when one or two PP escapes to continuous spectrum. The PPs, composing the nucleon, allow defining the magnetic momenta of structureless particles in Dirac’s way. The interactions of different pairs of PP (uu, ud and dd) contain the Coulomb and three-dimensional harmonic oscillator (spring) potentials, having four free parameters. Together with PP masses the model Hamiltonian has six free parameters. The conditions for this model are as follows. Firstly, it has to be Galilei invariant. Secondly, finite ranges of potential wells are applied in order to avoid the appearance of nonexistent bound excited states of the nucleon. Finally, the number of parameters of nucleon Hamiltonian has to be equal with the number of nucleon characteristics, applied for fitting. These are the best known characteristics of the proton and neutron―masses, magnetic momenta and charge distribution radii. The values of experimental results, given in Particle Data Group 2014 report [5] and corresponding model results are presented in Table 1. It is shown that six parameters of model Hamiltonian can be chosen so that the mentioned characteristics of nucleon could be predicted with experimental precision.
Thus, the eigenfunctions of introduced Hamiltonian application for nucleon structure investigation are the next interesting problem. This paper is devoted for electric and magnetic elastic form-factors and corresponding radii description.
2. The Galilei Invariant Form Factor Operator
The elastic form factor of nucleon is defined as density operator’s Fourier image:
 (1)
(1)
Here 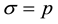 denotes the proton,
denotes the proton,  stands for the neutron, while
stands for the neutron, while
 (2)
(2)
is density operator in the nucleon’s center-of-mass reference frame (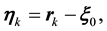 where
where 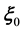 is center-of-mass radius vector).
is center-of-mass radius vector). 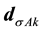 are k-th particle
are k-th particle 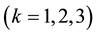 characteristics, given in Table 2.
characteristics, given in Table 2.
For charge density 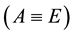 they equal the PP charge
they equal the PP charge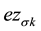 , for magnetization density
, for magnetization density ―the PP magnetic momentum operator
―the PP magnetic momentum operator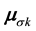 , defined in [4] , while for mass distribution density
, defined in [4] , while for mass distribution density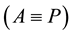 ―the mass of the PP’s
―the mass of the PP’s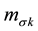 . For PP density distribution
. For PP density distribution 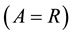 they equal 1/3, i.e. the baryon number of PP. The values of
they equal 1/3, i.e. the baryon number of PP. The values of 


Table 1. Nucleon characteristics, applied for Hamiltonian parameters fitting (experiment; data are from Ref. [5] ), and results of present model (theory).
Table 2. Parameters and operators, present in density definition, Equation (2).
It is well-known that the form factors, defined experimentally, are independent of angles of the momentum transfer




one obtains that

Here 

Written in Jacobi coordinates

it takes the form

Here 

it equals the nucleon charge, magnetic momentum, mass 

so that its value in zero equals one. The only exception is the electric form factor of the neutron



Thus,

is proportional to the square of corresponding radius operator, i.e.:

Inserting the charges of PP’s one obtains the expressions presented in [4] for the squared charge radius operators of the proton and neutron.
3. Expectation Values of Form Factor Operator
Elastic form-factors of nucleon as functions of momentum transfer 

Here both basic functions are bound angular and spin momenta functions

where the parentheses indicate the operation of momenta binding, 








where 




nodes).

the area where a potential equals zero, radial function equals spherical Hankel function of imaginary argument 
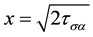

condition

Integration of the first member of right side of Equation (9) is straightforward. For calculation of the second and third integrals one needs spherical Bessel function expansion [8] :

The sum of two functions of this kind present in (9) equals

Having in mind the structure of nucleon wave function, only two first terms of expansion, corresponding 
Finally, after some angular momentum algebra, the form factor can be presented as

where



Here, the radial wave functions as functions of


where 

Obviously, the momentum transfer q in all given expressions has dimension fm−1. The widely accepted dimension of this momentum Q is GeV/c. Therefore, the slight modification is necessary due to these momenta dependence:

Here, in square brackets the dimensions of corresponding quantities are written. The value of conversion factor 
Operators, present in right hand side of Equation (13), having in mind the definitions (14), (11) and (10) are necessary for radii calculation. Together with precise calculation, the values of radii can be determined from the slopes of corresponding form factors in the limit of zero momentum transfer
4. Results
The obtained charge, magnetic, mass and point particles radii are present in the “theory” column of Table 3.
The known experimental values of corresponding radii are given in the “experiment” column. The charge radii of nucleon are applied for fitting, hence their values are equal to the ones, recommended by the Particle Data Group 2014 report [5] . The straightforward evaluation of magnetic radii of nucleon is problematic, hence only few estimates of proton and only one―for neutron magnetic radius are known. The evaluations for mass and point particles radii are absent in literature.
Table 3. Values of different radii of the proton and neutron.
In Figure 1 and Figure 2, the electric and magnetic form factors for the proton 


with parameters 

The neutron electric form factor 
The comparison of calculated and given by standard dipole approximation

with 

The all four obtained form factors demonstrate good enough comparison with known experimental data at low values of momentum transfer, that characterises the nucleons, present in an atomic nucleus. Moreover, ratio of electric and magnetic form factors of neutron at 
The mass and point particles form factors for proton




5. Conclusions
The most interesting result of radii calculation is that the neutron appears as a more compact system than the proton, although the results of the magnetism distribution radii, presented in [5] , show different relations. The obtained compactness of the neutron nicely fits with the well-known fact that the surface of the heavy nuclei is
Figure 1. The electric form factor of the proton (solid line). The fit 
Figure 2. The magnetic form factor of the proton (solid line). The fit 
Figure 3. The electric form factor of the neutron (solid line). The double-polarization data from Ref. [17] .
Figure 4. The magnetic form factor of the neutron (solid line). The standard dipole form factor, Equation (29) (dashed line).
more well-defined than the one of the proton [19] . As follows from our investigation, the proton’s density decreases smoothly and is much more spread out through the sphere than the one of the neutron. There is a surplus of the neutrons in heavy nuclei which usually distribute on the surface of the nucleus and can determine the mentioned effect. Moreover, compact distribution of neutron constituents gives larger probability of weak process, producing its decay.
Therefore, the obtained precision of nucleon description allows concluding that the calculations of other characteristics of the proton and neutron with obtained wave function may give some interesting and rather reliable results. It is well known that realistic potentials of nucleon-nucleon interaction, carefully fitted with the two- nucleon data, give smaller than experimental nuclear binding energies. It looks like that the introduced model is able to give a chance for this problem solution. As it is known from the solid state theory, when the distance between two potential wells decreases, the isolated levels of each well convert to the system of two levels, one of them is more bound than the other one. If Pauli principle allows the constituents of nucleon to occupy the best bound level, this may help us to improve the description of atomic nuclei, taking into account the changes of nucleon structure when merging into groups.
Cite this paper
Gintautas P.Kamuntavičius, (2015) Structure of Schrödinger’s Nucleon: Elastic Form-Factors and Radii. Journal of Applied Mathematics and Physics,03,1352-1360. doi: 10.4236/jamp.2015.310162
References
- 1. Strauch, S., et al. (2003) Polarization Transfer in the 4He(e,e’p)3H Reaction up to Q2 =2.6 (GeV/c)2. Physical Review Letters, 91, Article ID: 052301.
http://dx.doi.org/10.1103/PhysRevLett.91.052301 - 2. Close, F.E. and Roberts, R.G. (1988) A-Dependence of Shadowing and the Small-X EMC Data. Physics Letters, 213B, 91-94.
http://dx.doi.org/10.1016/0370-2693(88)91053-2 - 3. Ashman, J., et al. (European Muon Collaboration) (1988) Measurement of the Ratios of Deep Inelastic Muon-Nucleus Cross-Sections on Various Nuclei Compared to Deuterium. Physics Letters, 202B, 603-610.
http://dx.doi.org/10.1016/0370-2693(88)91872-2 - 4. Kamuntavicius, G.P. (2014) Nucleon as a Nonrelativistic Three Point Particles System. SOP Transactions on Theoretical Physics, 1, 44-56.
http://dx.doi.org/10.15764/TPHY.2014.04004 - 5. Olive, K.A., et al. (Particle Data Group) (2014) Review of Particle Physics. Chinese Physics, C38, Article ID: 090001.
http://dx.doi.org/10.1088/1674-1137/38/9/090001 - 6. Kamuntavicius, G.P. (2014) Galilei Invarint Technique for Quantum System Description. Journal of Mathematical Physics, 55, Article ID: 042103.
http://dx.doi.org/10.1063/1.4870617 - 7. Bateman, H. and Erdelyi, A. (1953) Higher Transcendental Functions, Vol. 1. McGraw-Hill, New York.
- 8. Abramowitz, M. and Stegun, I.A., Eds. (1964) Handbook of Mathematical Functions. NBS, New York.
- 9. Mohr, P.J., Taylor, B.N. and Newell, D.B. (2008) CODATA Recommended Values of the Fundamental Physical Constants: 2006. Reviews of Modern Physics, 80, 633-730.
http://dx.doi.org/10.1103/RevModPhys.80.633 - 10. Bernauer, J., et al. (2010) High-Precision Determination of the Electric and Magnetic Form Factors of the Proton. Physical Review Letters, 105, Article ID: 242001.
http://dx.doi.org/10.1103/physrevlett.105.242001 - 11. Pohl, R., Antognini, A., Nez, F., Amaro, F.D., Biraben, F., Cardoso, J.M.R., et al. (2010) The Size of the Proton. Nature, 466, 213-216.
http://dx.doi.org/10.1038/nature09250 - 12. Borisyuk, D. (2010) Proton Charge and Magnetic Rms Radii from the Elastic ep Scattering Data. Nuclear Physics A, 843, 59-67.
http://dx.doi.org/10.1016/j.nuclphysa.2010.05.054 - 13. Lorenz, I.T., Meissner, U.-G., Hammer, H.-W. and Dong, Y.B. (2015) Theoretical Constraints and Systematic Effects in the Determination of the Proton Form Factors. Physical Review D, 91, Article ID: 014023.
http://dx.doi.org/10.1103/PhysRevD.91.014023 - 14. Kopecky, S., Harvey, J.A., Hill, N.W., Krenn, M., Pernicka, M., Riehs, P. and Steiner, S. (1997) Neutron Charge Radius Determined from the Energy Dependence of the Neutron Transmission of Liquid 208Pb and 209Bi. Physical Review C, 56, 2229-2237.
http://dx.doi.org/10.1103/PhysRevC.56.2229 - 15. Aleksandrov, Y.A. (1999) The Sign and Value of the Neutron Mean Squared Intrinsic Charge Radius. Physics of Particles and Nuclei, 30, 29-48.
http://dx.doi.org/10.1134/1.953096 - 16. Venkat, S., Arrington, J., Miller, G.A. and Zhan, X. (2011) Realistic Transverse Images of the Proton Charge and Magnetization Densities. Physical Review C, 83, Article ID: 015203.
http://dx.doi.org/10.1103/PhysRevC.83.015203 - 17. Gentile, T.R. and Crawford, C.B. (2011) Neutron Charge Radius and the Neutron Electric form Factor. Physical Review C, 83, Article ID: 055203.
http://dx.doi.org/10.1103/PhysRevC.83.055203 - 18. Schlimme, B.S., Achenbach, P., Gayoso, C.A.A., Bernauer, J.C., Böhm, R., Bosnar, D., et al. (2013) Measurement of the Neutron Electric to Magnetic Form Factor Ratio at Q2=1.58 GeV2 Using the Reaction 3He(e,e’n)pp. Physical Review Letters, 111, Article ID: 132504.
http://dx.doi.org/10.1103/PhysRevLett.111.132504 - 19. Henley, E.M. and Garcia, A. (2007) Subatomic Physics. 3rd Edition, World Scientific, Hackensack, 158-174.
http://dx.doi.org/10.1142/6263








