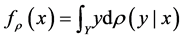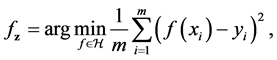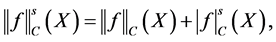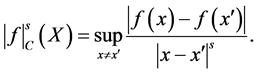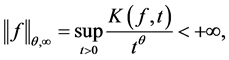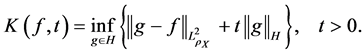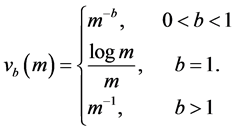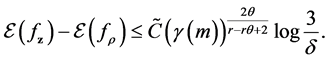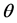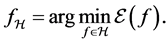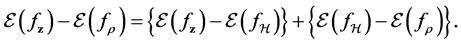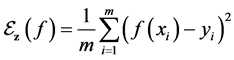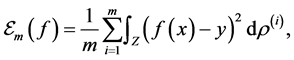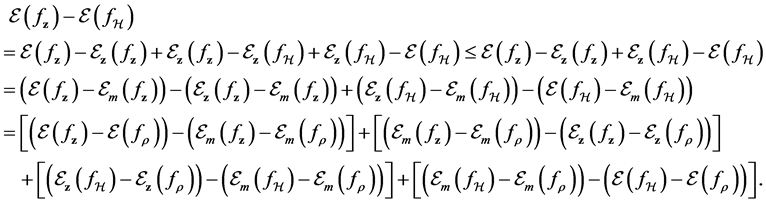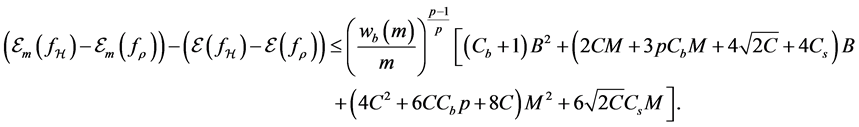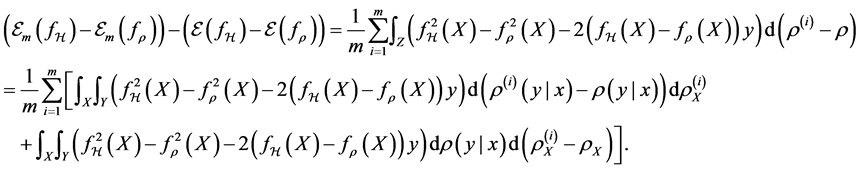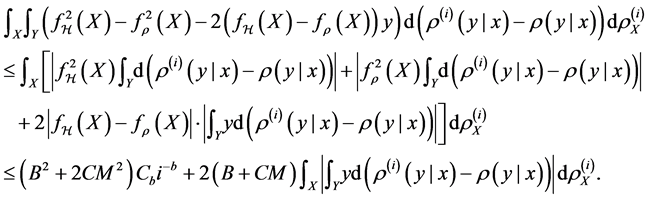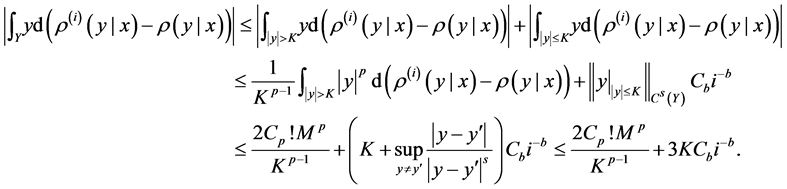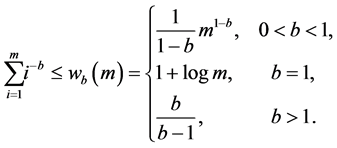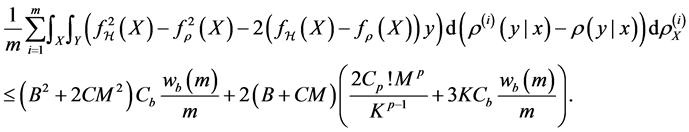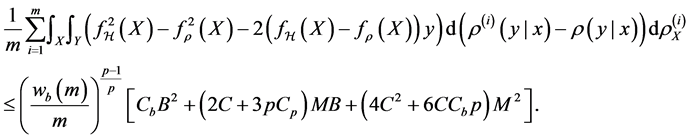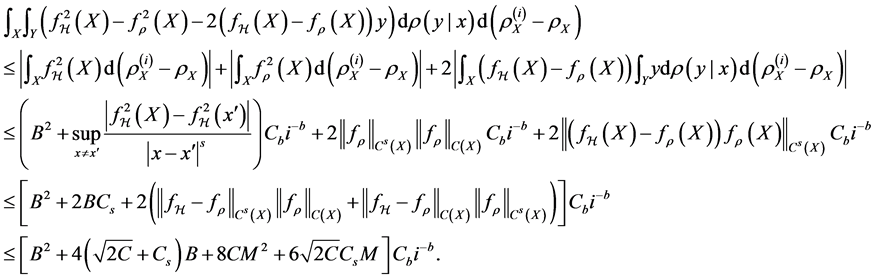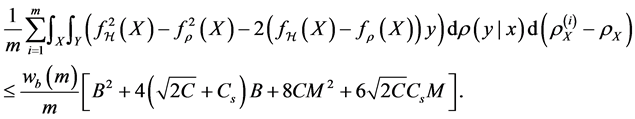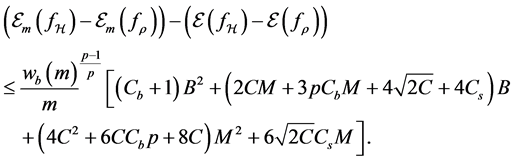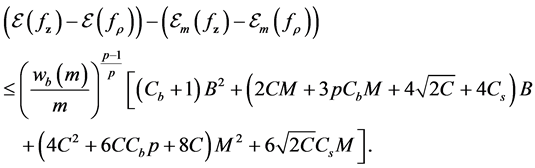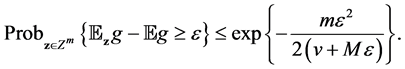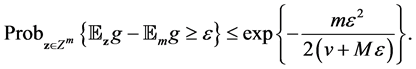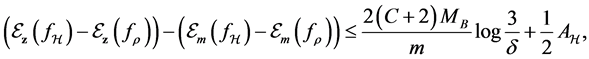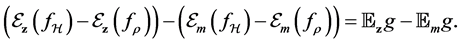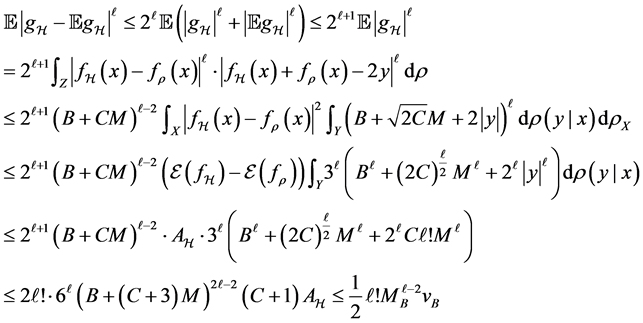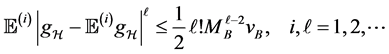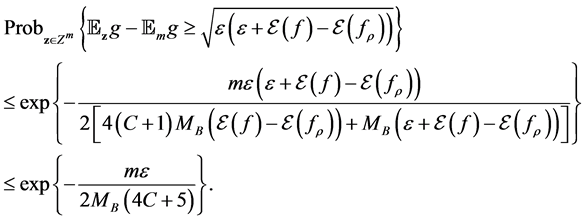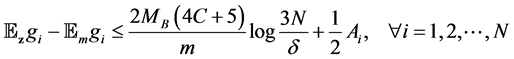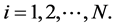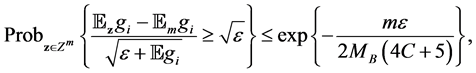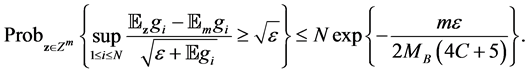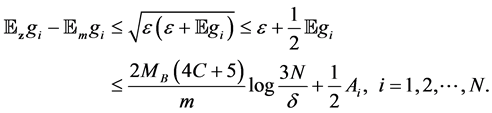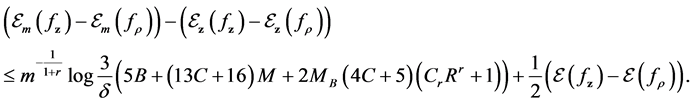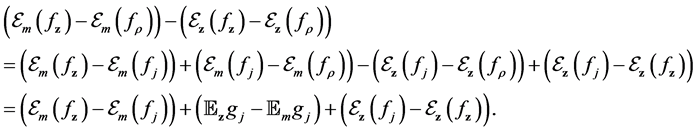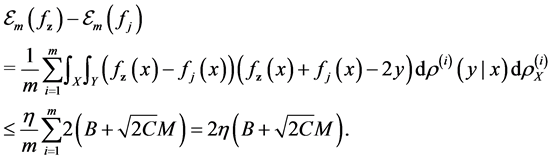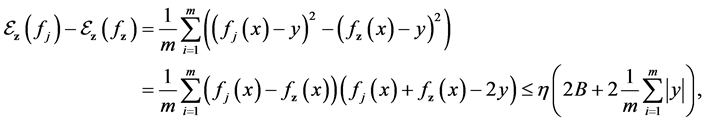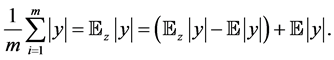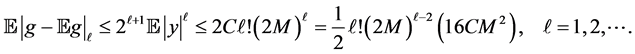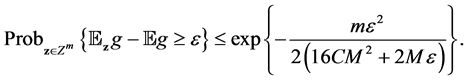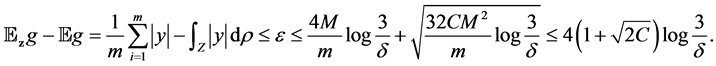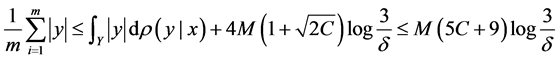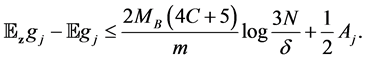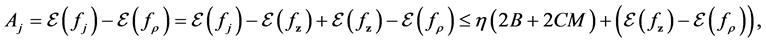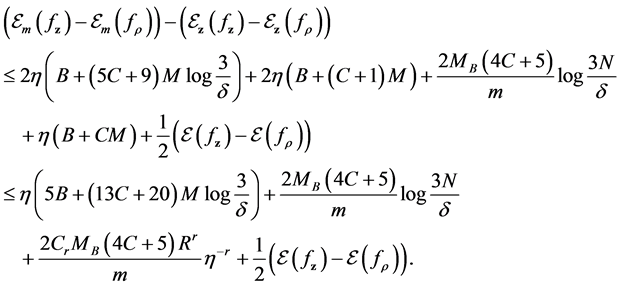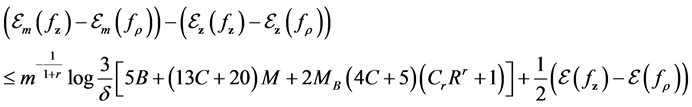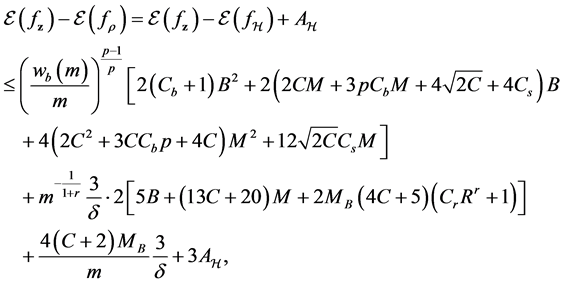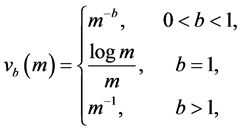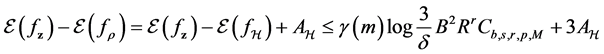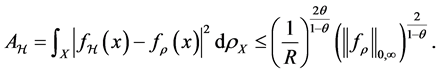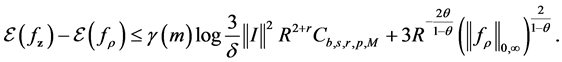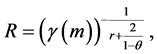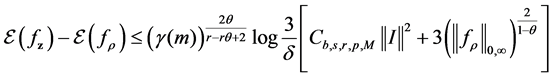Journal of Applied Mathematics and Physics
Vol.04 No.01(2016), Article ID:63080,13 pages
10.4236/jamp.2016.41019
Error Analysis of ERM Algorithm with Unbounded and Non-Identical Sampling*
Weilin Nie, Cheng Wang#
Department of Mathematics, Huizhou University, Huizhou, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 November 2015; accepted 24 January 2016; published 27 January 2016
ABSTRACT
A standard assumption in the literature of learning theory is the samples which are drawn independently from an identical distribution with a uniform bounded output. This excludes the common case with Gaussian distribution. In this paper we extend these assumptions to a general case. To be precise, samples are drawn from a sequence of unbounded and non-identical probability distributions. By drift error analysis and Bennett inequality for the unbounded random variables, we derive a satisfactory learning rate for the ERM algorithm.
Keywords:
Learning Theory, ERM, Non-Identical, Unbounded Sampling, Covering Number

1. Introduction
In learning theory we study the problem of looking for a function or its approximation which reflects the relationship between the input and the output via samples. It can be considered as a mathematical analysis of artificial intelligence or machine learning. Since the exact distributions of the samples are usually unknown, we can only construct algorithms based on an empirical sample set. A typical setting of learning theory in mathe- matics can be like this: the input space X is a compact metric space, and the output space  for regression. (When
for regression. (When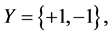 ,it can be regarded as a binary classification problem.) Then
,it can be regarded as a binary classification problem.) Then  is the whole sample space. We assume a distribution
is the whole sample space. We assume a distribution 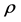 on Z, which can be decomposed to two parts: marginal distribution
on Z, which can be decomposed to two parts: marginal distribution 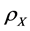 on X and conditional distribution
on X and conditional distribution 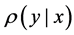 given some
given some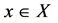 . This implies
. This implies
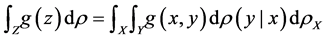
for any integrable function 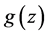 [1] .
[1] .
To evaluate the efficiency of a function  we can choose the generalization error:
we can choose the generalization error:
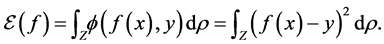
Here 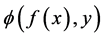 is a loss function which measures the difference between the prediction
is a loss function which measures the difference between the prediction 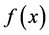 via f and the actual output y. It can be hinge loss in SVM (support vector machine) or pinball loss in quantile learning and etc.. In this paper we focus on the classical least square loss
via f and the actual output y. It can be hinge loss in SVM (support vector machine) or pinball loss in quantile learning and etc.. In this paper we focus on the classical least square loss  for simplicity. [2] shows that
for simplicity. [2] shows that
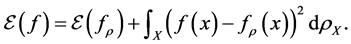 (1)
(1)
From this we can see the regression function
is our goal minimizing the generalization error. The empirical risk minimization (ERM) algorithm aims to find a function which approximates the goal function 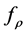
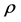
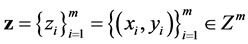
where function space 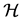
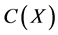
Then the error produced by ERM algorithm is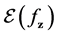
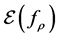
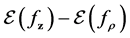
Dependent sampling has considered in some literature such as [3] for concentration inequality and [4] [5] for learning. More recently, in [6] and [7] , the authors studied learning with non-identical sampling and dependent sampling, and obtained satisfactory learning rates.
In this paper we concentrate on the non-identical setting that each sample 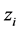
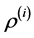
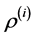
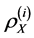
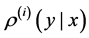
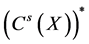
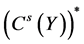
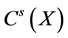
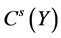
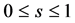
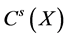
where
We assume a polynomial convergence condition for both sequences 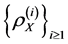
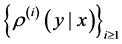
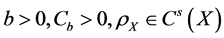
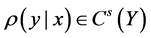
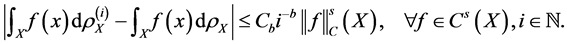
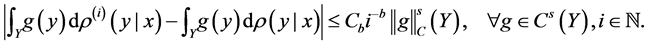
Power index b measures quantitatively differences between the non-identical setting and the i.i.d. case. The distributions are more similar as b is larger, and when 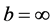
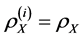
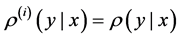
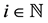
Example 1. Let 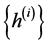
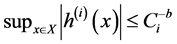
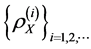
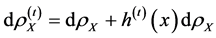
On the other hand, most literature assume the output space is uniformly bounded, that is, 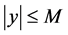
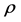
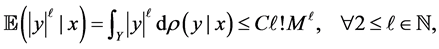
and
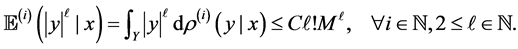
We can see the Gaussian distribution satisfies this setting.
Example 2. Let 
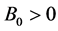
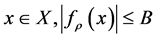
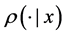
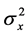
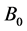
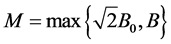
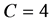
Next we need to introduce the covering number and interpolation space.
Definition 1. The covering number 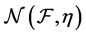
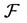
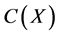
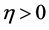
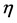
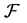
Let the hypothesis space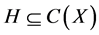
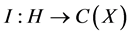
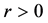
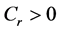
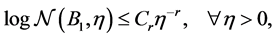
where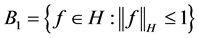
The sample error will decrease but approximation error will increase when covering number of H is larger (or simply say H is larger). So how to choose an appropriate hypothesis space is the key problem of ERM algorithm. We will demonstrate this in our main theorem.
Definition 2. The interpolation space 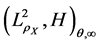
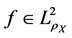
where 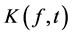
Interpolation space is used to characterize the position of the regression function, and it is related with the approximation error. Now we can state our main result as follow.
Theorem 1. If 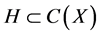
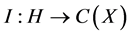
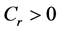
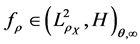
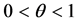
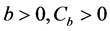
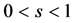
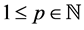
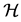
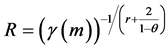
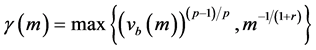
Moreover, we assume all functions in H and 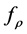
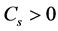
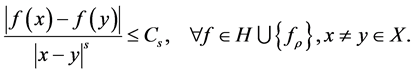
Then for any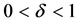
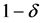
Here 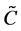
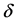
Remark 1. In [6] , the authors pointed out that if we choose the hypothesis space to be the reproducing kernel Hilbert space (RKHS) 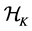
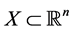
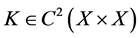
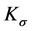
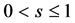
In all, we extend the polynomial convergence condition on the conditional distribution sequense and accordingly, set the moment inremental condition for the sequence in the least squares ERM algorithm. By error decomposition, truncate technique and unbounded concentration inequality, we can finally obtain the total error bound Theorem 1.
Compared with the non-identical settings in [6] and [17] , our setting is more general since the conditional distribution sequence 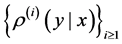
For the classical i.i.d. and bounded conditions, [9] indicates that 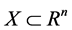
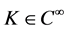
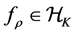
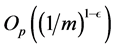
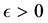
under some conditions on kernel, object function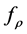
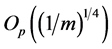
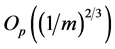
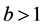
tends to 1 and 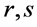
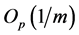
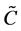
2. Error Decomposition
Our aim, the error 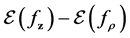
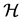
Then the generalization error can be written as
The first term on the right hand side is the sample error, and the second term 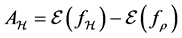
Now we break the sample error to some parts which can be bounded using truncate technique and unbounded concentration inequality. We refer the error decomposition 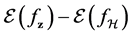
then 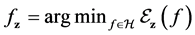
In the following, we call the first and fourth brackets drift errors, and the left sample errors. We will bound the two types of errors respectively in the following sections, and finally obtain the total error bounds.
3. Drift Errors
Firstly we consider the drift error involving 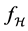
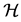
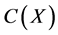
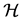
Proposition 1. Assume 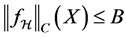
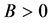
Proof. From the definition of 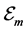
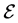
Since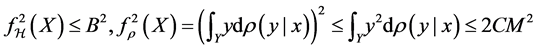
But for any 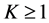
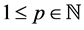
From (3.12) in [6] , we have
Then we can bound the sum of the first term as
Choose K to be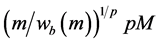
For the second term, notice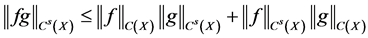
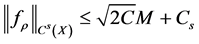
Therefore
Combining the two bounds, we have
And this is indeed the proposition.
For the drift error involving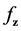
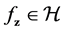
Proposition 2. Assume 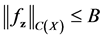
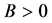
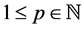
4. Sample Error Estimate
We devote this section to the analysis of the sample errors. For the sample error term involving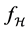
Bennett inequality to fit our setting. Denote 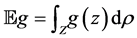

Lemma 1. Assume 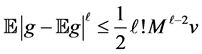
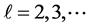
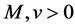
For our non-identical setting, we can have a similar result from the same idea of proof. By denoting 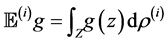
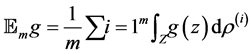
Lemma 2. Assume 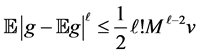
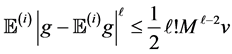
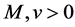
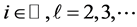
Now we can bound the sample error term 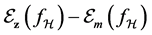
Proposition 3. Under the moment incremental condition (4), (5) and notations above, with probability at least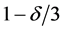
where 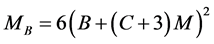
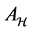
Proof. Let
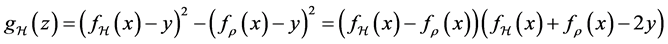
Since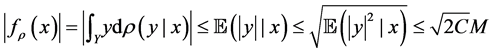
for any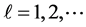
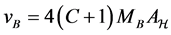
as well. Then from Lemma 2 above, we have
Set the right hand side to be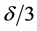
Therefore with confidence at least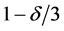
This proves the proposition.
For the sample error term involving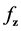
Lemma 3. Denote 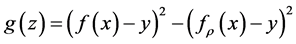
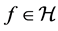
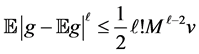
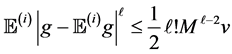
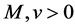
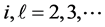
Proof. Let 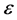
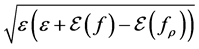
Note that 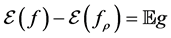
Then we have the following result.
Lemma 4. For a set of functions 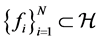
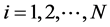
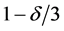
where 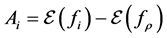
Proof. Since 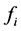
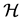
then there holds
Set the right hand side to be 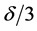

Here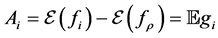
Now by a covering number argument we can bound the sample error term involving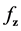
Proposition 4. If 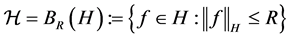
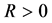
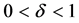
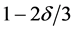
Proof. Denote 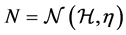
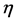
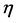
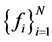
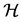
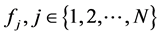
For the first term, since 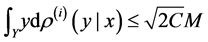
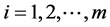
And for the third term,
we need to bound
Let 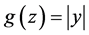
From Lemma 1 we have
Set the right hand side to be 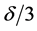
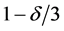
And this means,
with probability at least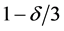
The second term can be bounded by 4 above. That is, with confidence at least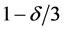
Since 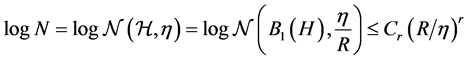
combining the three parts above, we have the following bound with confidence at least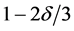
By choosing 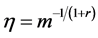
with confidence at least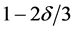
5. Approximation Error and Total Error
Combining the results above, we can derive the error bound for the generalization error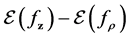
Proposition 5. Under the moment condition for the distribution of the sample and capacity condition for the hypothesis space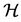
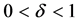
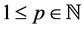
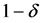
where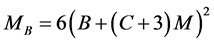
What is left to be determined in the proposition is the approximation error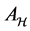
Proof of Theorem 1. Let
and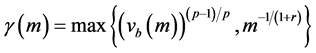
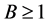
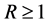
holds with confidence at least 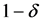
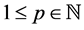
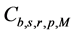
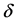
For the approximation error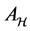
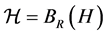
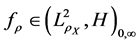
The upper bound B is now chosen to be 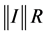
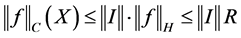
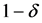
By choosing
we have
holds with confidence at least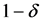
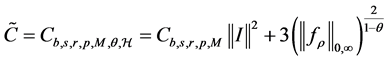
6. Summary and Future Work
We investigate the least squares ERM algorithm with non-identical and unbounded sample, i.e., polynomial convergence for 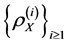
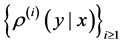
error decomposition as classical analysis for least sqaures regularization [9] [11] is conducted. Truncate techni- que is introduced for handling unbounded setting, and Bennett concentration inequality is used for the sample error. By the above analysis we finally get the error bound and learning rate.
However, our work only considers the ERM algorithm. It is neccesary for us to extend this to the regulari- zation algorithms which are more widely used in practice. A more recent relative reference can be found in [21] . Another interesting topic in future study is dependent sampling [7] .
Cite this paper
Weilin Nie,Cheng Wang, (2016) Error Analysis of ERM Algorithm with Unbounded and Non-Identical Sampling. Journal of Applied Mathematics and Physics,04,156-168. doi: 10.4236/jamp.2016.41019
References
- 1. Cucker, F. and Zhou, D.X. (2007) Learning Theory: An Approximation Theory Viewpoint. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511618796 - 2. Cucker, F. and Smale, S. (2002) On the Mathematical Foundations of Learning. Bulletin of the American Mathematical Society, 39, 1-49.
- 3. Dehling, H., Mikosch, T. and Sorensen, M. (2002) Empirical Process Techniques for Dependent Data. Birkhauser Boston, Inc., Boston.
http://dx.doi.org/10.1007/978-1-4612-0099-4 - 4. Steinwart, I., Hush, D. and Scovel, C. (2009) Learning from Dependent Observations. Journal of Multivariate Analysis, 100, 175-194.
- 5. Steinwart, I. and Christmann, A. (2009) Fast Learning from Non-i.i.d. Observations. In: Bengio, Y., Schuurmans, D., Lafferty, J.D., Williams, C.K.I. and Culotta, A., Eds., Advances in Neural Information Processing Systems 22, Curran and Associates, Inc., Yellowknife, 1768-1776.
- 6. Xiao, Q.W. and Pan, Z.W. (2010) Learning from Non-Identical Sampling for Classification. Advances in Computational Mathematics, 33, 97-112.
- 7. Pan, Z.W. and Xiao, Q.W. (2009) Least-Square Regularized Regression with Non-i.i.d. Sampling. Journal of Statistical Planning and Inference, 139, 3579-3587.
- 8. Hu, T. and Zhou, D.X. (2009) Online Learning with Samples Drawn from Non-identical Distributions. Journal of Machine Learning Research, 10, 2873-2898.
- 9. Wu, Q., Ying, Y. and Zhou, D.X. (2006) Learning Rates of Least-Square Regularized Regression. Foundations of Computational Mathematics, 6, 171-192.
- 10. Capponnetto, A. and De Vito, E. (2007) Optimal Rates for the Regularized Least Squares Algorithm. Foundations of Computational Mathematics, 7, 331-368.
- 11. Wang, C. and Zhou, D.X. (2011) Optimal Learning Rates for Least Squares Regularized Regression with Unbounded Sampling. Journal of Complexity, 27, 55-67.
- 12. Guo, Z.C. and Zhou, D.X. (2013) Concentration Estimates for Learning with Unbounded Sampling. Advances in Computational Mathematics, 38, 207-223.
- 13. He, F. (2014) Optimal Convergence Rates of High Order Parzen Windows with Unbounded Sampling. Statistics & Probability Letters, 92, 26-32.
- 14. Zhou, D.X. (2002) The Covering Number in Learning Theory. Journal of Complexity, 18, 739-767.
- 15. Zhou, D.X. (2003) Capacity of Reproducing Kernel Spaces in Learning Theory. IEEE Transactions on Information Theory, 49, 1743-1752.
- 16. Zhou, D.X. (2008) Derivative Reproducing Properties for Kernel Methods in Learning Theory. Journal of Computational and Applied Mathematics, 220, 456-463.
- 17. Smale, S. and Zhou, D.X. (2009) Online Learning with Markov Sampling. Analysis and Applications, 7, 87-113.
- 18. Smale, S. and Zhou, D.X. (2003) Estimating the Approximation Error in Learning Theory. Analysis and Applications, 1, 17-41.
- 19. Wang, C. and Guo, Z.C. (2012) ERM Learning with Unbounded Sampling. Acta Mathematica Sinica, English Series, 28, 97-104.
- 20. Bennett, G. (1962) Probability Inequalities for the Sum of Independent Random Variables. Journal of the American Statistical Association, 57, 33-45.
- 21. Cai, J. (2013) Coefficient-Based Regression with Non-Identical Unbounded Sampling. Abstract and Applied Analysis, 2013, Article ID: 134727.
http://dx.doi.org/10.1155/2013/134727
NOTES
*This work is supported by NSF of China (Grant No. 11326096, 11401247), Foundation for Distinguished Young Talents in Higher Education of Guangdong, China (No. 2013LYM 0089), Doctor Grants of Huizhou University (Grant No. C511.0206) and NSF of Guangdong Province in China (No. 2015A030313674).
#Corresponding author.