Received 25 July 2015; accepted 22 September 2015; published 25 September 2015

ABSTRACT

In this paper, we study the existence and uniqueness of positive solution for 2mth-order nonlinear differential equation with boundary conditions, by using the fixed point theorems on compression and expansion of cones.

Keywords:

2mth-Order, Uniqueness, Existence, Fixed Point Theorems on Compression and Expansion of Cones

1. Introduction

Recently, many authors studied the existence and multiplicity of positive solutions for the boundary value problem of even-order differential equations since it arose naturally in many different areas of applied mathematics and physics (see [1] -[3] ).

In [4] by applying the theory of differential inequalities, the author established the existence of positive solution for the third-order differential equation. In [5] , the authors derived the Green function of the 2mth-order nonlinear differential equation, and established the existence of positive solutions for BVP, by using the fixed point theorems on compression and expansion of cones. However, there are a few articles devoted to the uniqueness problem by using the fixed point theorem. In [6] , the authors studied the existence and multiplicity of positive periodic solutions for second-order nonlinear damped differential equations by combing the analysis of positiveness of the Green function for a linear damped equation. Our nonlinearity may be singular in its dependent variable. The proof of the main result relies on the Guo-Krasnosel’ skii fixed point theorem on compression and expansion of cones.

In this paper, we consider 2mth-order nonlinear differential equation

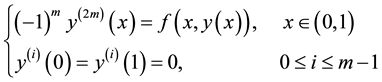, (1)

The existence and the uniqueness of positive solution are obtained, by means of the fixed point theorems on compression and expansion of cones.

Throughout this paper, we always suppose that

(H₁) 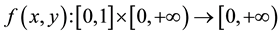is continuous;

(H₂), for any compact subinterval in 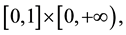is nonincreasing in,;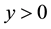

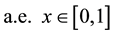(H₃),;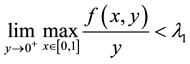

(H₄)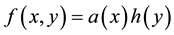, ,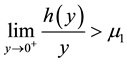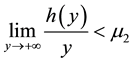. where,

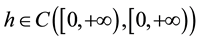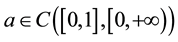, for any compact subinterval in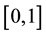. Here, , , satisfied, , ,. , with, ,.

Definition is the positive solution of boundary value problem (1), if satisfied

1), , , and,;

2), and,.

2. Preliminary

By a direct calculation, we can easily obtain

,

following from [5] , can be written by

, (2)

Define an operator,.

Lemma 1 The function defined by (2) satisfied the following conditions

,

where

Proof By Newton binomial formula, we have

, (3)

Put (3) into (2), and integral by item

,

and we can get

If

the upper and lower bound of is

.

Lemma 2 Let E be a Banach space, and is a cone, satisfied

,

where, then K is an closed convex cone.

Proof 1) Let, , we have

,

i.e.

,

so

.

2) Because, if, , and, then. from 1) and 2), we prove that

is an closed convex cone .

Lemma 3 is completely continuous.

Proof Let is bounded, then, ,we have

,

and

,

Hence, is bounded.

Next, we show that is compact set. In fact

,

then

For, , then

So is equicontinuous. By means of the Ascoli-Arzela theorem, is compact set, is an compact operator.

Let, , with, because of the convergence properties, we have

, ,. Now we show that. In fact

where

,

and

Because is continuous on, so is uniform-

ly continuous on., , , when, and,

, , then, , with

, as, also notice that

,

i.e., a.e.. And

,

By using Lebesgue control convergence theorem as, , so is continuous operator on. In conclusion, is completely continuous operator.

3. Main Results

Theorem 1 suppose (H₁)-(H₃) or (H₁), (H₂), (H₄) holds, BVP (1) has at least one positive solution.

Proof We prove. Since, we have

then, for, i.e..

It follows form (H₃), , where, there exist, such that, i.e.. Let,

for any, and, since, we have

From, where, , there exists, such that, , i.e..

Let, and. Then for any, , and , we have, and

According to the theorems on compression and expansion of cones, has at least a fixed point, i.e.

, an y satisfied integral equation,

so, y is the positive solution of (1).

From (H₄), we know, where,. There exists,

such that, we have. Let, for any

, we have

i.e.

From, where. We know, , such that.

In the following, we consider two cases:

1) If bounded on, Let, ,

, since and,so

i.e..

2) If is unbounded on, Let, such that,

. Since is unbounded, then, we have

i.e..

In conclusion, according to the theorems on compression and expansion of cones, has at least one fixed point. This showed that, and y satisfied integral equation

So, is the positive of BVP (1), where.

Theorem 2 If condition (H₁)-(H₄) holds, then the BVP (1) has a uniqueness positive solution.

Proof If, are the positive solution of BVP (1), Let, where

satisfied boundary value problem

,

Notice that , integral the left from 0 to 1, notice that

So we obtain

,

Thus, i.e.,. And since, we have,

, i.e.. Repeat above process, and conditions, ,

In the last, we have,. It is obvious that,. The uniqueness has been proved.

Cite this paper

JiyingLiu, (2015) Existence and Uniqueness of Positive Solution for 2mth-Order Nonlinear Differential Equation with Boundary Conditions. Journal of Applied Mathematics and Physics,03,1178-1185. doi: 10.4236/jamp.2015.39145

References