Journal of Applied Mathematics and Physics
Vol.02 No.13(2014), Article ID:52542,14 pages
10.4236/jamp.2014.213145
Reliability Modelling and Analysis of Redundant Systems Connected to Supporting External Device for Operation Attended by a Repairman and Repairable Service Station
Ibrahim Yusuf1, Rabia Salihu Said2, Fatima Salman Koki2, Mansur Babagana3
1Department of Mathematical Sciences, Bayero University, Kano, Nigeria
2Department of Physics, Bayero University, Kano, Nigeria
3Department of Computer Science and Information Technology, Bayero University, Kano, Nigeria
Email: iyusuf.mth@buk.edu.ng, rssaidu.phy@buk.edu.ng, FatimaSK2775@gmail.com, mbabagana.cs@buk.edu.ng
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 October 2014; revised 1 November 2014; accepted 24 November 2014
ABSTRACT
In this paper, probabilistic models for three redundant configurations have been developed to analyze and compare some reliability characteristics. Each system is connected to a repairable supporting external device for operation. Repairable service station is provided for immediate repair of failed unit. Explicit expressions for mean time to system failure and steady-state availability for the three configurations are developed. Furthermore, we compare the three configurations based on their reliability characteristics and found that configuration II is more reliable and efficient than the remaining configurations.
Keywords:
Availability, Supporting Device, Service Station, Redundancy

1. Introduction
High system reliability and availability play a vital role towards industrial growth as the profit is directly dependent on production volume which depends upon system performance. Thus the reliability and availability of a system may be enhanced by proper design, optimization at the design stage and by maintaining the same during its service life. Because of their prevalence in power plants, manufacturing systems, and industrial systems, many researchers have studied reliability and availability problem of different systems (see, for instance, Ref [1] -[8] and the references therein). In real-life situations we often encounter cases where the systems that cannot work without the help of external supporting devices connect to such systems. These external supporting devices are systems themselves that are bound to fail. Where such systems exist, a repairable service station is provided for the immediate repair of failed unit. Such systems are found in power plants, manufacturing systems, and industrial systems. Ref [9] [10] performed comparative analysis of some reliability characteristics between redundant systems requiring supporting units for their operation.
The problem considered in this paper is different from the work of Ref [9] [10] . The objectives of the present paper are three. The first is to develop the explicit expressions for the mean time to system failure (MTSF) and steady- state availability. The second objective is to perform a parametric investigation of various system parameters on mean time to system failure (MTSF) and steady-state availability and capture their impact on the mean time to sys- tem failure (MTSF) and steady-state availability. The third objective is to perform comparative analysis between the three configurations based on assumed numerical values in order to determine the optimal configuration.
2. Description of the Systems
We consider three redundant systems connected to an external supporting device for their operation as follows. The first system is a 2-out-of-3 system connected to a supporting device and has a repairable service station. The second is also a 2-out-of-3 system connected to supporting device and has two standby repairable service stations. The third system is a 3-out-of-4 system connected to a supporting device and has a repairable service station. We assume that switching is perfect and instantaneous. We also assume that two units cannot fail simultaneously. Whenever a unit fails with failure rate , it is immediately sent to a service station for repair with service rate
, it is immediately sent to a service station for repair with service rate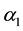 . However, on the course of repairing failed unit, the service is bound to fail with failure rate of
. However, on the course of repairing failed unit, the service is bound to fail with failure rate of 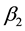 and service rate of
and service rate of 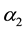 and failed unit must wait whenever the service station is under repair for first and third system, while the standby service will continue repairing failed unit for the second system. The supporting device is a system that is prone to failure. Whenever the supporting device failed with rate
and failed unit must wait whenever the service station is under repair for first and third system, while the standby service will continue repairing failed unit for the second system. The supporting device is a system that is prone to failure. Whenever the supporting device failed with rate  it is attended by a repairman, the system stop working and must wait until the supporting device is repaired with rate
it is attended by a repairman, the system stop working and must wait until the supporting device is repaired with rate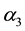 .
.
3. Mean Time to System Failure Models Formulation
3.1. MTSF Formulation for Configuration I
For configuration I, we define  to be the probability that the system at time
to be the probability that the system at time  is in state
is in state . Also let
. Also let 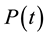 be the probability row vector at time
be the probability row vector at time , we have the following initial condition:
, we have the following initial condition:
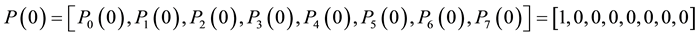
We obtain the following differential equations:
 (1)
(1)
This can be written in the matrix form as
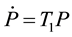 (2)
(2)
where
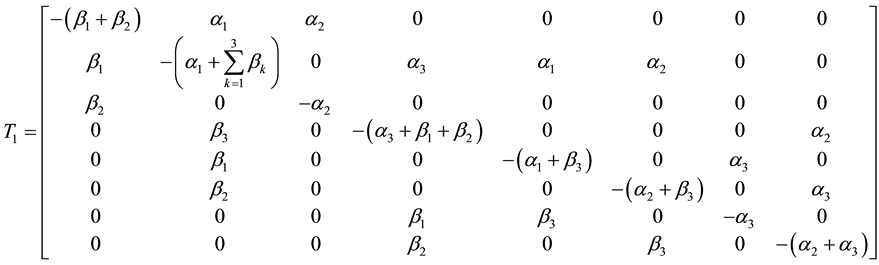
It is difficult to evaluate the transient solutions, the procedure to develop the explicit expression for 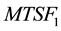 is to delete the rows and column of absorbing states of matrix
is to delete the rows and column of absorbing states of matrix 


where
3.2. MTSF Formulation for Configuration II
For configuration II, we define 




The differential equations are expressed in the form

where
and
Using the procedure described in Subsection 3.1, the expected time to reach an absorbing state is

where
3.3. MTSF Formulation for Configuration III
For configuration II, we define 




The differential equations are expressed in the form

where
Using the procedure described in Subsection 3.1, the expected time to reach an absorbing state is

where
4. Availability Models Formulation
4.1. Availability Model Formulation for Configuration I
For the analysis of availability case of configuration I we use the same initial condition as in Subsection 3.1
The differential equations above are expressed in the form
The steady-state availability is given by

In the steady-state, the derivatives of the state probabilities become zero and therefore Equation (2) become

which is in matrix form
Using the following normalizing condition

Substituting (10) in the last row of (9) to compute the steady-state probabilities, the expression for steady- state availability is given by

4.2. Availability Model Formulation for Configuration II
For the analysis of availability case of configuration II we use the same initial condition as in Subsection 3.2
The differential equations are expressed in the form
The steady-state availability is given by

In the steady-state, the derivatives of the state probabilities become zero and therefore Equation (4) become

which is in matrix form
Using the following normalizing condition

Substituting (14) in the last row of (13) to compute the steady-state probabilities, the expression for steady- state availability is given by

4.3. Availability Model Formulation for Configuration III
For the analysis of availability case of configuration III we use the same initial condition as in Subsection 3.3
The differential equations are expressed in the form
The steady-state availability is given by

In the steady-state, the derivatives of the state probabilities become zero and therefore Equation (6) become

which is in matrix form
Using the following normalizing condition

Substituting (18) in the last row of (17) to compute the steady-state probabilities, the expression for steady- state availability is given by

5. Comparison of the Three Configurations
In this section, we numerically compare the results for availability and MTSF for the developed models for the three configurations.
Case I:
We fix











Case II:
We fix











Figure 1. Availability against
Figure 2. Availability against
Figure 3. Availability against
Figure 4. Availability against
Case III:
We fix











Case IV:
We fix
















From Figure 1, the availability results for the three systems being studied against the repair rate
Figure 5. Availability against
Figure 6. Availability against
Figure 7. MTSF against
Figure 8. MTSF against
Figure 9. MTSF against
Figure 10. MTSF against
Figure 11. MTSF against
clear from the Figure that configuration II has higher availability with respect to 



However, one can say that the results from Figure 3 show slight distinction between availability of three configurations with respect to


ty than configuration I as 


Results from Figure 5 and Figure 6 show slight distinction between availability of three configurations with respect to 



II has higher availability than configuration I and III as 


Simulations of MTSF for the three configurations depicted in Figures 7-9 show that MTSF increases as 












6. Conclusion
In this paper, we studied the reliability characteristics of three dissimilar systems connected supporting device. We developed the explicit expressions for steady-state availability and mean time to system failure (MTSF) for each configuration and performed comparative analysis numerically to determine the optimal configuration. It is evident from Figures 1-6 that configuration II is optimal configuration using steady-state availability while using MTSF, the optimal configuration depends on the values of




References
- Khatab, A., Nahas, N. and Nourelfath, M. (2009) Availability of k-out-of-n: G Systems with Non Identical Components Subject to Repair Priorities. Reliability Engineering & System Safety, 94, 142-151. http://dx.doi.org/10.1016/j.ress.2008.02.017
- Fathabadi, H.S. and Khodaei, M. (2012) Reliability Evaluation of Network Flows with Stochastic Capacity and Cost Constraint. International Journal of Mathematics in Operational Research, 4, 439-452. http://dx.doi.org/10.1504/IJMOR.2012.048904
- Khalili-Damghani, K. and Amiri, M. (2012) Solving Binary-State Multi-Objective Reliability Redundancy Allocation Seriesparallel Problem Using Efficient Epsilon Constraint, Multi-Start Partial Bound Enumeration Algorithm, and DEA. Reliability Engineering and System Safety, 103, 35-44. http://dx.doi.org/10.1016/j.ress.2012.03.006
- Khalili-Damghani, K., Abtahi, A.R., and Tavana, M. (2013) A New Multi-Objective Particle Swarm Optimization Method for Solving Reliability Redundancy Allocation Problems. Reliability Engineering and System Safety, 111, 58- 75. http://dx.doi.org/10.1016/j.ress.2012.10.009
- Wang, K.-H., Yen, T.-C. and Fang, Y.-C. (2012) Comparison of Availability between Two Systems with Warm Standby Units and Different Imperfect Coverage. Quality Technology and Quantitative Management, 9, 265-282
- Srinivasan, S.K. and Subramanian, R. (2006) Reliability Analysis of a Three Unit Warm Standby Redundant System with Repair. Annals of Operations Research, 143, 227-235. http://dx.doi.org/10.1007/s10479-006-7384-z
- Singh, V.V., Singh, B., Mangeyram and Goel, C.K. (2010) Availability Analysis of a System Having Three Units Super Priority, Priority and Ordinary under Peemmptive Resume Repair Policy. International Journal of Reliability and Applications, 11, 41-53.
- Singh, V.V. and Rawal, D.K. (2011) Availability Analysis of a System Having Two Units in Series Configuration with Controller and Human Failure under Different Repair Policies. International Journal of Scientific and Engineering Research, 2, 1-9.
- Yusuf, I. (2013) Comparison of Some Reliability Characteristics between Redundant Systems Requiring Supporting Units for Their Operation. Journal of Mathematical and Computational Sciences, 3, 216-232.
- Yusuf, I. (2014) Comparative Analysis of Profit between Three Dissimilar Repairable Redundant Systems Using Supporting External Device for Operation. Journal of Industrial Engineering International, 10, 2-9. http://dx.doi.org/10.1007/s40092-014-0077-3
- Wang, K.H. and Kuo, C.C. (2000) Cost and Probabilistic Analysis of Series Systems with Mixed Standby Components. Applied Mathematical Modelling, 24, 957-967. http://dx.doi.org/10.1016/S0307-904X(00)00028-7
- Wang, K., Hsieh, C. and Liou, C. (2006) Cost Benefit Analysis of Series Systems with Cold Standby Components and a Repairable Service Station. Journal of Quality Technology and Quantitative Management, 3, 77-92.









































