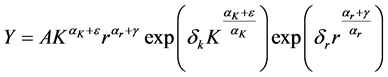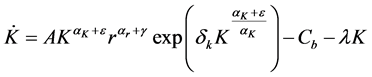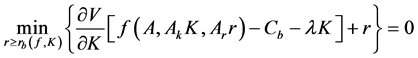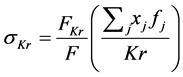Theoretical Economics Letters
Vol.06 No.03(2016), Article ID:67191,10 pages
10.4236/tel.2016.63053
Sustainable Consumption with an Essential Exhaustible Resource Re-Examined
Juan Sesmero*, Lilyan Fulginiti
Purdue University, West Lafayette, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2016; accepted 5 June 2016; published 8 June 2016
ABSTRACT
This study derives conditions for existence of a positive sustainable consumption in an economy with an essential exhaustible resource. It does so by approximating technology with a variable elasticity of substitution production function, instead of the constant elasticity of substitution specification widely assumed in previous studies. This approach permits examination of the robustness of results previously derived in the literature to key technological assumptions. It also generates new insights regarding the role of substitutability and technical progress on existence. We find that a capital-resource elasticity of substitution greater than one is sufficient for existence even when the resource is strictly essential; a situation precluded by constant elasticity of substitution specifications. Under an elasticity of substitution lower than one, existence can still be attained (in contrast to the constant elasticity of substitution case) but only through capital-aug- menting technical progress. Hicks-neutral technical progress is neither necessary nor sufficient for existence. A sufficiently high resource-augmenting technical progress thwarts existence of a positive sustainable consumption.
Keywords:
Sustainable Consumption, Essential Exhaustible Resource, Variable Elasticity of Substitution, Non-Neutral Technical Progress

1. Introduction
This paper examines the role of input substitutability and technical progress on the existence of positive sustainable consumption in an economy with an essential exhaustible resource. The framework used in the literature to study the existence issue (e.g. [1] - [5] ) is known as the Dasgupta-Heal-Solow-Stiglitz (DHSS) model. This literature has two important limitations. First, technology is modeled with a constant elasticity of substitution (CES) function.1 Under a CES specification, input substitutability and essentiality (i.e. an input is essential if positive production requires a positive amount of that input) are fundamentally linked to each other. An elasticity of substitution between the exhaustible resource and capital (which we denote by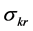 ) greater than one implies inessentiality of the resource.2 Consequently, high substitutability and non-essentiality are confounded and their individual roles in intertemporal sustainability of consumption cannot be identified. Under these technological assumptions the aforementioned studies found that
) greater than one implies inessentiality of the resource.2 Consequently, high substitutability and non-essentiality are confounded and their individual roles in intertemporal sustainability of consumption cannot be identified. Under these technological assumptions the aforementioned studies found that  is sufficient for existence of a positive sustainable consumption. This framework leaves an important question unanswered: is high substitutability (i.e.
is sufficient for existence of a positive sustainable consumption. This framework leaves an important question unanswered: is high substitutability (i.e. ) still sufficient for sustainability when essentiality is preserved?
) still sufficient for sustainability when essentiality is preserved?
Moreover, under a CES specification, 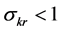 implies bounded average product of the resource as its quantity approaches zero. Consequently, low substitutability and limited resource productivity are also confounded. Under these technological assumptions studies found that
implies bounded average product of the resource as its quantity approaches zero. Consequently, low substitutability and limited resource productivity are also confounded. Under these technological assumptions studies found that 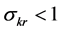 is sufficient for inexistence of a positive sustainable consumption. But it remains unclear whether limited substitutability (i.e.
is sufficient for inexistence of a positive sustainable consumption. But it remains unclear whether limited substitutability (i.e.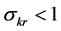 ) is still sufficient for inexistence when average product of the resource is unbounded?
) is still sufficient for inexistence when average product of the resource is unbounded?
The second limitation is related to technical progress. Previous analyses have been conducted under the assumption of Hicks-neutral technical progress. One exception is [4] who have looked at capital-augmenting technical progress but have not considered resource-augmenting technical progress, nor have they considered neutral and non-neutral technical progress simultaneously. Therefore many questions also remain unanswered pertaining the effect of technical progress on sustainable consumption. Can limited capital-resource substitutability ( ) be compensated by technical progress to guarantee existence of a positive consumption path? If so, what kind of technical progress?
) be compensated by technical progress to guarantee existence of a positive consumption path? If so, what kind of technical progress?
We develop a framework capable of 1) linking capital-resource substitutability with the existence of positive sustainable consumption when the resource is strictly essential regardless of the value of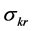 , 2) linking biased technical progress with existence, and 3) capturing compensations between
, 2) linking biased technical progress with existence, and 3) capturing compensations between 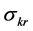 and technical progress that result in existence of a positive sustainable consumption.
and technical progress that result in existence of a positive sustainable consumption.
2. Model
The economy is described by the DHSS model:
 (1)
(1)
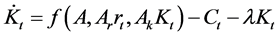 (2)
(2)
where 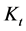 is the stock of human-made capital at time t,
is the stock of human-made capital at time t,  is the level of non-renewable resource stock,
is the level of non-renewable resource stock, 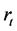 is the flow of the natural resource used in production, A is an efficiency factor capturing Hicks-neutral technological progress,
is the flow of the natural resource used in production, A is an efficiency factor capturing Hicks-neutral technological progress,  is an efficiency factor corresponding to the ith input (
is an efficiency factor corresponding to the ith input (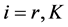
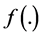
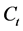
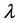
This economy evolves according to the following constraints:
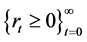
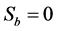
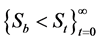
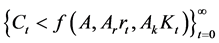
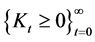
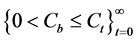
where 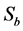
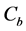
The combination of Equations (4) and (5) prevents depletion of the resource in finite time. Equations (2)-(8) can be combined to obtain:
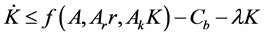
We are left with a system of one differential Equation (Equation (1)) and one differential inclusion (Equation (9)) denoting the set of all feasible paths. By solving the system formed by (1) and (9) we find a constant level of the control variable (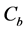
Due to the aforementioned limitations of a CES specification we approximate production technology by the following variable elasticity of substitution specification:
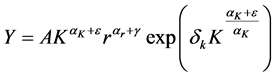
where
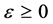
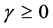
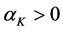
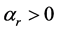
The function in Equation (10) is a particular case of the more general transcendental function
where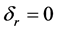
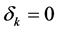
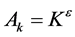
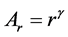
3. Analysis
We first examine sufficiency of 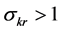
Proposition 1. Let the DHSS economy be constrained by production function (10). If 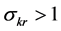
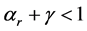
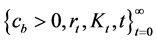
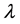
Corollary 1. Positive technical progress is not necessary for existence despite essentiality and capital depreciation. Proof: the conditions 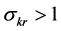
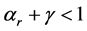
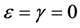
Corollary 2. Resource-augmenting technical progress can prevent existence. Proof: while the integral in inequality (A.7), Appendix A, converges due to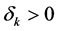
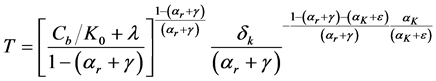
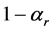
We prove in Appendix B that our framework replicates sustainability conditions obtained with a Cobb Douglas approximation by [4] in the case of positive capital depreciation (Proposition B.1), and by [2] under zero capital depreciation (Proposition B.2).
The analysis in [2] found that, under a CES specification, 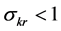
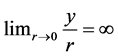
Proposition 2. Let the DHSS economy be constrained by production function (10) and let 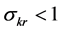
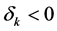
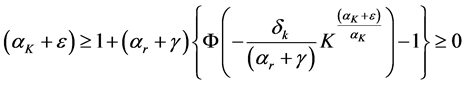
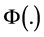
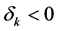
This proposition shows that limited substitutability does not necessarily puts the economy in an unsustainable path. It also underscores the importance of capital-augmenting technical progress, as shown in the following corollary.
Corollary 3. If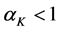
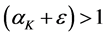
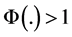
Notice that both capital-augmenting (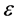
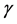
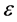
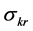
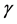
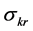
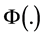
4. Discussion
Studies approximating technology with a CES specification, generated two important predictions. First, 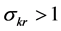
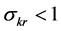
Our analysis confirms that 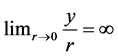
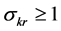
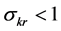
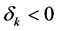
economy to unsustainability. It reveals that the hurdles of limited substitutability can be overcome with a sufficiently high productivity of capital. Equation (A.4) in Appendix A reveals that Hicks-neutral technical progress is beneficial for sustainability in the sense of reducing the minimum level of the resource required to sustain positive consumption. In contrast, resource-augmenting technical progress (
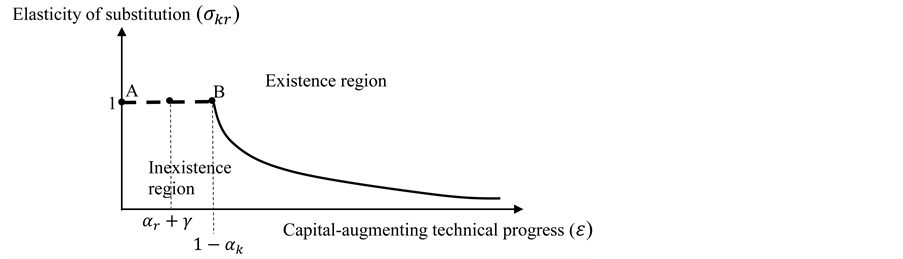
Assuming that 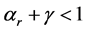
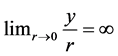
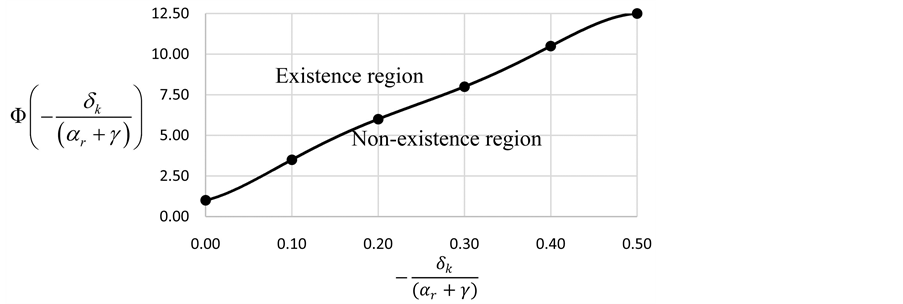
as a countervailing force to limited substitutability is conceptually illustrated in Figure 1. An elasticity of substitution greater than one guarantees existence of positive sustainable consumption. When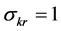
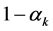
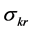
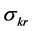
Figure 1. Existence requires higher capital-augmenting technical progress as substitutability decreases.
5. Conclusions
This study revisits the issue of existence of positive sustainable consumption in an economy with an essential exhaustible resource. It does so by utilizing a transcendental approximation to technology. Such parametric specification allows formal examination of the effect of capital-resource substitutability while preserving essentiality. We also highlight the role of non-neutral technical progress on existence.
Our analysis offers two important insights. First, 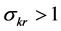
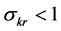
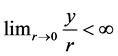
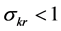
augmenting technical progress can be an effective countervailing force to limited substitutability, while resource-augmenting and Hicks-neutral technical progress cannot. This issue has not received adequate attention in the literature.
This study extends previous analyses of sustainability under an essential exhaustible resource by considering a particular production function that allows for co-existence of 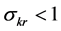
Cite this paper
Juan Sesmero,Lilyan Fulginiti, (2016) Sustainable Consumption with an Essential Exhaustible Resource Re-Examined. Theoretical Economics Letters,06,464-473. doi: 10.4236/tel.2016.63053
References
- 1. Dasgupta, P. and Heal, G. (1974) The Optimal Depletion of Exhaustible Resources. Review of Economic Studies, 41, 1-28.
http://dx.doi.org/10.2307/2296369 - 2. Solow, R.M. (1974) Intergenerational Equity and Exhaustible Resources. Review of Economic Studies, 41, 9-45.
http://dx.doi.org/10.2307/2296370 - 3. Stiglitz, J. (1974) Growth with Exhaustible Natural Resources: Efficient and Optimal Growth Paths. Review of Economic Studies, 41, 123-137.
http://dx.doi.org/10.2307/2296377 - 4. Martinet, V. and Doyen, L. (2007) Sustainability of an Economy with an Exhaustible Resource: A Viable Control Approach. Resource and Energy Economics, 29, 17-39.
http://dx.doi.org/10.1016/j.reseneeco.2006.03.003 - 5. Mitra, T., Asheim, G.B., Buchholz, W. and Withagen, C. (2013) Characterizing the Sustainability Problem in an Exhaustible Resource Model. Journal of Economic Theory, 148, 2164-2182.
http://dx.doi.org/10.1016/j.jet.2013.04.019 - 6. Nordhaus, W.D. and Tobin, J. (1972) Is Economic Growth Obsolete. In: Economic Growth, Fiftieth Anniversary Colloquium, V, National Bureau of Economic Research, New York.
- 7. Aubin, J.P. (1991) Viability Theory. Springer Verlag, Birkhauser.
- 8. Gautschi, W. (1979) A Computational Procedure for Incomplete Gamma Functions. ACM Transactions on Mathematical Software (TOMS), 5, 466-481.
http://dx.doi.org/10.1145/355853.355863
Appendix
Appendix A
Proof of Proposition 1.
The problem at hand is to minimize the natural resource extraction rate subject to technology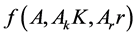
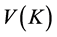
Therefore 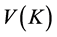
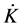
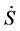
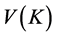
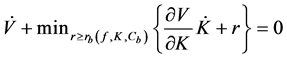
where r is the flow of the natural resource (to minimize it subject to equations of motion is the primal objective), 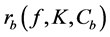
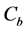
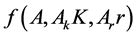
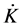
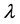
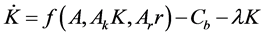
where K is the capital stock, and 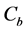
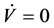
where 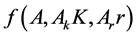
The first order condition of this problem is:
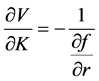
Plugging this back into the HJB equation and solving for the resource flow yields:
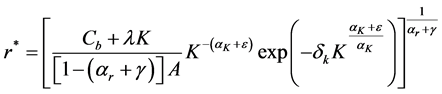
The viability kernel of an economy with accumulated capital 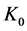
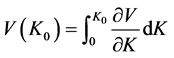
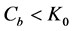
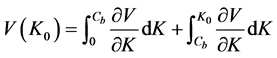
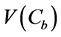
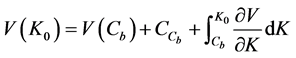
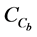
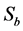
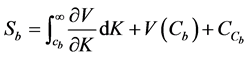
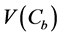
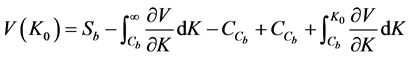
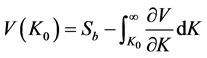
Combining (A.1) and (A.2) and inserting the resulting expression in (A.3) yields:
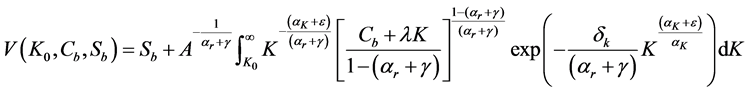
An interior path exists if and only if the second term in (A.4) is finite. This occurs whenever the integral converges. We show then that the integral converges if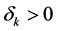
The integral, which we denote by I, can be rearranged in the following way:
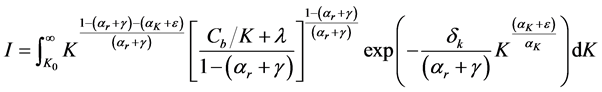
Since the term in brackets depends negatively on the capital stock then the following inequality holds:
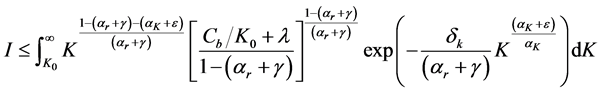
Therefore if the right hand side of inequality (A.6) converges, the left hand side converges. We can re-express the integral in (A.6) as an upper incomplete gamma function. We start with a variable transformation. We first re-define 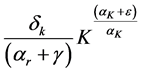
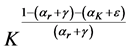
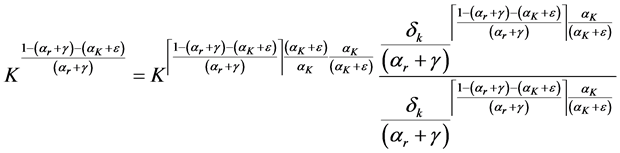
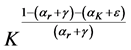
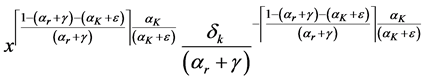
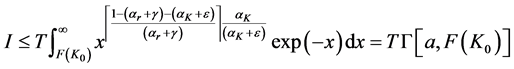
where 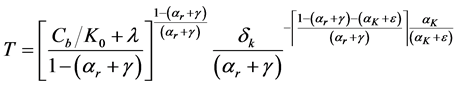
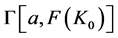
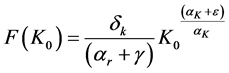
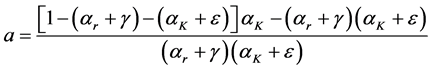
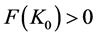
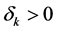
The Allen-Uzawa elasticity of substitution between capital and resource is
where F is the determinant of the bordered Hessian of the production function, 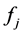
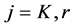
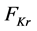
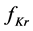
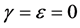
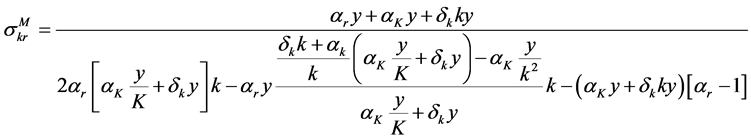
After some algebraic manipulation, this can be re-expressed as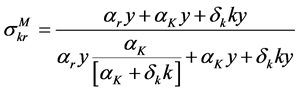
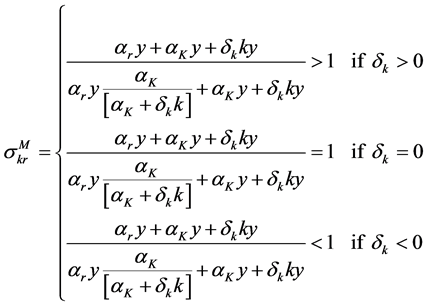
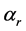
Therefore the condition 
Appendix B
Proposition B.1.
If 
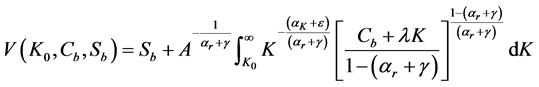
Let us denote the integral on the right hand side of (B.1) as I. This integral can be re-expressed as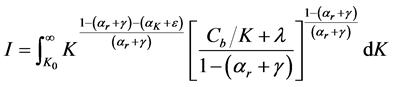
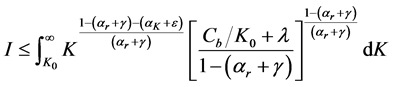
Therefore if the right hand side of the inequality converges, the left hand side converges. Solving the integral on the right hand side of the inequality yields:
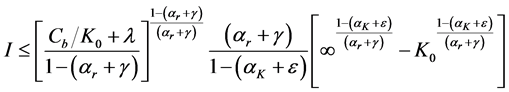
The right hand side converges (is a finite number) if and only if 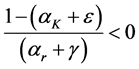
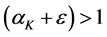
Proof of Proposition B.2.
If 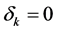
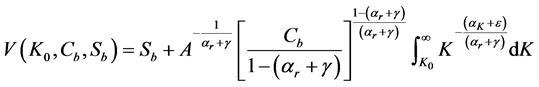
Solving the integral in (B.4) yields:
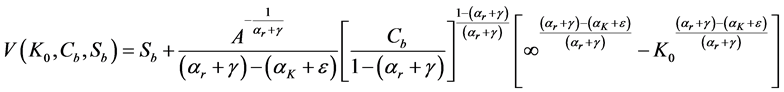
Therefore the minimum level of resource stock needed to sustain consumption at 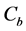
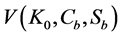
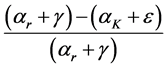
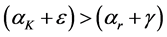
Appendix C
Proof of Proposition 2.
Existence of a positive sustainable consumption in this case depends upon convergence of the right hand side of inequality (A.6) which, once the constant part is removed from the integral, can be re-expressed as:
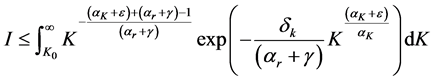
Convergence of the right hand side of (C.1) depends on how fast the integrand converges to zero as K tends to infinity. Since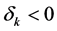
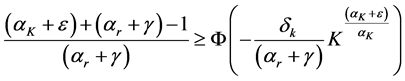
where 
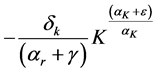
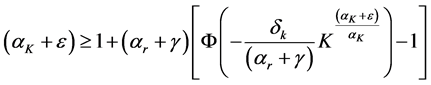
Figure C1. Parametric combinations and existence of sustainable consumption.
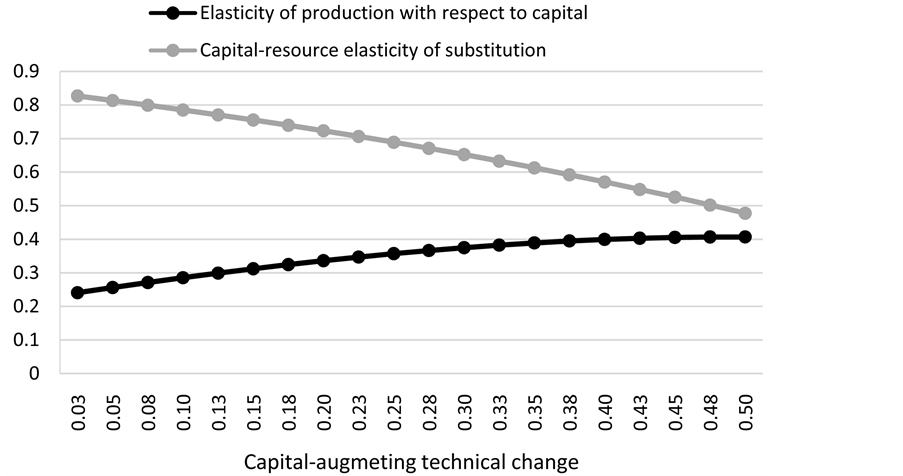
Figure C2. Parametric combinations and existence of sustainable consumption.
We compute the function 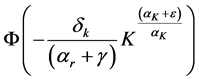
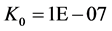
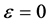
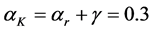
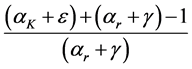
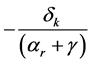
Provided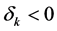
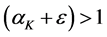
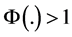
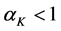
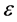
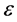
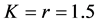
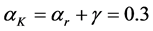
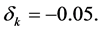
NOTES
*Corresponding author.
1 [5] uses a generic approximation to the production technology. The downside of this is the impossibility to tie existence conditions to specific technological parameters such as technical progress and elasticity of substitution.
2In this situation, as argued by [6] , the existence of an exhaustible input is no longer a “fundamental” problem.
3Such a specification permits combination of essentiality with unbounded average product of the resource.