Theoretical Economics Letters
Vol.05 No.06(2015), Article ID:62349,5 pages
10.4236/tel.2015.56091
Winter Transport via Trucks with Chains and the Fraction of Time Spent in Accidents
Amitrajeet A. Batabyal
Department of Economics, Rochester Institute of Technology, Rochester, New York, USA

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 October 2015; accepted 26 December 2015; published 29 December 2015
ABSTRACT
In this note, we analyze hitherto unstudied aspects of winter transport provision via trucks with chains on tires. Specifically, we first construct a discrete-time Markov chain (DTMC) model of transport provision that focuses on the movements of a representative truck in a firm’s fleet of trucks. Second, we specify the limiting probabilities of our DTMC model of truck transport. Third, we derive the fraction of time that the representative truck is involved in accidents. Finally, we solve an optimization problem whose solution tells us when the fraction of time the representative truck spends in accidents, is maximal.
Keywords:
Accident, Tire Chain, Transport, Truck, Uncertainty

1. Introduction
Harsh winter weather affects not only large parts of the United States but also many other parts of the world. Although driving in the winter is potentially dangerous for all automobiles, it is particularly so for trucks that are large, possess limited maneuverability, but at the same time are used routinely to transport goods from one location to another. Therefore, it is not surprising that in the United States, since the 1950s, trucks in general have been advised to use chains on their tires to reduce the hazards of winter driving1.
Trucks are now an important part of the transportation industry in the United States. Therefore, focusing on US trucks, the decision about whether to use or not use chains on tires in the winter months is often not optional. Although different states have different “chain laws,” they all frequently require that trucks use chains and other traction generating devices depending on weather conditions on the highways. For instance, consider the case of California. As noted by the website The American Driver2, the Department of Transportation in this state notifies truckers about when chains on tires are required. Eastbound trucks on Interstate 80 which travel through the Donner summit are stopped in Applegate, California, to ensure that drivers are carrying the correct amount of chains. Similarly, westbound trucks on Interstate 80 are screened in Verdi, Nevada, to ensure that they are in compliance with current chain laws. Noncompliant trucks are routinely ordered to turn around and such trucks can also be subject to monetary penalties.
Despite the frequently required use of tire chains by trucks during the winter months in the United States, to the best of our knowledge, the subject of winter transport provision by trucks using chains on tires and the related question of the fraction of time spent in accidents by such trucks has received no theoretical attention in the literature thus far. What has been studied thus far is the behavior of truck drivers in a couple of circumstances. Therefore, we now briefly summarize this literature in the following two paragraphs and then proceed to the specific questions to be analyzed in this note.
In an early paper, Golob and Hensher [7] econometrically analyzed the relationship between drug taking, compliance with schedules, and the propensity to speed by long distance truck drivers in Australia. They showed that increasing speed is positively influenced by the propensity to take stay awake pills which itself is positively affected by the tendency to self-impose schedules. Which characteristics of truck drivers are most pertinent in predicting crashes? This question has been studied by Cantor et al. [8] using what they call a crash prediction model. Their analysis shows that driver age, weight, height, gender, and employment stability are the most useful predictors of truck crashes.
Arentze et al. [9] examine the factors that are germane in determining the route choices of truck drivers. Their choice experiment based study yields two noteworthy conclusions. First, road accessibility characteristics and the variation in travel times are significant determinants of observed route choices. Second, when truck drivers select travel routes, they pay more attention to road pricing schemes and less attention to what these researchers call environmental bonuses. Finally, Guest et al. [10] compare the crash performances of older versus younger heavy goods vehicle drivers in Australia. The empirical analysis undertaken in this paper shows that relative to younger drivers, older male professional drivers have a lower risk of crashes in rigid vehicles.
Given the absence of prior research on winter transport provision by trucks using tire chains and the related question of the fraction of time spent in accidents by such trucks, we analyze hitherto unstudied aspects of these two issues. We discuss our theoretical framework in Section 2. In particular, in Section 2.1, we construct a discrete-time Markov chain (DTMC) model3 of transport provision that concentrates on the movements of a representative truck in a firm’s fleet of trucks. Section 2.2 specifies the limiting probabilities of our DTMC model of truck transport. In Section 3, we analyze accidents that the representative truck may get into. Specifically, Section 3.1 computes the fraction of time that the representative truck is involved in accidents. Section 3.2 solves an optimization problem whose solution tells us when the fraction of time the representative truck spends in accidents, is maximal. Finally, Section 4 concludes and then suggests two ways in which the research delineated in this note might be extended.
2. The Theoretical Framework
2.1. The Discrete-Time Markov Chain Model
Consider a firm that owns a fleet of trucks that is used to transport goods between various locations. In what follows, without loss of generality, we shall focus on a representative truck in this fleet and analyze its movements. To this end, suppose that in a time period―such as a day, a week, or a month―this representative truck makes deliveries of goods either from location A to location B or, in the opposite direction, from location B to location A.
Because we are interested in analyzing truck transport in the winter time, we suppose that the driver of the representative truck owns c > 0 sets of tire chains. Depending on weather conditions, the driver will find it necessary to use these chains in his movements from location A to B and vice versa. If the representative truck driver is in location A (B) at the beginning (end) of the time period and it is snowing heavily―which means that tire chains are legally required―then he will fit his truck tires with one set of chains and then travel to location B (A) provided that there is a set of chains to use.
If it is not snowing heavily―which means that tire chains are not legally required―then the representative truck driver will not fit his truck tires with a set of chains. We suppose that independent of the past, in the time period of interest, it snows heavily―hence requiring the legal use of tire chains―with exogenous probability p > 0. Note that in our theoretical framework, to reduce the weight of the goods carrying truck and to improve its maneuverability, the driver does not carry with him all the c sets of tire chains that he owns. Instead, a set of chains that he uses in location A (B) is kept in location B (A) upon his arrival here.
Our goal now is to define a discrete-time Markov chain with c + 1 states which will help us determine the proportion of time that our representative truck is in an accident. To this end, note that our truck gets into an accident if it is snowing heavily and the driver has not fitted his truck with the legally required set of chains because all the tire chain sets are in the other location. In other words, in the model that we are describing, the representative truck gets into an accident if and only if the driver of this truck is driving illegally.
Let
 denote the DTMC of interest. Let the state of this DTMC be the number of tire chain sets
denote the DTMC of interest. Let the state of this DTMC be the number of tire chain sets
the truck driver has with him at his current location. Then, the transition probabilities of our DTMC model are given by
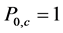 , (1)
, (1)
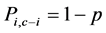 , (2)
, (2)
and
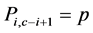 , (3)
, (3)
where the index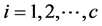 . Our next task is to stipulate the limiting probabilities of the DTMC model of truck transport that we have just described.
. Our next task is to stipulate the limiting probabilities of the DTMC model of truck transport that we have just described.
2.2. The Limiting Probabilities
Let us denote the limiting probabilities by πi, . Given the structure of the DTMC model that we have been working with thus far, we conjecture that the limiting probabilities we seek are given by
. Given the structure of the DTMC model that we have been working with thus far, we conjecture that the limiting probabilities we seek are given by
 , (4)
, (4)
and
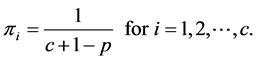 (5)
(5)
We now have to show that the above conjectured probabilities are valid limiting probabilities. In other words, using theorem 4.1 in Ross ([5] , pp. 200-201), we have to demonstrate that the solution proposed in Equation (4) and Equation (5) satisfies the condition
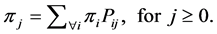 (6)
(6)
In the DTMC model with c + 1 states that we are studying, the above condition reduces to
 (7)
(7)
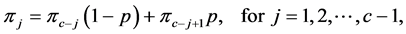 (8)
(8)
and
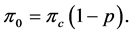 (9)
(9)
Straightforward algebra shows that our proposed solution in Equations ((4) and (5)) satisfies the three conditions given in Equations ((7)-(9)). Therefore, we conclude that the probabilities specified in Equations ((4) and (5)) are indeed the valid limiting probabilities that we seek. We now proceed to study accidents that the representative truck may get into. In this regard, the first item on the agenda is to compute the fraction of time that our representative truck is involved in accidents.
3. The Analysis of Accidents
3.1. Fraction of Time in Accident
Recall from the discussion in Section 2.1 that the driver of our representative truck gets into an accident if it is snowing heavily and he has not fitted his truck with the legally required set of chains because all the tire chain sets are in the other location. Mathematically, we are concerned now with state 0 and the limiting probability π0 that our truck driver is in this state. Note that the event in which it snows heavily and our driver is required to fit his truck tires with chains is not deterministic but stochastic and given by the probability p. Therefore, to obtain the correct expression for the fraction or proportion of time that our truck is involved in accidents, we have to multiply the limiting probability π0 with the probability p. This tells us that the proportion of time our truck is involved in accidents is given by
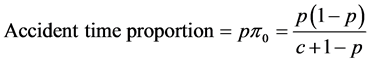 , (10)
, (10)
where we have used Equation (4) to substitute for π0.
Inspecting the right-hand-side (RHS) of Equation (10), we see that in general, the impact of a change in the probability p on the fraction of time our representative truck is in accidents is ambiguous. However, the same is not true of the number of sets of tire chains or c. Specifically, all else being equal, when the driver increases the number of tire chain sets he has at his disposal, the proportion of time spent in accidents clearly declines. We now proceed to our last task in this note and that is to solve an optimization problem whose solution tells us when the proportion of time our representative truck spends in accidents, is maximal.
3.2. The Optimization Problem
The fraction of time spent in accidents is closely related to the tires of our representative truck not being fitted with chains when such an action is legally required. In turn, the legal requirement to drive with tire chains is very closely related to the occurrence of a heavy snowfall in the time period of interest. Clearly, a regulatory authority such as the California Department of Transportation cannot control the winter weather. Even so, from a policy perspective, this entity would like to know for what values of the probability of a heavy snowfall, the proportion of time spent by our representative truck in accidents, is maximal.
To answer this question, we need to solve an optimization problem in which we select the probability p to
maximize the RHS of Equation (10). Formally, we want to solve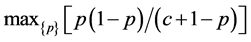 . Now, if we do
. Now, if we do
not specify a particular value for c then this maximization problem gets algebraically unwieldy and the resulting solution is not easy to interpret. Therefore, to illustrate our approach and essentially without any loss of generality, we suppose that our truck driver owns ten sets of tire chains. This means that c = 10. Using this value, our optimization problem becomes
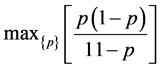 . (11)
. (11)
Note that the maximand in (11) is concave in the choice variable p and hence this maximization problem is well posed. Now, differentiating the maximand in (11) with respect to the choice variable p and then setting the resulting derivative equal to zero gives us the first order necessary condition for an optimum. That condition is a quadratic equation in p given by

The only sensible solution to the above equation is p ≈ 0.51.
The above result says that in the time period of interest, when the probability of a heavy snowfall is approximately 0.51, the proportion of time spent by our representative truck in accidents, is maximal. In addition, substituting p = 0.51 into the maximand in Equation (11) and then simplifying the resulting expression tells us that the maximum proportion of time our representative truck spends in accidents is only about 0.02. In other words, our truck will spend only about 2 percent of the total available time in accidents.
4. Conclusion
We shall not repeat our basic conclusions from Sections 2 and 3. Having said this, our main summary point is that in this note, we theoretically analyzed hitherto unstudied aspects of winter transport provision via trucks with chains on tires. The analysis conducted here can be extended in a number of different directions. Here are two suggestions for extending this note’s research. First, it would be useful to analyze the fraction of time spent in accidents in a model with more than two locations and in which a representative truck delivers goods to and from the various locations in a probabilistic manner. Second, to make the model richer, one could also analyze a scenario in which an appropriate regulatory authority first observes the current weather and then selects the probability with which it will require the use of tire chains or other traction generating devices. In such a scenario, one would want to explicitly account for the likelihood of fines if a truck driver is caught driving without chains when such chains are mandated by law. Studies of winter truck transport which incorporate these features of the problem into the analysis will provide additional insights into the connections between legally mandated driving rules, the response of truck drivers to such rules, and the occurrence of accidents.
Acknowledgements
Batabyal thanks two anonymous reviewers for their helpful comments on a previous version of this paper and Cassandra Shellman for her assistance in formatting the paper. In addition, he acknowledges financial support from the Gosnell endowment at RIT.
Cite this paper
Amitrajeet A.Batabyal, (2015) Winter Transport via Trucks with Chains and the Fraction of Time Spent in Accidents. Theoretical Economics Letters,05,805-809. doi: 10.4236/tel.2015.56091
References
- 1. Anonymous (1953) Use of Tire Chains Advised by State. New York Times, November 7.
- 2. Anonymous (1963) Tips for Winter Motorists. New York Times, December 29.
- 3. Cobb, J.G. (2002) A Turning Point for Big Trucks. New York Times, February 3.
- 4. Fisher, P. (2005) Ch-ch-Chains. Tire Business, November 7.
- 5. Ross, S.M. (2003) Introduction to Probability Models. 8th Edition, Academic Press, San Diego.
- 6. Tijms, H.C. (2003) A First Course in Stochastic Models. Wiley, Chichester.
http://dx.doi.org/10.1002/047001363X - 7. Golob, T.E. and Hensher, D.A. (1996) Driving Behavior of Long Distance Truck Drivers: The Effects of Schedule Compliance on Drug Use and Speeding Citations. International Journal of Transport Economics, 23, 267-301.
- 8. Cantor, D.E., Corsi, T.M., Grimm, C.M. and Ozpolat, K. (2010) A Driver Focused Truck Crash Prediction Model. Transportation Research Part E, 46, 683-692. http://dx.doi.org/10.1016/j.tre.2009.08.011
- 9. Arentze, T., Feng, T., Timmermans, H. and Robroeks, J. (2012) Context-Dependent Influence of Road Attributes and Pricing Policies in Route Choice Behavior of Truck Drivers: Results of a Conjoint Choice Experiment. Transportation, 39, 1173-1188. http://dx.doi.org/10.1007/s11116-012-9391-z
- 10. Guest, M., Boggess, M.M. and Duke, J.M. (2014) Age Related Annual Crash Incidence Rate Ratios in Professional Drivers of Heavy Goods Vehicles. Transportation Research Part A, 65, 1-8. http://dx.doi.org/10.1016/j.tra.2014.04.003
NOTES
1See Anonymous ([1] [2] ), Cobb [3] , and Fisher [4] for additional details on this point.
2Go to http://www.theamericandriver.com/files/info/chain_up_info.html for more details on the chain laws of different states. Accessed on September 23, 2015.
3See Ross ([5] , pp. 181-268]) or Tijms ([6] , pp. 81-139) for lucid textbook treatments of discrete-time Markov chains.



