Received 30 June 2015; accepted 15 August 2015; published 18 August 2015

ABSTRACT

To explain fluctuations of base metals prices we propose a model of short-run pricing based on trade in international exchanges. We introduce the critical tradeoff of choosing the share of material input from risky mining extraction versus risk-free recycling. We show that if more producers participate in the international exchange, or producers are less risk averse, the prices of base metals fluctuate more. If there are more traders, or producers are less risk averse, the prices of base metals fluctuate less. These observations may shed light on price movement during the recent financial crisis and possible future liquidity crises.

Keywords:

Base Metals, Price Fluctuations, Investment, Risk Aversion, Metals Industry, LME, International Exchange

1. Introduction

Aluminum, copper, lead, nickel, tin, and zinc (industrial non-ferrous metals) are commonly known as base metals. Their extensive use in the economy leads to the hypothesis that base metals consumption and futures can predict economic trends. Famed trader Dennis Gartman uses copper―among other base metals―as a leading economic indicator. According to him a recent rise in base metals prices signals a comeback of long-waited economic growth. He also states that prior to 2007-2009 financial crisis, “many base metals prices moved downwards long before the data signaled weakness in the global economy”.¹ Thus fluctuations of base metals prices are of a significant economic importance. Figure 1 presents the dynamics of base metals prices from 2000 to 2015. The main observation is that volatility in prices increases dramatically before and during the 2007-2009 crisis. In addition, after 2011 prices fluctuate less.

In this paper we study short-run price determinants of base metals in the global market where producers and

traders are selling and buying in well-organized commodity exchanges.² We answer the question: what drives fluctuations in base metals prices? We link price fluctuations to agents’ risk preferences in exchanges and to trading activity. Prior to trade, producers have to decide on the structure of supply for smelters. Recycling constitutes a less risky supply for producers than mining. Producers have to choose the share of risky―but potentially more profitable-mining. We introduce the critical share above which the market “correctly” responds to an increase in risk aversion. We provide an explanation of higher volatility in the prices of base metals during the crisis of 2007-2009. There are two effects which contribute to this increase in volatility. Firstly, during a crisis the traders are more risk averse. Secondly, there are more producers who want to get rid of stocks during a crisis. Both effects contribute positively to the increase in price volatility.

Literature Review

There is an empirical literature on the volatility of metals prices. [1] presents an empirical study of the volatility of 21 metals prices. He found that if volatility is commodity-specific rather than “global” then metals-exporting countries can smooth income via diversification. [2] studies the monthly price volatility of precious metals and the macroeconomic determinants such as the business cycle, the monetary environment, and the financial market sentiment of this volatility. Our paper fills the gap in this literature by offering a theoretical treatment of pricing which includes trade in metal exchanges.

Studies of crude oil and precious metals pricing are closely related to base metals pricing. [3] examines co- movements and information transmission among the spot prices of precious metals, oil, and the US dollar/euro exchange rate. They find evidence of a weak relationship in the long run equilibrium but strong feedback in the short run. The spot precious metal markets respond significantly (but temporarily) to a shock in any of the prices of the other metals prices and the exchange rate. Investors may diversify away at least a portion of the risk by investing in precious metals, oil, and the euro.

Newbery in [4] considers a theoretical model of risky choice by farmers. Risky production increases price risk. Thus speculators will tend to increase price instability. Using the same analysis on the market as [4] [5] study impacts of forward markets on international trade, using the optimal control approach to expose the behavior of producers. We build our model on works by [4] and [6] to draw conclusions which help us to explain the higher price volatility during the financial crisis of 2007-2009. Further, we introduce the critical feature of choosing the share of risky mining in smelting (with the complement taken up by risk-free recycling). This allows us to draw conclusions about the links between fluctuations in base metals prices and market conditions.

Finally, [8] tests the hypothesis that prices for metals are more stable in concentrated markets and investigates whether markets in which buyers are consumers have more stable prices than those with suppliers and specu- lators. She offers an explanation of the increase in metal price instability through changes in market structure and organization variables. The main reason for this is the increased reliance on commodity exchanges; declines in concentration are of less importance.

2. The Model

Base metals are produced from the smelting of ore extracted from mines and/or from recycled materials. Firms in the manufacturing sector (producers) choose a share i of extracted ore; the rest 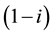comes from recycling. Producers face variation in the content of valuable elements found in nature.³ Suppose that the drilling exploration, sampling, and sample analysis reveal that is normally distributed with expected value 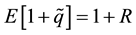and variance. The recycled materials generate a certain productivity which is normalized to 1. We assume price p is a realization of a random variable 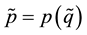which will be realized expost. International exchanges allow producers to sell futures to traders at known price 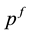before the price p is known.

Globally, the major centers for trading base metals are the Commodity Exchange of New York (COMEX), the London Metal Exchange (LME), and the Shanghai Futures Exchange (SHFE). Commodity futures are standardized contracts for the purchase and sale of physical commodities for future delivery on a regulated commodity futures exchange. The commodity futures contract price is determined by the equilibrium between supply and demand among competing buy and sell orders.

Suppose that in the international exchange there are I identical producers and J identical traders. The quantities of futures that producers and traders are selling are 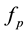and respectively. If the traders buy

futures then 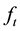takes a negative value. The utility function of producers and traders is given by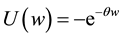, where 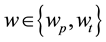is income and 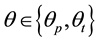is the coefficient of absolute risk aversion of the producer and trader respectively.

Remark: In recent years huge investments in mining have taken place in Latin America, Africa, and parts of Asia. These are likely to escalate in the next ten years [9] . Such investments generate uncertainty in each of the stages of mining (see Figure 2).

On the other hand, recycling constitutes a more certain type of supply of materials for smelters. According to the International Copper Study Group (ICSG), recycled content in copper production has remained steadily in the 33.7% - 36.8% range over the last decade. The International Zinc Association states that 60% of zinc produc-

tion comes from mined ores and the rest from secondary materials. The Yale University Center of Ecology reports that the recycling input rate of nickel production is 33%. The International Lead Association says that the recycled content of lead production is 52.6%. In general those figures have remained stable over the last ten years.⁴

3. Trade Equilibrium

Producers choose the share of extracted ore i before realization of the random variable. The total productivity of the base metal industry for is

. (1)

Consider price elasticity at the point. If price increases by then revenue increases by and decreases by, so that the price in the short run is⁵

. (2)

Therefore the price is normally distributed. Substituting (2) into (1) yields the price as a function of the optimal investment level

. (3)

The variance of the price is

. (4)

Importantly, the volatility in prices depends on the optimal share. This is the instrument which will affect the prices. We obtain the following.

Proposition 1: The price of base metals varies with the scales of production, the elasticity of demand, and the distribution of ore content in nature

.

Proof: Follows directly from (4).

We define a coefficient that combines the size and risk preferences of the agents in the market.

Definition 1: The generalized risk aversion coefficient of the futures market is.

Notice that. If traders are infinitely risk averse, , then the coefficient. If traders are risk neutral, , then the coefficient. Thus this coefficient is a measure of traders' riskiness; the higher, the riskier are traders. Other properties of are

. (5)

If producers sell tonnes of base metal in the futures market at price to traders and the remaining tonnes will be sold at price p, then a representative producer’s expected profit is

. (6)

A representative trader earns

. (7)

With a normal distribution of income and utility function, a producer’s expected utility maximization is equivalent to solving the program. Equipped with this formulation of the agents’ problems we have the following :

Lemma 1: Under the equilibrium in the international exchange, the optimal choices of producer and trader on are the following:

, (8)

, (9)

. (10)

Proof : See Appendix A1.

Equilibrium of the futures market in international exchanges requires that the total selling and buying quantity of futures equals zero. Therefore, from Lemma 1 we have

.

From this we obtain the condition for the optimal value of i (see Appendix A3)

. (11)

Denote and. Then from (11) we have.

Note that up to this point calculations are similar to the [4] model of farmers’ choice. Now we are going to define the critical level of input shares. The idea is that when the market risk aversion increases one can expect that the equilibrium choice of i should move towards safe technology. Equilibrium implies. Taking the derivative of i with respect to yields

. (12)

Thus only if, which is equivalent to. Define the critical level of i.

Definition 2: The critical level of uncertain production scale is.

We suppose that the share in risky production is larger than the critical level of investment:. To justify this, consider the values for nickel,^{6 7} and.⁸ Thus. Note that [4] establishes that is more likely to be positive when the demand is elastic. However, [10] finds that the

price elasticity of base metals is between 0.2 and 0.8 (aluminum 0.7 to 0.8; copper 0.4; lead 0.2; tin and zinc 0.2 to 0.4). By introducing the critical level of investments and observing that in reality we have, for inelastic demand,

. (13)

From Proposition 1 and Inequalities (5), (13) we have

(14)

and

(15)

We obtain the following :

Proposition 2: Suppose that, if there are more speculators (J increases) or they are less risk averse (decreases), then the price of base metals fluctuates less.

Also we have

(16)

and

. (17)

This leads to

Proposition 3: Suppose that, if there are more producers (I increases) or they are less risk averse (decreases), then the price of base metals fluctuates more.

Figure 1 shows that the prices fluctuated more in the period before and during the financial crisis of 2007-2009. This can be explained by two factors present in our model. Traders tend to be more risk averse (is high) during liquidity shocks, and more producers are interested in selling futures contracts (I is high). Thus, the price fluctuates more during crises. In [11] , liquidity premiums increase in volatile times. Traders become more risk-averse because higher fundamental volatility increases the likelihood that their performance falls short of the threshold. This will lead to costly withdrawal of funds.

4. Conclusion

In the theoretical literature on base metals, the price is defined only by the mining industry (see for example [8] ). Participation of speculative traders in metals exchanges is not considered. We show that in the short-run, price fluctuations respond to risk preferences of agents and the scale of international exchanges. We focus on the critical point of what share of input comes from risky mining (as opposed to less risky recycling) and show that the actual level is higher than the critical one. This allows us to explain the high volatility being seen during liquidity shocks.

Acknowledgements

The authors thank Zhiqi Chen, Jean-Francois Tremblay, Gamal Atallah for careful reading of the manuscript and many helpful comments. Our sincere thanks go to Margaret Slade, Nguyen Van Quyen for useful suggestions and David Stambrook for extensive discussions. We also thank participants of CEA Annual Conference at Ryerson 2015 and the discussant Martin Stuermer for helpful comments and suggestions. The paper was a part of a bigger project: “Trends and Fluctuations in Base Metals Prices”, which was awarded the prize for the best paper at Vietnam Economist Annual Meeting 2015 in Thai Nguyen City, Vietnam. The authors thank SSHRC for financial supports.

Cite this paper

Nguyen BaoAnh,AggeySemenov, (2015) Fluctuations in Base Metals Prices. Theoretical Economics Letters,05,545-554. doi: 10.4236/tel.2015.54064

References

Appendix

A1. Proof of Lemma 1

Proof. The metal producer maximizes his expected utility Let income be normally distributed and assume the utility function. Applying the second order approximation to the utility function this is equivalent to

(18)

Similarly the maximization problem of the trader is

(19)

From (6) the variance of producer’s income is

(20)

Substituting (20) and (6) into (18) the problem of a metal producer is

The first order condition with respect to i is From this the optimal choice of the share of mining as an input is

(21)

The first order condition with respect to is The optimal choice of futures to be sold by producer is

(22)

From (7) the variance of a trader’s income is is

(23)

Substituting (7) and (23) into (19), the problem of a trader is

(24)

The first order condition with respect to is The optimal choice of futures to be sold by the trader is

(25)

A2. Applying Taylor Approximation for the Variance of pq

By definition, the is

Using the first order Taylor approximation expanded around R we have

(26)

By the definition of covariance

(27)

Substituting, and (27) into (26) yields

(28)

Thus we have.

A3. The Optimal Value of i

The equilibrium condition is

Rearranging this yields

(29)

Substituting (29) into (9) for and collecting the variables leads to

Using the definition of the coefficient we have

(30)

Substituting (30) into (8) gives

(31)

As per the definition the term is the correlation coefficient of the price and the sales of base metal extraction. As p and pq are price and revenue, suppose, i.e. perfect negative correlation. We have

(32)

The variance of price is

(33)

The expected value of revenue by mined extraction is

(34)

The variance of revenue by mined extraction is. Note that p and q are not independent, so to calculate we apply the Taylor approximation (see (28) above) The covariance of the price and mined extraction revenue is

(35)

Substituting (28), (33), (34), (35) into (31) yields

(36)

NOTES

^*Corresponding author.

¹ http://www.marketfolly.com/2009/04/trader-dennis-gartman-says-watch-base.html; http://www.investopedia.com/articles/economics/11/base-metals-economic-indicator.asp

²In a companion paper “Trends in Base Metals Prices”, [7] we study non-systematic price determinants. The model used there is very different and has little overlap with the current paper.

³In the feasibility study phase of a mining and metallurgy project, drilling exploration is executed in the metal deposit to evaluate the metal content and reserve size. The content of base metals in ore varies across deposits. The coefficient of variation 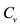and standard deviation 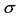have been used (we observed this fifty years ago in former Soviet Union) to evaluate the degree of risk, which directly affects to the profit of the base metals producer. and, where is the content of the metal in sample i, n is the number of samples, and is the mean value of.

⁴Metal Bulletin, 30 January 2012, Report of the United Nations Environment Program 2011.

⁵This expression is similar to one in [6] (A13). However, because we are interested in short run price fluctuations, we do not postulate the linear demand function. Alternatively, if we are interested in a longer period when p is realized we can assume linear demand.

⁶For nickel mines in Canada.

⁷Economic Research Center, the University of Western Australia.

⁸See http://www.victorynickel.ca/