Theoretical Economics Letters
Vol.05 No.02(2015), Article ID:55732,5 pages
10.4236/tel.2015.52031
Value Data and the Fisher Index
Robin M. Cross*, Rolf Färe
Oregon State University, Corvallis, USA
Email: *robin.cross@oregonstate.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 March 2015; accepted 12 April 2015; published 16 April 2015
ABSTRACT
In this paper we show how to use value data (price times quantity) to construct Fisher price and quantity indexes. In particular, we think of revenue and expenditure data. This model extends the work of Cross and Färe, who showed how to recover relative prices from value data with no explicit price or quantity information. We examine the accuracy of our model over a range of price changes, firm sample sizes, and response variation, in a Monte Carlo experiment in which firms respond to price changes with error. The model outperforms it component indexes with accuracy levels that increase with response variation.
Keywords:
Constrained Equilibrium, Index Number Theory, Nonlinear Programming, Value Data, Weak Axiom

1. Introduction
Most economic models are expressed in terms of prices and quantities. In practice, however, economic data is often available only in terms of revenues or expenditures (value data). Value data is the product of prices and quantities, but does not provide explicit price and quantity information. Cobb and Douglas [1] and Farrell [2] are two canonical examples using such data. Shephard [3] developed duality theory to utilize value data1. However, his results depend on price information.
Bowley [4] introduced a ratio-based price index, calculated as the geometric mean of the Paasche and Laspeyres indexes2. Fisher [5] identified it as “ideal” for satisfying a set of mathematical properties, collectively the Test Approach (see Fisher [6] ), and emphasized its use as a quantity index. Konüs [7] showed Fisher’s ideal index to be an exact solution for a quadratic production function. Diewert [8] demonstrated its exactness for a flexible second-order quadratic mean aggregator (utility or production) function, showing it to be superlative and completing the Economic Approach. Finally, Diewert [9] extended its use to Malmquist [10] output, input, and productivity indexes.
In a separate line of inquiry, Afriat [11] exploited properties of the Weak Axiom3 (Cyclical Consistency) to recover unobserved utility from consumer-level price and quantity data and later unobserved technology from production prices and quantities [12] . Cross and Färe [13] extended Afriat’s approach, using nonlinear programing to recover unobserved price relatives from firm-level revenues and expenditures.
Balk [14] uses dimensional invariance to construct Fisher ideal price and quantity indexes with value data and price relatives, instead of prices and quantities. Statistical agencies utilize this method, augmenting value data with secondary price surveys and constructing elementary price indexes [14] .
In this article, we show how to construct Fisher ideal price indexes directly from value data, without price relatives or the secondary price survey. In the next section, we review the value-based Fisher index, expressed in terms of value data and price relatives. We then recover the Fisher index price relatives from value data, without prices. In Section 3, we evaluate the accuracy of our value-based index in a simple Monte Carlo experiment in which firms respond rationally, but not optimally, to price changes. We then conclude.
2. A Value-Based Fisher Index
Let 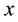 and
and 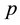 be vectors of (input) quantities and their prices, and denote output/utility
be vectors of (input) quantities and their prices, and denote output/utility 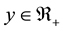 and the production/utility function
and the production/utility function
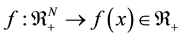 . (1)
. (1)

3We use the term Weak Axiom of Profit Maximization (Weak Axiom) discussed by Varian [15] , though many alternatives exist, notably Afriat’s [11] Cyclical Consistency.
4For the existence of a minimum, see Färe and Primont [16] . Note that  is the inner product of prices and quantities.
is the inner product of prices and quantities.
5Constant price relative across firms is a weaker restriction than constant prices, the so called “Law of One Price” [17] .
The cost function4 is defined
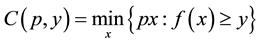 . (2)
. (2)
Konüs [7] defines a price index for situations 0 and 1 as the ratio of cost functions,
 . (3)
. (3)
Here, the price index is defined for a fixed output level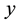 .
.
Consider a unit cost function  which is homogeneous, quadratic mean of order
which is homogeneous, quadratic mean of order . Here
. Here 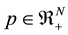 is the price vector for goods
is the price vector for goods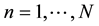 . According to Diewert [9] , this cost function is flexible, since it can provide a second order differential approximation to any linearly homogeneous, twice continuously differentiable, positive function. When a price function is exact for a flexible function, like the quadratic mean, it is said to be superlative.
. According to Diewert [9] , this cost function is flexible, since it can provide a second order differential approximation to any linearly homogeneous, twice continuously differentiable, positive function. When a price function is exact for a flexible function, like the quadratic mean, it is said to be superlative.
The Fisher index 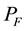 is exact for a second-order Quadratic cost function
is exact for a second-order Quadratic cost function . It is the geometric mean of two component indexes. The Laspeyres index
. It is the geometric mean of two component indexes. The Laspeyres index 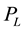 is a ratio of prices, weighted by past period quantities
is a ratio of prices, weighted by past period quantities



The Fisher is then
Following Balk [14] , we can write the value-based Fisher index 



The expenditure share is given by

3. The Programming Problem
We wish to recover price information from the inner product of price and quantity

Here, all inputs and outputs are included 
Identification is trivial when firms are strictly cost minimizing and the technology 




Price relatives may still be recovered from this system when firms are not strictly cost minimizing, but are instead weakly rational. To illustrate how this is possible, consider first an economy in which there is no quantity response to price change, due to some regulation, capital constraint, or information asymmetry. The response vector 




This economy is not cost minimizing, but satisfies Afriat’s [12] Weak Axiom of Profit Maximization,

In fact, the perfectly constrained firm defines the null vector 0 of Weak Axiom’s convex response-cone, and the profit maximizing firm defines its upper bound, illustrated in Figure 1.
Figure 1. Monte Carlo example-production response with error.
Under dimensional invariance (see Balk [14] ), the inequality (9) can be rewritten in value and price relative terms:

The vector of shadow price relatives 


4. Monte Carlo
To explore the accuracy of the proposed value-based Fisher index, we simulate a two-period, two-input, unit output economy and recovered price relatives 
Both response magnitude and direction are random variables, following two independent 2-parameter Beta distributions, with identical shape parameter sets


Define accuracy 






4.1. Technology
We consider a Translog unit cost function and impose parameter restrictions




4.2. Results
Table 1 reports accuracy levels for the value-based Fisher index and its two elementary components for firm sample sizes increasing from 15 to 30 firms, with a 200% increase in the second input price. Price response variation (standard deviation) ranges from 0.14 to 0.41, corresponding to shape parameter 
The value-based Fisher index is understated, 


Value-based Paasche and Laspeyres component indexes are under and overstated, respectively, at all levels of volatility and price deviations. This is reasonable, because they reference only a single-period market basket, whereas the Fisher index averages over the two-period market basket.
Table 2 illustrates accuracy levels for a range of price increases, from 50% to 200%, and three volatility levels. Firm sample size K is 15. The value-based index is overstated for larger price increases 

5. Conclusion
Economic data are frequently available in value terms, rather than price and quantity terms. We extended the superlative Fisher index to value data and recovered price relatives by exploiting the Weak Axiom. Our value-
Table 1. V-price index accuracy for a 200% price increase, reported for three firm sample sizes and three firm-response standard deviation levels.
Table 2. V-price index accuracy for 15 firms, reported for three price relatives (percentage increase) and three firm-response standard deviation levels.
based Fisher model eliminates the need for supplementary price information. The value-based model’s accuracy is encouraging, when firms respond to price changes rationally, but with error. We did not explore econometric approaches to price recovery. We also did not explore the accuracy of the value-based model when firms respond irrationally to price changes, violating the Weak Axiom. Such would be the case when the response error term is two-sided. Both extensions would be of practical interest.
Acknowledgements
Authors thankfully acknowledge Bert Balk’s extensive criticisms and suggestions for this project.
References
- Cobb, C.W. and Douglas, P.H. (1928) A Theory of Production. American Economic Review, 18, 139-165.
- Farrell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society, Series A, 120, 253-281. http://dx.doi.org/10.2307/2343100
- Shephard, R.W. (1953) Cost and Production Functions. Princeton University Press, Princeton.
- Bowley, A.L. (1899) Wages, Nominal and Real. In: Palgrave, R.H.I., Ed., Dictionary of Political Economy, Macmillan, London.
- Fisher, I. (1921) The Best Form of Index Number. Journal of the American Statistical Association, 17, 533-537. http://dx.doi.org/10.2307/2965310
- Fisher, I. (1922) The Making of Index Numbers. Houghton-Mifflin, Boston.
- Konüs, A.A. (1939) The Problem of the True Index of the Cost of Living. Econometrica, 7, 10-29. http://dx.doi.org/10.2307/1906997
- Diewert, W.E. (1976) Exact and Superlative Index Numbers. Journal of Econometrics, 4, 115-145. http://dx.doi.org/10.1016/0304-4076(76)90009-9
- Diewert, W.E. (1992) Fisher Ideal Output, Input, and Productivity Indexes Revisited. Journal of Productivity Analysis, 3, 211-248. http://dx.doi.org/10.1007/BF00158354
- Malmquist, S. (1953) Index Numbers and Indifference Surfaces. Trabajos de Estatistica, 4, 209-242. http://dx.doi.org/10.1007/BF03006863
- Afriat, S.N. (1967) The Construction of Utility Functions from Expenditure Data. International Economics Review, 8, 67-77. http://dx.doi.org/10.2307/2525382
- Afriat, S.N. (1972) Efficiency Estimation of Production Functions. International Economics Review, 13, 568-598. http://dx.doi.org/10.2307/2525845
- Cross, R.M. and Färe, R. (2009) Value Data and the Bennet Price and Quantity Indicators. Economics Letters, 102, 19- 21. http://dx.doi.org/10.1016/j.econlet.2008.10.003
- Balk, B.M. (2008) Price and Quantity Index Numbers. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511720758
- Varian, H.R. (1984) The Nonparametric Approach to Production Analysis. Econometrica, 52, 579-597. http://dx.doi.org/10.2307/1913466
- Färe, R. and Primont, D. (1995) Multi-Output Production and Duality: Theory and Applications. Kluwer Academic Pub- lishers, Netherlands. http://dx.doi.org/10.1007/978-94-011-0651-1
- Kuosmanen, T., Cherchye, L. and Simplanen, T. (2006) The Law of One Price in Data Envelopment Analysis: Restricting Weight Flexibility across Firms. European Journal of Operational Research, 170, 735-757. http://dx.doi.org/10.1016/j.ejor.2004.07.063
NOTES
*Corresponding author.
1Shephard [3] notes: “Statistical studies of cost functions are generally more accessible than corresponding empirical investigations of production functions, because economic data are most frequently in price and monetary (value) terms.”
2Fisher [6] acknowledges (page XV) Bowley’ [4] early identification (page 641) of the “ideal” index in an addendum added shortly before going to press in October, 1922.




