Theoretical Economics Letters
Vol.04 No.07(2014), Article ID:48737,4 pages
10.4236/tel.2014.47076
Optimal Environmental Policy under Endogenous Terms of Trade and Economic Growth
Alejandro Sampaolesi
School of Economics, University of Business and Social Science, Buenos Aires, Argentina
Email: asampaolesi@campus.uces.edu.ar
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 April 2014; revised 10 May 2014; accepted 28 June 2014
ABSTRACT
The aim of this work is to depict the main characteristics of the optimal environmental policy under endogenous terms of trade and economic growth. Here, endogenous terms of trade are inferred from the price of an aggregate consumption good. Our results show that when emissions of a global pollutant affect the environment and, therefore, the utility of the economic agents, the optimal policy consists in a pollution tax on production.
Keywords:
Growth, Trade, Environment, Political Economy

1. Introduction
In the last two decades many studies have tried to explain the existing trade-offs among economic growth, international trade, and the environment (see, for example, [1] -[3] ). However, from a theoretical perspective, their main results were based on economic models in which the terms of trade were defined as an exogenous variable. Therefore, the analysis of such trade-offs under endogenous terms of trade represents a missing subject in the economic literature. In this framework, the present analysis departs from previous ones in the modeling of the optimal environmental policy when we deal with both endogenous terms of trade and economic growth. Then, working in a simple representative agent model, we allow for the possibility that the domestic economy might be big enough to modify its terms of trade, where the latter are indirectly delineated by means of the price of an aggregate consumption good. Hence, as long as emissions of a global pollutant, coming from the production process of a pollution-intensive good, affect negatively the quality of the environment and, therefore, the utility of the economic agents, we find that the optimal policy represents a pollution tax on production.
2. The Basic Model
Let us assume that there are two traded goods in the world and that the domestic economy is completely specialized in the production of one of them, a pollution-intensive good, which can be consumed, invested, or traded overseas1. Moreover, it has the power to modify the international price of its exported good and, therefore, the terms of trade. Finally, it is assumed that trade is balanced, which rules out the possibility of lending or borrowing from abroad. Preferences: the instantaneous utility function of the representative agent is defined as: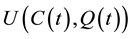 , where C represents an aggregate consumption good, i.e., a subutility function of the consumption of both domestic and imported goods, and Q denotes a stock variable measuring the quality of the environment. Furthermore, it is assumed that the utility function is increasing and strictly concave in both of its arguments, i.e.,
, where C represents an aggregate consumption good, i.e., a subutility function of the consumption of both domestic and imported goods, and Q denotes a stock variable measuring the quality of the environment. Furthermore, it is assumed that the utility function is increasing and strictly concave in both of its arguments, i.e.,
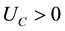 ,
,
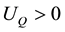 ,
,
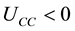 ,
,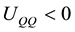 . Finally, we assume that the sign of the cross-partial derivative between consumption and environmental quality,
. Finally, we assume that the sign of the cross-partial derivative between consumption and environmental quality,
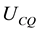 , is ambiguous. This conveys the possibility of a “win-win” outcome when both the equilibrium growth rate increases and the environment improves. Production and Environmental quality: The production process is modeled as a linear function of the stock of physical capital,
, is ambiguous. This conveys the possibility of a “win-win” outcome when both the equilibrium growth rate increases and the environment improves. Production and Environmental quality: The production process is modeled as a linear function of the stock of physical capital, . On the other hand, given the negative effect that domestic emissions generate on the quality of the environment, the latter is defined as:
. On the other hand, given the negative effect that domestic emissions generate on the quality of the environment, the latter is defined as: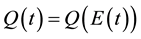 , where E stands for the total amount of emissions. Hence, assuming, for simplicity, that the emission level (in units of measurement) is proportional to the production level, i.e.,
, where E stands for the total amount of emissions. Hence, assuming, for simplicity, that the emission level (in units of measurement) is proportional to the production level, i.e.,
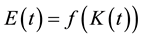 , we can express
, we can express
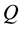 as:
as:
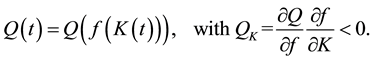 (1)
(1)
This implies that the quality of the environment is a decreasing function of the stock of capital. Note that as we focus on steady-state situations and not on the dynamic properties of the economy, the introduction of more realistic functions and pollution-abatement activities does not affect qualitatively the main results of our analysis2.
2.1. The Decentralized Path
Now, since we abstract from any government intervention, each agent perceives the stock of the environment as exogenous, although Q, in the aggregate, varies over time. Therefore, in the second stage of the maximization process, the representative agent, who has already solved his temporal allocation problem, selects the time path for consumption that maximizes3
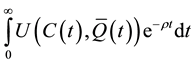 , (2)
, (2)
subject to
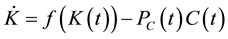 , (3)
, (3)


where



where



These results are quite intuitive. From (7), the static efficiency condition, the shadow price of capital adjusted by the price of the aggregate consumption good must equal the marginal utility of consumption. The dynamic condition (8) is Ramsey’s rule, which requires that the shadow price of physical capital rises at a rate given by the difference between the social discount rate and the marginal product of capital. Hence, if we differentiate totally (7) with respect to time and substitute for



where


2.2. The Efficient Path
The social planner’s problem is to select the time path of consumption decisions, assuming Q endogenous, that maximizes the present value of the utility. Formally, the decision maker’s problem, dropping the time arguments, will be to maximize the intertemporal utility function,

subject to (3), (4), and (5).Therefore, the current value Hamiltonian is given by:

where the first order conditions for an interior solution are:


Then, differentiating totally (12) with respect to time and using (13), we can express the efficient growth rate of consumption as:

Note that as

capital accumulation on the environment and, consequently, on the efficient growth path. That is, a higher level of emissions coming from an increase in physical capital decreases the utility associated with a given path of consumption.
2.3. Environmental Policy
In this section we introduce a Pigovian tax-cum-subsidy scheme in order to internalize the environmental externality. Therefore, to calculate this policy, sustainable through a lump-sum transfer, we set up an ad valorem tax or subsidy,




From (15), the optimal policy represents a pollution tax on production. This can be expressed as the modified ratio, via the price of the aggregate consumption good, between social marginal benefits,


3. Conclusions
In this essay we model endogenous terms of trade and economic growth in order to analyze the optimal environmental policy that maximizes social welfare. To accomplish this, we work with an AK model of economic growth and deduce endogenous terms of trade from the price of an aggregate consumption good. Thus, as long as households derive utility from consumption and the environment and pollution is generated through domestic production, we conclude that the optimal policy consists in a pollution tax on production.
There are many additional areas of research that could be pursued. A natural extension would be to admit the possibility that the environment may affect productivity. Another development implies the introduction of a natural resource in the production function.
Acknowledgements
I would like to thank an anonymous referee for his valuable suggestions.
Cite this paper
AlejandroSampaolesi, (2014) Optimal Environmental Policy under Endogenous Terms of Trade and Economic Growth. Theoretical Economics Letters,04,608-611. doi: 10.4236/tel.2014.47076
References
- 1. Elbasha, E.H. and Roe, T.L. (1996) On Endogenous Growth: The Implications of Environmental Exter-nalities. Journal of Environmental Economics and Management, 31, 240-268. http://dx.doi.org/10.1006/jeem.1996.0043
- 2. Copeland, B.R. and Taylor, M.S. (2004) Trade, Growth, and the Environment. Journal of Economic Literature, 42, 7-71. http://dx.doi.org/10.1257/002205104773558047
- 3. Sirakaya, S., Turnovsky, S.J. and Alemdar, N.M. (2009) Economic Growth, Trade, and Environmental Quality. Review of International Economics, 17, 906-926. http://dx.doi.org/10.1111/j.1467-9396.2008.00800.x
- 4. Smulders, S. and Gradus, R. (1996) Pollution Abatement and Long-Term Growth. European Journal of Political Economy, 12, 505-532. http://dx.doi.org/10.1016/S0176-2680(96)00013-4
- 5. Huang, C. and Cai, D. (1994) Constant Returns Endogenous Growth with Pollution Control. Environmental and Resource Economics, 4, 383-400. http://dx.doi.org/10.1007/BF00692231
- 6. Bovenberg, A.L. (1986) Capital Income Taxation in Growing Open Economies. Journal of Public Economics, 31, 347-77. http://dx.doi.org/10.1016/0047-2727(86)90065-4
NOTES|

1It could be the case of a manufactured good that generates air pollution through its production process.
2See, for example, [4] and [5] for a previous discussion of these arguments.
3Note that the maximization problem is discomposed into the temporal solution, involving the choice of those goods that maximizes the subutility function at each period of time, and the intertemporal solution, concerning the stream of consumption that maximizes the present value of the utility.
4That is,
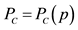 , with
, with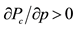 , and where p represents the terms of trade (see, for example, [6] ).
, and where p represents the terms of trade (see, for example, [6] ).
5Note that, given the absence of distorted taxes, the consolidation of firms and households in a representative composite worker-entrepreneur constitutes an adequate representation of the private sector.


