Theoretical Economics Letters
Vol.2 No.3(2012), Article ID:21505,6 pages DOI:10.4236/tel.2012.23055
Market Expansion Effects with Differentiated Goods: Monopoly versus Atomistic Competition
1School of Social Sciences, University of Manchester, Manchester, UK
2Business Economics and Management, Xi’an Jiaotong-Liverpool University, Suzhou, China
Email: simon.rudkin@xjtlu.edu.cn
Received April 16, 2012; revised May 18, 2012; accepted June 20, 2012
Keywords: Market Expansion Effects; Differentiated Goods; Socially Desirable Monopoly
ABSTRACT
In a horizontally differentiated goods market, where consumers face heterogeneous costs of entering the market and exhibit a taste for variety (via CES preferences) over the continuum of substitute goods, lowering the general market price level leads to increased consumer entry—the market expansion effect. Since atomistic competitors (each supplying 1 good) cannot influence this general price level, whilst a (multi-product) monopolist can, monopoly may lead to lower prices. In a model where market expansion effects are potentially large, the paper shows how monopoly leads to socially desirable lower prices, and greater variety, even when goods are arbitrarily close substitutes.
1. Introduction
An elementary result in microeconomics is that, for a market where firms produce a homogeneous good at constant, symmetric marginal cost, monopoly leads to higher prices and a less socially desirable outcome than perfect competition amongst a large number of (atomistic) firms. In what follows these elementary conclusions are reversed—monopoly offers lower prices and the socially better outcome—in a model with constant, symmetric marginal production costs, and where goods are not quite homogeneous but slightly differentiated in the eyes of consumers who have a taste for variety.
To be more precise, a market where a continuum of horizontally differentiated goods is studied. In this model the goods on offer are imperfect substitutes and all goods are produced at the same constant marginal cost. The performance of (multi-product) monopoly provision of the goods with that of atomistic (monopolistic) competetion is then compared. Consumers face (heterogeneous) costs of accessing the market and when shopping they exhibit a taste for variety via CES preferences. Lowering of the general price level on the market thus leads to a market expansion effect, the number of entering consumers increasing. But, whilst individual atomistic competetors are too small to affect the general price level, this is not so for the monopolist, who may therefore set lower prices in a socially preferable way.
The general idea of the last paragraph is quite wellknown, as discussed below. The contribution of this note is to provide a model with sufficiently large market expansion effects that the desirability of monopoly survives to markets where goods are arbitrarily close substitutes. The demonstration is provided both for a short-run model, where the number of goods on offer is fixed, and a longrun model where monopoly has a further desirable impact on the extent of variety on offer.
The idea in the second paragraph can be found in Stahl [1], Smith and Hay [2], and Nocke et al. [3]. In [1] consumers have a quadratic utility function defined over the 2 varieties available, and monopoly provision of the 2 goods leads to lower prices than duopoly, provided goods are not too close substitutes. Reference [2] provides a number of comparisons between multi-product monopoly (supermarket) and other market forms, their High Street alternative equating to the atomistic competition presented here; again lower monopoly prices can emerge in their setting, where goods are independent (i.e. on the border between substitutes and complements). In the terminology of [3], the market is a platform where consumers gain access to a variety of products and the compareson that follows in this paper is between open integrated platform ownership (atomistic competition) and monopoly integrated platform ownership. The latter is not studied in [3]—see p. 1150—and, again in their terminology, our CES example shows how large market expansion effects can always produce strong platform effects, and the desirability of the monopoly ownership; the CES examples in [3] pertaining to other comparisons also produce strong platform effects, if goods are sufficiently complementary. To demonstrate the importance of market expansion effects Peng [4] considers a spatial monopolist and their ability to determine market size when consumer access cost is a linear function, although no attempt is made to study the atomistic alternative. Reference [4] is thus analogous to a special case of the monopolist discussed here.
Focus on multi-product purchase, of the type studied in this note, is limited however. There is a related literature which studies the role of product search in determining which provision method is socially optimal. Seminal works in this setting are Schulz [5] and Schulz and Stahl [6]. They find that the incentive to offer a consumer their preferred variety can cause a monopolist to offer a greater product range from the full set of possible varieties desired by shoppers. Anderson and Renault [7] find that a strong preference for variety can cause prices to fall as competition increases, but that this only serves to partially counter the search effect. As this paper considers multiple products the results from search theory serve as a reference point only.
A second related literature is in the area of product bundling. Chen and Riordan [8] find that a multiproduct monopolist will set a higher price than two competing firms when it sells both of the goods that are sold by the duopolists to consumers who want both goods. Here it is the internalizing of the effect of one product on demand for the other that generates the result. Davis and Murphy [9] is among a series of papers which apply these ideas to anti-trust cases. Specifically in [9] the case studied of Microsoft and its decision to bundle Internet Explorer with its’ Windows operating platform. Following the result of [8] it is shown that the monopoly provision harms consumer welfare. Although many effects from this area can transfer to the multi-product setting, the suggested welfare results of [8,9] do not apply here.
Section 2 sets out the short-run model and Section 3 the long-run model. Section 4 then compares the resulting equilibrium from each provision method with the social optimum. Section 5 concludes.
2. The Short-Run Model
There is a continuum of goods 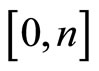 available in the market. If
available in the market. If  denotes the price of good
denotes the price of good 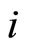 and
and 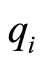 the quantity of good
the quantity of good 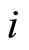 consumed by a consumer entering the market, the consumer’s utility is of the following quasi-linear, symmetric CES form1;
consumed by a consumer entering the market, the consumer’s utility is of the following quasi-linear, symmetric CES form1;
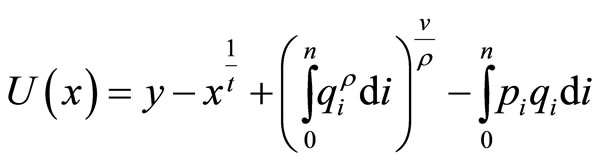
Here  is the consumer’s heterogeneity parameterand
is the consumer’s heterogeneity parameterand 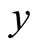 is the consumer’s income (or numeraire endowment).
is the consumer’s income (or numeraire endowment).  would also be the consumer’s utility if the market was not entered. It is assumed
would also be the consumer’s utility if the market was not entered. It is assumed  is large enough to never prevent a potential consumer from entering the market. If they enter, the access cost is
is large enough to never prevent a potential consumer from entering the market. If they enter, the access cost is 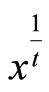 where
where 
and  is uniformly distributed on
is uniformly distributed on . On entering the market the consumer purchases generate net utility corresponding to the last 2 terms in
. On entering the market the consumer purchases generate net utility corresponding to the last 2 terms in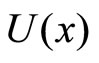 , where
, where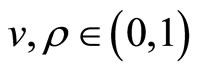 , and
, and .
.  implies goods are always net substitutes, and (as is seen in (2) below)
implies goods are always net substitutes, and (as is seen in (2) below) 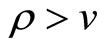 implies they are also gross substitutes. As usual, the quasi-linear form chosen for
implies they are also gross substitutes. As usual, the quasi-linear form chosen for  legitimizes the use of consumer surplus as a welfare measure.
legitimizes the use of consumer surplus as a welfare measure.
Suppose  is the price of all goods apart from good
is the price of all goods apart from good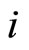 . Any consumer entering the market will buy quantities derived from the following first-order conditions defining the desired
. Any consumer entering the market will buy quantities derived from the following first-order conditions defining the desired 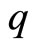 (for each good other than good
(for each good other than good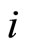 ) and
) and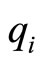 ;
;

and

Hence2;
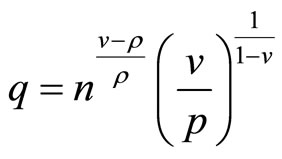 (1)
(1)
 (2)
(2)
Thus, a consumer with heterogeneity parameter x who enters the market would have utility;
 (3)
(3)
The consumer would in fact enter the market if this exceeds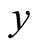 , so the market size at price
, so the market size at price 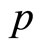 (i.e. the mass of entering consumers, denoted
(i.e. the mass of entering consumers, denoted ) will be the
) will be the  thatequates the right hand side of Equation (3) to y;
thatequates the right hand side of Equation (3) to y;
 (4)
(4)
Notice that 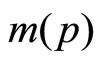 does not depend on
does not depend on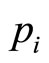 , since
, since 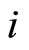 is negligible. Notice also that market size is, naturally, decreasing in
is negligible. Notice also that market size is, naturally, decreasing in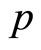 , and the size of the market expansion effect as
, and the size of the market expansion effect as 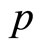 falls can be measured by the (absolute value of the) elasticity of
falls can be measured by the (absolute value of the) elasticity of 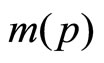 with respect to
with respect to , namely
, namely
 ; in particular, for any given
; in particular, for any given , the market expansion effect will range in size from 0 to
, the market expansion effect will range in size from 0 to  as t increases from 0 to
as t increases from 0 to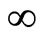 . Letting
. Letting 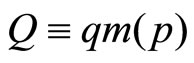 denote aggregate consumer demand for each good other than i, and
denote aggregate consumer demand for each good other than i, and  the corresponding demand for good i, it follows from Equations (1), (2) and (4) that;
the corresponding demand for good i, it follows from Equations (1), (2) and (4) that;
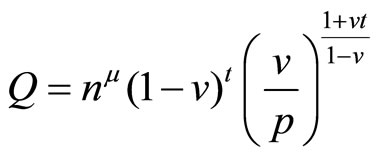 (5)
(5)
 (6)
(6)
where
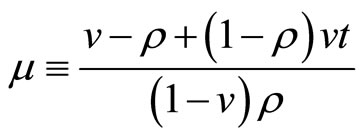 (7)
(7)
Consider first atomistic provision in which each good i is provided by an independent profit-maximizing firm, . These firms produce their particular product variety at constant marginal cost
. These firms produce their particular product variety at constant marginal cost 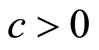 to meet the desired consumer demand. They select a price
to meet the desired consumer demand. They select a price  in order to maximise their profits. If all other firms choose the price p, the profit of firm i is;
in order to maximise their profits. If all other firms choose the price p, the profit of firm i is;

Using Equation (6),  has the sign of
has the sign of 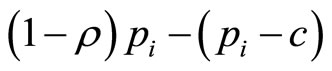 which equals 0 when
which equals 0 when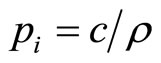 .
.  is increasing to the left of this stationary point, and decreasing to its right, and thus the stationary point is the global profit maximum for all firms. Hence
is increasing to the left of this stationary point, and decreasing to its right, and thus the stationary point is the global profit maximum for all firms. Hence  is the short-run equilibrium price under atomistic competition. Of course,
is the short-run equilibrium price under atomistic competition. Of course, 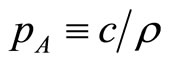 is also the familiar expression for equilibrium under Dixit-Stiglitz monopolistic competition with CES preferences; notice that it does not depend on n.
is also the familiar expression for equilibrium under Dixit-Stiglitz monopolistic competition with CES preferences; notice that it does not depend on n.
Now consider multi-product monopoly provision of the goods  in which each good continues to be produced at constant marginal cost
in which each good continues to be produced at constant marginal cost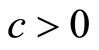 . It is assumed that the monopolist meets the desired consumer demands. Given the symmetry of preferences and demands for the goods, the monopolist will set a symmetric price p for all goods, generating demands given by Equation (5) for each good. The monopolist’s profit from the sale of the n goods is;
. It is assumed that the monopolist meets the desired consumer demands. Given the symmetry of preferences and demands for the goods, the monopolist will set a symmetric price p for all goods, generating demands given by Equation (5) for each good. The monopolist’s profit from the sale of the n goods is;
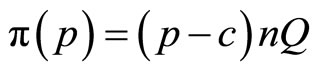
 has the sign of
has the sign of  which equals 0 when
which equals 0 when .
.  is increasing to the left of this stationary point, and decreasing to its right, and so
is increasing to the left of this stationary point, and decreasing to its right, and so  is the global profit maximum for the monopolist. Thus
is the global profit maximum for the monopolist. Thus 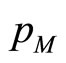 is the short-run equilibrium price under monopoly, and again this does not depend on n.
is the short-run equilibrium price under monopoly, and again this does not depend on n.
Notice that the individual firm under atomistic competition cannot influence market size (which depends on p but not ), whereas the monopolist is large enough to be aware that reductions in their goods’ price will expand the market. For this reason it is possible that
), whereas the monopolist is large enough to be aware that reductions in their goods’ price will expand the market. For this reason it is possible that , a possibility which is easily confirmed (using the previous formulae for
, a possibility which is easily confirmed (using the previous formulae for ) when the size of the market expansion effect is sufficiently large;
) when the size of the market expansion effect is sufficiently large;
 (8)
(8)
Now Equation (8) holds if and only if 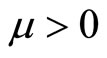 so that
so that  (which is increasing in
(which is increasing in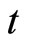 ) becomes an alternative measure of the size of the market expansion effect, from now on
) becomes an alternative measure of the size of the market expansion effect, from now on 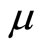 will be used to measure this effect.
will be used to measure this effect.
The following summarises findings so far;
Proposition 1. For any 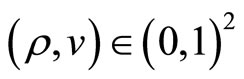 with
with , and thus in particular for a market where goods are arbitrarily close substitutes (
, and thus in particular for a market where goods are arbitrarily close substitutes (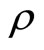 close to 1), the short-run equilibrium price under atomistic competition
close to 1), the short-run equilibrium price under atomistic competition
(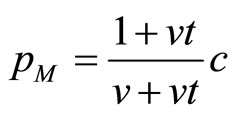 ) exceeds that under monopoly
) exceeds that under monopoly
(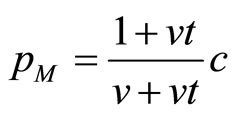 ) if and only if the size of the market expansion effect is sufficiently large (
) if and only if the size of the market expansion effect is sufficiently large (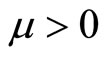 ).
).
It is worth remarking that the exposited short-run model inverts the slope ranking of the DD and dd curves in the familiar textbook Chamberlin diagram. In that diagram, the firms in a monopolistically competitive industry produce substitute goods but without market expansion effects; the DD curve indicates demand per firm if all firms (say) lower price and is naturally steeper than the dd curve which indicates demand for just one firm that lowers price. In our model, the market expansion effect kicks in when all firms lower price, and causes DD to flatten and become less steep than dd.
When the atomistic competition price exceeds the monopoly price the welfare consequences are immediate. First, consumers who enter the atomistic market are also in the monopoly market and are made better off by the lower monopoly price; the lower monopoly price causes new consumers to enter, who are also better off under monopoly; and the remaining consumers enter neither market and are indifferent. Monopoly is Pareto superior to atomistic competition for consumers, and aggregate consumer surplus is certainly higher under monopoly. Secondly, the profit-maximizing monopolist could have chosen the atomistic equilibrium price, but didn’t. Hence monopoly profit (aggregate producer surplus) must be higher than under atomistic competition.
Corollary to Proposition 1. When the short-run equilibrium price under atomistic competition exceeds that under monopoly, aggregate consumer and producer surplus are higher under monopoly.
3. The Long-Run Model
The previously exogenous number of goods on offer in the market (n) is now endogenised. Throughout market expansion effects are assumed to be large, that is . Consequently it is possible to develop long-run analogues of Proposition 1 and its Corollary.
. Consequently it is possible to develop long-run analogues of Proposition 1 and its Corollary.
Under atomistic competition, it is assumed that there is a large mass of potential entrant firms to the market, each of whom face heterogeneous fixed entry costs. Firms with lower entry costs enter first, and the increasing function f(n) indicates the entry cost for the nth entrant. If there are n entrants the market outcome is the short-run equilibrium given n from Section 2. The resulting profit per firm (gross of the fixed entry cost) is;

The entry dynamics are that some further firms enter if, 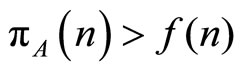 , and some firms leave if
, and some firms leave if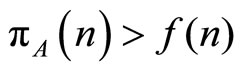 . Long-run equilibrium under atomistic competition is then defined as a locally stable equilibrium of this dynamic process.
. Long-run equilibrium under atomistic competition is then defined as a locally stable equilibrium of this dynamic process.
In the monopolised market, the monopolist now chooses n, as well as the goods’ price. In making its choice it attracts fixed costs that are equivalent to those in the atomistic market when it provides n goods, namely
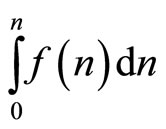 . Given n, the monopolist would choose the corresponding short-run price from Section 2, so profits (gross of the fixed cost) are;
. Given n, the monopolist would choose the corresponding short-run price from Section 2, so profits (gross of the fixed cost) are;
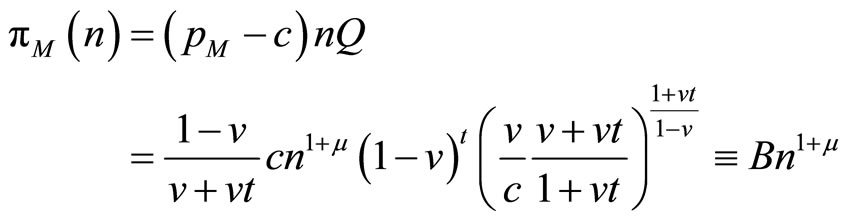
The long-run equilibrium under monopoly is then defined to be a global maximum of
 . The long-run possibilities are quite rich for a general
. The long-run possibilities are quite rich for a general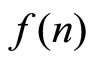 . Here focus is on a special case that illustrates the main point adequately, namely
. Here focus is on a special case that illustrates the main point adequately, namely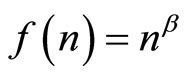 , where
, where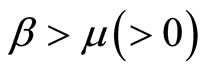 .
.
Steady-states of the entry dynamic under atomistic competition satisfy , producing 2 solutions,
, producing 2 solutions, 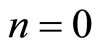 and
and . Since
. Since
 ,
,  is unstable, whilst
is unstable, whilst  is locally stable. Thus
is locally stable. Thus 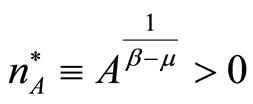 is the unique long-run equilibrium under atomistic competition.
is the unique long-run equilibrium under atomistic competition.
For monopoly, 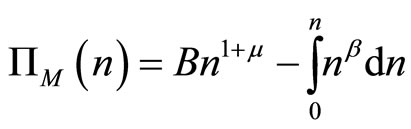 and so
and so
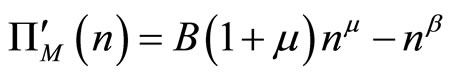 . This satisfies
. This satisfies 
when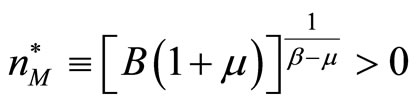 , is increasing to the left of this stationary point and decreasing to the right. Thus
, is increasing to the left of this stationary point and decreasing to the right. Thus 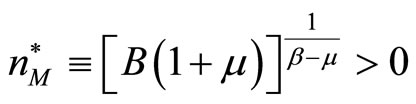 is the unique global maximum of
is the unique global maximum of  and is the unique long-run equilibrium under monopoly.
and is the unique long-run equilibrium under monopoly.
It is straightforward to check that, under the assumption ,
,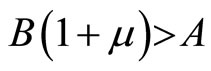 and so
and so . For prices
. For prices
 can be shown readily.
can be shown readily.
Thus in the long-run (with , monopoly offers both lower prices (which do not vary with n) and greater variety than atomistic competition.
, monopoly offers both lower prices (which do not vary with n) and greater variety than atomistic competition.
The desirable welfare consequences of monopoly in the short-run are further enhanced by these long-run variety consequences. Consumers who enter the atomistic market are also in the monopoly market and are made better off by the lower monopoly price and greater variety; the lower monopoly price and greater variety cause new consumers to enter, who are also better off under monopoly, whilst the remaining consumers enter neither market and are indifferent. In the long-run, monopoly is again Pareto superior to atomistic competition for consumers and aggregate consumer surplus is certainly higher under monopoly. Secondly, the profit-maximizing monopolist could have chosen the atomistic equilibrium price and variety, but didn’t. Hence monopoly profit (aggregate producer surplus) must be higher than under atomistic competition in the long-run.
Summarising:
Proposition 2. In the long-run monopoly model with , not only is the equilibrium price lower than under atomistic competition, but the extent of variety on offer is higher, creating a Pareto improvement for consumers, higher aggregate consumer surplus and higher aggregate producer surplus.
, not only is the equilibrium price lower than under atomistic competition, but the extent of variety on offer is higher, creating a Pareto improvement for consumers, higher aggregate consumer surplus and higher aggregate producer surplus.
4. The Social Optimum
A planner now chooses p and n so as to maximize aggregate social welfare. As usual, the optimal choice of p will be marginal cost c, in which case the utility of an entering consumer and the market size will be;


Continuing to assume that the mass of potential consumer entrants is large ( ) aggregate social welfare
) aggregate social welfare 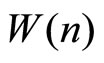 is then:
is then:
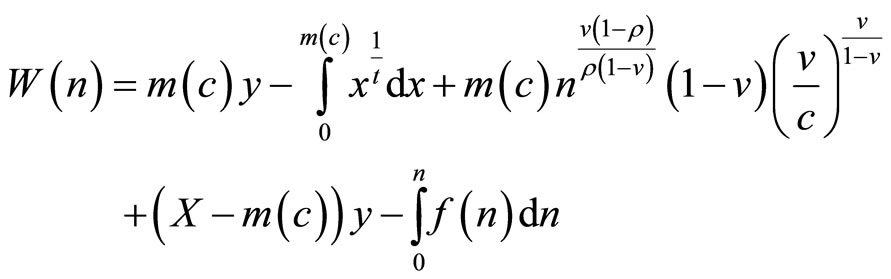
Substituting for , ignoring the constant
, ignoring the constant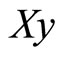 , reintroducing
, reintroducing 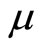 and rearranging and simplifying gives:
and rearranging and simplifying gives:
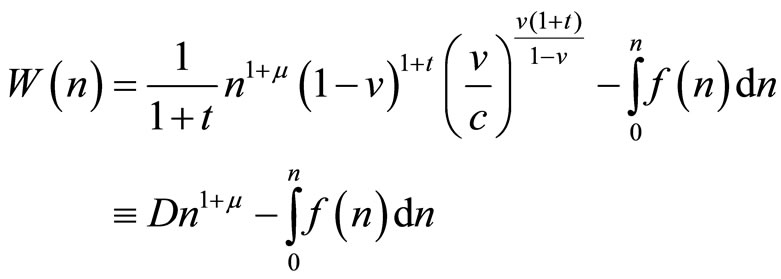
with  it can be seen that
it can be seen that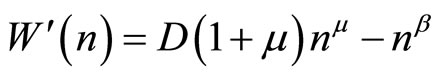 . This is stationary,
. This is stationary,
 , when
, when .
. 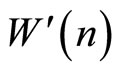 is increasing to the left of this stationary point and decreasing to the right. Thus
is increasing to the left of this stationary point and decreasing to the right. Thus  is the unique global maximum of
is the unique global maximum of , and is the unique socially optimal level of variety.
, and is the unique socially optimal level of variety.
Under the assumption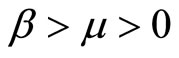 , it is straightforward to check that
, it is straightforward to check that 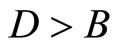 and so
and so . Thus although monopoly provides a welfare increasing level of variety compared to atomistic competition, that level is still short of the socially optimal level. Analogously, although monopoly provides a welfare enhancing reduction in price, compared to atomistic competition, that level still exceeds the socially optimal, marginal cost price.
. Thus although monopoly provides a welfare increasing level of variety compared to atomistic competition, that level is still short of the socially optimal level. Analogously, although monopoly provides a welfare enhancing reduction in price, compared to atomistic competition, that level still exceeds the socially optimal, marginal cost price.
Figure 1 illustrates  and
and 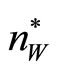 with
with 
 , in a diagram similar to that used extensively in [2]. The ranking of the three levels of variety is clear, with
, in a diagram similar to that used extensively in [2]. The ranking of the three levels of variety is clear, with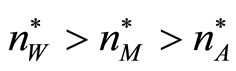 .
.
5. Conclusion
The paper has compared the performances of multiproduct monopoly and atomistic competition in a market for the provision of a continuum of differentiated goods where consumers have a taste for variety. The presence of heterogeneous consumer access costs means that low-

Figure 1. Long run equilibrium and welfare variety comparison.
ering of the general price level on the market generates a market expansion effect that may lead to lower prices under monopoly. The novelty is that market expansion effects can be so large in the model that monopoly leads to lower prices, greater product variety, and higher social welfare than atomistic competition, even if the goods are arbitrarily close substitutes.
REFERENCES
- K. Stahl, “Location and Spatial Pricing Theory with NonConvex Transportation Cost Schedules,” Bell Journal of Economics, Vol. 13, No. 2, 1982, pp. 575-582. doi:10.2307/3003478
- H. Smith and D. Hay, “Streets, Malls and Supermarkets,” Journal of Economics & Management Strategy, Vol. 14, No. 1, 2005, pp. 29-59. doi:10.1111/j.1430-9134.2005.00033.x
- V. Nocke, K. Stahl and M. Peitz, “Platform Ownership,” Journal of the European Economic Association, Vol. 5, No. 6, 2007, pp. 1130-1160. doi:10.1162/JEEA.2007.5.6.1130
- S. Peng, “Spatial Monopoly with Product Differentiation,” Southern Economic Journal, Vol. 70, No. 3, 2004, pp. 646-660. doi:10.2307/4135336
- N. Schulz, “Are Markets More Competitive if Commodties Are Closer Substitutes?” International Economic Review, Vol. 36, No. 4, 1996, pp. 963-983. doi:10.2307/2527268
- N. Schulz and K. Stahl, “Do Consumers Search for TheHighest Price? Oligopoly Equilibrium in DifferentiatedProducts Markets,” RAND Journal of Economics, Vol. 27, No. 3, 1996, pp. 542-562. doi:10.2307/2555843
- S. Anderson and R. Renault, “Pricing, Product Diversity and Search Costs: A Bertrand-Chamberlain-Diamond Model,” RAND Journal of Economics, Vol. 30, No. 4, 1999, pp. 719-735. doi:10.2307/2556072
- Y. Chen and M. H. Riordan, “Price-Increasing Competition,” RAND Journal of Economics, Vol. 39, No. 4, 2008, pp. 1042-1058. doi:10.1111/j.1756-2171.2008.00049.x
- S. J. Davis and K. M. Murphy, “A Competitive Perspective on Internet Explorer,” American Economic Review, Vol. 90, No. 2, 2000, pp. 184-187. doi:10.1257/aer.90.2.184
- S. Rudkin, “The Impact of Supermarkets on Prices, Consumer Behaviour and Welfare; Theoretical and Empirical Issues,” Ph.D. Thesis, University of Manchester, Manchester, 2008.
NOTES
1In Rudkin [10] the author provides a similar analysis to here, with quadratic rather than CES utility.
2From Equation (2) 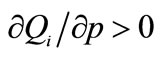 and goods are gross substitutes iff
and goods are gross substitutes iff , as remarked earlier.
, as remarked earlier.

