ABSTRACT

In this note, we compare two strategic general equilibrium concepts: the Stackelberg-Walras equilibrium and the Cournot-Walras equilibrium. We thus consider a market exchange economy embodying atoms and a continuum of traders. It is shown that, when the preferences of the small traders are represented by Cobb-Douglas utility functions, the Stackelberg-Walras and the Cournot-Walras equilibria can coincide only if 1) the endowments and preferences of atoms are identical and 2) the elasticity of the followers’ best response functions is equal to zero in equilibrium.

1. Introduction

The Cournot-Walras equilibrium (CWE) models opened by Gabszewicz and Vial [1], and developed in exchange economies by Codognato and Gabszewicz [2,3], Gabszewicz and Michel [4] and Busetto, Codognato and Ghosal [5,6] feature the consequences of strategic interactions in general equilibrium. The strategic traders manipulate the equilibrium relative prices by restricting their supplies on the markets. Some contributions aim at comparing the CWE with other strategic equilibria. Codognato [7] studies the equivalence between the CWE and the Cournot equilibrium, while Codognato [8] compares two Cournot-Nash equilibrium models. In this note, we compare the CWE and the Stackelberg-Walras equilibrium (SWE) defined in Julien and Tricou [9]. From the benchmark of Cournot-Walras exchange economies, the SWE concept inserts Stackelberg competition into interrelated markets. We determine the conditions under which the CWE and the SWE are equivalent.

We thus consider a mixed market exchange economy as developed in Shitovitz [10] and Codognato [7]. Therefore, strategic interactions prevail here in one sector only. We characterize and define the SWE in this framework. It is shown that, when the preferences of the small traders are represented by Cobb-Douglas utility functions, the SWE and the CWE can coincide only if 1) the atoms have the same endowments and preferences and 2) the elasticity of the best response functions is zero. So, in mixed markets exchange economies, the SWE and the CWE coincide when two kinds of conditions are satisfied: one stems from the fundamentals, another is based on consistent expectations formed by the atomic part of the economy.

The paper is organized as follows. Section 2 provides a characterization and a definition of the SWE in a mixed-markets exchange economy. Section 3 is devoted to the statement and the proof of the proposition. In section 4, an example is given. In section 5, we conclude.

2. The Stackelberg-Walras Equilibrium

The space of commodites is. There is a finite set 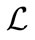of divisible commodities, indexed by. Let 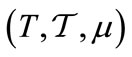be a measure space of agents, where T denotes the set of traders, 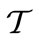a -field of Lebesgue measurable subsets of T (the class of coalitions), and 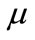a Lebesgue measure on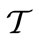. Large traders are represented by atoms and small traders by an atomless sector. 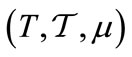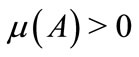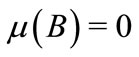An atom of the measure space is a coalition A with, such that, for each coalition, one has either or 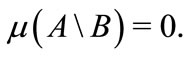The set embodies atoms, while 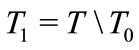is the atomless sector. The set of atoms embodies two subsets: the subset of leaders 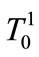and the subset of followers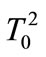, so .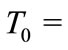

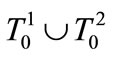An assignment (of commodity bundles to traders) is an integrable function 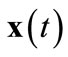from T to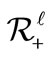. All integrals are with respect to t. Any trader 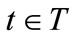has a measurable, continuous, strictly increasing and strictly quasi-concave utility function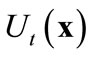, which represents his preferences among the commodity bundles x. The distribution of initial endowments satisfies:

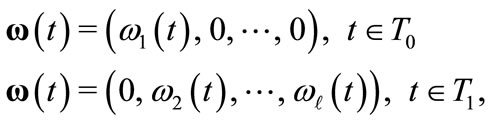(1)

with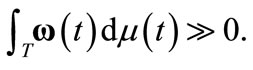      

A feasible allocation is an assignment

.

The price vector is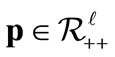. Since no a trader is subject to money illusion, we let, with

.

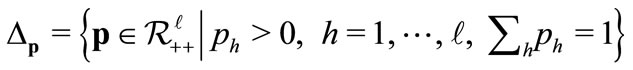Any trader t, 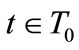, behaves stragically, while any trader t, 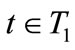, behaves competitively. The strategic behavior consists in contracting the quantity of commodity 1 brought to the market to manipulate the price system. We denote by s the pure strategy of trader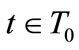. A strategy profile for 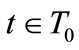is a real valued integrable function defined on 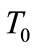such that, for all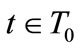,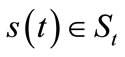. The strategy set of t may be written

,

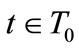: it involves all the possible quantities that trader t, 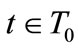, may bring to the markets. The characterization and the definition of a CWE for this economy is given in Codognato [7]. We now characterize the SWE.

The SWE concept can be modeled as a sequential structure in three steps: it is based on a two-stage game which relies on a competitive moment. Before, the strategic interactions, the general equilibrium price vector deduced from the competitive behaviors is computed for any strategy profile. Then, traders make quantity decisions within a Stackelberg game.

Given a price vector, trader 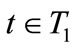solves:

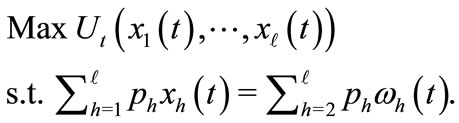(2)

The unique solution to this program is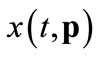. Given and a strategy profile, the program of any trader 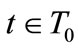may be written:

(3)

The vect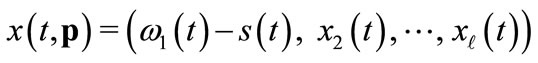or for denotes the unique solution to this program. Let 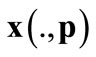be the function on T with values in defined by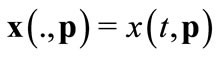. For all, 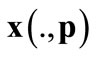is an assignment. Given a strategy profile, the equilibrium price system is the solution to:

(4)

We assume that 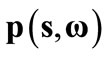exists and is unique. We here follow the argument developed by Codognato and Gabszewicz [3] for the CWE concept. So, we denote by 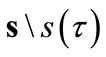the strategy profile which coincides with s for all 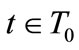except for, , 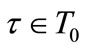with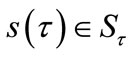. We denote by 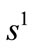(resp.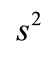) the pure strategies of any leader (follower), whom respective strategy selections are integrable functions 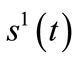and. Given a vector of strategy profiles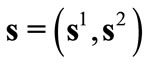, 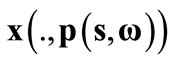is an allocation.

In the second step, the followers determine their best response functions. The strategic plan 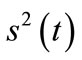of any follower 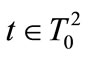solves:

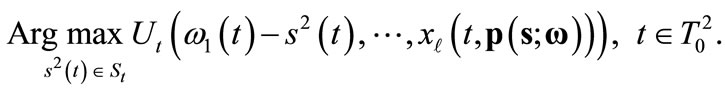(5)

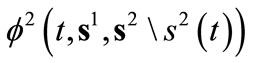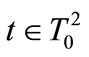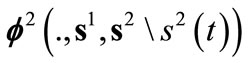The solution to this program yields the best response function of follower. Let be the real valued integrable function on 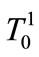with values in 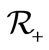defined by

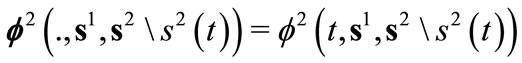
for all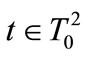. When considering all followers, one gets:

(6)

The system of equations given by (9) determines a consistency among the best response functions, each of which depending on and. The solution to this system is denoted by.

In the third step, trader t solves the program:

(7)

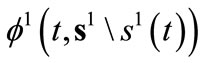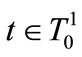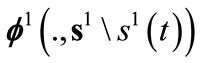The solution to this program yields the best response function denoted by of leader. Let be the real valued integrable function on 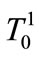with values in 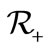defined by

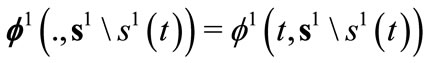
for all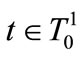. When considering all leaders, one has:

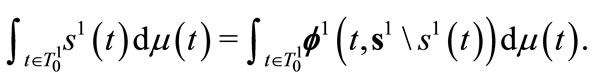(8)

In the symmetric equilibrium (8) yields the strategy profile. One deduces, and thereby the vector of equilibrium relative prices 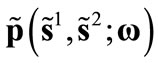and the equilibrium allocations 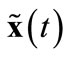for all.

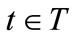A SWE is a general equilibrium which embodies a non cooperative equilibrium of a game where the players are the atoms, the strategies are their supply decisions and the payoffs are their utility levels.

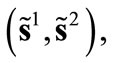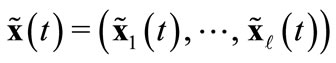DEFINITION (SWE). A Stackelberg-Walras equilibrium is given by a vector of strategy profiles a price system and an allocation such that:

1)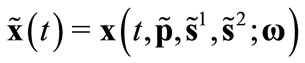, for all2)3)

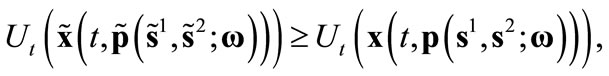
4)

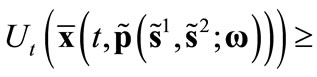
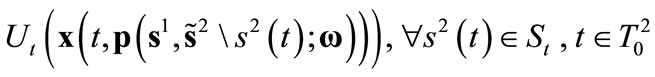
5)

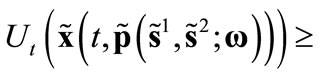
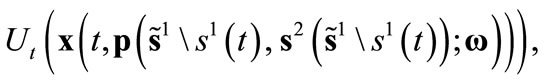
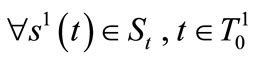
3. Equivalence between the SWE and the CWE

PROPOSITION: Suppose the preferences of traders in the atomless continuum are represented by Cobb-Douglas utility functions. The Stackelberg-Walras and the Cournot-Walras equilibria coincide only if 1) the atoms have the same endowments and preferences and 2) the elasticity of the best-response functions is equal to zero in equilibrium.

Proof. Consider commodities indexed by h, 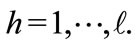There are n atoms indexed by i, 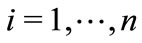, with m leaders and followers. There is also a continuum of traders, each being indexed by t,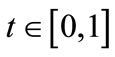. We make the following assumptions:

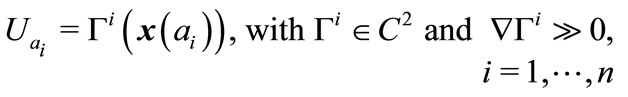
We first determine the SWE.

The competitive step is determined before the strategic steps. Given a price vector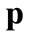, trader 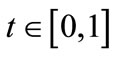solves:

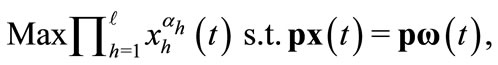
It leads to

,

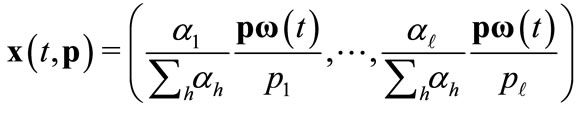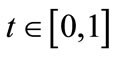. Given, the program of any trader i may be written:

When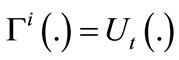, it leads to

,

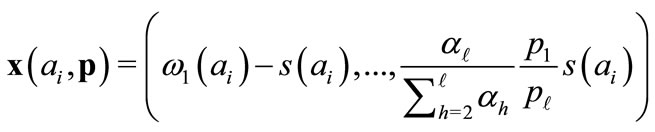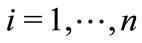. Given a strategy profile

and from Walras’ law, the price system 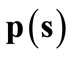is the solution to:

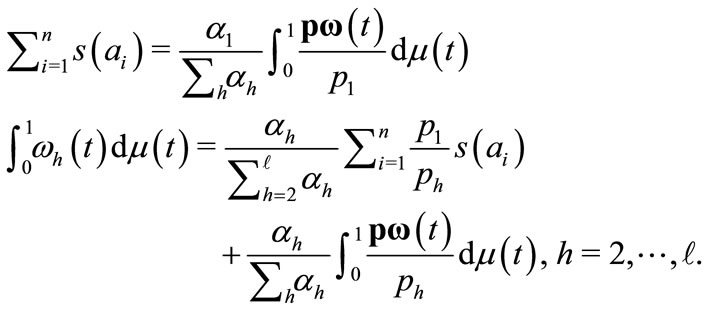
It leads to the equilibrium relative prices:

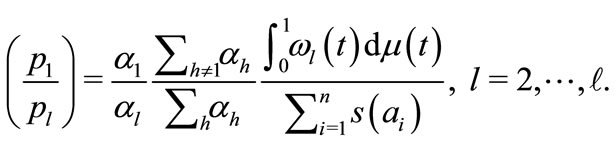
In the first strategic step, follower i, 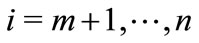, determines his best response function, which is the solution to:

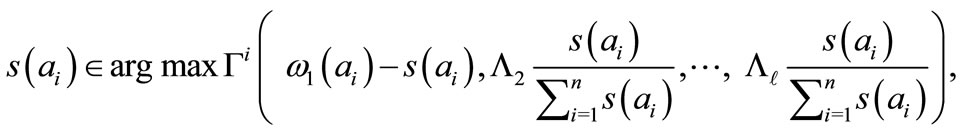
where,.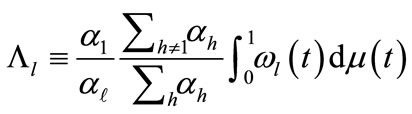

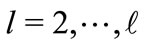The first-order condition is:

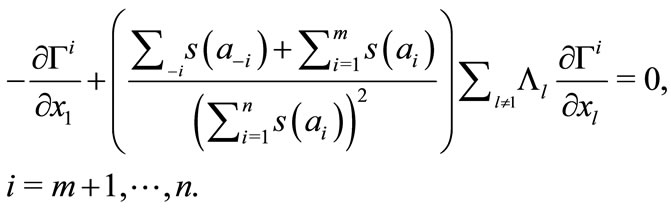
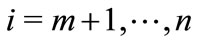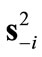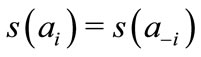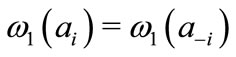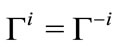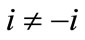The preceding equation yields the best-response of follower i, , where and represent respectively the vector of leaders’ strategies and the vector of all followers strategies but i. In the symmetric case, one gets, which requires and for all i and all, with, so,.

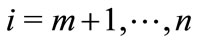The second strategic step consists in determining the equilibrium strategy of any leader i,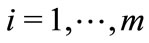. The program of any leader i, 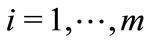, may then be written:

.

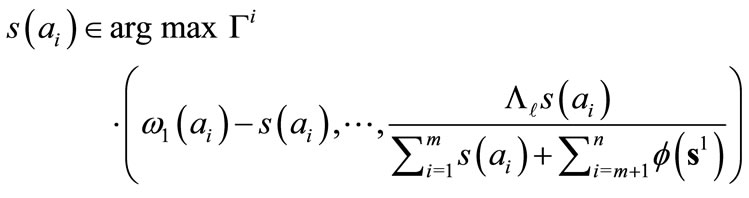At the symmetric SWE, one has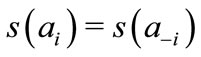, which requires 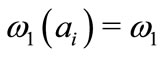and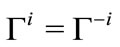, , so the first-order conditions may be written:

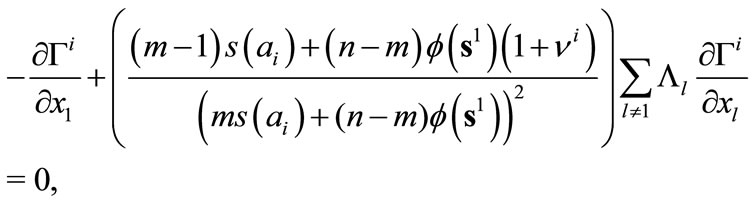(C1)

where           ,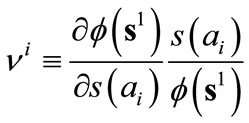

, represents the elasticity of the best response function of any follower i, 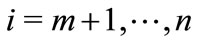, correctly perceived by any i,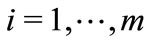. Equations (C1) yield the equilibrium strategy 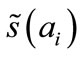of any leader i, 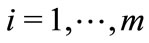, from which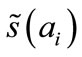, , 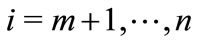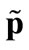and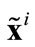, 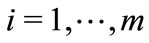are deduced.

Let us now proceed to the characterization of the CWE. There is only one strategic step: the atoms plays a simultaneous move game between themselves. Any trader i, 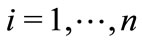solves:

In the symmetric equilibrium, the first-order condition for i, 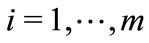, leads to the equilibrium strategy 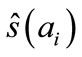of trader i, which is the solution to:

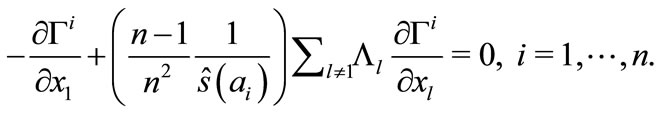(C2)

If for any i, ,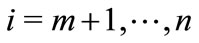

,

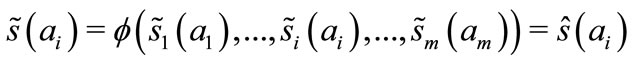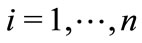, then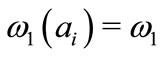, 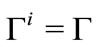and,. One concludes that the SWE and CWE allocations coincide. QED.

When the best response functions have a zero elasticity in equilibrium, any leader rationally expects that a change in his strategy will elicit no reaction from the followers. The elasticity thus coincides with the true slope of the best response functions (here zero): conjectures are fulfilled and are thus consistent. It is as if the leaders made no expectations regarding the reactions of the followers to a change in their decisions. Consequently, the traders take the decisions of their rivals as given when optimizing, and thus behave as if they played a simultaneous move game, believing in the same way their rivals behave following a Cournotian reaction function. This condition on consistent conjectures is necessary but not sufficient. It may also hold when both equilibria do not coincide. In addition, the shape of the reaction functions and their slopes at equilibrium depend notably on the market demand function. The CobbDouglas specification leads to an isoelastic aggregate market demand function. Thus, the market demand which addresses to the atoms has a constant unitary price elasticity. So, when all atoms have the same endowments and preferences, their market shares are equal, which implies that their (Cournotian) equilibrium strategies are identical. If strategic traders did not have the same endowments and preferences, their equilibrium strategies would differ and could not correspond to the Cournotian ones (the same result can hold in industrial organization when firms have not the same marginal costs). Therefore, we extend a result obtained in partial equilibrium by Julien [11] to cover exchange economies.

4. An Example

Consider the case for which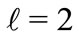. The price system is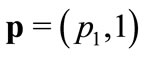. The economy embodies two atoms 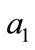(the leader) and (the follower), each of measure , , 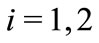and an atomless continuum of traders represented by the unit interval 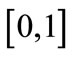with the Lebesgue measure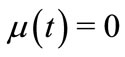,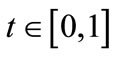. The following assumptions are made:

(9)

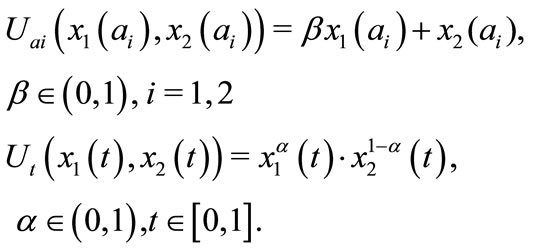(10)

The strategy set of i is given by

,

. Let us determine the competitive step. Given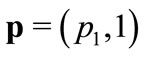, t solves:

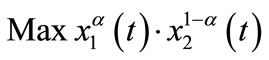s.t.,.

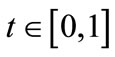It leads to.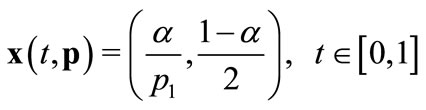

Given 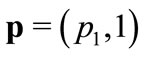and, , 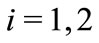one get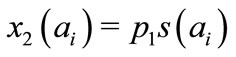s,. Thus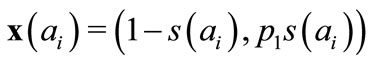,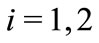. Given a strategy profile, and from Walras’ law, the relative price 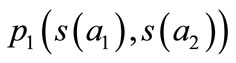is the solution to

.

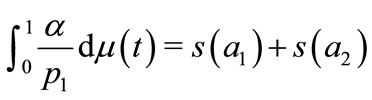The equilibrium price system is then:

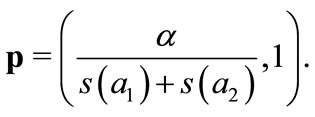(11)

The first strategic step may be written:

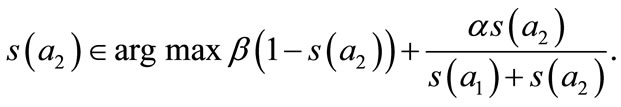(12)

This leads to the best response function of the follower:

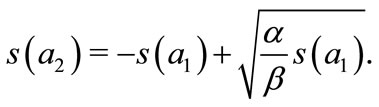(13)

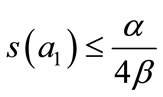One has when, and.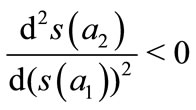

The program of the leader may then be written:

(14)

The SWE strategies are:

(15)

The equilibrium price and allocations are given by:

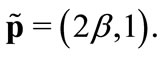(16)

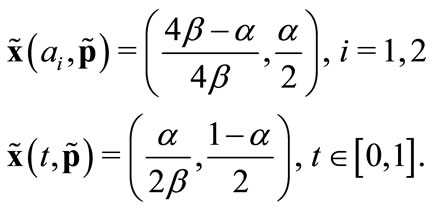(17)

We finally determine the CWE. Given

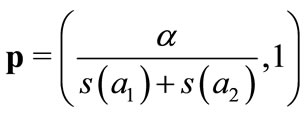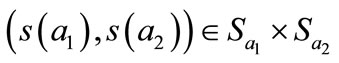andthe program of any trader may be written:

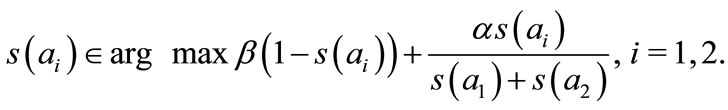(18)

It leads to the equilibrium strategies:

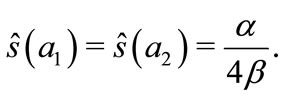(19)

The equilibrium price system and allocations are then:

(20)

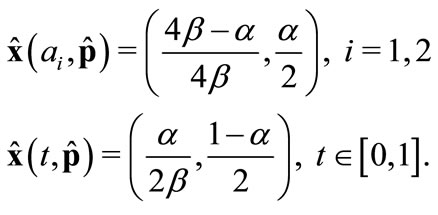(21)

Then the SWE and the CWE coincide. We also check that from (13).

5. Conclusion

In mixed markets exchange economies the CWE and the SWE can coincide: one condition stems from the fundamentals (endowments and preferences), while the other concerns consistent expectations formed by the atomic part of the economy.

6. Acknowledgements

I am grateful to an anonymous referee for her/his remarks and suggestions. All remaining deficiencies are mine.

REFERENCES