Journal of Mathematical Finance
Vol.08 No.01(2018), Article ID:82776,17 pages
10.4236/jmf.2018.81013
A Linear Regression Approach for Determining Option Pricing for Currency-Rate Diffusion Model with Dependent Stochastic Volatility, Stochastic Interest Rate, and Return Processes
Raj Jagannathan
Department of Management Sciences, Tippie College of Business, The University of Iowa, Iowa City, USA
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 14, 2017; Accepted: February 25, 2018; Published: February 28, 2018
ABSTRACT
A three-factor exchange-rate diffusion model that includes three stochastically-dependent Brownian motion processes, namely, the domestic interest rate process, volatility process and return process is considered. A linear regression approach that derives explicit expressions for the distribution function of log return of foreign exchange rate is derived. Subsequently, a closed form workable formula for the call option price that has an algebraic expression similar to a Black-Scholes model, which facilitates easier study, is discussed.
Keywords:
Option Pricing, Interest-Rate Parity Condition, Black-Scholes Model, Linear Regression Approach, Spot Option, Ito Calculus

1. Introduction
A foreign exchange rate depends on the supply and demand dynamics of a currency. The exchange rate is a function of trade balance, the interest rate differential and differential inflation expectations between the two countries [1] [2] .
Let S(u), 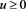 = exchange rate process over the time interval:
= exchange rate process over the time interval: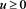 , where u = number of domestic currency units, e.g., $, per unit of foreign currency = $-price of foreign currency.
, where u = number of domestic currency units, e.g., $, per unit of foreign currency = $-price of foreign currency.
As interest rate 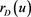 increases, $ appreciates because investors prefer $-denominated bonds. Assuming a frictionless, arbitrage-free continuous-time economy in [1] , we define a diffusion process model for S(u). In addition, using interest-rate parity condition we have
increases, $ appreciates because investors prefer $-denominated bonds. Assuming a frictionless, arbitrage-free continuous-time economy in [1] , we define a diffusion process model for S(u). In addition, using interest-rate parity condition we have
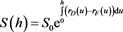 , see [1] .
, see [1] .
In the following section, the formula for valuations of currency spot options is considered, where we obtain a closed form formula for the call option price that has a simple algebraic expression, which is similar to the call option price expression of a Black-Scholes model, making it much easier to compute its value and study. As in [2] , we can define an implied volatility function and derive its skewness property.
Subsequently, the proposed three-factor exchange-rate diffusion model is discussed, such that the stochastic volatility process and the stochastic domestic interest rate process each have a stochastically dependent Brownian motion return process.
In the next section, a linear regression approach that derives explicit expressions for the distribution function of 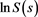 is treated.
is treated.
Foreign exchange rate option modeling is the subject of several well-known papers and in chapters within [3] [4] [5] [6] . Leveraging Heston’s model [4] for this application would introduce complexity due to the need to numerically integrate conditional characteristic functions obtained as solutions of nonlinear pdf to derive the call option prices. An equivalent two-factor Black-Derman-Toy model [2] can be formulated with introduction of H(u).
The method suggested in this paper results in Black-Scholes type formula for call option pricing, which is easily computable.
Finally, we provide concluding remarks and suggestions for future direction.
2. Currency Spot Option
Given the spot rate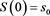 , consider the present value of option
, consider the present value of option
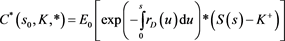 (1)
(1)
where K is the known strike price and 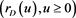 is a mean-reverting stochastic process given in (2) below.
is a mean-reverting stochastic process given in (2) below. 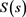 is the value of the exchange rate at the option’s maturity price. The option to purchase foreign currency over the counter can be exercised when S(s) > the strike price exchange rate K.
is the value of the exchange rate at the option’s maturity price. The option to purchase foreign currency over the counter can be exercised when S(s) > the strike price exchange rate K.
3. A Diffusion Process Model
A continuous-time risk-adjusted and risk-neutral exchange rate model, under a Martingale Measure Q, is defined below as a diffusion process (2), mean-reverting stochastic processes: Volatility 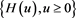 (3) and domestic interest rate
(3) and domestic interest rate 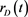 process (4), and foreign interest rate
process (4), and foreign interest rate  is a known constant.
is a known constant.
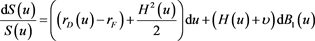 (2)
(2)
 (3)
(3)
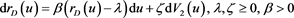 (4)
(4)
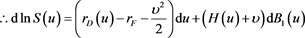 (5)
(5)
Equation (5) is obtained from Equation (2) by the application of Ito calculus [7] .
Assumption:
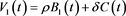 , where
, where 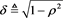 and
and 


and 

From the assumption above, the return processes 


Then it follows, see [2] [3] , that the distributions of 

Alternatively, 


where 


Remark 1:
From (8), choosing 

If, alternatively, we assume that 

where 

Assuming

The Brownian motion processes 



In addition, the Brownian motion processes 

Remark 2:

It follows from [2] that the distribution of 

Alternatively, 

where 

See [9] for a similar assumption. See also [2] and [3] .
Note that 






For

Define
deviation in the case of uncorrelated Brownian motion process

Proposition 1:

where

Proof: See Appendix B.
We consider a mean-reverting Gaussian process model (2), the volatility stochastic processes 





Assumption 1:

In (4), we define the domestic interest rate process 





Assumption 2:
It follows from [2] that the distribution of

Now we use the results obtained in Proposition 1 to derive an explicit expression for
Proposition 2:

Remark 3:
From the expression for









Then, using the results in [2] , Proposition 1 and those in Appendix A and Appendix B we have:

Therefore,
Remark 4:
Note that 

due to our treatment of a stochastic interest rate:
In the case of






Case 1:
Let
Let
Assumption 3: 

Assumption 4:
Assumption 5: 

If Assumptions (4) and (5) hold, then the conditional risk-neutral distribution of 
Proposition 3:

where

If



In other words, 

Remark 5:
Since we know the CDF of lnS(s) we can estimate the parameters of the underlying model (2)-(5).
Case 2: Conditional Risk-neutral Distribution function of



where
Example 1


Then
Remark 6:
From the expression for
the stochastic terms 




Proof:
Apply a proof similar to the one in Appendix A of [2] using the result for 
Remark 7:
Assume

If Assumption (3) holds then the conditional risk-neutral distribution of 

where

If



In other words, 

Call option price:
Proposition 4:
where from Proposition 1
See Appendix B.
Remark 8:
Given the formula for







Let

Then
Hedge Ratio:
D-Neutral Portfolio
Delta-Neutral Portfolio
Consider the following portfolio that includes a short position of one European call and a long position of delta units of the domestic currency.
The portfolio of delta-neutral positions is defined as:
We obtain below Conditional Risk-neutral Distribution function of

by considering the cases of: h = 1, 0 and −1
We use a discrete approximation (see [2] , (28)).
Suppose

Again, we consider the Equations (1)-(4) to define Example 1 below.




Let
Then,
And
If Assumption (2) holds then the unconditional risk-neutral distribution of

Then Figure 1 depicts the unconditional risk-neutral distribution of

Remark 9:
Future movement of values of risk-free interest rate and volatility are uncertain and as they increase, they affect call option values as depicted in the above Figure 2, Figure 3 ( [5] , p. 204). Sudden changes in their values may occur because of economic shock. See the models suggested in [11] [12] .
Figure 1. Unconditional risk-neutral CDF of lnS(s), strike price (cents) k from 1.1 to 16.2.
Figure 2. Unconditional call option price with strike price k (cents) from 1.1 to 26.
Figure 3. Unconditional hedge ratio with strike price k (cents) from 1.1 to 26.
4. Conclusion
We define a three-factor exchange-rate diffusion model with 1) stochastic volatility process, 2) stochastic domestic interest rate process, and 3) return process which are Brownian motion return processes that are stochastically dependent. Further generalization is possible with the assumption of domestic and foreign stochastic interest rate processes which are subject to economic shocks [11] [12] . The results are applicable to bond option models ( [5] , p. 783).
Cite this paper
Jagannathan, R. (2018) A Linear Regression Approach for Determining Option Pricing for Currency-Rate Diffusion Model with Dependent Stochastic Volatility, Stochastic Interest Rate, and Return Processes. Journal of Mathematical Finance, 8, 161-177. https://doi.org/10.4236/jmf.2018.81013
References
- 1. Krugman, P.R. and Obstfeld, M. (2000) International Economics. 3rd Edition, Addison Wesley, Boston, 360-362.
- 2. Jagannathan, R. (2016) A Linear Regression Approach to Two-Factor Option Pricing Model. Journal of Math Finance, 6, 317-337.
- 3. Vasicek, O. (1977) An Equilibrium Characterization of the Term Structure. Journal Financial Economics, 5, 177-188. https://doi.org/10.1016/0304-405X(77)90016-2
- 4. Heston, S. (1993) A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Review of Financial Studies, 6, 327-344. https://doi.org/10.1093/rfs/6.2.327
- 5. Hull, J.C. (2009) Options, Futures and Derivatives. Pearson, Prentice Hall, Upper Saddle River.
- 6. Garman M.B. and Kohlhagen, S.W. (1983) Foreign Exchange Option Values. Journal of International Money and Finance, 2, 231-237. https://doi.org/10.1016/S0261-5606(83)80001-1
- 7. Oksendal, B. (2003) Stochastic Differential Equations—An Introduction with Applications. Springer, New York.
- 8. Cox, J.C., Ingersoll, J.E. and Ross, S.A. (1985) A Theory of the Term Structure of Interest Rates. Econometrics, 53, 385-407. https://doi.org/10.2307/1911242
- 9. Trolle, A.B. and Schwarz, E.S. (2009) A General Stochastic Volatility Model for the Pricing of the Interest Rate Derivatives. The Review of Financial Studies, 22, 2007-2057. https://doi.org/10.1093/rfs/hhn040
- 10. Duffie, D. (1996) Dynamic Asset Pricing Theory. 2nd Edition, Princeton University Press, Princeton.
- 11. Merton, R.C. (1976) Option Pricing When the Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144.
- 12. Jagannathan, R. (2008) A Class of Asset Pricing Models Governed by Subordinated Processes That Signal Economic Shocks. Journal of Economic Dynamics and Control, 32, 3820-3846. https://doi.org/10.1016/j.jedc.2008.04.004
- 13. Bakshi, G., Cao, C. and Chen, Z. (1997) Empirical Performance of Alternative Option Pricing Models. The Review of Financial Studies, 52, 2003-2049. https://doi.org/10.1111/j.1540-6261.1997.tb02749.x
- 14. Wilks, S.S. (1962) Mathematical Statistics. John Wiley, Hoboken.
Appendix A
is the regression coefficient.

Then the regression equation is

Assumption 6:

Note that 

Assumption 7:

(2A4)
Proof of Proposition 1:
Appendix A from [2]
where
where
Appendix B
See [13] .
because
Let
where
Let
Let
where applying Wilk’s linear regression [14] , we get




























































