Journal of Mathematical Finance
Vol.3 No.1(2013), Article ID:28401,7 pages DOI:10.4236/jmf.2013.31013
Optimal Investment under Price and Wage Uncertainty*
School of Finance, Shanghai University of Finance and Economics, Shanghai, China
Email: eyesonme_hmily@msn.com
Received November 24, 2012; revised December 28, 2012; accepted January 9, 2013
Keywords: Optimal Investment; Output Price; Wage Rate; Uncertainty
ABSTRACT
The effects of future output price uncertainty and wage uncertainty on a firm’s investment decision are examined in this paper, by assuming the competitively risk-neutral firm maximizes the expected value of the sum of discounted cash flows. We find that the optimal investment behavior is such that the expected proportional growth rate of investment is invariant over time, although there exists a tradeoff between the effects of the two uncertainty on firm’s investment because the shift in output price has positive effects on firm’s investment, whereas the shift in wage has negative impacts on firm’s investment. And what’s more important, fluctuations in output price and wage are correlated so that changes in output price tend to be accompanied by changes in wage.
1. Introduction
During the past decades, many scholars studied the effects of uncertainty on a firm’s input and output decisions. Regarding to this topic, one can see references we enumerate at the end of the paper and etc. Within those papers, considerable results and conclusions have been achieved. For example, Hartman [1] examined the impacts that increased uncertainty in future output prices, wage rates and investment costs has on the quantity of investment undertaken by a firm, and pointed out current investment doesn’t decrease with increased uncertainty in future output prices as well as wage rates, and invariant to increased uncertainty in future investment costs. The sign of the investment-uncertainty relationship is negative, and that the quantitative negative impact is substantially greater in industries dominated by small firms are shown in Ghosal and Lougani [2] by studying the impact of profit uncertainty on investment and whether or not this response is different in industries that are dominated by small firms versus those that are dominated by relatively larger firms. These results are robust to accounting for potential endogeneity of the uncertainty measure, alternate procedures for measuring uncertainty, and alternate ways of segmenting industries into smalland-large firm groups. In Peeters [3], empirical results proved that both demand and price uncertainty correlate significantly with corporate investment, and that output price uncertainty depresses investment in Belgium and Spain. Applying dynamic panel data methods, Temple, et al. [4] found that all sources of uncertainty exert a considerable negative impact on investment while financial factors may be important in some industries. Bloom offered a structural framework to analyze the impact of these uncertainty shocks and built a model with a timevarying second moment, which is numerically solved and estimated using firm-level data in Bloom [5]. The parameterized model demonstrated higher uncertainty causes firms to temporarily pause their investment and hiring, and the increased volatility from the shock induces an overshoot in output, employment, and productivity. Thus, uncertainty shocks generate short sharp recessions and recoveries. In Lee and Shin [6], they discovered that in the absence of fixed adjustment cost, a higher labor share strengthens the positive relationship between investment and uncertainty, whereas in the presence of a lumpy adjustment cost, optimal investment will drop to zero as uncertainty increases if labor share is low, but will increase if labor share is high. Both the case in which the firm faces an uncertain price in a perfectly competitive commodity market and the case in which the firm faces an uncertain downward sloping demand function are studied in Nielsen [7], the results showed higher expected price increases optimal output, and a quantity setting policy implied a tendency towards smaller quantities and higher price, while on the contrary, a price setting policy implied a tendency towards lager quantities and lower price, than under certainty.
Besides, Lucas and Prescott [8] made an extension of “cost-of-adjustment” type investment theory to situations involving demand uncertainty, and determined the time series behavior of investment, output, and price in a competitive industry with a stochastic demand. The effects of demand and cost uncertainty on a firm’s investment, output and pricing decisions are examined in Pindyck [9], the conclusion suggested the desired capital stock and output level will be higher/lower if marginal adjustment costs are rising at an increasing/decreasing rate, under the condition that demand shifts stochastically. At the same time, when the marginal adjustment costs of a risk-averse firm rise at an increasing or constant rate, uncertainty will increase the desired capital stock and output. Furthermore, the effects of stochastic fluctuations in factor costs are the same as demand fluctuations on a firm’s behavior. And what’s more important, these results are robust and consistent whether a firm is competitive or monopolistic. In particular, Abel [10] demonstrated the results of Hartman [1] continue to hold using the stochastic specification of Pindyck [9] and the analysis of Pindyck’s applies to a so called “target” investment rate which is not optimal in general, by developing a special case of the model in Pindyck’s to verify the effects of output price uncertainty on investment decision for a risk-neutral competitive firm with convex adjustment costs. Abel and Eberly [11] extended the theory of investment under uncertainty to incorporate fixed costs of investment, a wedge between purchase price and sale price of capital, and potential irreversibility of investment. They found investment is a nondecreasing function of shadow price of installed capital, and the optimal rate of investment relies on the value of shadow price relative two critical values. By using information on the subjective probability distribution of future demand for firm’s products, Guiso and Parigi [12] investigated the effects of uncertainty on the investment decisions of some Italian firms. The results suggest uncertainty weakens the response of investment to demand, and the negative effects of uncertainty on investment can’t be explained by uncertainty proxying for liquidity constraints. In Bloom, et al. [13], they showed that with (partial) irreversibility higher uncertainty reduces the responsiveness of investment to demand shocks, and uncertainty increases real option values making firms more cautious when investing or disinvesting, which confirmed both numerically for a model with adjustment costs and time-varying uncertainty. And so on (See [14- 27]).
Ultimately, it’s worth mentioning that the shortcoming of Pindyck [9] is that it didn’t derive an expression for the optimal rate of investment in the general model, but analyzed it by stochastic phase diagram approach instead, of which the problem is that it’s unreasonable for a firm to be on the locus with zero expected change in investment, even in the long-run. In view of this, we construct a concrete case can be solved explicitly herein. In addition, our model is an extension to that in Abel [10], since we take output price uncertainty and wage rate uncertainty into account simultaneously, rather than consider output price uncertainty only. Evidently, it’s sensible and logical to consider the price uncertainty and wage uncertainty together because fluctuations in output price tend to be accompanied by variations on wage in general, that is, changes in output price and wage are correlated.
The major contributions, in brief, of this paper relative to existing literatures are, on the one hand, an explicit solution is derived and firm’s investment behavior is analyzed qualitatively and quantitatively rather than just qualitatively, on the other hand, both price and wage uncertainty are taken into account reasonably and simultaneously rather than consider the price uncertainty only. What’s more important, so far to our knowledge, the question we discussed in the paper is still open. As we expected, our conclusion is consistent with that in Abel [10], which shows that the optimal investment behavior is such that the expected proportional rate of change of investment is constant over time. The remaining of this paper is organized as follows. In Section 2, we describe our model at length. Section 3 analyzes the effects of uncertainty on investment. Finally, conclusion is presented in Section 4.
2. Model Description
In this section, we will introduce the model again in detail for the sake of intactness, although it’s a special case of the model in Pindyck [9], and is an extension to the model in Abel [10]. For our purpose, we give hypothesis as below.
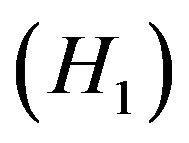 The firm is risk-neutral and competitive with strictly quasi-concave production function as well as with convex costs of adjustment function. But for simplicity and operability, production function is adopted by CobbDouglas type, namely
The firm is risk-neutral and competitive with strictly quasi-concave production function as well as with convex costs of adjustment function. But for simplicity and operability, production function is adopted by CobbDouglas type, namely
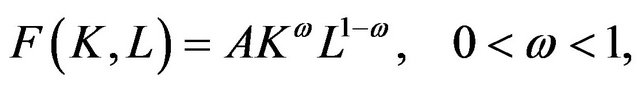
where,  and
and 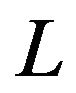 are respectively capital stock and labor, and
are respectively capital stock and labor, and  denotes technology. Without loss of generality, we normalize
denotes technology. Without loss of generality, we normalize  to unit one hereafter, i.e.,
to unit one hereafter, i.e.,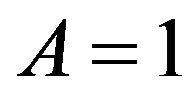 . It’s obviously that
. It’s obviously that 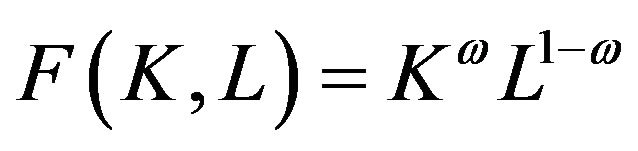 satisfies the conditions of quasi-concave, i.e.,
satisfies the conditions of quasi-concave, i.e., 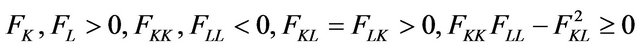 And the convex costs of adjustment function is adopted by the form as
And the convex costs of adjustment function is adopted by the form as  is the purchase price of one unit capital(equipment),
is the purchase price of one unit capital(equipment),  is the constant elasticity, and
is the constant elasticity, and  is the gross investment. As many literatures suggested previously,
is the gross investment. As many literatures suggested previously,  confirms with
confirms with  and
and , for any
, for any . Note that the convexity of the adjustment costs function
. Note that the convexity of the adjustment costs function  implies that it is more costly to increase capital stock quickly than slowly.
implies that it is more costly to increase capital stock quickly than slowly.
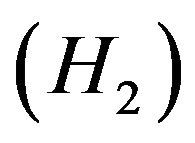 Capital accumulation equation at time t is defined by
Capital accumulation equation at time t is defined by
 (1)
(1)
here, 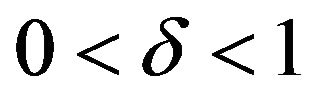 is the depreciation rate.
is the depreciation rate.
 The stochastic behavior of output price p and of wage rate w at time t follows geometric Brownian motion, that is
The stochastic behavior of output price p and of wage rate w at time t follows geometric Brownian motion, that is
 (2)
(2)
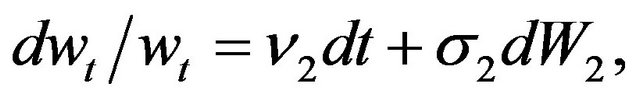 (3)
(3)
where,  and
and  are two Wiener processes with zero mean and unit variance,
are two Wiener processes with zero mean and unit variance, 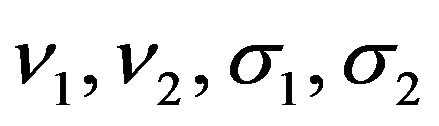 are all non-zero constants. As a matter of fact,
are all non-zero constants. As a matter of fact, 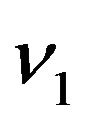 and
and 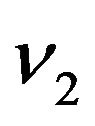 can be regarded as inflation rates. Besides, we set
can be regarded as inflation rates. Besides, we set
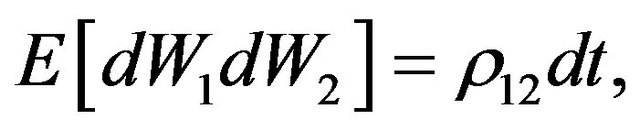 (4)
(4)
here, 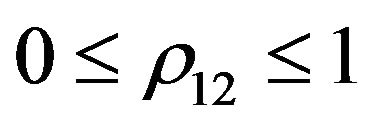 is the instantaneous correlation coefficient for the two Wiener processes
is the instantaneous correlation coefficient for the two Wiener processes  and
and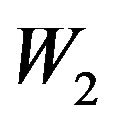 .
.  is the expectation operator.
is the expectation operator.
For a risk-neutral and competitive firm, its objective is to maximize the expected present value  of cash flow by selecting labor
of cash flow by selecting labor 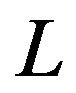 and investment
and investment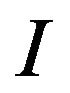 . Mathematically, the optimal problem can be described as
. Mathematically, the optimal problem can be described as
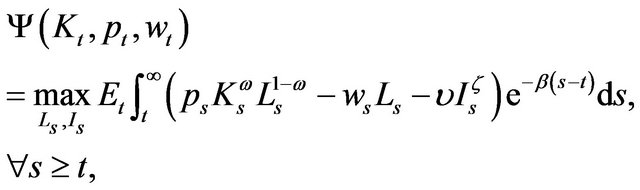
subject to constraints in (1)-(4). Of course, discount rate 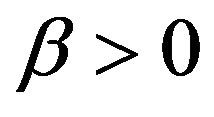 is set to be constant here.
is set to be constant here.
Remark 1. In Pindyck [9], the general model can be rewritten as

subject to (1) and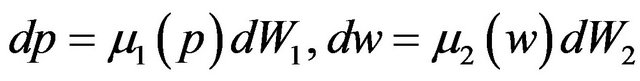 , where,
, where, 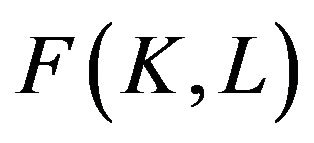 is a general production function with strictly quasi-concavity and
is a general production function with strictly quasi-concavity and  is a general adjustment-cost function with convexity, and
is a general adjustment-cost function with convexity, and  are two functions respectively with respect to
are two functions respectively with respect to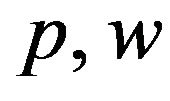 . In the general case, Pindyck did not obtain an explicit solution for the optimal investment, but analyzed the firm’s investment behavior qualitatively by using stochastic phase diagram approach instead. However, our model will collapse to the the special case expressed in Abel [10] by setting
. In the general case, Pindyck did not obtain an explicit solution for the optimal investment, but analyzed the firm’s investment behavior qualitatively by using stochastic phase diagram approach instead. However, our model will collapse to the the special case expressed in Abel [10] by setting 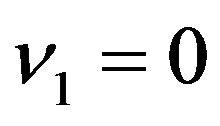 as well as
as well as , i.e., the wage is non-stochastic. In this special case, Abel derived an explicit solution and found the optimal investment rate is such that the expected proportional rate of change of investment is a non-zero constant over time.
, i.e., the wage is non-stochastic. In this special case, Abel derived an explicit solution and found the optimal investment rate is such that the expected proportional rate of change of investment is a non-zero constant over time.
Remark 2. We argue that it is not nonsense to assume that the wage rate follows a stochastic process in reality. Also, it’s feasible in practice. For example, Hartman [14] has considered the wage rate as a random variable and perfect results have been achieved. Differently, however, we here need not presume that the distribution of price  and of wage rate
and of wage rate 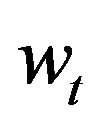 are independent, which was proposed in Hartman’s. Conversely, the dependence of them is allowed in our paper. Fortunately, we will prove later that this case is feasible too. Alternatively, it’s logical to think wage rate changes with the fluctuation of output price. Indeed, by supposing that the firm’s goal is to pursuit the maximum profit, then, at least in the short-run, the employers would cut back their costs by reducing wage rate if the price of output falls due to some reasons. By contrary, if the price of output rises, then the firm would raise the wage rate to make employees work harder to produce more.
are independent, which was proposed in Hartman’s. Conversely, the dependence of them is allowed in our paper. Fortunately, we will prove later that this case is feasible too. Alternatively, it’s logical to think wage rate changes with the fluctuation of output price. Indeed, by supposing that the firm’s goal is to pursuit the maximum profit, then, at least in the short-run, the employers would cut back their costs by reducing wage rate if the price of output falls due to some reasons. By contrary, if the price of output rises, then the firm would raise the wage rate to make employees work harder to produce more.
It’s not difficult to prove that , reduced by
, reduced by  hereafter, obeys formula
hereafter, obeys formula
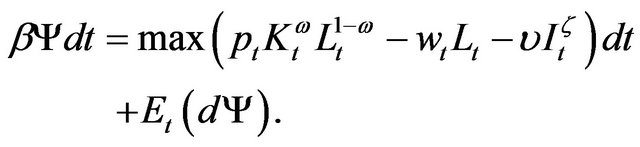 (5)
(5)
Straightforwardly, the left-hand side of (5) can be regarded as the total mean return desired by the firm over the time interval dt, if the firm requires a mean return rate . On the contrary, the right-hand side of (5) is the whole return expected by the firm, which is the sum of cash flow and expected capital gain or loss
. On the contrary, the right-hand side of (5) is the whole return expected by the firm, which is the sum of cash flow and expected capital gain or loss . In other words, optimality means the desired mean return is equal to the expected return.
. In other words, optimality means the desired mean return is equal to the expected return.
Now, we will derive the expression of the optimal investment rate  step by step. To begin, we present the following Proposition 1.
step by step. To begin, we present the following Proposition 1.
Proposition 1. The firm’s optimal rate of investment 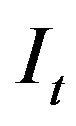 can be expressed as
can be expressed as
 (6)
(6)
where
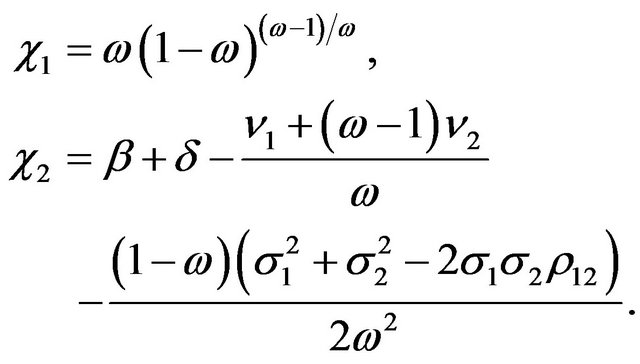 (7)
(7)
It is clear to see from (6) that the optimal rate of investment 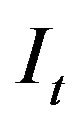 does not depend on
does not depend on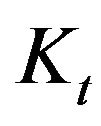 , but increases with
, but increases with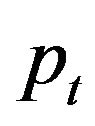 , decreases with
, decreases with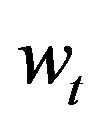 , since
, since .
.
Proof. First of all, we claim that Itô’s Lemma is applicable under the hypothesis . Thus, applying Itô’s Lemma to calculate the capital gain or loss
. Thus, applying Itô’s Lemma to calculate the capital gain or loss , we have
, we have
 (8)
(8)
Inserting (1)-(4) into (8), meanwhile recalling that 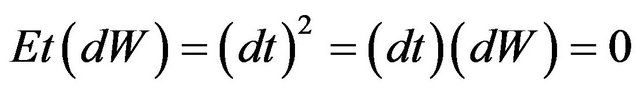 and
and 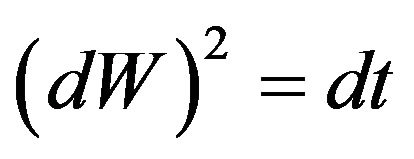 for any standard Wiener process
for any standard Wiener process , we get
, we get

(9)
Substituting (9) into (5), we obtain
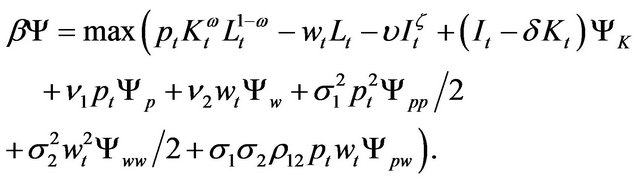 (10)
(10)
By simple computation, it yields
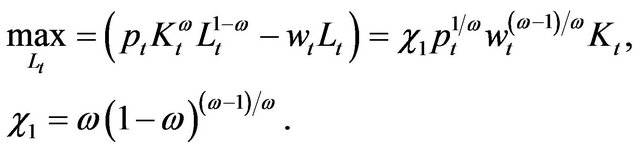 (11)
(11)
Notice that,  is the marginal revenue product of capital.
is the marginal revenue product of capital.
Next, differentiating the right-hand side of (10) with respect to , there holds
, there holds
 (12)
(12)
An economic interpretation can be seen straightly from (12), i.e., the optimal investment rate is such that the marginal cost of investment equals the marginal valuation of capital. Plugging (11) and (12) into (10), we have
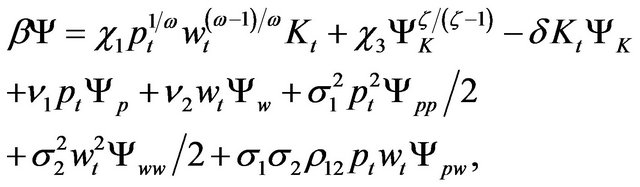 (13)
(13)
where
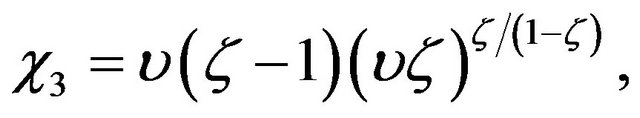 and
and  as in (7). (14)
as in (7). (14)
It’s well known that we can rewrite (12) and (13) as a nonlinear second-order partial differential equation, despite such equations are unsolvable in general case. But fortunately, an explicit solution can be derived herein due to our assumptions. Note that we can strictly prove that there exists a  to satisfy the nonlinear second-order partial differential equation given by (12) and (13) together. The argument process, however, is not the emphasis in the paper. Hence, we omit the details here. Now that the solution
to satisfy the nonlinear second-order partial differential equation given by (12) and (13) together. The argument process, however, is not the emphasis in the paper. Hence, we omit the details here. Now that the solution  exists and taking the form of (12) and (13) into account, we guess the form of
exists and taking the form of (12) and (13) into account, we guess the form of  as
as
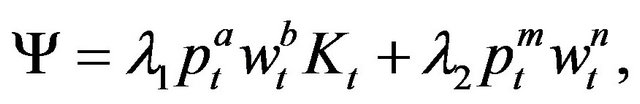 (15)
(15)
where,  and
and 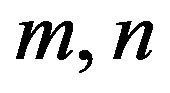 are all undetermined coefficients.
are all undetermined coefficients.
In terms of (15), it yields
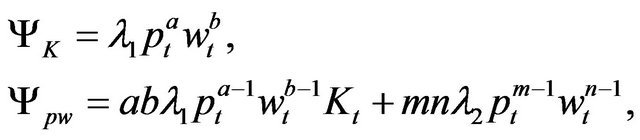 (16)
(16)
 (17)
(17)
 (18)
(18)
Lastly, applying method of undetermined coefficients, and combining (13) as well as (16)-(18), it’s not difficult to get
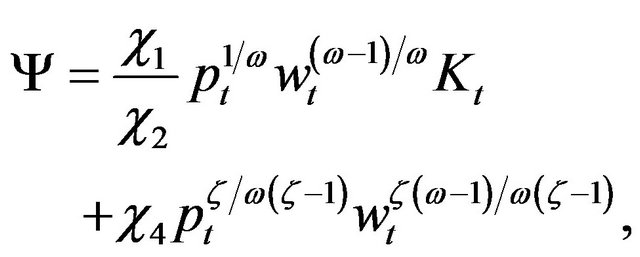 (19)
(19)
where

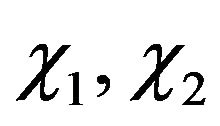 as in (7),and
as in (7),and 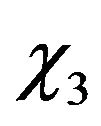 as in (14).
as in (14).
Following (12) and (19), we see immediately that
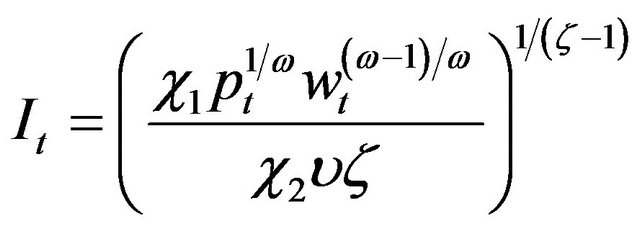 ,
,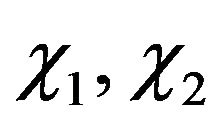 as in (7) (20)
as in (7) (20)
Obviously, some results can be obtained directly from (19) and (20). The firm’s value , for instance, is a linear function of the capital stock . The optimal rate of investment It does not depend on
. The optimal rate of investment It does not depend on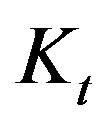 , but increases with
, but increases with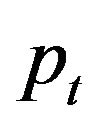 , decreases with
, decreases with , since
, since .
.
3. The Effects of Uncertainty on Investment
We will analyze the qualitative effects of price and wage uncertainty on investment in this section, for given the current level of output price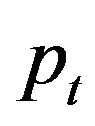 , and of wage rate
, and of wage rate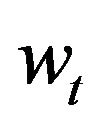 .
.
Proposition 2. If
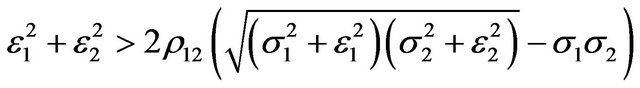 , then the increases in uncertainty of output price and of wage rate together will have positive effects on the optimal investment rate
, then the increases in uncertainty of output price and of wage rate together will have positive effects on the optimal investment rate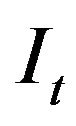 . Conversely, if
. Conversely, if
 , then the increases in the two uncertainty will have negative effects on the optimal rate of investment. Particularly, there will be no effects of shifts in uncertainty on the investment so long as
, then the increases in the two uncertainty will have negative effects on the optimal rate of investment. Particularly, there will be no effects of shifts in uncertainty on the investment so long as
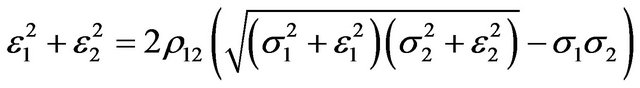 . Here,
. Here,
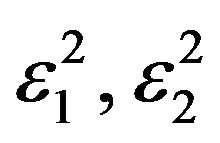 are respectively the fluctuations in uncertainty
are respectively the fluctuations in uncertainty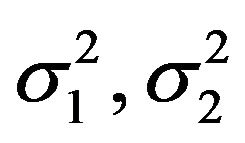 , which associate with
, which associate with , correspondingly.
, correspondingly.
Proof. As a matter of fact, in order to analyze the effects of uncertainty on investment behavior, we just need to determine the effects of uncertainty on
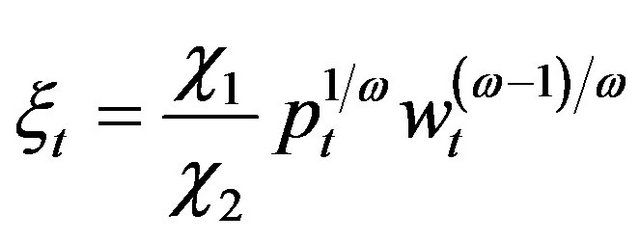 , because
, because  relies on
relies on 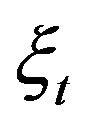 only. To this end, taking the expression of
only. To this end, taking the expression of  into account, we only require focusing on the change of
into account, we only require focusing on the change of
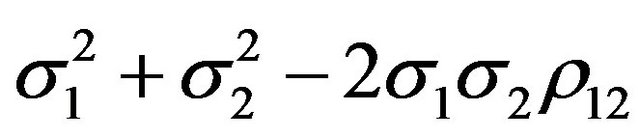 . By simple analysis, we see the changes in uncertainty of output price and of wage rate together will result in a rising in the optimal investment rate
. By simple analysis, we see the changes in uncertainty of output price and of wage rate together will result in a rising in the optimal investment rate 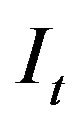 if
if
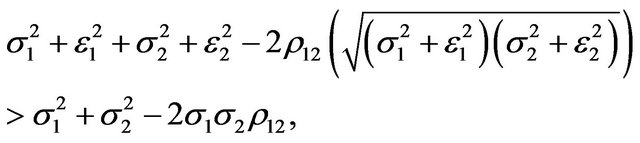
i.e.,
 . Similarlythe changes in the two uncertainty will lead to a falling in the optimal rate of investment if Specially, as long
. Similarlythe changes in the two uncertainty will lead to a falling in the optimal rate of investment if Specially, as long
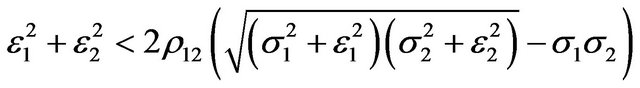 . Specially, as long as
. Specially, as long as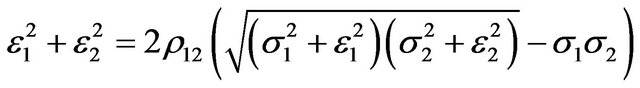 then there will be no effects of changes in uncertainty on the investment behavior.
then there will be no effects of changes in uncertainty on the investment behavior.
Remark 3. Certainly, the conclusion above will hold as long as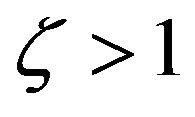 , but no matter the marginal adjustment cost function is convex
, but no matter the marginal adjustment cost function is convex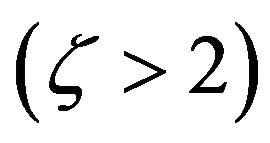 , concave
, concave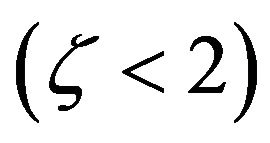 , or linear
, or linear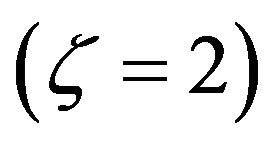 .
.
Subsequently, we will explain the effects of uncertainty on investment. To achieve this goal, it’s a good choice to simulate the idea in Abel [10]. As mentioned in (11),  is the marginal revenue product of capital(
is the marginal revenue product of capital( hereafter), thus
hereafter), thus
 (21)
(21)
Here, we used (2)-(4) to get the second equality. Naturally, the expected present value of the marginal revenue product of capital is
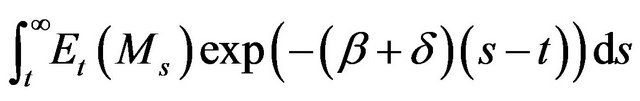 . Inserting (21) into this integral directly, we see that the integral is actually equal to
. Inserting (21) into this integral directly, we see that the integral is actually equal to , this indicates
, this indicates 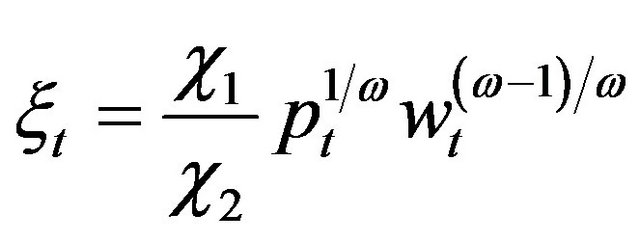 is the expected present value of the marginal revenue product of capital
is the expected present value of the marginal revenue product of capital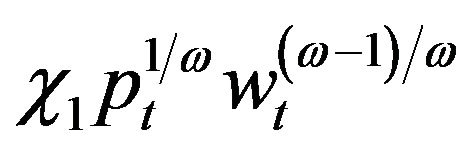 . Hence, we can say that the uncertainty affects investment by means of influencing the expected value of future marginal revenue product of capital.
. Hence, we can say that the uncertainty affects investment by means of influencing the expected value of future marginal revenue product of capital.
Finally, the dynamic behavior of investment will be explored at the end of this section.
Proposition 3. The optimal investment behavior is such that the expected proportional growth rate of investment(non-zero in general) is constant over time.
Proof. Applying Itô’s Lemma to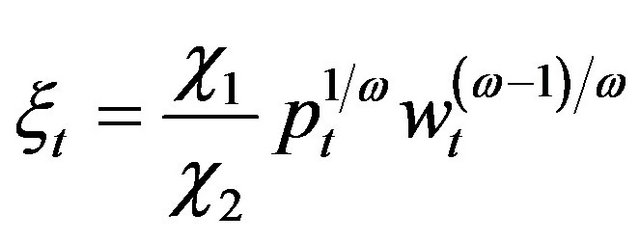 , it yields
, it yields
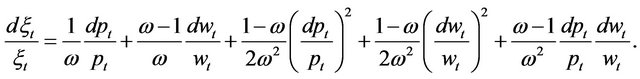 (22)
(22)
Substituting (2)-(4) into (22), it’s easily to obtain
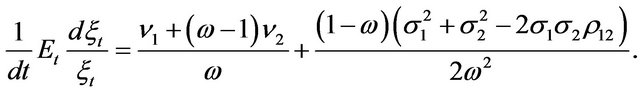 (23)
(23)
Applying Itô’s Lemma to (20), there holds
 (24)
(24)
Substituting (2)-(4) into (24), it’s easily to get
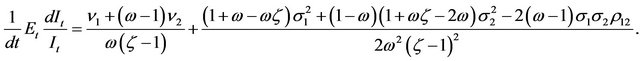 (25)
(25)
So far, from (23) and (25), we observe that both the expected growth rate of marginal revenue product of capital and the expected proportional growth rate of investment are constants over time, neither they depends on output price or wage. Simultaneously, it’s clearly to see the two expected growth rates are zero in the case without uncertainty.
4. Concluding Remarks
The objective of this paper is to analyze the effects of uncertainty on a competitively risk-neutral firm’s investment decision. By referring the methods presented in Abel [10] and Pindyck [9], we find that given the current output price and wage rate, then the fluctuations in uncertainty of output price and of wage rate together will result in positive impacts on the optimal investment rate
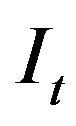 if
if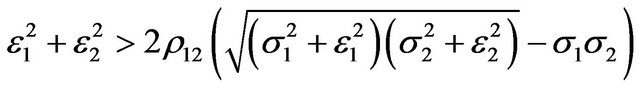 whereas the fluctuations in uncertainty will lead to negative impacts on the optimal rate of investment if
whereas the fluctuations in uncertainty will lead to negative impacts on the optimal rate of investment if
 , and there won’t have any effects of fluctuations in uncertainty on the investment so long as
, and there won’t have any effects of fluctuations in uncertainty on the investment so long as
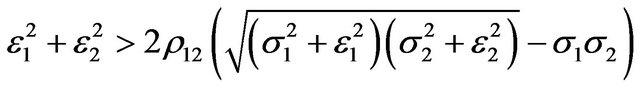 , where
, where
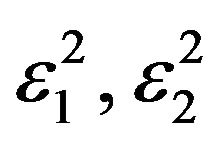 are changes in uncertainty of output price
are changes in uncertainty of output price 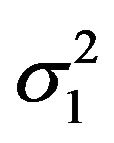 and of wage rate
and of wage rate , respectively.
, respectively.
The expected growth rate of marginal valuation of capital and of investment are both invariant over time. And moreover, by observing (23) and (25) carefully, we see that the expected growth rate of marginal valuation of capital multiplies the elasticity of investment with respect to marginal valuation of capital,  , is equal to the expected growth rate of investment when the marginal adjustment costs function is linear, i.e.,
, is equal to the expected growth rate of investment when the marginal adjustment costs function is linear, i.e., . As to the convex marginal adjustment costs function and the concave type, the relationship between the two expected growth rates are uneasy to determine, which is unlike the case demonstrated in Abel [10].
. As to the convex marginal adjustment costs function and the concave type, the relationship between the two expected growth rates are uneasy to determine, which is unlike the case demonstrated in Abel [10].
We remark that it’s unnecessary to confine the production function to Cobb-Douglas type, and strictly speaking, the argument presented in the paper can be applied to any production function obeys homogeneous of degree one. Besides, we derived our results without considering whether the marginal revenue product of capital is convex, concave or linear, which is different from Pindyck [9]. Self-evidently, our model will collapse to the one in Abel
[10], if set 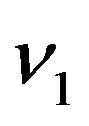 to be zero and assume the wage rate
to be zero and assume the wage rate 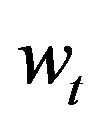 without uncertainty.
without uncertainty.
At last, we mention the major contribution of this paper. For one thing, an explicit solution is derived and firm’s investment behavior is analyzed qualitatively and quantitatively rather than just qualitatively. For another thing, both price and wage uncertainty are examined simultaneously since fluctuations in output price tend to be accompanied by fluctuations in wage, rather than consider the price uncertainty only. What’s more important, so far to our knowledge, the question we discussed in the paper is still open.
5. Acknowledgements
The author would like to express his sincere thanks to the anonymous referees for their helpful comments and suggestions, which greatly improved the presentation of this paper. The author also would like to thank the editors for their help.
REFERENCES
- R. Hartman, “The Effects of Price and Cost Uncertainty on Investment,” Journal of Economic Theory, Vol. 5, No. 2, 1972, pp. 258-266. doi:10.1016/0022-0531(72)90105-6
- V. Ghosal and P. Lougani, “The Differential Impact of Uncertainty on Investment in Small and Large Businesses,” Review of Economics and Statistics, Vol. 82, No. 2, 2000, pp. 338-349. doi:10.1162/003465300558722
- M. Peeters, “Does Demand and Price Uncertainty Affect Belgian and Spanish Corporate Investment?” Recherches Economiques de Louvain, Vol. 67, No. 3, 2001, pp. 235- 255.
- P. Temple, G. Urga and C. Driver, “The Influence of Uncertainty on Investment in the UK: A Macro or Micro Phenomenon?” Scottish Journal of Political Economy, Vol. 48, No. 4, 2001, pp. 361-382. doi:10.1111/1467-9485.00204
- N. Bloom, “The Impact of Uncertainty Shocks,” Econometrica, Vol. 77, No. 3, 2009, pp. 623-685. doi:10.3982/ECTA6248
- J. Lee and K. Shin, “The Role of Variable Input in the Relationship between Investment and Uncertainty,” American Economic Review, Vol. 90, No. 3, 2001, pp. 667- 680. doi:10.1257/aer.90.3.667
- N. C. Nielsen, “The Price and Output Decisions of the Firm under Uncertainty,” Swedish Journal of Economics, Vol. 77, No. 4, 1975, pp. 459-469. doi:10.2307/3439339
- R. E. Lucas and E. C. Prescott, “Investment under Uncertainty,” Econometrica, Vol. 39, No. 5, 1971, pp. 659-681. doi:10.2307/1909571
- R. S. Pindyck, “Adjustment Costs, Uncertainty, and the Behavior of the Firm,” American Economic Review, Vol. 72, No. 3, 1982, pp. 415-427.
- A. B. Abel, “Optimal Investment under Uncertainty,” American Economic Review, Vol. 73, No. 1, 1983, pp. 228- 233.
- A. B. Abel and J. C. Eberly, “A Unified Model of Investment under Uncertainty,” American Economic Review, Vol. 84, No. 5, 1994, pp. 1369-1384.
- L. Guiso and G. Parigi, “Investment and Demand Uncertainty,” Quarterly Journal of Economics, Vol. 114, No. 1, 1999, pp. 185-227. doi:10.1162/003355399555981
- N. Bloom, S. Bond and J. Van-Reenen, “Uncertainty and Investment Dynamics,” Review of Economics Studies, Vol. 74, No. 2, 2007, pp. 391-415. doi:10.1111/j.1467-937X.2007.00426.x
- R. Hartman, “Adjustment Costs, Price and Wage Uncertainty, and Investment,” Review of Economic Studies, Vol. 40, No. 2, 1973, pp. 259-267. doi:10.2307/2296652
- R. Bachmann, S. Elstner and E. Sims, “Uncertainty and Economic Activity: Evidence from Business Survey Data,” NBER Working Paper, No. 16143, 2010. http://www.nber.org/papers/w16143
- N. Bloom, “Uncertainty and the Dynamics of R&D,” American Economic Review, Vol. 97, No. 2, 2007, pp. 250- 255. doi:10.1257/aer.97.2.250
- A. Carruth, A. Dickerson and A. Henley, “What Do We Know about Investment under Uncertainty?” Journal of Economic Surveys, Vol. 14, No. 2, 2000, pp. 119-153. doi:10.1111/1467-6419.00107
- T. Dunne and X. Y. Mu, “Investment Spikes and Uncertainty in the Petroleum Refining Industry,” Journal of Industrial Economics, Vol. 58, No. 1, 2010, pp. 190-213. doi:10.1111/j.1467-6451.2010.00407.x
- J. P. Gould, “Adjustment Costs in the Theory of Investment of the Firm,” Review of Economic Studies, Vol. 35, No. 1, 1968, pp. 47-55. doi:10.2307/2974406
- R. Hartman, “Factor Demand with Output Price Uncertainty,” American Economic Review, Vol. 66, No. 4, 1976, pp. 675-681.
- M. Kurz and M. Motolese, “Endogenous Uncertainty and Market Volatility,” Journal of Economic Theory, Vol. 17, No. 4, 2001, pp. 497-544.
- J. A. List and M. S. Haigh, “Investment under Uncertainty: Testing the Options Model with Professional Traders,” The Review of Economics and Statistics, Vol. 92, No. 4, 2010, pp. 974-984. doi:10.1162/REST_a_00041
- R. E. Lucas, “Adjustment Costs and the Theory of Supply,” Journal of Political Economy, Vol. 75, No. 4, 1967, pp. 321-334. doi:10.1086/259289
- R. S. Pindyck, “Irreversibility, Uncertainty, and Investment,” Journal of Economic Literature, Vol. 29, No. 3, 1991, pp. 1110-1148.
- R. S. Pindyck, “Investments of Uncertain Cost,” Journal of Financial Economics, Vol. 34, No. 1, 1993, pp. 53-76. doi:10.1016/0304-405X(93)90040-I
- R. S. Pindyck, “A Note on Competitive Investment under Uncertainty,” American Economic Review, Vol. 83, No. 1, 1993, pp. 273-277.
- E. Zabel, “Multiperiod Monopoly under Uncertainty,” Journal of Economic Theory, Vol. 5, No. 3, 1972, pp. 524- 536. doi:10.1016/0022-0531(72)90053-1
NOTES
*This work is supported by Research Innovation Foundation of Shanghai University of Finance and Economics under Grant No. CXJJ-2011- 336.

