Received 21 December 2015; accepted 22 February 20146; published 25 February 2016

ABSTRACT

When the event of interest never occurs for a proportion of subjects during the study period, survival models with a cure fraction are more appropriate in analyzing this type of data. Considering the non-linear relationship between response variable and covariates, we propose a class of generalized transformation models motivated by Zeng et al. [1] transformed proportional time cure model, in which fractional polynomials are used instead of the simple linear combination of the covariates. Statistical properties of the proposed models are investigated, including identifiability of the parameters, asymptotic consistency, and asymptotic normality of the estimated regression coefficients. A simulation study is carried out to examine the performance of the power selection procedure. The generalized transformation cure rate models are applied to the First National Health and Nutrition Examination Survey Epidemiologic Follow-up Study (NHANES1) for the purpose of examining the relationship between survival time of patients and several risk factors.

Keywords:

Link Functions, Mixture Cure Rate Models, Noninformative Improper Priors, Proportional Hazards Models, Proportional Odds Models

1. Introduction

Survival data analysis is an important topic in statistics that focuses on analyzing the expected duration of time until one or more events occur, such as death or cancer in a targeted population. In a standard survival model, it is often assumed that all uncensored subjects will eventually experience the event of interest, which is described by a monotone decreasing survival function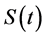. The function 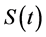goes to 0 when time t tends to infinity. Survival time T is a continuous nonnegative random variable representing the time of an event. The probability of a subject’s surviving till time t is given by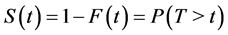, where 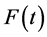is the distribution function with probability density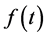. The hazard function 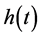is defined as the instantaneous failure rate at time t conditional on survival until time t or later. The cumulative hazard 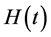is defined as

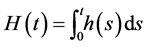, which represents the total amount of risk up to time t. Usually covariates, such as gender, age,

weight, blood pressure, heart rate, stage of surgery, etc., are modeled through survival models. In this paper, we assume that the covariates are independent of time.

Cox [2] brought the idea of separating time t and individual covariate vector in the hazard function, which led to the popular proportional hazard model with

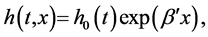
where 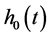was the baseline hazard function and 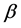was a vector of regression coefficients.

However, in some situations, the event of interest never occurs for a significant proportion of subjects. For example, in a cancer clinical trial, the endpoint of interest is often recurrence. For some patients, the disease will never relapse after being treated. These patients are considered cured. Sometimes, subjects with long-term censored times can be viewed as “cured” as well. Survival models with a cure fraction are very popular in analyzing this type of cancer clinical trials.

Motivated by the transformed proportional time cure model introduced by Zeng et al. [1] , we propose a class of generalized transformation models to characterize the non-linear relationship between survival function 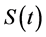and relate covariates. Statistical properties of the proposed models are investigated, which include iden- tifiability, asymptotic consistency, and asymptotic normality of the estimated regression coefficients. Powers of fractional polynomials within the proposed models are selected based on the likelihood function. A simulation study is carried out to examine the performance of the power selection procedure. The generalized trans- formation cure rate models are applied to coronary heart disease and cancer related medical data from both observational cohort studies and clinical trials.

The first cure rate model is the mixture cure rate model proposed by Berkson and Gage [3] , which combines the cured and non-cured populations by using a summation function. In their model, the survival function for the entire population, denoted by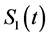, is given by

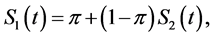
where is the proportion in the cured group and is the survival function for the non-cured group in the entire population. Notice that is not a proper survival function since. This mixture model has been fully discussed by many authors, including Farewell [4] , Gary and Tsiatis [5] , Sposto et al. [6] , Laska and Meisner [7] , Sy and Taylor [8] , and Lu and Ying [9] .

Even though the mixture model introduced by Berkson and Gage [3] , is attractive and widely used, it has several drawbacks. One of them is that the mixture model cannot have a proportional hazards structure if the covariates are modeled through. Ibrahim et al. [10] also pointed out that a mixture model sometimes yields improper posterior distribution when noninformative improper priors are used from the Bayesian point of view.

Yakovlev and Tsodikov [11] , Tsodikov [12] , Chen et al. [13] , and Zeng et al. [1] proposed and studied promotion time cure model. Instead of dividing the population into two sub-populations so that some subjects are long-term survivors with probability and others have a proper survival function with probability, the promotion time cure model takes long-term survivors into account by putting a restriction on the cumulative hazard function. In general, the population survival function is represented as. However, in a cure rate model the function is improper in the sense of, which also implies that is bounded by some positive number, say. When t goes to, we have. Tsodikov [12] suggested to consider, where is the distribution function of a nonnegative random variable with and covariates can be modeled through,

(1.1)

The promotion time cure model avoids the drawbacks of a mixture model and has a proportional hazards structure through the cure rate parameter. Chen et al. [13] also proposed classes of noninformative and infor- mative priors for promotion time cure rate model that lead to proper posterior distributions.

The promotion time cure rate model and the mixture cure rate model are linked by a mathematical relation- ship, and can be rewritten in a uniform format. Zeng et al. [1] proposed a general promotion time cure model with transformation. Their model includes proportional hazards model and proportional odds model as special cases. To take into account the unknown and unobservable risk factor for each individual, they used a subject- specific frailty variable, in model (1.1). The survival function for the time to relapse is given by

(1.2)

Different parametric distributions may be applied to the frailty. The most commonly used one is the gamma distribution, where. The mean of the gamma distribution needs to be one due to the model identification issue. Taking expectations with respect to on both sides in (1.2), the survival function becomes

(1.3)

As Zeng et al. [1] pointed out, (1.3) provides a very wide class of transformation cure models with the form:

(1.4)

where

(1.5)

When takes other distributions, we may get different transformations. A Box-Cox type transformation is also considered in Zeng et al. [1] with

(1.6)

The proportional hazards model in (1.1) is a special case of the transformation families (1.5) and (1.6) corre- sponding to and, respectively. Another popular survival model, the proportional odds model, is also a special case of (1.5) and (1.6) when and, respectively.

From model (1.4) the cure fraction is, and the model can be written as a standard cure rate model,

where is the survival function for the non-cured population,

The covariates can be modeled through a known and strictly positive increasing link function , where is the regression vector including an intercept term.

In this paper, we extend the transformed proportional time cure model proposed by Zeng et al. [14] to a more general class of transformation models, in which fractional polynomials are used instead of the simple linear combination of the covariates. The statistical properties of our proposed models will be investigated. Estimation and model selection procedures will be discussed. The rest of the paper is organized as follows. In Section 2, we introduce the generalized transformation models and study the identifiability and asymptotic properties of the proposed models. In Section 3, simulation studies are conducted for the purpose of assessing the performance of the power selection procedure. In Section 4, the proposed models will be applied to some real datasets and compared with other models. Conclusions and some discussions are given in Section 5. Proofs of the theorems in Section 2 are provided in Appendix.

2. Proposed Models and Their Properties

In survival data analysis, the relationship between hazard rates and covariates is quite often nonlinear. Motivated by Zeng et al. [1] , we propose a generalized transformation cure model by using a general additive function of instead of the strictly positive increasing link function.

The additive models were introduced by Stone [15] , which is defined by, where

is a constant term and are arbitrary univariate functions, one for each covariate. Additive models retain the important additive feature of the linear regression models and are much more flexible to use in practice. Royston and Altman [14] suggested using fractional polynomials for each, which is a family of functions of positive covariates. For simplicity, let us consider a single covariate X first. A fractional poly- nomial with degree m is described as, where

(2.1)

and, is a real-valued vector of powers. If for any i, is defined to be by the Box-Tidwell transformation. For example,

is a fractional polynomial with degree and. Royston and Altman [14] pointed out that special attention should be paid to low-order fractional polynomials with degrees one and two, since models with degree higher than two are rarely used in practice. They also suggested that the powers could be chosen from the set , since the set is rich enough to cover all conventional polynomials of interest. It is well known that the best estimates of the powers in a transformation model may be determined based on the maximum likelihood method.

For some data sets, especially data from medical studies, fractional polynomials may give a better fit com- pared to the conventional polynomial. In our proposed models we use a fractional polynomial instead of in the link function. Even though in practice fractional polynomials with degree higher than two are not used very often, we consider the following general form for the function in (1.2),

(2.2)

where, are categorical covariates such as ordinal covariates or

dummy variables, and are positive continuous covariates. An intercept term is also con-

sidered in (2.2) when we assume that. Moreover, we assume that for, i.e., a degree of three fractional polynomial is used for each continuous covariate. For example, for a given if, the powers for predictor are based on the definition in (2.1).

In a typical survival analysis setting, survival times are often right censored, which means for some subjects we do not know when exactly the failures occurred, but we do know that the survival time is at least beyond some certain time point C. Suppose that there are n right censored subjects. For the ith individual the survival time and the fixed censoring time are denoted by and, respectively. The’s are assumed to be independent and identically distributed with a distribution function F.

The observed time point for the ith subject is. The exact survival time will be observed only if the failure occurred before being censored, otherwise is equal to the censoring time. A triple of random variables is used to describe each subject, where is the covariate vector and is defined as the following,

In a proportional hazard model, the regression coefficient is estimated by maximizing the partial likelihood function,

In the model (1.4) with link function (2.2), if the parameter is given the likelihood function is expressed by

(2.3)

Given observations (,) and following the discussion in Zeng et al. [1] , the maximum likelihood estimates of, denoted by, are derived from the modified semi-parametric version of (2.3),

(2.4)

where is the jump size of F at and.

The three pieces of products in (2.4) are for failures, censored cases, and subjects who never experience failure or censoring, respectively. The estimate of, denoted by, can be obtained by using the nonparametric maximum likelihood estimation approach and Newton-Raphson algorithm iteratively.

2.1. Model Identifiability

For the statistical properties of our proposed models, we first discuss the identifiability of generalized trans- formation models. Suppose that we use models (1.4) and (1.5) with the link function defined in (2.2). The observed-data likelihood function of parameters is given by

(2.5)

The following two lemmas give sufficient conditions of identifiability to a more general class of transfor- mations that include the transformation (1.5) as a special case. Proofs of the lemmas are given in Appendix.

Lemma 1. If satisfies the following conditions:

(G1) is strictly monotonic and twice continuously differentiable with and.

(G2) If, then.

Then implies that, and, i.e., is identi- fiable.

It can be shown that the transformation family given in (1.5) satisfies both conditions (G1) and (G2). Speci- fically, we have and.

Other transformation families can also be considered as long as the conditions (G1) and (G2) hold. For example, the Box-Cox type transformation discussed in Zeng et al. [1] , also satisfies conditions (G1) and (G2) with and.

Next, we consider the following function

(2.6)

where is strictly monotonic, , and are not equal to zeros simultaneously, and is used for a finite summation since the number of parameters in our proposed models is finite.

Function in (2.6) is a more general function than that defined in (2.2). The following lemma show that the parameters’s and’s in the function are all identifiable.

Lemma 2. For the function defined in (2.6), if, then, i.e., para- meters in are identifiable.

Based on the results in Lemma 1 and Lemma 2, we have the following theorem on the identifiability of the generalized transformation models.

Theorem 1. For the generalized transformation models defined in (1.4) and (1.5) with the link function specified in (2.2), if, for any and any X, then, and. In other words, the generalized transformation models are identifiable.

2.2. Estimation

Zeng et al. [1] discussed semiparametric transformation models for survival data with a cure fraction and estab- lished theorems describing the asymptotic properties of the maximum likelihood estimation of, where is the vector of coefficients and is the promotion time cumulative distribution function in the model. In our proposed generalized transformation cure models, fractional polynomials are used instead of the simple linear combination of the covariates. Similar to Theorem 1 and Theorem 2 in Zeng et al. [1] , we can prove the asymptotic properties of the maximum likelihood estimation of in the proposed models.

To obtain consistency and asymptotic normality, we make the following assumptions:

(C1) The covariate X belongs to a compact set.

(C2) The vector of regression coefficients belongs to a compact set. The true value of, denoted by, belongs to the interior of set.

(C3) is a distribution function with jumps when. The true F, denoted by, is differentiable with for all.

(C4) Conditional on, the right censoring time C is independent of T, and.

(C5) The positive link function is a strictly increasing and twice continuously differentiable for.

(C6) The transformation satisfies, , and exists and is conti- nuous.

Under conditions (C1)-(C6), we can prove the following theorems.

Theorem 2. The maximum likelihood estimates based on (2.4) are strongly consistent, that is

Theorem 3. converges weakly to a Gaussian process.

Sketched proofs of Theorem 2 and Theorem 3 are provided in Appendix.

3. Simulations

In this section, we conduct simulations to study the empirical properties of the generalized transformation models and to examine the performance of the proposed power selection procedure on generalized transfor- mation models. The model used in this simulation was given in Zeng et al. [1] and has a survival function of the form:

(3.1)

where is given in (1.5).

For the purpose of illustration, only one continuous variable and one categorical variable are con- sidered in the simulation. Specifically, we take equal to zero in (1.5) and consider the following link func- tion,

(3.2)

where is a nonzero power varying from −2 to 2. Covariate is a uniformly distributed random variable in [0.5, 2] and covariate is a Bernoulli random variable with probability 0.5. The coefficients, , and are assumed to be constants. When, we use

(3.3)

is a proper distribution function. We choose in this simulation.

Survival times of subjects with covariates and are generated. Each subject has a chance of being cured. We assume the survival life times T equal to for the cured population. For example, the ith individual in the simulated data set has a cure rate equal to, which means the survival life time equals with probability. Moreover, with probability, the survival time is finite and follows the distribution, where is the generalized transformation model given in (3.1) and (1.5). Therefore, the life time T will be generated from

(3.4)

with probability, where u has a uniform distribution in [0, 1].

Assume each subject being right-censored with a probability, for example q = 80%. So, the censoring time for the ith individual in the data set will equal with a 20% of chance. For the rest of the population, the censoring time is generated from an exponential distribution with mean one.

The complete data set is given by

(3.5)

The whole population is categorized into three groups: right-censoring events when, failure events when, and cured population when.

The coefficients, , and in model (3.2) are arbitrary constants. We set, , and. As changes from −2 to 2, the cured proportions vary from 5% to 10%. For each simulated date set, we choose a from the set A = (−2, −1.5, −1, 0.5, 0, 0.5, 1, 1.5, 2) based on the likelihood function given in (2.3).

Table 1 shows the power selection results under the proposed generalized transformation model based on 200 simulated data sets with q = 80% and sample sizes 2000 and 5000, respectively. The columns labeled “mean” are the average of the selected powers and the columns labeled “freq.” are the number of times of selecting the

true power in the 200 simulations. When the sample size is 5000, the power selection procedure work well. The accurate rates of choosing the true power are higher than 50% and the means of the selected powers are very close to the true value for most of the cases. For example, when the true power is selected for 104 times and the estimated mean is −1.005. When the sample size decreases to 2000, the power selection results are less accurate. For both sample sizes, the accurate rates are higher when or than other cases since we select the powers only in the range of −2 to 2. This also explains why the absolute values of means of the selected powers when or tends to be smaller. If powers beyond −2 and 2 are allowed to be selected, or should have less chance to be underestimated.

Table 2 presents more results on power selection with and q = 80% based on 200 simulations. In the table each column represents one scenario. For example, when, the true power −1 is selected 104 times; Powers −1.5 and −0.5 are selected 44 and 42 times, respectively; and powers −1 and 0 are selected 5 times each. These results indicates that the selected powers are all centering around the true power.

In this simulation we assume that the probability of each subject being censored is q = 80%. In fact, the probability q basically does not affect the performance of the power selection procedure. When q takes different values while other factors in the simulation remain the same, the power selection results show a very similar pattern as that when q = 80%.

4. Applications

In this section, we will illustrate the applications of the proposed generalized transformation models and compare the proposed models with the Cox proportional hazards model and the Zeng et al. [1] transformation cure model by analyzing data from the First National Health and Nutrition Examination Survey Epidemiologic Follow-up Study (NHANES1). The NHANES1 data set is from the Diverse Populations Collaboration (DPC), which is a pooled database contributed by a group of investigators to examine issues of heterogeneity of results in epidemiological studies. The database includes 21 observational cohorts studies, 3 clinical trials, and 3 national samples. In the dataset NHANES1, information for 14,407 individuals was collected in four cohorts from 1971 to 1992. In this analysis, we use data from two of the four cohorts, the black female cohort and the black male cohort. After dropping all missing observations, a total of 2027 patients remains in these two cohorts, including 1265 black females and 762 black males. Survival times of the 2027 patients are used as the response variable. The endpoint is the overall survival time collected in 1992. In the two cohorts 848 patients, about 40% of the total number of patients, died at the end of followup with a maximum survival life time of 7691 days. There were 1179 patients whose survival times were right censored, among them 115 patients had survival time longer than 7691 days. We consider these 115 patients as cured subjects.

Covariates selected by fitting the Cox model and using the stepwise backward elimination algorithm will be

included to compare different survival models. These covariates are Age, Systolic blood pressure (Sbp), Sex, Body Mass Index (BMI), Diabetes (Diab), and Coronary heart disease (Chd). Summary statistics of continuous covariates are list in Table 3. Diab and Chd are categorical and only take the values of 0 and 1 for absence and presence of the corresponding disease. Among the 2027 patients in the two cohorts, there were 121 of them having diabetes and 82 of them having coronary heart disease.

The results of the Cox proportional hazard model are summarized in Table 4. All covariates are highly signi- ficant at the level. The results show that males have a higher hazard rate than females and older patients have a higher hazard rate than younger patients. People with diabetes or coronary heart disease face a higher hazard rate than people who did not have such disease. The hazard of death increases by 0.4% when the Sbp level of a patient increases 1 mmHg. The results also show that the higher the value of BMI of a patient the lower the hazard rate she/he will face. Particularly, the hazard will decrease about 1.2% when the value of BMI increases by 1 kg/m², which is not quite reasonable. The values of BMI often ranges from 15 kg/m² to 60 kg/m². BMI in the range of 21 kg/m² to 25 kg/m² is considered as normal weight; 30 kg/m² or greater is considered as obesity. It is well known that being obesity will increase the hazard to develop many coronary heart diseases or even death. The relationship between survival time and BMI may not be linear. Therefore, a transformation on the covariate BMI may be needed for the NHANES1 data.

A transformation of is chosen with maximum likelihood from Zeng et al. [1] model with trans- formation family (1.5). The observed log-likelihood is shown in Figure 1 with different values of γ. The corre- sponding estimates of regression coefficients are summarized in Table 5. The results are comparable with that in the Cox proportional hazards model.

There are three continuous covariates in our analysis, Age, BMI, and Sbp. The main relationship of interest is between mortality and the factor BMI. In the next step, we will focus on choosing an appropriate power from the set A = (−2, −1.5, −1, −0.5, 0, 0.5, 1, 1.5, 2) for BMI within our proposed models. To do so, we fit models

with link function. In stead of using the linear terms as in Zeng et al. [1] models, we use the following four expressions in the function:

(4.1)

(4.2)

(4.3)

(4.4)

In model (4.1), when we fix Age and Sbp, power is selected for BMI. The observed log-likelihood is plotted in Figure 2(a). In the next model (4.2), we fix BMI and Sbp, trying to find a transformation for Age. Power is selected based on the log-likelihood, which is plotted in Figure 2(b). The selected model corresponds to Zeng et al’s model. In many statistical models, the inverse of BMI, , lean body mass index is used. So we fit a model (4.3) where and Sbp are fixed. In model (4.4), and Sbp fixed. Both model (4.3) and model (4.4) select power=1 for Age. The results are plotted in Figure 2(c) and Figure 2(d). As a summary, the best transformation based on log-likelihood from model (4.1)-(4.4) is

(4.5)

The corresponding estimates of regression coefficients are listed in Table 6.

Now let us compare the Cox model, Zeng et al. [1] models, and the proposed models by using the Brier score. The Brier score was originally proposed by Brier [16] to verify the accuracy of weather forecasts and then

extended by May et al. [17] to survival models. The Brier score (BS) at time is given by

(4.6)

where n is the total sample size, is the observed survival time of the ith patient, is the indicator function representing the occurrence of the event, and is the predicted probability of the ith patient surviving beyond time. The choices of the time can be arbitrary, such as the quartiles of follow up time, the quartiles of the survival time, or a fixed number of years.

It is obvious that the Brier score takes minimum value of 0 for perfect prediction of survival status and its range is from 0 to 1. The lower the value of the Brier score, the better the prediction. To compare the Cox model, Zeng et al. [1] models, and proposed models, we calculated the Brier scores at the first quartile Q1, median Q2, and last quartile Q3 of 848 uncensored survival times in the NHANES1 study. The results are summarized in Table 7. We can see that the proposed models has the smallest Brier scores at all there time points. For example, at the median uncensored survival time Q2 = 3894.5 days, the Brier score is 0.1396 for the Cox model. It is 0.1308 for Zeng et al. [1] model. The value of Brier score drops to 0.1297 for the selected proposed model, which indicates the chosen proposed model can well predict the survival outcome as the other two models, and sometimes better.

5. Conclusions and Discussion

In this paper, we proposed a class of generalized transformation models. Zeng et al. [14] introduced semi- parametric transformation models for survival data with a cure fraction, which included the commonly used proportional hazards cure rate models and proportional odds models as special cases. Similar to the structure suggested in Zeng et al. [1] , covariates related to the event of interest were modeled through a link function, where was a known and strictly positive increasing function, such as exponential functions. In our proposed models, we used generalized additive models instead of in the link function. Specifically, we considered fractional polynomials proposed by Royston and Altman [14] . We proved that the proposed model was identifiable as long as the transformation families to satisfy some very general conditions. To select transformation powers in fractional polynomials, we proposed choosing powers from set A = (−2, −1.5, −1, 0.5, 0, 0.5, 1, 1.5, 2) by comparing likelihood functions. Simulation results showed the power selection procedure works well. An improvement in this direction could consider the power as a parameter and estimate the power by using maximum likelihood methods rather than selecting the power from set A.

The proposed generalized transformation models can be applied to a variety of survival data. Even though the cure models are motivated from clinical trials where the end point is not death, such as relapse-free survival time, it can be used to overall survival time as well. In this article, the applications of the proposed models are illu- strated by examining the relationship between the survival time of a patient and several risk factors based on two cohorts data from the First National Health and Nutrition Examination Survey Epidemiologic Follow-up Study. In terms of the Brier scores, the selected proposed model provides better fitting compared with the Cox proportional hazards model and the Zeng et al. [1] transformation cure model. It should be pointed out that even though the Brier score is commonly used in practice for model comparison, it has its own disadvantages. For instance, although the Brier score can be calculated at any arbitrary time point, but it dose not discriminate competing models over the whole time period. Other model comparison methodologies will be explored in our future study. For example, receiver operating characteristic (ROC) curves may be used to measure the diffe- rences of the models over all the relevant time periods.

Acknowledgements

The authors would like to thank Dr. Donglin Zeng from the University of North Carolina at Chapel Hill for sharing his original MATLAB code with us, and to thank the Diverse Populations Collaboration Group for providing data from their studies. The authors would also like to thank the Editor, the Associate Editor, and the referees for their insightful comments and suggestions that provide guidelines for the authors to revise the paper.

Cite this paper

YangLiu,QiushengChen,XufengNiu, (2016) Transformation Models for Survival Data Analysis with Applications. Open Journal of Statistics,06,133-155. doi: 10.4236/ojs.2016.61013

References

Appendix: Proofs of the Main Results

In Appendix, we first prove the Lemmas on model identifiability listed in Section 2.1. Then we will show the asymptotic properties of the semi-parametric estimates in the proposed models under conditions (C1)-(C6) given in Section 2.2. Proofs of the Theorems 2 and 3 are similar to those of Theorems 1 and 2 in Zeng et al. [14] with some modifications.

a. Proofs of Model Identifiability

Proof of Lemma 1: Suppose that can take two different non-zero values and, such that

then we will have the following two equations about,

(A.1)

The inverse function of exists because of the monotonicity of. Applying to the above we get,

(A.2)

We want to show that is an identity function. Function is monotonic since both and are monotonic, which implies that both and can not be zero. Otherwise when y takes different values. Take the ratio of the two equations in (A.2) and let. The following equation holds for,

(A.3)

Suppose that and the conditions (G1) and (G2) hold. Noting that, we have

(A.4)

Calculating the first and second order derivatives in both sides of (3), plugging in, and taking ratio of the two equations, we will have. This contradiction leads to. This concludes that is an identity function. Therefore,. Letting, we get and there- fore.

Proof of Lemma 2: Suppose that. Since is a strictly monotonic function, we have

. Now, let’s fix and for ex-

ample, and only consider, where is a continuous covariate,

(A.5)

Without loss of generality, assume that and, since we can always add more terms with coefficients zero to both sides of (A.5).

Let and, we have the following equation,

(A.6)

Because the function in the left side on (A.6) is analytic in some interval, it holds for any. For different or,’s have different orders when. But since their summation is always zero, the coefficients for each term must be zero. Therefore, we have. Similarly, we can prove that for.

To prove the identifiability of the coefficient of a categorical covariate, for example, fixing we have. Coefficient is identifiable if can take at least two different values.

Thus all parameters in are identifiable.

b. Proofs of Strong Consistency of the Maximum Likelihood Estimates

Let be the empirical measure of n iid observations and E be the expectation, respectively. For any mea-

surable function, define. Suppose that there are n in-

dependent right censored observations. For the ith observation, we have, , where

(A.7)

(A.8)

In applications we may use

to differ the cured and uncured population. which will not affect the proof of consistency and asymptotic nor- mality of the maximum likelihood estimates.

The modified semi-parametric version observed-data likelihood function of parameters, denoted by

, is given in (2.4). Let, be the estimates of and such that

reaches its maximum. The log likelihood function is given by

(A.9)

where satisfy the restricted condition with when

and when. When for, we have

(A.10)

by the method of Lagrange multipliers, where is the Lagrange multiplier. That is,

(A.11)

for, where

(A.12)

Equation (A.11) can be written as

(A.13)

for i when. When, we have the same expression for considering. Therefore,

(A.14)

Since is bounded, the sequence is also bounded. Thus we can choose a subsequence

from such that almost surely; choose a further subsequence of such that

almost surely since belong to a compact set; choose a subsequence of such that

pointwise. Notice that is monotone and. Later we will prove and is a proper distribution function.

The structure of the limit function can be derived from the results of Lemmas 3 and 4. In particular, Lemma 3 shows the convergence of. Proof of the lemma was given in Zeng et al. [1] .

Lemma 3. Under conditions (C1)-(C6), uniformly in y, where

(A.15)

Actually, the right hand side of Equation (A.14) converges to

. For the difference, we have the following result.

Lemma 4. Under conditions (C1)-(C6), for, and

Proof: Because, we have

(A.16)

Letting, then, we obtain

(A.17)

We then calculate the right hand side of (A.17) by using conditional expectations.

(A.18)

where

(A.19)

Function is positive and continuous on. When

, exists and is positive. Therefore there exists positive con-

stants such that, for any T. Hence for any T. Combining (A.17) and

(A.18), we then have.

It can be shown that is Lipshitz continuous and for any. Because of

the continuity of and for, we have

. Therefore, for any i we have

which implies that and. Taking, we have

for any.

Based on the results in Lemma 4, for a given M there exists such that for

any. Define class. Class is a Donsker class (van der Vaart,

A. W. and Wellner, J. A. [18] ) because is bounded away from zero. Thus, converges to

uniformly in, i..e,

(A.20)

Following the calculations in (A.18), we have with the density function.

Based on the expression of, we can construct a sequence of distribution functions with jumps such that for any. For and, define

(A.21)

where is a constant such that and is defined in (A.19). Let

(A.22)

Then it is obviously. Because is bounded away from zero, we have

(A.23)

The calculation here is similar to that in (A.18) with in the denominator instead of. Therefore, combining (A.22) and (A.23) we have

(A.24)

Because are the maximum likelihood estimates, from (A.9) we have

(A.25)

For the strong convergency of the maximum likelihood estimates, we need to show that.

Letting in (A.25), we have. By the Jenson inequality, we have

, where “=” holds if and only if which con-

cludes since the model is identifiable. Therefore, We only need to show.

Theorem 2. Under conditions (C1)-(C6),. The maximum likelihood estimates

based on the modified likelihood function are strongly consistent, that is and

a.s., where is the true value of and function is the true promotion time cumulative distribution function.

Proof: First of all, we want to prove. In fact, from (A.9) we have

(A.26)

by a direct calculation.

Because and is a monotone decreasing function, which implies that

and

Thus from (A.26) we have. Thus, which concludes

and also concludes.

We have proved that any subsequence of, which is also denoted by, converges to almost surely. Therefore, we conclude that the whole sequence converges to with probability 1.

We also proved that converges to uniformly in y on for any fixed M and converges to pointwise on since. Therefore, converges to uniformly in y on because of the continuity of.

c. Proofs of Asymptotic Normality of the Maximum Likelihood Estimates

We consider the likelihood function

(A.27)

and write as, where

Then the log likelihood function, denoted by, can be written as

(A.28)

Lemma 5. For any and any distribution function F with a density, we have

(A.29)

where is the likelihood function given in (A.27), is the true value of and is the true promotion time cumulative distribution function.

Proof: By Jensen inequality. Thus, it suffices to show that

. The proof is similar to that of Theorem 2 thus omitted.

From (A.29) we can derive a differential equation with. Let us consider function such that:

(1) is continuously differentiable with.

(2),.

(3) For and is small enough,.

Under conditions (1)-(3), is a density function with corresponding distribution. For any, where d is the dimension of, we have, and

when is small. Therefore,

(A.30)

Particularly, we can construct satisfying conditions (1)-(3) through a function, which is defined on with bounded total variation. The total variation of is given by

, where the supreme is taken over all finite partitions

.

Define

(A.31)

We can show in (A.31) satisfies conditions (1)-(3). Equation (A.30) can be written as

(A.32)

Let us consider a modified semiparametric version likelihood function,

(A.33)

where

(A.34)

For any and any step function, where

we have

(A.35)

where is the maximum likelihood estimate of based on (A.33).

Similar to the continuous case, now we can derive a differential equation with. Consider function satisfying the following conditions:

(1)′has a jump of size at when and a value of zero elsewhere.

(2)′ The summation of over all is zero, that is.

(3)′ When is small enough, for any.

Under conditions (1)′ -(3)′, is a qualified distribution function for likelihood (A.33). Take such that. Therefore, because of (A.35) we have

, when is small enough. After some algebra, we obtain

(A.36)

Define

(A.37)

With such a function in (A.37), we have

(A.38)

Now, let us consider functions h with bounded total variation such that and define a set of such functions as. For any, define

(A.39)

where

Lemma 6. With the notations defined in (A.39), we have

(A.40)

where and is the likelihood function given in (A.27).

Proof: It follows from (A.32) and (A.38) that

(A.41)

We consider a class,

(A.42)

is a Donsker class. By Theorem 3.3.1 in van der Vaart and Wellner [18] , the left hand side of (A.41) equals

(A.43)

Using the Taylor expansion at for the right hand side of (A.41) and notations (A.39), Equation (A.41) can be simplified as

(A.44)

Lemma 7. The linear operator is invertible from to itself.

Proof: Decompose as a summation of and, and

(A.45)

We can show is an invertible operator from to, and is a compact operator. Rewrite as. To prove is invertible, we only need to show

. Suppose that. Because

(A.46)

with probability one, we have

(A.47)

which implies and.

Theorem 3. Under condition (C1)-(C6), converges weakly to a Gaussian process in.

Proof: Because has an inverse, denoted by, Equation (A.44) can be written as

(A.48)

Immediately from (A.44) and (A.48), we have. Back to (A.48), we obtain

(A.49)

Equation (A.49) holds uniformly for any and. By using Theorem 3.3.1 in van der Vaart and Wellner [18] , converges weakly to a Gaussian process in.