Open Journal of Statistics
Vol.04 No.09(2014), Article ID:50989,7 pages
10.4236/ojs.2014.49074
A New Regression Type Estimator with Two Auxiliary Variables for Single-Phase Sampling
Everline Chemutai Tum, John Kung’u, Leo Odongo
Department of Statistics and Actuarial Science, Kenyatta University, Nairobi, Kenya
Email: everlinechemutai@yahoo.com, johnkungu08@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 August 2014; revised 16 September 2014; accepted 28 September 2014
ABSTRACT
In this paper, we have proposed an estimator of finite population mean using a new regression type estimator with two auxiliary variables for single-phase sampling and investigated its finite sample properties. An empirical study has been carried out to compare the performance of the proposed estimator with the existing estimators that utilize auxiliary variables for finite population mean. It has been found that the new regression type estimator with two auxiliary variables for to be more efficient than mean per unit, ratio and product estimator and exponential ratio and exponential product estimators and exponential ratio-product estimator.
Keywords:
Regression Estimator, Exponential Ratio-Product Estimator, Auxiliary Variables, Mean Squared Error

1. Introduction
The history of using auxiliary information in survey sampling is as old as history of the survey sampling. The work of Neyman [1] may be referred to as the initial work where auxiliary information has been used to improve precision of an estimator. Cochran [2] used auxiliary information in single-phase sampling to develop the ratio estimator for estimation of population mean. In the ratio estimator, the study variable and the auxiliary variable had a high positive correlation and the regression line was passing through the origin. Watson [3] used the regression estimator of leaf area on leaf weight to estimate the average area of the leaves on a plant.
Olkin [4] was the first author to deal with the problem of estimating the mean of survey variable when auxiliary variables were made available. He suggested the use of information on more than one auxiliary variable, highly positively correlated with the study variable. Murthy [5] used auxiliary information in single-phase sampling to develop the product estimator for estimation of population mean. Singh [6] gave a multivariate expression of Murthy’s [5] product estimator while Raj [7] put forward a method for using multi-auxiliary variables through a linear combination of single difference estimators.
Singh [8] considered the extension of the ratio-cum-product estimators to multi-auxiliary variables while Rao and Mudholkar [9] considered a multivariate estimator based on a weighted sum of single ratio and product estimators. John [10] suggested two multivariate generalizations of ratio and product estimators which actually reduced to the Olkin’s [4] and Singh’s [6] estimators.
Bahl and Tuteja [11] proposed ratio and product type exponential estimators while Singh and Vishwakarma [12] extended the exponential ratio and product type estimators to double-phase sampling. Singh and Espejo [13] proposed a class of ratio-product estimators in single-phase sampling with its properties and identified asymptotically optimum estimators from the proposed class of estimators. Singh and Espejo [14] also extended the ratio-product estimators to two-phase sampling. Hanif, Hamad and Shahbaz [15] and [16] proposed a modified regression type estimator in survey sampling where they combined regression estimator with the ratio-product estimator in both single and two-phase sampling. Hamad, Hanif and NajeebHaider [17] extended the estimator to two-phase sampling under partial information case.
In this paper, we will extend the modified regression estimator proposed by Hanif, Hamad and Shahbaz [15] to a new regression type estimator with two auxiliary variables for single-phase sampling estimator and incorporate Arora and Bansi [18] approach in writing down the mean squared error. We will use natural both simulated and natural population by Johnson [19] .
2. Preliminaries
2.1. Notation and Assumption
Let us consider a finite population 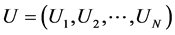 of size N units. A first phase large sample of size n units is drawn from population U following simple random sampling without replacement (SRSWOR) scheme.
of size N units. A first phase large sample of size n units is drawn from population U following simple random sampling without replacement (SRSWOR) scheme.
Let 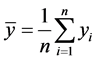 and
and 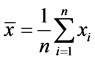 be the unbiased estimators of
be the unbiased estimators of 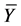 and
and  the population mean of y and x respectively. Let
the population mean of y and x respectively. Let  then
then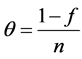 . Let
. Let ,
, 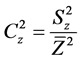 and
and  be the squares of coeffi-
be the squares of coeffi-
cient of variation of study variable and the auxiliary variables respectively. Where the variances and covariance are given by,
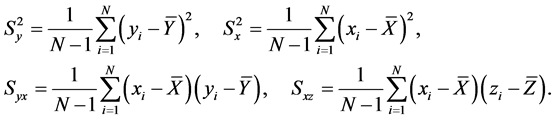 (1.0)
(1.0)
The correlation coefficients between study variable and auxiliary variables are given by;
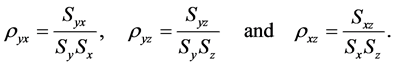 (1.1)
(1.1)
Let 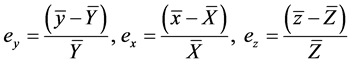 be sampling errors and are assumed to be very small. We as-
be sampling errors and are assumed to be very small. We as-
sume that
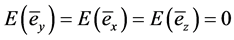 . (1.2)
. (1.2)
The sampling error can also be written as,
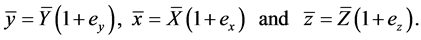 (1.3)
(1.3)
Then for simple random sampling without replacement for both single-phase, we write by using phase wise operation of expectations as:
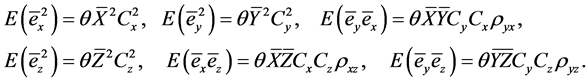 (1.4)
(1.4)


The following notations will be used in deriving the mean square errors of proposed estimator.





















2.2. Mean per Unit in Single-Phase Sampling
It is obtained by taking a sample of size n from N using simple random sampling without replacement.

Its variance is given by,

2.3. Ratio, Product and Regression Estimators
Classical ratio estimator by Cochran [2] is given by,

The mean squared error of the estimator 

Classical regression estimator by Watson [3] is given by,

Mean squared error of estimator 

Classical product estimator by Murthy [5] is given by,

The mean squared error of the estimator 

2.4. Ratio-Product Estimator
Singh and Espejo [13] proposed the following ratio-product estimator

The mean squared error of the estimator 

2.5. Exponential Ratio-Type and Exponential Product-Type Estimators
Bahl and Tuteja [11] suggested an exponential ratio-type and exponential product-type estimator defined as


The mean squared error of 



2.6. Exponential Ratio-Product Estimator Using Auxiliary Variable
The exponential ratio-product estimator proposed by Singh and Espejo [13] is given by,

The mean squared error is given by,

In general these estimators have a bias of order




is usually unimportant in samples of moderate and large sizes.
In this paper, we have extended the modified regression estimator by Hanif, Hamad and Shahbaz [15] in single-phase sampling to a new regression type estimator with two auxiliary variables for single-phase for estimating the population mean.
3. Methodology
3.1. Mixture Ratio Estimators Using Multi-Auxiliary Variable and Attributes for Single-Phase Sampling
If we estimate a study variable when information on all auxiliary variables is available from the population, it is utilized in the form of their means. A new regression type estimator using two auxiliary variables for single variables is proposed as:

Substituting (1.3) equation in (3.0) we get,

Ignoring the second and higher terms for each expansion of product and after simplification we can write 

Expanding the exponential in (3.2) and ignoring the second and higher terms for each expansion we get,

Simplifying (3.3) we get,

Expanding (3.4) and ignoring the second and higher terms we get,

The mean squared error of 

Squaring the right sides of (3.6) and taking expectation, we get,

Differentiating (4.7) with respect to 



Using normal equations that are used to find the optimum values of 


Taking expectation in (3.10) we get,

Taking expectation and using (1.4) in (3.11) we get

Substituting the optimum value (3.8) and (3.9) in (3.12), we get

Simplifying (3.13) we get

Or

Or

We can also rewrite (3.16) as,

Using (1.6) in (3.17) we get

where 


3.2. Bias of the New Regression Type Estimator with Two Auxiliary Variables
The regression-cum-exponential ratio-product estimator using multiple auxiliary variables in single-phase sampling is biased. However, this bias is negligible for moderate large samples. It is easily shown that the new regression type estimator with two auxiliary variables for single-phase is consistent estimator using two auxiliary variables since it is a linear combination of consistent estimators it follows that it’s also consistent.
4. Simulation, Result and Discussion
We carried out some data simulation experiments to compare the performance of the new regression type estimator with mean per unit, ratio and product estimator using one auxiliary variable, ratio-product estimator, exponential ratio estimator, exponential product estimator and exponential ratio-product estimators in single-phase sampling for finite population.
1) Simulated population
1) Study variable 
ii) For ratio estimator the auxiliary variable is strongly positively correlated with the study variable and the line passes through the origin.

iii) For regression estimator the auxiliary variable was strongly positively correlated with the study variable and the regression line does not pass through the origin.
Auxiliary variable
iv) For product estimator the auxiliary variable was strongly negatively correlated with the study variable.
Auxiliary variable
2) Natural population by Johnson (1996)
Lists estimates of the percentage of body fat determined by underwater weighing and various body circumference measurements for 252 men and data set was used to illustrate multiple regression techniques.
i) Body fat 
ii) For ratio estimator the auxiliary variable (simulated) is strongly positively correlated with the study variable (body fat).

iii) For regression estimator the auxiliary variable (hips circumference) was strongly positively correlated with the study variable (body fat).
Auxiliary variable
iv) For product estimator the auxiliary variable (simulated) was strongly negatively correlated (body fat) with the study variable.
Auxiliary variable
In order to evaluate the efficiency gain we could achieve by using the proposed estimators, we have calculated the variance of mean per unit and the mean squared error of all estimators we have considered. We have then calculated percent relative efficiency of each estimator in relation to variance of mean per unit. We have then compared the percent relative efficiency of each estimator, the estimator with the highest percent relative efficiency is considered to be the more efficient than the other estimators. The percent relative efficiency is calculated using the following formulae.

Table 1 shows percent relative efficiency of proposed estimator with respect to mean per unit estimator for single-phase sampling. It is very clear from Table 1 that our proposed new regression type estimator is the most
Table 1. Relative efficiency of existing and proposed estimator with respect to mean per unit estimator for single-phase sampling.
efficient compared to mean per unit, ratio and product estimator using one auxiliary variables, ratio-product estimator, exponential ratio estimator, exponential product estimator and exponential ratio-product estimator estimators for population mean since it has the highest percent relative efficiency.
5. Conclusion
The proposed new regression type estimator with two auxiliary variables for single-phase sampling is recommended for estimating the finite population mean since it is the most efficient estimator compared to mean per unit, ratio and product estimator using one auxiliary variables, ratio-product estimator, exponential ratio estimator, exponential product estimator and exponential ratio-product estimator in term of efficiency in single-phase sampling.
References
- Neyman, J. (1938) Contribution to the Theory of Sampling Human Populations. Journal of the American Statistical Association, 33, 101-116. http://dx.doi.org/10.1080/01621459.1938.10503378
- Cochran, W.G. (1940) The Estimation of the Yields of the Cereal Experiments by Sampling for the Ratio of Grain to Total Produce. Journal of Agricultural Science, 30, 262-275. http://dx.doi.org/10.1017/S0021859600048012
- Watson, D.J. (1937) The Estimation of Leaf Areas. Journal of Agricultural Science, 27, 474. http://dx.doi.org/10.1017/S002185960005173X
- Olikin, I. (1958) Multivariate Ratio Estimation for Finite Population. Biometrika, 45, 154-165. http://dx.doi.org/10.1093/biomet/45.1-2.154
- Murthy, M.N. (1964) Product Method of Estimation. Sankhya, 26, 294-307.
- Singh, M.P. (1967) Multivariate Product Method of Estimation for Finite Populations. Journal of the Indian Society of Agricultural Statistics, 31, 375-378.
- Raj, D. (1965) On a Method of Using Multi-Auxiliary Information in Sample Surveys. Journal of the American Statistical Association, 60, 270-277. http://dx.doi.org/10.1080/01621459.1965.10480789
- Singh, M.P. (1967) Ratio-Cum-Product Method of Estimation. Metrika, 12, 34-42. http://dx.doi.org/10.1007/BF02613481
- Rao, P.S.R.S. and Mudholkar, G.S. (1967) Generalized Multivariate Estimators for the Mean of a Finite Population. Journal of the American Statistical Association, 62, 1009-1012. http://dx.doi.org/10.1080/01621459.1967.10500911
- John, S. (1969) On Multivariate Ratio and Product Estimators. Biometrika, 56, 533-536. http://dx.doi.org/10.1093/biomet/56.3.533
- Bahl, S. and Tuteja, R.K. (1991) Ratio and Product Type Exponential Estimator. Information and Optimization Sciences, 12, 159-163. http://dx.doi.org/10.1080/02522667.1991.10699058
- Singh, H.P. and Vishwakarma, G.K. (2007) Modified Exponential Ratio and Product Estimators for Finite Population Mean in Double Sampling. Austrian Journal of Statistics, 36, 217-225.
- Singh, H.P. and Espejo, M.R. (2003) On Linear Regression and Ratio-Product Estimation of a Finite Population Mean. The Statistician, 52, 59-67. http://dx.doi.org/10.1111/1467-9884.00341
- Singh, H.P. and Espejo, M.R. (2007) Double Sampling Ratio-Product Estimator of a Finite Population Mean in Sample Survey. Journal of Applied Statistics, 34, 71-85. http://dx.doi.org/10.1080/02664760600994562
- Hanif, M., Hamad, N. and Shahbaz, M.Q. (2009) A Modified Regression Type Estimator in Survey Sampling. World Applied Sciences Journal, 7, 1559-1561.
- Hanif, M., Hamad, N. and Shahbaz, M.Q. (2010) Some New Regression Type Estimators in Two-Phase Sampling. World Applied Sciences Journal, 8, 799-803.
- Hamad, N., Hanif, M. and Haider, N. (2013) A Regression Type Estimator with Two Auxiliary Variables for Two- Phase Sampling. Open Journal of Statistics, 3, 74-78. http://dx.doi.org/10.4236/ojs.2013.32010
- Arora, S. and Lal, B. (1989) New Mathematical Statistics. Satya Prakashan, New Delhi.
- Johnson, R.W. (1996) Fitting Percentage of Body Fat to Simple Body Measurements. Journal of Education, 4.








