Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27401,10 pages DOI:10.4236/ojdm.2013.31013
Dominating Sets and Domination Polynomials of Square of Paths
1Department of Mathematics, Nesamony Memorial Christian College, Marthandam, India
2Department of Mathematics, Mar Ephraem College of Engineering and Technology, Kanayakumari District, India
Email: naacnmccm@gmail.com, lalgipson@yahoo.com
Received August 30, 2012; revised September 30, 2012; accepted October 8, 2012
Keywords: Domination Set; Domination Number; Domination Polynomials
ABSTRACT
Let G = (V, E) be a simple graph. A set S Í V is a dominating set of G, if every vertex in V-S is adjacent to at least one vertex in S. Let 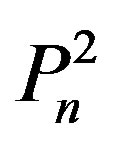 be the square of the Path
be the square of the Path 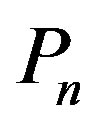 and let
and let 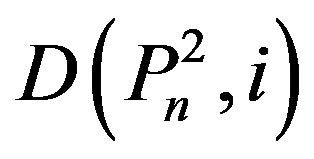 denote the family of all dominating sets of
denote the family of all dominating sets of 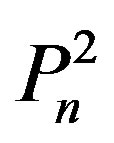 with cardinality i. Let
with cardinality i. Let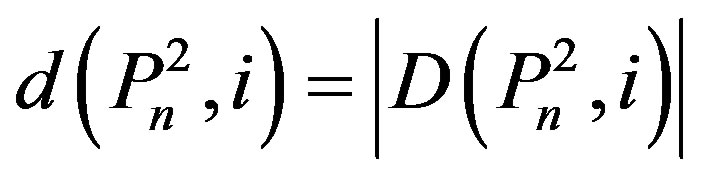 . In this paper, we obtain a recursive formula for
. In this paper, we obtain a recursive formula for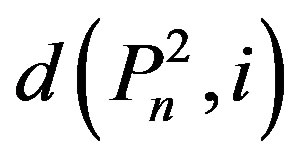 . Using this recursive formula, we construct the polynomial,
. Using this recursive formula, we construct the polynomial, 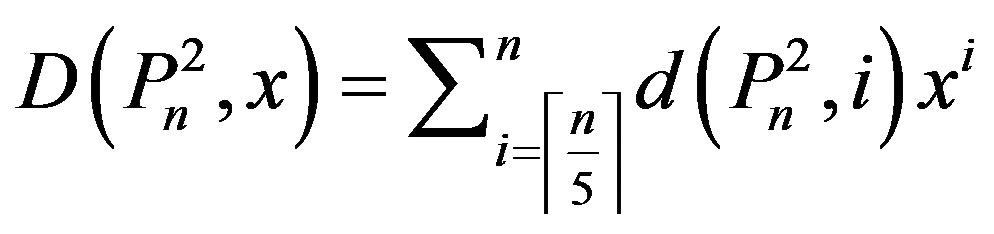 , which we call domination polynomial of
, which we call domination polynomial of 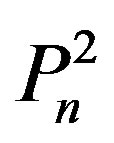 and obtain some properties of this polynomial.
and obtain some properties of this polynomial.
1. Introduction
Let G = (V, E) be a simple graph of order |V| = n. For any vertex v Î V, the open neighbourhood of n is the set 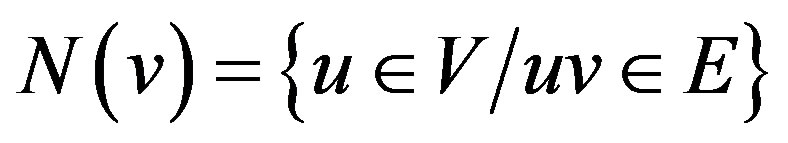 and the closed neighbourhood of n is the set
and the closed neighbourhood of n is the set . For a set S Í V, the open neighbourhood of S is
. For a set S Í V, the open neighbourhood of S is 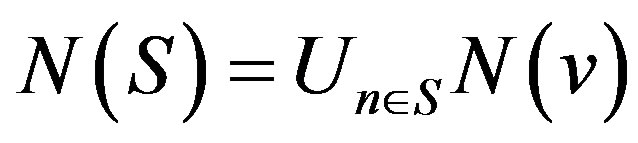 and the closed neighbourhood of S is
and the closed neighbourhood of S is . A set S
. A set S
Í V is a dominating set of G, if N[S] = V, or equivalently, every vertex in V-S is adjacent to at least one vertex in S. The domination number of a graph G is defined as the minimum size of a dominating set of vertices in G and it is denoted as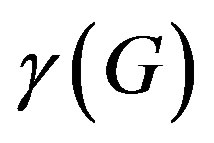 . A simple path is a path in which all its internal vertices have degree two, and the end vertices have degree one and is denoted by
. A simple path is a path in which all its internal vertices have degree two, and the end vertices have degree one and is denoted by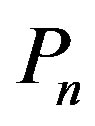 .
.
Definition 1.1.: Let 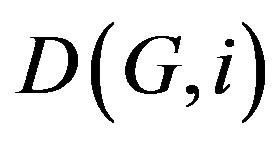 be the family of dominating sets of a graph G with Cardinality i and let
be the family of dominating sets of a graph G with Cardinality i and let
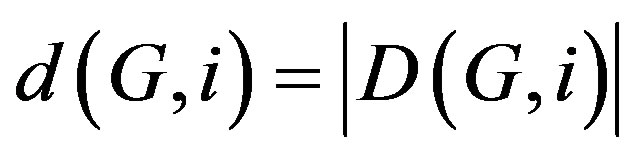 .
.
Then the domination polynomial 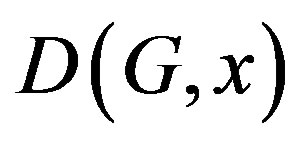 of G is defined as
of G is defined as
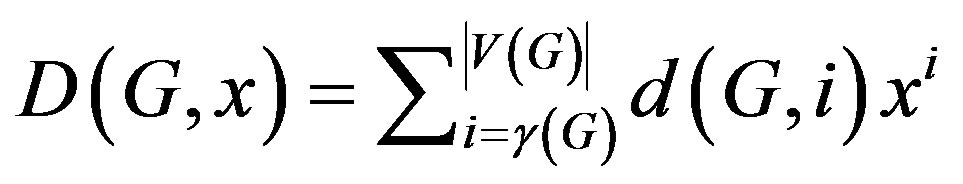 .
.
where  is the domination number of G.
is the domination number of G.
Result 1.2. [1]: If a graph G consists of m components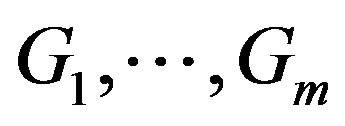 , then
, then
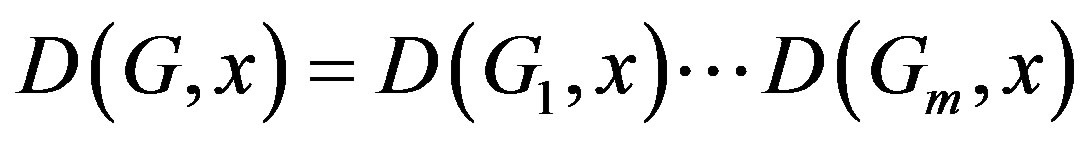 .
.
Result 1.3. [1]: Let 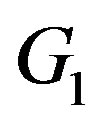 and
and 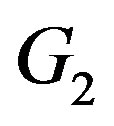 be graphs of order
be graphs of order 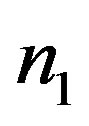 and
and 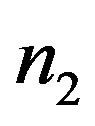 respectively. Then
respectively. Then

Result 1.4. [1]: Let G be a bipartite graph with bipartition (X,Y). Then G contains a matching that saturates every vertex in X if and only if for all S Í V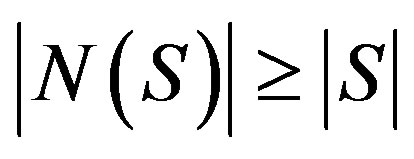 .
.
Result 1.5. [1]: Let G be a graph of order n. Then for every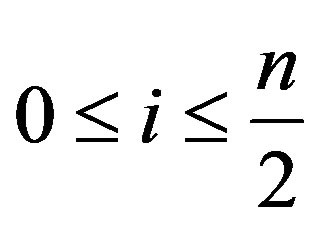 , we have
, we have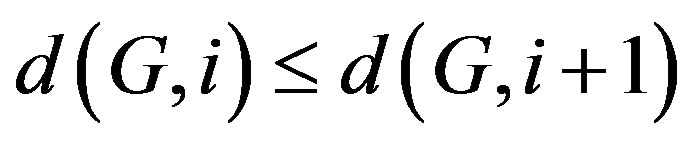 .
.
Result 1.6. [1]: For any graph G of order n, .
.
Result 1.7. [1]: For any graph G of order n and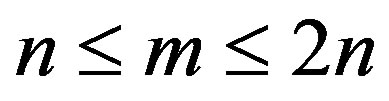 , we have
, we have
 .
.
Hence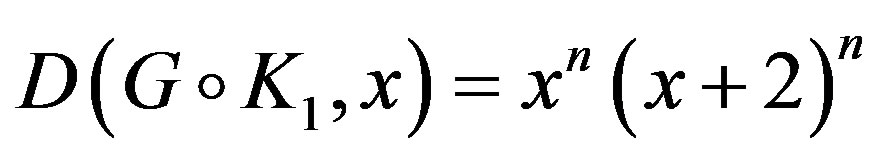 .
.
Definition 1.8: The Square of a graph with the same set of vertices as G and an edge between two vertices if and only if there is a path of length at most 2 between them. The second power of a graph is also called its Square.
Let  be the square of the path
be the square of the path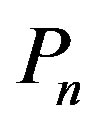 (2nd power )with n vertices. Let
(2nd power )with n vertices. Let  be the family of dominating sets of the graph
be the family of dominating sets of the graph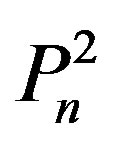 with cardinality i and let
with cardinality i and let
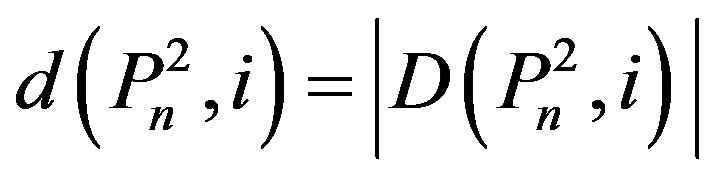 .
.
We call the polynomial
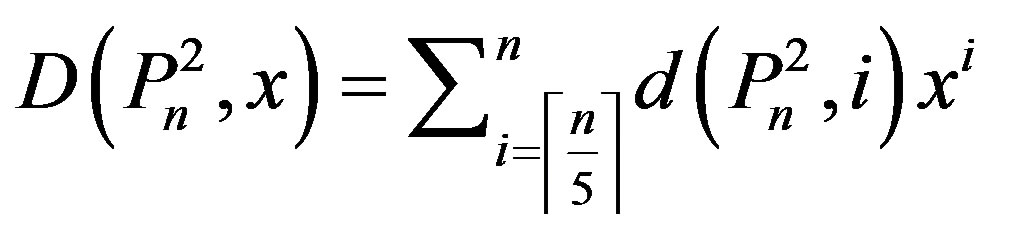
the domination polynomial of the graph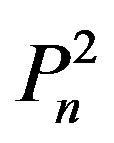 [2].
[2].
In the next section, we construct the families of the dominating sets of the square of paths by recursive method.
As usual we use 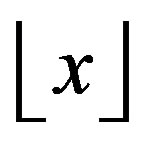 for the largest integer less than or equal to x and
for the largest integer less than or equal to x and 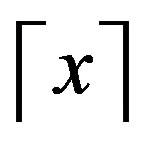 for the smallest integer greater than or equal to x. Also, we denote the set
for the smallest integer greater than or equal to x. Also, we denote the set 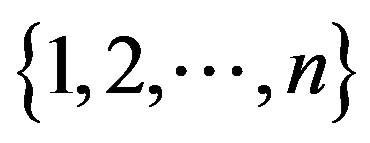 by [n], throughout this paper.
by [n], throughout this paper.
2. Main Result
Let 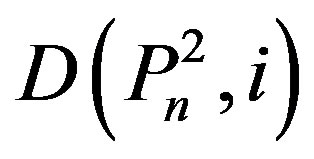 be the family of dominating sets of
be the family of dominating sets of 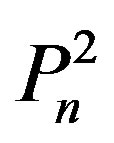 with cardinality i. We investigate the dominating sets of
with cardinality i. We investigate the dominating sets of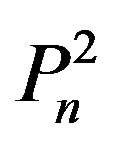 . We need the following lemma to prove our main results in this section.
. We need the following lemma to prove our main results in this section.
Lemma 2.1. [3]:  By Lemma 2.1 and the definition of domination number, one has the following Lemma:
By Lemma 2.1 and the definition of domination number, one has the following Lemma:
Lemma 2.2. 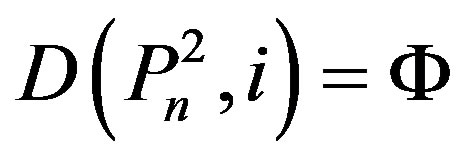 if and only if
if and only if 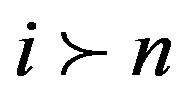 or
or
 . A simple path is a path in which all its internal vertices have degree two, and the end vertices have degree one. The following Lemma follows from observation [2].
. A simple path is a path in which all its internal vertices have degree two, and the end vertices have degree one. The following Lemma follows from observation [2].
Lemma 2.3. [2]: If a graph G contains a simple path of length 5k – 1, then every dominating set of G must contain at least k vertices of the path.
In order to find a dominating set of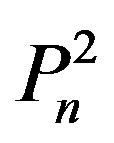 , with cardinality i, we only need to consider
, with cardinality i, we only need to consider
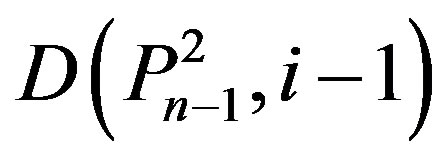 ,
,  ,
,
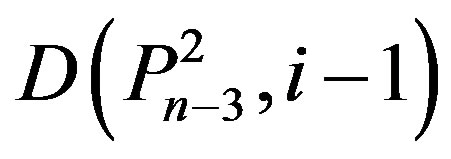 ,
, 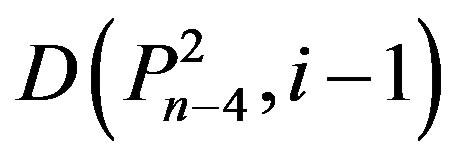
and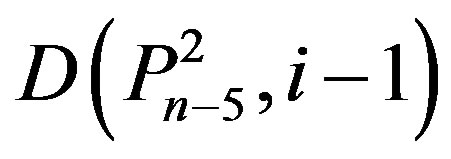 . The families of these dominating sets can be empty or otherwise. Thus, we have eight combinations, whether these five families are empty or not. Two of these combinations are not possible (Lemma 2.5(i), & (ii)). Also, the combination that
. The families of these dominating sets can be empty or otherwise. Thus, we have eight combinations, whether these five families are empty or not. Two of these combinations are not possible (Lemma 2.5(i), & (ii)). Also, the combination that


does not need to be considered because it implies that  (See Lemma 2.5 (iii)). Thus we only need to consider five combinations or cases. We consider those cases in Theorem 2.7.
(See Lemma 2.5 (iii)). Thus we only need to consider five combinations or cases. We consider those cases in Theorem 2.7.
Lemma 2.4.: If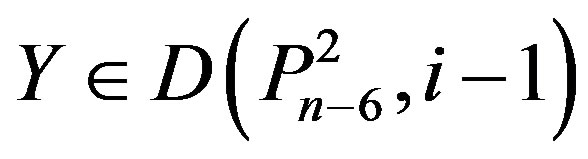 , and there exists x
, and there exists x
Î [n] such that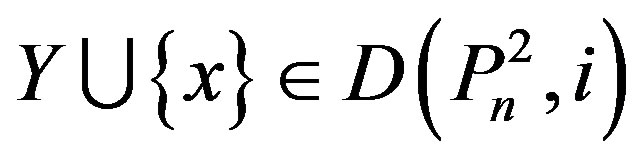 , then
, then
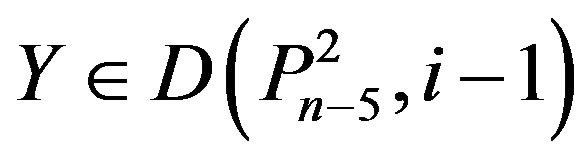 .
.
Proof: Suppose that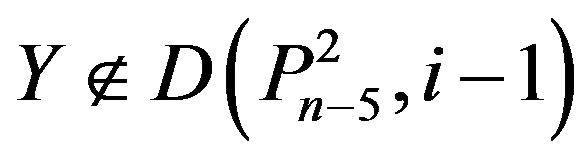 . Since
. Since
 Y contains at least one vertex labeled n – 6, n – 7 or n – 8.
Y contains at least one vertex labeled n – 6, n – 7 or n – 8.
![]() If
If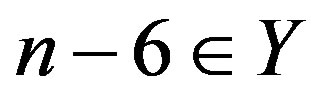 , then
, then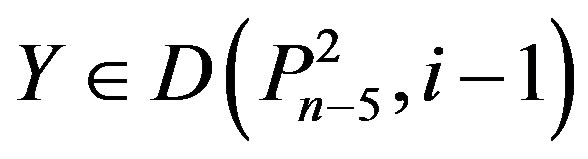 , a contradiction. Hence n – 7 or n – 8 Î Y, but then in this case,
, a contradiction. Hence n – 7 or n – 8 Î Y, but then in this case, 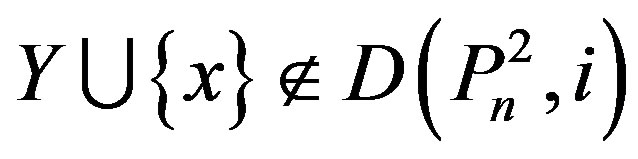 , for any xÎ [n], also a contradiction.
, for any xÎ [n], also a contradiction.
Lemma 2.5.:
1) If
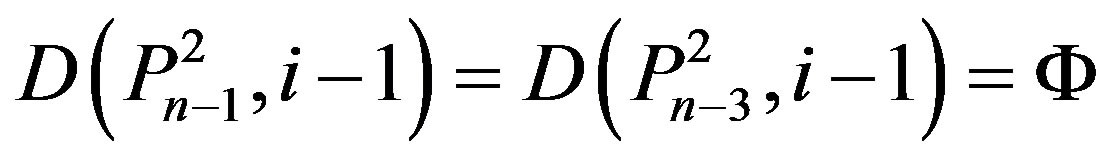
then

2) If
 ,
, 
then
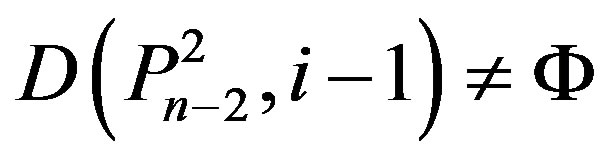 3) If
3) If
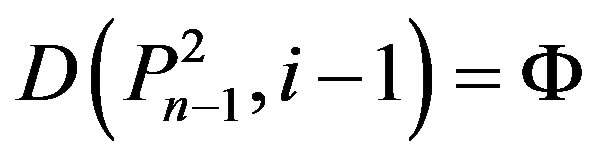 ,
, 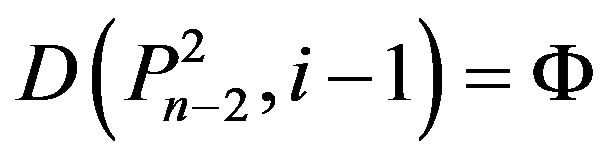 ,
,
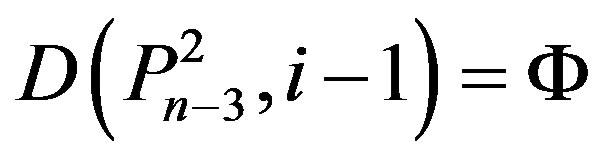 ,
, 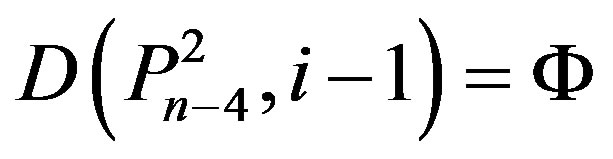 ,
,
 , then
, then 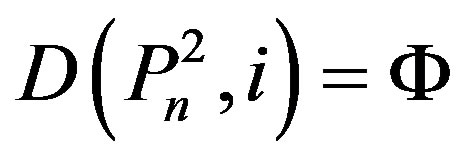
Proof:
1) Since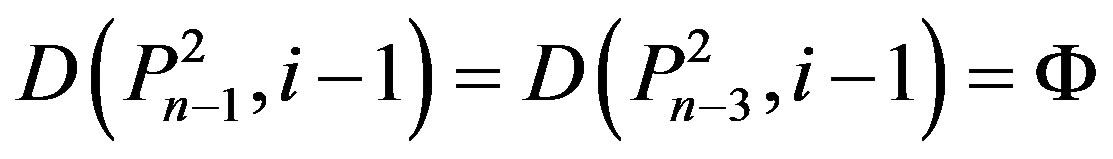 , by Lemma 2.2,
, by Lemma 2.2,  (or)
(or)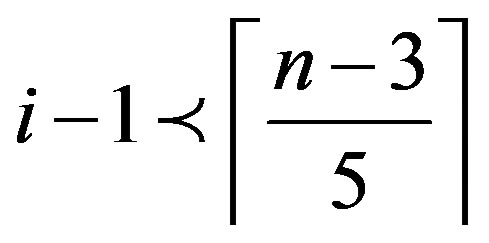 . In either case, we have
. In either case, we have  .
.
2) Suppose that , so by Lemma 2.2we have
, so by Lemma 2.2we have 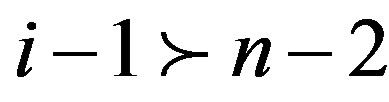 or
or 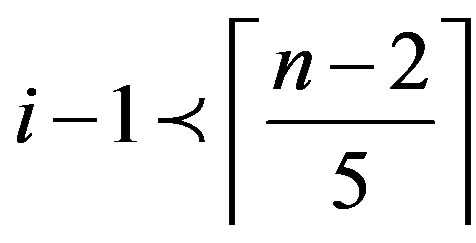 If
If then
then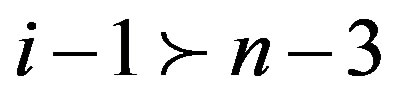 . Therefore
. Therefore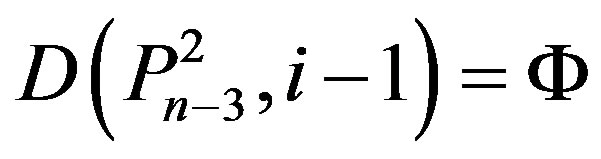 , a contradiction.
, a contradiction.
3) Suppose that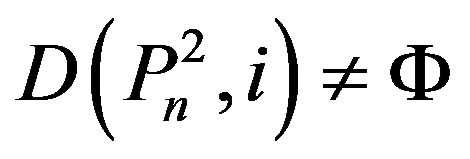 , Let
, Let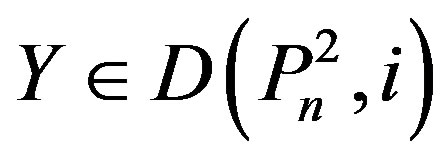 . Thus, at least one vertex labeled n or n – 1 or n – 2 is in Y. If n Î Y, then by Lemma (2.3), at least one vertex labeled n – 1, n – 2, n – 3, n – 4 or n – 5 is in Y. If n – 1 Î Y or n – 2 Î Y, then
. Thus, at least one vertex labeled n or n – 1 or n – 2 is in Y. If n Î Y, then by Lemma (2.3), at least one vertex labeled n – 1, n – 2, n – 3, n – 4 or n – 5 is in Y. If n – 1 Î Y or n – 2 Î Y, then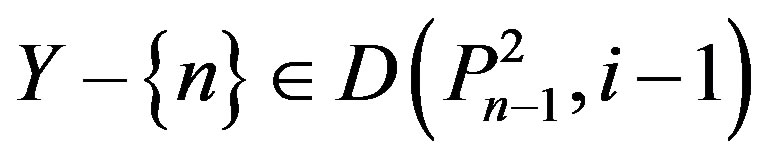 , a contradiction.
, a contradiction.
If n – 3 Î Y, then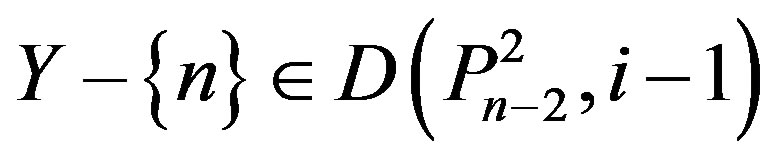 , a contradiction. Now, suppose that n – 1 Î Y. Then, by Lemma 2.3, at least one vertex labeled n – 2, n – 3, n – 4, n – 5 or n – 6 is in Y. If n – 2 Î Y or n – 3 Î Y, then
, a contradiction. Now, suppose that n – 1 Î Y. Then, by Lemma 2.3, at least one vertex labeled n – 2, n – 3, n – 4, n – 5 or n – 6 is in Y. If n – 2 Î Y or n – 3 Î Y, then
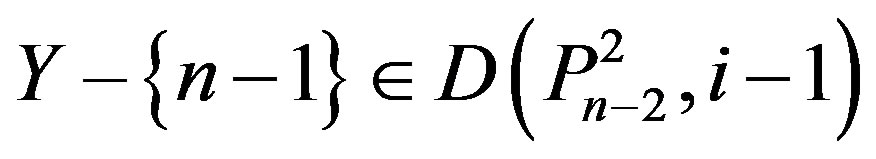 a contradiction. If n – 4 Î Ythen
a contradiction. If n – 4 Î Ythen , a contradiction.
, a contradiction.
If n – 5 Î Y, then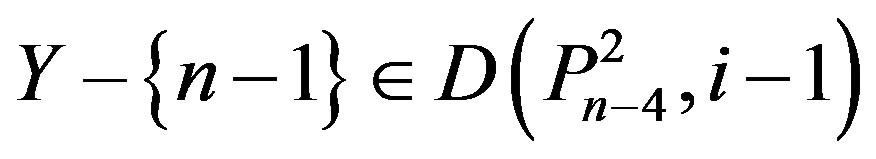 , a contradiction If n – 6 Î Y, then
, a contradiction If n – 6 Î Y, then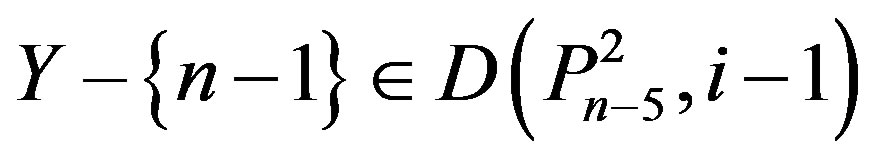 , a contradiction. Therefore,
, a contradiction. Therefore,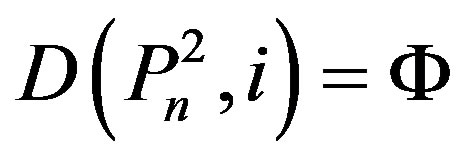 .
.
Lemma 2.6.: If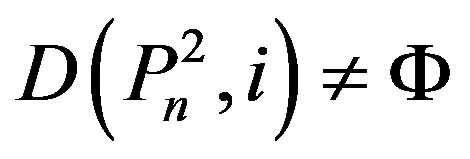 , then 1)
, then 1) 
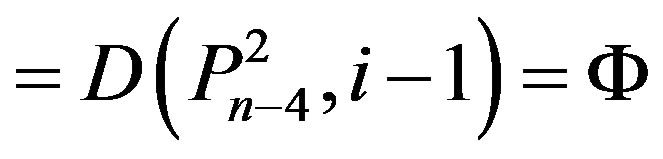 and
and 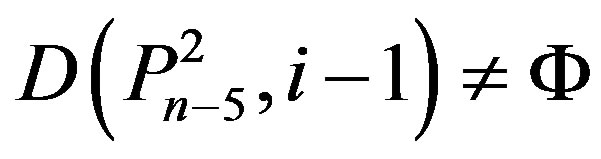 if and only if n = 5k and i = k for some k Î N;
if and only if n = 5k and i = k for some k Î N;
2) 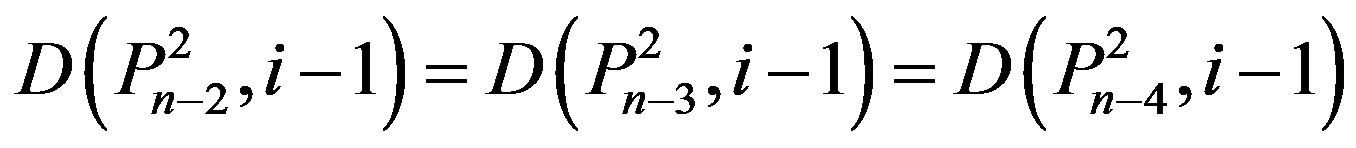
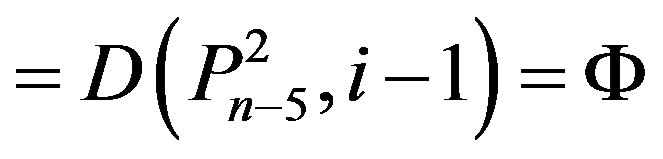 then
then 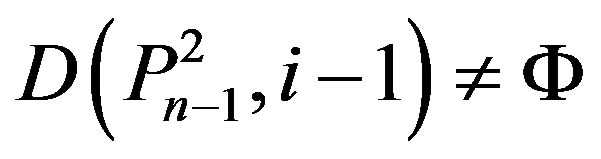 if and only if i = n;
if and only if i = n;
3) ,
,  ,
,
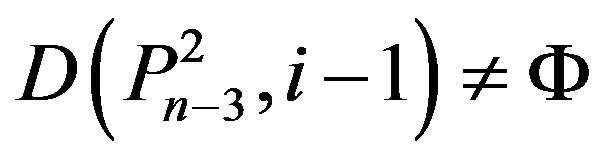 ,
, 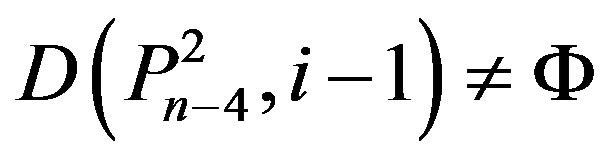 ,
,
 , if and only if n = 5k + 2 and
, if and only if n = 5k + 2 and
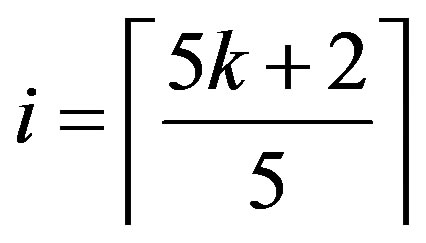 for some kÎN;
for some kÎN;
4)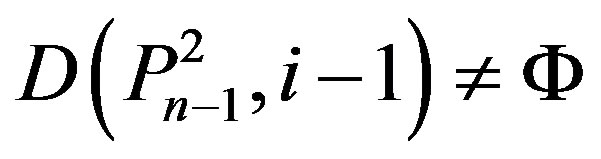 ,
, 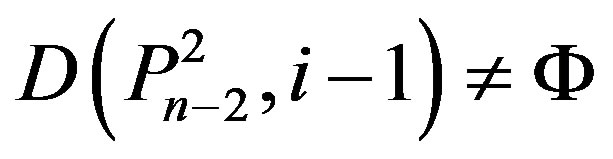 ,
,
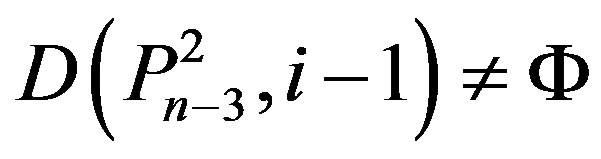 ,
, 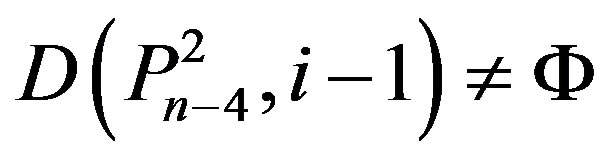 , and
, and
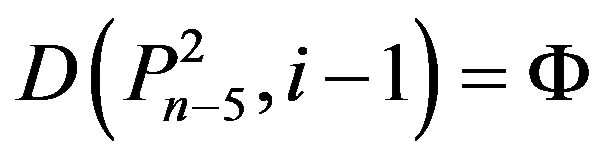 if and only if i = n – 3.
if and only if i = n – 3.
5)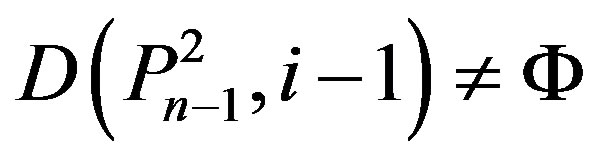 ,
, 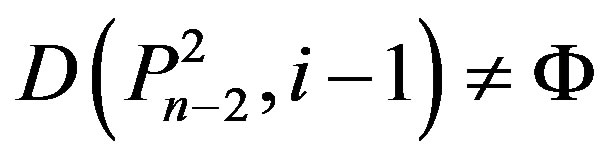 ,
,
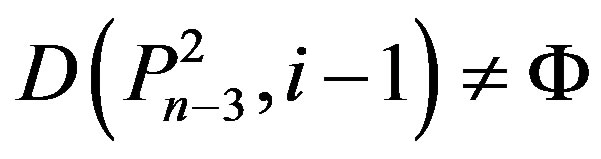 ,
,  , and
, and
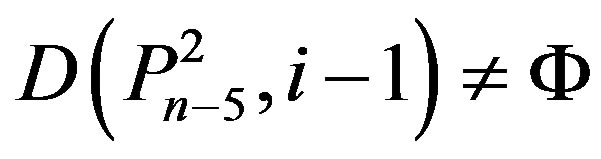 if and only if
if and only if
 .
.
wang#title3_4:spwang#title3_4:spwang#title3_4:spwang#title3_4:spProof:
1) (Þ)
Since

by Lemma 2.2,
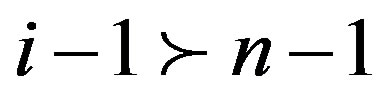 or
or 
If , then
, then 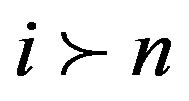 and by Lemma 2.2,
and by Lemma 2.2, 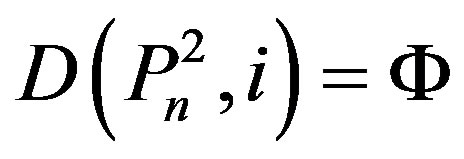 , a contradiction.
, a contradiction.
So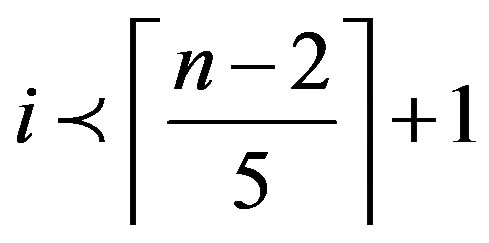 , and since
, and since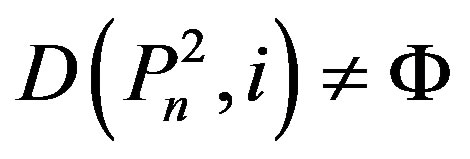 , we have
, we have
 , which implies that n = 5k and i = k for some kÎN.
, which implies that n = 5k and i = k for some kÎN.
(Ü) If n = 5k and i = k for some kÎN, then by Lemma 2.2,
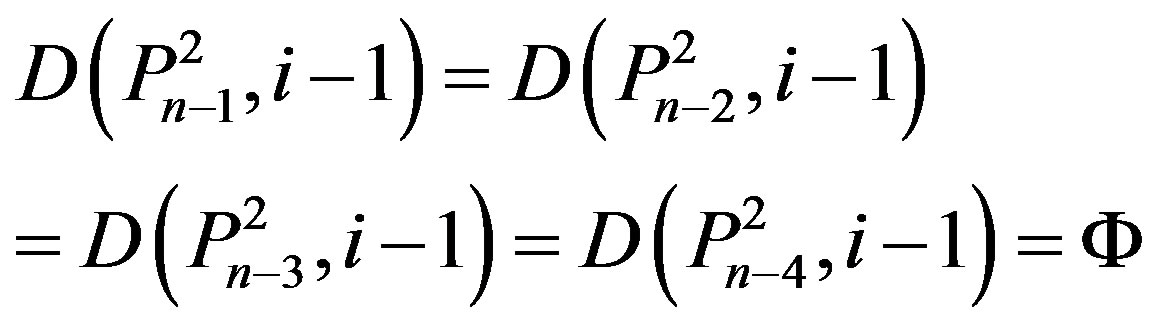 and
and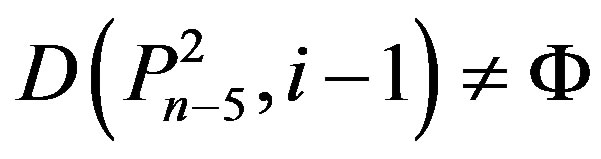 .
.
2) (Þ) Since
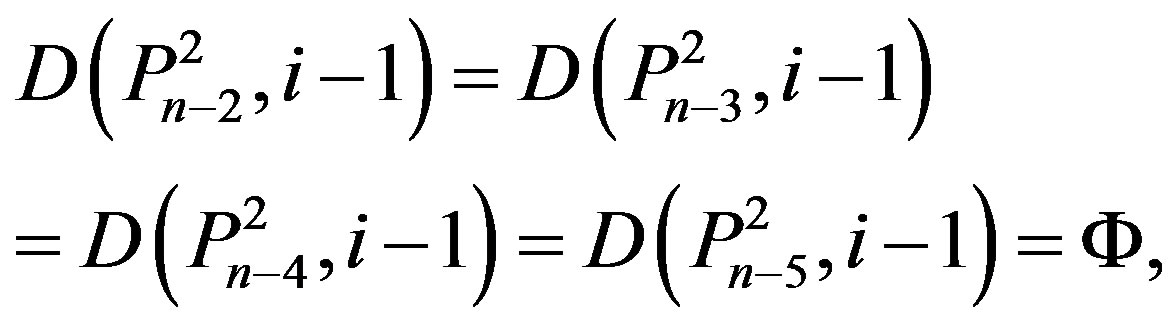
by Lemma 2.2,
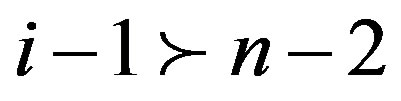 or
or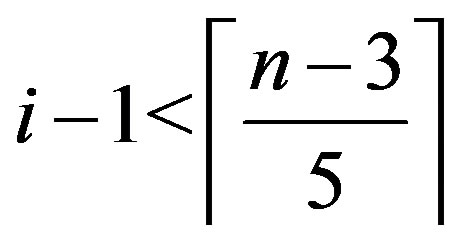 .
.
If
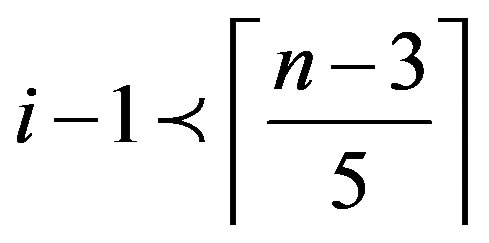 , then
, then 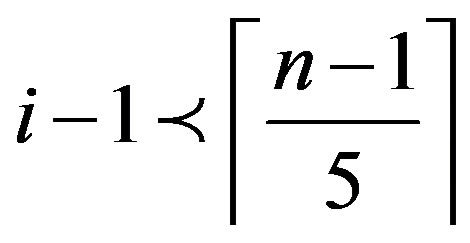
and hence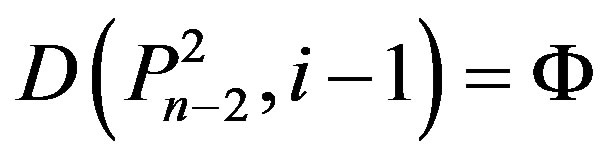 , a contradiction.
, a contradiction.
So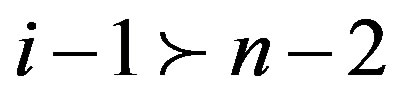 . Also,
. Also,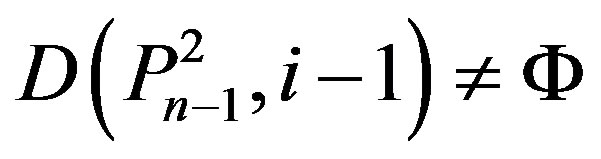 .
.
Therefore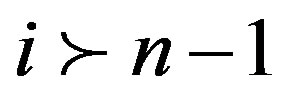 . Therefore
. Therefore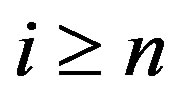 . But
. But . Hence i = n.
. Hence i = n.
(Ü) If i = n, then by lemma 2.2,

then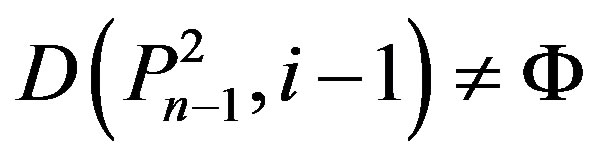 .
.
3) (Þ) Since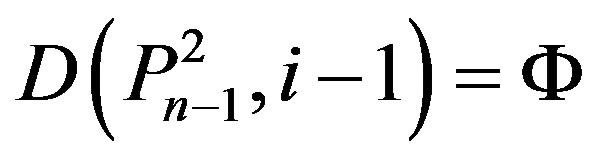 , by Lemma 2.2,
, by Lemma 2.2,
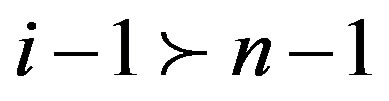 or
or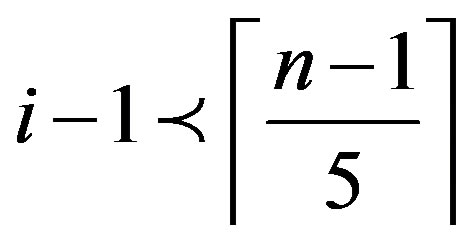 .
.
If , then
, then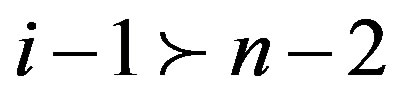 , by Lemma 2.2,
, by Lemma 2.2,

a contradiction.
Therefore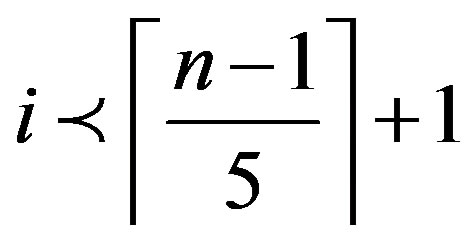 .
.
But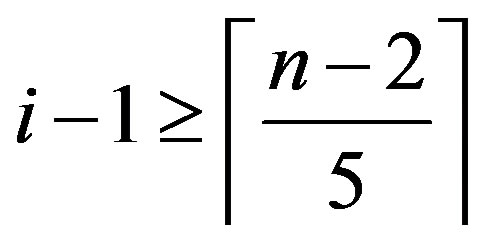 , because
, because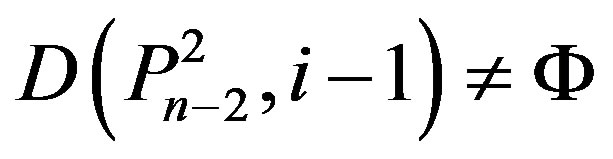 .
.
Therefore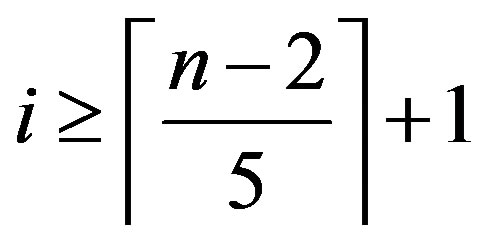 .
.
Hence,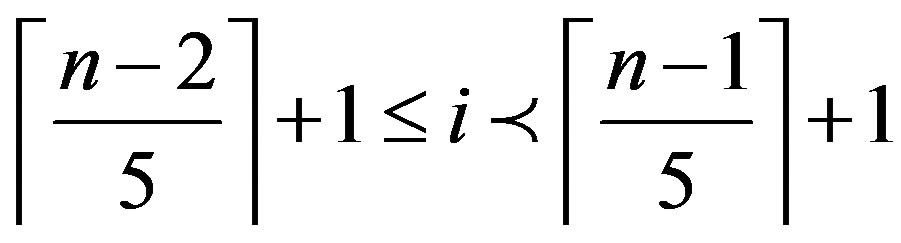 .
.
This holds only if n = 5k + 2 and
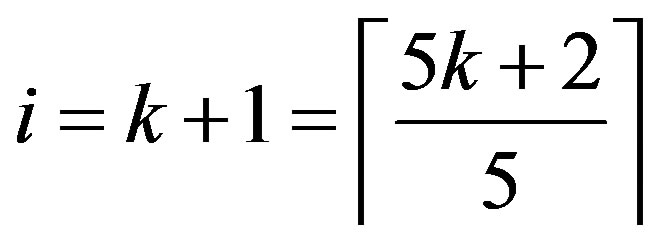 for some k Î N.
for some k Î N.
(Ü) If n = 5k + 2 and 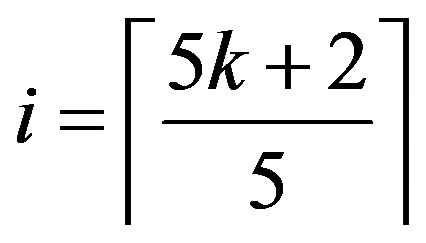 for some k Î N, then by Lemma 2.2,
for some k Î N, then by Lemma 2.2,
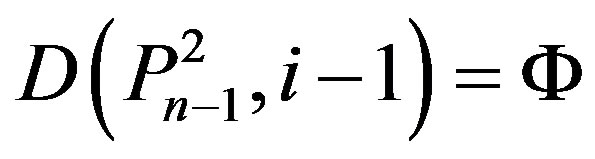 ,
, 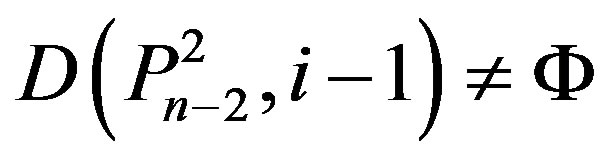 ,
,
 ,
, 
and
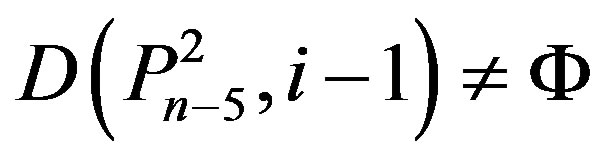 .
.
4) (Þ) Since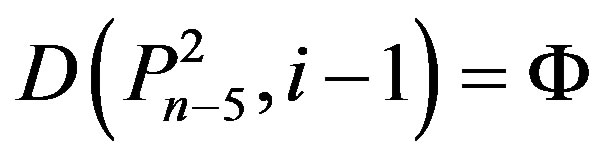 , by Lemma 2.2,
, by Lemma 2.2,
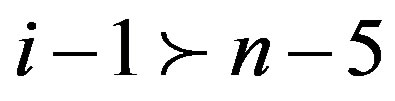 or
or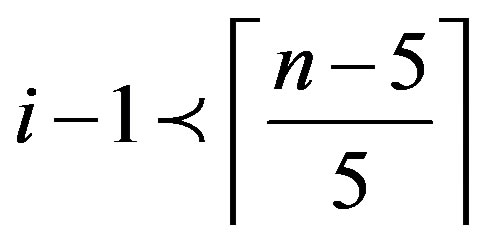 .
.
Since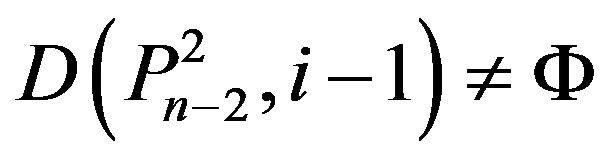 , by Lemma 2.2,
, by Lemma 2.2,
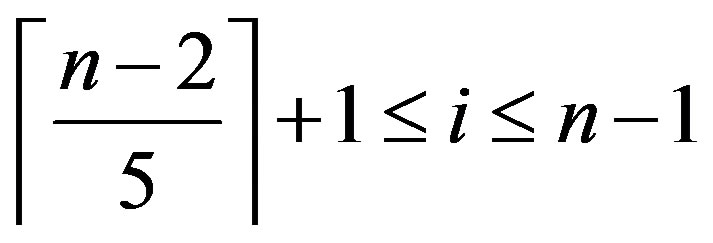 .
.
Therefore 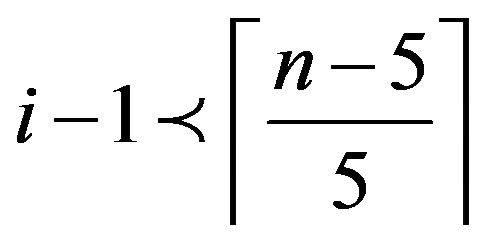 is not possible. Therefore
is not possible. Therefore
 . Therefore
. Therefore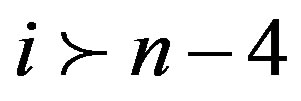 .
.
Therefore .
.
Since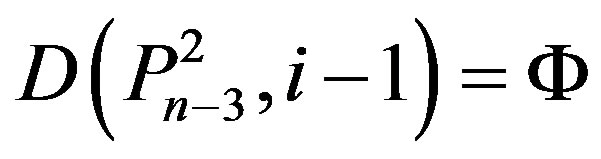 ,
,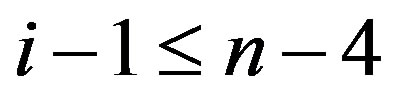 .
.
Therefore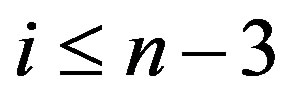 . Hence
. Hence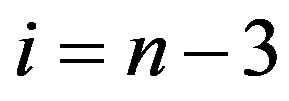 .
.
(Ü) if 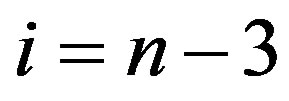 then By Lemma 2.2,
then By Lemma 2.2,
 ,
,  ,
,
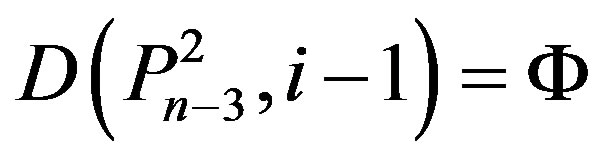 ,
, 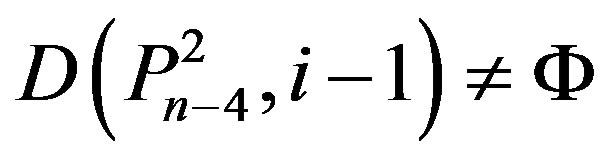
and
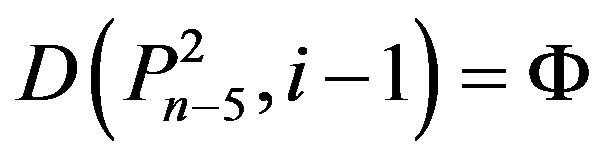 .
.
5) (Þ) Since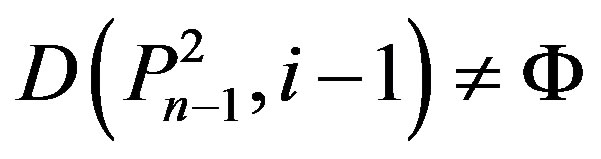 ,
, 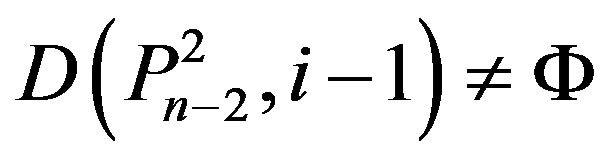
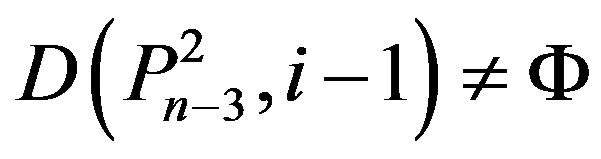 , and
, and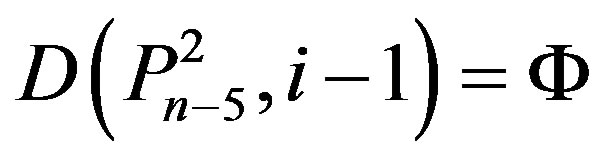 , then by applying Lemma (2.2),
, then by applying Lemma (2.2),
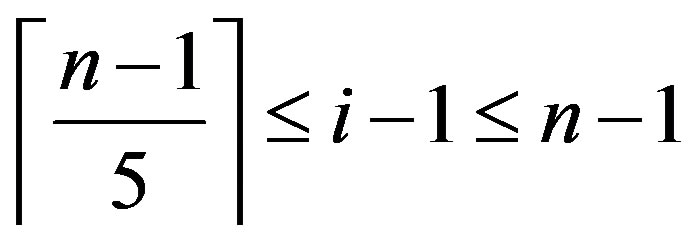 ,
, 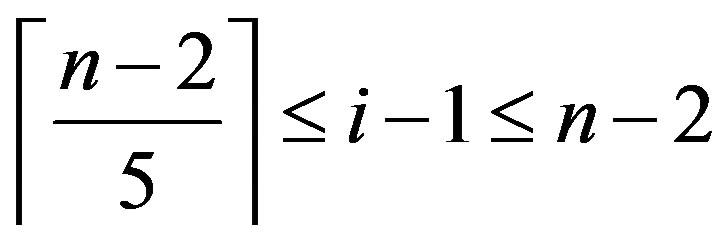 ,
,
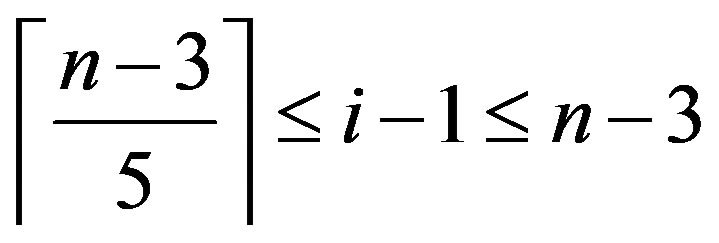 ,
, 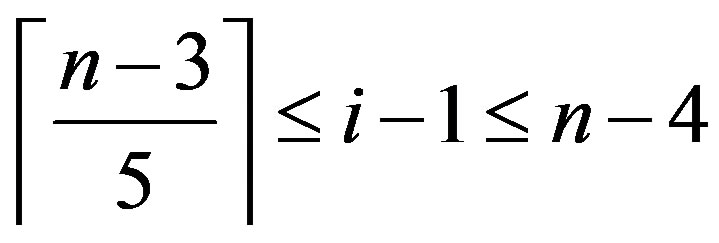
and
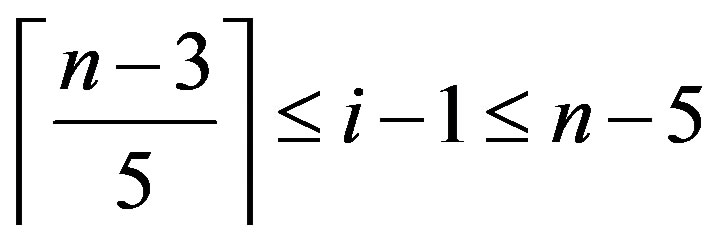 .
.
So
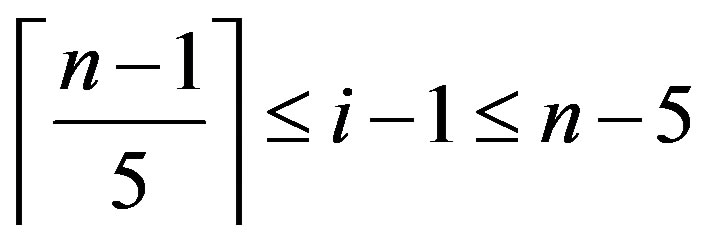
and hence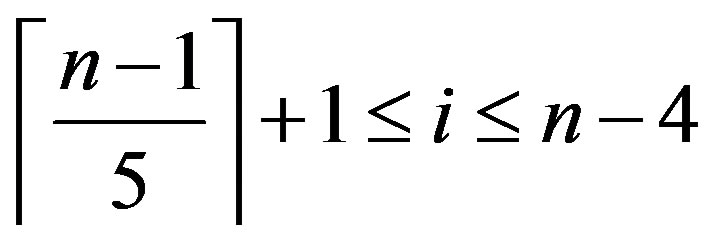 .
.
(Ü) If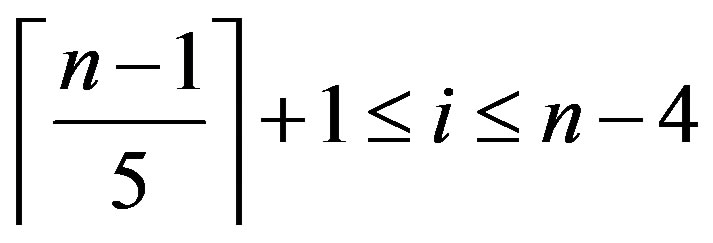 , then the result follows from Lemma 2.2.
, then the result follows from Lemma 2.2.
Theorem 2.7.: For every 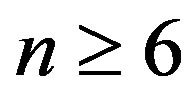 and
and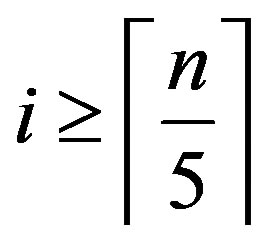 1) If
1) If

and
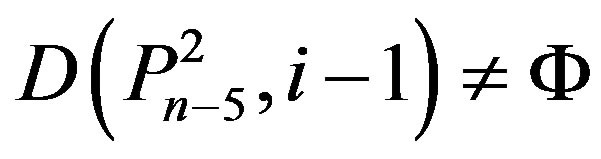
then
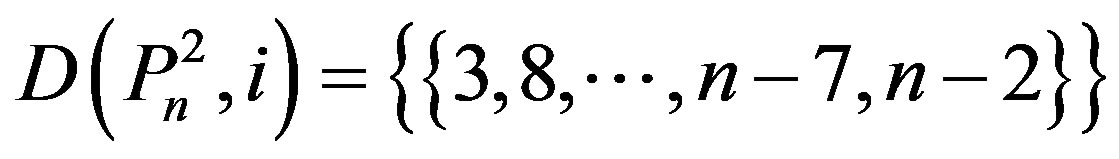 .
.
2) If
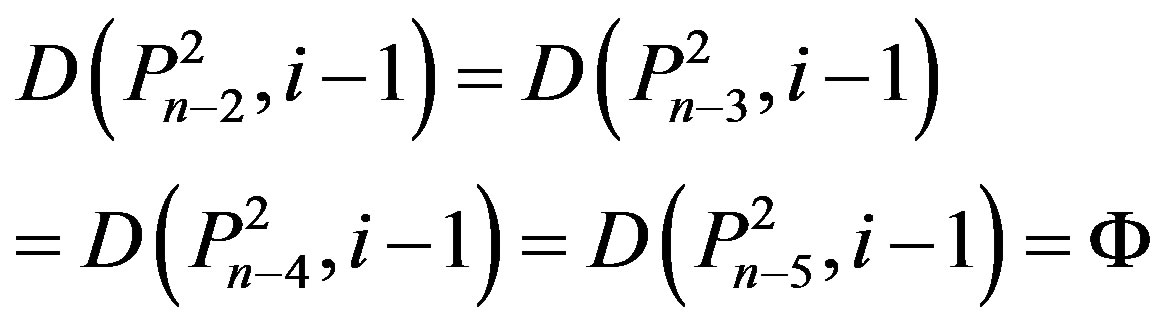
and
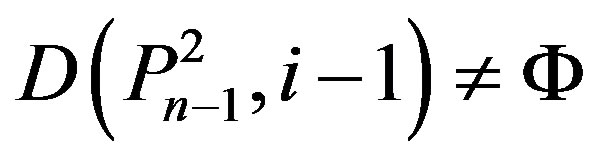
then
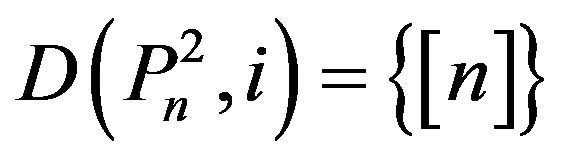 .
.
3) If
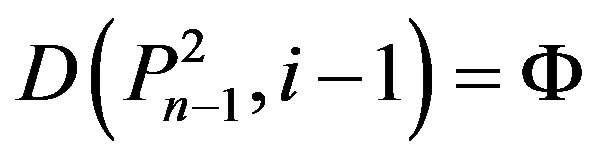 ,
,  ,
,
 ,
, 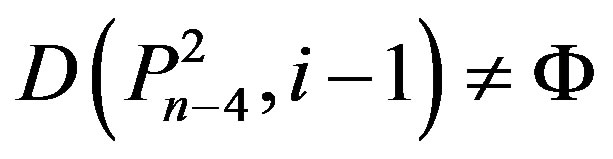
and
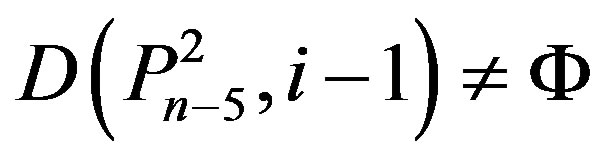
then
 (2.1)
(2.1)
4) If ,
,  ,
,
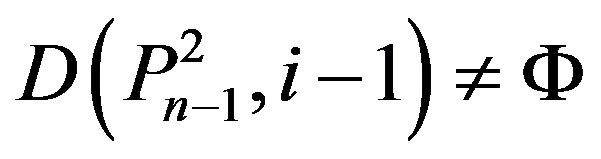 then
then
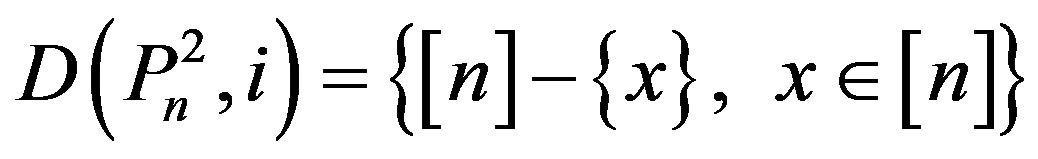 .
.
5) If
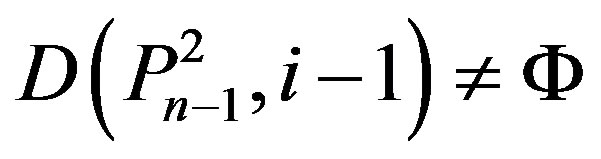 ,
, 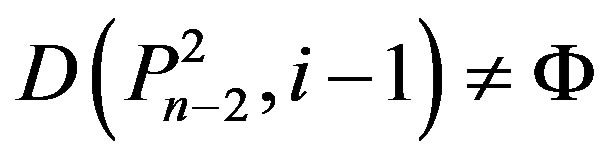 ,
,
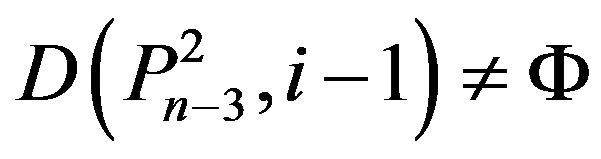 ,
, 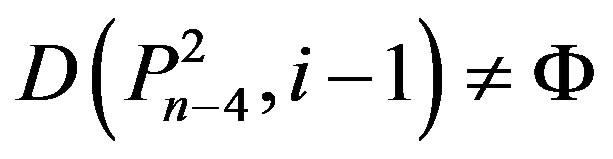 ,
, 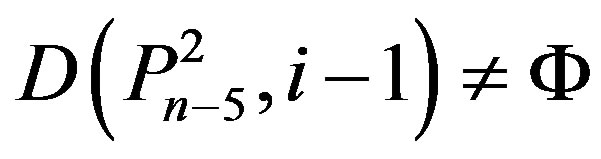
then
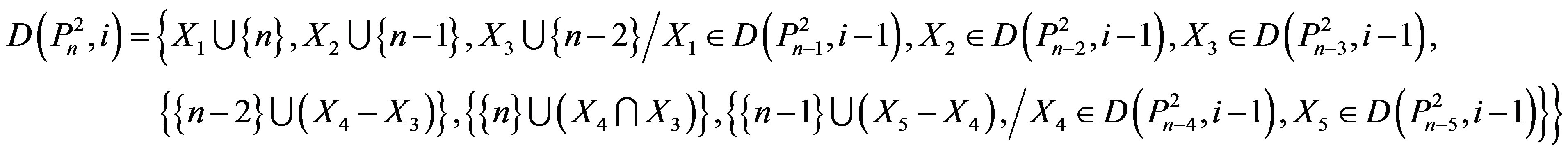 (2.2)
(2.2)
wang#title3_4:spwang#title3_4:spwang#title3_4:spwang#title3_4:spProof:
1) Since
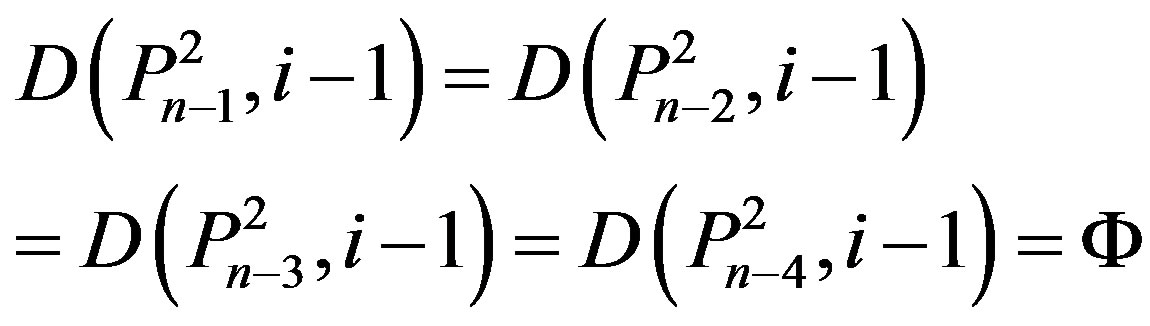
and 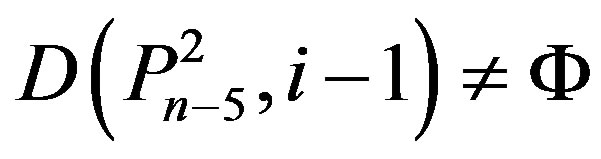 by Lemma 2.6 i) n = 5k, and i = k for some k Î N.
by Lemma 2.6 i) n = 5k, and i = k for some k Î N.
Clearly the set 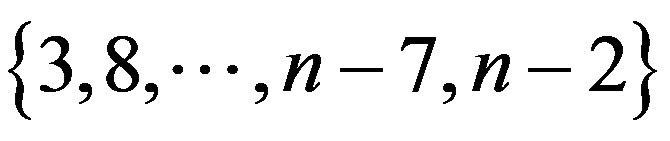 has
has 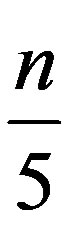 elements.
elements.
By the definition of , 3 has joining with 1, 2, 4, 5, and 8 has joining with 6, 7, 9, 10. Therefore 3 and 8 covers all the vertices up to10for n = 10. Proceeding like this, we obtain that
, 3 has joining with 1, 2, 4, 5, and 8 has joining with 6, 7, 9, 10. Therefore 3 and 8 covers all the vertices up to10for n = 10. Proceeding like this, we obtain that 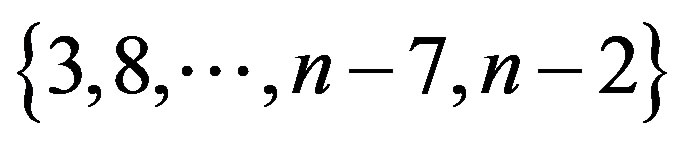 covers all Vertices up to n. The other sets with cardinality
covers all Vertices up to n. The other sets with cardinality 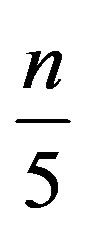 are
are
 ,
, 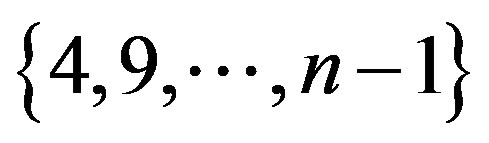 etc. In the first set,
etc. In the first set, 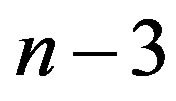 does not cover the vertex n. The second set does not cover the vertex 1and so on.
does not cover the vertex n. The second set does not cover the vertex 1and so on.
Therefore  is the only dominating set of cardinality
is the only dominating set of cardinality .
.
2) We have
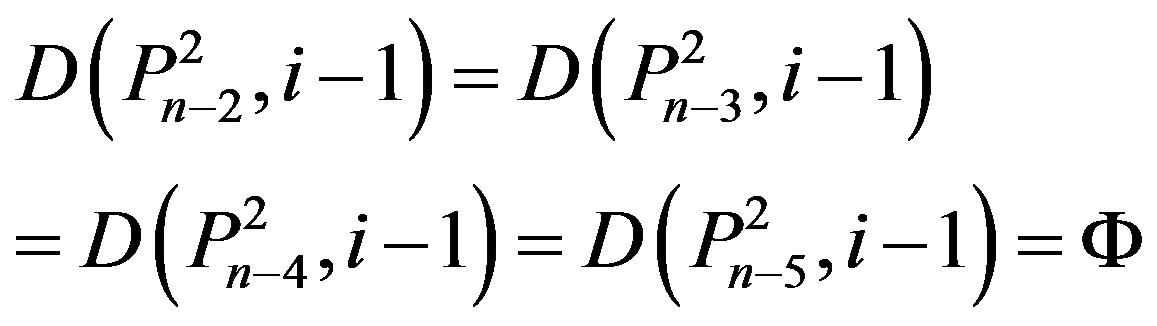
and
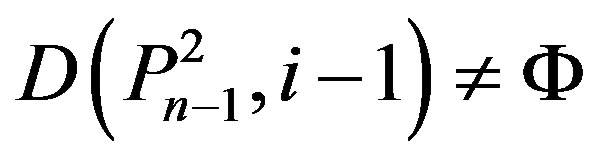 .
.
By Lemma 2.6 (ii), we have i = n. So,
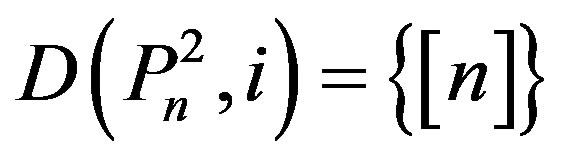 .
.
3) We have
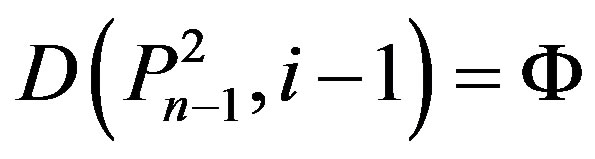 ,
, 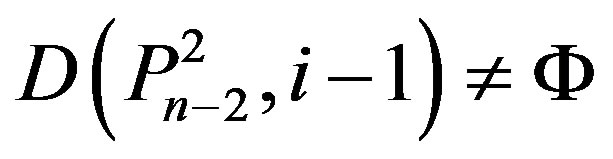 ,
,
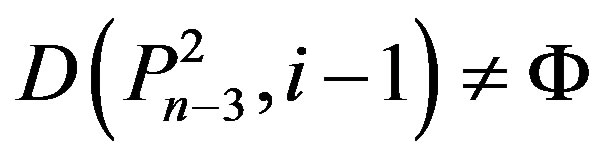 ,
, 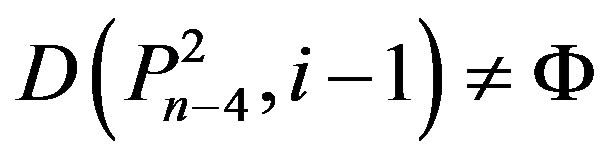
and
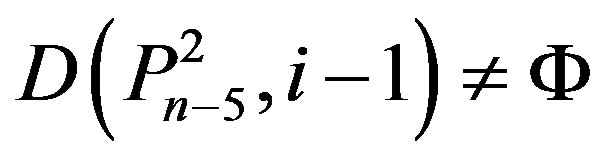 .
.
By Lemma 2.6 (iii), n = 5k + 2 and
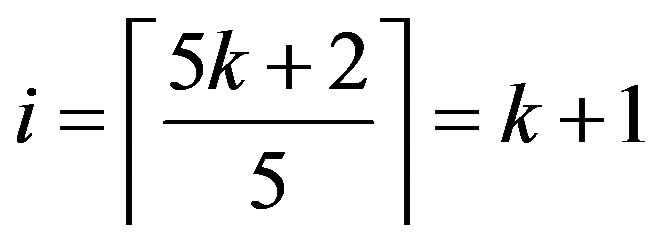
for some k Î N.
Since
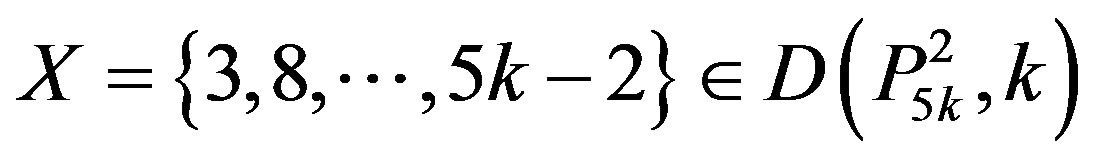 ,
,
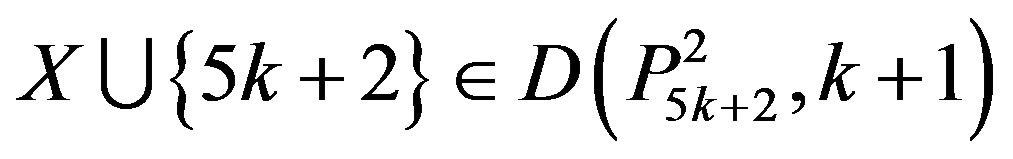 .
.
Also, if 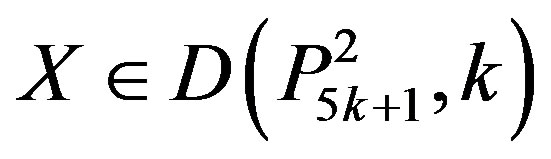 then
then
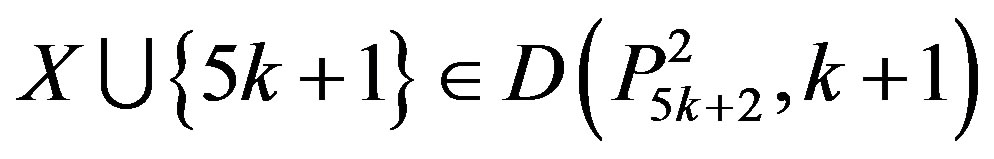
Therefore, we have
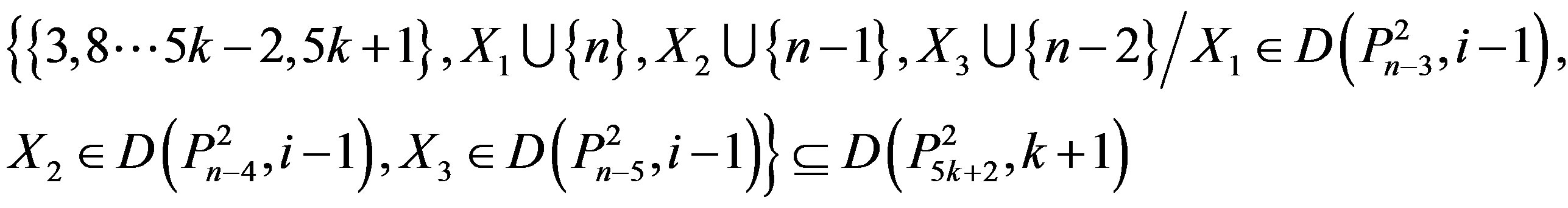 (2.3)
(2.3)
Now let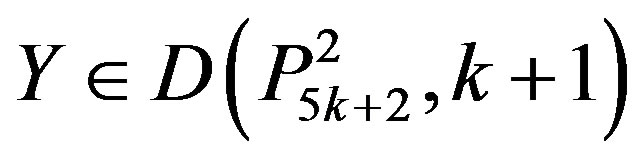 . Then 5k + 2, or 5k + 1 is in Y. If 5k + 2 ÎY, then by Lemma 3, at least one vertex labeled 5k + 1, 5k or 5k – 1 is in Y. If 5k + 1 or 5k is in Y, then
. Then 5k + 2, or 5k + 1 is in Y. If 5k + 2 ÎY, then by Lemma 3, at least one vertex labeled 5k + 1, 5k or 5k – 1 is in Y. If 5k + 1 or 5k is in Y, then
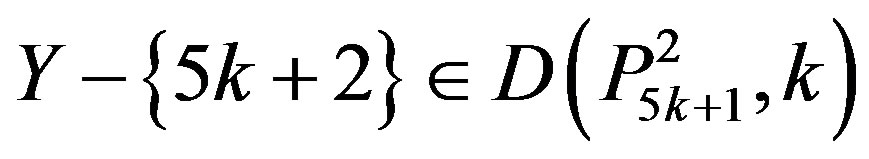 a contradiction; because
a contradiction; because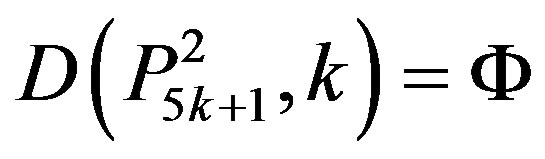 .
.
Hence 5k – 1 Î Y, 5k Ï Y and 5k + 1 Ï Y.
Therefore,  for some
for some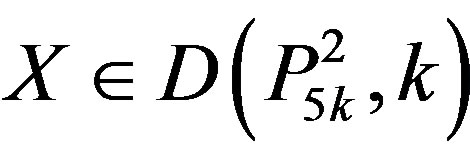 ;
;
that is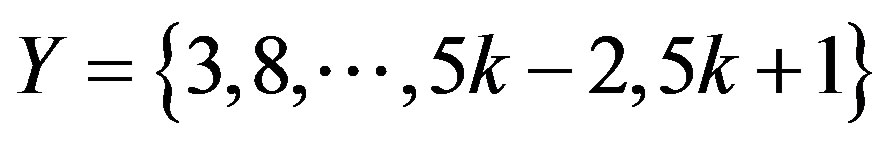 . Now suppose that 5k + 1 ÎY and 5k + 2 Ï Y. By Lemma 2.3 at least one vertex labeled 5k, 5k – 1 or 5k – 2 is in Y. If 5k Î Y then
. Now suppose that 5k + 1 ÎY and 5k + 2 Ï Y. By Lemma 2.3 at least one vertex labeled 5k, 5k – 1 or 5k – 2 is in Y. If 5k Î Y then
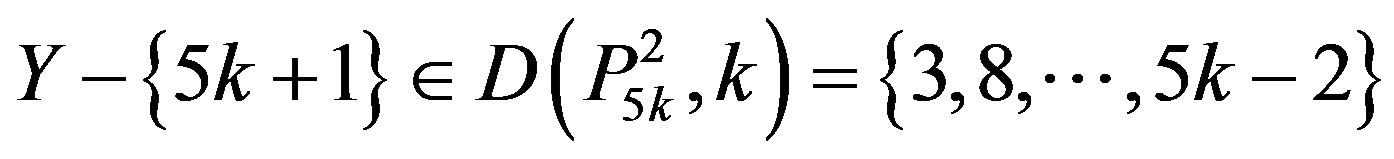 a contradiction because 5k Ï X for all
a contradiction because 5k Ï X for all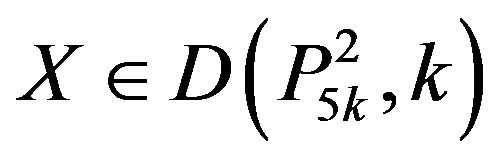 .
.
Therefore 5k – 1, or 5k – 2 is in Y, but 5kÏY.
Thus 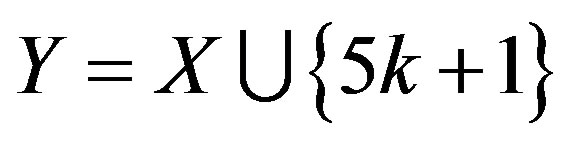 for some
for some . So
. So
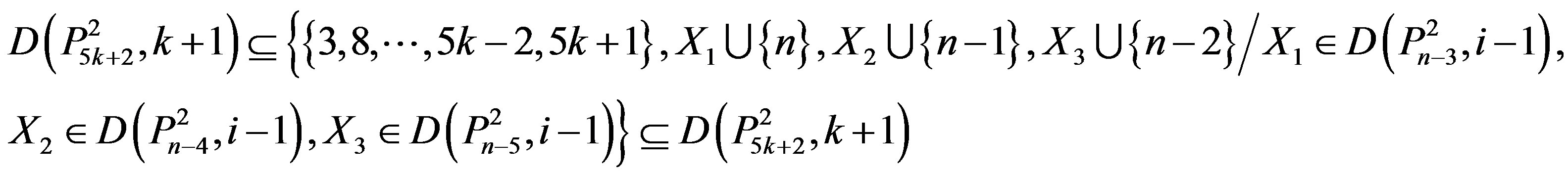 (2.4)
(2.4)
From (2.3) and (2.4),

4) If
 ,
,
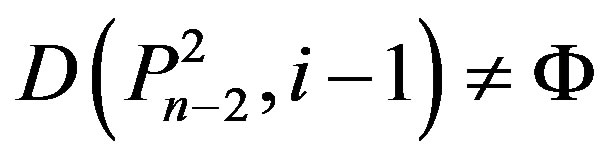 ,
,
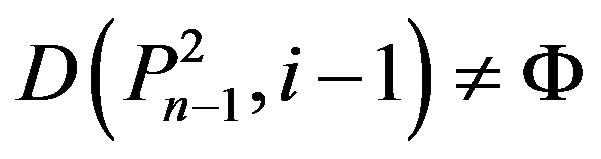 by Lemma 2.6 (iv) i = n – 1.
by Lemma 2.6 (iv) i = n – 1.
Therefore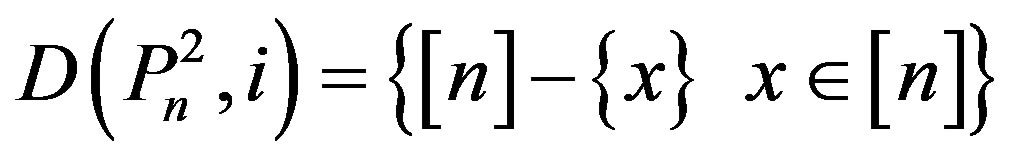 .
.
5) ,
, 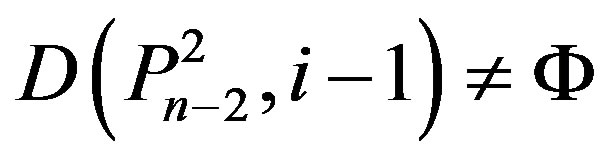 ,
,
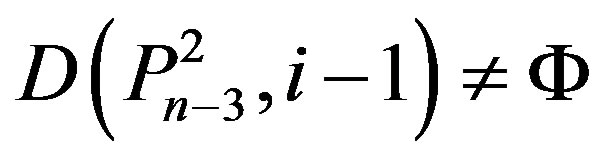 ,
, 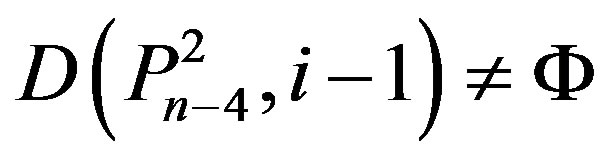 ,
,
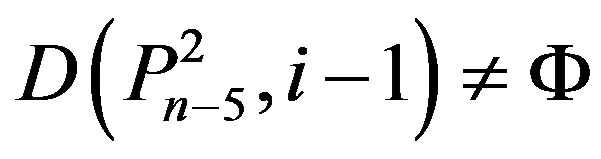 .
.
Let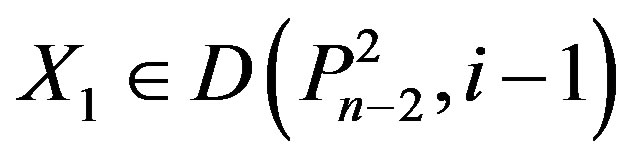 , so at least one vertex labeled n – 1, n – 2 or n – 3 is in X1. If n – 1, n – 2 or n – 3 ÎX1, then
, so at least one vertex labeled n – 1, n – 2 or n – 3 is in X1. If n – 1, n – 2 or n – 3 ÎX1, then
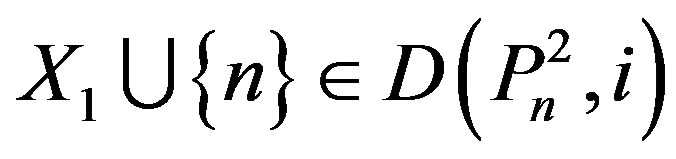 .
.
Let , then n – 2 or n – 3 or n – 4 is inX2.
, then n – 2 or n – 3 or n – 4 is inX2.
If n – 2, n – 3 or n – 4 Î X2, then
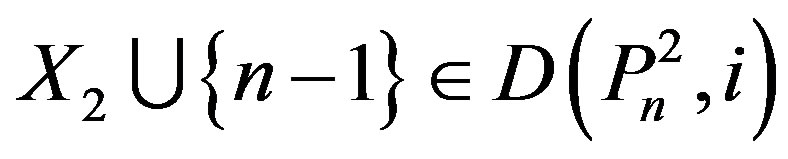 .
.
Now let 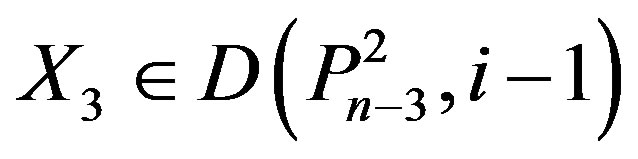 then n – 3, n – 4 or n – 5 is in X3. If n – 3 or n – 4 or n – 5 Î X3, then
then n – 3, n – 4 or n – 5 is in X3. If n – 3 or n – 4 or n – 5 Î X3, then
 .
.
Now let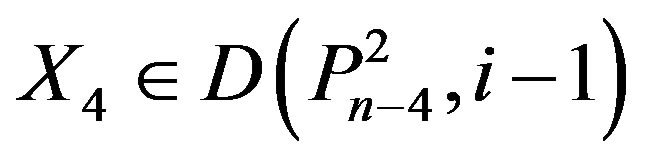 , then n – 4, or n – 5 or n – 6 is in X4.
, then n – 4, or n – 5 or n – 6 is in X4.
If n – 4 Î X4, then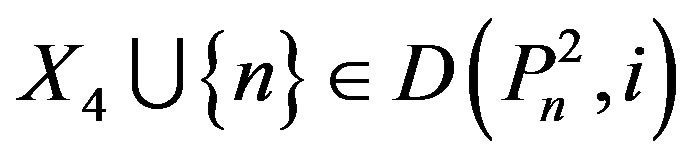 . If n – 5 Î X4, then
. If n – 5 Î X4, then
 .
.
If n – 6 Î X4, then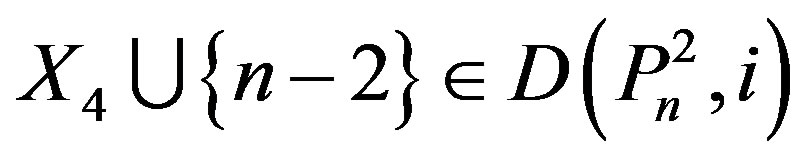 . Thus we have
. Thus we have
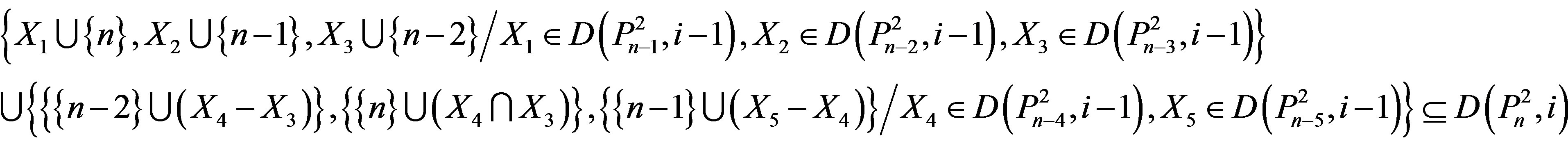 (2.5)
(2.5)
Now suppose that n – 1Î Y, n Î Y then by Lemma 2.3, at least one vertex labeled n – 2, n – 3 or in Y. If n – 2 Î Y then  for some
for some
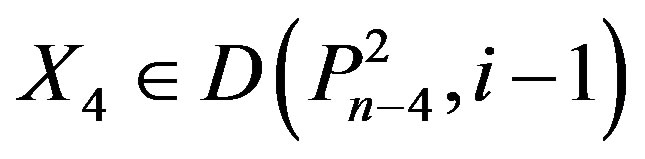 ,
, 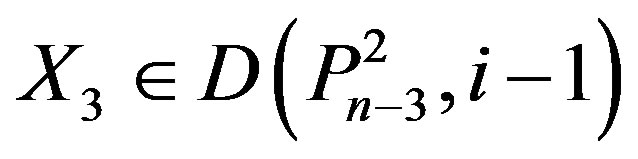 .
.
Now suppose that, n – 5 ÎY & n – 4 Î Y, then by Lemma 2.3 one vertex labeled n – 6, n – 7, in Y.
If n – 4 Î Y, then 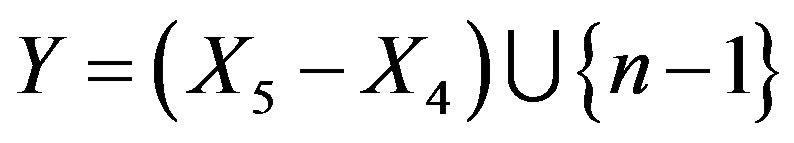 for
for
 ,
, 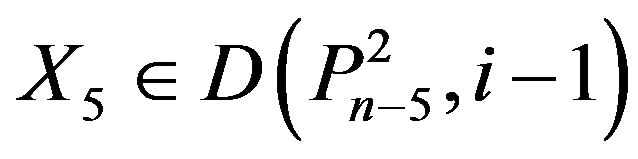 So
So
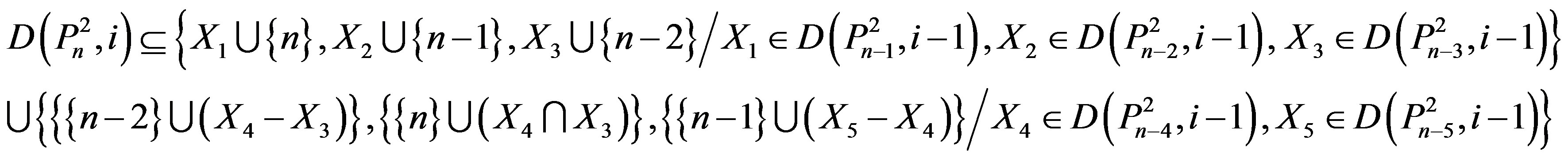 (2.6)
(2.6)
From (2.5) & (2.6)
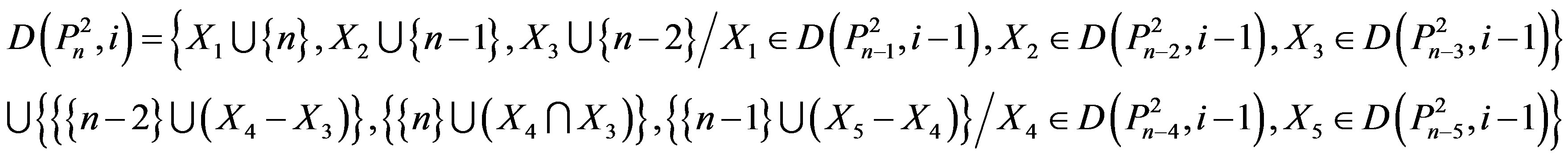
3. Domination polynomial of 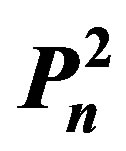
Let 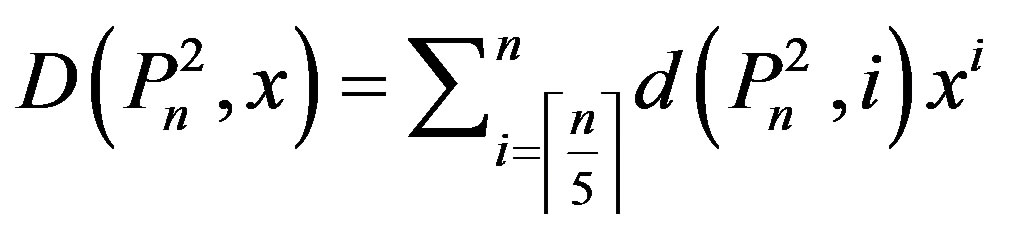 be the domination polynomial of a path
be the domination polynomial of a path . In this section, we derive the expression for
. In this section, we derive the expression for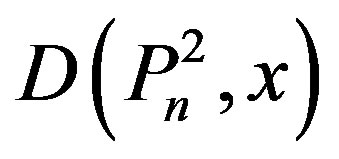 .
.
Theorem 3.1.
a) If 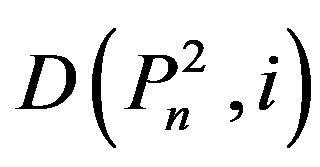 is the family of dominating sets with cardinality i of
is the family of dominating sets with cardinality i of , then
, then
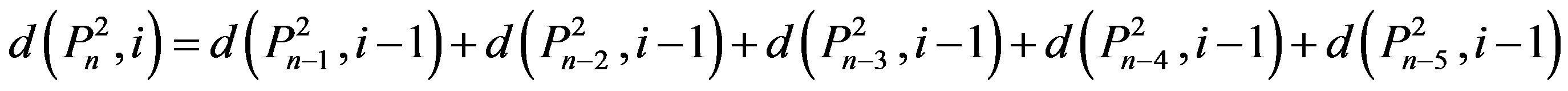
where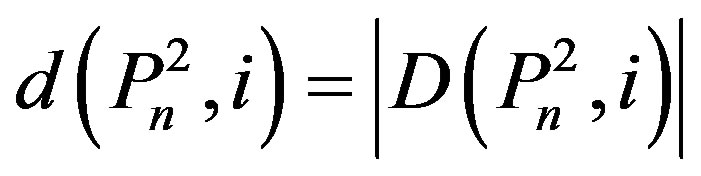 .
.
b) For every ,
,
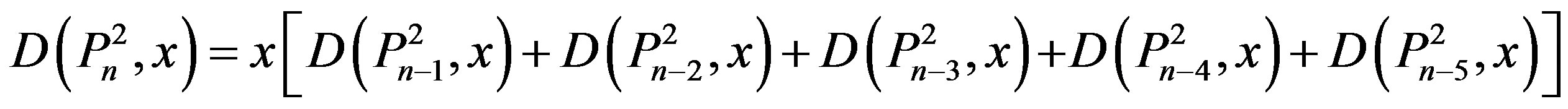
with the initial values
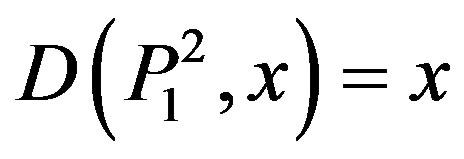 ,
,  ,
,
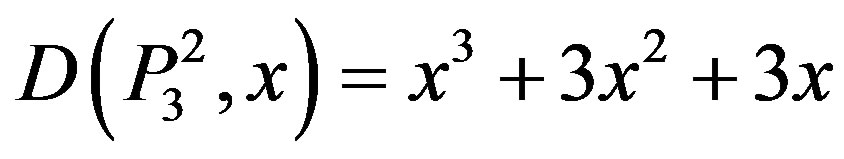 ,
,
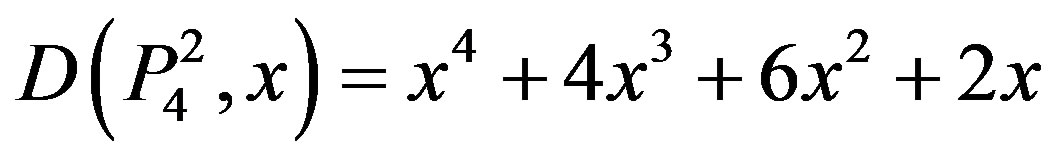 ,
,
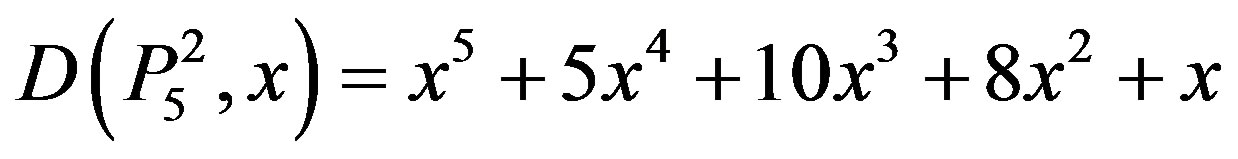 .
.
wang#title3_4:spwang#title3_4:spwang#title3_4:spwang#title3_4:spProof:
a) Using (i), (ii), (iii), (iv) and (v) of Theorem 2.7, we prove (a) part.
1) Suppose (i) of Theorem 2.7 holds.
From (v), we have
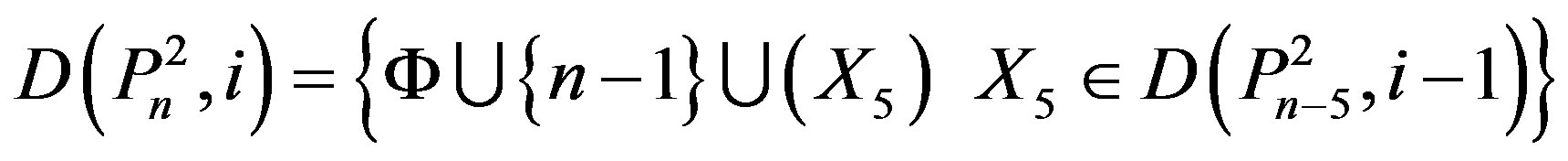 .
.
Since
 ,
,
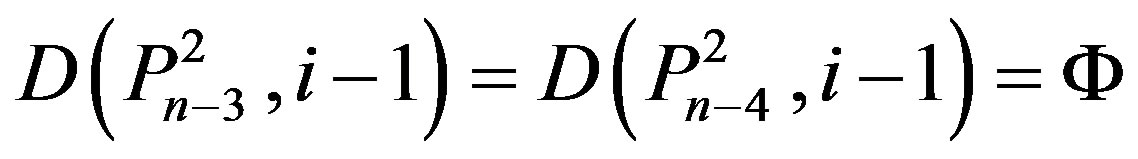
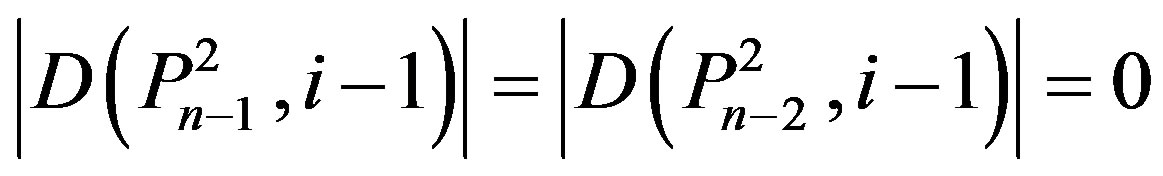
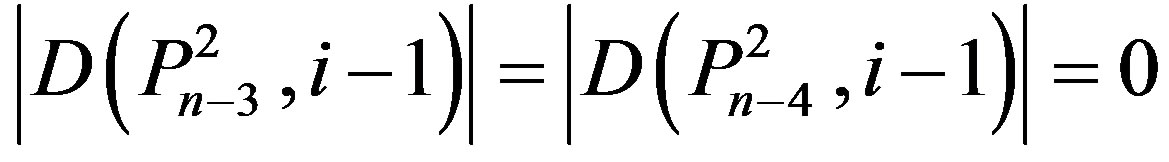
Therefore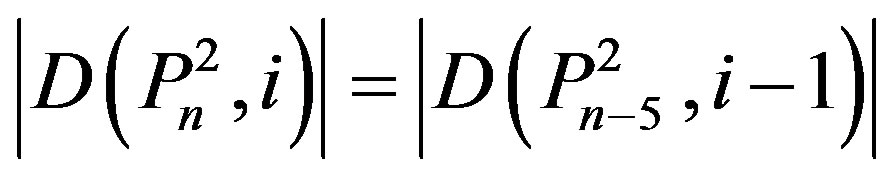 .
.
Therefore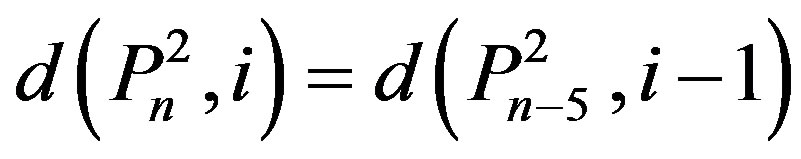 .
.
Therefore, in this case 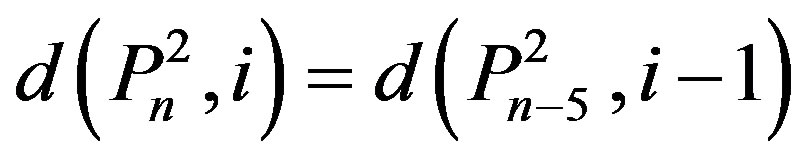 holds.
holds.
2) Suppose (ii) of Theorem 2.7 holds.
From (v), we have
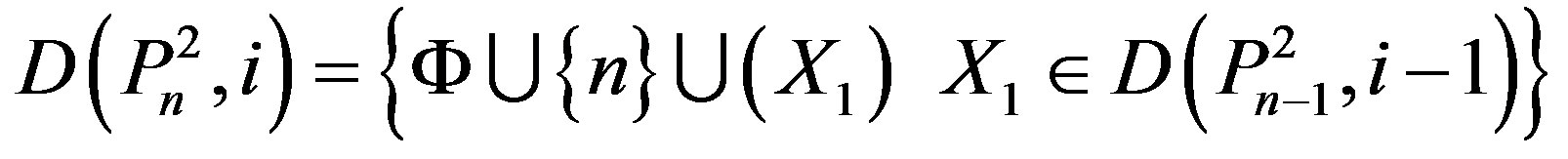 .
.
Since 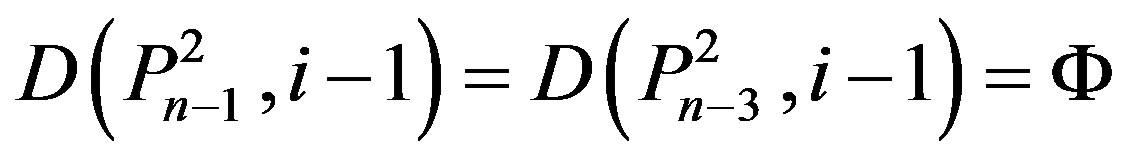


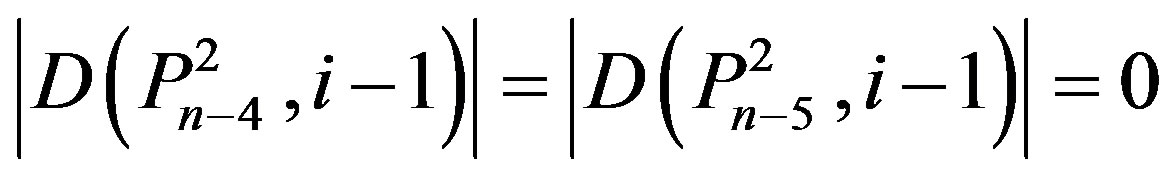
Therefore 
Therefore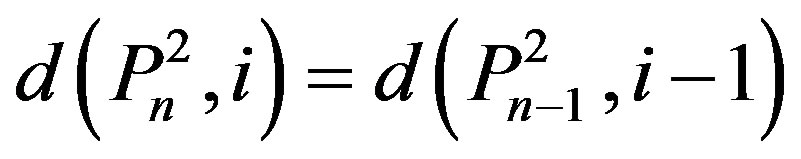 .
.
Therefore, In this case 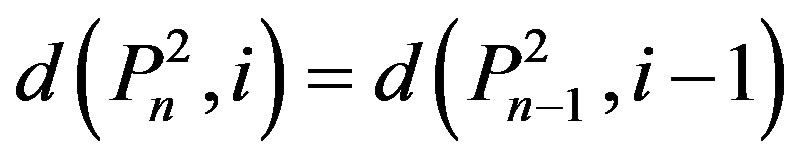 holds.
holds.
3) Suppose (iii) of Theorem 2.7 holds.
From (v), we have
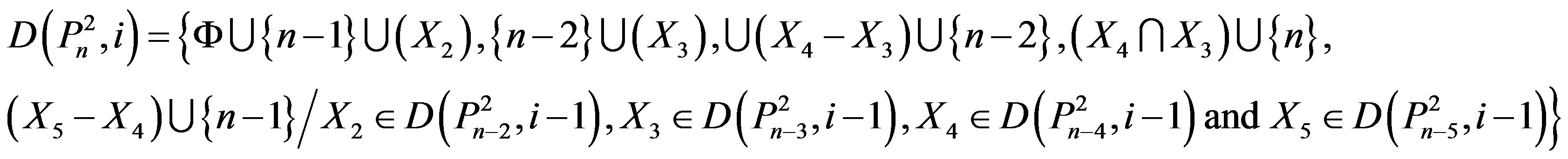 .
.
Since
 ,
,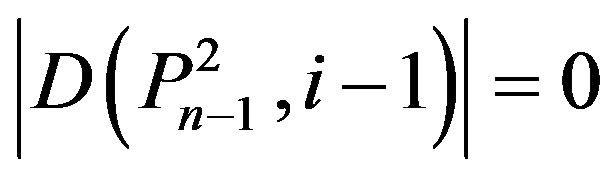 .
.
Therefore
 .
.
Therefore
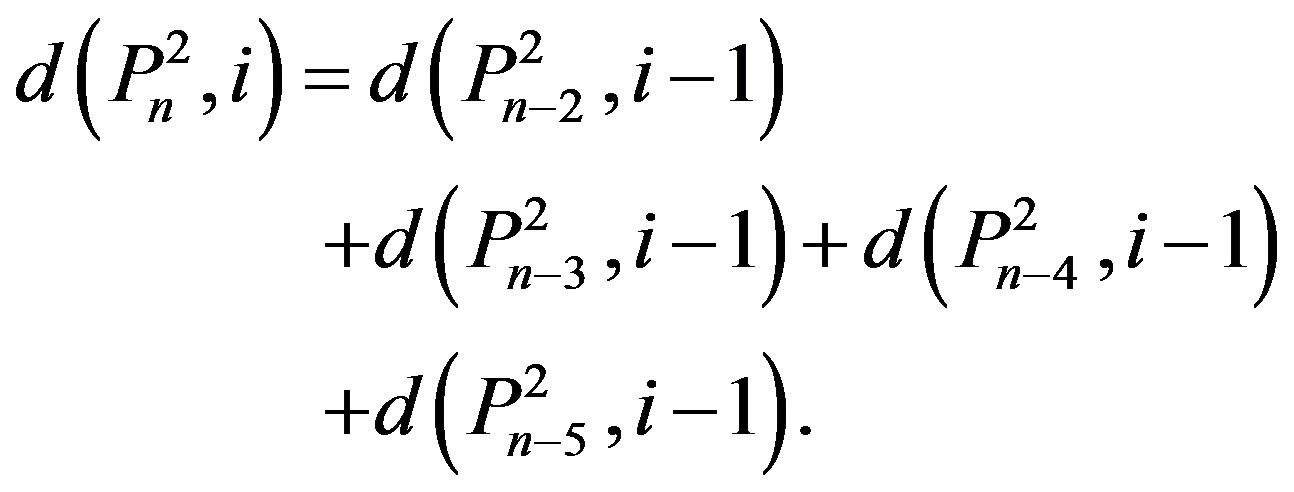 .
.
4) Suppose (v) of Theorem 2.7 holds.
From (v), we have

Therefore
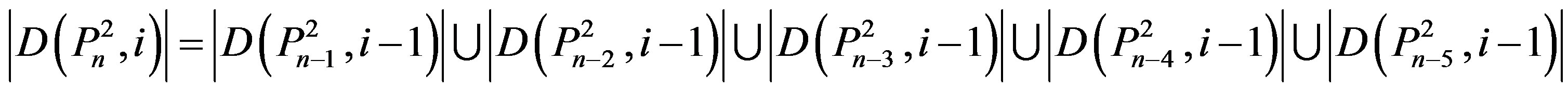 .
.
Therefore
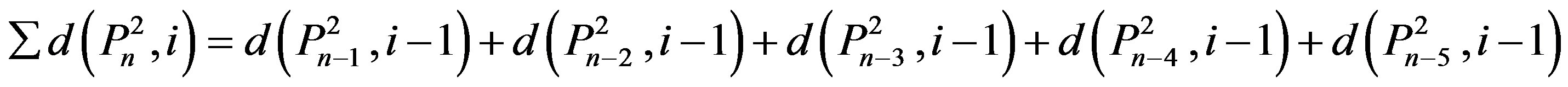 .
.
Therefore, we have the theorem.
b)
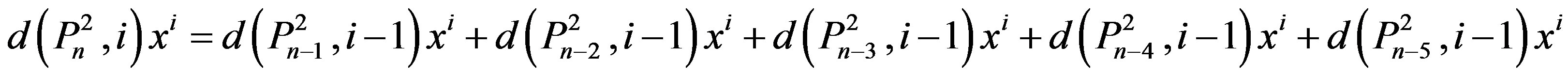
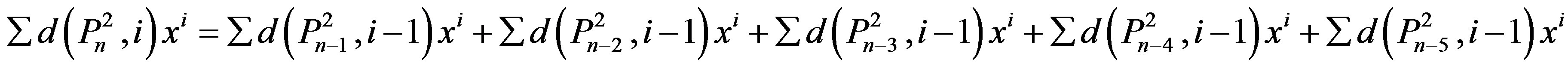
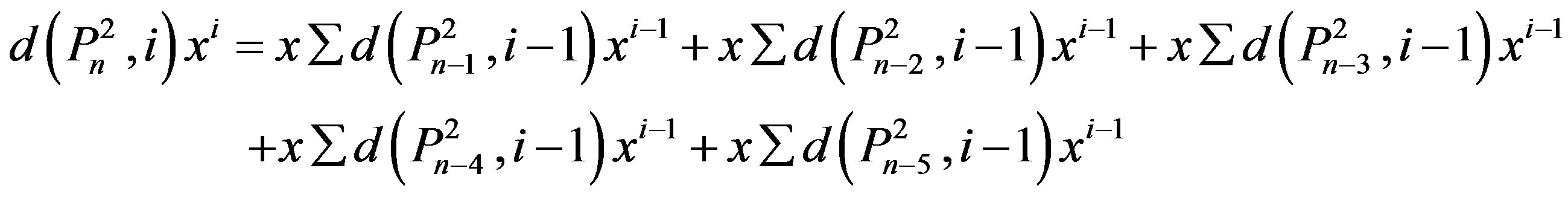
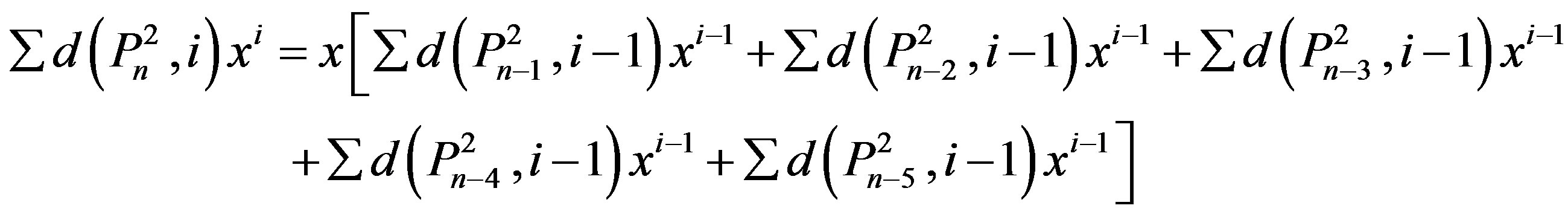
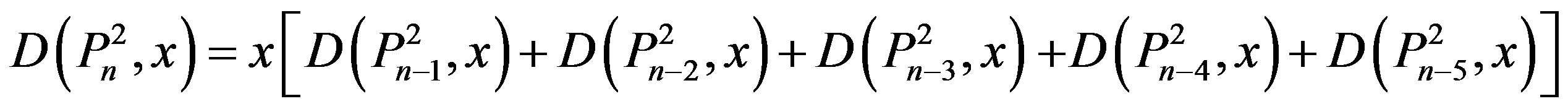
with the initial values
 ,
,
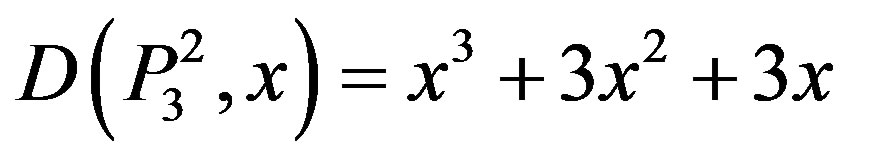
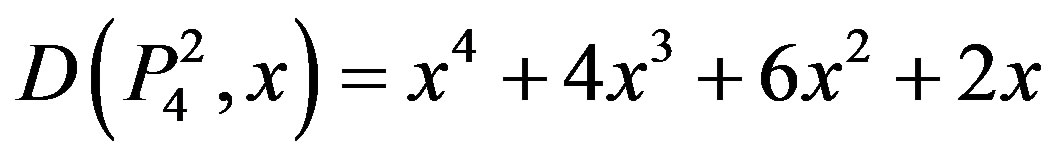 ,
,
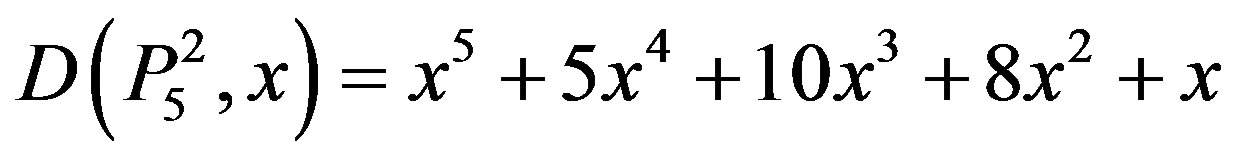 .
.
We obtain 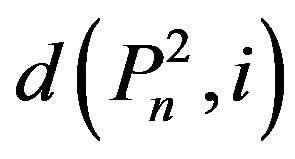 for 1 ≤ n ≤ 10 as shown in Table 1.
for 1 ≤ n ≤ 10 as shown in Table 1.
Table 1.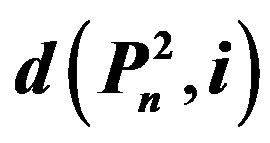 , the number of dominating set of
, the number of dominating set of with cardinality i.
with cardinality i.

In the following Theorem, we obtain some properties of 
Theorem 3.2. The following properties hold for the coefficients of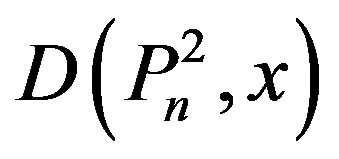 ;
;
1) 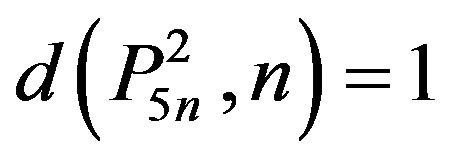 for every n Î N.
for every n Î N.
2) 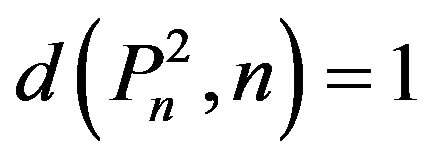 for every n Î N 3)
for every n Î N 3)  for every
for every 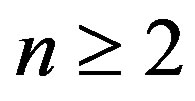
4) 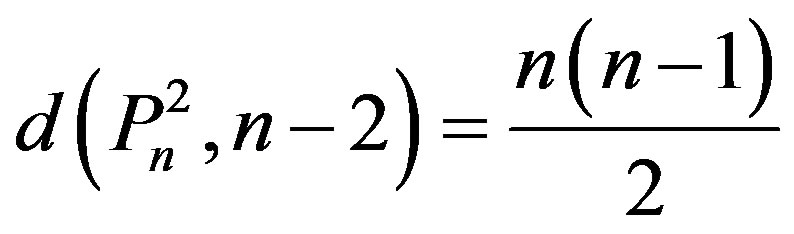 for every
for every 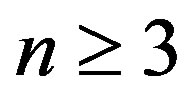
5) 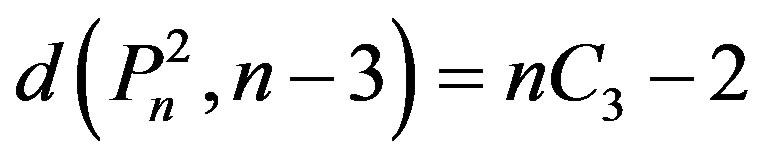 for every
for every 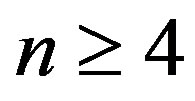
6) 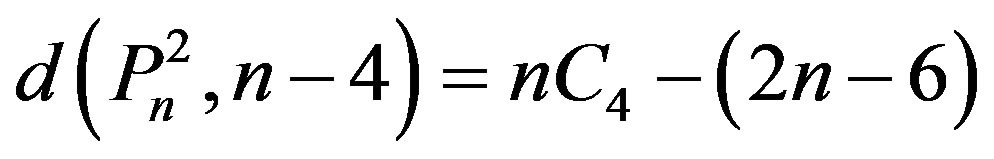 for every
for every 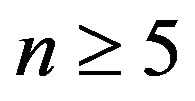
7) 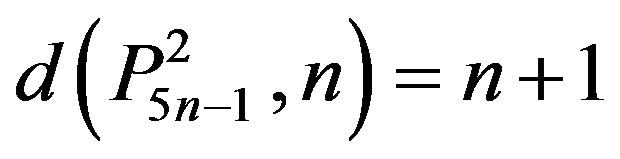 for every n Î N.
for every n Î N.
wang#title3_4:spwang#title3_4:spwang#title3_4:spwang#title3_4:spProof:
1) Since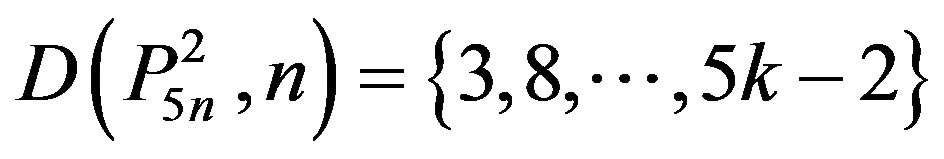 , we have
, we have 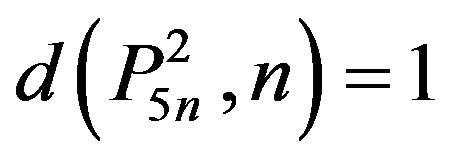 .
.
2) Since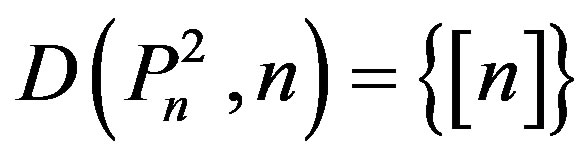 , we have the result 3) Since
, we have the result 3) Since , we have
, we have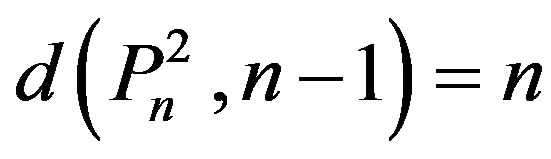 .
.
4) By induction on n. The result is true for n = 3.
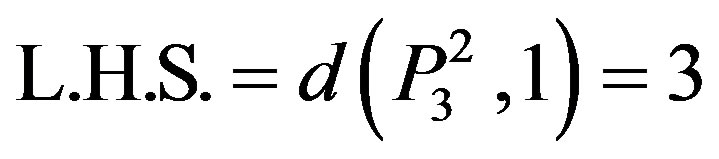 (from table)
(from table)
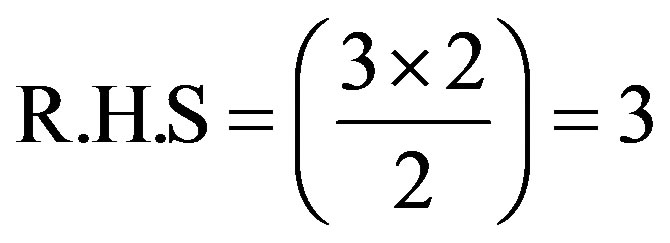
Therefore, the result is true for n = 4.
Now suppose that the result is true for all numbers less than “n” and we prove it for n.
By Theorem 3.1,
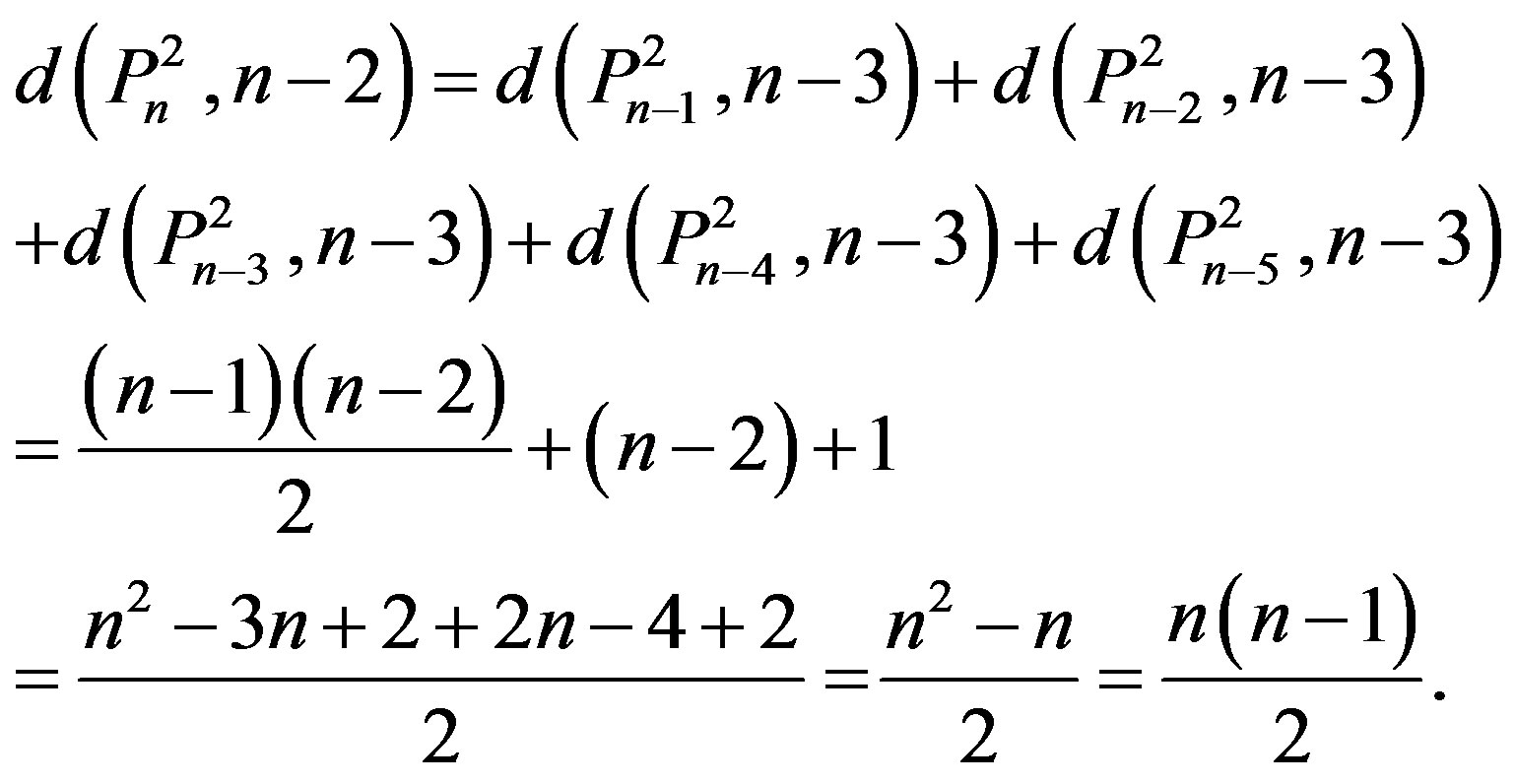
5) By induction on n. The result is true for n = 4.
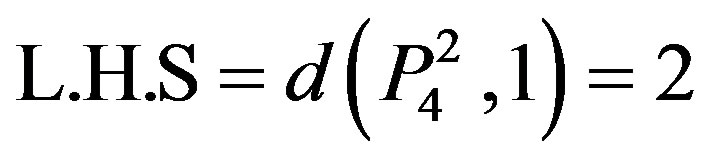 (from table)
(from table)
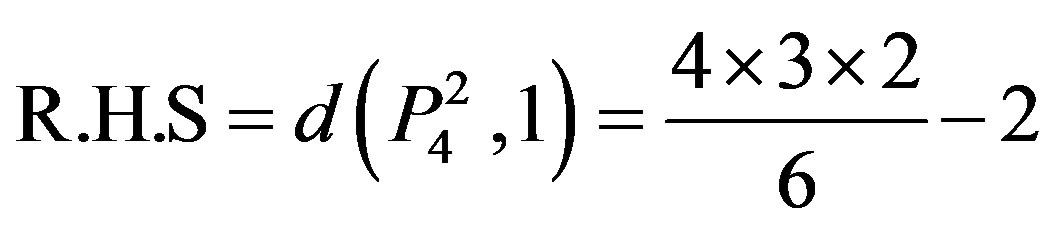
Therefore the result is true for n = 1. Now suppose the result is for all natural numbers less than n.
By Theorem 3.1,
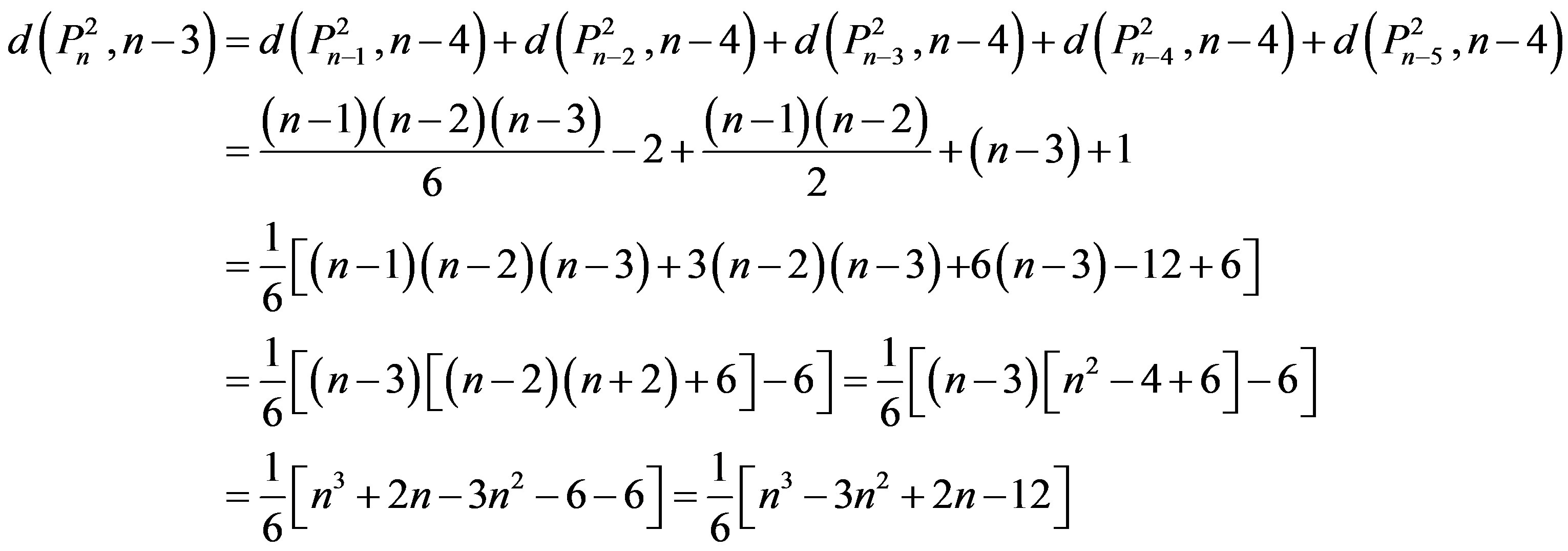
6) By induction on n. Let n = 5
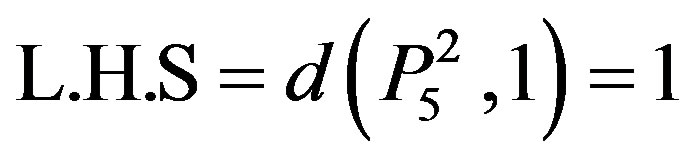 (from table)
(from table)
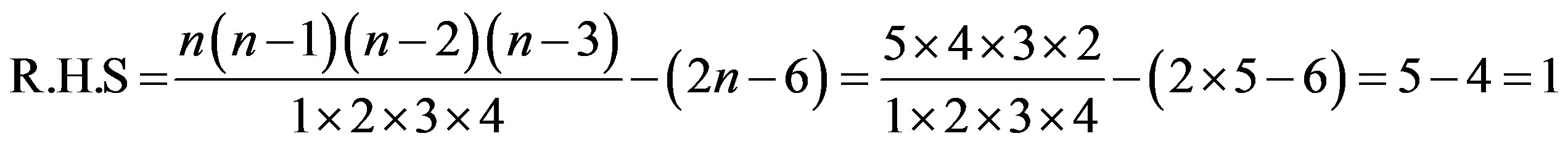
Therefore the result is true for n =1.
Now suppose that the result is true for all natural numbers less than or equal to n.
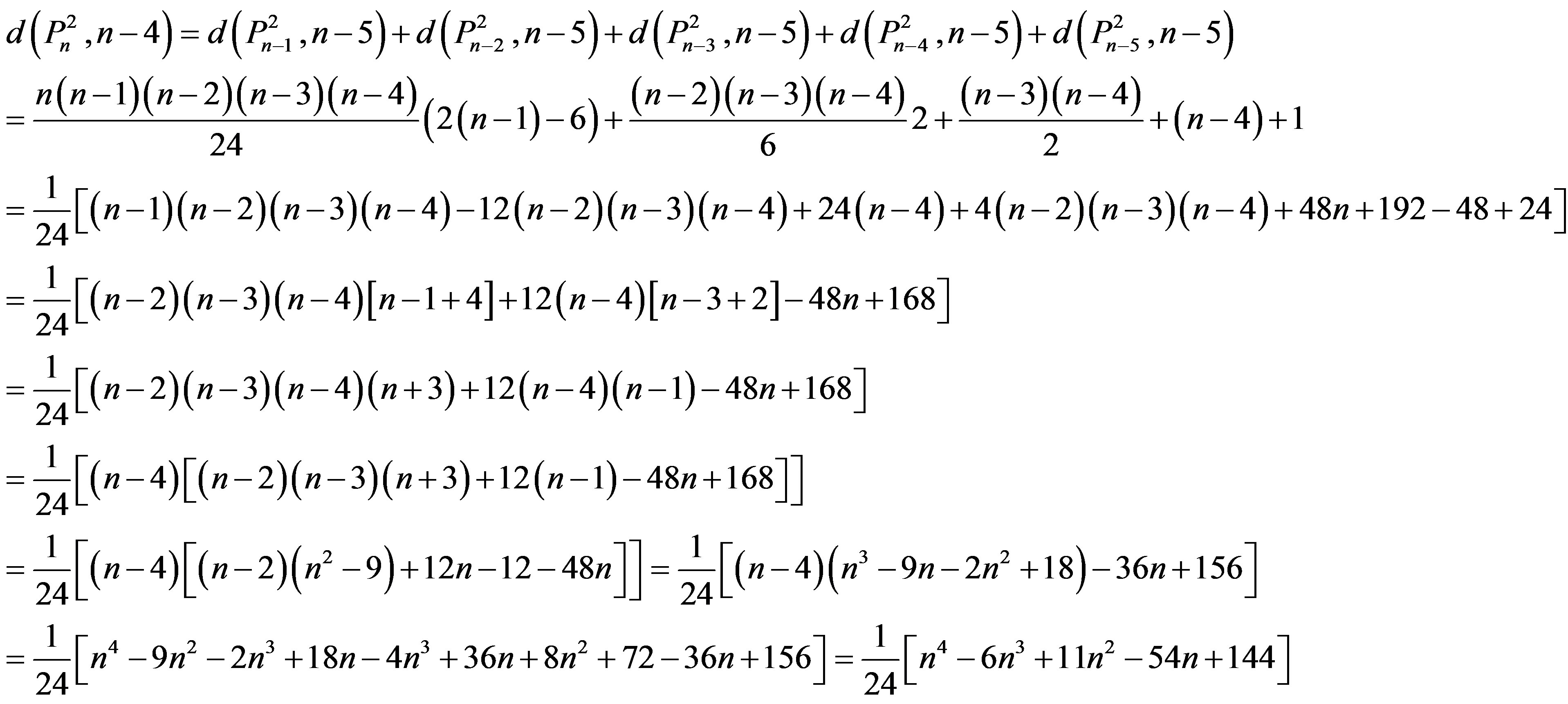
7) From the table it is true.
Theorem 3.3.
1) 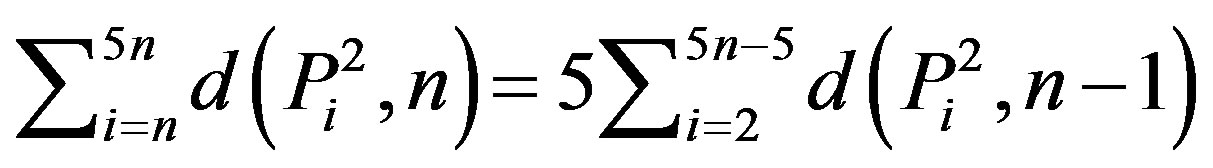
2) For every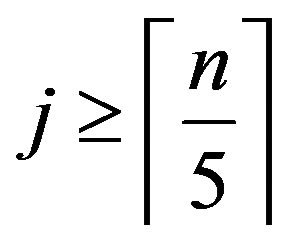 ,
,

3) If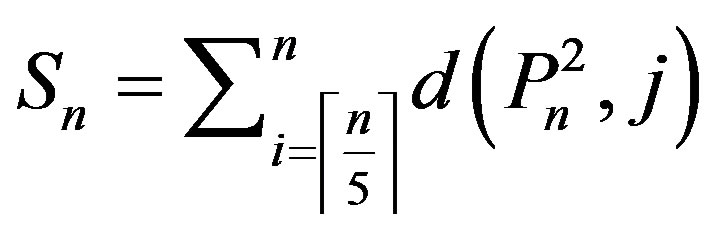 , then for every n ≥ 6,
, then for every n ≥ 6,
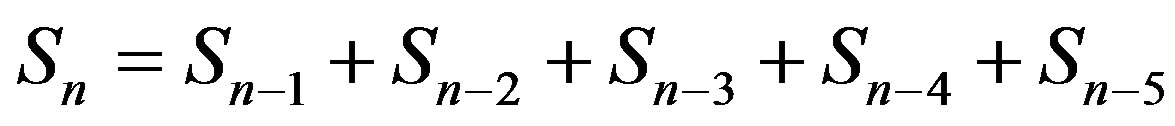 with initial values S1
with initial values S1
= 1, S2 = 3, S3 = 7, S4 = 13 and S5 = 25.
wang#title3_4:spwang#title3_4:spwang#title3_4:spwang#title3_4:spProof:
1) Proof by induction on n First suppose that n = 2 then,
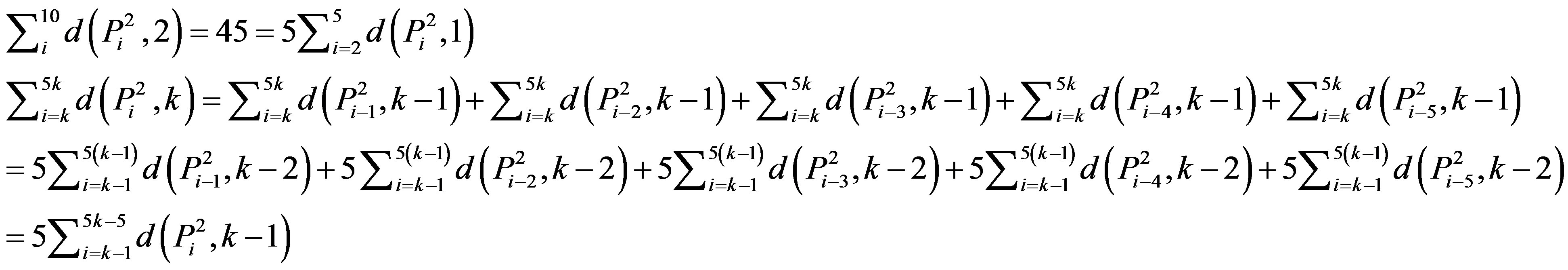
We have the result.
2) By Theorem 3.1, We have
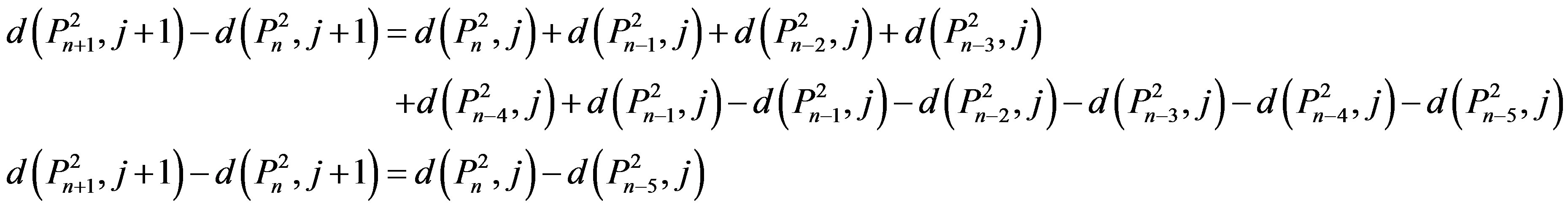
Therefore we have the result 3) By theorem (3.1), we have
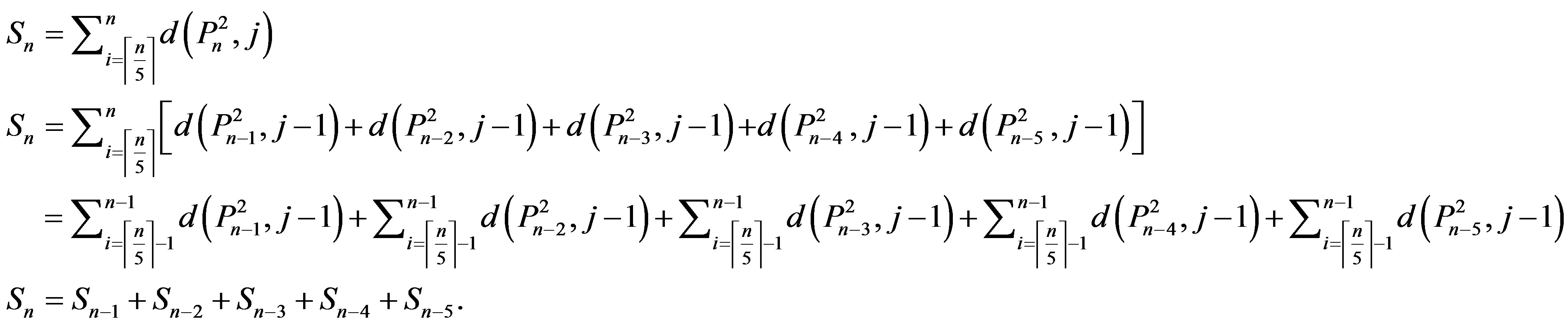 .
.
4. Conclusions
In [2], the domination polynomial of path was studied and obtained the very important property,
 .
.
It is interesting that we have derived an analogues relation for the square of path of the form
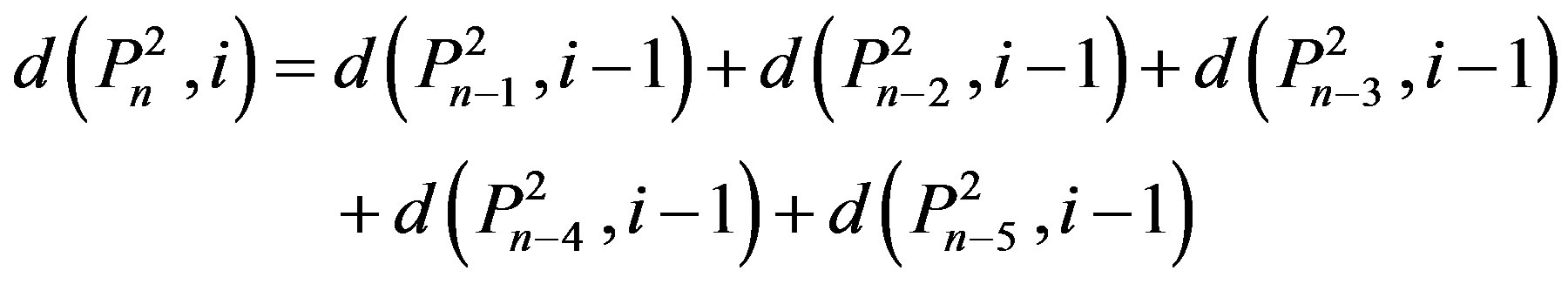
One can characterise the roots of the polynomial  and identify whether they are real or complex. Another interesting character r to be investigated is whether
and identify whether they are real or complex. Another interesting character r to be investigated is whether 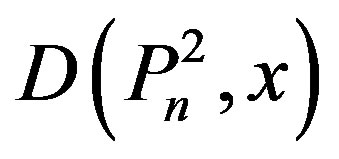 is log concave are not.
is log concave are not.
REFERENCES
- S. Alikhani and Y.-H. Peng, “Introduction to Domination Polynomial of a Graph,” .arXiv:0905.2251v1[math.co], 2009.
- S. Alikhani and Y.-H. Peng, “Domination Sets and Domination Polynomials of Paths,” International Journal of Mathematics and Mathematical Sciences, Vol. 2009, 2009, Article ID: 542040.
- G. Chartand and P. Zhang, “Introduction to Graph Theory,” McGraw-Hill, Boston, 2005.

