American Journal of Computational Mathematics
Vol.2 No.2(2012), Article ID:20136,7 pages DOI:10.4236/ajcm.2012.22021
Solution of Singular Integrals in Mathematical Model of Mode I Crack Near Strength Mismatched Interface
1School of Mechanical and Building Sciences, VIT University, Vellore, India
2Department of Mechanical Engineering, Indian Institute of Technology, Mumbai, India
Email: sbhat_789@rediffmail.com
Received April 5, 2012; revised May 2, 2012; accepted May 10, 2012
Keywords: Crack Opening Displacement; Singular Integrals; Strength Mismatch; Weld Interface; Cauchy’s Principal Value Theorem
ABSTRACT
Characteristics of Mode I crack near the interface of elasticity matched but plasticity and strength mismatched materials differ from those of the crack in a homogenous body. Interface body of different strength influences the plastic or cohesive zone at the crack tip in parent body. The mathematical model for load line opening of the crack near the interface in linear elastic regime involves singular integrals. The paper presents explicit solution of these integrals with the help of Cauchy’s principal value theorem. Cases of thin and thick welds between the materials are investigated. Solutions of the integrals are well substantiated. Final results are provided in a consolidated form.
1. Introduction
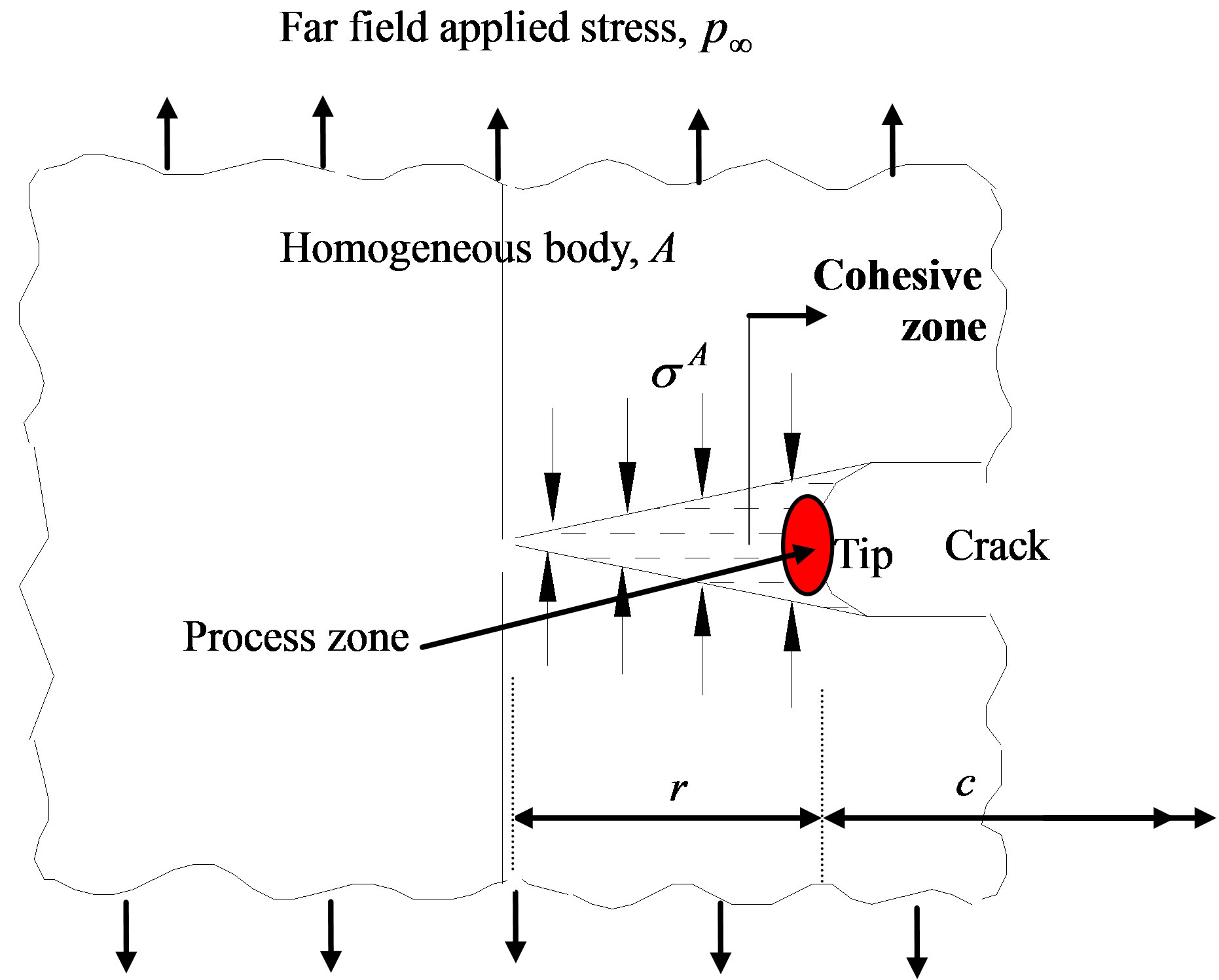
The material behaviour at the tip of the Mode I crack in a homogenous body is in general very complex and difficult to describe by continuum mechanical models. The crack tip region where the material undergoes degradation or damage is known as the process region. Refer Figure 1(a). Micro-mechanical processes, viz. microcracking in brittle materials and void initiation and coalescence in ductile materials create new traction free surfaces or cracks in process region. Yielding occurs outside the process region. This zone is called as the plastic or cohesive zone. Cohesive zone is considered as the crack extension under the action of closing cohesive stress generated by elastic constraint exerted by surrounding non-yielded material over the cohesive zone. The cohesive stress is assumed equal to material yield strength in plane stress and 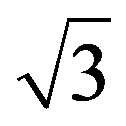 times the yield strength in plane strain conditions. Qualitative characteristics of the cohesive zone were experimentally verified by Hahn et al. [1]. They conducted experiments on cracked steel specimens and found the cohesive zone, as shown in Figure 1(b), by etching the polished surface in front of the crack tip.
times the yield strength in plane strain conditions. Qualitative characteristics of the cohesive zone were experimentally verified by Hahn et al. [1]. They conducted experiments on cracked steel specimens and found the cohesive zone, as shown in Figure 1(b), by etching the polished surface in front of the crack tip.
In a bimaterial comprising elasticity identical but plasticity and strength mismatched constituents (like steels), the Mode I crack near the interface has the characteristics similar to the one in homogeneous parent body as long as the cohesive zone is in the parent body alone. The effect of approaching interface body of different strength is not felt by the crack in such a stage because of similar elastic properties across the interface. But as the crack grows and reaches nearer to the interface, the increasing magnitude of crack tip stress field causes the cohesive zone to develop in the interface body. Consequently, the part of cohesive zone in the interface body is subjected to cohesive stress different from that acting over its portion in the parent body that triggers the effect of strength mismatch across the interface over the crack tip. The effect continues with increasing intensity as the cohesive zone spreads deeper into the interface body with crack growth and reaches the maximum when the crack tip touches the interface body with the cohesive zone fully in the interface body.
Cases of thin and thick welds between the steels are examined. Thin weld, obtained by non-fusion, solid state like friction welding between dissimilar steels leads to a single thin interface whereas a thick weld by fusion bonding from electron or laser beam welding results in two interfaces, one between the parent body and the weld and the other between the weld and the interface body. The parent body, the weld and the interface body have similar elastic properties but variable strengths of comparable magnitudes.
2. Problem Definition
Solution for load line opening of the crack is obtained by modeling its cohesive zone. Complex potentials are used
 (a)
(a)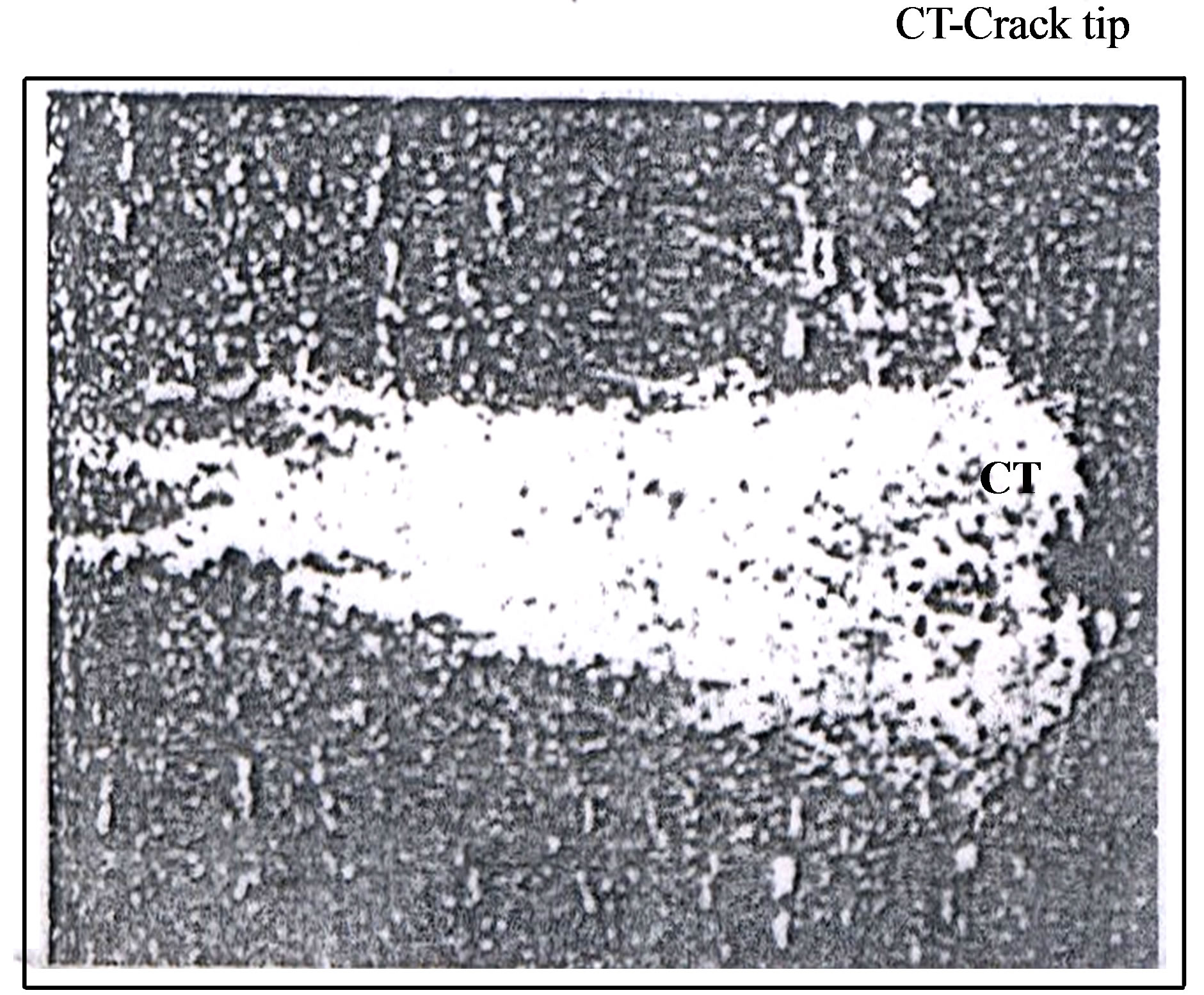 (b)
(b)
Figure 1. Crack tip cohesive zone and its experimental validation; (a) Crack tip cohesive zone; (b) Cohesive zone observed experimentally by Hahn et al. [1].
for this purpose in linear elastic regime.
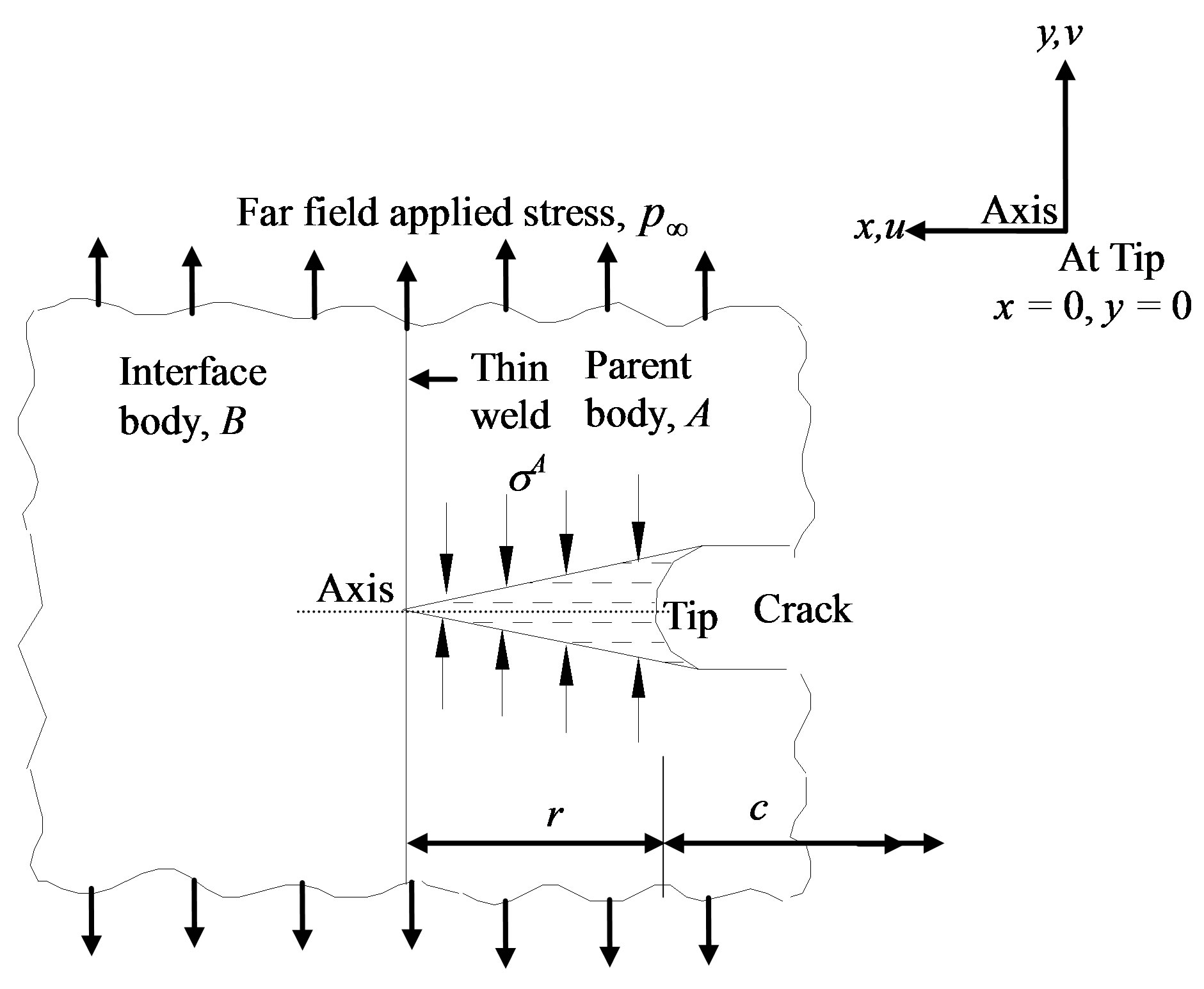
2.1. Crack Near Thin Weld (Refer Figure 2)
Half load line crack opening, v, in the cohesive zone of size, r, in parent body A in stage I, Figure 2(a), subjected to cohesive stress, 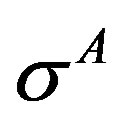 , under far field applied stress intensity parameter,
, under far field applied stress intensity parameter, 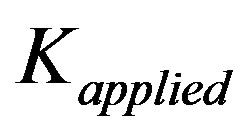 , is of the following form [2]:
, is of the following form [2]:
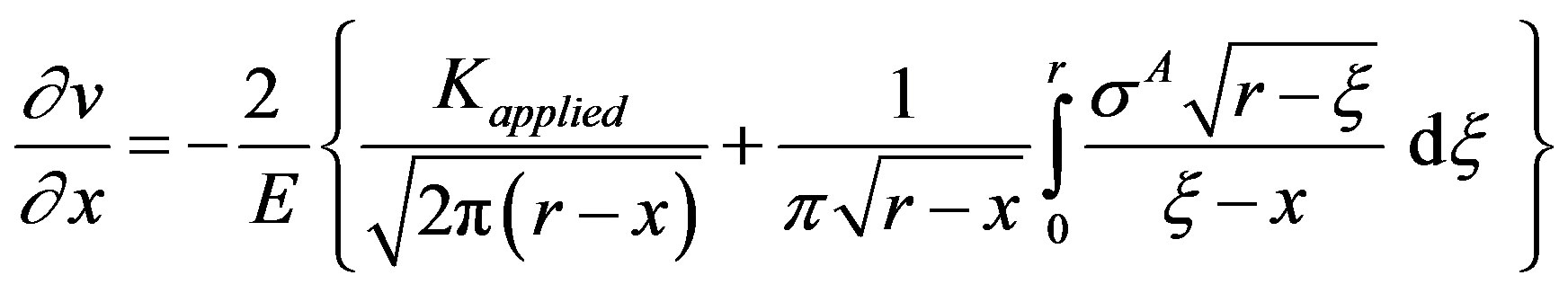 (1)
(1)
where, 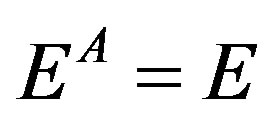 , is the modulus of elasticity of parent body, A. On integrating Equation (1), the expression for v, as the function of distance x from the crack tip in the cohesive zone is obtained as
, is the modulus of elasticity of parent body, A. On integrating Equation (1), the expression for v, as the function of distance x from the crack tip in the cohesive zone is obtained as
 (a)
(a)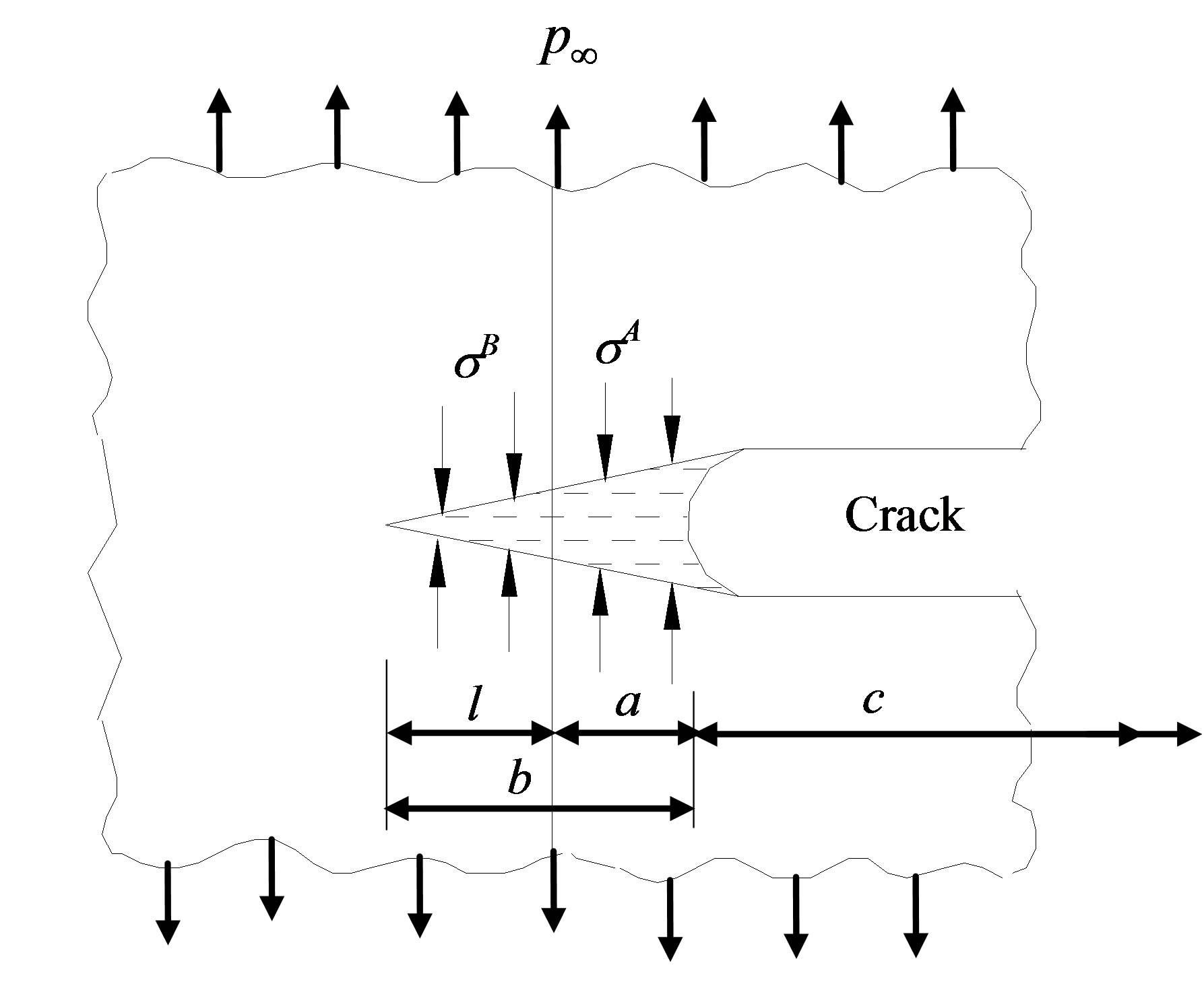 (b)
(b)
Figure 2. Stages of crack advancement towards a thin weld; (a) Stage I (Cohesive zone in parent body); (b) Stage II (Extension of cohesive zone into interface body).
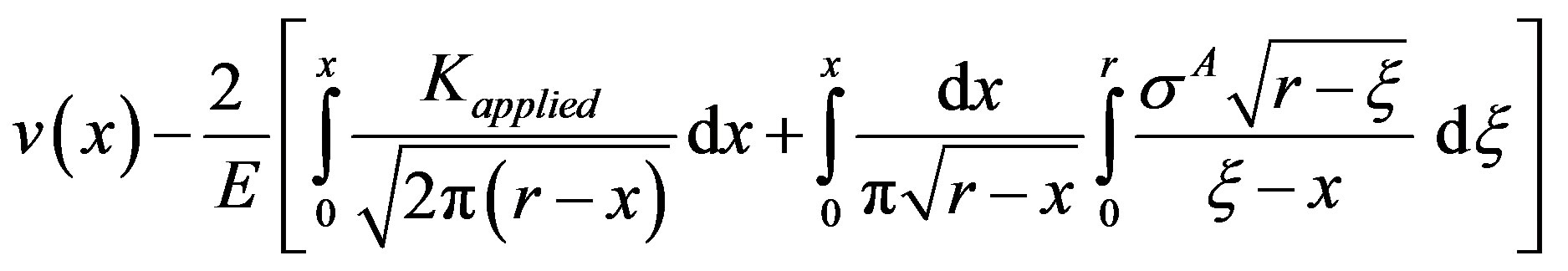 (2)
(2)
Stage I is valid till the cohesive zone lies in the parent body i.e. the distance of the crack tip from the interface, a, fulfills the condition,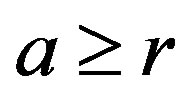 .
.
Refer Figure 2(b). The crack has grown ahead from Stage I such that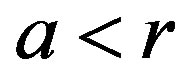 . The cohesive zone has developed in interface body, B, with its extent up to distance, l, from the interface. Length of the cohesive zone, b, is equal to (a + l). Since,
. The cohesive zone has developed in interface body, B, with its extent up to distance, l, from the interface. Length of the cohesive zone, b, is equal to (a + l). Since, 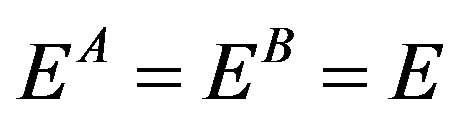 , the following expression is written for v(x) in Stage II under simultaneous action of different cohesive stresses
, the following expression is written for v(x) in Stage II under simultaneous action of different cohesive stresses 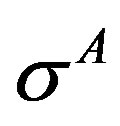 and
and 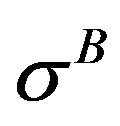 in parent and interface bodies respectively with the help of Equation (2)
in parent and interface bodies respectively with the help of Equation (2)
 (3)
(3)
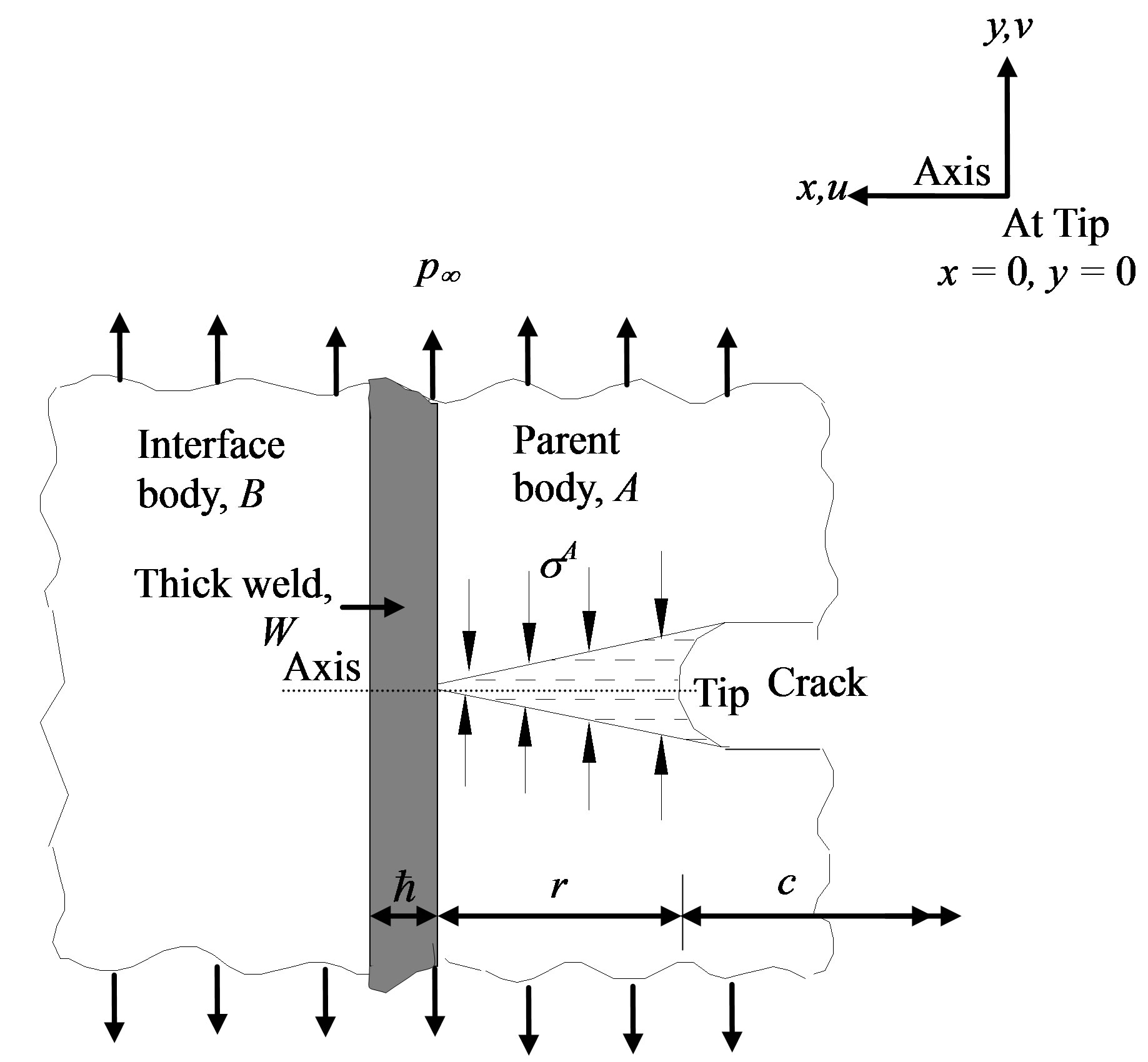
2.2. Crack Near Thick Weld (Refer Figure 3)
Using similar principles as in thin weld, the expressions for 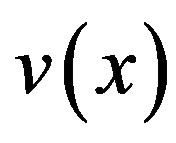 assume the following forms in Stages I, II and III in the case of thick weld:
assume the following forms in Stages I, II and III in the case of thick weld:
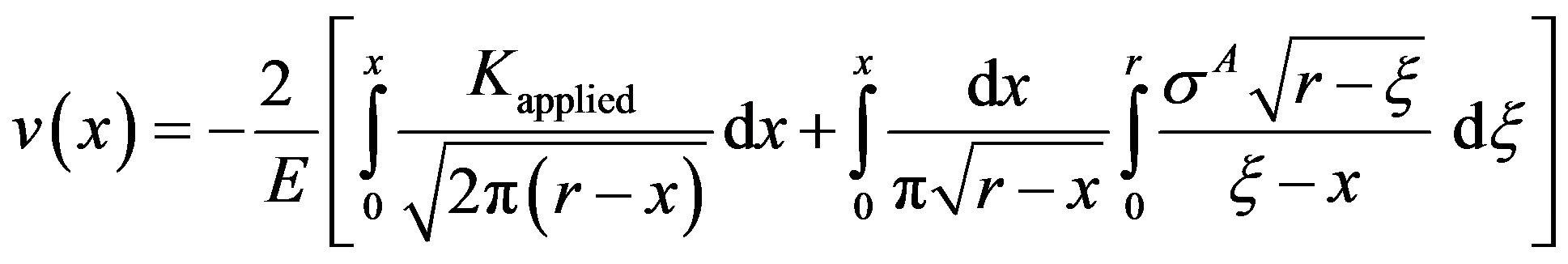 (4)
(4)
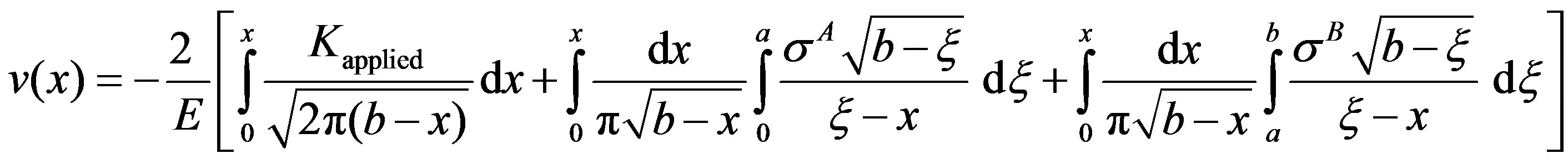 (5)
(5)
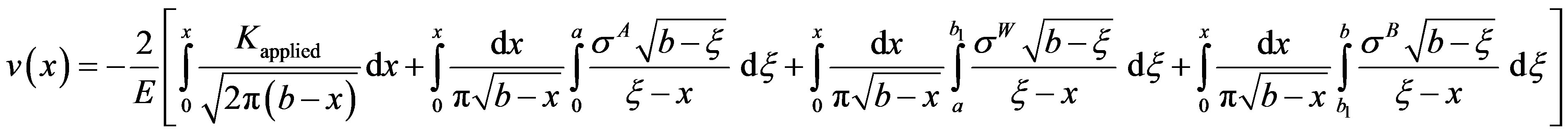 (6)
(6)
 (a)
(a)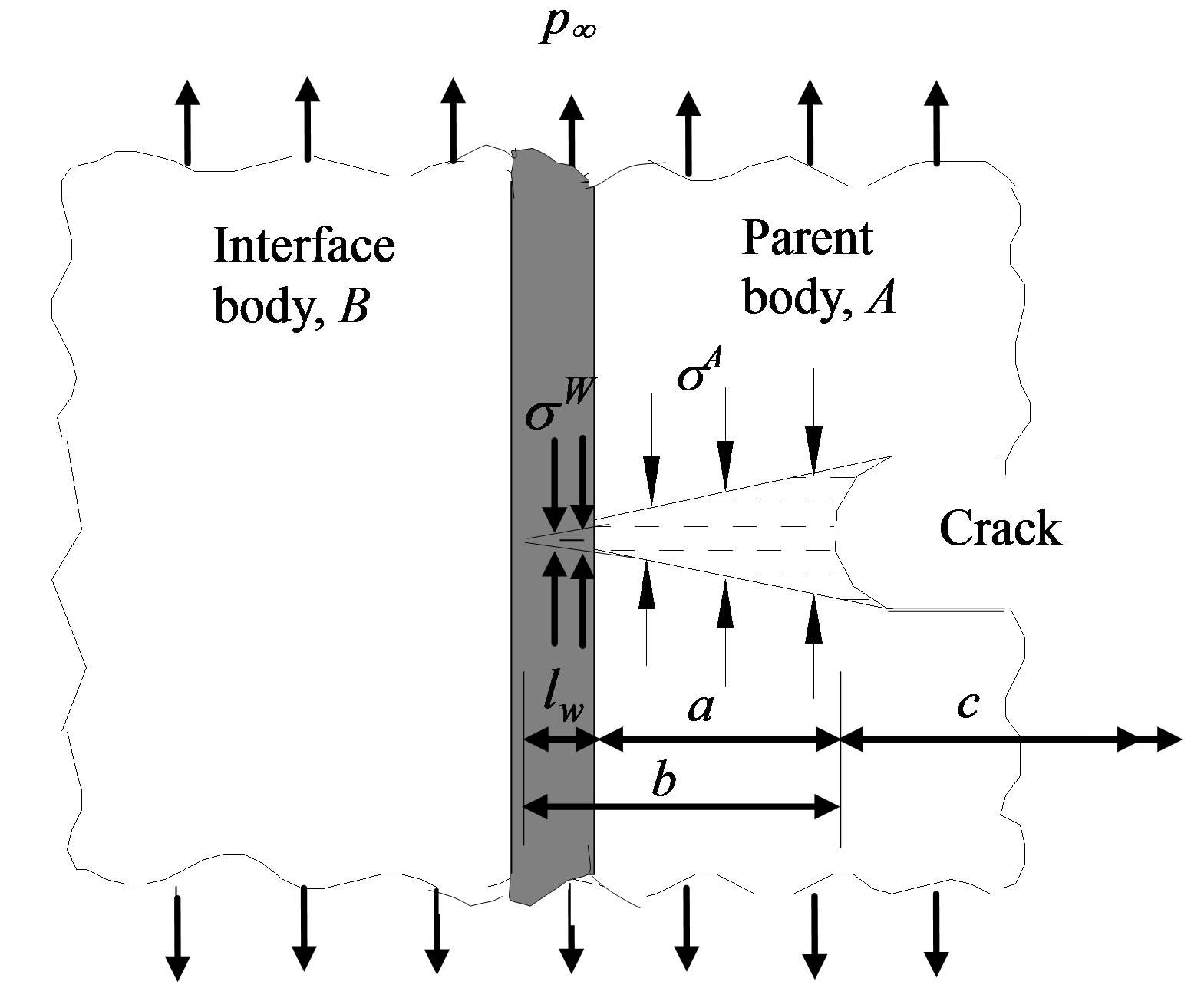 (b)
(b) (c)
(c)
Figure 3. Stages of crack advancement towards a thick weld; (a) Stage I (Cohesive zone in parent body); (b) Stage II (Spread of cohesive zone to weld); (c) Stage III (Extension of cohesive zone into interface body).
All the integrals, especially non-singular ones, in Equation (1) to Equation (6) need to be solved for obtaining a usable form of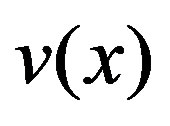 .
.
3. Solution
Equations in important stages of crack growth towards the interface in bodies with thin and thick welds are solved as follows.
3.1. Crack Near Thin Weld
In Stage II,
 (7)
(7)
where
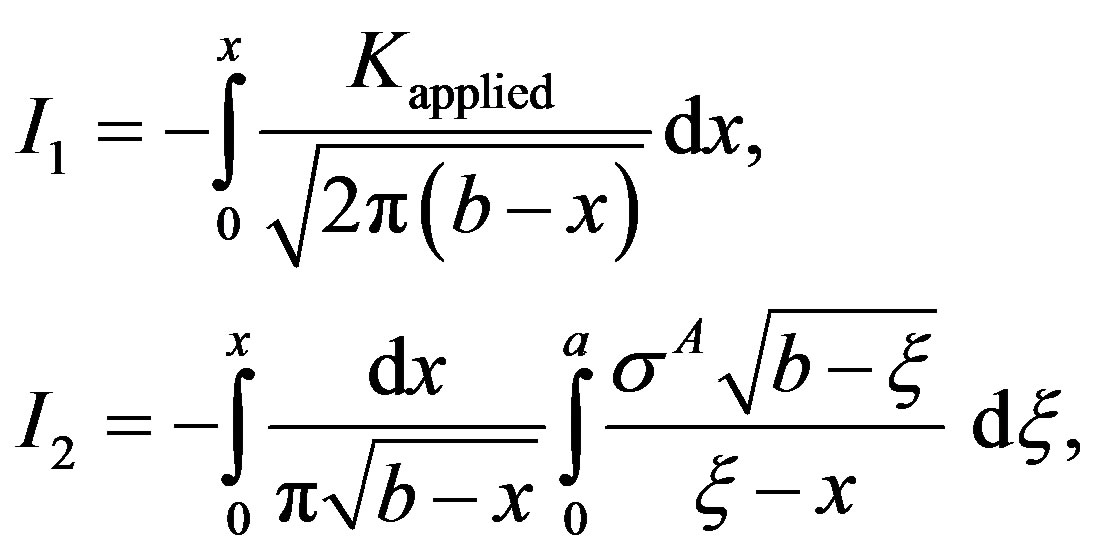
and
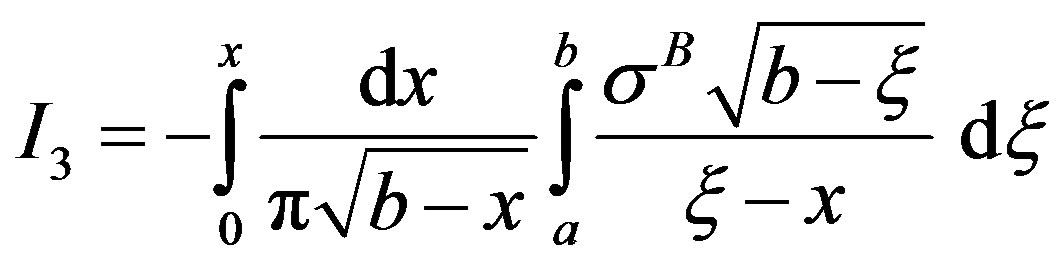
Integral I1 is easily solved as
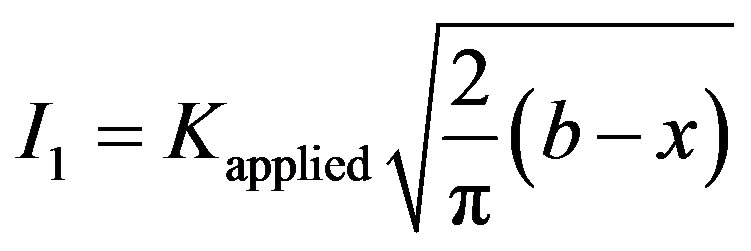
Integrals I2 and I3 are singular in nature and are evaluated as follows:
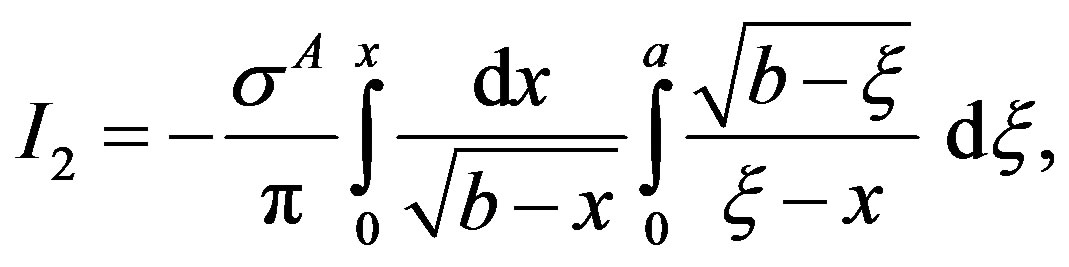
Use of Cauchy’s principal value theorem [3] enables to write for 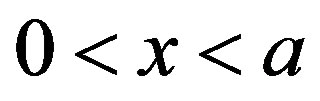 and continuous
and continuous 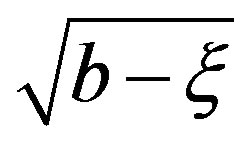 as
as
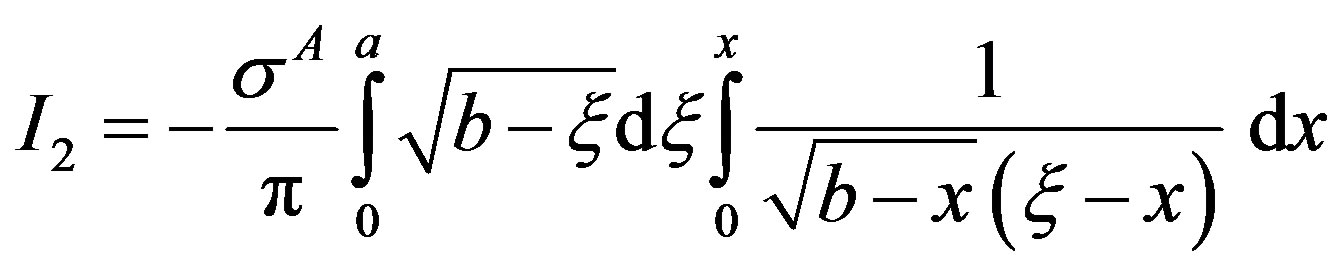 .
.
On using the following substitutions
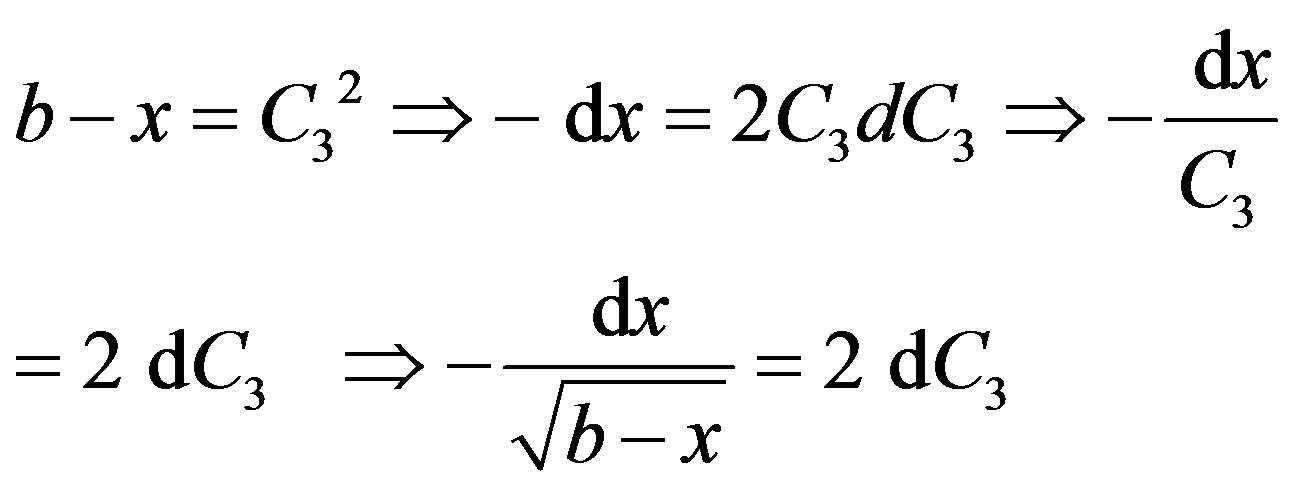
in integral I2, one obtains
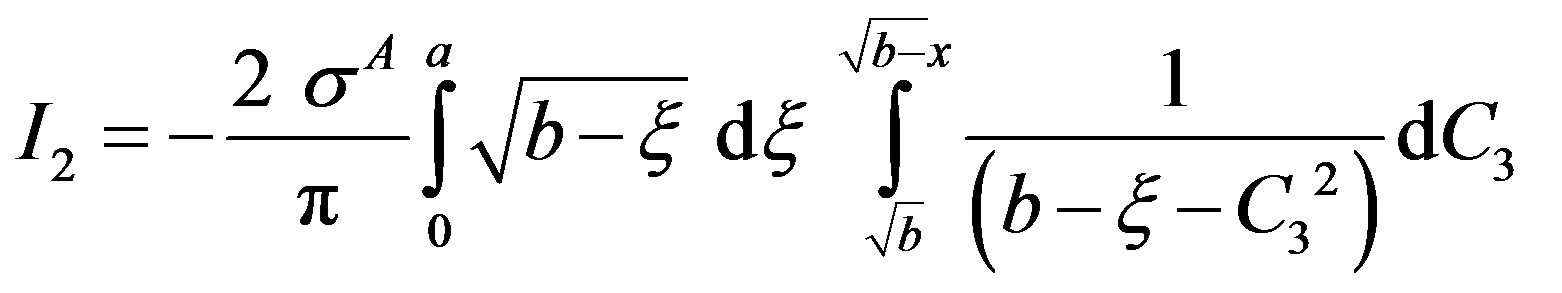
On evaluating the inner integral, one obtains
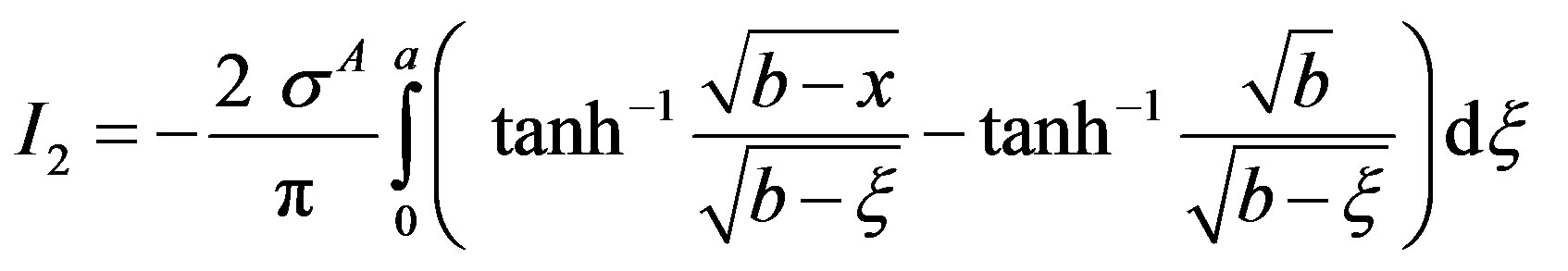
Since for +ve , term
, term 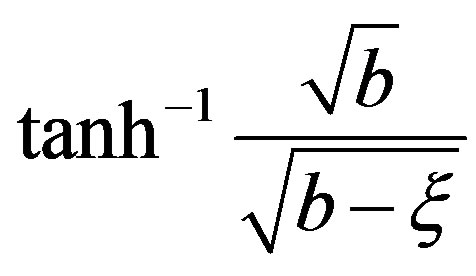 causes singularity in the solution and is not considered further. Therefore
causes singularity in the solution and is not considered further. Therefore
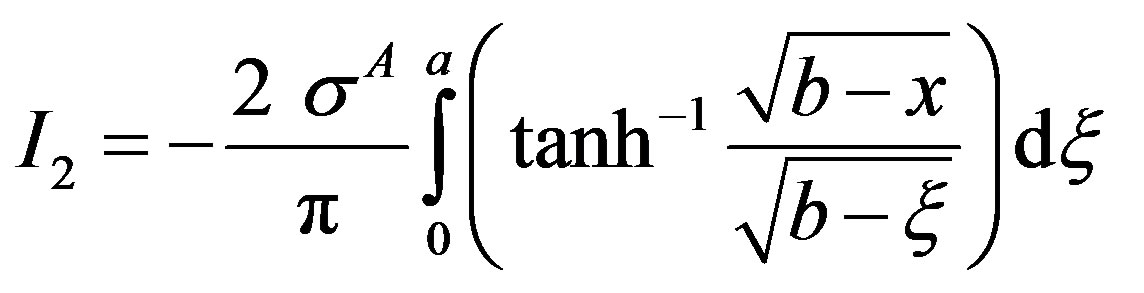
which can also be written as
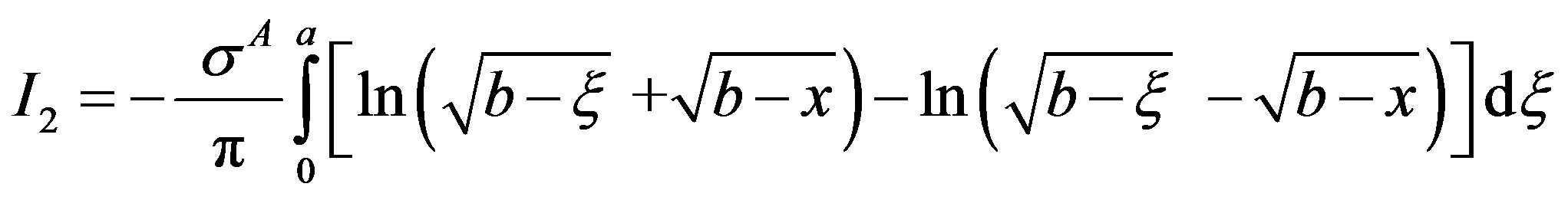
On defining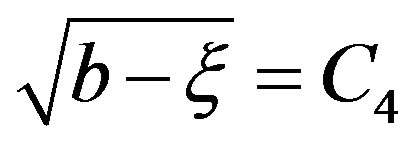 , one obtains
, one obtains 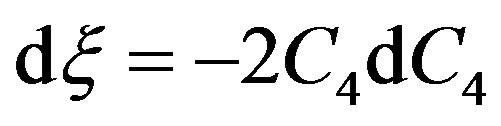 Therefore
Therefore
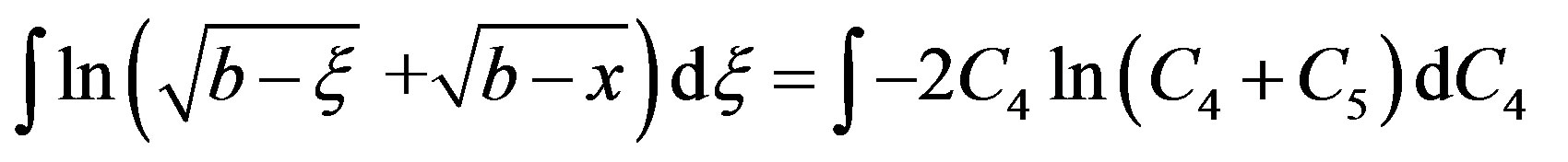
where constant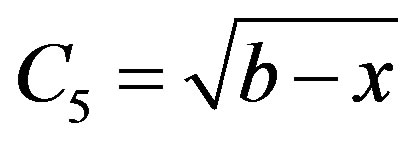 . Solution of the integral
. Solution of the integral 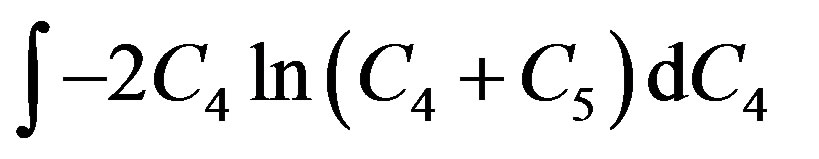 is obtained as
is obtained as
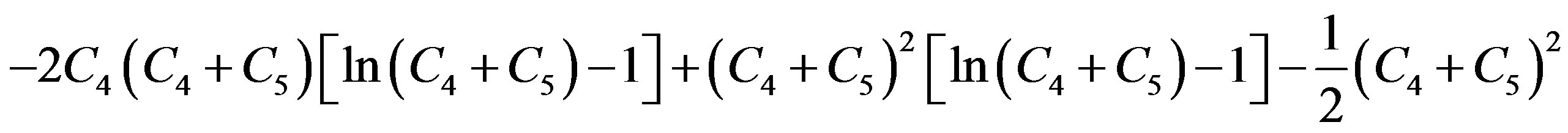
Similarly, other term 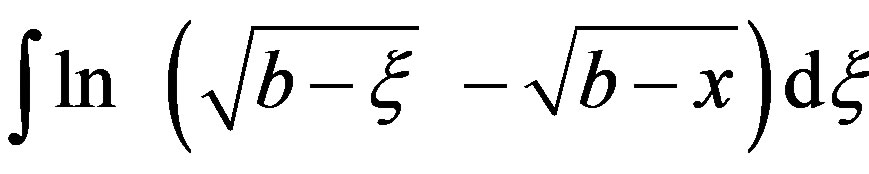 in integral I2 is obtained as
in integral I2 is obtained as
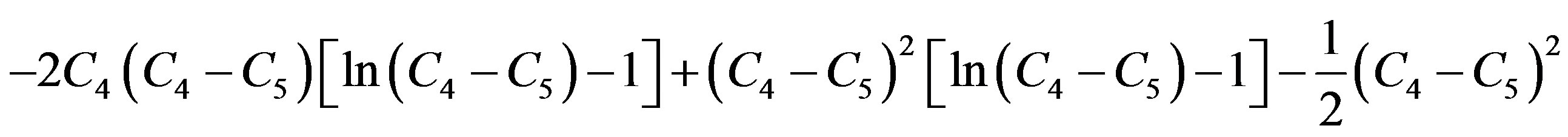
Integral I2 is finally written as
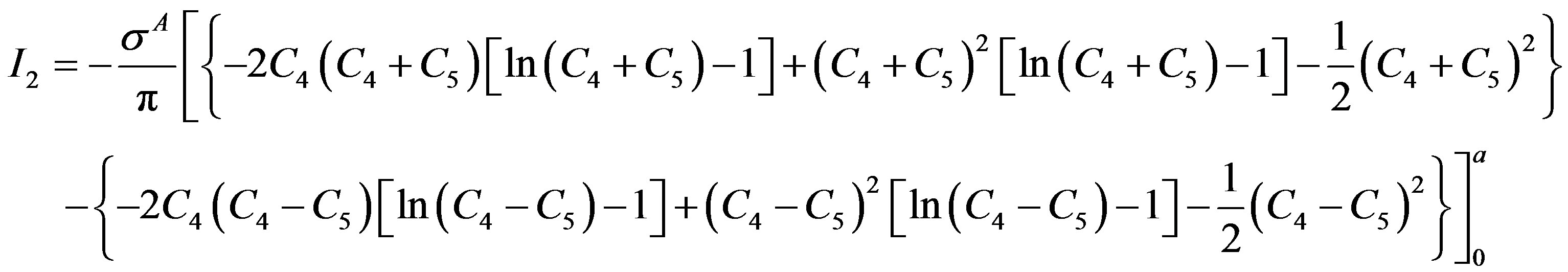
On re-substituting  and
and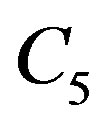 , one obtains
, one obtains
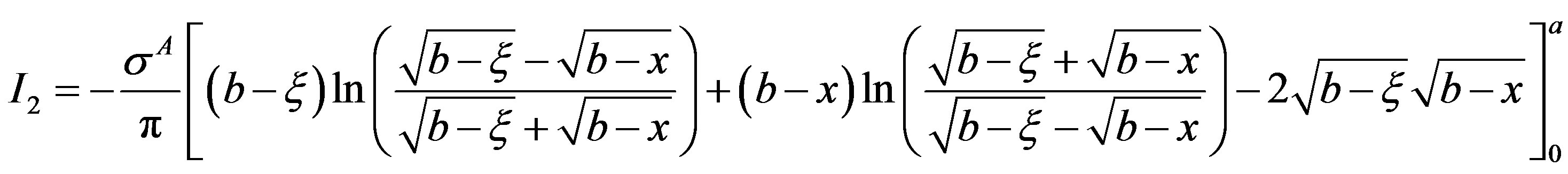
Applying the limits of integration results in the following
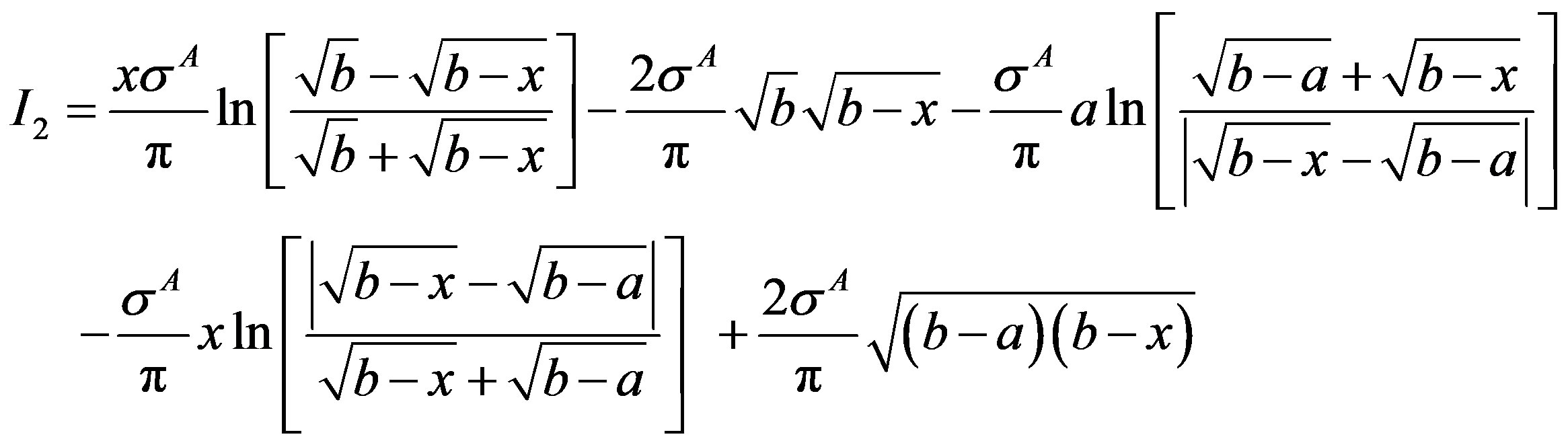
Similarly, Integral I3 is written as
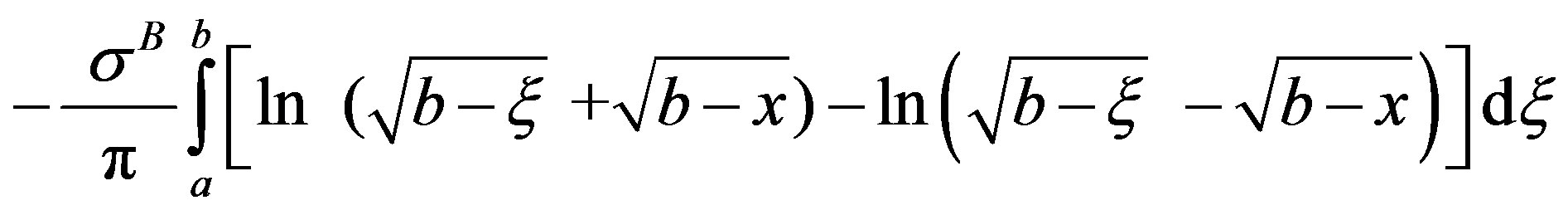
and is evaluated in similar manner as integral I2.
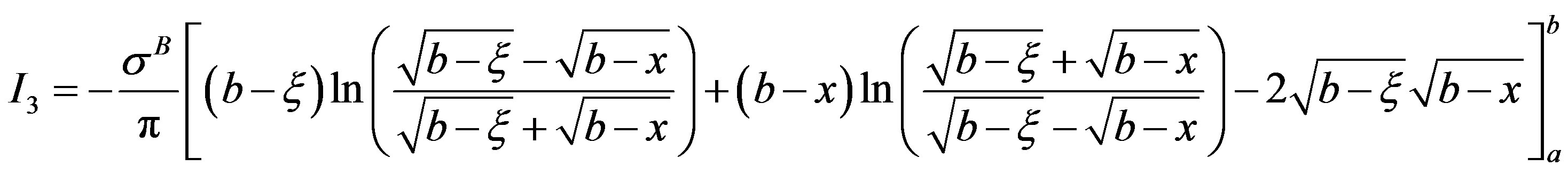
On applying the limits of integration, one obtains
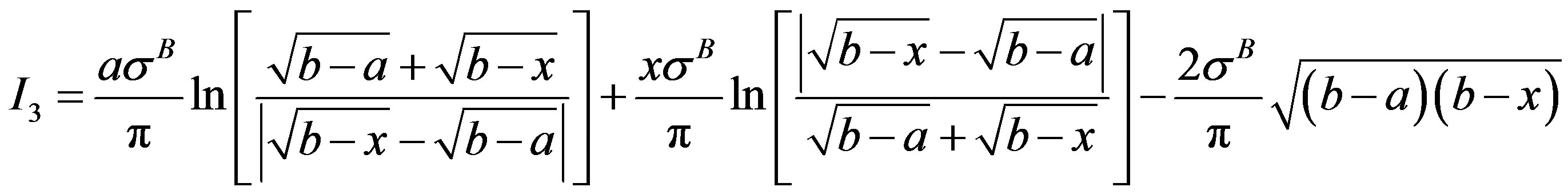
Substitution of integrals I1, I2 and I3 in Equation (7) on using, b = a + l, results in closed form expression for load line displacement, v(x), in the cohesive zone spread across the interface of bodies A and B as
 (8)
(8)
3.2. Crack Near Thick Weld
Solution in Stage II is obtained upon replacing 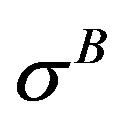 by
by 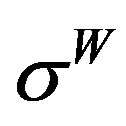 and
and 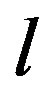 by
by 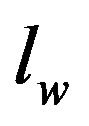 in Equation (8).
in Equation (8).
In Stage III,
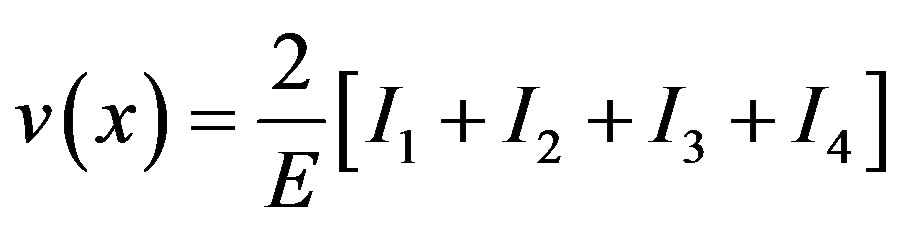 (9)
(9)
where 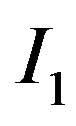 and
and 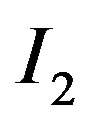 are similar as in Equation (7).
are similar as in Equation (7).
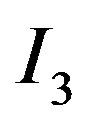 is written as
is written as
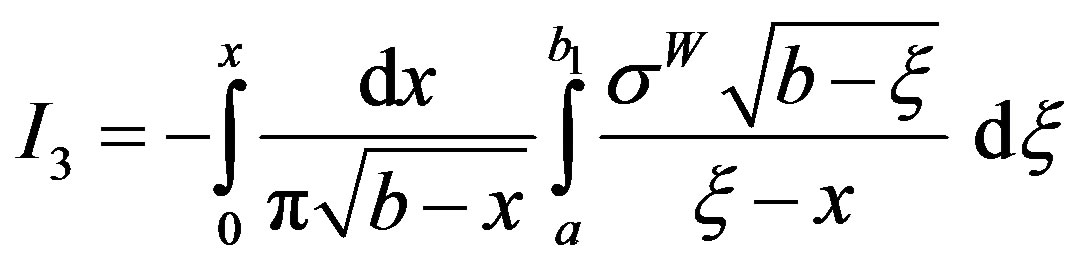
or
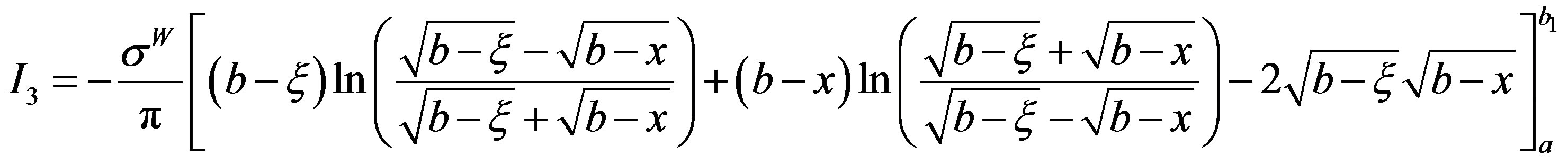
or
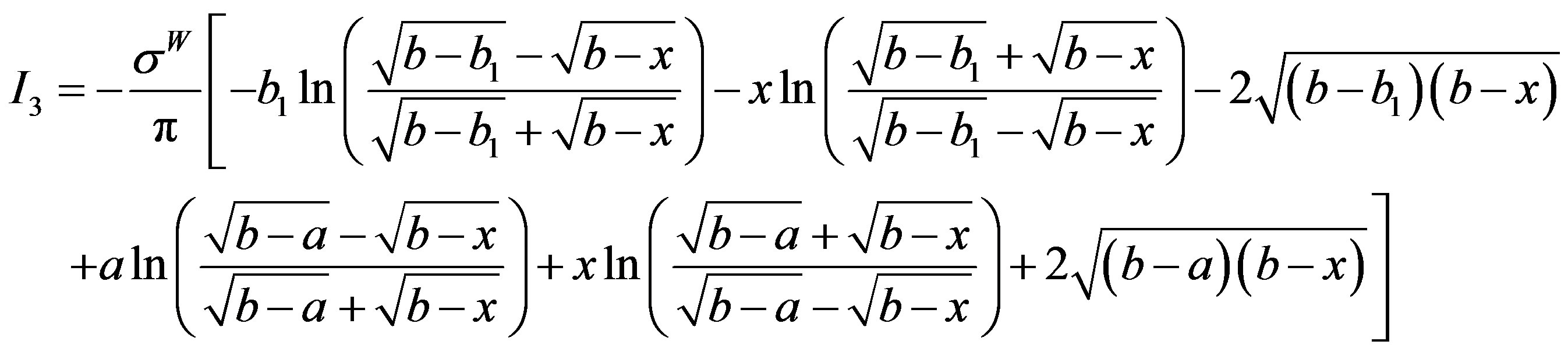
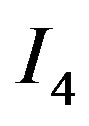 is written as
is written as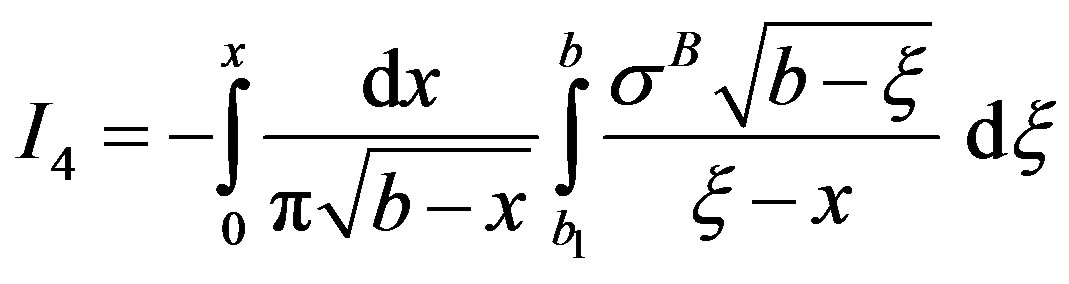
or
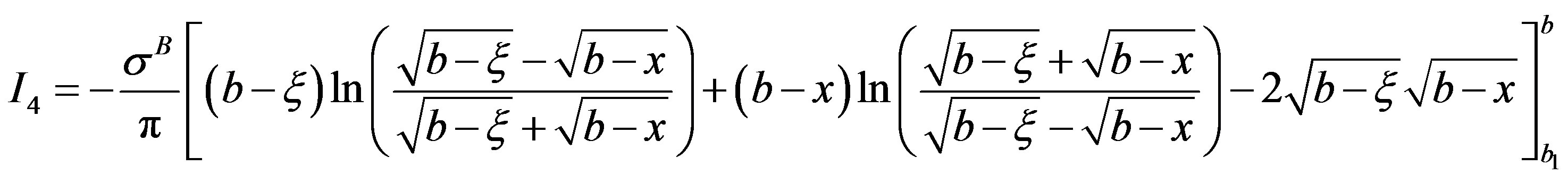
or
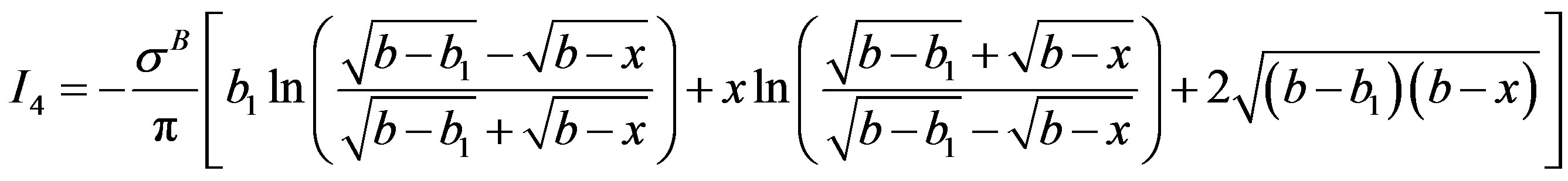
Substitution of integrals I1 to I4 in Equation (9) results in closed form expression for displacement, v(x), in the cohesive zone spread across parent body, A, weld, W and interface body, B, as
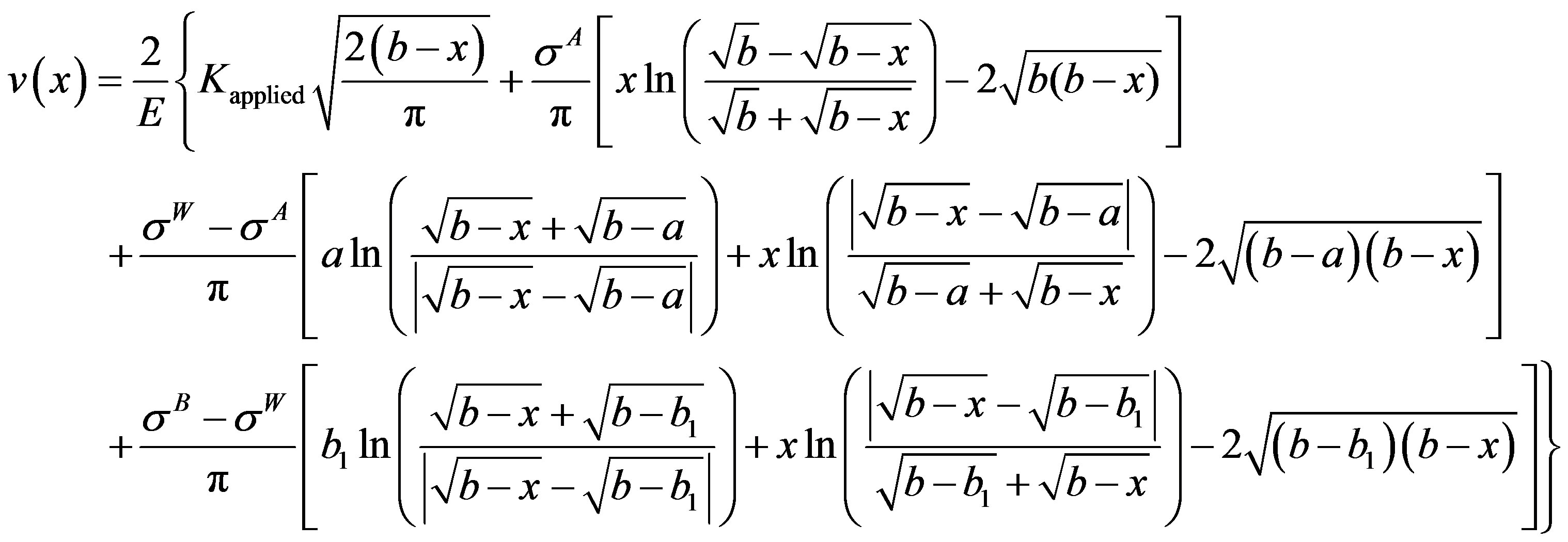 (10)
(10)
4. Validation
Solution of integrals is validated by once again reverting to Stages I and II of crack near thin weld. Refer Equation
(2). In Stage I, solution of integral
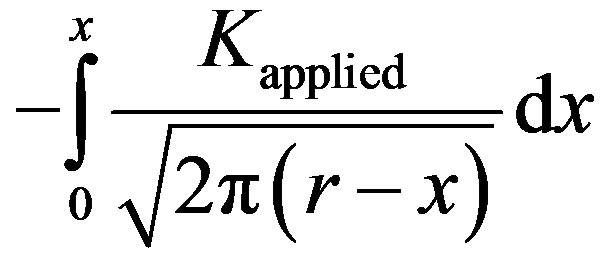 is
is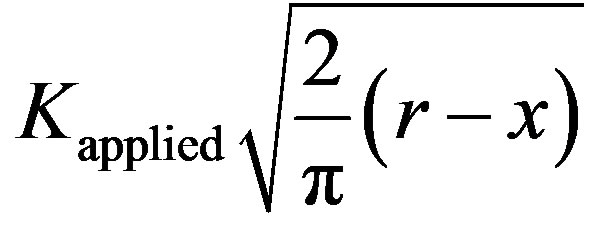 .
.
Lower limit is disregarded since value of 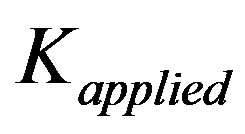 at upper limit acts over the specific location in the cohesive zone. Singular integral
at upper limit acts over the specific location in the cohesive zone. Singular integral
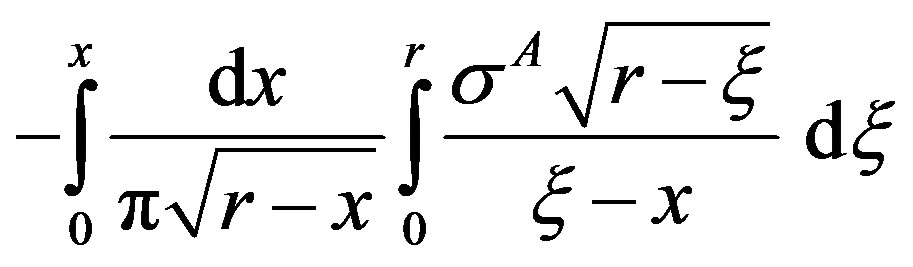
is evaluated as
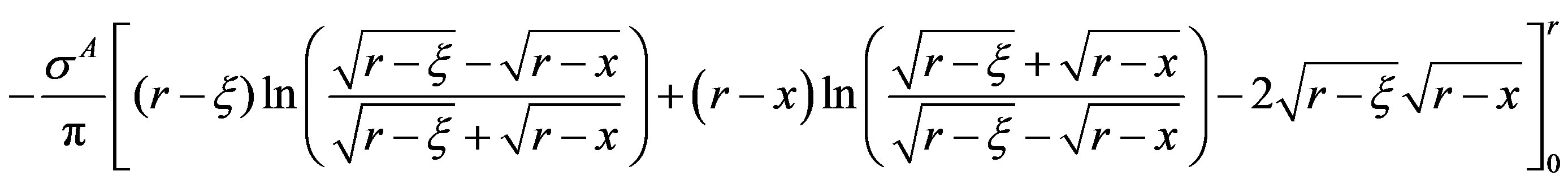
which simplifies to
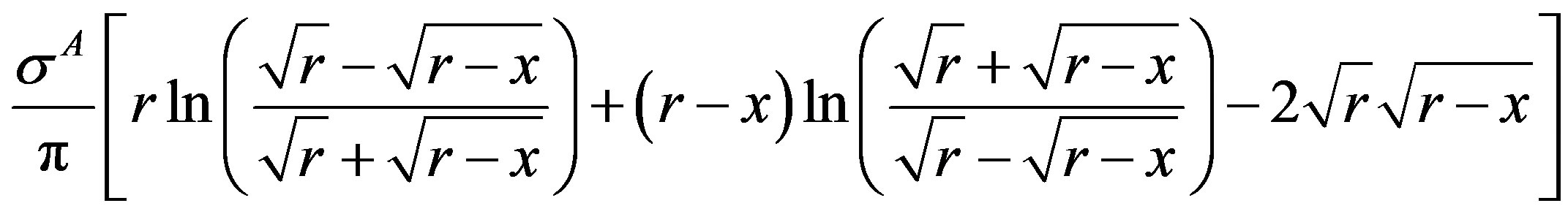
Crack tip opening displacement (CTOD), 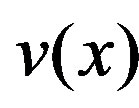 at x = 0i.e.,
at x = 0i.e., 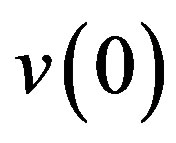 is obtained as
is obtained as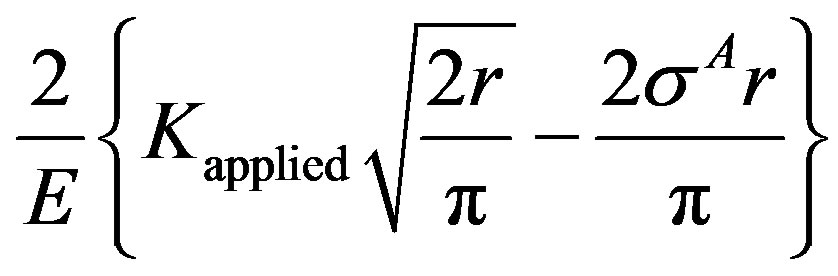 . On applying Dugdale’s cohesive zone criterion,
. On applying Dugdale’s cohesive zone criterion,
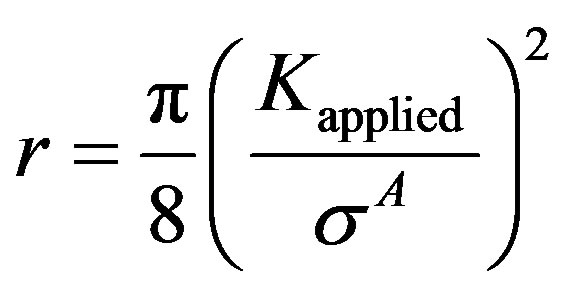 ,
,  reduces to
reduces to 
which is the well known solution for half crack tip opening displacement in homogenous body A in linear elastic regime.
In Stage II, J integral at crack tip,  , expressed as
, expressed as
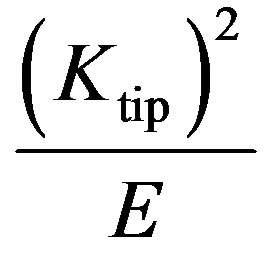 , is equal to
, is equal to 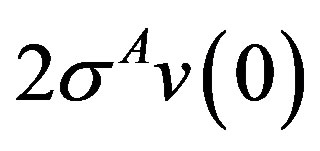 whereas J integral at interface,
whereas J integral at interface,  , is equal to
, is equal to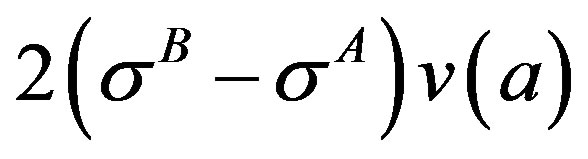 . Since
. Since
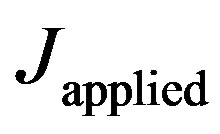 is given by
is given by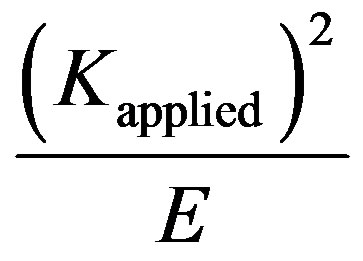 , the following equation is obtained upon using conservation of energy release rate,
, the following equation is obtained upon using conservation of energy release rate, 
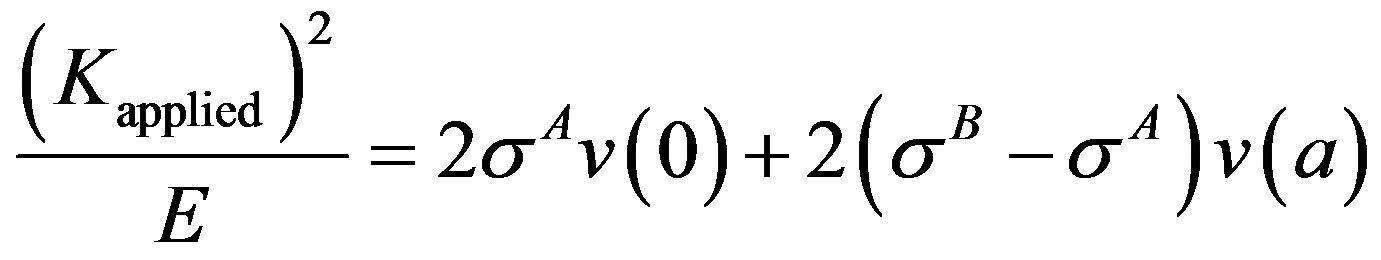 (11)
(11)
Equation (8) leads to the following expressions
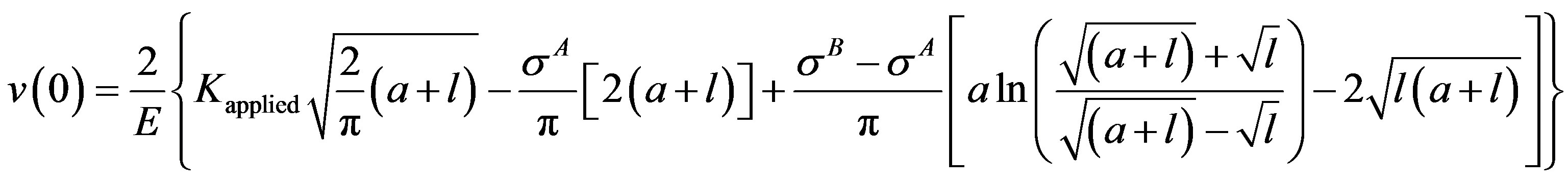 (12)
(12)
and
 (13)
(13)
Stress intensity parameter applied over the crack with its cohesive zone split across the interface in Stage II [4] is written as
 (14)
(14)
With Equation (12) and Equation (13), R.H.S. of Equation (11) results in the expression
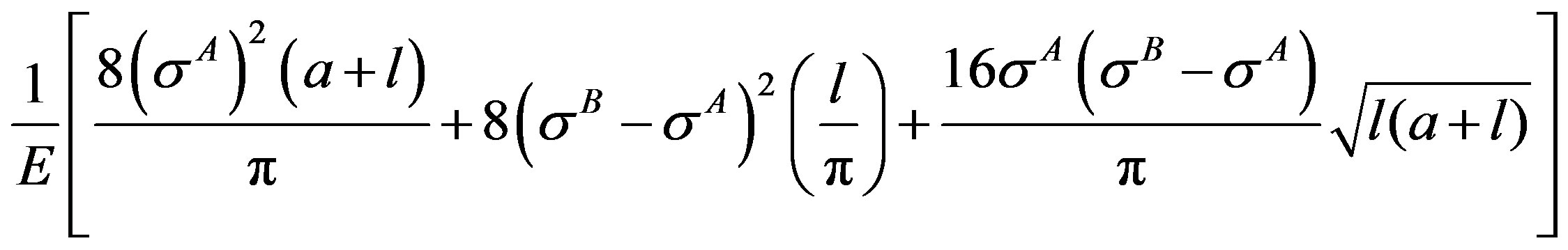
which equals 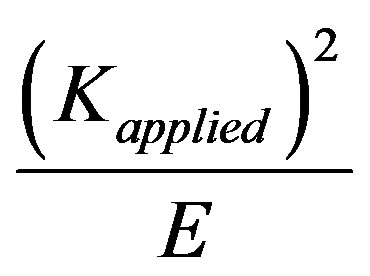 i.e. L.H.S upon using Equation (14) that validates the solutions of singular integrals.
i.e. L.H.S upon using Equation (14) that validates the solutions of singular integrals.
5. Conclusion
Singular integrals in mathematical model of load line opening of Mode I crack near the interface of elasticity identical but strength and plasticity mismatched materials in linear elastic regime are solved. The solution is well validated.
6. Acknowledgements
Support received from the School of Mechanical Building Sciences, VIT University, Vellore, India during the course of this work is gratefully acknowledged.
REFERENCES
- G. T. Hahn and A. R. Rosenfield, “Local yielding and extension of a crack under Plane Stress,” Acta Metallurgica, Vol. 13, No. 3, 1965, pp. 293-306. doi:10.1016/0001-6160(65)90206-3
- D. Wappling, J. Gunnars and P. Stahle, “Crack growth across a strength Mismatched Bimaterial Interface,” International Journal of Fracture, Vol. 89, No. 3, 1998, pp. 223-243. doi:0.1023/A:1007493028039
- D. Porter and D. S. G. Stirling, “Integral equations—a Practical Treatment, from Spectral Theory to Applications,” Cambridge University Press, Cambridge, 1990.
- F. O. Reimelmoser and R. Pippan, “The J-integral at Dugdale Cracks Perpendicular to interfaces of materials with Dissimilar Yield Stresses,” International Journal of Fracture, Vol. 103, No. 4, 2000, pp. 397-418. doi:10.1023/A:1007605224764

