Energy and Power Engineering, 2010, 10-17
doi:10.4236/epe.2010.21003 Published Online February 2010 (http://www.scirp.org/journal/epe)
Three-Level Five-Phase Space Vector PWM
Inverter for a Two Five-Phase Series Connected
Induction Machine Drive
N. R. ABJADI1, J. SOLTANI2, J. ASKARI2, Gh. R. Arab MARKADEH1
1Department of Engineering, Shahrekord University, Shahrekord, Iran
2Department of Electrical and Computer Engineering, Isfahan University of Technology, Isfahan, Iran
Abstract: This paper describes the decoupled torque and flux control of a two series connected five-phase
Induction Machine (IM) drive that is supplied by a three-level five phase SVPWM inverter, using a well
known phase transposition in the series connection. At the first, the decoupled torque and flux controller is
developed based on variable-structure control (VSC). Then, a sliding-mode (SM) flux observer in employed
to estimate the stator flux; that uses a two reference frames which result in eliminating the speed adaptation.
Moreover simple control strategy is introduced for three-level SVPWM voltage source inverter (VSI) that can
be easily implemented in practice for a two-series five phase IM drive. Finally, the effectiveness and
capability of the proposed control method is verified by computer simulation.
Keywords: multiphase systems, multilevel VSI, sliding mode control
1. Introduction
In electrical drive applications, three-phase drives are
widely used for their convenience. However, high-ph-
ase number drives possess several advantages over
conventional three-phase drives such as: reducing the
amplitude and increasing the frequency of torque puls-
ations, reducing the rotor harmonic currents, reducing the
current per phase without increasing the voltage per
phase, and lowering the dc-link current harmonics and
higher reliability. By increasing the number of phases, it
is also possible to increase the torque per rms ampere for
the same volume machine [1].
Multi-phase machines have found wide applications in
transport, textile manufacturing and aerospace since few
years [2–14]. The recent research works on multi-
phase machines can be categorized into multi-phase
pulse width modulation (PWM) techniques for multi-
phase machines [2–14], harmonic injection to produce
more torque and to achieve better stability [5], fault
tolerant issues of multi-phase motor drives [6], series/
parallel connected multi-phase machines [7–14].
Applications involving high power may require
multiphase systems, in order to reduce stress on the
switching devices. There are two approaches to
supplying high power systems; one approach is the use
of multilevel inverters supplying three-phase mac-
hines and the other approach is multileg inverters sup-
plying multiphase machines. Much more work has
been done on multilevel inverters. It is interesting to
note the similarity in switching schemes between the
two approaches: for the multilevel inverter the
additional switching devices increase the number of
voltage levels, while for the multileg inverter, the
additional number of switching devices increases the
number of phases [15].
In [16], Kelly et al. also verified that an n-phase
space vector PWM (SVPWM) scheme can be described
in terms of the applying times of available switching
vectors on the basis of the space vector concept. How-
ever, the paper only focuses on how to realize a sinu-
soidal phase voltage. As is widely known, most multi-
phase motors are designed to have the nonsinusoidal
back-EMF voltage.
Hamid A. Toliyat have made much research on control
method and running performance aim at five-phase drive
[1], but their subject investigated is the system feeding
with two level inverter. Another research work has been
done in [17] on a multiphase two level nonsinusoidal
SVPWM.
The power rating of the converter should meet the
required level for the machine and driven load. However,
the converter ratings can not be increased over a certain
range due to the limitation on the power rating of
semiconductor devices. One solution to this problem is

N. R. ABJADI ET AL.
11
Figure 1. Two five-phase machine drive supplied by a single
inverter
using multi-level inverter where switches of reduced
rating are employed to develop high power level
converters. The advent of inverter fed motor drives
also removed the limits of the number of motor phases.
This fact made it possible to design machine with more
than three phases and brought about the increasing
investigation and applications of multi-phase motor
drives [18,19].
In [20], Qingguo Song, introduced a method to
supply a single five-phase permanent magnetism syn-
chronous motor (PMSM) with a three level SVPWM
VSI. But the method is not capable to control more
series connected multiphase machines or producing
nonsinusoidal voltages.
Space-vector modulation (SVM) is an advanced
technique for the generation of output voltages or cur-
rents in inverters based on the spatial visualization of
their variables. In the conventional approach of this
technique, the inverter is understood as a whole, allow-
ing full control over the switching sequences of the swit-
ches and achieving maximum use of the dc-link voltage.
The five-phase induction motor drives have many
more space voltage vectors than the three-phase induc-
tion motor drives. The increased number of vectors
allows the generation of a more elaborate switching
vector table in which the selection of the voltage vectors
is made based on the real-time values of the stator flux
and torque variations.
In this paper, a five-phase 3 level SVPWM algorithm
is developed to control a two series IM drive system.
Recognizing the VSC merits and the advantages of using
the SVM, this paper presents a VSC-DTC solution for
series-connected induction motor drives. Direct torque
and flux control is achieved by means of VSC.
2. Description and Modeling of the Drive
System
The drive consists of two five-phase squirrel cage induc-
tion machines. Referring to Figure 1 the five-phase stator
windings of the two machines are connected in series,
with an appropriate phase transposition [19]. The two-
motor drive system is supplied from a single five-phase
VSI.
From Figure 1 the relationship between voltage and
currents are given as:
12
12
12
12
12
A
as as
Bbs cs
Ccses
D
ds bs
E
es ds
vv v
vv v
vv v
vv v
vv v






,
12
12
12
12
12
Aas as
B
bs cs
Ccs es
D
ds bs
E
es ds
ii i
ii i
ii i
ii i
ii i





(1)
Each machine is supposed to have its own parameters.
Using the decoupling Clark’s transformation, the original
phase variables are correlated to new (

 ) variable as
C ff
abcde 

, where C is the power-invariant
transformation matrix:
1coscos 2cos 3cos4
0sinsin2sin 3sin4
21cos2cos 4cos 6cos8
50sin2sin4sin6sin 8
01/ 21/ 21/ 21/ 21/2
Cx
y



























(2)
The (

,

) and (
x
, y) voltages and currents of the
five-phase VSI are obtained as:
12 12
2 112
12 12
12 12
0
012
INV vv
vvv
vas as
A
s
xs
INV
vvv
vvv
cs
bs B
s
ys
INV CC
vv v
vxvv
cs es
C
x
ss
INV
vyvv
vvv
Dds bsys s
INV
vvvv
Ees ds





 
 

 
 
 
 

 
 
 

  

 
 
 
 

 
 
 
 
  

 
 










(3)
Figure 2. Five-phase IM equivalent circuits of one machine

N. R. ABJADI ET AL.
12
12
12
12
12
INV
iii
s
xs
INV
ii i
s
ys
INV
iii
x
x
ss
INV
iii
yys s








(4)
The torque equations of the two series-connected
machines are given as follow
()
ii ii TPL
ekk mkrkskrk sk  

(5)
here k=1,2 andPk are pole pairs.
From these equations and (4), one can note that the
torque production currents of the first motor (,
11
ii
s
s


)
are equal to none producing torque currents of the second
motor (,
22
ii
x
sys
). As a result, the two motors can be
controlled independently through a single VSI.
The stator voltage equations of each machine are
()
()
()
()
d
vii i RLL
sksk mk
s
ksk skrk
dt
d
vii i RLL
sksk mk
s
kskskrk
dt
d
vi i RL
sk lsk xsk xskxsk
dt
d
vi i RL
sk lsk ysk yskysk
dt
 
 
 
 


(6)
where k=1,2.
The rotor voltage equations of each machine are
0( )
1
()
iii RLL
rkrk mk
rk rrksk
dii
LL
rk mk rk sk
dt



 

0( )
()
iii RLL
rkrk mk rk rkrksk
dii
LL
rk mk rk sk
dt



 
 (7)
where k=1,2.
In Figure 2 the five-phase IM equivalent circuits of
one machine is shown.
3. Sliding-Mode Controller
Block diagram of the variable-structure direct torque
controlled drive (VSC-DTC) under consideration is
shown in Figure 3. As can be seen from this figure, for
each motor the control quantities are the stator flux
magnitude and torque.
A reference stator voltage, ** *
s
ds qs
j
vv v
 , is obtained
at the output of the VSC, where *
ds
v is generated by the
flux control law and
*
qs
v by the torque control law. The
Figure 3. Block diagram of the VSC-DTC
control law is of the “Relays with constant gains” type
[21],
*1
()sgn( )
PI ds d
s
vS KK

 (8)
*1
()sgn( )ˆ
ˆs
PT IT qs q
s
s
vS KK



 (9)
where s=d/dt, sgn is the signum function, ,
P
K

I
K

,PT
K
and
I
T
K
are the PI controller gains,

dq
j
SS S
is the sliding surface, and superscript “ ^ ”
stands for estimated quantities. In order to accelerate the
voltage response during speed transients, the torque
control law contains a feedforward compensation for the
dynamic electromotive force (EMF). The PI controllers
help to reduce the chattering associated with VSC and
define the system’s behavior when it is not in the sliding
mode (during the reaching phase). The sliding surface is
designed so as to enforce SM operation with first-order
dynamics,
()
eee
sss
dq
jsjs
TTT
SSSe ceece

  (10)
where *ˆ
ss
s
e



 and *ˆ
eee
T
eTT
 ;
s
c

and e
T
care
design constants.
In the sliding mode, the control law (8) and (9) restrict
the system state onto the surface , and its behavior is
exclusively governed by 0
S [21].
4. Sliding-Mode Observer
In [21,22], an inherently sensorless SM observer has
been developed. It uses two reference frames allows
eliminating the speed adaptation. This feature is
significant in drives that do not need the speed estimation
for control (torque-controlled drives) and it is expected
to produce better results than conventional observers.
An SM observer for IM is
1sgn( )
ˆˆ ˆ
se
sss
s
ss
dj
dt ivi
i RK  
  (11)
2
1
(( ))
sgn( )
ˆˆ ˆ
ˆ
m
er
rs r
sr r
ss
dj
dt
L
LTT
ii
K






 (12)
2
ˆˆ
rm
s
r
s
L
L
i
L




 (13)
In order to eliminate the rotor speed adaptation, the
stator Equation (11) is implemented in stator reference

N. R. ABJADI ET AL.
13
Figure 4. Scheme of a five-phase three-level inverter
Figure 5. The switching vectors on α-β and x-y planes
frame, and the rotor Equation (12) is implemented in
rotor flux frame (superscript “ r ”), which rotates with
rotor flux speed,


r
1sgn( )
ˆˆ
sss s
s
s
d
dt iv ii
RK

  (14)
2
1
(( ))
sgn( )
ˆˆ ˆ
ˆ
r
rr r
m
r
rs r
sr r
r
r
ss
dj
dt
L
LT T
ii
K








(15)
Taking into consideration that the rotor flux is aligned
with the reference frame, the rotor model (15) turns out
to be simple:
2
1
(sgn( ))
ˆˆˆ
ˆ
rrr
m
drds dr
sr r
r
r
ss
d
dt
e
L
LT T
ii
K






(16)
0 ˆr
qr


(17)
It can be shown that the observer is stable if its gains
are large enough [21].
5. Three Level Space Vector Pwm
In [20], a technique of vector space control of three-level
voltage source inverter fed five-phase machines was
presented.
Using the same idea described in [20], in this paper a
SVPWM voltage source is developed which is capable of
supplying the two motor drive system with different rotor
speeds. The SVPWM scheme is designed to generate an
arbitrary reference voltage space vector which consti-
tutes the motors main frequencies 1

and 2

.
Figure 4 shows the scheme of a five-phase three-level
inverter. There are 243(35) voltage vectors; the mag-
nitude and distributing of voltage vectors are far more
complex than five-phase two-level inverter. However,
not all of vectors are suitable to vector synthesizing.
Consider voltage vectors with magnitude VL

0.6472VDC , 0.6156
VV
M
DC

, 0.3236
VV
SDC

and zero voltage vectors as efficient working vectors.
There are 43 efficient vectors in each plane, including 30
non-zero vectors, 10 redundant and 3 zero vectors, as
shown in Figure 5.
The decimal numbers in Figure 5 denote the switching
modes. When each decimal number is converted to a five
digit number in base 3, the 2's in this number indicate
that the two upper switches in the corresponding
switching arms are “on” and the 1's in this number
indicate that the two middle switches are “on”, while the
0's indicate the “on” state of the lower switches. The
MSB (most significant bit) of the number represents the
switching state of phase a, the second MSB for phase b,
and so on. As shown in Figure 5, selected working
voltage vectors equally divide the decagon into ten sec-
tions 1, 2, ..., 10.
From the average vector concept during one sampling

N. R. ABJADI ET AL.
14
*
n
V

a
V
b V
Figure 6. Reference vector and switching vectors in section
1 of α-β plane
Figure 7. Flowchart to realize reference voltage vectors
period, the reference voltage vectors on the α-β and x-y
planes can be realized by adjusting the applying times of
3 vectors. Figure 6 shows each section can be divided
into four smaller triangle regions, and the reference
voltage vector is formed by three apical voltage vectors
in this triangle [20]. For example if the reference vector
is between vectors 218 and 216 in α-β plane (sector 1),
and moreover it is located in region C, as shown in
Figure 6, the active switching vectors are 217, 216, 108
(or 229).
To control 2 series-connected motor, in half of each
switching period, the α-β reference vector, in α-β plane,
is used as the reference vector and in half other, the x-y
reference vector, in x-y plane, is used to determine the
switching vectors. This strategy can be repeated in all of
the sectors and shown in flowchart of Figure 7. It is
worthwhile to note using the switching vectors for
example in α-β plane, by above suggested method, the
x-y components are negligible and vice versa. In this way,
both α-β reference vector and x-y reference vector are
realized.
It is better to normalize vectors by 0.3236
VV
SDC
,
then each switching vector coordinate becomes integer as
shown in Figure 6.
From Figure 6, the coordinates of reference vector are
obtained as follow
*
(c) sin
36
o
an
tg ctg
VV
  (18)
*
sin
sin 36
o
bn
VV

 (19)
where

is the angle between reference vector and
a-axis in each section. The space vector PWM strategy is
accomplished by the following equations
E
FGs Ea Fa Gaa
E
FGs Eb Fb Gbb
EFGs
VVV V TTTT
VVV V TTTT
TTTT
 




(20)
where
E
T,
F
T and G Tare the apical switching vectors
in each triangle region; and
s
T is half of the switching
period.
For simplicity the switching times for all of the
regions are calculated in Table 1.
6. Simulation Results
The proposed control scheme is implemented in a block
diagram shown in Figure 8. In this figure, only control of
IM1 is illustrated (some subscripts are omitted for the
sake of brevity), the same can be applied to IM2.
Notice that the SM controller and observer gains are
obtained by trial and errors. Similarly the coefficients of
sp eed PI controller are obtained as 10
p
k,1.1
i
k.
Simulation results are obtained for a two different five-
phase squirrel cage IM with parameters shown in Table 2.
The IMs speeds and stator fluxes control results are
obtained and shown in Figure 9(a) and Figure 9(b)
respectively. These results obtained for an exponential
reference rotor speed from zero to 80 rad/s for machine 1
and an exponential reference rotor speed from zero to 40
rad/s for machine 2. The amplitudes of stator fluxes are
Table 1. Calculation of switching times in each region
Region A: V
(,)(0,0)
(,)(1,0)
(,)(0,1)
FsEa Eba
GsFa Fbb
E
sFGGa Gb
VV V
TT
VV V TT
VV TTTT
 








Region B: (,)(0,1)(1 )
(,)(1,0) (1 )
(,)(1,1)
EsEa Eba
FsFa Fbb
GsEF Ga Gb
VV V TT
VV V TT
VV TTTT

 

 



 
Region C: (,)(0,1) (2 )
(,)(1,1)
(, )(0,2)
E
sEa Ebab
Fs Fa Fba
GsEF Ga Gb
VVV V
TT
VV V TT
VV TTTT
  







Region D:
(,)(1,0) (2 )
(,)(2,0)
(,)(1,1)
E
s Ea Ebab
Gs Fa Fbb
FsEGGa Gb
VV VV TT
VV V TT
VV TTTT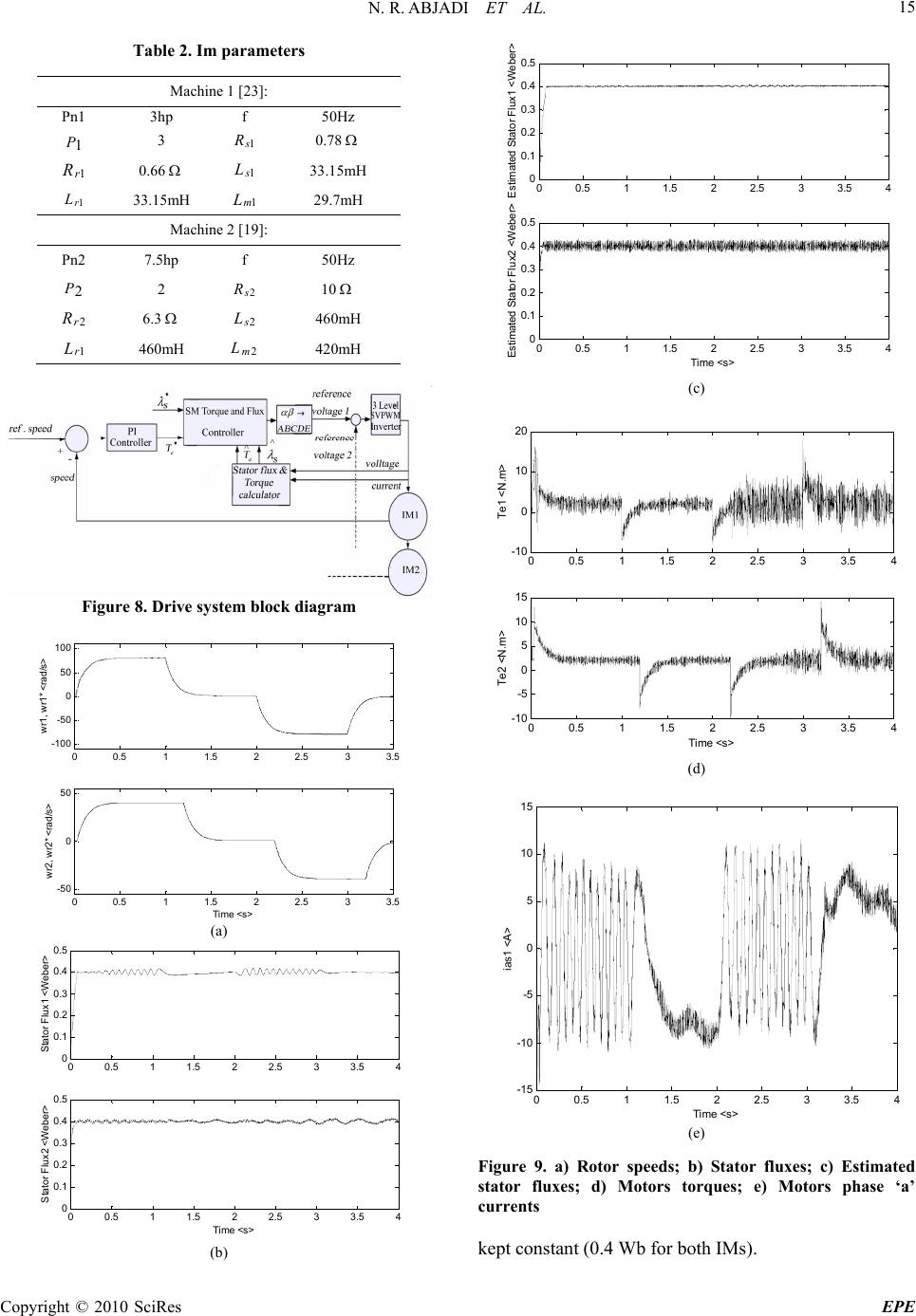
  

 





N. R. ABJADI ET AL.
15
Table 2. Im parameters
Machine 1 [23]:
Pn1 3hp f 50Hz
1
P
3 1
s
R
0.78 
1r
R 0.66  1
s
L 33.15mH
1r
L
33.15mH 1m
L 29.7mH
Machine 2 [19]:
Pn2 7.5hp f 50Hz
2
P
2 2
s
R 10 
2r
R
6.3 2
s
L 460mH
1r
L 460mH 2m L 420mH
Figure 8. Drive system block diagram
00.5 11.5 22.5 33.5
-10 0
-50
0
50
100
wr1, wr1* < rad/ s>
00.5 11.5 22.5 33.5
-50
0
50
Time <s>
wr 2, wr2* < r a d /s>
(a)
00.5 11.5 22.5 33.5 4
0
0.1
0.2
0.3
0.4
0.5
Stator Flux1 <Weber>
00.5 11.5 22.5 33.5 4
0
0.1
0.2
0.3
0.4
0.5
Time <s>
Stat or Flux2 <W eber >
(b)
00.511.522.5 33.5 4
0
0.1
0.2
0.3
0.4
0.5
Estimat ed St at or Flux1 <Weber >
00.511.522.5 33.5 4
0
0.1
0.2
0.3
0.4
0.5
Time <s>
Estimat ed Stator Flux2 <Weber >
(c)
00.5 11.5 22.5 33.5 4
-10
0
10
20
Te1 <N. m >
00.5 11.5 22.5 33.5 4
-10
-5
0
5
10
15
Time <s>
Te2 <N.m>
(d)
00.5 11.5 22.533.54
-15
-10
-5
0
5
10
15
Time <s>
ias 1 <A>
(e)
Figure 9. a) Rotor speeds; b) Stator fluxes; c) Estimated
stator fluxes; d) Motors torques; e) Motors phase ‘a’
currents
kept constant (0.4 Wb for both IMs).

N. R. ABJADI ET AL.
16
The speeds and fluxes track their references with a
good dynamics. It is evident from these Figs. that the
flux of the IM2 remains unaffected during the transient
of the speed of IM1 and vice versa, moreover the speeds
are also almost unaffected. These results verify the
ability of the proposed control and SVPWM technique
during speed start up and speed reversal.
In addition, the motors stator flux estimated results are
shown in Figure 9(c).
Finally the torque and phase a current of IMs are
shown in Figures 9(d) and 9(e) respectively. The inverter
phase ‘a’ current (1
ias ) includes two frequencies to run
both IMs.
7. Conclusions
This paper has discussed a two five-phase series-connec-
ted IM drive which is supplied by a 3 level five-phase
SPWM VSI.
An SM controller is used that is capable of controlling
the stator flux and torque of each motor separately.
The proposed controller in this paper is capable to
track the speed reference and the flux reference in spite
of motor resistances mismatching. In addition, the
transient dynamic of the motors stator fluxes and torques
is precisely regulated by the design of SM controller.
Moreover an algorithm is suggested to produce α-β and
x-y voltage components with a 3 level SVPWM VSI.
The effectiveness and validity of the proposed control
method is verified by simulation results.
REFERENCES
[1] H. A. Toliyat, “Analysis and simulation of five-pha-
se variable-speed induction motor drives under asym-
metrical connections,” IEEE Transactions on Power
Electronics, Vol. 13, No. 4, pp. 748–756, July 1998.
[2] D. Dujic, G. Grandi, M. Jones, and E. Levi, “A space
vector PWM scheme for multifrequency output voltage
generation with multiphase voltage-source inverters,”
IEEE Transactions on Industrial Electronics, Vol. 55, No.
5, pp. 1943–1955, May 2008.
[3] E. Levi, D. Dujic, M. Jones, and G. Grandi, “Analytical
determination of DC-Bus utilization limits in multip-
hase VSI supplied AC drives,” IEEE Transactions on
Energy Conversion, Vol. 23 No. 2, pp. 433–443, June 2008.
[4] V. Oleschuk, F. Profumo, and A. Tenconi, “Analysis of
operation of symmetrical dual three-phase converters
with hybrid schemes of synchronised PWM,” Internati-
onal Review of Electrical Engineering (IREE), Vol. 2, No.
6, December 2007.
[5] M. J. Duran, F. Salas, and M. R. Arahal, “Bifurcation
analysis of five-phase induction motor drives with third
harmonic injection,” IEEE Transactions on Industrial
Electronics, Vol. 55, No. 5, pp. 2006–2014, May 2008.
[6] R. Kianinezhad, B. Nahid-Mobarakeh, L. Baghli, F. Betin,
and G.-A. Capolino, “Modeling and control of six-phase
symmetrical induction machine under fault condition due
to open phases,” IEEE Transactions on Industrial Elec-
tronics, Vol. 55, No. 5, pp. 1966–1977, May 2008.
[7] N. R. Abjadi, J. Soltani, and J. Askari, “Nonlinear
sliding-mode control of a multi-motors web winding sys-
tem without tension sensor,” IEEE International Con-
ference on Industrial Technology (ICIT 2008), pp. 1–6,
April 21–24, 2008.
[8] E. Levi, S. N. Vukosavic, and M. Jones, “Vector control
schemes for series-connected six-phase two-motor drive
systems,” IEE Proceedings-Electronics Power Applica-
tions, Vol. 152, No. 2, pp. 226–238, March 2005.
[9] M. Jones, S. N. Vukosavic, E. Levi, and A. Iqbal, “A
six-phase series-connected two-motor drive with de-
couple-ed dynamic control,” IEEE Transactions on Indus-
trial Applications, Vol. 41, No. 4, pp. 1056–1066, July–
August 2005.
[10] K. K. Mohapatra, R. S. Kanchan, M. R. Baiju, P. N.
Tekwani, and K. Gopakumar, “Independent field-orient-
ed control of two split-phase induction motors from a
single six-phase inverter,” IEEE Transactions on Indus-
trial Electronics, Vol. 52, No. 5, pp. 1372–1382, Octo-
ber 2005.
[11] M. Jones, S. N. Vukosavic, and E. Levi, “Parallel-con-
nected multiphase multidrive systems with single inverter
supply,” IEEE Transactions on Industrial Electronics, Vol.
56, No. 6, pp. 2047–2057, June 2009.
[12] E. Levi, M. Jones, S. N. Vukosavic, and H. A. Toliyat,
“A five-phase two-machine vector controlled induction
motor drive supplied from a single inverter,” EPE Journal,
Vol. 14, No. 3, pp. 38–48, August 2004.
[13] K. K. Mohapatra, M. R. Baiju, and K. Gopakumar,
“Independent speed control of two six-phase induction
motors using a single six-phase inverter,” EPE Journal,
Vol. 14, No. 3, pp. 49–62, June–August 2004.
[14] M. Jones, E. Levi, and A. lqbal, “A five-phase series-
connected two-motor drive with current control in the
rotating reference,” 35th Annual IEEE Power Electronics
Specialists Conference, Aochen, Gemany, pp. 3278–3284,
2004.
[15] J. W. Kelly, E. G. Strangas, and J. M. Miller, “Multiphase
space vector pulse width modulation,” IEEE Transactions
on Energy Conversion, Vol. 18, No. 2, pp. 259–264, June
2003.
[16] J. W. Kelly, E. G. Strangas, and J. M. Miller, “Multiphase
inverter analysis,” Proceedings of IEEE International
Electric Machines Drives Conference (IEMDC), pp. 147–
155, 2001.
[17] H.-M. Ryu, J.-H. Kim, and S.-K. Sul, “Analysis of
multiphase space vector pulse-width modulation based
on multiple d-q spaces concept,” IEEE Transactions on
Power Electronics, Vol. 20, No. 6, pp. 1364–1371,
November 2005.

N. R. ABJADI ET AL.
17
[18] L. Parsa, “On advantages of multi-phase machines,” 32nd
Annual Conference of IEEE Industrial Electronics Socie-
ty (IECON), pp. 1574–1579, 2005.
[19] E. Levi, A. Iqbal, S. N. Vukosavic, and H. A. Toliyat,
“Modeling and control of a five-phase series-connected
two-motor drive,” The 29th Annual Conference of the
IEEE Industrial Electronics Society (IECON), Vol. 1, pp.
208–2132, 003.
[20] Q. Song, X. Zhang, F. Yu, and C. Zhang, “Research on
space vector PWM of five-phase three-level inverter,”
Proceedings of the Eighth International Conference on
Electrical Machines and Systems, ICEMS, Vol. 2, pp.
1418–1421, 2005..
[21] C. Lascu, I. Boldea, and Frede Blaabjerg, “Direct torque
control of sensorless induction motor drives: A sliding-
mode approach,” IEEE Transactions on Industrial App-
lications, Vol. 40, No. 2, pp. 582–590, March–April 2004.
[22] C. Lascu and G.-D. Andreescu, “Sliding-mode observer
and improved integrator with DC-Offset compensation
for flux estimation in sensorless-controlled induction
motors,” IEEE Transactions on Industrial Electronics, Vol.
53, No. 3, pp. 785–794, June 2006.
[23] K. N. Pavithran, R. Parimelalagan, and M. R. Krishna-
murthy,” Studies on inverter-fed five-phase induction
motor drive,” IEEE Transactions on Power Electronics,
Vol. 3, No. 2, pp. 224–235, April 1988.