Energy and Power Engineering, 2010, 1-5
doi:10.4236/epe.2010.21001 Published Online February 2010 (http://www.scirp.org/journal/epe)
A Tabu Search Algorithm for Fast Restoration of
Large Area Breakdown in Distribution Systems
Jian LIU, Hongli CHENG, Xiaojun SHI, Jingqiu XU
School of Electrical Engineering, Xi’an University of Science and Technology, Xi’an, China
Abstract: To restore the distribution systems in emergency states with the minimum load shedding, a novel
Tabu search approach is put forward. The set of tripped switches is used as candidate solution. Some virtual
tripped nodes are defined at the ends of the terminal nodes and by the source nodes. The neighborhood
searching is committed by moving a tripped switch to the adjacent node of its upper stream and down stream,
respectively. A Tabu list is formed for the tripped switches. The ind ex is to energize as much as possible loads
with as less as possible operated times. The electrical limitations and the voltage criterions are used as con-
strictions. The global aspiration criterion is adopted. An example is given, which shows that the proposed ap-
proach is feasible and can deal with complicated indexes.
Keywords: distribution systems, restoration, large area break down, load shedding, Tabu search
1. Introduction
Although many achievements have been made on fault
isolation and restoration, most of them are for fault on a
certain feeder section [1–5].
More serious faults, such as failure on a HV transmis-
sion line, a main transformer or a bus, may also occur
and sometimes cause large area break down in the dis-
tribution systems.
Moreover, in some con tingent situ ations of main tran s-
former over loaded, bulk loads need to be transferred to
the adjacent substations and sometimes load shedding is
necessary, which is quit similar to the restoration process
of large area break down.
A fast restoration approach of large area break down
based on numerical optimization is put forward in [6].
Although it is smart, it can only deal with the simple
index of the minimum load shedding.
In the practice, some other considerations are also
needed to be included, such as the times of switching
operation, losses, etc.
Tabu search is a promising evolutionary algorithm,
which can deal with complicated indexes and constraints.
It has been successfully applied into the distribution
network reconfiguration [7].
But the conventional Tabu search based network re-
configuration approaches are not suitable to solve the
problem of large area break down restoration with a few
load shedding, because the numbers of tripped switches
before and after reconfiguration must be equal.
In this paper, a novel Tabu search based approach is
proposed to solve above problems.
2. Basic Principles
2.1 Construction of Solutions
In the Tabu search based distribution network reconfigu-
ration, the set of tripped switches can be used as candi-
date solution.
The initial solution s(0) based on the current topology
of the distribut i on net w ork is
],...,,[ )0()0(
2
)0(
1
)0( M
ssss (1)
where, )0(
i
s is the sequence number of the i-th tripped
switch of the current operation mode, M is the number of
the tripped switches.
A candidate solution of the k-th iteration s(k) is
],...,,[)()(
2
)(
1
)( k
N
kkk ssss (2)
If some loads are shed, we have
MN (3)
2.2 Virtual Tripped Nodes
In order to meet the requirement of N>M, we should
define virtual tripped switches, which are shown in
Figure 1.
The initial positions of virtual tripped switches are at
the end of terminal nodes and behind the source nodes.
The total number of virtual tripped switches is the sum-
mation of the number of terminal nodes and the number
of the source nodes.

J. LIU ET AL.
2
Virtual
tr ipped node Virtual
tripped node
Virtual
tr ipped node
Figure 1. Illustration of virtual tripped switch-nodes
Actual tripped switches and virtual tripped switch-
es are all called tripped switches. With the help of the
virtual tripped switches, the Tabu search based dis-
tribution network reconfiguration approach can deal
with the network reconfiguration problem with load
shedding.
In the initial positions, the virtual tripped switches
have no influence on the feeder as shown in Figure 1.
But when their positions are shifted, some loads may be
shed, which are shown in Figures 2(a), (d), (e) and (f). In
Figure 2, the reenergized feeder sections are labeled with
dotted lines.
2.3 Neighborhood Searching
In the iteration of Tabu search, the neighborhood search-
ing is committ ed, in which, each tripped switch is moved
to the adjacent node of its upper stream or down stream
while the other switches keep their states not changed.
Therefore, the candidate solution set is formed.
Assuming that the selected solution of the k-th itera-
tion is shown in Figure 1, its candidate solutions of the
k+1-th itera tion produ ced by th e neighbo rhood sear ching
are shown in Figure 2.
The arrows in Figure 2 indicate the shifting direction
of a certain tripped switch.
In each iteration, the best solution in the candidate so-
lution set without being tabooed is taken as s(k+1) and the
corresponding newly tripped switch is taken into the
Tabu list.
The global aspiration criterion is adopted, i.e., once
the best candidate in the candidate solution set is superior
than the ‘best so far ’ solution, it is taken as s(k+1) and the
new ‘best so far’ solution, no matter whether it is in ta-
booed state.
Above process is committed repeatedly until the stop
criterion of no more improvement or reaching the maxi-
mum iteration times is satisfied.
2.4 Fitness Function
Complicated fitness functions, i.e., indexes, can be used.
As an example, a typical fitness function is
Virtual
tr ipped node Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped nodeVirtual
tr ipped node
Virtual
tr ipped node
(a) (b)
Virtual
tr ipped node Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
(c) (d)
Virtual
tr ipped node Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
Virtual
tr ipped node
(e) (f)
Figure 2. The candidate solutions

J. LIU ET AL.
3
12
3
1










γ
γ
i
i
i
i
pP
Pp
Max fT (4)
where,  P is the total load within the investigating
area,  is the set of energized sections after reconfigu-
ration,


γ
i
i
p is the summation of the energized loads
after reconfiguration, P is the total line losses, T is
the times of switching operation, 
1,

2 and

3 are
weighted va lue s.
The index of (4) indicates that it is encouraged to en-
ergize as much as possible loads with as less as possible
operating times and line lo sses.
In most emergency states, the main task is to restore
loads as much as possible without considering the line
losses. But the difference of importance of various loads
should be described in the index. Thus, the fitness func-
tion become s
3
1




γ
ii
i
kp
Max fT (5)
where, ki is the weight of the importance of the i-th load.
2.5 Constraints
Typical constraints are as follows:
-Topology constraints, i.e., no loop exists.
-The times of switching operation should not exceed
the max imum value allowed.
-Constraints of electrical limitations, i.e., ,max

ii
I
I
where, ,maxi
I
is the current limitation of the i-th branch.
-Voltage constraints, i.e., each node voltage is within
the range of voltage criterions.
-Other constraints such as locking the switches con-
nected to the malfunctioned buses and keep the switches
in reparation in tripped states, etc.
2.6 Initial Solution
In contingent situations of main transformer over loaded,
the current network topology can be used as the initial
solution.
In emergency states due to faults, the steps to form the
initial solution are as follows:
Step 1: Isolate of the deenergized buses by tripping all
the switches connected to the corresponding buses and
lock them in the tripped states, therefore, some feeder
sections are deenergized.
Step 2: Close the loop switches (if exist) connecting
the deenergized feeder sections to the healthy parts of the
distribution network. If there are more than one restora-
tion path for a certain deenergized feeder section, choose
any one of them.
Step 3: Take the obtained topology as the initial solu-
tion.
2.6 Tabu Length and Stop Criterion
The ability of escaping from the local optimal points is
improved with the Tabu length grows larger. But a larger
Tabu length may hamper the convergence. As for a
small-scale distribution network, it is possible to face the
situation of no feasible candidate solution with a too
large Tabu length . Th erefor e, th e selectio n of Tabu length
may be in accordance with the number of nodes of the
distribution network. In most cases, it ranges from three
to five.
The Tabu search based optimization process will ter-
minate if the best solution remains the same within sev-
eral successive iterations or the times of iteration reaches
its maximum value set before hand.
2.7 Discussions
The optimal topology obtained by the above approach
may contain redundant switching operations. As for the
obtained optimal topology, if a certain switch is in
tripped state and its adjacent feeder sections are all deen-
ergized, the tripping operation of the switch is redundan t
and should be eliminated from the switching schedule.
The following measures may improve the efficiency of
the proposed approach:
-Never locate any virtual tripped switch at the end of
the feeder sections without sectionalizing switches.
-Only the feeders suffering from the failed apparatus
and their corresponding connected parts [8] (In [8], a
connected part is defined as a feeder gr oup, in which , the
load may be transferred from one feeder to the other) are
included in the process of Tabu search.
-The Tabu search based optimization processes are
performed in each connected part, respectively.
3. Case Study
The approach described in Section 2 will now be illus-
trated with results for Case Study based on a realistic
distribution netw ork shown in Figure 3.
There are two HV transmission line paths and three
substations, such as, Sb.A, Sb.B and Sb.C and six main
transformers labeled from No.1 Tr. to No.6 Tr. The volt-
age of primary distribution system is 10kV. There are six
10kV buses, such as B75, B79, B80, B84, B85 and B89.
The solid circles and the hollow indicate the closed
and tripped switches, respectively. The numbers besides
the circles are the sequence number of the co rresponding
nodes.
Assuming that the power factors of the loads are of the
same value, the loads can be measured in Ampere. The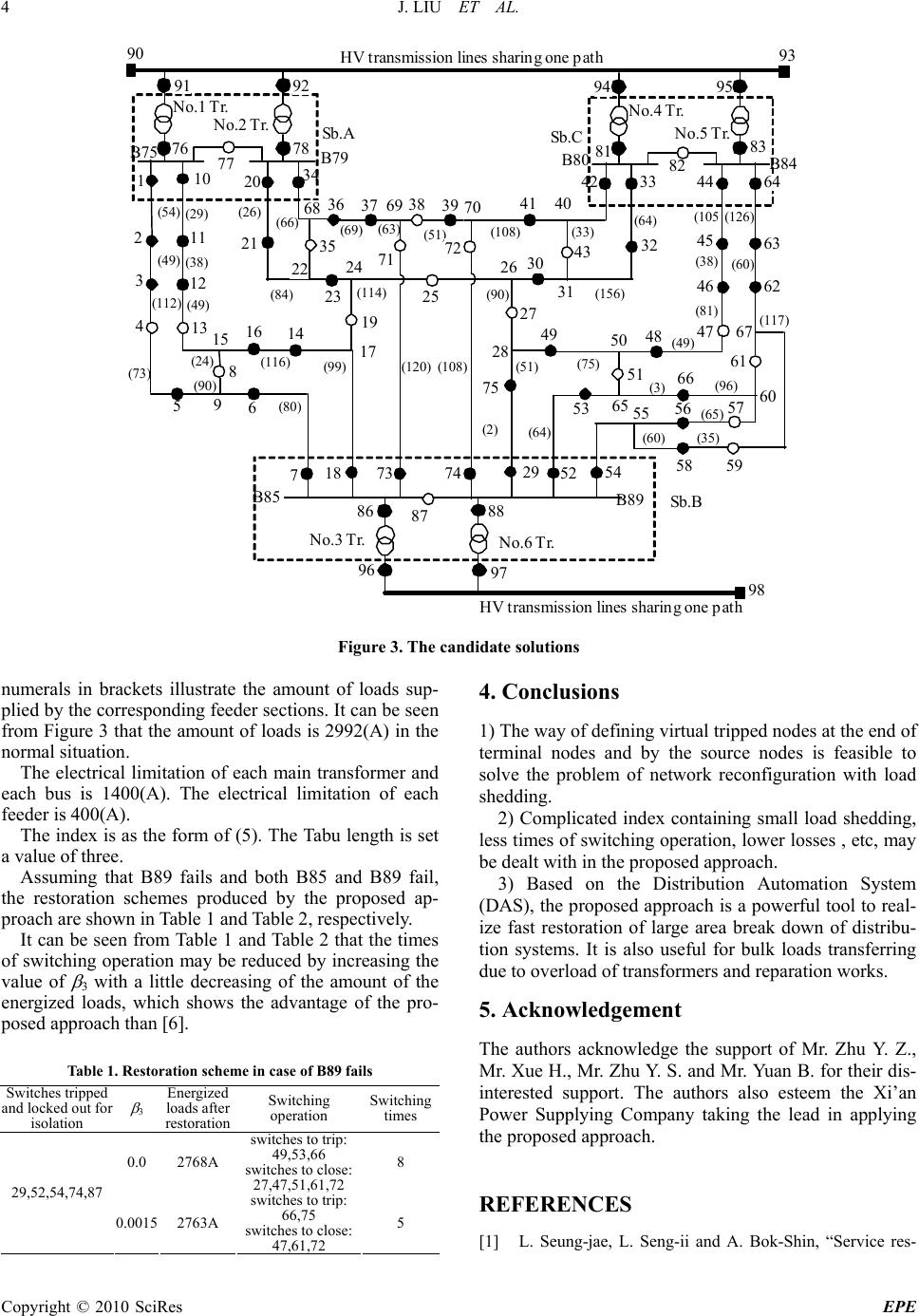

J. LIU ET AL.
4
HV transmission lines sharing one path
N
o.1 Tr .
N
o.2 Tr .
HV transmission lines sharing one path
56
28
96
Sb.C
77 64
(49)
94
1 10 20
86
16
2
3
4
5 6
7
8
9
11
12
13 15 14
18
21
23
22
29
34 44
45
46
48
52 54
62
63
B85
35
Sb.B
(
54
)
(49)
(112)
(73)
(29)
(38)
(
24
)
(26)
(
84
)
(66)
(80)
(
90
)
(
116
)
(105
(38)
(126)
(60)
No.3 Tr .
98
N
o.4 Tr .
B
75
B79 B80 B84
82
68
73
81
95
83
93
90
N
o.5 Tr .
74
87
76
91
78
92
88
97
Sb.A
No.6 Tr .
B89
47
58
61
(
49
)
(81)
(
117
)
(
96
)
(
65
)
57
59
(
35
)
60
67
(
3
)
49
17
19
23
24
25
26
27 31
30 32
33
36 37 38 39 4140 42
43
51
50
53 55
35
(
69
)
(
63
)
(
51
)
(
108
)
(
33
)
(
99
)
(90)
(114)
(5 1 )
(6 4 )
(75)
(156)
(64)
(
60
)
65
71
69
(
120
)
70
72
(108) 66
75
(2)
Figure 3. The candidate solutions
numerals in brackets illustrate the amount of loads sup-
plied by the corresponding feeder sections. It can be seen
from Figure 3 that the amount of lo ads is 2992(A) in the
normal situation.
The electrical limitation of each main transformer and
each bus is 1400(A). The electrical limitation of each
feeder is 400(A).
The index is as the form of (5). The Tabu length is set
a value of three.
Assuming that B89 fails and both B85 and B89 fail,
the restoration schemes produced by the proposed ap-
proach are shown in Table 1 and Table 2, respectively.
It can be seen from Table 1 and Table 2 that the times
of switching operation may be reduced by increasing the
value of 
3 with a little decreasing of the amount of the
energized loads, which shows the advantage of the pro-
posed approach than [6].
Table 1. Restoration scheme in case of B89 fails
Switches tripped
and locked out for
isolation

3 Energized
loads after
restoration
Switching
operation Switching times
0.0 2768A
switches to trip:
49,53,66
switches to close:
27,47,51,61,72
8
29,52,54,74,87
0.0015 2763A
switches to trip:
66,75
switches to close:
47,61,72
5
4. Conclusions
1) The way of defining virtual tripped nodes at the end of
terminal nodes and by the source nodes is feasible to
solve the problem of network reconfiguration with load
shedding.
2) Complicated index containing small load shedding,
less times of switching operation, lower losses , etc, may
be dealt with in the proposed approach.
3) Based on the Distribution Automation System
(DAS), the proposed approach is a powerful tool to real-
ize fast restoration of large area break down of distribu-
tion systems. It is also useful for bulk loads transferring
due to overload of transformers and reparation works.
5. Acknowledgement
The authors acknowledge the support of Mr. Zhu Y. Z.,
Mr. Xue H., Mr. Zhu Y. S. and Mr. Yuan B. for their dis-
interested support. The authors also esteem the Xi’an
Power Supplying Company taking the lead in applying
the proposed approach.
REFERENCES
[1] L. Seung-jae, L. Seng-ii and A. Bok-Shin, “Service res-

J. LIU ET AL.
5
toration of primary distribution systems based on fuzzy
evaluation of multi-criteria [J],” IEEE Transaction on
Power Systems, Vol. 13, No. 3, pp. 1156–1163. 1998
[2] S. Curcic, C. S. Ozveren, and K. L. Lo, “Computer based
strategy for t he restoration proble m in electric power distri-
bution systems [J],” IEE Proceedings-Generation, Trans-
mission, Distribution, Vol. 144, No. 5, pp. 389–398, 1997.
[3] J. Nahman and G. Strbac, “A new algorithm for service
restoration in large-scale urban distribution systems,” Elec-
tric Power System Research [J], No. 29, pp. 181–192, 1994.
[4] A. Augugliaro, L. Dusonchet, and E. Riva Sansevvrino,
“Multi-objective service restoration in distribution net-
works using an evolutionary approach and fuzzy sets
[J],” Electric Power and Energy Systems, No. 22, pp.
103–110, 2000.
[5] A. Pahwa, “Role of distribution automation in restoration
of distribution systems after emergencies [C],” Proceedings
of the IEEE Power Engineering Society Transmission and
Distribution Conference, No. 1, pp. 737–738, 2007.
[6] J. Liu, J. Q. Xu, and H. L. Cheng, “Fast restoration of
large area breakdown for power distribution systems [J],”
Frontiers of Electrical and Electronic Engineering in
China, No. 2, 2006.
[7] G. J. Chen, K. K. Li, and G. Q. Tang, “A Tabu search
approach to distribution network reconfiguration for loss
reduction [J],” Proceedings of the CSEE, Vol. 22, No. 10,
pp. 28–33 (Ch), 2002.
[8] J. Liu, P. X. Bi, and H. P. Dong, “Simplified Analysis and
Optimization for Complicated Distribution Systems [M],”
China Electric Power Press, Beijing 2002.