Communication and Network, 2010, 2, 50-53
doi:10.4236/cn.2010.21007 Published Online February 2010 (http://www.scirp.org/journal/cn)
ADPF Algorithm for Target Tracking in WSN
Chunhe Song, Hai Zhao, Wei Jing, Dan Liu
Institute of Information and Technology, Northeastern University, Shenyang, China
Received October 27, 2009; accepted December 29, 2009
Abstract: Particle filtering (PF) has been widely used in solving nonlinear/non Gaussian filtering problems.
Inferring to the target tracking in a wireless sensor network (WSN), distributed PF (DPF) was used due to the
limitation of nodes’ computing capacity. In this paper, a novel filtering method—asynchronous DPF (ADPF)
for target tracking in WSN is proposed. There are two keys in the proposed algorithm. Firstly, instead of
transferring value and weight of particles, Gaussian mixture model (GMM) is used to approximate the poste-
riori distribution, and only GMM parameters need to be transferred which can reduce the bandwidth and
power consumption. Secondly, in order to use sampling information effectively, when target moving to the
next cluster head region, the GMM parameters are transfer to the next cluster head, and combine with the
new local GMM parameters to compose the new GMM parameters incrementally. The ADPF can also deal
with the situation of different number of nodes in different cluster when using the dynamic cluster structure.
The proposed ADPF is compared to some other DPF for WSN target tracking, and the experimental results
show that not only the precision is improved, but also the bandwidth and power is reduced.
Keywords: WSN, target tracking, asynchronous distributed particle filtering
1. Introduction
One of the major goals of WSN is to detect and track
changes. The problem concerned is performing on-line
state estimation for multi-dimensional signals that can be
modeled using markovian state-space models that are
nonlinear and non-Gaussian, Particle filter is one of the
widely used tracking algorithms in non-linear/ Gaussian
dynamic systems. When using such algorithm in sensor
networks the energy cost related to computation in each
sensor node and communication between sensor nodes is
significant. Currently there are several distributed parti-
cle filters [1–3], in which the distributed nature is
achieved by either transmitting local statistics of particles
to a centralized unit or using the parameters passing me-
thod. Transmitting local statistics of particles to a cen-
tralized unit is not an efficient approach. Failure of the
centralized unit is vital to the entire network. In the pa-
rameters passing method, the algorithms construct a path
through the networks, which passes through all nodes.
Global statistics of particles are accumulated by adding
local statistics in each node through a forward pass. Then
there needs a backward pass, which runs the important
sampling and selection steps in each sensor node by us-
ing the accumulated global statistics.
In this paper, a novel filtering method – asynchronous
DPF (ADPF) for target tracking in WSN is proposed.
There are two keys in the proposed algorithm. Firstly,
instead of transferring value and weight of particles,
Gaussian mixture model (GMM) is used to approximate
the posteriori distribution, and only GMM parameters
need to be transferred which can reduce the bandwidth
and power consumption. Secondly, in order to use sam-
pling information effectively, when target moving to the
next cluster head region, the GMM parameters are trans-
fer to the next cluster head, and combine with the new
local GMM parameters to compose the new GMM pa-
rameters incrementally. Because of computing asyn-
chronously, this process can be regarded as ADPF.
The remaining of the paper is organized as follows: a
brief description of PF and DPF in WSN are presented in
Section 2. The details of the new PF this paper proposed
– ADPF is presents in Section 3. In Section 4 the pro-
posed algorithm is compared to other DPFs and finally,
we give some concluding remarks in Section 5.
2. Tracking in WSN
Issues considered in this paper is tracking a moving tar-
get based on position measurements from multiple dis-
tributed sensors.
2.1 Target Motion Model
The target motion model used in this paper is the same as [4]:
1
(),1, 2,...
kk k
xfxGv k

 
(1)
where the target state vector [,, ,,]
T
k
x
xxyyw , consist
of the position, velocity and the turn rate; ~(0, )
kk
vNQ

C. H. SONG ET AL. 51
is white process nosie: and
sin( )(1cos( ))
10 0
0cos( )0sin( )0
() (1cos( ))sin( )
01 0
0sin( )0cos( )0
00 001
kk
kk
kk
kk
kk
kk
TT
x
TTx
fx TT y
y
TT w
























 




(2)
2
2
/2 00
00
0/20
00
00
T
T
Gk T
T
T








(3)
2.2 Target Moti on Model
In this paper, measurements of range and bearing are
given by [5]:
() ,1,2,...,
i
kkk
zhx wiN  (4)
with
22
1
()
tan ()
kk
kk
k
xy
ri
hx y
bi
x



 

 
 

(5)
And white measurement noise ~(0,)
ii
kk
wNR
.
3. Basic PF and DPF in WSN
3.1 Basic Particle Filter
In the bayes filtering framework, the posterior distribu-
tion is updated recursively over the current state xt given
all observations 1
{}
t
tii
Zz

 up to and including time t as
follows[6]:
1111
(| )(|)(| )
ttttt tk
px YpxxpxYdx

 (6)
1
1
(|)(|)
(|) (| )
tt tt
tt
tt
pyxpx Y
px Ypy Y


 (7)
11
(| )(|)(|)
tttt ttk
pyYpyxpxYdx

 (8)
Using Monte Carlo sampling points, particle filter
executes the filtering process by generating weighted
sampling points of state variances recursively. Generic
particle filter algorithm can be found in [4].
3.2 Distributed Particle Filter in WSN
Particle filter has been widely used in target tracking. In
WSN, the information transferred between nodes and the
computing process in nodes are limited due to the re-
striction of power, computing capacity and bandwidth, so
some changes must be conducted in particle filter in or-
der to use it in WSN target tracking. The main idea of
distributed particle filter is to deal with the computation
at different sensor rather than at a central unit.
One typical DPF is the forward-backward type of dis-
tributed particle filter [6], which may be the first DPF for
WSN. Supposing K nodes in WSN, and N particles for
each node, in this algorithm, firstly, it is assumed that
measurements at sensor are independent with each others,
and in the particle filtering process, the likelihood
(|)
tt
p
yxcan be approximated by a parametric model
1
(|)(;|)
kK
tt ttk
py xLx 

. Secondly, only a single commu-
nication chain exists from node 1 to node k, with any
node i in the interior of the chain communicating only
with nodes i-1 and i+1. In the initialization step, each
node samples N particles from0
()
p
x. At time t, Node i
sample from its importance distribution to generate N
particles. Node i calculates the value of its likelihood for
each one of these particles for the current observ
ation and then trains the model()
1
{(, (;{})
j
ki
tttk
x
Lx
p



()
1
(| ))}
kjN
tt j
py x
. The parameters 1
{}
ki
tk

are then appro-
priately quantized and transmitted to node i+1 in the
chain. In the next phase of this algorithm, the estimated
parameters 1
{}
kK
tk


are propagated back along the
communication chain. And each node uses the parame-
ters to calculate estimates of likelihood for its samples
()
1
{}
j
N
tj
x

, which will be used to calculate the importance
weights of particles. In the mentioned process above, it is
assumed that the sensors act synchronously and record
their measurements at the same time. So it can be re-
garded as synchronously particle filter.
There is complicated training process in this algorithm,
and all nodes compute synchronously during target
tracking. One simple idea is to transfers value and weight
of particles directly between nodes and represents the
posterior distribution. But there are N particles in each
node and the transferred bits will be very large, so the
posterior distribution of particle filter is assumed to be a
GMM with C mixture probabilities. [2] is such type of
DPF. In this algorithm, firstly, the WSN is divided into a
series of group misrelated, and a single particle filter
runs in each group. Through the head of current group,
parameters of filter are transferred to the next head and
update the posterior distribution. On the last group of
sensors target tracking was estimated. As need transfer
number of value and weight of particle, in this algorithm,
low dimension GMM is used to approximate the likeli-
hood distribution of DPF. To implement a distributed
particle filter (DPF), particles and weights are distributed
over entire network. Each sensor should maintain N par-
ticles () ,
n
mk
x
and weights()
,
n
mk
w. The posterior distribution of
particle filter is assumed to be a GMM with C mixture

C. H. SONG ET AL. 52
probabilities. For each unobserved state yc, observation
zm, k follows a Gaussian distribution with mean μc and
variance c
:
1
,,
1()()
2
,
1
(|,)
2
T
mk ccmk c
zz
mkc c
c
pz e




 
 (9)
The Gaussian mixture distribution for observation
,mk
z is:
,,,
(|) (|,)
mkmcmkc c
pz pz   
 (10)
where θ is the set of the distribution parameters to be
estimated,


,,,;1,..., ,1,..., mccc cCmM
 
.
Assume all observed data from all nodes are sent to a
centralized unit where a standard EM algorithm is used
to estimate the parameter set θ. The log-likelihood for
the observed data satisfies:
,,
11 11
,,
11
(|)log( |)( |)
(|,)
Mk Mk
mj mj
mj
mj
Mk
mcmkc c
mj
L zpzpz
pz










 (11)
4. Asynchronous Distributed Particle Filter
4.1 Dynamic Cluster Structure
In some former DPF, the cluster structure is fixed. In the
ADPF, dynamic cluster structure is used. Supposing all
nodes have the same detecting capacity, choose one
cluster head, forming all nodes in the range of sing-hop
of cluster head into a cluster, and this cluster head is used
to deal with the sampling data and get local estimation.
Supposing C is the max distance of sing-hop communi-
cation, R is the max range of detecting, and D is the dis-
tance of cluster head and other node. When target enter-
ing into the detecting region of WSN, and the number of
node already detecting the target is over a predefined
threshold, choose the nearest node as the cluster head.
Forming the cluster and recall all nodes in this cluster.
Following the movement of target, some nodes in the
cluster will be out of the detecting region. If the number
of nodes out of the detecting region is over a predefined
threshold or D+C>R, choose a new cluster head and
construct a new cluster. Otherwise predict the new loca-
tion of target using filtering algorithms.
4.2 Gaussian Mixture Model Using EM
Using EM algorithm, the parameters of Equation 7) can
be calculated. Given observation z and current parameter
set t

where t is the time step between two consecutive
sensor observations at k and k+1, the conditional expec-
tation of joint distribution (,| )pzy

is defined as:
,,
111
,, ,
111
(, )log[(,|))](|, )
log[(|,)] (|,)
CM k
tt
mkccmj
cm j
CM k
t
mkmkcccm j
cm j
Qpzypyz
pzpy z


 






Detail information about the Gaussian mixture model
using EM algorithm can be found in [6].
4.3 Asynchronous Updating GMM Parameters
When running DPF in WSN asynchronously using GMM
approximate posterior distribution, after getting into the
new cluster region, former sampling information will be
lost. Here propose a new GMM incrementally updating
algorithm using PCA concept.
Supposing m0 nodes in the first cluster, each node
send its parameters ,
[,,]
T
mccc


to the first cluster
head, and compose the parameters matrix 010 [,... ]
n
P



.
It will be used to approximate the posterior distribution
and transfer to the next cluster head.
Supposing the former cluster is the (i-1)th cluster with
ni-1 sensors, parameters matrix is Pi-1, the current cluster
is the ith cluster with ni sensors, parameters matrix is
i
P.1i P

and i Pare the raw average vectors of 1i P

and
i
P.
decomposing i
Pwith SVD:
T
i
PUV

 (12)
and denote i
P as the row average vector of i P.
Using the i
Pand 1i P

to compose a new matrix
*
1
[, ]
iii
P
PP

, decomposing it with SVD:
*
1
[, ]T
iii
PPPUV



  (13)
where *
[, ]UUU
,1
*
1
0
T
i
T
i
UP
UP










 and 0
0
T
TV
VI







;
1
1
1
*
[|( )*()]
ii
ixiii i
ii
nn
PPPsqrt PP
nn



 
 (14)
*(* )
T
iy ix
P
PIUU , calculate the QR decomposing of
iy
P:()
iz iy
P
QR P. Using T
V, U,ix
Pand iz P to compose
the matrix i
P
:
**
0*(*)
ix
iTT
iy ix
ff VUT P
PPPIUU










 (15)
where ff is the forgotten factor with value in the range of
[0, 1]. It indicates the weights of last parameters in the
current computing time. In this experiment, the ff is set
to 0.8.
Calculating SVD of i
P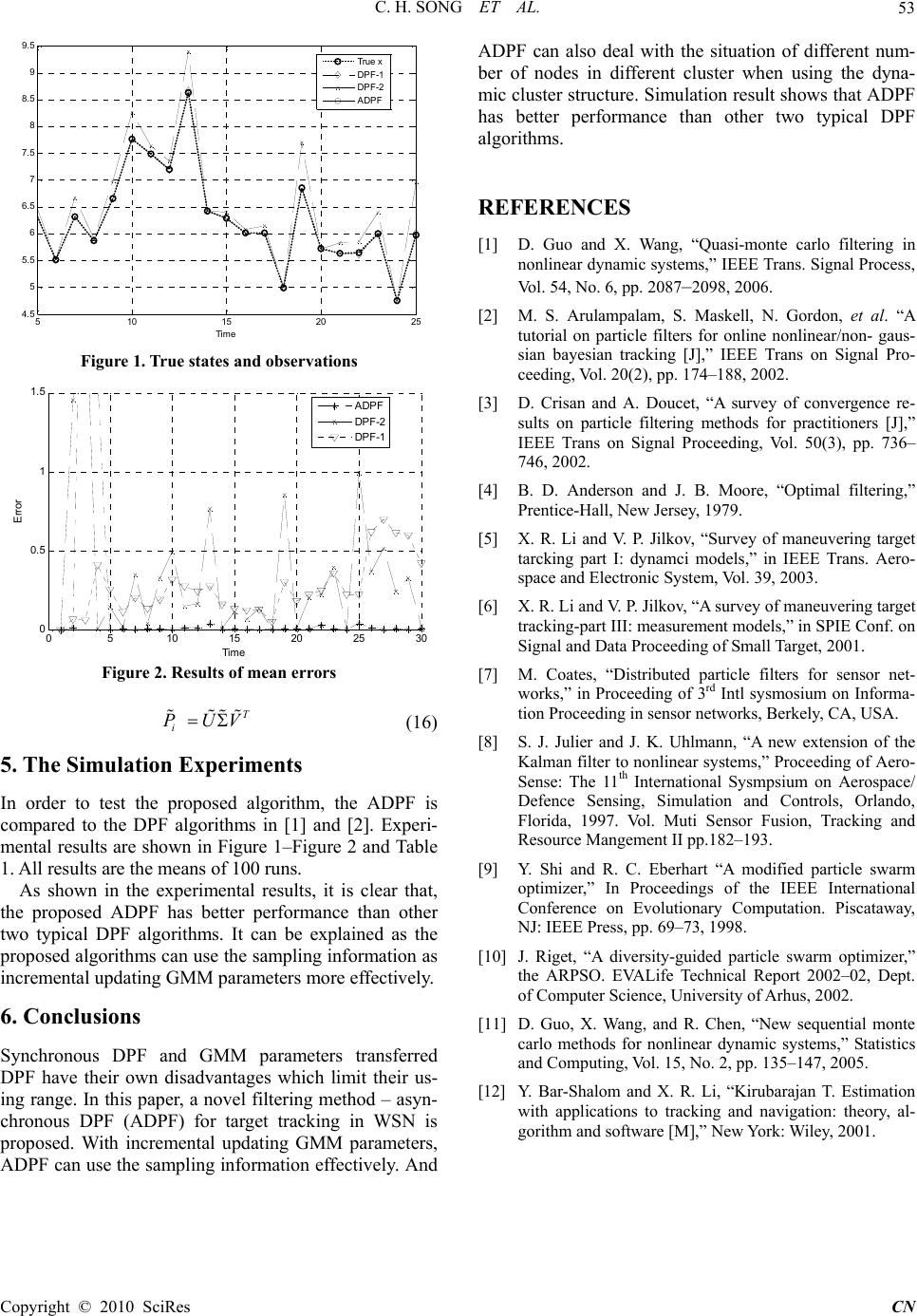
:

C. H. SONG ET AL. 53
510 15 20 25
4. 5
5
5. 5
6
6. 5
7
7. 5
8
8. 5
9
9. 5
Ti me
Tr ue x
DPF-1
DPF-2
ADPF
Figure 1. True states and observations
05 10152025 30
0
0.5
1
1.5
Time
Error
ADPF
DP F -2
DP F -1
Figure 2. Results of mean errors
T
i
PUV
  (16)
5. The Simulation Experiments
In order to test the proposed algorithm, the ADPF is
compared to the DPF algorithms in [1] and [2]. Experi-
mental results are shown in Figure 1–Figure 2 and Table
1. All results are the means of 100 runs.
As shown in the experimental results, it is clear that,
the proposed ADPF has better performance than other
two typical DPF algorithms. It can be explained as the
proposed algorithms can use the sampling information as
incremental updating GMM parameters more effectively.
6. Conclusions
Synchronous DPF and GMM parameters transferred
DPF have their own disadvantages which limit their us-
ing range. In this paper, a novel filtering method – asyn-
chronous DPF (ADPF) for target tracking in WSN is
proposed. With incremental updating GMM parameters,
ADPF can use the sampling information effectively. And
ADPF can also deal with the situation of different num-
ber of nodes in different cluster when using the dyna-
mic cluster structure. Simulation result shows that ADPF
has better performance than other two typical DPF
algorithms.
REFERENCES
[1] D. Guo and X. Wang, “Quasi-monte carlo filtering in
nonlinear dynamic systems,” IEEE Trans. Signal Process,
Vol. 54, No. 6, pp. 2087–2098, 2006.
[2] M. S. Arulampalam, S. Maskell, N. Gordon, et al. “A
tutorial on particle filters for online nonlinear/non- gaus-
sian bayesian tracking [J],” IEEE Trans on Signal Pro-
ceeding, Vol. 20(2), pp. 174–188, 2002.
[3] D. Crisan and A. Doucet, “A survey of convergence re-
sults on particle filtering methods for practitioners [J],”
IEEE Trans on Signal Proceeding, Vol. 50(3), pp. 736–
746, 2002.
[4] B. D. Anderson and J. B. Moore, “Optimal filtering,”
Prentice-Hall, New Jersey, 1979.
[5] X. R. Li and V. P. Jilkov, “Survey of maneuvering target
tarcking part I: dynamci models,” in IEEE Trans. Aero-
space and Electronic System, Vol. 39, 2003.
[6] X. R. Li and V. P. Jilkov, “A survey of maneuvering target
tracking-part III: measurement models,” in SPIE Conf. on
Signal and Data Proceeding of Small Target, 2001.
[7] M. Coates, “Distributed particle filters for sensor net-
works,” in Proceeding of 3rd Intl sysmosium on Informa-
tion Proceeding in sensor networks, Berkely, CA, USA.
[8] S. J. Julier and J. K. Uhlmann, “A new extension of the
Kalman filter to nonlinear systems,” Proceeding of Aero-
Sense: The 11th International Sysmpsium on Aerospace/
Defence Sensing, Simulation and Controls, Orlando,
Florida, 1997. Vol. Muti Sensor Fusion, Tracking and
Resource Mangement II pp.182–193.
[9] Y. Shi and R. C. Eberhart “A modified particle swarm
optimizer,” In Proceedings of the IEEE International
Conference on Evolutionary Computation. Piscataway,
NJ: IEEE Press, pp. 69–73, 1998.
[10] J. Riget, “A diversity-guided particle swarm optimizer,”
the ARPSO. EVALife Technical Report 2002–02, Dept.
of Computer Science, University of Arhus, 2002.
[11] D. Guo, X. Wang, and R. Chen, “New sequential monte
carlo methods for nonlinear dynamic systems,” Statistics
and Computing, Vol. 15, No. 2, pp. 135–147, 2005.
[12] Y. Bar-Shalom and X. R. Li, “Kirubarajan T. Estimation
with applications to tracking and navigation: theory, al-
gorithm and software [M],” New York: Wiley, 2001.