Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2008, 1, 195-199 Published Online November 2008 in SciRes. http://www.srpublishing.org/journal/jbise JBiSE Application of modified superposition model to viscoelastic behavior of periodontal ligament 1Javad Hazrati Marangalou, 1Farzan Ghalichi & 2Behnam Mirzakouchaki 1Division of Biomechanics, Mechanical Engineering Department, Sahand University of Technology, Tabriz, Iran. 2Division of Orthodontics, School Of Dentistry, Tabriz University of Medical Sciences, Tabriz, Iran. Correspondence should be addressed to J. Hazrati (hazrati_biomech@yahoo.com). Received July 17, 2008; revised October 17, 2008; accepted October 17, 2008 ABSTRACT The periodontal ligament (PDL) is a soft bio- logical tissue which shows a strongly nonlinear and time dependent mechanical behavior. Re- cent experiments on rabbit PDL revealed that the rate of stress relaxation is strain dependent. This nonlinear behavior of PDL cannot be de- scribed well by the separable quasi linear vis- coelasticity theory which is usually used in tis- sue biomechanics. Therefore, PDL requires a more general description which considers this nonlinearity and time dependency. The purpose of this study was to model strain dependent stress relaxation behavior of PDL using modi- fied superposition method. It is shown herein that modified superposition method describes viscoelastic nonlinearties well and shows a good compatibility with available experimental PDL data. Hence, the modified superposition model is suggested to describe periodontal ligament data, because it can suitably demon- strate both elastic nonlinearity and strain-dependent stress relaxation behavior of PDL. Keywords: periodontal ligament, viscoelasticity, modified superposition method, stress relaxa- tion 1. INTRODUCTION A tooth is secured to the alveolar bone by fibrous con- nective tissue that is called the periodontal ligament (PDL) and schematically is showed in Figure 1. The human PDL stabilizes the tooth in bone and provides nutritive, proprioceptive and reparative functions [1]. It is composed of collagenous fibers and a gelatinous ground substance including cells and neurovascular tis- sue [2]. The PDL not only strongly binds the tooth root to the supporting alveolar bone but also absorbs occlusal loads and distributes the resulting stress over the alveolar bone [3]. This causes PDL to play a major role in tooth mobility which is very important in prosthodontic and orthodontic treatment and selection of an optimal force system for orthodontic treatment [4]. The PDL has a de- terminant influence on tooth instantaneous mobility be- cause of lower stiffness in comparison with surrounding tissues [5], and also long term movement because of bone remodeling [6]. Ligaments display time dependent behavior which is typical of viscoelastic materials [7]. Viscoelastic behav- ior has been observed and studied in articular cartilage [8, 9], periodontal ligament [10-12], ligament [7]. For- mulation for modeling viscoelasticity in nonlinear mate- rial was first used for modeling the time dependent be- havior in soft tissue by Fung [13] and called it “quasi linear viscoelasticity” (QLV). The QLV theory has been applied for PDL by Natali et al. [14]; Toms et al. [2]. These models are composed of two parts: an instantane- ous elastic response (often a hyperelastic strain energy function) and a relaxation function. Relaxation function governs the fading memory of current constitutive state on deformation history [15]. It is known from literature, periodontal ligament is a nonlinear viscoelastic material [16, 17], and stress re- laxation behavior is a nonlinear function of strain. The rate of stress relaxation decreases with increasing strain [7]. The behavior in these data cannot be described well using Fung quasi linear method [13], because in this formulation stress relaxation is independent of strain. Therefore, two previously presented QLV model for PDL is discussed: 1) Komatsu et al. [12] studied stress relaxation on PDL at different deformations. Experiments were done on seventeen 4-month-old rabbits. The stress relaxation process was well described by a function (relaxation function) with three exponential decay terms and a con- stant. On the other hand the experiment showed that stress relaxation is a function of strain too, and G (t) (re- laxation function) differs at different strains. Komatsu's model for relaxation function is as follows: 0.390.09 exp(/0.35) 0.13exp(/ 4.12)0.39exp(/ 403) () t tt Gt =+− + −+ − (1) In the present study, experimental data obtained by Komatsu et al. [12] has been used to describe stress re- laxation process for PDL. SciRes Copyright © 2008  196 J. Hazrati / J. Biomedical Science and Engineering 1 (2008) 195-199 SciRes Copyright © 2008 JBiSE Figure 1. Transversal section of a double rooted tooth sur- rounded by PDL and alveolar bone. 2) Toms et al. [2] studied the quasi linear viscoelastic model and applied to mechanical tests of the human PDL. Transverse sections of cadavric premolars were subjected to relaxation tests. In their study the relaxation function described by using an exponential equation. This model was similar to Komatsu's model. Many reasonably general constitutive models have been proposed to describe nonlinearly viscoelastic mate- rials. A brief description of these models has been stud- ied by Provenzano et al.[7]. In this paper, we have used the modified superposition (or nonlinear superposition) method to describe nonlinear viscoelasticity of PDL to determine whether this method can model strain de- pendent stress relaxation behavior of PDL. 2. MATERIAL AND METHODS 2.1. Modified Superposition Method The single integral formulation of the modified super- position method [18, 19] allows the relaxation function to depend on strain level: 0 () (,)(, ()) td tEt d d ετ σ ετεττ τ −=∫ (2) The form of the relaxation modulus will be chosen as a non separable strain-dependent power law: (,)() (,)Et AGt ε εε =⋅ (3) () (,) B Gtt ε ε = (4) The function()A ε represents the initial modulus0 E, which can be obtained from a stress–strain curve or iso- chronal curve describing the nonlinear elastic behavior. (,)Gt ε is the relaxation function which itself is function of strain and time. The function()B ε describes the strain-dependent rate of stress relaxation. Substituting a Heaviside function into Eq.(2) results in: 00 () () (,) BB tEt t ε ε σεε σ == (5) where 0 Eand 0 s represent isochronal values of the tan- gent modulus and stress, respectively, and can be func- tions of strain to account for nonlinearities in the elastic Figure 2. Histological section through an anterior tooth is taken from a pig mandible. The periodontal ligament is enclosed by the alveolar bone (B) and the tooth roots (T) and is pervaded by a dense network of collagen fibers. (staining: hematoxylin and eosin, original magnification ×400). response. In addition, Eq.(5) can take on a more predic- tive form once relaxation rates over a range of strain values are obtained, the dependence of the rate function ()B ε as a function of strain is known. Stress–strain or isochronal curves can be used to obtain the initial modulus or stress terms,()A ε and a polynomial can be fit to the rate range to obtain the function()B ε ; so me- chanical behavior of the tissue can be predicted. Hence, the non separable form of modified superposition is able to represent both the elastic and strain-dependent rate nonlinearities that are experimentally observed. 2.2. Application of Modified Superposition Method to PDL Modified superposition method Eqs.(2-5) was applied to experimental stress relaxation data from rabbit periodon- tal ligament [12]. As mentioned above, these data dem- onstrate that the rate of stress relaxation decreases sig- nificantly with increasing tissue strain, this behavior have shown in Figure 10. For rabbit PDL modified su- perposition method fits the experimental data well for all strain levels:0.078 ε =,0.124 ε =,0.17 ε =, 0.215 ε =. 0 σ values are 0.265, 0.53, 1.19, 1.85, MPa for 0.078, 0.124, 0.17, 0.215 strain respectively.0 s is the stress at the start of stress relaxation test (1t= sec), this is rea- sonable if assumed that the stress relaxation have not started up to 1 sec, so it is supposed that 1t= sec is ini- tial time for this method. Strain dependent rate of stress relaxation term or ()Be can be seen to decrease in mag- nitude as strain increase (-0.172, -0.127, -0.102, -0.096 for 0.078, 0.124, 0.17, 0.215 strain, respectively) which shows a nonlinearity in the strain dependent rate of stress relaxation. The rate function or ()e B and ()e A is a polyno- mial which is obtained by curve fitting using commercial software MATLAB 7.0 (The Mathwork Inc., Natick, MA). Curve fitting rate function (Fig 4), and initial modulus (Fig 5) versus strain were done using experi- mental data from Komatsu et al. [12]. 3. RESULTS 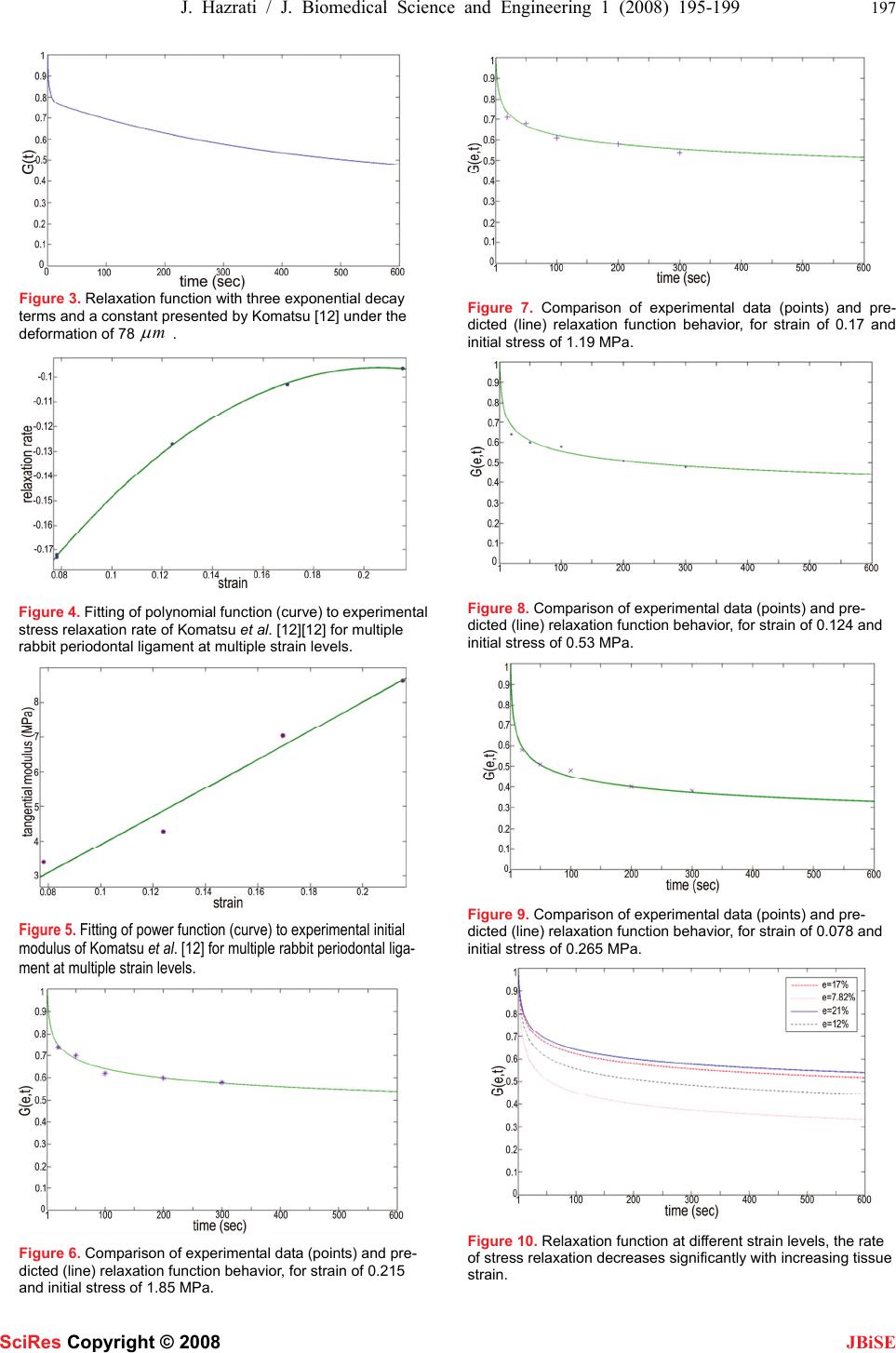 J. Hazrati / J. Biomedical Science and Engineering 1 (2008) 195-199 197 SciRes Copyright © 2008 JBiSE Figure 3. Relaxation function with three exponential decay terms and a constant presented by Komatsu [12] under the deformation of 78m μ . Figure 4. Fitting of polynomial function (curve) to experimental stress relaxation rate of Komatsu et al. [12][12] for multiple rabbit periodontal ligament at multiple strain levels. Figure 5. Fitting of power function (curve) to experimental initial modulus of Komatsu et al. [12] for multiple rabbit periodontal liga- ment at multiple strain levels. Figure 6. Comparison of experimental data (points) and pre- dicted (line) relaxation function behavior, for strain of 0.215 and initial stress of 1.85 MPa. Figure 7. Comparison of experimental data (points) and pre- dicted (line) relaxation function behavior, for strain of 0.17 and initial stress of 1.19 MPa. Figure 8. Comparison of experimental data (points) and pre- dicted (line) relaxation function behavior, for strain of 0.124 and initial stress of 0.53 MPa. Figure 9. Comparison of experimental data (points) and pre- dicted (line) relaxation function behavior, for strain of 0.078 and initial stress of 0.265 MPa. Figure 10. Relaxation function at different strain levels, the rate of stress relaxation decreases significantly with increasing tissue strain.  198 J. Hazrati / J. Biomedical Science and Engineering 1 (2008) 195-199 SciRes Copyright © 2008 JBiSE Figure 11. Stress relaxation curve for rabbit PDL at the strain of 21.5% and initial stress of 1.86 MPa. In order to obtain a set of constitutive parameters for PDL, invitro experimental data were analyzed, and the fit of the rate function was done with2 R value of 0.999 for tension relaxation using nonlinear least square method. The results of curve fitting have been depicted in Figure 4. The rate function obtained as follows: 5.9377.2992.286 0.3094 32 ()B ε εεε =−+− (6) The function ()A ε was determined by fitting the tan- gential modulus as a function of strain using nonlinear least square method from typical stress–strain data for the rabbit periodontal ligament with 2 Rvalue of 0.967. The results of curve fitting have been depicted in Figure 5. The function ()A ε obtained as follows: 1.039 42.66 ()A εε =∗ (7) So, the relaxation modulus will take the following form: 32 42.66 1.039 5.9377.2992.286 0.3094 (,)Et t εεε εε =∗∗ −+− (8) Four separate stress relaxation tests at four different strains were then fitted using the predicted rate function. The results for each strain and comparison between the experimental data and the model curve have been dem- onstrated in Figures 6-9. Figure 10 shows that the rate of stress relaxation decreases significantly with increas- ing tissue strain which shows the dependence of relaxa- tion function to tissue dilatation. Stress relaxation proc- ess for the initial stress of 1.86 MPa and strain of 0.215 which is followed by a gradual reduction up to 600s has been depicted in Figure 10, after 600s the stress de- creases approximately to 1.0 MPa and the relaxation function reaches 0.54. 4. DISCUSSION In this study the ability of modified superposition (nonlinear superposition) method as a nonlinear viscoe- lastic model has been investigated to describe periodon- tal ligament behavior which has been experimentally observed. In previous studies, QLV model had been ap- plied for PDL, with QLV theory, the time dependent portion of model G(t) (relaxation function) is independ- ent of strain, however, as experimental data shows the relaxation behavior differs at different strain levels and depends on tissue dilatation too. In this study the time dependent portion of model depends on strain to consider strain history dependence of tissue, too. The stress relaxation property of PDL was expressed by a non separable strain dependent power law, which showed a good fitting with experimental data under dif- ferent deformations, but in previous studies stress relaxa- tion property of PDL had been often expressed by expo- nential decay terms which were functions of time alone, as in the human [2]; rabbit [12]; bovine [20]; pig [14], and strain history dependence of tissue had not been taken into account. The mechanisms driving viscoelastic behavior in ligament are not yet completely defined. It has been speculated that ‘‘the decrease in relaxation rate with in- creasing strain could be the result of larger strains caus- ing greater water loss (wringing out effect) which causes the tissue to be more elastic (less viscous) than tissues subjected to lower strains’’ [21]. In other words, at greater deformations because of water loss, the viscous components (matrix) have less influence in tissue me- chanics than elastic components, and this causes the tis- sue to show more elastic properties than viscous. There are several limitations which must be consid- ered while examining the presented model in this study. In the presented model other effects such as diseased state, effects of age, biochemical changes, temperature, hydration and others have not been considered. The other limitation is related to experimental data, in which col- lagen fiber bundles in PDL of the specimens are assumed to run almost parallel to the direction of testing. REFERENCES [1] B.KB. Berkovitz, B.J. Moxham, et al. (Eds.).( 1982) The Perio- dontal Ligament in Health and Disease. Pergamon Press, Elms- ford, NY. [2] S.R. Toms, G.J. Dakin, J.E. Lemons, A.W. Eberhardt, (2002) Quasi linear viscoelastic behavior of the human periodontal ligament. Journal of Biomechanics. 35, 1411–1415. [3] Nishihira, M., Yamamoto, K., Sato, Y., Ishikawa, H., Natali, A.N. (2003) Mechanics of periodontal ligament. In: Natali, A.N. (Ed.), Dental Biomechanics. Taylor & Francis, London, 20–34. [4] C. Dorow, N. Krstin, F.G Sander. (2002) Determination of the Mechanical Properties of the Periodontal Ligament in a Uniaxial Tensional Experiment. Journal of Orofacial Orthopedics, 64, 100– 7. [5] A.N. Natali, E.L. Carniel, P.G. Pavan, C. Bourauel, A. Ziegler, L. Keilig, (2006) Experimental–numerical analysis of minipig’s multi-rooted teeth. Journal of Biomechanics, 37, article in press, 1- 8. [6] A. Kawarizadeh, C. Bourauel, D. Zhang, W. Gotz, A. Jager, (2004) Correlation of stress and strain profiles and the distribution of os- teoclastic cells induced by orthodontic loading in rat. European Journal of Oral Science, 112, 140–147. [7] P. Provenzano, R. Lakes, R. Vanderby, (2002) Application of nonlinear viscoelastic models to describe ligament behavior. Bio- mechan Model Mechanobiol. 1, 45–57. [8] G.A. Ateshian, W.H. Warden, J.J. Kim, R.P. Grelsamer, V.C. Mow,  J. Hazrati / J. Biomedical Science and Engineering 1 (2008) 195-199 199 SciRes Copyright © 2008 JBiSE (1997) Finite Deformation Biphasic Material Properties of Bovine Articular Cartilage From Confined Compression Experiments. J. Biomech, 30, 1157–1164. [9] J.J. Garc ia, D.H. Cortes, A nonlinear viscohyperelastic model for articular cartilage. Journal of Biomechanics. 2006; 39, 2991–2998. [10] A.N. Natali, P.G. Pavan, B.A. Schre.er, S.A. Secchi, (2002) multi- phase media formulation for biomechanical analysis of periodontal ligament. Meccanica, 37, 407–418. [11] A.N. Natali, E.L. Carniel, P.G. Pavan, A. Gasparetto, F.G. Sander, C. Dorow, M. Geiger. (2006) Constitutive formulation for numeri- cal analysis of visco-hyperelastic damage phenomena in soft bio- logical tissues. 8th Biennial ASME Conference on Engineering Systems Design and Analysis. Proceedings of ESDA. [12] K. Komatsu, C. Sanctuary, T. Shibata, A. Shimada, J. Botsis. (2007) Stress–relaxation and microscopic dynamics of rabbit periodontal ligament. Journal of Biomechanics. 40, 634–644. [13] Fung, Y.C. Biomechanics, (1993) Mechanical Properties of Living Tissues, second ed. Springer, New York. [14] A.N. Natali, P.G. Pavan, E.L. Carniel, C. Dorow, (2004) Visco- elastic response of the periodontal ligament: an experimental- numerical analysis. Connective Tissue Research, 45, 222–230. [15] J.E. Bischoff, E.M. Arruda, K. Grosh. (2004) A rheological net- work model for the continuum anisotropic and viscoelastic behav- ior of soft tissue. Biomechanics Model Mechanobiol, 3, 56–65. [16] M. Pini, H.W.A. Wiskott, S.S. Scherrer, J. Botsis, U.C. Belser, (2002) Mechanical characterization of bovine periodontal liga- ment. Journal of Periodontal Research, 37, 237–244. [17] C. Dorow, N. Krstin, F.G. Sander. (2001) Experiments to Deter- mine the Material Properties of the Periodontal Ligament. Journal of Orofacial Orthopedics, 63, 94–104. [18] Findley, W.N., Lai, J.S., Onaran, K. (1976) Creep and relaxation of nonlinear viscoelastic materials. Dover, NewYork. [19] Lakes, R.S., (1998) Viscoelastic solids. CRC Press, New York. [20] M. Pini, P. Zysset, J. Botsis, R. Contro, (2004) Tensile and com- pressive behaviour of the bovine periodontal ligament. Journal of Biomechanics, 37, 111–119. [21] P. Provenzano, R. Lakes, T. Keenan, R. Vanderby, (2001) Nonlin- ear ligament viscoelasticity. Annals of Biomedical Engineering. 29, 908–914. |

