Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3: 65-72 doi:10.4236/jsea.2010.31008 Published Online January 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes JSEA Element Retrieval Using Namespace Based on Keyword Search over XML Documents Yang WANG1, Zhikui CHEN1, Xiaodi HUANG2 1School of Software, Dalian University of Technology, Dalian, China; 2School of Computing and Mathematics, Charles Sturt Uni- versity, Australia. Email: Wayag2000@yahoo.com.cn, zkchen@dlut.edu.cn, xdhuang@csu.edu.au Received July 31st, 2009; revised September 12th, 2009; accepted September 22nd, 2009. ABSTRACT Querying over XML elements using keyword search is steadily gaining popularity. The traditional similarity measure is widely employed in order to effectively retrieve various XML documents. A number of authors have already proposed different similarity-measure methods that take advantage of the structure and content of XML documents. However, they do not consider the similarity between latent semantic information of element texts and that of keywords in a query. Although many algorithms on XML element search are available, some of them have the high computational complexity due to searching for a huge number of elements. In this paper, we propose a new algorithm that makes use of the se- mantic similarity between elements instead of between entire XML documents, considering not only the structure and content of an XML document, but also semantic information of namespaces in elements. We compare our algorithm with the three other algorithms by testing on real datasets. The experiments have demonstrated that our proposed method is able to improve the query accuracy, as well as to reduce the running time. Keywords: Semantics, Namespace, SVD, Text Matching 1. Introduction Keyword search querying over XML elements has emer- ged as one of the most effective paradigms in information retrieval. To identify relevant results for an XML key- word query, different approaches lead to various search results in general. Some authors calculated the similarity between the content of XML documents and query, only analyzing the content and structure of XML (e.g., [1–3]). Many algorithms calculate the degree of text of elements matching with the keywords to produce the ranked re- sult-list (e.g., DIL Query processing algorithm [4] and Top-k algorithm [5]). The classical methods focus on TF-IEF formula to calculate the cosine similarity between elements and query (e.g., Tae-Soon Kim et al. [6]; Maria Izabel M et al. [7]; Yun-tao Zhang et al. [8]). In particular, overlaps of elements in XML documents must be considered. For several overlapping relevant ele- ments, we have to choose which one should be avoided to ensure that users do not see the same information for several times. Su Cheng Haw et al. [9] presented the TwigINLAB algorithm to improve XML Query process- ing. In this paper, we modify it to deal with the elements overlap occurring in keyword search results. On the basis of previous work, we make the following contributions in this paper. Firstly, we utilize the seman- tic information of namespaces in elements to filter the relevant components since the text of elements are com- monly related with semantic information of namespace. Secondly, the precision and recall of our algorithm show that the non-text matching but semantic relevant ele- ments with respect to the keyword can be effectively retrieved. Compared with traditional work, our algorithm also shows the better performance on time execution over a large collection of elements. The rest of this paper is organized as follows: Section 2 introduces the element-rank schema by keyword search. Section 3 presents the Namespace Filter Algorithm (NFA). The experiments on the comparison of NFA and related methods are reported in Section 4. Related work is presented in Section 5, followed by the conclusion. 2. Element-Rank Schema In this section, we utilize the namespace of elements to describe our element rank schema. Another goal of util- izing namespace is to filter relevant elements with the keyword in a query to reduce time execution compared with traditional algorithms. Interestingly, namespaces can distinguish different ele-  Element Retrieval Using Namespace Based on Keyword Search over XML Documents 66 ments containing the same markup that refers to different semantic meanings. As an illustration, we consider two elements with the same markup of <table>: <table> <td>apple</td> <td>banana<td> </table> <table> <name>coffee table</name> <width>80</width> </table> This will lead to the confliction when they are in the same XML document. Thus, we utilize different name- spaces of 'h' and 'f' to distinguish them as below. <h:table xmlns:h = "http://.../fruit"> <h:td>apple</h:td> <h:td>banana</h:td> </h:table> <f:table xmlns:f = "http://.../furniture"> <f:name>coffee table</f:name> <f:width>80</f:width> <f:length>120</f:length> </f:table> As discussed above, the text of elements is commonly related with the semantic information of their namespaces. Given the semantic information of namespace that is ir- relevant to the keyword, it is not desirable to access all the elements containing this namespace. In order to calculate the semantic similarity between namespaces and key- words, we map semantic information of namespaces and keywords into different vectors in a concept vector space created by Singular Value Decomposition (SVD) [10] over a collection of elements. In order to do this, Defini- tions 1 and 2 are provided as follows. Definition 1: : a function that maps the namespace of element v into a vector and represents a special meaning in the concept vector space created by SVD. )(vprefix Definition 2:: the degree of relevance calculated by the cosine similarity between the namespace vector of element v and the key- word vector in concept vector space created by SVD. )),(( keywordvprefixncorrelatio The value of the correlation is commonly normalized between the range [-1,1]. If the semantic meaning of namespaces is very close to that of the keywords, the value of ‘correlation’ will be around 1. Nobert Govert et al. [2] proposed the concept of degree of relevance be- tween elements. We extend it to include several intervals in [-1,1] to describe the degree of the semantic similarity of namespaces and keywords. Without loss of generality, some definitions are provided to describe the degree of relevance between namespaces and keywords. Definition 3: High relevance: the high correlation between namespaces and keywords which satisfies 1)),(( 1 keywordvprefixncorrelatio (1) Definition 4: Common relevance: the median corre- lation between namespaces and keywords which satisfies 12 )),(( keywordvprefixncorrelatio (2) Definition 5: Irrelevance: the lower correlation be- tween namespaces and keywords which satisfies 2 )),((1 keywordvprefixncorrelatio (3) In the above equations, we have 10 12 , our ranking algorithm accesses the elements containing the namespaces that satisfy either Equation (1) or Equation (2) rather than Equation (3). 3. Espace Filter Algorithm In this section, we introduce some preliminary knowl- edge, followed by presenting our algorithm called the Namespace Filter Algorithm (NFA). 3.1 Preliminaries The idftf weight is commonly used to calculate the term weight in documents in the field of traditional in- formation retrieval. The purpose of our work is to re- trieve the appropriate nested elements that contain the relevant text to keywords instead of entire XML docu- ments. So we extend idftf to for ele- ments in XML documents. ieftf et , Notations: et tf , the number of times that keyword t occurs in the text of element e. qt tf , the number of times that keyword t occurs in the query q. ef N ief 10 log whereis the total number of elements over a collection of XML documents, and is the number of elements that contain the keyword. We then give Definition 6 as below. N ef Definition 6: keyword weights in elements and query otherwise tfifieftf Wetet et 0 0)log1( ,,10 , (4) ieftfW qtqt )log1( ,10, (5) where is keyword weight in the text of element , and keyword weight in a query . We calculate the cosine similarity between query vector et W, qt, e Wq q and ele- ment vector e in Equation (6) on text matching factor. n ii n ii n iii eq eq eq eq eqscore 1 2 1 2 1 ),( (6) Copyright © 2010 SciRes JSEA  Element Retrieval Using Namespace Based on Keyword Search over XML Documents67 Figure 1. Example of elements with the label ID in the XML document tree where is the ith keyword weight in i ee , and is the ith keyword weight in i q q . Their weight values are calcu- lated using Equation (4) and Equation (5), respectively. In XML documents, elements are of varying size and nested. Since relevant elements can be at any level of granularity, either an element or its children can be rele- vant to a given query. These facts commonly lead to a problem that the same resulting elements of a query based on keyword search will be presented to users for several times. As an illustration, Consider the structure of an XML document that is shown as the labeled tree in Figure 1. Besides, let us suppose the relevant element list after key- word search are listed in Table 1. Elements with ID 0.2.1 and 0.2 are overlapping, so are with 0.1, 0.1.1, and 0.12. If one element's parent is the component of another element, the two relevant compo- nents can be merged into one. An element will be merged into its parent only if the number of the keyword occur- ring in this particular element is less than that of its par- ent element. In this way, there will be no overlap in the resulting list shown in Table 2. Furthermore, we denote value[v] calculated by NFA in Section 3.2 as element v. Combining with Definition 2. The final comprehensive evaluation formula about rele- Table 1. Example of ranked list Rank Self Parent 1 0.2.1 0.2 2 0.2 Root 3 0.1 Root 4 0.1.1 0.1 5 0.1.2 0.1 Table 2. Result list without overlap Rank Self Parent 1 0.2.1 0.2 2 0.1 Root vant elements ranking is given as Equation (7). ][)),(()( 21 vvalueakeywordvprefixncorrelatioavrank (7) where 1 21 aa . In order to highlight the factor of namespace's semantic, we have . 10 12 aa 3.2 NFA Description In the following discussion, we will focus on presenting the Namespace Filter Algorithm (NFA) and how it per- forms based on the keyword search over a collection of elements. Let A be a set consisting of different elements to be accessed by NFA, and the namespaces of elements in set A satisfy either Equation (1) or Equation (2). Other ele- ments not included in A will be neglected by NFA. The length[e] in Equation (6) is defined as n ii e 1 2. Value[e] in Figure 2 gives the degree of text matching between the text of element and keywords. 3.3 An Example To evaluate the effectiveness of NFA, using an example, we perform it with different pair values of 1 and 2 in Equations (1) and (2). We empirically provide an XML document named as record.xml in Figure 3 which con- sists of many elements with namespace 'c' describing semantic "computer" and 'n' describing "joy". Let the query be "data and space in algorithm". Meanwhile, we set 1 in Equation (1) and 2 in Equation (2) to 0.8 and 0.6, respectively. SVD is commonly applied to docu- ments in traditional information retrieval. We extend it to NFA : retrieve the ranked element based on the keyword Input:query, a collection of relevant elements denoted as A Output: top k elements of ranked result list Description: 01 float value[N] = 0//N is the number of elements A 02 float Length[N] 03 for each keyword t in the query 04 do for each pair(element A,tf(t,e)) 05 do value[e] += //Equations.(4) and (5) qtet WW ,, 06 end-for 07 end-for 08 for each element e 09 do value[e] = value[e] / length[e] 10 end-for 11 merge the overlap 12 calculate the rank[] with Equation (7) 13 return top K elements of rank[] over all documents Figure 2. Namespace filter algorithm Copyright © 2010 SciRes JSEA  Element Retrieval Using Namespace Based on Keyword Search over XML Documents Copyright © 2010 SciRes JSEA 68 Table 3. Term-element matrix M <root1> <c:cs xmlns:c = "http://....../computer"> <c:DBMS> <c:DB>attribute</c:DB> <c:DB>Management</c:DB> </c:DBMS> <c:programming> <c:complexity>data and space</c:complexity> <c:time>data in computer's Algorithm</c:time> </c:programming> <c:java>data of Algorithm in computer science</c:java> </c:cs> <n:joy xmlns:n = "http://....../happiness"> <n:entertainment> <n:in>no space with audience's joy</n:in> <n:out>jackson dance in large space</n:out> </n:entertainment> </n:joy> </root1> 0.1.1.1 0.1.1.2 0.1.2 0.1.3.1 0.1.3.2 0.1.4 0.2.1.1 0.2.1.2 Computer 0 0 1 0 1 1 0 0 Data 0 0 1 1 1 1 0 0 Space 0 0 1 1 1 0 1 1 A Algorithm 0 0 0 0 1 1 0 0 Joy 0 0 0 0 0 0 1 0 elements in this example. Each element in record.xml corresponds to a node in the tree with labeled IDs in Figure 4. Given the correlation value between the semantic meaning of namespaces: 'c', and 'n', and that of the key- words :"data","space", and "Algorithm", we construct a term-element matrix denoted as M, the elements of which are term frequencies occurring over all of ele- ments in record.xml in Table 3. Then we normalize matrix M denoted by M1 as fol- lows 07071.0000000 005774.05774.00000 17071.0007071.05774.000 005774.05774.07071.05774.000 005774.05774.005774.000 M1 is decomposed into the following three matrixes by SVD Figure 3. Example of record.xml 1403.04420.08437.02458.01122.0 7261.03172.03754.04147.02435.0 1073.02915.01155.06863.06474.0 0637.06617.03163.03361.05874.0 6614.04256.01839.04285.04050.0 U 0003433.00000 00004126.0000 000006569.000 0000003770.10 00000008397.1 S Figure 4. Tree structure of record.xml 0003124.07066.01757.04984.03519.0 0000681.02579.07839.04786.02920.0 2877.04082.05.02159.01133.02135.04945.03878.0 2887.04082.05.02159.01133.02135.04945.03878.0 0003520.06345.04647.01798.04746.0 0008250.00774.02179.00328.05146.0 5722.07654.02946.000000 7113.02843.06428.000000 V 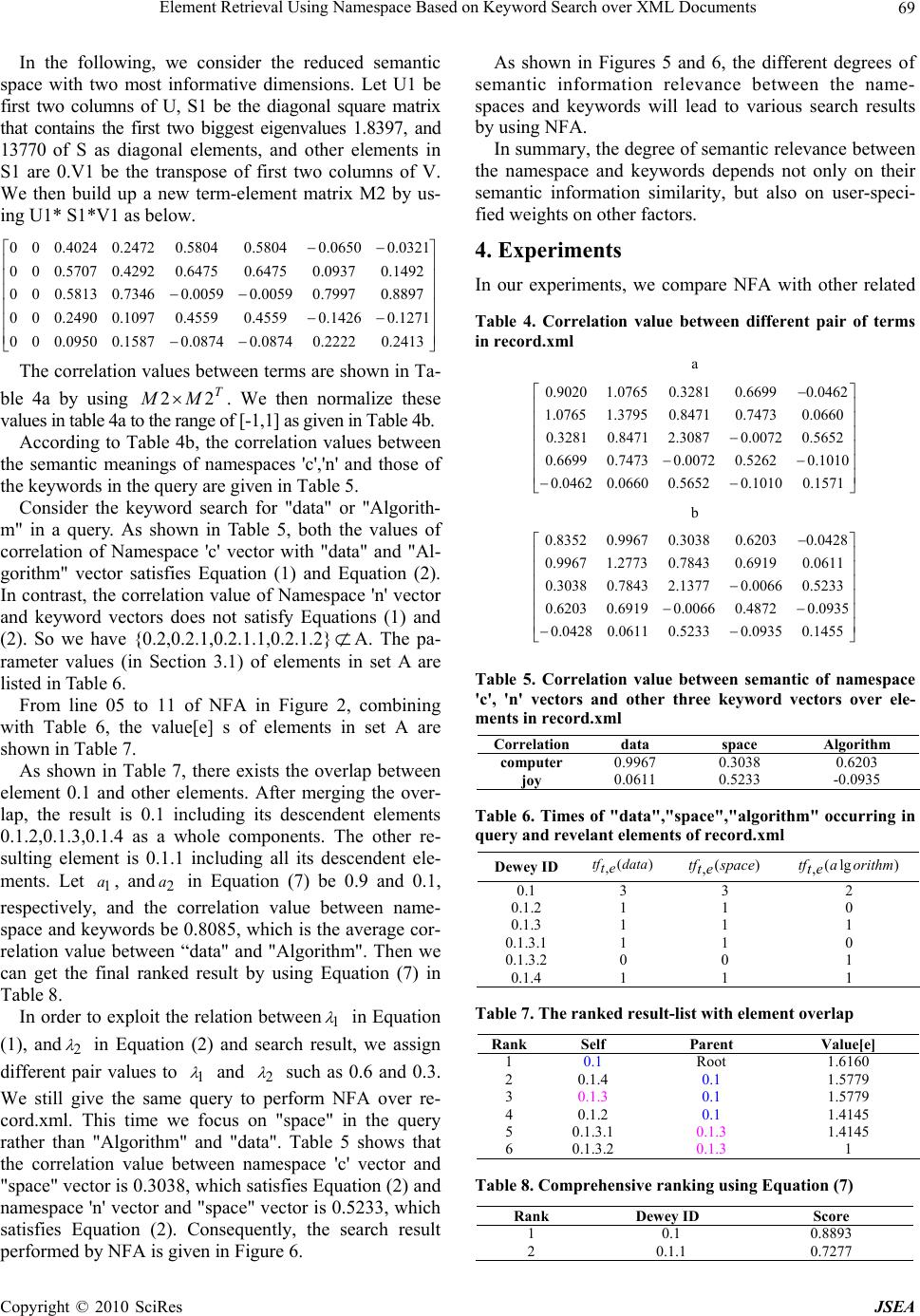 Element Retrieval Using Namespace Based on Keyword Search over XML Documents69 In the following, we consider the reduced semantic space with two most informative dimensions. Let U1 be first two columns of U, S1 be the diagonal square matrix that contains the first two biggest eigenvalues 1.8397, and 13770 of S as diagonal elements, and other elements in S1 are 0.V1 be the transpose of first two columns of V. We then build up a new term-element matrix M2 by us- ing U1* S1*V1 as below. 2413.02222.00874.00874.01587.00950.000 1271.01426.04559.04559.01097.02490.000 8897.07997.00059.00059.07346.05813.000 1492.00937.06475.06475.04292.05707.000 0321.00650.05804.05804.02472.04024.000 The correlation values between terms are shown in Ta- ble 4a by using T M M 22. We then normalize these values in table 4a to the range of [-1,1] as given in Table 4b. According to Table 4b, the correlation values between the semantic meanings of namespaces 'c','n' and those of the keywords in the query are given in Table 5. Consider the keyword search for "data" or "Algorith- m" in a query. As shown in Table 5, both the values of correlation of Namespace 'c' vector with "data" and "Al- gorithm" vector satisfies Equation (1) and Equation (2). In contrast, the correlation value of Namespace 'n' vector and keyword vectors does not satisfy Equations (1) and (2). So we have {0.2,0.2.1,0.2.1.1,0.2.1.2}A. The pa- rameter values (in Section 3.1) of elements in set A are listed in Table 6. From line 05 to 11 of NFA in Figure 2, combining with Table 6, the value[e] s of elements in set A are shown in Table 7. As shown in Table 7, there exists the overlap between element 0.1 and other elements. After merging the over- lap, the result is 0.1 including its descendent elements 0.1.2,0.1.3,0.1.4 as a whole components. The other re- sulting element is 0.1.1 including all its descendent ele- ments. Let , and in Equation (7) be 0.9 and 0.1, respectively, and the correlation value between name- space and keywords be 0.8085, which is the average cor- relation value between “data" and "Algorithm". Then we can get the final ranked result by using Equation (7) in Table 8. 1 a2 a In order to exploit the relation between in Equation (1), and in Equation (2) and search result, we assign different pair values to and such as 0.6 and 0.3. We still give the same query to perform NFA over re- cord.xml. This time we focus on "space" in the query rather than "Algorithm" and "data". Table 5 shows that the correlation value between namespace 'c' vector and "space" vector is 0.3038, which satisfies Equation (2) and namespace 'n' vector and "space" vector is 0.5233, which satisfies Equation (2). Consequently, the search result performed by NFA is given in Figure 6. 1 2 1 2 As shown in Figures 5 and 6, the different degrees of semantic information relevance between the name- spaces and keywords will lead to various search results by using NFA. In summary, the degree of semantic relevance between the namespace and keywords depends not only on their semantic information similarity, but also on user-speci- fied weights on other factors. 4. Experiments In our experiments, we compare NFA with other related Table 4. Correlation value between different pair of terms in record.xml a 1571.01010.05652.00660.00462.0 1010.05262.00072.07473.06699.0 5652.00072.03087.28471.03281.0 0660.07473.08471.03795.10765.1 0462.06699.03281.00765.19020.0 b 1455.00935.05233.00611.00428.0 0935.04872.00066.06919.06203.0 5233.00066.01377.27843.03038.0 0611.06919.07843.02773.19967.0 0428.06203.03038.09967.08352.0 Table 5. Correlation value between semantic of namespace 'c', 'n' vectors and other three keyword vectors over ele- ments in record.xml Correlation data space Algorithm computer 0.9967 0.3038 0.6203 j oy 0.0611 0.5233 -0.0935 Table 6. Times of "data","space","algorithm" occurring in query and revelant elements of record.xml Dewey ID )( ,data et tf )( ,space et tf )lg( ,orithma et tf 0.1 3 3 2 0.1.2 1 1 0 0.1.3 1 1 1 0.1.3.1 1 1 0 0.1.3.2 0 0 1 0.1.4 1 1 1 Table 7. The ranked result-list with element overlap Rank Self Parent Value[e] 1 0.1 Root 1.6160 2 0.1.4 0.1 1.5779 3 0.1.3 0.1 1.5779 4 0.1.2 0.1 1.4145 5 0.1.3.1 0.1.3 1.4145 6 0.1.3.2 0.1.3 1 Table 8. Comprehensive ranking using Equation (7) Rank Dewey ID Score 1 0.1 0.8893 2 0.1.1 0.7277 Copyright © 2010 SciRes JSEA 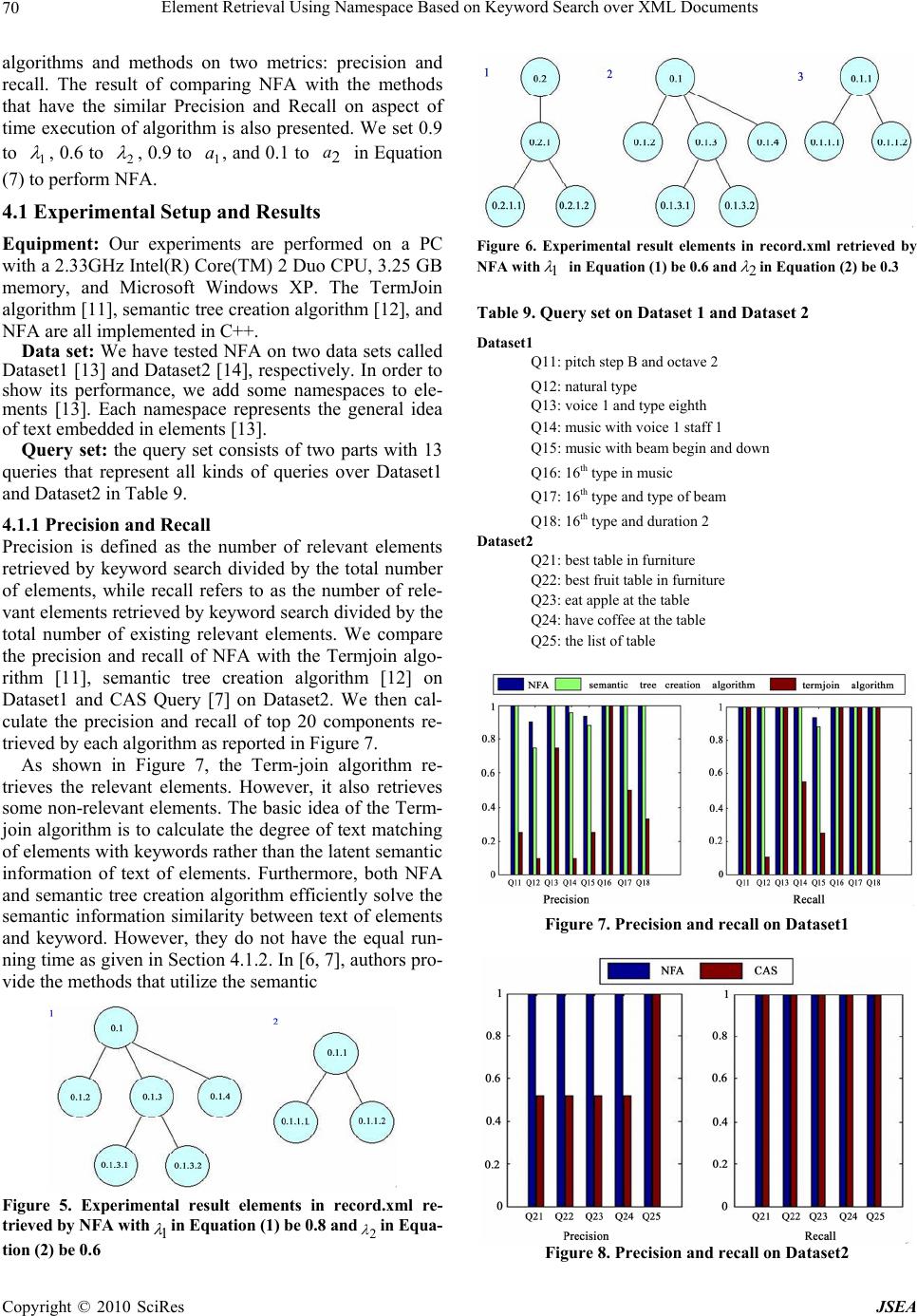 Element Retrieval Using Namespace Based on Keyword Search over XML Documents 70 algorithms and methods on two metrics: precision and recall. The result of comparing NFA with the methods that have the similar Precision and Recall on aspect of time execution of algorithm is also presented. We set 0.9 to 1 , 0.6 to 2 , 0.9 to , and 0.1 to in Equation (7) to perform NFA. 1 a2 a 4.1 Experimental Setup and Results Equipment: Our experiments are performed on a PC with a 2.33GHz Intel(R) Core(TM) 2 Duo CPU, 3.25 GB memory, and Microsoft Windows XP. The TermJoin algorithm [11], semantic tree creation algorithm [12], and NFA are all implemented in C++. Data set: We have tested NFA on two data sets called Dataset1 [13] and Dataset2 [14], respectively. In order to show its performance, we add some namespaces to ele- ments [13]. Each namespace represents the general idea of text embedded in elements [13]. Query set: the query set consists of two parts with 13 queries that represent all kinds of queries over Dataset1 and Dataset2 in Table 9. 4.1.1 Precision and Recall Precision is defined as the number of relevant elements retrieved by keyword search divided by the total number of elements, while recall refers to as the number of rele- vant elements retrieved by keyword search divided by the total number of existing relevant elements. We compare the precision and recall of NFA with the Termjoin algo- rithm [11], semantic tree creation algorithm [12] on Dataset1 and CAS Query [7] on Dataset2. We then cal- culate the precision and recall of top 20 components re- trieved by each algorithm as reported in Figure 7. As shown in Figure 7, the Term-join algorithm re- trieves the relevant elements. However, it also retrieves some non-relevant elements. The basic idea of the Term- join algorithm is to calculate the degree of text matching of elements with keywords rather than the latent semantic information of text of elements. Furthermore, both NFA and semantic tree creation algorithm efficiently solve the semantic information similarity between text of elements and keyword. However, they do not have the equal run- ning time as given in Section 4.1.2. In [6, 7], authors pro- vide the methods that utilize the semantic Figure 5. Experimental result elements in record.xml re- trieved by NFA within Equation (1) be 0.8 andin Equa- tion (2) be 0.6 1 2 Figure 6. Experimental result elements in record.xml retrieved by NFA with in Equation (1) be 0.6 andin Equation (2) be 0.3 1 2 Table 9. Query set on Dataset 1 and Dataset 2 Dataset1 Q11: pitch step B and octave 2 Q12: natural type Q13: voice 1 and type eighth Q14: music with voice 1 staff 1 Q15: music with beam begin and down Q16: 16th type in music Q17: 16th type and type of beam Q18: 16th type and duration 2 Dataset2 Q21: best table in furniture Q22: best fruit table in furniture Q23: eat apple at the table Q24: have coffee at the table Q25: the list of table Figure 7. Precision and recall on Dataset1 Figure 8. Precision and recall on Dataset2 Copyright © 2010 SciRes JSEA 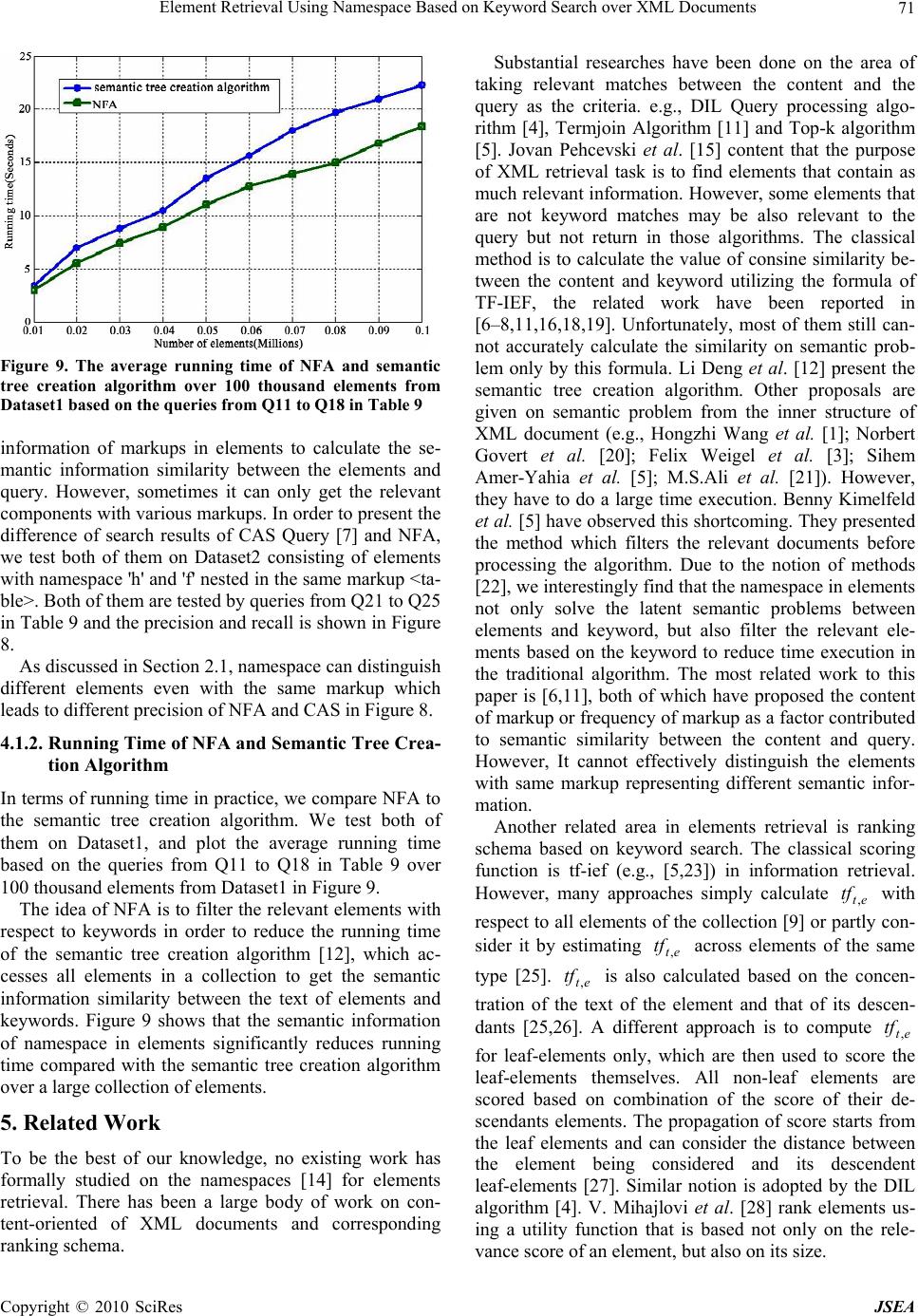 Element Retrieval Using Namespace Based on Keyword Search over XML Documents71 Figure 9. The average running time of NFA and semantic formation of markups in elements to calculate the se- ussed in Section 2.1, namespace can distinguish di In terme in practice, we compare NFA to ts with re knowledge, no existing work has earches have been done on the area of ta er related area in elements retrieval is ranking sc the tree creation algorithm over 100 thousand elements from Dataset1 based on the queries from Q11 to Q18 in Table 9 in mantic information similarity between the elements and query. However, sometimes it can only get the relevant components with various markups. In order to present the difference of search results of CAS Query [7] and NFA, we test both of them on Dataset2 consisting of elements with namespace 'h' and 'f' nested in the same markup <ta- ble>. Both of them are tested by queries from Q21 to Q25 in Table 9 and the precision and recall is shown in Figure 8. As disc fferent elements even with the same markup which leads to different precision of NFA and CAS in Figure 8. 4.1.2. Running Time of NFA and Semantic Tree Crea- tion Algorithm s of running tim the semantic tree creation algorithm. We test both of them on Dataset1, and plot the average running time based on the queries from Q11 to Q18 in Table 9 over 100 thousand elements from Dataset1 in Figure 9. The idea of NFA is to filter the relevant elemen spect to keywords in order to reduce the running time of the semantic tree creation algorithm [12], which ac- cesses all elements in a collection to get the semantic information similarity between the text of elements and keywords. Figure 9 shows that the semantic information of namespace in elements significantly reduces running time compared with the semantic tree creation algorithm over a large collection of elements. 5. Related Work To be the best of our formally studied on the namespaces [14] for elements retrieval. There has been a large body of work on con- tent-oriented of XML documents and corresponding ranking schema. Substantial res king relevant matches between the content and the query as the criteria. e.g., DIL Query processing algo- rithm [4], Termjoin Algorithm [11] and Top-k algorithm [5]. Jovan Pehcevski et al. [15] content that the purpose of XML retrieval task is to find elements that contain as much relevant information. However, some elements that are not keyword matches may be also relevant to the query but not return in those algorithms. The classical method is to calculate the value of consine similarity be- tween the content and keyword utilizing the formula of TF-IEF, the related work have been reported in [6–8,11,16,18,19]. Unfortunately, most of them still can- not accurately calculate the similarity on semantic prob- lem only by this formula. Li Deng et al. [12] present the semantic tree creation algorithm. Other proposals are given on semantic problem from the inner structure of XML document (e.g., Hongzhi Wang et al. [1]; Norbert Govert et al. [20]; Felix Weigel et al. [3]; Sihem Amer-Yahia et al. [5]; M.S.Ali et al. [21]). However, they have to do a large time execution. Benny Kimelfeld et al. [5] have observed this shortcoming. They presented the method which filters the relevant documents before processing the algorithm. Due to the notion of methods [22], we interestingly find that the namespace in elements not only solve the latent semantic problems between elements and keyword, but also filter the relevant ele- ments based on the keyword to reduce time execution in the traditional algorithm. The most related work to this paper is [6,11], both of which have proposed the content of markup or frequency of markup as a factor contributed to semantic similarity between the content and query. However, It cannot effectively distinguish the elements with same markup representing different semantic infor- mation. Anoth hema based on keyword search. The classical scoring function is tf-ief (e.g., [5,23]) in information retrieval. However, many approaches simply calculate et tf , with respect to all elements of the collection [9] or p con- sider it by estimating et tf , across elements of the same type [25]. et tf , is also calculated based on the concen- tration of thxt of the element and that of its descen- dants [25,26]. A different approach is to compute et tf , for leaf-elements only, which are then used to score leaf-elements themselves. All non-leaf elements are scored based on combination of the score of their de- scendants elements. The propagation of score starts from the leaf elements and can consider the distance between the element being considered and its descendent leaf-elements [27]. Similar notion is adopted by the DIL algorithm [4]. V. Mihajlovi et al. [28] rank elements us- ing a utility function that is based not only on the rele- vance score of an element, but also on its size. artly e te Copyright © 2010 SciRes JSEA  Element Retrieval Using Namespace Based on Keyword Search over XML Documents Copyright © 2010 SciRes JSEA 72 s the keyword search over elem nymous reviewers for their REFERENCES [1] H. Z. Wang, J X. M. Lin, “Cod uhr, and M. Lalmas, “Evalua gasundaram, A. Marian, D. Srivastava, and D Lee, J. W. Song, and D. H. Kim, “Similar- g, and Y. C. Wang, “An improved aw and C. S. Lee, “TwigINLAB: A decomposi- Schutze,” Introduc- C. Yu, and H. V. Jagadish, “Querying oral cxml.org/xml/elite.xml. www.w3schools. [15] “HixEval: Highlighting ring similarity of , G. Lin, C. Botev, and J. Shanmugasundaram, “XML “A novel method for onsens, and M. Lalmas, “Structural , Y. Sagiv, and D. Yahav, “Using anmugasundaram, “Context-sensitive ct XXL . Callan, “Parameter estimation for a sim- t XML,” IR at INEX 2005. 6. Conclusions This paper addresseents tion to information retrieval,” Cambridge Press, April, 2008. [11] S. Al-Khalifa, in XML documents. Using the namespaces of elements, we have presented the Namespace Filter Algorithm (NFA) that retrieves the relevant components of XML docu- ments with respect to keyword queries. In addition, we provide a new approach that can remove effectively the element overlaps occurring in query results. Using an evaluation formula, our approach is able to produce a ranking result-list without element overlaps. Compared with previous algorithms, NFA has demonstrated a better performance not only on time execution but also on the precision and recall of query results. Our future work will study the relation of the previous factors on the back- ground of graph structures in XML documents. 7. Acknowledgments We are grateful to the ano stru helpful comments. . Z. Li, W. Wang, and- sem ing-based join algorithm for structure queries on graph-structured XML document,” World Wide Web, Vol. 11, pp. 485–510, 2008. [2] N. Govert, G. Kazai, N. Fting retrieval: What about using contextualrelevance?” SAC, pp. 1114–1115, April 23–27, 2006. [20] B. Jeong, D. Lee, H. Cho, and J. Lee, the effectiveness of content-oriented XML retrieval,” In- formation Retrieval, Vol. 9, No. 6, pp. 699–722, 2006. [3] F. Weigel, H. Meuss, and K. U. Schulz, “Francois bry me content and structure in indexing and ranking XML,” WebDB, Vol. 17–18, pp. 68–72, June 2004. [4] G. Lin, S. Feng, C. Botev, and J. Shanmu “XRank: Ranked keyword search over XML documents,” ACM International Conference Proceeding, SIGMOD, pp. 7–11, June 9–12, 2003. [5] S. A. Yahia, N. Koudas, . rel Toman, “Structure and content scoring for XML,” Pro- ceedings of the 31st VLDB Conference, pp. 362–372, 2005. [6] T. S. Kim, J. H. ity measurement of XML documents based on structure and contents,” International Conference on Computational Science (ICCS), Part 3, LNCS 4489, pp. 902–905, 2007. [7] M. Izabel, M. Azevedo, L. P. Amorim, and N. Ziviani, “A of st universal model for XML information retrieval,” LNCS pp. 312–318, 2005. [8] Y. T. Zhang, L. Gon TF-IDF approach for text classification,” Journal of Zhejiang University Science, Vol. 6A, No. 1, pp. 49–55, 2005. [9] S. C. H tion-matching-merging approach to improving XML query processing,” American Journal of Applied Sciences, Vol. 5, No. 9, pp. 1199–1205, 2008. [10] C. D. Manning, P. Raghavan, and H. structured text in an XML database,” ACM International Conference Proceeding, SIGMOD, June 9–12, 2003. [12] D. Li, X. J. Wang, and L. H. Wang, “Indexing temp XML using semantic tree index,” IEEE Xplore, pp. 448– 451, 2008. [13] http://www.musi [14] Namespaces in XML Available: http:// com/XML/xml_namespaces.asp/. J. Pehcevski and J. A. Thom, XML retrieval evaluation,” LNCS 3977, pp. 43–57, 2006. [16] T. S. Kim, J. H. Lee, J. W. Song, and S. L. Lee, “Semantic ctural similarity for clustering XML documents,” Inha University Technical Report, 2006. http://webbase.inha. ac.kr/TechnicalReport/tech_04.pdf. [17] C. Yang and N. Liu, “Measu i-structured documents with context weights,” ACM International Conference Proceeding, pp. 719–720, Au- gust 6–11, 2006. [18] S. Feng “Efficient keyword search over virtual XML views,” VLDB, pp. 1057–1065, September 23–28, 2007. [19] K. Sauvagnat, L. Hlaoua, and M. Boughanem, asuring semantic similarity for XML schema match- ing,” Expert Systems with Applications, Vol. 24, pp. 1651–1658, 2008. [21] M. S. Ali, M. P. C evance in XML retrieval evaluation,” Proceedings of the SIGIR Workshop on XML and Information Retrieval, pp. 2–8, July 27, 2007. [22] B. Kimelfeld, E. Kovacs language models and the HITS algorithm for XML re- trieval,” LNCS 4518, Springer-Verlag Berlin Heidelberg, pp. 253–260, 2007. [23] C. Botev and J. Sh keyword search and ranking for XML,” WebDB, 2005. [24] B. Sigurbjornsson, J. Kamps, and M. de Rijke, “The effe ructured Queries and selective Indexing on XML re- trieval,” INEX’05, LNCS 3977, pp. 104–118, 2006. [25] M. Theobald, R. Schenkel, and G. Weikum, TopX & at INEX 2005. [26] P. Ogilvie and J ple hierarchical generative model for XML component re- trieval,” INEX, 2004. [27] S. Geva, “GPX-gardens poin [28] V. Mihajlovic, G. Ramirez, T. Westerveld, D. Hiemstra, H. E. Blok, and A. P. de Vries, “Vague element selection, image search, overlap, and relevance feedback,” INEX 2005. |

