Engineering, 2010, 2, 65-77
doi:10.4236/eng.2010.21009 lished Online January 2010 (http://www.SciRP.org/journal/eng/).
65
Pub
An Adaptive Differential Evolution Algorithm to Solve
Constrained Optimization Problems in Engineering Design
Youyun AO1, Hongqin CHI2
1School of Computer and Information, Anqing Teachers College, Anqing, China
2Department of Computer, Shanghai Normal University, Shanghai, China
Received July 28, 2009; revised August 23, 2009; accepted August 28, 2009
Abstract
Differential evolution (DE) algorithm has been shown to be a simple and efficient evolutionary algorithm for
global optimization over continuous spaces, and has been widely used in both benchmark test functions and
real-world applications. This paper introduces a novel mutation operator, without using the scaling factor F,
a conventional control parameter, and this mutation can generate multiple trial vectors by incorporating dif-
ferent weighted values at each generation, which can make the best of the selected multiple parents to im-
prove the probability of generating a better offspring. In addition, in order to enhance the capacity of adapta-
tion, a new and adaptive control parameter, i.e. the crossover rate CR, is presented and when one variable is
beyond its boundary, a repair rule is also applied in this paper. The proposed algorithm ADE is validated on
several constrained engineering design optimization problems reported in the specialized literature. Com-
pared with respect to algorithms representative of the state-of-the-art in the area, the experimental results
show that ADE can obtain good solutions on a test set of constrained optimization problems in engineering
design.
Keywords: Differential Evolution, Constrained Optimization, Engineering Design, Evolutionary Algorithm,
Constraint Handling
1. Introduction
Many real-world optimization problems involve multiple
constraints which the optimal solution must satisfy. Usu-
ally, these problems are also called constrained optimiza-
tion problems or nonlinear programming problems. En-
gineering design optimization problems are constrained
optimization problems in engineering design. Like a con-
strained optimization problem, an engineering design
optimization problem can be generally defined as follows
[1–4]:
Minimize )(xf

, n
n
xxxx  ],...,,[ 21

Subject to q
j
x
g
j,...,2,1,0)( 
 (1)
mqqjxhj,...,2,1,0)(



where DiU
x
Liii ,...,2,1, 
Here, is the number of the decision or parameter
variables (that is,
n
x

is a vector of size ), the
variable varies in the range . The function
Dthi
i
x],[ ii UL
)(xf

is the objective function, )(xg j

is the ine-
quality constraint and
thj
)(xhj

is theequality con-
straint. The decision or search space is written as
, the feasible space expressed as
th
S
0
j
)(;

S
{

D
iiiUL 1],[
(|,1,,0) ,...,2,1







qjjxhq j

xgSxj F


},..., m2q

is one subset of the decision space (ob-
viously, ) which satisfies the equality and ine-
quality constraints.
S
SF
Population-based evolutionary algorithm, mainly due
to its ease to implement and use, and its less suscepti-
bleness to the characteristics of the function to be opti-
mized, has been very popular and successfully applied to
constrained optimization problems [5]. And many suc-
cessful applications of evolutionary algorithms to solve
engineering design optimization problems in the special-
ized literature have been reported. Ray and Liew [6] used
a swarm-like based approach to solve engineering opti-
mization problems. He et al. [7] proposed an improved
particle swarm optimization to solve mechanical design

Y. Y. AO ET AL.
66
optimization problems. Zhang et al. [8] proposed a dif-
ferential evolution with dynamic stochastic selection to
constrained optimization problems and constrained en-
gineering design optimization problems. Akhtar et al. [9]
proposed a socio-behavioural simulation model for en-
gineering design optimization. He and Wang [10] pro-
posed an effective co-evolutionary particle swarm opti-
mization for constrained engineering design problems.
Wang and Yin [11] proposed a ranking selection-based
particle swarm optimizer for engineering design optimi-
zation problems. Differential evolution (DE) [12,13], a
relatively new evolutionary technique, has been demon-
strated to be simple and powerful and has been widely
applied to both benchmark test functions and real-world
applications [14]. This paper introduces an adaptive dif-
ferential evolution (ADE) algorithm to solve engineering
design optimization problems efficiently.
The remainder of this paper is organized as follows.
Section 2 briefly introduces the basic idea of DE. Section
3 describes in detail the proposed algorithm ADE. Sec-
tion 4 presents the experimental setup adopted and pro-
vides an analysis of the results obtained from our em-
pirical study. Finally, our conclusions and some possible
paths for future research are provided in Section 5.
2. The Basic DE Algorithm
Let’s suppose that ],...,,[ ,2,1,
t
Di
t
i
t
i
t
ixxxx 

are solutions
at generation
t
, },...,,{ 21
t
N
ttt xxxP



 is the population,
where denotes the dimension of solution space,
is the population size. In DE, the child population
D N
1t
P
is generated through the following operators [12,15]:
1) Mutation Operator: For each t
i
x

in parent popu-
lation, the mutant vector 1t
i
v

is generated according to
the following equation:
)( 321
1t
r
t
r
t
r
t
ixxFxv





 (2)
where are randomly chosen and
mutually different, the scaling factor
iNrrr \},...,2,1{,,321
F
controls ampli-
fication of the differential variation .
)(3
t
r
x


2
t
r
x

2) Crossover Operator: For each individual t
i
x

, a
trial vector 1t
i
u

is generated by the following equation:








otherwise ,
]),1[||(if ,
,
1
,
1
,t
ji
t
ji
t
ji x
DrandjCRrandv
u (3)
where is a uniform random number distributed be-
tween 0 and 1, is a randomly selected index
from the set {, the crossover rate
rand
],1[ Drand
},...,2,1 D]1,0[

CR
controls the diversity of the population.
3) Selection Operator: The child individual 1t
i
x

is
selected from each pair of t
i
x

and 1t
i
u

by using gree-
dy selection criterion:








,
)))(if ,11
1
t
i
tt
i
t
ix
u
x(t
i
xf
otherwise
(i uf



 (4)
where the functionis the objective function and the
condition
f
f)()( 1t
i
t
ixuf



 means the individual 1t
i
u

is better than t
i
x

.
Therefore, the conventional DE algorithm based on
scheme DE/rand/1/bin is described in Figure 1 [15].
3. The Proposed Algorithm ADE
3.1. Generating Initial Population Using
Orthogonal Design Method
Usually, the initial population },...,,00
2N
xxP{0
1
0x




(rjU
D
of
evolutionary algorithms is randomly generated as follows:
):, 0
jjji LLxDjNi  ,j (5)
where is the population size, is the number of
variables, is a random number between 0 and 1, the
variable of
N
j
r
thj0
i
x

is written as , which is initial-
ized in the range . In order to improve the
search efficiency, this paper employs orthogonal design
method to generate the initial population, which can
make some points closer to the global optimal point and
improve the diversity of solutions. The orthogonal design
method is described as follows [16]:
0
,ji
x
,...,, 21 x
]
j
x
,
jUL[
For any given individual ][D xx

, the thi
1: Generate initial population }{0
1N
xx  ,...,,0
2
0x

0
P
2: Let
0t
3: repeat
4: for each individualt
i
x

in the populationdo
t
P
2
r
,...,2,1 D
5: Generate three random integersand
1
r,
6: , with
iNr \},...,2,1{
33
r
21 rr 
j 7: Generate a random integer }{
rand 
8: for each parameter
j
do
9:











otherwise
( if
),(
,
,,
1
,
13
tji
t
jr
t
jr
tji
x
randrand
xFx
u

,
||
,
2
t
jr
jCR
x
]),1[ D
10: end for
11: Replacet
i
x

with the childin the population,
1t
i
u
1t
P
12: if1t
i
u

is better, otherwiseis retained
t
i
x

13: end for
14: 1


tt
15: until the termination condition is achieved
Figure 1. Pseudocode of differential evolution based on
scheme DE/rand/1/bin.

Y. Y. AO ET AL. 67
decision variablevaries in the range . Here,
each is regarded as one factor of orthogonal design.
Suppose that each factor holds levels, namely, quan-
tize the domain into Q levels
i
x
[i L
],[ ii UL
i
x
Q
], i UQ



,...,
ji,

,21 .
The level of the factor is written as ,
which is defined as follows:
thjthi










QjU
QjjL
jL
a
i
Q
LU
i
i
ji
ii
,
12 , ))(1(
1,
1
, (6)
And then, we create the orthogonal array

M
with factors and Q levels, where is
the number of level combinations. The procedure of con-
structing one orthogonal array is de-
scribed in Figure 2.
DNji
b )(,DN
DNji
b )( , M
Therefore, the initial population is
generated by using the orthogonal array ,
where the variable of individual
DNji
xP  )( 0
,
0
Nji
bM  )( ,
0
i
x
D
thj

is

0
,ji
x
.
ji
bj
a,
,
3.2. Multi-Parent Mutation Scheme
According to the different variants of mutation, there are
several different DE schemes often used, which are for-
mulated as follows [12]:
"DE/rand/1/bin": (7) )( 321
1t
r
t
r
t
r
t
ixxFxv  

"DE/best/1/bin": )( 21
1t
r
t
rbest
t
ixxFxv





 (8)
"DE/current to best/2/bin":
)()( 21
1t
r
t
r
t
ibest
t
i
t
ixxFxxFxv







 (9)
"DE/best/2/bin":
)()( 4321
1t
r
t
r
t
r
t
rbest
t
ixxFxxFxv 
 (10)
"DE/rand/2/bin":
)()( 54321
1t
r
t
r
t
r
t
r
t
r
t
ixxFxxFxv







 (11)
1: for ()
iNii ;;1
2: {int() mod ;mod Q}

1,i
bQi/)1( Q)1(
2, ibi
3: for ()
 jDjj ;;3
4: for ()
 iNii ;;1
5: {mod }
))2(( 2,1,, iiji bjbb  Q
6: Increment by one for
ji
b,DjNi 1,1
Figure 2. Procedure of constructing one orthogonal array
DN
i
j)(bM
.
best
x

is the best individual of the current popula- where
tion. Usually, based on both the control parameter F and
the selected multiple parents, using these DE schemes
can only generate a vector after a single mutation. Tsutsui
et al. [17] proposed a multi-parent recombination with
simplex crossover in real coded genetic algorithms to
utilize the selected multiple parents and improve the di-
versity of offspring. Inspired by multi-parent recombina-
tion with simplex crossover, this paper proposes a novel
multi-parent mutation in differential evolution. The multi-
parent mutation is described in the following.
For each individual t
i
x

from the population t
P
with
population size N, Ni ,...,2,1

. A perturbedector
1t
i
v
v

is generatedccor following formula:
K

ading to the





k
t
r
t
rk
t
i
t
ikkxxwxv
1
1)( 1 (12)
where iNrrr K\},...,2,1{,...,, 21

,
K
r
d
andomly chosen
integers t
r
t
rxxK11
are mutually different, an


. The
weighted valuek wis defined as follows:
),1( Kdn  ran

,/  )( 



sumw  (13)
where is a 1-by),1(Krandn -
K
matrix with normally
distribunumbers, )(

ted random

su is used for calcu-
lating the sum of all componhe vector

m
nts eof t

, and
],...,,[ 21 K wwww


.
varyAccording to the ingw

, repeat Formulas (13) and
(12) for
K
times,
K
new vectors }1{
1t
i
v

, }2{
1t
i
v

, ... ,
}{
1Kv t
i


are genated from theerse
K
seleents.
n
cted par
And the
K
vectors }1{
1t
i
x

, }2{
1t
i
x

,... , }{
1Kx t
i


are
created byossover andtrt de-
scribed in Subsections 3.3-3.5 respectively. Finally, an
offspring individual 1t
i
x
cr, repair consainhandling

of the th)1( tgeneration
population 1t
P
is obd by selecting the best indi-
vidual from
taine
these
K
offspring and their common parent
t
i
x

.
.3. Adaptive Crossover Rate
rateis a constant
3CR
conventional DE, the crossoverCRIn
value between 0 and 1. This paper prop an adaptive
crossover rate CR , which is defined as follows:
oses
))^(exp(
0baCR T
t
 CR (14)
where the initial crossover rate is
and usually is set to 0.8 or 0.85
0
CR
,
a constant value
t
is the current genera-

Y. Y. AO ET AL.
68
tion number and
T
is the max generation number,
b is a shape parameter determing the degree of de-
pendency on the geration number, a and b are po-
sive constants, usually a is set to 2, b is set to 2 or 3.
At the early stage, DE uses a bigger crossoverate CR
to preserve the diversity o solutions andrevent prema-
ture; at the later stage, DE employs a smaller crossover
rate CR to enhance the local search and prevent the
better solutions found from being destroyed.
3.4. Repair Method
imal
in
more of t
w
en
it
e
r
variables in t
f
r
p
After crossover, if one ohe he
n vector 1t
i
u

are bd their baritheyonoundes, e vio-
lated variable value 1
,
t
ji
u

is either reflected back from
the violated bdary r set to the corresponding bound-
ary value using the repair rule as follows [18,19]:
oun o












1
,
t
ji
e p
num
zation p




)()3/1(if ,1
,
1
,
j
t
ji
t
jij Lup
uL



(
j
e
e









()3/2 2
23 ,
)()3/(
2
()3/2 2
)(23/ ,
2
,
1
,
,
j
j
t
jij
t
ji
t
ij
jj
j
t
ij
UuU
UupU
up
uU
LuL
LupL
u
er uniform y distributed ran-
ber ing
g chniof
olv constre
mthod ha


)
)
1
1
j
j
ain
to




)3/
)3/
1
,
1
,
t
ji
t
ji
u
U
u
l
qu
ing
on m

(if
/1(if
1
(if
1(if
p
p
e,0[
n



,
if ,
,
1
,
1
,
1
,
t
ji
j
t
ji
is a probability and
the ran
Feasibility-Based Rule
)
(15)
d opti-
ndle
wh
dom
In e
i
]1 .
3.5. Constraint HandliTe
volutionary algorithms for s
roblems, the most comm
constraints is to use penalty functions. In general, the
constraint violation function of one individual x

is
transformed by m equality and inequality constraints as
follows [4]:


m
q
j
j
wxG )(

 (16)

qj
jj xwx
11
))(max((max

re the
|  )) j hg,0(
nt
|,0
whe expone

is usually set to 1 or 2,

is a
tolerance allowed (a very small value) for the equality
constraints and the cfficient j w is greater than zero.
If x
oe

is a feasible solution,0)(xG

, otherwise
0)(xG

. The function value)(x G

shows that the
deg of constraints violation oal x reef iundivid

.

is
d j w is set to 1 in this study.
In this study, a simple and efficient constraintand ing
technique of feasibility-based rule is intro
also a co
set to
hl
duced, which is
ra
with the better
le, the one with smaller
roposed algorithm ADE
tion Problems in
use
b, which are commonly used
2: orthogonal design method, set nd let
3: repeat
4: for each individual
2 an
nstraint handling technique without using pa-
meters. When two solutions are compared at a time, the
following criteria are always applied [1]:
1) If one solution is feasible, and the other is infeasible,
the feasible solution is preferred;
2) If both solutions are feasible, the one
objective function value is preferred;
3) If both solutions are infeasib
constraint violation function value is preferred.
3.6. Algorithm Framework
The general framework of the p
is described in Figure 3.
4. Experimental Study
4.1. Constrained Optimiza
Engineering Design
In order to validate the proposed algorithm ADE, we
enchmark test problemssix
1: Generate initial population},...,,{00
2
0
1
0N
xxxP using
0
CR a 0t
t
i
x

in the populationdo
5: Generateandom integer
6:
t
P
Krs 1 r,2 r,... ,K r
iN \},...,2,1{

, they are also mutually different
7: for each},...2,1{ Kk

do
8: Apply multi-parent mutation to generate new
9: vector}{
1kvt
i

10: for each parameter
j
do
11:











otherwise ,
]),1[|| ( if
},{
}{
,
1
,
1
,
tji
tji
tji
x
DrandjCRrand
kv
ku

12: Ifis beyond its lower or upper boundaries,
13: repair rule is enforced
14: end for
15: end for
16: Find out the best one of the children
17:
1
,
tji
u
1t
i
u

}}{},...,2{},1{{ 111Kuuu t
i
t
i
t
i



/*apply the
18 feasibility–based rule */
19: Replacet
i
x

with 1t
i
u

in the populatio,
20: if
n1t P
1t
i
u

is better, otherwiseis retained
21: end for
22:
t
i
x

1


tt
23: until the termination condition is achieved
Figure 3. The general framework of the ADE algorithm.

Y. Y. AO ET AL.
69
in thd which are ded in
the following.
1)
M
e specialized literature, an scribe
Three-bar truss design [8]:
inimize lxxf  )22()( 21 x

Subject to0
22 21
2
1

xxx
,
2
(1   P
xx
xg)2
1
0)( 2
2
2
 Pxg
22 211 xxx
x

,
0
2
1
)( xg
21
3

 P
xx

wher and e 101 x;10 2

x ,cm100

l
,KN/cm2 and
2P.KN/cm2 2

2) desi
M
Spring gn [8]:
inimize )(xf 2
213 )2( xxx

Subject to0
71785
1)( 4
1
1 x
xg ,
2
3
3
x
x
01
51)125 2 08
1
(66
4
)(
2
1
x xg
2
21 
x
xx,
4
2
3
21
2xxx
0
45.140
12  x )(
3xg
3
2
1

xx

,
01)( 21 

xx xg5.1
4

w1 2 here ,3.125.0  x ,0.205.0

x and .1523

x
3) Pressure vessel design [9,20]:
Minimize 431 16224.0)( xxxxf  4
2
1
2
321661.37781. xxxx 

3
2
1
84.19 xx
Subject to00193.0)(311 xxxg

,
000954.0)( 322  xxxg

,
0000,296,1
3
4
)( 3
34
2
33  xxxxg


,
0240)( 44

 xxg

where ,0625.0 11 nx ,0625.0 22 nx

,991 1

n
. ,99 10 3x12 n
4) Wdesign
,200 20010 4 x
elded beam [9]:
Minimize
)0.14(04811.0 243 xxx 10471.1)( 2
2
1xxxf 

Subject to0)()( max1


xxg

,
0)()( max2 


xxg

,
0)(413 xxxg

)0.14(04811.010471.0)( 243
2
14 xxxxxg
00.5  ,
0125.0)( 15  xxg

0)()( max6 


xxg

,
0)()(
7


xPPxg c

The other parameters are defined as follows:
,)"(
2
)'()22   R x
"'2

x
(2 
,
221xx
' 
P,"
J
MR
 
),
2
2
x,)
2
(
4
2 31
2
2xx
x
R  (LPM 
,
212
2
2
2
31
2
221









xx













 xx
x
J ,
6
)( 2
34xx
PL
x


,
4
)(3
34
3
xEx
PL
x


,
42
1
36/013.4
)( 3
2

L
6


4
2
3


 G
E
L
x
xEGx
xP
c

where .,lb 6000

P ,in 14L.,in 25.0
max


,psi600,13
max ,psi 106
 G30E,psi 106  12

,psi 000,30
max


,0.211.0

x ,0.101.0 2

x
,0.101.0 3


x and .0.2
41.0

x
5) Speed reducer design [8]:
Minimize
)0934.439334.3333. 3
2
3 xx143(7854.0)(2 21
xxxf

)(4777.7)(508.1 2
7
3
6
2
7
2
61 xxxx  x
)(7854.0 2
75
2
64xxxx 
Subject to01)(
3
2
27
21
1xxx
xg

,
01
5.397
)( 2
3
2
21
2 xxx
xg

,
01
93.1
)( 4
632
3
4
3 xxx
x
xg ,
01
93.1
)( 4
732
3
5
4 xxx
x
xg,
01
0.110
]109.16))/(745[(
)( 3
6
2/162
324
5

x
xxx
xg ,
01
0.85
]105.157))/(745[(
)( 3
7
2/162
325
6

x
xxx
xg ,
01
40
)( 32
7
x
x
xg

,01
5
)(
1
2
8x
x
xg

,
01
12
)(
2
1
9x
x
xg

,
01
9.15.1
)(
4
6
10  x
xg 
x

,
01
9.11.1
)(
5
7
11 

x
x
xg


Y. Y. AO ET AL.
70
where ,6.36.2 1 x,807.02.

x
,3.83.7 5 ,28 3.7 4 x17 3x,3.8

x
,9.3 0.57 x9.2 6 x.5 5.
r6) Himmelblau’s Nonlinea Optimization Problem
This problem was proposed by Himmelblau and simi-
lar to problem [22] of the hmark except for
the second coefficient of the first constraint. There are
five design variables. The problem can be stated as fol-
lows:
Minimize
Subject t
[21]:
04g benc
51
2
38356891.03578547.5)( xxxxf

141.40792293239.37 1x
o521 0056858.0334407.85)( xxxg

5341 0022053.000026.0 xxxx  ,
092 
522 0056858.0334407.85)( xxxg

00022053.000026.0 5341

 xxxx ,
523 0071317.051249.80)( xxxg



2,
321 0021813.00029955.0 xxx
0110
524 0071317.051249.80)(xxxg 

2
321 0021813.00029955.0 xxx ,
090 
535 0047026.0300961.9)( xxxg



4331 0019085.00012547.0 xxxx, 
025 
536 0047026.0300961.9)( xxxg 

4331 0019085.00012547.0 xxx  , x
020 
where,10278 1x ,4533 2

x and 4527


i
x
(i).5,4,3
Figure 5. Convergence graph for spring design.
Figure 6. Convergence graph for pressure vessel design.
4.2. Convergence of ADE
In this section, Figures 4-9 depict the convergence graphs
for 6 engineering optimization problems described above
respectively. From Figures 4-6, we know that ADE and
DE all can be quickly convergent. In the figures, FFES is
the number of fitness function evaluations.
4.3. Comparing ADE with Respect to Some
S
In this experimental study, the parameter values used in
ADE are set as follows: the population size
tate-of-the-Art Algorithms
50

N
e level num
, the
maximal generation number , thber 300T


NQ , the mutation pareer nt numb1

D
K
, the
Figure 4. Convergence graph for three-bar truss design.

Y. Y. AO ET AL.
71
Fir
optimization problem.
initial crossover rate
gure 9. Convergence graph for Himmelblau’s nonlinea
Figure 7. Convergence graph for welded beam design.
8.0
0

CR , the coefficient 2

a,
the shape parameter 3

b, the exponent 2


. The
s equalnumber of fitness fuuations (FF
to
nction evalES) i
KTN


. The acu hieved soltion at the end of
KTN


. Convergence graph for speed regn. Figure 8ducer desi
FFES is easure the pe
ADE. ADE is independently run 30 times on each test
problem above. The optimized objective function values
(of 30 runs) arranged in ascending order and the 15th
value in the list is called the median optimized function
value. Experimental results are presented in Tables 1-12.
And NA is the abbreviation for “Not Available”.
For three-bar truss design problem, the experimental results
are given in Tables 1-2. According to Table 1, ADE and
DSS-MDE [8] can obtain the approximate best and median
Table 1. Comparison of statistical results f over 30 ru
Algorithms Best Median
used to mrformance of
values, which are slightly better than those obtained by Ray
or three-bar truss designns.
Mean Worst Std FFES
ADE 263.89584338 263.89584338 263.89584338 263.89584338 4.72e-014 45,000
DSS-MDE [8] 263.8958434 263.8958434
Ray and Liew [6] 263.8958466 263.8989
263.8958436 263.8958498 9.72e-07 15,000
263.9033 263.96975 1.26e-02 17.610
Table 2. Comparison of best solutions
Function ADE DSS-MDE [8] Ray a
found for three-bar truss design.
nd Liew [6] ECT [23] Ray and Saini [24]
1
x 0.7886751376014 0.7886751359 0.7886210370 0.78976441 0.795
2
x 0.4082482819599 0.4082482868 0
263.8958466 263.896710000 264.300
FFES 45,000 15,000 17,610 55,000 2712
.4084013340 0.40517605 0.395
)(xf 263.895843376 263.8958434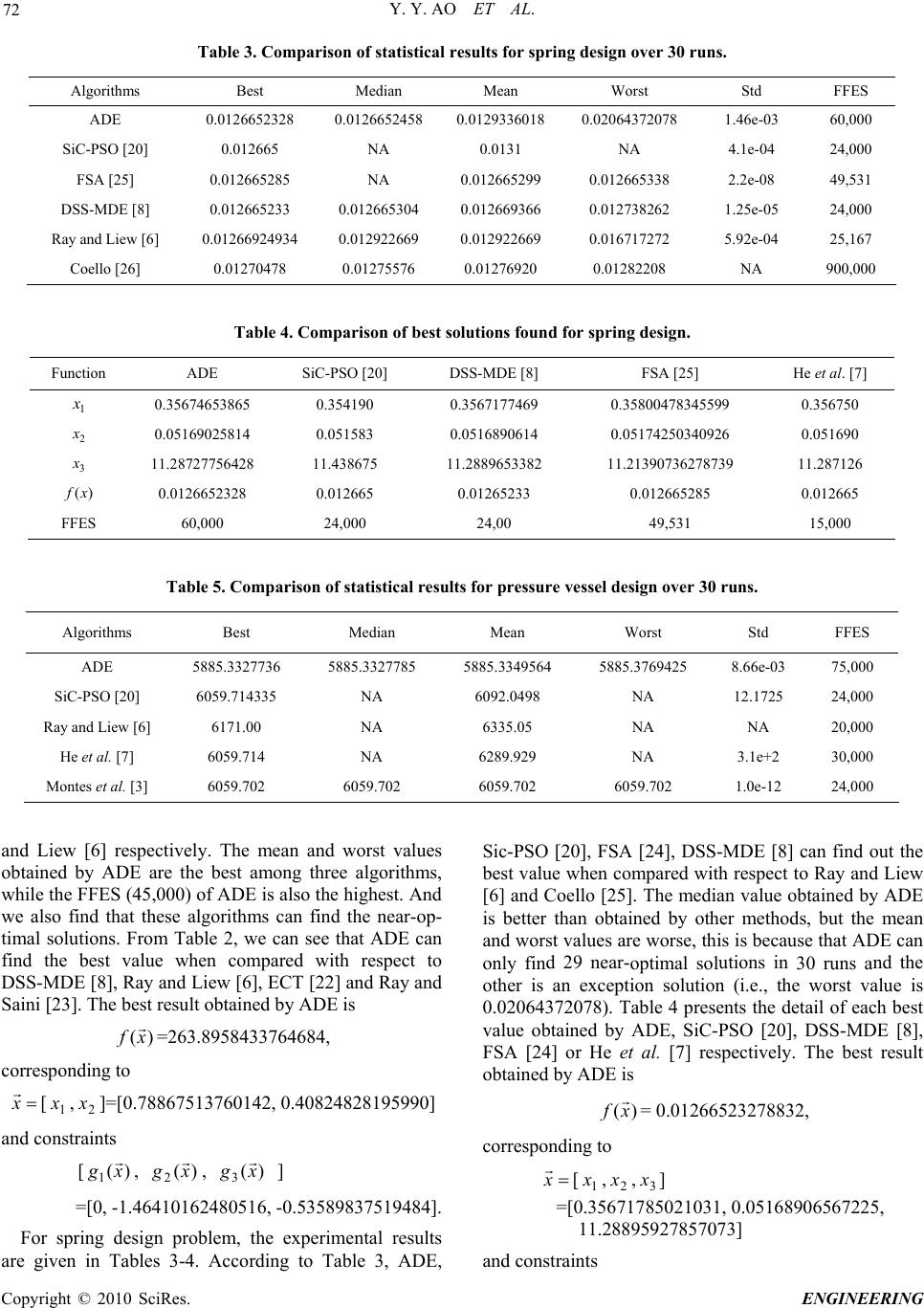

Y. Y. AO ET AL.
72
Table 3. Comparison of statistical results for spring design over 30 runs.
Algorithms Best Median Mean Worst Std FFES
ADE 60,000 0.0126652328 0.0126652458 0.0129336018 0.02064372078 1.46e-03
SiC-PSO [20] 0.012665 NA 0.0131 NA 4.1e-04 24,000
F0.012660.0126 0.012 2.
DSS-M] 0.000. 0
Ray0.01 0.0.0 0.
0.00.0 0.01 0.0
SA [25] 5285 NA 65299 6653382e-0849,531
DE [812665233 .012665304 012669366 .012738262 1.25e-05 24,000
and Liew [6] 266924934 012922669 12922669 016717272 5.92e-04 25,167
Coello [26] 1270478 1275576 276920 1282208 NA 900,000
Table 4. Comparison of best solutions found for spring design.
SDiC-PSO [20] SS-MDE [8] FSA [25] He et al. [7] Function ADE
1
x 0.35674653865 0.354190 0.30.399 50 567177469 580047834550.3567
2
x 0.05169025814 0.051583 0.00.026 90
111.219 6
0.01 8 0.00.0120.85 65
FFES 6015,000
516890614 517425034090.0516
3
x 1.28727756428 11.438675 889653382 1.213907362787311.28712
)(xf 266523212665 65233 01266520.0126
,000 24,000 24,00 49,531
Table 5. Comparison of statsults fore ver 30 r
Mrst
istical re pressurssel design oveuns.
Algorithms Best edian Mean WoStd FFES
ADE 585885.385 5 85.3327736 32775885.3349564 5885.3769428.66e-0375,000
SiC-PSO [20] 6
R
H2
Montes et al. [3] 6059.702 6059.702 6059.702 6059.702 1.0e-12 24,000
059.714335 NA 6092.0498 NA 12.1725 24,000
ay and Liew [6] 6171.00 NA 6335.05 NA NA 20,000
e et al. [7] 6059.714 NA 6289.929 NA 3.1e+30,000
and Lrespectivhe mean
obtained b ADE mong trithms,
while the FFES (45 the hest. And
we also find that ths can fear-op-
timal solutions. Fr can see that ADE can
find the best valuepared with respect to
DSS-MDE [], Ray and], ECT [22 and
Saini [2e best resined by AD
iew [6] ely. T and worst values
yare the best a
,000) of ADE is also
hree algo
igh
ese algorithmind the n
om Table 2, we
when com
Liew [68] and Ray
3]. Thult obtaE is
)(xf

=263.8958433764684,
corresponding to
x

[1,2 x]=[0.7x886751372, 0.4082490]
and constr
6014 8281959
aints
[)(
1xg

, )(
2xg

, )(
3xg

]
162 -0.5358989484].
For gn prob experimeresults
are given in Tables 3-4. According to Table 3, ADE,
[20], FSA MDE [8ut the
e whenespect to Ray and Liew
oello [25]ue ob ADE
han obmethode mean
t value becauE can
d 29 near-utions in nd the
tio (i.e., the alue is
64372078). Tabesents the detach best
value obtained by ADE, SiC-PSO [20], DSS-MDE [8],
ely. The best result
=[0, -1.46410480516,3751
spring desilem, thental
Sic-PSO[24], DSS-] can find o
best valu
[6] and C
compared with r
. The median valtained by
is better ttained by other s, but th
and worss are worse, this isse that AD
only fin
other is an excep
optimal sol
n solution
30 runs a
worst v
0.020le 4 prail of e
FSA [24] or He et al. [7] respectiv
obtained by ADE is
)(xf

= 0.01266523832,
ing
278
correspondto

x

[1 x,2 x,3 x]
=[0.3567021031, 0.051689065
11.288 7073
and constraints
1785 67225,
9592785]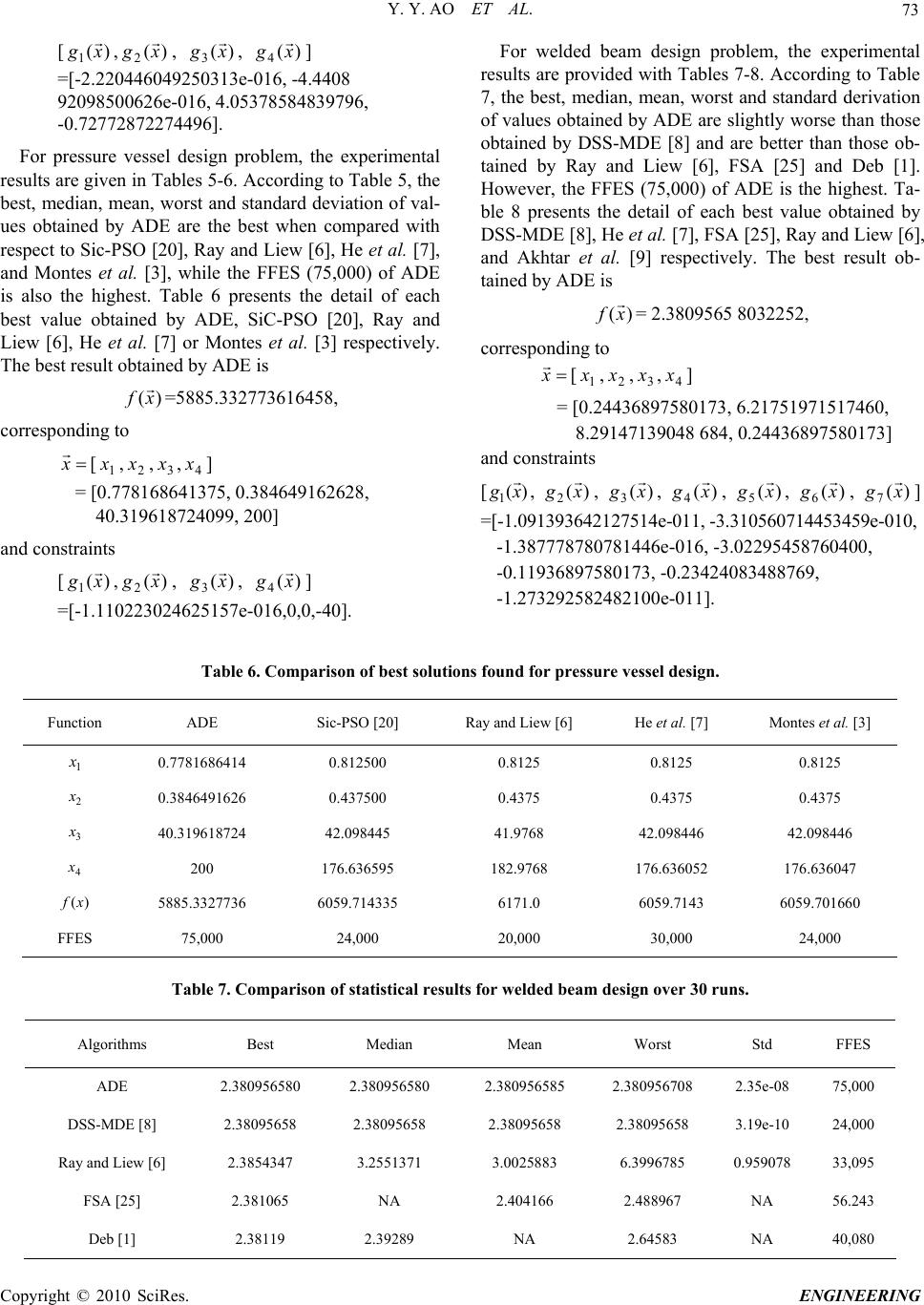

Y. Y. AO ET AL. 73
[)(
1xg

,(
2xg )

, )(
3xg

, g)(
4x

]
=[-2.220446049250313e-016, -4.4408
) of ADE
is also the highest.etail of each
ed by20], Ray and
l. [7] or Montes et al. [3] respectively.
The best
92098500626e-016, 4.05378584839796,
-0.72772872274496].
For pressure vessel design problem, the experimental
results are given in Tables 5-6. According to Table 5, the
best, median, mean, worst and standard deviation of val-
ues obtained by ADE are the best when compared with
respect to Sic-PSO [20], Ray and Liew [6], He et al. [7],
and Montes et al. [3], while the FFES (75,000
Table 6 presents the d
ADE, SiC-PSO [best value obtain
Liew [6], He et a
result obtained by ADE is
)(xf

=5885.332773616458,
corresponding to
and constraints
[1 x,2 x,3 x,4 x] x

= [0.778168641375, 0.384649162628,
40.319618724099, 200]
[)(
1xg

,)(
2xg

, )(
3xg

, )(
4xg

]
=[-1.110223024625157e-01 6,0,0,-40].
elded bgn prothe eental
results are provided with Tables 7-8. According to Table
7, the best, median, mean, worst and standard derivation
For weam desiblem, xperim
of values obtained by ADE are slightly worse than those
obtained by DSS-MDE [8] and are better than those ob-
tained by Ray and Liew [6], FSA [25] and Deb [1].
However, the FFES (75,000) of ADE is the highest. Ta-
ble 8 presents the detail of each best value obtained by
DSS-MDE [8], He et al. [7], FSA [25], Ray and Liew [6],
and Akhtar et al. [9] respectively. The best result ob-
tained by ADE is
)(xf

= 2.3809565 8032252,
corresponding to

x

[1 x,2 x,3 x,4 x]
= [0.24436897580173, 6.21751971517460,
.2141348 684, 0.24436897580173]
and constrai
897 90
n ts
[)(
1xg

, )x(
2
g

, )(
3xg

, )(
4xg

, (
5
g)x

, )(
6xg

, )(
7xg

]
27514e-011, -3.310560714453459e-010,
-1.7878144-016, -3.02295760400,
-0.
-1.27
Table 6. Comparison of best solutions
Function ADE Sic-PSO [20] R
=[-1.0913936421
387778 06e458
11936897580173, -0.23424083488769,
3292582482100e-011].
found for pressure vessel design.
ay and Liew [6] He et al. [7] Montes et al. [3]
1
x 0.7781686414 0.812500 0.8125 0.8125 0.8125
2
x 0.3846491626 0.437500
40.319618724 42.098445
200 176.636595
5885.3327736 6059.714335 6171.0 60
FFES 75,000 24,000 30,000 24,000
0.4375 0.4375
0.4375
41.9768 42.098446 42.098446
182.9768 176.636052 176.636047
3
x
4
x
)(xf 6059.7143 6059.7016
20,000
Table 7. Comparison of statistical results for welded
Algorithms Best Median Worst Std FFES
beam design over 30 runs.
Mean
ADE 2.380956580 2.380956580 2.380956585 2.3809708 2.35e-08 75,000 56
DSS-MDE [8] 2.38095658 2.38095658 2.38095,000
Ray and Liew [6] 2.3854347 3.2551371
FSA [25] 2.381065 NA
Deb [1] 2.38119 2.39289
658 2.38095658 3.19e-10 24
3.0025883 6.3996785 0.959078 33,095
2.404166 2.488967 NA 56.243
NA 2.64583 NA 40,080

Y. Y. AO ET AL.
74
ions found for
Ray and Liew [6] Akhtar et al. [9]
welded beam design. Table 8. Comparison of best solut
Function ADE DSS-MDE [8] He et al. [7]FSA [25]
1
x 0.24436897580 0.2443689758 0.244369 0.24435257 0.244438276 0.2407
2
x 6.21751971517 6.2175197152 6.217520
8.2 05 8.291471 9
7580 0.2443689758 0.244369 0.2497
2.3809 8032 2.38095658 2.380957 2.381065 2.3854347 2.4426
FFES 75,000 24,000 30,000 56,243 33,095 19,259
6.2157922 6.237967234 6.4851
8.2939046 8.288576143 8.239
0.24435258 0.244566182
3
x 9147139049 8.29147139
40.2443
x 689
565
)(xf
Table 9. Comparison of statistical resultscer desiruns.
Algorithms Mean Worst Std ES
for speed redugn over 30
Best Median FF
ADE 662 22 2994.472994.4710662 1.85e-012 ,000 2994.4710994.47106610662 120
DSS-MDE [8] 066 2994.4 2994.4713.58e-012 0
Ray and Liew [6] .744241 3001.73009.96423 6
Monte [27]689 2996.36NA 8.2e-03
et al. [9] 8.08 30123028 NA 154
2994.4712994.47106671066 066 30,00
2994 3001.758264 582264 4736 4.009154,45
s et al. 2996.356NA 7220 24,000
Akhtar 300NA .12 19,
FunctiADE DSS-MDE Ray and LMon [27] khtar et
Table 10. Comparison of best solutions found for speed reducer design.
on [8] iew [6] tes et al.Aal.[9]
1
x 3.5 3.5 3.50000681 3.500010 3.506122
2
x0.7 0.7
0.70
17 17 117
7.3 7.3
7.3276 7.5491
7.715319911478 7.7153199115 7.71532175 7.800027 7.859330
3.350214666096 3.3502146661 3.35026702 3.350221 3.365576
5.28665446 5.289773
2994.4710662 2994.471066 2994.744241 2996.356689 3008.08
1
000001 0.7 0.700006
3
x 7 17
4
x 0205 7.300156 26
5
x
6
x
7
x 4980 5.2866544650 5.28665450 5.286685
)(xf
FFES 20,00030,000 54,456 24,000 18,154
Tarisal resimmelinear problem.
Algorms Best ean WorStd S
able 11. Compon of statisticults for hlblau’s non optimization
ithMedian Mst FFE
ADE 4 4 5.560231025.55.91e-010 000 -31025.5602-31025.5602-3102 4 -6024 90,
COPSO [28] 56024 A 25.56024 NA 0 ,000
HU-PSO [29] -31025.56142 NA -31025.56142 NA 0 200,000
-31025.N -310200

Y. Y. AO ET AL.
75
Table 12. Comparison of best solutions found for himmelblau’s nonlinear optimization problem.
Function ADE[28] PSO [29] Colleo [21] Homaifar et COPSO HU- al. [30]
1
x 78.000 495 78.000000000000 78 78.078.0000
2
x 33.0000 070 33.00
0709 0 29.99
0000 45.0000 45.00
.969242 9242 924255 44.9400 36.77
-31025.56024249794 -31025.56024 -31025.56142 -31020.859 -30665.609
FFES 9NA
0000000000 33 33.033.000
3
x 27.9710517604 27.07099727.070997 27.08150
4
x 45.0000000000 4545.000
5
x 44 5501054944.9644.9660
)(xf
0,000 200,000 200,000 NA
F reducegn problemmental
results argiven in Taes 9-10. Accordio Table 9,
the best, median, mean, worst and standaerivation of
values obained by And DSS-MDE [re superior
to those obtained by R Liew [6], Ms et al. [27]
and Akhet al. [9ely, whe FFES
(120,000of ADE ishighest. Table shows the
detail ofh bned b-MDE
[8], Ray and Liew [6], Montes et al. [27] and Akhtar et
al. [9] respectiveult obE is
or speedr desi, the experi
e blng t
rd d
tDE a8] a
ay and
] respectiv
onte
ile thtar
) the 10
eacest value obtaiy ADE, DSS
ly. The best restained by AD
)x

x

[1 x,2 x,3 x,4 x,5 x]
= [78, 33971051760
44.96924010549]
constraints
, 27.07094, 45,
255
and
[1 g)(x

,)(
2xg

,)(
3xg

,)(
4xg

,(
5xg

, )(
6xg

)]
=[0, -92, -9.59476568762383, -10.40523431237617,
, 0].
m, comparespect to sev-of-the-
rithms, ADerform bettbench-
mark test problems. It is clearly shown that ADE is fea-
d effecte constrainmization
ems in engineeesign. The reahat ADE
uses multi-parent mutation to generate a better offspring,
and applies self-adaptive control parameter and effective
Conclusiond Future rk
paper pdaptintialution
) algorithm constrained timizatngi-
neering Design. Firstly, ADE employs the orthogonal
method toerate the initial popul im-
prove the diversity of solutions. Secondly, a multi-parent
mutation scheme is developed to improve the capacity of
DE. Thirdly,
in order to improve the adaptive capacity of crossover
w appdjustirate
is pted. In addiE introducw repair
ruleonstrainting technique he feasi-
ble- rule is also when como solu-
tme. Finally, ADE is tested onstrained
engiing design op problemom the
specialized literature. Cared with resperal
art algorie experimenlts show
highlye and ca re-
surms of a test set of constrainetimization
-5
In sued with reral state
art algoE can per on six
sible anive to solved opti
problring dson is t

= 2994.471(f06614
corresponding to
]
= [3.5, 0.7, 17, 7.3, 7.71531991147825,
3.3
and constraints
682020,
x
[1
x,2 x,3 x, 4 x,5 x,6 x,7 x
5021466609645, 5.28665446498022] repair rule etc.
[(
1xg

),)(xg

,)(
3xg

,)
4x

,)(
5xg

,
2(g)(xg

6,)( 7xg

,
)(
8xg

,
5. s anWo
This roposes an ave differe evol
(ADE foropion in E
design genation to
)(
9xg

,g(
10 x

,)(
11 xg

] )
=[-0.073915280
49917224810
39787, -0.1979985
2, -0.904643
2714195,
7, -0.249045560
-65090.7025000000,
-2.22003133333333,
-0.05132575354183, -8.881784197001252e-016].
For Himme
best, median, mean, worst and standard derivation of
valuwn in Tab-12, it is cleat
ADE, COO [28][29] all can d one
near-optimal solu. Adnally,
ADE only requirewhich is suior to
other sev ral algoOPSO [00
FFES and HU-PSFES. The bresult
obtained by ADE i
.6613381477
44604925
39e-016, 0, -
3e-016, -0.58
0000
3333
lblau’s nonlinear optimization problem, the exploration and the convergence speed of A
es is sholes 11arly seen th
PS, and HU-PSO
tion after a single run
fin
ditio
s 90,000 FFES, per
erithms, such as C28] 200,0
O [29] 200,000 Fest
s
)
operator, a neroach to ang the crossover
resen
and a c
tion, AD
handl
es a ne
of t
based appliedparing tw
ions at a ti six con
neer timization
omp
s taken fr
ect to sev
state-of-the-thms, thtal resu
that ADE is competitivn obtain good
lts in ted op
(xf

=-3.1025.5602424979
corres
4,
ponding to

Y. Y. AO ET AL.
76
roblems in engineering design. However, there are still
so
genetic algorithplied Me-
ngineering, Vol. 186, No. 2, pp. 311–338,
[2] E. Mezuraoes Aale, “Parame-
ter cd opti-
miza -
putation
ontes, C. A. Coello Coello, J. Velázquez-
Res, and . Muñoz-Dávila, “Multiple trial ctors i
differential evolution for e design,” Engineer-
ing Optimization, Vol. 39, No. 5, pp. 567–589, 2007.
merical con-
th-
, No.
[5]
for mechanical design optimiz
problems,” Eng.
.
.. Luo, and X. F. Wang, “Differential
lution withymselection for constrained
optim . 178, pp.
3043
. Tai, and T. Ray, “A socio-behavioural
odel for engineering design optimization
Engineering Optimization, Vo34, No. 4, pp. 354,
[10]
[12] R. Storn and K. Price, “Differential evolution—A simple
, 1997.
ferential evolu-
tion,” Berlin:
Springer-Verlag, 2005.
nina, S. C. Esquivel, and C. A. Coello Coello,
“Solving engineering optimization problems with the
rained particle swarm optimizer,” Infor-
2, pp. 319–326, 2008.
[21] C. A. Coello Coello, “Use of a self-adaptive penalty ap-
evolutionary optimization,” IEEE Transactions on
al technique
ima, “Derivative-free filter
p
me things to do in the future. Firstly, we will further
validate ADE in the case of higher dimensions. Secondly,
we also will take some measures to improve the conver-
gence speed during the evolutionary process. Addition-
ally, testing some initial parameters of ADE is another
future work.
6. References
[1] K. Deb, “An efficient constraint handling method for
ms,” Computer Methods in Ap
chanics and E
2000.
-Mnt and. G. Pomque-Qrtiz
ontrol in differential evolution for constraine
tion,” 2009 IEEE Congress on Evolutionary Com
(CEC'2009), pp. 1375–1382, 2009.
[3] E. Mezura-M
ye Lven
ngineering
[4] C. A. Coello Coello, “Theoretical and nu
straint-handling techniques used with evolutionary algo-
rithms: A survey of the state of the art,” Computer Me
ods in Applied Mechanics and Engineering, Vol. 191
11-12, pp. 1245–1287, 2002.
R. Landa-Becerra and C. A. Coello Coello, “Cultured
differential evolution for constrained optimization,”
Computer Methods in Applied Mechanics and Engineer-
ing, Vol. 195, No. 33–36, pp. 4303–4322, 2006.
[6] T. Ray and K. M. Liew, “Society and civilization: An
optimization algorithm based on the simulation of social
behavior,” IEEE Transactions on Evolutionary Computa-
tion, Vol. 7, No. 4, pp. 386–396, 2003.
[7] S. He, E. Prempain, and Q. H. Wu, “An improved particle
swarm optimizeration proach for engineering optimization problems,” Com-
puters in Industry, Vol. 41, No. 2, pp. 113–127, 2000.
[22] T. P. Runarsson and X. Yao, “Stochastic ranking for con-
strained
ineering Optimization, Vol. 36, No. 5, pp
585–605, 2004
[8] M. Zhang, W Jevo-
Evolutionary Computation, Vol. 4, No. 3, pp. 284–294,
2000.
[23] K. Hans Raj, R. S. Sharma, G. S. Mishra, A. Dua, and C.
Patvardhan, “An evolutionary computation
dnaic stochastic
ization,” Information Sciences, Vol
–3074, 2008.
[9] S. Akhtar, K
simulation m,”
f
l. 41–3
2002.
Q. He and L. Wang, “An effective co-evolutionary parti-
cle swarm optimization for constrained engineering de-
sign problems,” Engineering Applications of Artificial
Intelligence, Vol. 20, No. 1, pp. 89–99, 2007.
[11] J. H. Wang and Z. Y. Yin, “A ranking selection-based
particle swarm optimizer for engineering design optimi-
zation problems,” Structural and Multidisciplinary Opti-
mization, Vol. 37, No. 2, pp. 131–147, 2008.
and efficient heuristic for global optimization over con-
tinuous spaces,” Journal of Global Optimization, Vol. 11,
pp. 341–359
[13] K. Price, R. Storn, and J. Lampinen, “Dif
tion: A practical approach to global optimiza
[14] Z. Y. Yang, K. Tang, and X. Yao, “Self-adaptive differ-
ential evolution with neighborhood search,” 2008 Con-
gress on Evolutionary Computation (CEC'2008), pp.
1110–1116, 2008.
[15] H. A. Abbass, R. Sarker, and C. Newton, “PDE: A
Pareto-frontier differential evolution approach for mul-
tiobjective optimization problems,” Proceedings of IEEE
Congress on Evolutionary Computation, Vol. 2, pp. 971–
978, 2001.
[16] Y. W. Leung and Y. P. Wang, “An orthogonal genetic
algorithm with quantization for global numerical optimi-
zation,” IEEE Transactions on Evolutionary Computation,
Vol. 5, No. 1, pp. 40–53, 2001.
[17] S. Tsutsui, M. Yamamure, and T. Higuchi, “Multi-parent
recombination with simplex crossover in real coded ge-
netic algorithms,” Proceedings of the Genetic and Evolu-
tionary Computation Conference, pp. 657–664, 1999.
[18] J. Brest, V. Zumer, and M. S. Maucec, “Self-adaptive
differential evolution algorithm in constrained real-pa-
rameter optimization,” 2006 IEEE Congress on Evolu-
tionary Computation (CEC'2006), pp. 919–926, 2006.
[19] Y. Wang and Z. X. Cai, “A hybrid multi-swarm particle
swarm optimization to solve constrained optimization
problems,” Frontiers of Computer Science in China, Vol.
3, No. 1, pp. 38–52, 2009.
[20] L. C. Cag
simple const
matica, Vol. 3
or constrained optimisation in engineering design,”
Journal of the Institution of Engineers India Part Me Me-
chanical Engineering Division, Vol. 86, pp. 121–128,
2005.
[24] T. Ray and P. Saini, “Engineering design optimization
using a swarm with intelligent information sharing among
individuals,” Engineering Optimization, Vol. 33, No. 33,
pp. 735–748, 2001.
[25] A. R. Hedar and M. Fukush
simulated annealing method for constrained continuous
global optimization,” Journal of Global Optimization,
Vol. 35, No. 4, pp. 521–549, 2006.

Y. Y. AO ET AL.
77
Evolu-
sity in differential
ing
ence Symposium, pp. 53–57,
[26] C. A. Coello, “Self-adaptive penalties for GA- based
optimization,” Proceedings of the Congress on
tionary Computation 1999 (CEC'99), Vol. 1, pp. 573–580,
1999.
[27] E. Mezura-Montes, C. A. Coello, and J. V. Reyes, “In-
creasing successful offspring and diver
and C
evolution for engineering design,” Proceedings of the
Seventh International Conference on Adaptive Comput-
ing in Design and Manufacture (ACDM 2006), pp. 131–
139, 2006.
[28] A. E. Muñoz Zavala, A. Hernández Aguirre, E. R. Villa
Diharce, and S. Botello Rionda, “Constrained optimiza-
tion with an improved particle swarm optimization algo-
rithm,” International Journal of Intelligent Comput
ybernetics, Vol. 1, No. 3, pp. 425–453, 2008.
[29] X. H. Hu, R. C. Eberhart, and Y. H. Shi, “Engineering
optimization with particle swarm,” Proceedings of the
2003 IEEE Swarm Intellig
2003.
[30] A. Homaifar, S. H. Y. Lai, and X. Qi, “Constrained opti-
mization via genetic algorithms,” Simulation, Vol. 62, No.
4, pp. 242–254, 1994.