Technology and Investment
Vol.3 No.3(2012), Article ID:22087,5 pages DOI:10.4236/ti.2012.33028
Competitive Innovation Diffusion in Small-World Network: Agent-Based Modeling and Simulation*
Department of Management Science and Engineering, School of Business, East China University of Science and Technology, Shanghai, China
Email: liying@ecust.edu.cn
Received July 10, 2012; revised August 10, 2012; accepted August 17, 2012
Keywords: Small-World Network; Innovation Diffusion; Competitive Innovations; Diffusion Model
ABSTRACT
The main purpose of this paper is to analyze the dynamic process when two competitive innovations diffuse simultaneously in the small world network. To illustrate the micro diffusion process, an agent-based modeling and simulation method is applied. In the agent based model, there are two competitive innovations. Agents make decisions to adopt one of the innovations according to the utility value. The sensitivity of the parameters of the utility function is analyzed. The result indicates that in the early stage and the late stage the advertisement strategy is better; while in the middle stage the word-of-mouth will be better.
1. Introduction
Innovation could be a product, a method or a theory. To the innovation adopters, innovation diffusion is a slow process, which depends on the network and the diffusion. Just like Rogers [1] said, innovation is the process which propagates among the social system members in a specific channel over time. He also points out that the innovation diffusion process is made of four key actors: innovation, information channel, time and social system. Innovation diffusion theory is mainly focus on which channel the new technology propagated.
The competition is a must in the innovation diffusion in the real work under the market mechanism. At the same time, many replaceable innovations may occur. Many researches are on the competitive innovation diffusion, whatever in or out China. Reccardo L. [2] studied the market segmentation mechanism in the same market for two products and validated it by a digital experiment. Chihiro Watanabe [3] studied the replace orbit in innovation replacement by the utilization of L-V model and does the empirical study on the diffusion of the digital TV in Japanese. In China, studied the competition and diffusion for two products and did the empirical study in Chinese communication market [4,5]. According to the relationship of the products and technology, the competitive innovation models can be divided into: competitive models, complementarily models, replaceable models and technology innovation models [6].
The model we constructed in this paper is a replaceable model. At the same time, there are two innovations exist in the market. They are competitive products. The purpose of this paper is to analyze which factors will influence the competitive diffusion and the effect of the word of mouth and the advertisement.
2. Competitive Diffusion Model
All the innovation diffusions need the diffusion medium. Generally, innovation diffusion is in a specific network. Many networks in the real social, for example, finance market, personal relationships, Industrial clusters [7] and so on, are just like what Watts and Strongatz [8] said the small world networks. So it is meaningful to analyze the diffusion in small world networks. The network applied in this paper is the small world network which contains 1000 nodes.
There are two and only two innovations in the model. And at the start of the diffusion, the market share for each innovation is different in order to investigate how lower one to catch up with the higher ones.
2.1. Diffusion Model for a Single Innovation
The component of our model is derived from the model in reference [9]. In the model, there are a set of actors who differ in the social ties, and they make decisions to adopt or reject an innovation. At each time step every actor has to decide whether to adopt the innovation, or if already adopted, whether to give up it. Each actor’s decision is based on (a) his/her attitude towards the innovation and (b) the adoption behavior of his/her social network.
Two thresholds are assigned to each agent. The first threshold L governs adoption; the second threshold R is always a fixed fraction of the first and governs the giving up of the adoption of the innovation. Also, the agents have their memory. In this way they can make their adoption decision based on their perception of how well this innovation has been established in the past. To take the observed trend in innovation use into account we define an actor a’s “personal network trend” as the weighed sum of:
1) The average number of adopters in a’s personal network and;
2) The average gain/loss of adopters within a’s network over a period of ten time steps.
If a’s personal network trend exceeds a’s threshold for adoption, a will adopt; if this degree falls below a’s threshold for giving up the adoption, a will give up adopting the innovation. The memory that allows actors to take trends into consideration and the threshold for giving up adoption distinguish our model from other threshold models 3. These components, as we shall see, enable our actors to give up adopting an innovation.
 (1)
(1)
where, W1 means the weight for the average number of adopters in a personal network; W2 means the weight for average gain/loss of adopters in personal net (observed trend).
In this paper, we add two factors: 1) the word of mouth Mt, which means the innovation adopters’ evaluation on the innovation, the effect of word of mouth is in direct proportion to m; and 2) the advertisement At, which is like the public medium in BASS model. The advertisement is in direct proportion to (m – Nt).
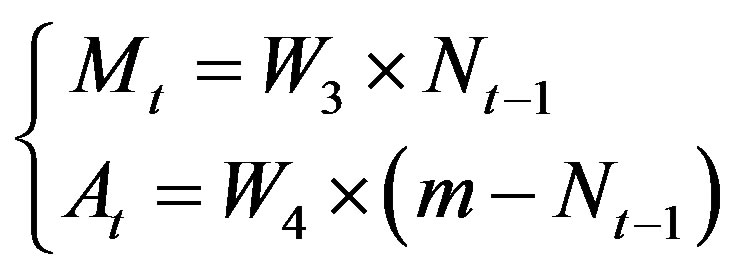 (2)
(2)
where, W3 means word of mouth coefficient, which can be changed by adjust the W3. Item (m – Nt–1) means the number of the adopters who have not adopted the innovation. W4 is advertisement coefficient, which can be changed by the change of W4.
The utility value to each innovation for each node in model is not only related to the number of the node’s neighbor in 10 steps, but also related to innovation diffusion trend and word of mouth and advertisement. More specifically, the utility value of node j in time t is shown in Equation (3).
Next, we will simulate the competitive innovations diffusion in the small world network. For innovation A and B, we assume A has higher market share at the beginning of the simulation.
2.2. Two Competitive Innovations Diffusion Model
1) Model Assumptions For each agent, it could have one of the three statuses at time t:
Sj(t) = 0 means node adopts no innovation.
Sj(t) = 1 means node j adopt innovation A.
Sj(t) = 2 means node j adopt innovation B.
We have the assumptions below in the two competitive innovations model:
• There are two innovations A and B in the network and they are replaceable;
• At the beginning of the simulation, the market share of A is higher than B;
• The status of a node can be 0, 1, or 2. A node can only have one status in a time;
• The nodes can adopt or drop the innovations.
2) The Procedure of Innovation Diffusion The nodes accept or drop the innovation depends on the utility value E. If E is bigger than threshold value L, the node adopts the node. If E is smaller than refuse threshold (R × L), the node drop the node. The judgment function is shown in Table 1.
From the Table 1, we can see: in the diffusion process, when Sj(t – 1) = 0, if EjA > L, then Sj(t) = 1; else Sj(t) = 0. When Sj(t – 1) = 1, if EjA ≥ R × L, Sj(t) = 1; else Sj(t) = 0. The simulation flow chart is shown in Figure 1.
3. Simulation Results
We set market share of A is bigger than B. And the diffusion
 (3)
(3)

Table 1. Decision model.
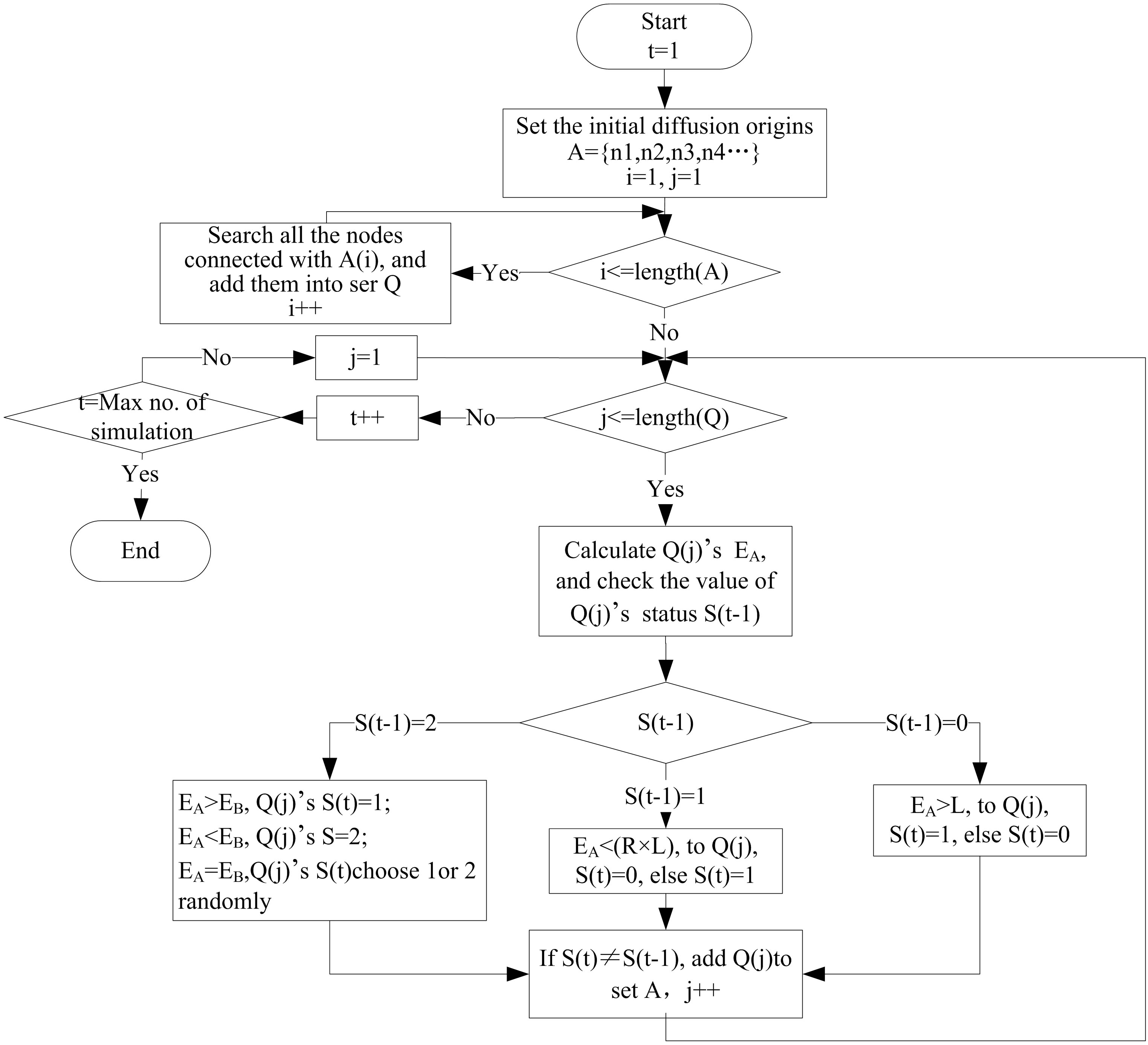
Figure 1. Flow chart of the simulation algorithm.
point of A is 8 and of B is 4. The rest parameters is W1A = 0.3; W1B = 0.3; W2A = 0.7; W2B = 0.7; W3A = 0.1; W3B = 0.1; W4A = 0.2; W4B = 0.2; R = 0.5; L = 0.75.
3.1. The Sensitive Analysis of W1
Then we change the value of W1 to check how W1 influence the diffusion. W1 is the one to influence the “Innovation Perceive”. The bigger the W1, the bigger the “innovation perceive”. We then change W1 from 0.25 to 0.29. The increase step is 0.02. The result is shown in Figure 1.
According to the Figure 2, A’s initial market share is higher than s. So in the early stage of the diffusion, A’s market share is higher than s. In the middle stage of the diffusion, when A is in saturation, B is going on growing. So finally the number of nodes who adopt B is bigger than A’s (Blue line is for A and green dashed is for B). Then we increase W1. When W1 = 0.27, innovation A increased rapidly and exceeded B at last (Red line is for A when purple dashed is for B). Keep increasing A, when W1 = 0.29, A’s and B’s nodes become more. But the extent is less (Black line is for A and light blue dashed is for B). From the result above, we can conclude that at the beginning, the innovation perceive is little. And A is stroke into the “Lock-In” status.
The innovation A is diffused in the clusters. Diffusion didn’t cover all the network. That is why A is in saturation earlier than B. At first the “Innovation Perceive” is small and B’s diffusion points are less than A’s, which made B has less possibility to get into the status “Lock-In” and diffuse to the whole network. But the increase of “Innovation Perceive” produces the difference of the level of two innovations. And according to the analysis above, the increase of W1 can avoid the “Lock-In” status effectively. That is why A’s market share is bigger than s. When W1 = 0.27, there are about 500 nodes adopt A and there are about 300 nodes adopt B. Then we increase W1 again, the number of nodes added for both A and B is less. When W1 = 0.29, the situation is a little better than W1 = 0.27. That is means the effect of the increase of “Innovation Perceive” is decrease while the increase of “Innovation Perceive”. And at that moment, the competition mechanism influences the diffusion more.
3.2. The Sensitive Analysis of W3
First we simulate the totally diffusion. We set the parameter like W1A = 0.3; W1B = 0.3; W2A = 0.7; W2B = 0.7; W3A = 0.1; W3B = 0.1; W4A=0.2; W4B = 0.2; R = 0.5; L = 0.73. Under this condition, the market share of A is 631 while the market share for B is 349. That is because the A’s diffusion points is more than B’s (A’s initial market share is higher than B’s).
Then we adjust the B’s word of mouth W3B, to check how word of mouth influences the diffusion. By the increase of the value of B’s word of mouth continuously, we get the result which is demonstrated in the Figure 3. With the increase of s word of mouth, from 0.1 to 0.7, innovation s market share is upping. We can see how it catch up with A and finally exceed A. The detailed diffusion times and boost step of the value of word of mouth is in Figure 3.
From the Figure 3 we can find that the increase of word of mouth of B has little impact on diffusion. Just decrease some diffusion times. But it has the distinct boost on s market share.
The way to increase the word of mouth in the real world can through the better package, the better service
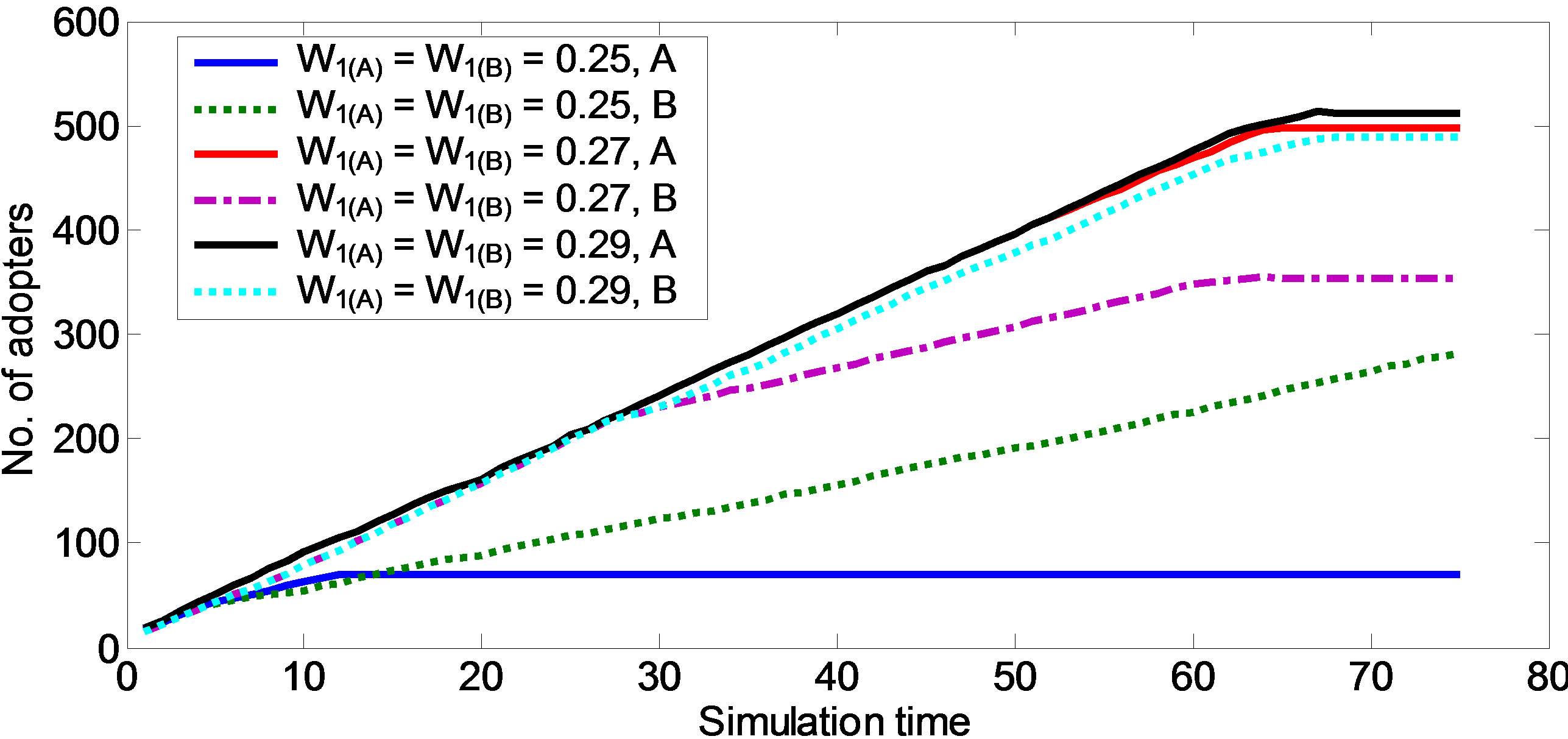
Figure 2. Influence of W1.
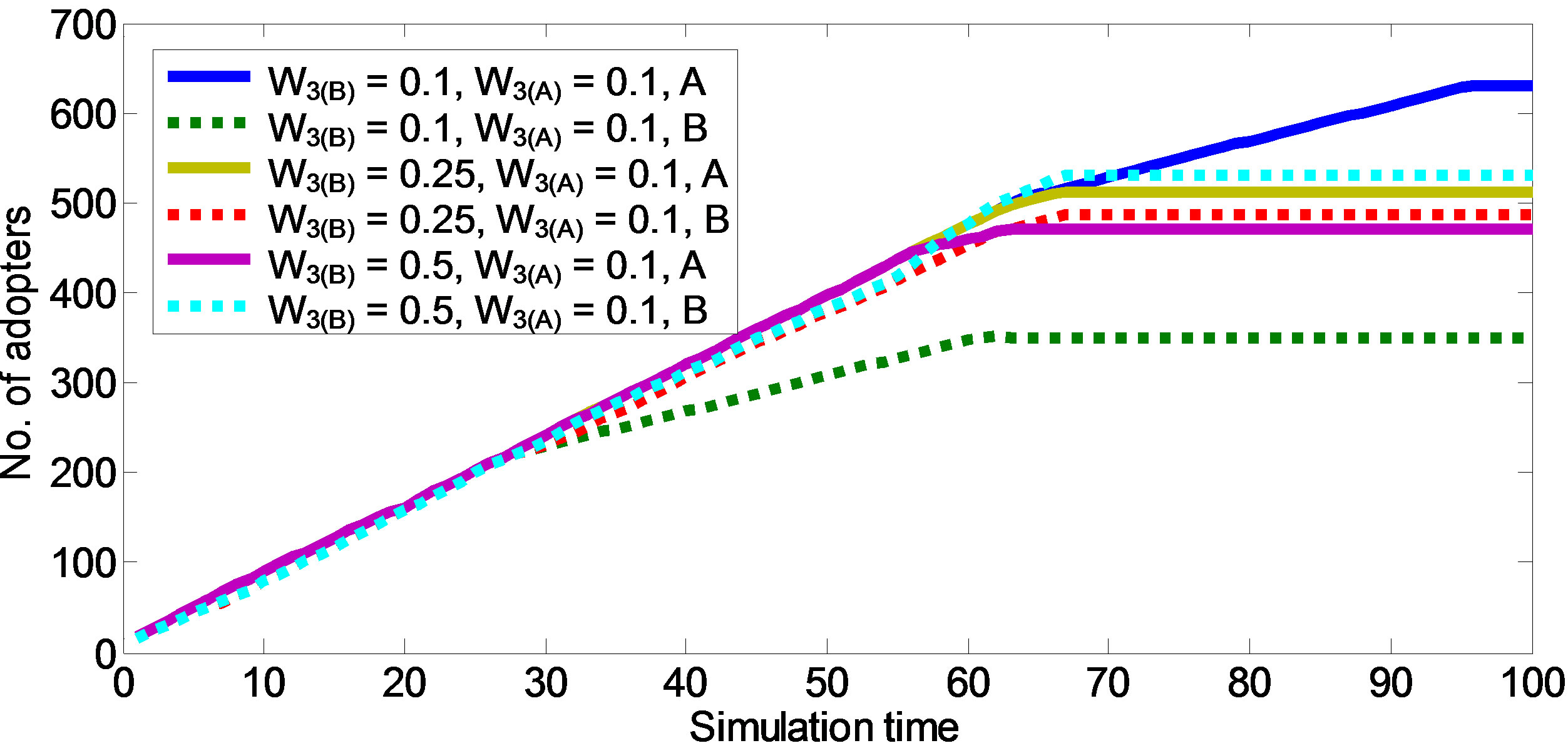
Figure 3. Influence of W3B.
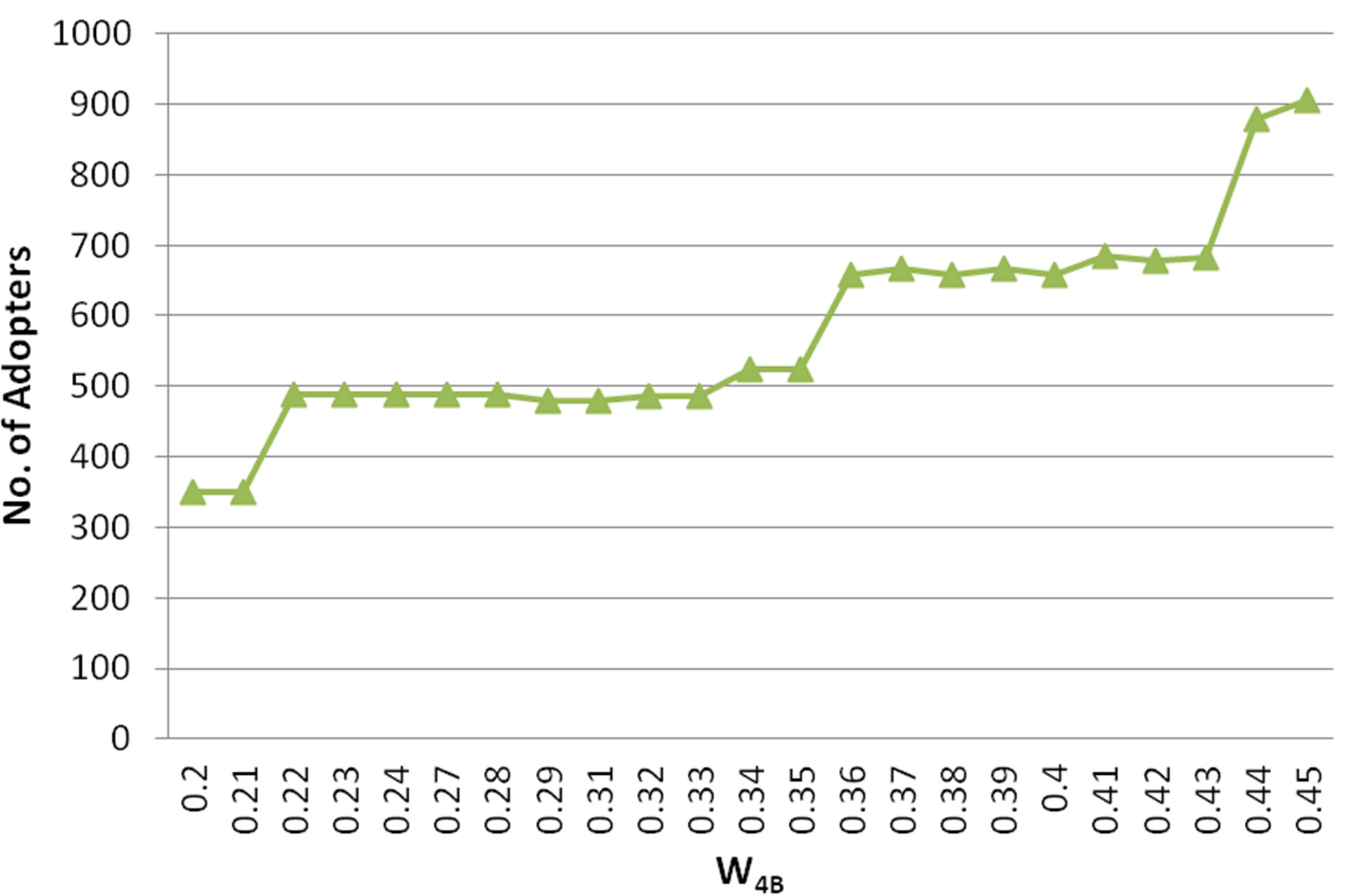
Figure 4. Influence of W4B.
or the customized design to make it. The simulation above is to demonstrate that if one with lower initial market share wants to catch up with the one with higher initial market share, it needs to increase its word of mouth.
3.3. The Sensitive Analysis of W4
Next we will adjust s W4B which is the advertisement parameter to see how it influences the diffusion of innovation B. By the increasing s advertisement continuously, we get the result shown in Figure 4.
From Figure 4 we can find that the increase of advertisement will enlarge s market share. When W4B increases from 0.2 to 0.45, s market share increases from 350 to 900. There are two special characters for the increase of advertisement according the figure above.
4. Conclusions
According to the simulation, we find that the middle stage is the time when to enlarge the market share. The one with higher initial market share is easier to get into the “Lock-In” status, which can be escaped by increasing the “Innovation Perceive”. In the real market, if there are two innovations and one is with higher market share comparing with the other, the government can decrease the market gap by increasing the entrance threshold which can be achieved by launching some policies or publishing some guides. For the one with higher market share, it can increase the nodes’ “Acceptance Trend” which can be achieved by publishing the innovation information to increase its market share and decrease the lower one’s market share.
Actually, the model proposed in this paper is still a simple one, with only one kind of agent. Also, the cost of accepting a new technology or product is ignored. And it will be better if the empirical study will be operated to adjust the parameter of the model.
REFERENCES
- E. M. Rogers and M. Everett, “Diffusion of Innovations,” 4th Edition, The Free Press, New York, 1995.
- L. Riccardo, “Segmentation and Increasing Returns in the Evolutionary Dynamics of Competing Techniques,” Metroeconomica, Vol. 52, No. 2, 2001, p. 2.
- C. Watanabe, “Reiko Kondo: A Substitution Orbit Model of Competitive Innovations,” Technological Forecasting & Social Change, Vol. 71, No. 4, 2004, pp. 365-390. doi:10.1016/S0040-1625(02)00351-7
- B. Zhang, L. Fang and R. B. Zhang, “A Dynamic Diffusion Model of Competitive Multi-Innovations and Its Applacation,” Technology Economics, Vol. 27, No. 9, 2008, pp. 5-9, 19.
- R. Nie, K. M. Qian and D. H. Pan, “The Innovative Technology Diffuse Models and Their Stability Analysis Base on Logistic Equation,” Journal of Industrial Engineering and Engineering Management, Vol. 20, No. 1, 2006, pp. 41-45.
- Y. H. Liu and J. R. Dong, “Innovation Produce and Technology Comparative Diffusion,” Journal of Industrial Technological Economics, Vol. 25, No. 7, 2006, pp. 48-52.
- F. M. Bass, “A New Product Growth Model for Consumer Durables,” Management Science, Vol. 15, No. 5, 1969, pp. 215-227. doi:10.1287/mnsc.15.5.215
- D. J. Watts and S. H. Strogatz, “Collective Dynamics of ‘Small-World’ Networks,” Nature, Vol. 393, No. 6684, 1998, pp. 440-442. doi:10.1038/30918
- D. Maienhofer, “Finding Optimal Targets for Change Agents: A Computer Simulation of Innovation Diffusion,” Computational & Mathematical Organization Theory, Vol. 8, No. 4, 2002, pp. 259-280. doi:10.1023/A:1025464501110
NOTES
*This paper is funded by Natural Science Foundation of Shanghai (09ZR1407300), Natural Science Fund of China (71071055), Social Science Fund of Chinese Ministry of Education (09YJC630069), and National Science Fund for Distinguished Young Scholars (71125002).

