Int'l J. of Communications, Network and System Sciences
Vol.2 No.6(2009), Article ID:699,7 pages DOI:10.4236/ijcns.2009.26061
A Rank-One Fitting Method with Descent Direction for Solving Symmetric Nonlinear Equations*
College of Mathematics and Information Science, Guangxi University, Nanning, Guangxi, China
Email: glyuan@gxu.edu.cn.
Received January 14, 2009; revised March 4, 2009; accepted May 31, 2009
Keywords: Rank-One Update, Global Convergence, Nonlinear Equations, Descent Direction
ABSTRACT
In this paper, a rank-one updated method for solving symmetric nonlinear equations is proposed. This method possesses some features: 1) The updated matrix is positive definite whatever line search technique is used; 2) The search direction is descent for the norm function; 3) The global convergence of the given method is established under reasonable conditions. Numerical results show that the presented method is interesting.
1. Introduction
Consider the following system of nonlinear equations:
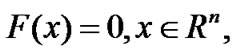 (1)
(1)
where F:Rn→Rn is continuously differentiable and the Jacobian ▽F(x) of F(x) is symmetric for all x∈Rn. Let θ(x) be the norm function defined by
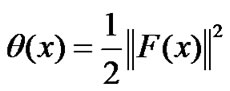
then the nonlinear Equation (1) is equivalent to the following global optimization problem
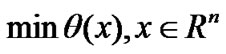 (2)
(2)
The following iterative method is used for solving (1)
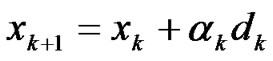 (3)
(3)
where xk is the current iterative point, dk is a search direction, and ak is a positive step-size.
It is well known that there are many methods [1–9] for the unconstrained optimization problems
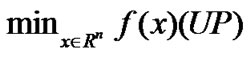 where the BFGS method is one of the most effective quasi-Newton methods [10–17]. These years, lots of modified BFGS methods (see [18–23]) have been proposed for UP. Different from their techniques, Xu [24] presented a rank-one fitting algorithm for UP and the numerical examples are very interesting. Motivated by their idea, we give a new rank-one fitting algorithm for (1) which possesses the global convergence, the method can ensure that the updated matrices are positive definite without carrying out any line search, the search direction is descent for the normal function, and the numerical results is more competitive than those of the BFGS method for the test problem.
where the BFGS method is one of the most effective quasi-Newton methods [10–17]. These years, lots of modified BFGS methods (see [18–23]) have been proposed for UP. Different from their techniques, Xu [24] presented a rank-one fitting algorithm for UP and the numerical examples are very interesting. Motivated by their idea, we give a new rank-one fitting algorithm for (1) which possesses the global convergence, the method can ensure that the updated matrices are positive definite without carrying out any line search, the search direction is descent for the normal function, and the numerical results is more competitive than those of the BFGS method for the test problem.
For nonlinear equations, the global convergence is due to Griewank [25] for Broyden’s rank one method. Fan [1], Yuan [26], Yuan, Lu andWei [27], and Zhang [28] presented the trust region algorithms for nonlinear equations. Zhu [29] gave a family of nonmonotone backtracking inexact quasi-Newton algorithms for solving smooth nonlinear equations. In particular, a GaussNewton-based BFGS method is proposed by Li and Fukushima [30] for solving symmetric nonlinear equations, and the modified methods [31,32] are studied.
The line search rules play an important role for solving the optimization problems. In the following, we briefly review some line search technique to obtain the stepsize ak.
Brown and Saad [33] proposed the following line search method:
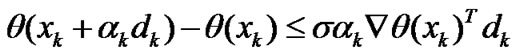 (4)
(4)
where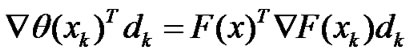 ,
, 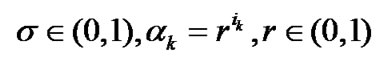 ik is the smallest nonnegative integer i such that (4). Zhu [29] gave the nonmonotone line search technique:
ik is the smallest nonnegative integer i such that (4). Zhu [29] gave the nonmonotone line search technique:

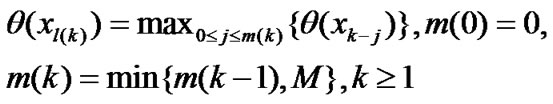
and M is a nonnegative integer. Yuan and Lu [32] presented a new backtracking inexact technique to obtain the stepsize ak:
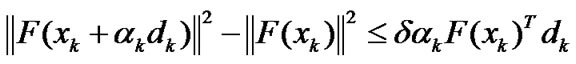 (5)
(5)
where δ∈(0,1) is a constant, and dk is a solution of the system of linear Equation (9). Li and Fukashima [11] give a line search technique to determine a positive step-size ak satisfying
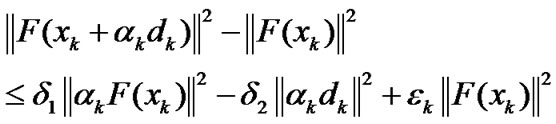 (6)
(6)
where δ1 andδ2 are positive constants, and {εk} is a positive sequence such that
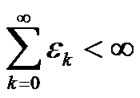 (7)
(7)
The Formula (7) means that {F(xk)} is approximately norm descent when k is sufficiently large. Gu, Li, Qi, and Zhou [14] presented a descent line search technique as follows
 (8)
(8)
whereδ1 andδ2 are positive constants. In this paper, we also use the Formula (8) as line search to find the step-size ak:
The search direction dk: play a main role in line search methods for solving optimization problems too, and dk: is a solution of the system of linear equation
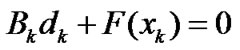 (9)
(9)
where Bk is often generated by BFGS update formula
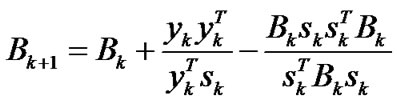 (10)
(10)
where
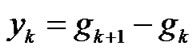 and
and 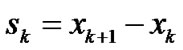 Is there another way to determine the update formula? Accordingly the search direction dk is determined by the way. In this paper, the updated matrix Bk is generated by the following rank-one updated formula
Is there another way to determine the update formula? Accordingly the search direction dk is determined by the way. In this paper, the updated matrix Bk is generated by the following rank-one updated formula
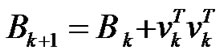 (11)
(11)
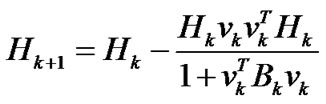 (12)
(12)
where, as k = 0, B0 is the given symmetric positive definite matrix,
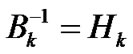 and
and 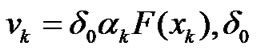
is a positive constant. Then we use the following formula to get the search direction,
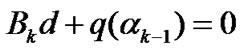 (13)
(13)
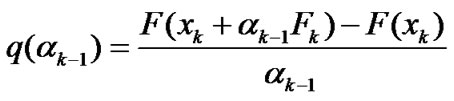 (14)
(14)
Bk follows (11), ak-1 is the steplength used at the previous iteration, and the Equation (14) is inspired by [34]. Throughout the paper, we use these notations: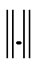 is the Euclidean norm, and F(xk) and F(xk+1) are replaced by Fk and Fk-1, respectively.
is the Euclidean norm, and F(xk) and F(xk+1) are replaced by Fk and Fk-1, respectively.
This paper is organized as follows. In the next section, the algorithm is stated. The global convergence convergence is established in Section 3. The numerical results are reported in Section 4.
2. Algorithm
In this section, we state our new algorithm based on Formulas (3), (8), (11), (12) and (13) for solving (1).
Rank-One Updated Algorithm (ROUA).
Step 0: Choose an initial point x0∈Rn constants
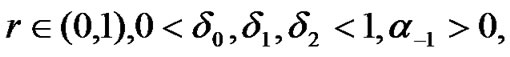
symmetric positive definite matrices B0 and B0-1=H0 . Let: k = 0;
Step 1: If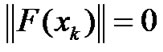 , stop. Otherwise, solving linear Equation (13) to get dk;
, stop. Otherwise, solving linear Equation (13) to get dk;
Step 2: Find ak is the largest number of {1,r,r2,…} such that (8);
Step 3: Let the next iterative point be xk+1= xk+akdk;
Step 4: Update Bk+1 and Hk+1 by the Formulas (11) and (12) respectively;
Step 5: Set k: = k + 1. Go to Step 1.
In this paper, we also give the normal BFGS method for solving (1), the algorithm which has the same conditions to ROUA is stated as follows.
BFGS Algorithm(BFGSA).
In ROUA, the Step 4 is replaced by: Update Bk+1 by the Formula (10).
Remark 1. a) By the Step 0 of ROUA, there should exist constants λ1≥λ0>0 such that
 (15)
(15)
b) By the Step 4 of ROUA, it is easy to deduce that the updated matrices are symmetric
3. Convergence Analysis
This section will establish the global convergence for ROUA. Let Ω be the level set defined by
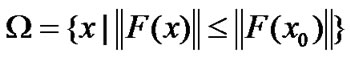 (16)
(16)
In order to establish the global convergence of ROUA, the following assumptions are needed [30,34,35].
Assumption A 1) F is continuously differentiable on an open convex set Ω1 containing Ω. 2) The Jacobian of F is symmetric, bounded and uniformly nonsingular on Ω1, i.e., there exist constants M≥m>0 such that
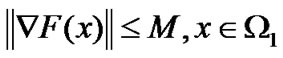 (17)
(17)
and
 (18)
(18)
Remark Assumption A 2) implies that
 (19)
(19)
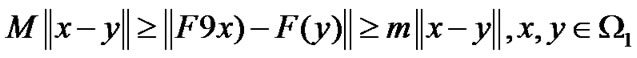 (20)
(20)
In particular, for all x∈Ω1, we have
 (21)
(21)
where x* stand for the unique solution of (1) in Ω1.
Lemma 3.1 Let Assumption A hold. Consider ROUA. Then for any d∈Rn, then there exist constants m0 such that
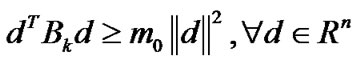 (22)
(22)
i.e., the matrix Bk is positive for all k.
Proof. By ROUA, we know that the initial matrix B0 is symmetric positive, and then we have (15). Using (11), for k≥1, we have
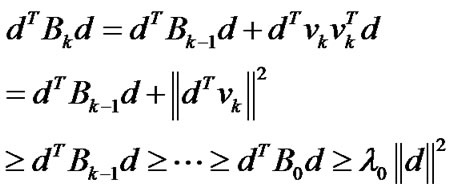 (23)
(23)
Let m0=λ0. Then we get (22). The proof is complete.
Since Bk is positive definite, then dk which is determined by (13) has the unique solution. The following lemma can found in [34], here we also give the process of this proof.
Lemma 3.2 Let Assumption A hold. If xk is not a stationary point of (2), then there exists a constant a'>0 depending on k such that when ak-1∈(0, a'), the unique solution d(ak-1) of (13) such that
 (24)
(24)
Moreover, inequality
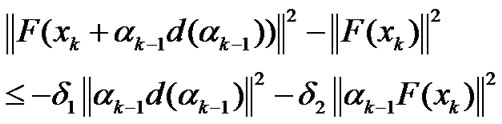 (25)
(25)
Proof. By (14), we can deduce that
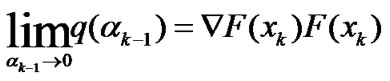 (26)
(26)
From (13), we get
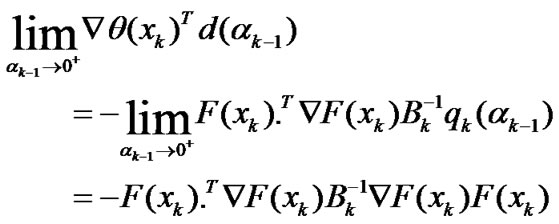 (27)
(27)
Since xk is not a stationary point of (2), we have ▽F(xk)F(xk)≠0. By ▽F(xk) is symmetric and Bk is positive. We obtain (24).

However, the right hand side of (25) is O(ak-1). Thus, inequality (25) holds for all ak-1>0 sufficiently small. The proof is complete.
The above lemma shows that line search technique (8) is reasonable, and the given algorithm is well defined. Lemma 3.2 also shows that the sequence {θ(xk)} is strictly decreasing. By Lemma 3.2, it is not difficult to get the following lemma.
Lemma 3.3 Let {xk} be generated by ROUA. Consider the line search (8). Then {xk}∈Ω moreover,  converges.
converges.
Lemma 3.4 Let Assumption A hold and
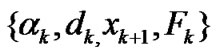
be generated by ROUA. Then we have
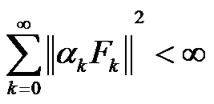 (28)
(28)
and
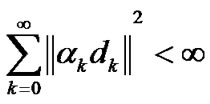 (29)
(29)
Proof. By the line search (8), we get
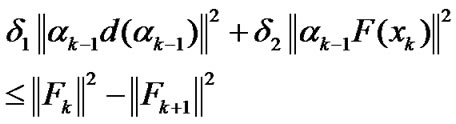 (30)
(30)
Summing these inequalities (30) for k from 0 to ∞ we obtain (28) and (29). Then we complete the proof of this Lemma.
Lemma 3.5 Let Assumption A hold. Consider ROUA. Then 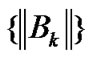 converges, for all k and any d∈Rn then there exist constants m0 and M0 such that
converges, for all k and any d∈Rn then there exist constants m0 and M0 such that
 (31)
(31)
and
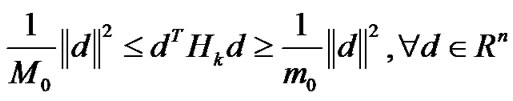 (32)
(32)
which mean that the updated matrices are all positive by ROUA.
Proof. By the updated Formula (11), we have
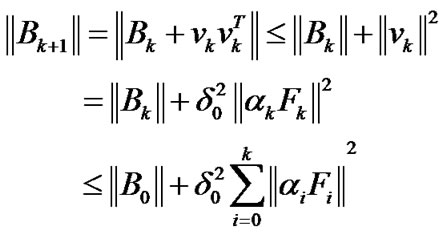 (33)
(33)
By (28), we know that
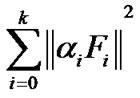
is convergent. Then we can deduce that 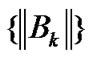 is convergent. So there exists a constant M0 such that
is convergent. So there exists a constant M0 such that
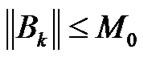 for all k (34)
for all k (34)
Accordingly, we get (28). By (32), (31), and the Remark 1(b), we can deduce that the updated matrices are all symmetric and positive. Consider 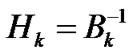 we obtain (32) immediately. So, we complete the lemma.
we obtain (32) immediately. So, we complete the lemma.
By (32), (31), and (34), we have
 (35)
(35)
Now we establish the global convergence theorem of ROUA.
Theorem 3.1 Let Assumption A hold and 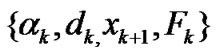 be generated by ROUA. Then the sequence {xk} converges to the unique solution x* of (1) in sense of
be generated by ROUA. Then the sequence {xk} converges to the unique solution x* of (1) in sense of
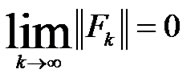 (36)
(36)
Proof. By Lemma 3.3, we know that  converges. By Lemma 3.4, we get
converges. By Lemma 3.4, we get
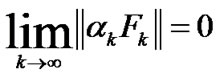 (37)
(37)
then, we have
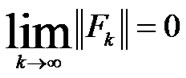 (38)
(38)
or
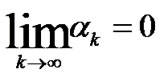 (39)
(39)
Therefore, we only discuss the case of (38). In this case, for all k sufficiently large and
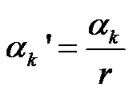
by (8), we obtain
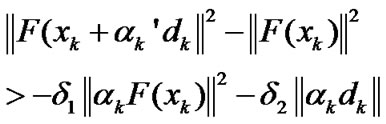 (40)
(40)
By Lemma 3.3, we know that {xk}∈Ω is bounded, considering (35), it is easy to deduce that {qk(ak-1) and {dk} are bounded. Let {xk} and {dk(a)} converge to x* and dx*, respectively. Then we have
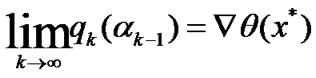 (41)
(41)
Let both sides of (40) be divided by ak' and take limits as k→∞ we obtain
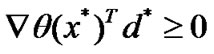 (42)
(42)
By (31) and (13), we have
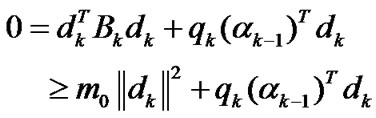 (43)
(43)
As k→∞ taking limits in both of (43) yields
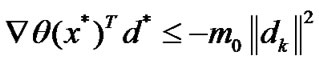
This together with (42) implies d*=0. From (35), we have
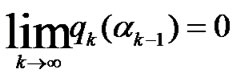
which together with (41), we obtain
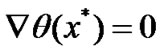 (44)
(44)
By 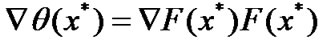 and using
and using 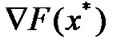 is nonsingular, we have
is nonsingular, we have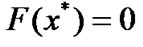 . This implies (36). The proof is complete.
. This implies (36). The proof is complete.
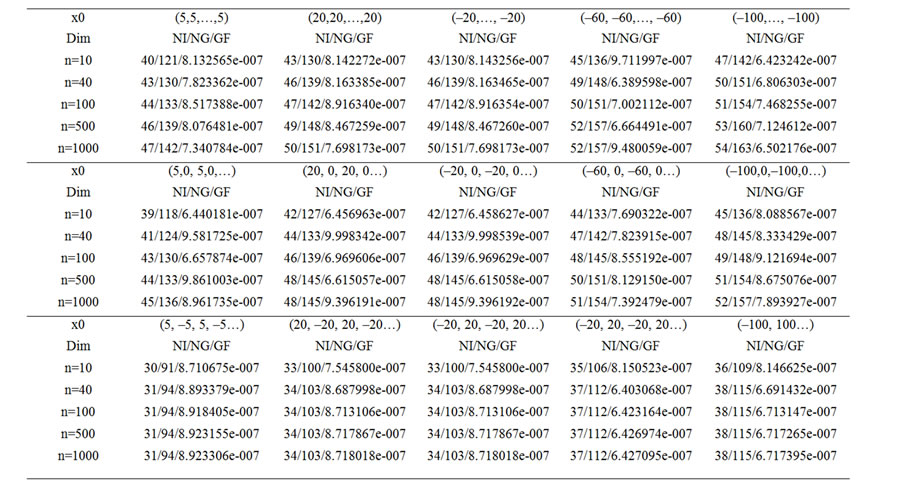
Table 1. Test results for ROUA.
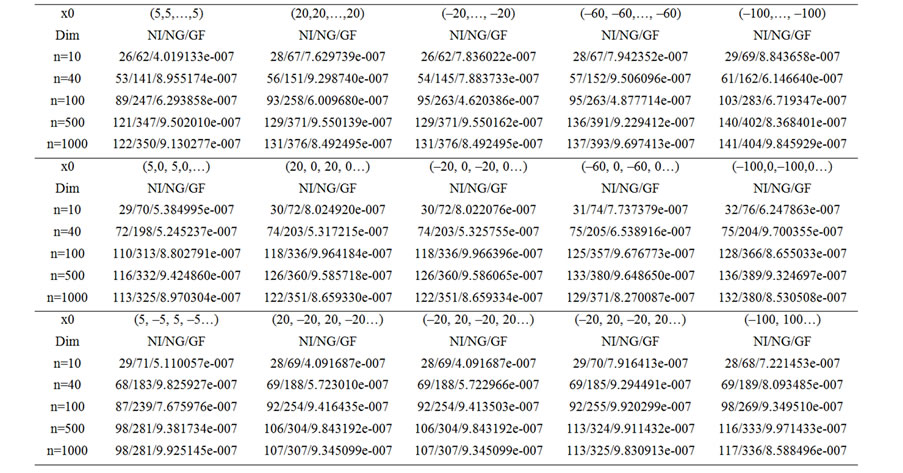
Table 2. Test results for BFGSA.
4. Numerical Results
In this section, we report results of some preliminary numerical experiments with ROUA. Problem. The discretized two-point boundary value problem is similar to the problem in [36]
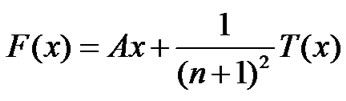
where A is the n×n tridiagonal matrix given by

and
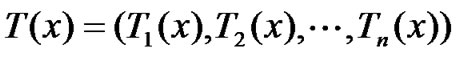
with  In the experimentsthe parameters in ROUA were chosen as
In the experimentsthe parameters in ROUA were chosen as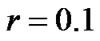 ,
,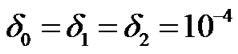 . The program was coded in MATLAB Subsection 6.5.1. We stopped the iteration when the condition
. The program was coded in MATLAB Subsection 6.5.1. We stopped the iteration when the condition 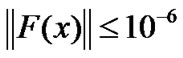 was satisfied.
was satisfied.
The columns of the tables have the following meaning:
Dim: the dimension of the problem.
NI: the total number of iterations.
NG: the number of the function evaluations.
GF: the function norm evaluations.
In the next table, the numerical results are to test ROUA.
In the Table 2, the numerical results are to test BFGSA.
From these two tables, we can see that the numerical results of the two methods are all interesting. The numerical results of the proposed method perform better, and more stationary than the method BFGSA. Moreover, for the method ROUA, the initial points and the dimension do not influence the number of iterations very much. However, for the BFGSA, the number of the iteration will increase quickly with the dimension becoming larger. One thing we like to point out is that δ0 should be chosen in such a way that it is not too large. Overall, from the numerical results, we can see that the ROUA is one of the robust methods for symmetric nonlinear equations.
5. Acknowledgements
We are very grateful to anonymous referees and the editors for their valuable suggestions and comments, which improve our paper greatly.
6. References
[1] R. Fletcher, Practical meethods of optimization, 2nd Edition, John Wiley & Sons, Chichester, 1987.
[2] A. Griewank and L. Toint, “Local convergence analysis for partitioned quasi-Newton updates,” Numerical Mathematics, No. 39, pp. 429–448, 1982.
[3] G. L. Yuan and X. W. Lu, “A new line search method with trust region for unconstrained optimization,” Communications on Applied Nonlinear Analysis, Vol. 15, No. 1, pp. 35–49, 2008.
[4] G. L. Yuan and X. W. Lu, “A modified PRP conjugate gradient method,” Annals of Operations Research, No. 166, pp. 73–90, 2009.
[5] G. L. Yuan, X. W. Lu, and Z. X. Wei, “New two-point step size gradient methods for solving unconstrained optimization problems,” Natural Science Journal of Xiangtan University, Vol. 1, No. 29, pp. 13–15, 2007.
[6] G. L. Yuan, X. W. Lu, and Z. X. Wei, “A conjugate gradient method with descent direction for unconstrained optimization,” Journal of Computational and Applied Mathematics, No. 233, pp. 519–530, 2009.
[7] G. L. Yuan and Z. X. Wei, “New line search methods for unconstrained optimization,” Journal of the Korean Statistical Society, No. 38, pp. 29–39, 2009.
[8] G. L. Yuan and Z. X. Wei, “A rank-one fitting method for unconstrained optimization problems,” Mathematica Applicata, Vol. 1, No. 22, pp. 118–122, 2009.
[9] G. L. Yuan and Z. X. Wei, “A nonmonotone line search method for regression analysis,” Journal of Service Science and Management, Vol. 1, No. 2, pp. 36–42, 2009.
[10] R. Byrd and J. Nocedal, “A tool for the analysis of quasi-Newton methods with application to unconstrained minimization,” SIAM Journal on Numerical Analysis, No. 26, pp. 727–739, 1989.
[11] R. Byrd, J. Nocedal, and Y. Yuan, “Global convergence of a class of quasi-Newton methods on convex problems,” SIAM Journal on Numerical Analysis, No. 24, pp. 1171–1189, 1987.
[12] Y. Dai, “Convergence properties of the BFGS algorithm,” SIAM Journal on Optimization, No. 13, pp. 693– 701, 2003.
[13] J. E. Dennis and J. J. More, “A characterization of superlinear convergence and its application to quasi-Newtion methods,” Mathematics of Computation, No. 28, pp. 549–560, 1974.
[14] J. E. Dennis and R. B. Schnabel, “Numerical methods for unconstrained optimization and nonlinear equations,” Pretice-Hall, Inc., Englewood Cliffs, NJ, 1983.
[15] M. J. D. Powell, “A new algorithm for unconstrained optimation,” in Nonlinear Programming, J. B. Rosen, O. L. Mangasarian and K. Ritter, eds. Academic Press, New York, 1970.
[16] Y. Yuan and W. Sun, Theory and Methods of Optimization, Science Press of China, 1999.
[17] G. L. Yuan and Z. X. Wei, “The superlinear convergence analysis of a nonmonotone BFGS algorithm on convex,” Objective Functions, Acta Mathematica Sinica, English Series, Vol. 24, No. 1, pp. 35–42, 2008.
[18] D. Li and M. Fukushima, “A modified BFGS method and its global convergence in nonconvex minimization,” Journal of Computational and Applied Mathematics, No. 129, pp. 15–35, 2001.
[19] D. Li and M. Fukushima, “On the global convergence of the BFGS methods for on convex unconstrained optimization problems,” SIAM Journal on Optimization, No. 11, pp. 1054–1064, 2001.
[20] Z. Wei, G. Li, and L. Qi, “New quasi-Newton methods for unconstrained optimization problems,” Applied Mathematics and Computation, No. 175, pp. 1156–1188, 2006.
[21] Z. Wei, G. Yu, G. Yuan, and Z. Lian, “The superlinear convergence of a modified BFGS-type method for unconstrained optimization,” Computational Optimization and Applications, No. 29, pp. 315–332, 2004.
[22] G. L. Yuan and Z. X. Wei, “Convergence analysis of a modified BFGS method on convex minimizations,” Computational Optimization and Applications, doi: 10.1007/ s10 589–008–9219–0.
[23] J. Z. Zhang, N. Y. Deng, and L. H. Chen, “New quasiNewton equation and related methods for unconstrained optimization,” Journal of Optimization Theory and Applications, No. 102, pp. 147–167, 1999.
[24] Y. Xu and C. Liu, “A rank-one fitting algorithm for unconstrained optimization problems,” Applied Mathematics and Letters, No. 17, pp. 1061–1067, 2004.
[25] A. Griewank, “The ‘global’ convergence of Broyden-like methods with a suitable line search,” Journal of the Australian Mathematical Society, Series B., No. 28, pp. 75– 92, 1986.
[26] Y. Yuan, “Trust region algorithm for nonlinear equations, information,” No. 1, pp. 7–21, 1998.
[27] G. L. Yuan, X. W. Lu, and Z. X. Wei, “BFGS trust-region method for symmetric nonlinear equations,” Journal of Computational and Applied Mathematics, No. 230, pp. 44–58, 2009.
[28] J. Zhang and Y. Wang, “A new trust region method for nonlinear equations,” Mathematical Methods of Operations Research, No. 58, pp. 283–298, 2003.
[29] D. Zhu, “Nonmonotone backtracking inexact quasi-Newton algorithms for solving smooth nonlinear equations,” Applied Mathematics and Computation, No. 161, pp. 875– 895, 2005.
[30] D. Li and M. Fukushima, “A global and superlinear convergent Gauss-Newton-based BFGS method for symmetric nonlinear equations,” SIAM Journal on Numerical Analysis, No. 37, pp. 152–172, 1999.
[31] G. Yuan and X. Li, “An approximate Gauss-Newtonbased BFGS method with descent directions for solving symmetric nonlinear equations,” OR Transactions, Vol. 8, No. 4, pp. 10–26, 2004.
[32] G. L. Yuan and X. W. Lu, “A new backtracking inexact BFGS method for symmetric nonlinear equations,” Computer and Mathematics with Application, No. 55, pp. 116–129, 2008.
[33] P. N. Brown and Y. Saad, “Convergence theory of nonlinear Newton-Kryloy algorithms,” SIAM Journal on Optimization, No. 4, pp. 297–330, 1994.
[34] G. Gu, D. Li, L. Qi, and S. Zhou, “Descent directions of quasi-Newton methods for symmetric nonlinear equations,” SIAM Journal on Numerical Analysis, Vol. 5, No. 40, pp. 1763–1774, 2002.
[35] G. Yuan, “Modified nonlinear conjugate gradient methods with sufficient descent property for large-scale optimization problems,” Optimization Letters, No. 3, pp. 11– 21, 2009.
[36] J. J. More, B. S. Garow, and K. E. Hillstrome, “Testing unconstrained optimization software,” ACM Transactions on Mathematical Software, No. 7, pp. 17–41, 1981.
NOTES
*National Natural Science Foundation of China (10761001) and the Scientific Research Foundation of Guangxi University (Grant No. X081082).

