Journal of Water Resource and Protection
Vol.5 No.11(2013), Article ID:40304,7 pages DOI:10.4236/jwarp.2013.511116
Regional Drought Severity Assessment at a Basin Scale in the Limpopo Drainage System
1Department of Geology, University of Botswana, Gaborone, Botswana
2WaterNet, University of Zimbabwe, Harare, Zimbabwe
Email: alemaw@mopipi.ub.bw, bfalemaw@gmail.com
Copyright © 2013 Berhanu F. Alemaw et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 21, 2013; revised March 24, 2013; accepted April 22, 2013
Keywords: Drought; Standardized Precipitation Index; Drought Severity; Drought Severity-Area-Frequency (SAF) Curves; Limpopo Basin
ABSTRACT
A spatial analysis of drought characteristics in the Limpopo basin is undertaken to evaluate its regional implications to water management challenges. In this study, drought duration, frequency and severity are investigated. In addition drought Severity-Area-Frequency (SAF) curves were constructed. The entire Limpopo River Basin is subdivided into four homogeneous regions based on topographic and climate variations in the basin, which was constructed with the K-Means Clustering algorithm. Using the medium range time series of the Standardized Precipitation Index (SPI) as an indicator of drought for each homogeneous region, monthly and annual SAF curves and maps of probability of drought occurrence were produced. The results indicated localized severe droughts in higher frequencies compared to moderate to severe low frequency droughts spread over wider areas in the basin. The approach can be used to develop improved drought indicators to assess the relationship between drought hazard and vulnerability and to enhance the performance of methods currently used for drought forecasting. In general, this preliminary investigation reveals that the western part of the basin will face a higher risk of drought when compared to other regions of the Limpopo Basin in terms of the medium-term drought patterns. The Limpopo Basin is water stressed and livelihood challenges remain high, thus impacts of droughts and related resilience options should be taken into account in the formulation of regional sustainable water resources development strategies.
1. Introduction
Droughts are common phenomena in the Limpopo River basin. In essence, droughts are long-term hydro-meteorological events affecting vast regions and causing significant non-structural damages. Droughts are some of the costliest natural disaster in the world and affect more people than floods, due to wider spatial effect and are analyzed in water resource planning and management studies. Main drought characteristics include the onset, termination time, severity and frequency [1-4]. Drought is a slowly-developing phenomenon that affects human life in different parts of the world. Both flooding and droughts have caused major environmental, social and economic problems in the basin.
Numerous drought indices have been proposed to quantify droughts. The most commonly used meteorological drought indices provided by [5] are the Palmer Drought Severity Index (PDSI) and the standardized precipitation index (SPI). The Palmer Drought Severity Index (PDSI) has been widely used to study aridity changes in modern and past climates, and different variates of DPSI are developed over years. The SPI quantifies the precipitation deficit for multiple time scales and reflects the impact of droughts on the availability of different types of water resources. Wetter and drier climates can be represented in the same way by the SPI, because it is a normalized index [1-3].
The properties of regional droughts can be studied through regional drought characteristics like the area covered by drought and total precipitation deficit over the drought area. A method to estimate Severity-Area-Frequency (SAF) curves has been proposed in this study to estimate the return periods of annual regional droughts and their relative severity. A combination of clustering, theory of runs and spatially-enabled stochastic modeling approaches were applied to estimate regional drought, its severity and areal distribution.
The approach illustrated in this manuscript can be used to develop and assist sub-regional and local drought mitigation and adaptation planning processes. Long-term planning and adaptive capacity for local, institutional and government actions can widely rely on the degree and extent of local drought severity and plan long lasting measures, which require commitment by national/transnational authorities. This will be an important policy option for African governments. It will result in a policy shift away from drought response actions that can be filled by several actors and NGOs. These actions are short-lived actions in the form of provision of emergency services and public assistance during or immediately after a disaster to save lives, reduce health impacts, ensure public safety and meet the basic subsistence needs of the affected people by droughts in a region.
2. Study Area and Data
The Limpopo River Basin which falls between 25˚'E - 35˚'E and 19˚S - 27˚S is one of the largest river basins in Southern Africa with an average rainfall of 530 mm per annum across the region. It is home to 14 million inhabitants in the four riparian countries bordering the basin. The Limpopo River Basin drainage area is 413,000 km² in extent and drains four riparian countries: Botswana, Zimbabwe, South Africa and Mozambique.
Precipitation data with monthly time scales of 94 stations within the region were collected. Most of the records for the stations spans from 1950 to early 2010 s which is adequate for drought-related study. The FAO CLIMWAT database was used to extract median precipitation data for stations where no national data were available for the study, mainly from Zimbabwe and South Africa Figure 1.
3. Methodology
3.1. Regionalization of Drought
The determination of homogenous drought regions was undertaken through clustering. The Fuzzy C-Means (FCM) clustering was employed for this purpose. The FCM algorithm is a modification of the K-means algorithm and minimizes intra-cluster variance [6] to include grouping of sites using the clustering algorithm. Factors that affect annual rainfall and seasonal variability considered in the study and used for clustering are: elevation, longitude, latitude and median monthly rainfall.
The algorithm assumes that the attributes are from a vector space and is targeted to achieve a minimized total intra-cluster variance function, Dv is given as [7,8]:
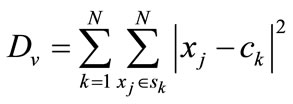 (1)
(1)
where ck is the centroid point of all the points in cluster k; N the total number of clusters; Sk the set of points in the kth cluster; xj the standardized vector for site j.

Figure 1. Meteorological stations used in the study and homogeneous regions of the Limpopo River Basin.
The FCM algorithm is initiated with an initial set of k groups and then it calculates the centroid point of each set. The next step is to construct a new partition by associating each point with the closest centroid. The centroids are recalculated for the new clusters and the algorithm is repeated by alternate application of these two steps until convergence [8] is achieved. As for K-means, this algorithm minimizes intra-cluster variance and this is obtained when the points no longer switch clusters. In contrast to the K-means algorithm, which assigns each site to only one cluster, partial membership is permitted in FCM. This entails that each point has a degree of membership in each of the clusters. Thus points on the edge of a cluster may be in that cluster to a lesser degree than points in the centre of a cluster. The degree of belonging of site i in the kth cluster is equal to the inverse of the distance of site i to the centroid of cluster as defined in [9]:
 (2)
(2)
where bk(i) is the degree that the site i belongs to the kth cluster, d(ck,i)the distance of site i to the centroid of cluster k. Each station is assigned to the cluster with which it has the highest degree of membership. The coefficients are normalized to ensure that the sum of membership of one site of interest to all different clusters is unity or one [6], that is
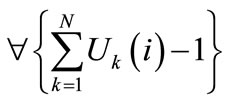 (3)
(3)
where Uk(i) is the normalized coefficient of site I in the kth cluster.
3.2. Drought Severity and Duration
The two important properties of drought namely drought duration and drought severity are analyzed for each drought event. The SPI was used to characterize drought. In this study, the theory of runs [10] was adopted to determine properties of droughts. Based on the classification of drought, the truncation level was maintained as –0.99 in the runs analysis. A hydrologic drought event is considered as an event during which SPI is continuously below the truncation level.
Drought duration is the period of time when SPI is continuously below the truncation level and drought severity is the cumulative deficit below the truncation level for the duration of a drought event. Drought categories were set from calculated standardized precipitation index (SPI) based on the criteria shown in Table 1.
3.3. Construction of SAF Curves
The standardized precipitation index (SPI) was considered as a drought variable. As droughts corresponding to
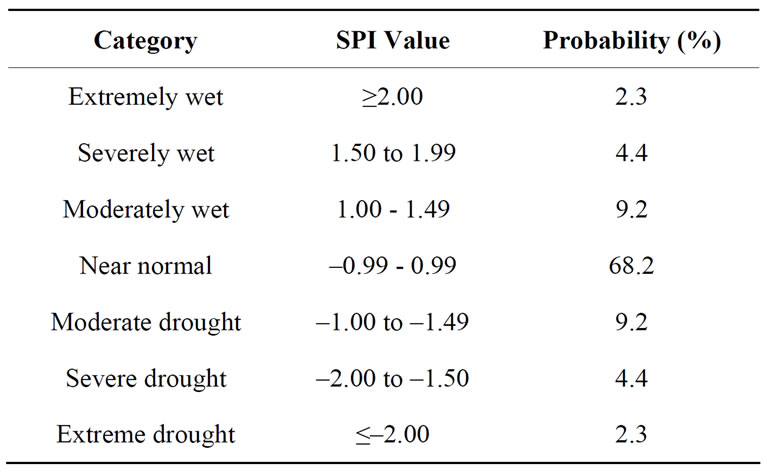
Table 1. SPI-based drought categories.
the short-, mediumand long-term periods are of great importance for different water resource management, then 3, 6, 9 and 12 month units are selected for the time scale of SPI to construct the Severity-Area-Frequency curves for each homogeneous region for this study.
In previous attempts, spatial interpolation of historical time series precipitation data was used to derive SPI and to construct SAF curves. GIS and other multi-temporal spatial interpolation techniques such as Inverse Distance Weighting (IDW) approach were used in several studies (e.g. [1,7]).
The thrust of this study is that the frequency modeling of drought frequency was used to derive spatial distribution of SPI. By avoiding data intensive, multi-temporal interpolation of all the monthly time series and the corresponding SPI, a robust solution was achieved. Spatial interpolation of the few parameters of the frequency models that control the precipitation over the basin and the consequential drought corresponding to the short-, mediumand long-term periods of 3, 6, 9 and 12 months was applied. For the respective periods, the hydrological annual values of drought severity are used for frequency analysis in this study. These severity values were fitted to Lognormal (LN), General Extreme Value (GEV), General Pareto (GP), Exponential (EXP) and 2-Parameter Gamma (G2) probability distributions.
The most important contribution of this study was to determine the SAF curves using a parsimonious modeling approach of relying on few model parameters of a robust frequency model to model drought frequency and construct the SAF curves.
4. Results and Discussions
4.1. Homogenous Regions in the Limpopo Basin
There was a marked variability of the monthly rainfall for the various stations used in the study. As the annual precipitation mode is different in heterogeneous regions, homogenous regions are formed by identifying FCM clusters in the space of site characteristics of the median of month precipitation in a year. Only a few stations were initially classified into regions which are geographically far away and were subject to further scrutiny to associate them to the respective nearby regions. The Limpopo River basin is divided into 4 homogenous regions (Tables 2 and 3).
The homogenous regions were formed by identifying FCM clusters and containing the stations (Figure 1) shown in Table 2.
4.2. SPI and SAF Curves
Time series of SPI corresponding to the time series events in all 94 stations was calculated and then the drought properties were extracted to derive SAF curves. Droughts corresponding to the short-, mediumand longterm are of great importance for different water resource management strategies. Once this was completed the drought Severity-Area-Frequency curves for each homogeneous region were constructed at a 3, 6 and 9 month time scale. All of the distributions have passed the Kolmogorov-Smirnov (K-S) test at the 90% confidence level for the homogeneous regions.
The predictive ability test results of the four frequency models in each region were determined and the 2-Parameter Gamma distribution has resulted in comparatively high accuracy in model predictions of drought severity in all regions, and this model was adopted for further drought spell and severity analysis in the basin.
The quantile estimates were in good agreement with the observed SPI in terms of lower standard of error (SE)
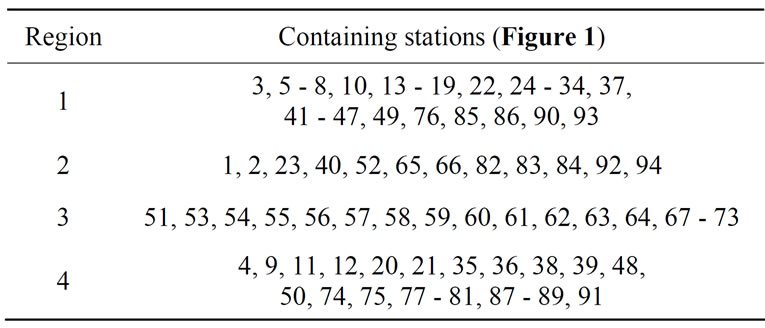
Table 2. Homogeneous regions identified and containing stations.
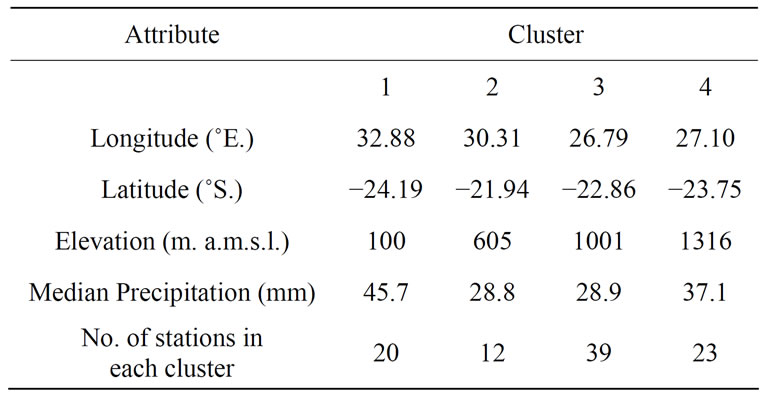
Table 3. Details of final cluster centers and number of cases in each cluster.
for the various return periods. For instance, a comparison among the 4 probability distributions in terms of quantiles of drought severity (QT) and return periods for a station at Xai Xai in Region 1 is shown in Table 4, where for station at Molepolole in Region 3 is shown in Table 5. A summary of quantile estimates (QT) and their standard error (SE) of 3-month (OND) drought severity in Region 3 (on arbitrarily selected 10 stations) for return periods of 2, 5, 10, 25, 50 and 100 years is shown in Table 6. Also estimates for two severe drought years 1986- 87 and 1994-95 in the region are presented here as an illustration.
4.3. Drought Characteristics
The quantile estimates were in good agreement with the observed SPI in terms of lower standard of error (SE) for the various return periods. Figure 2 shows a comparison between observed and simulated DSI, based on 2-parameter Gamma frequency model of fitted DSI 12 at two stations in Regions 1 and 3, respectively, in the Limpopo basin.

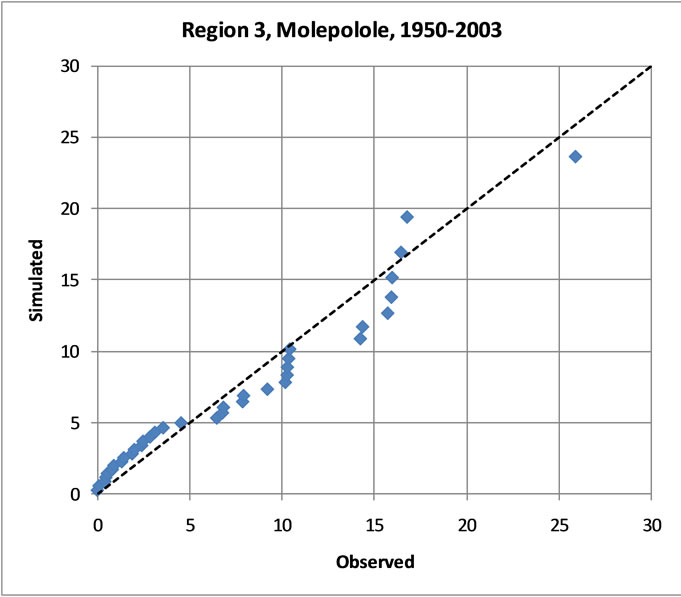
Figure 2. Comparison between observed and Gamma-simulated DSI at 2 stations in the Limpopo basin.
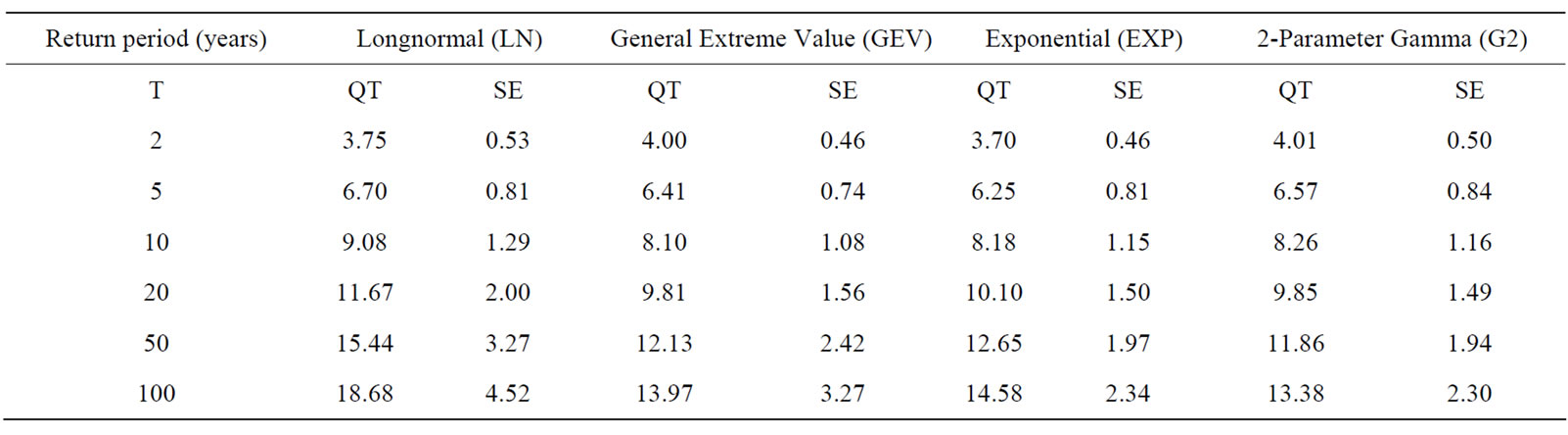
Table 4. Quantile estimates and their standard error of 3-month (OND) drought severity at Xai Xai station (Region 1).
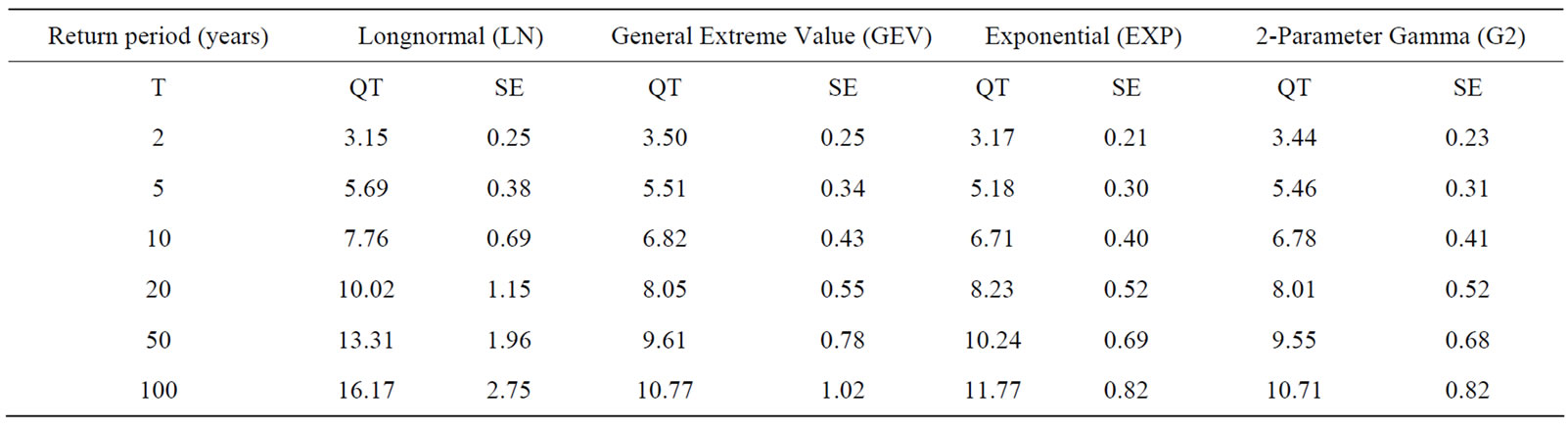
Table 5. Quantile estimates and their standard error of 3-month (OND) drought severity at Molepolole station (Region 3).
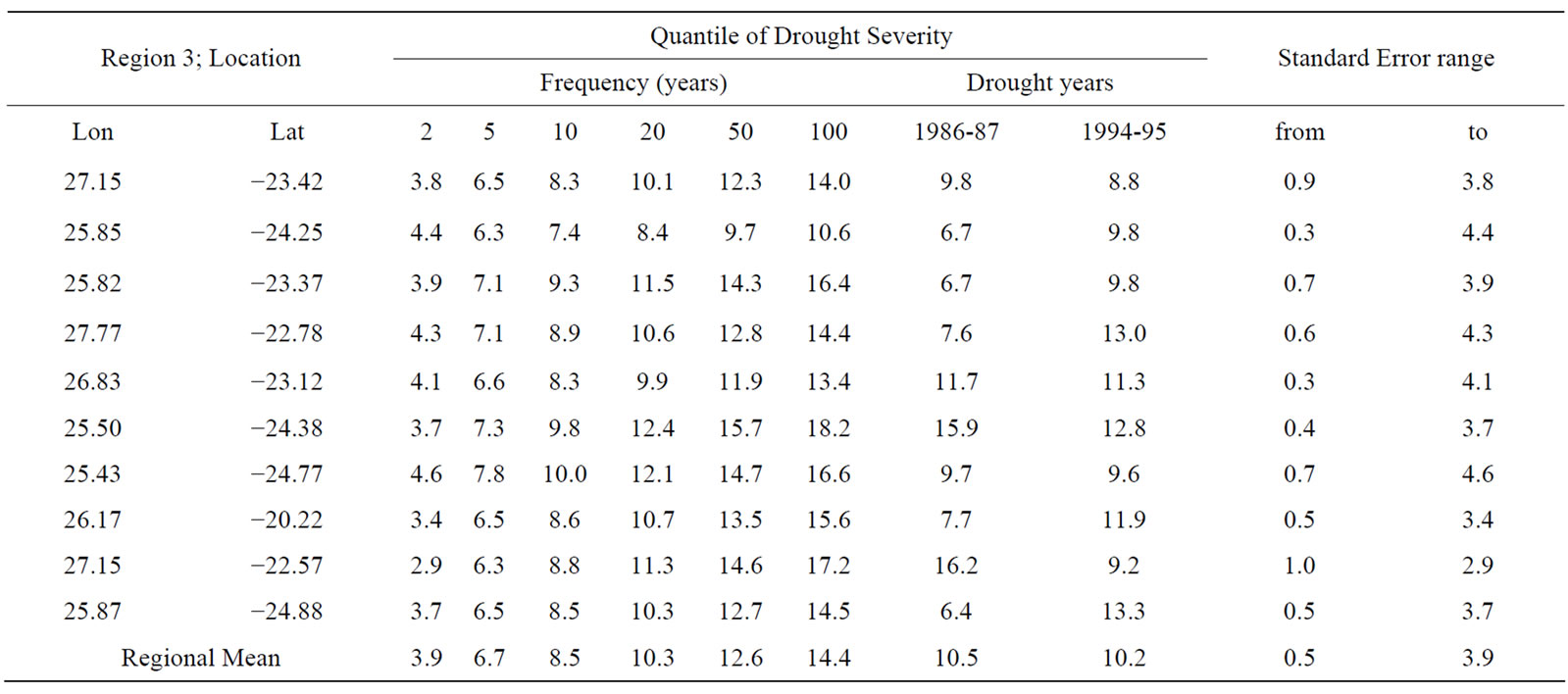
Table 6. Quantile estimates and their standard error of 3-month (OND) drought severity at 10 selected stations in Region 3 for return periods of 2, 5, 10, 25, 50 and 100 years. Also estimates for two severe drought years are presented.
Severity-Area-Frequency curves for each homogeneous region are illustrated. Figure 3 illustrates the drought Severity-Area-Frequency curves of SPI 6 for Region 3 with the two most severe drought years of 1986-87 and 1994-95. In the long-term, recurrence intervals of the droughts are 13 and 12.5 years over Region 3. Mean while, when compared to the Severity-Area-Frequency curves for each homogeneous region, it can be shown that, for the medium-term drought, the drought severity in Region 2 is higher than that in other regions with the same return period in the same area extent; while drought severity for droughts in Region 1 is relatively lower. For all the regions, the Severity-Area-Frequency curves for 3 and 9 month SPIs for each homogeneous region are illustrated. The regional distribution in terms of the mean of the regional drought severity is illustrated in Figure 4.
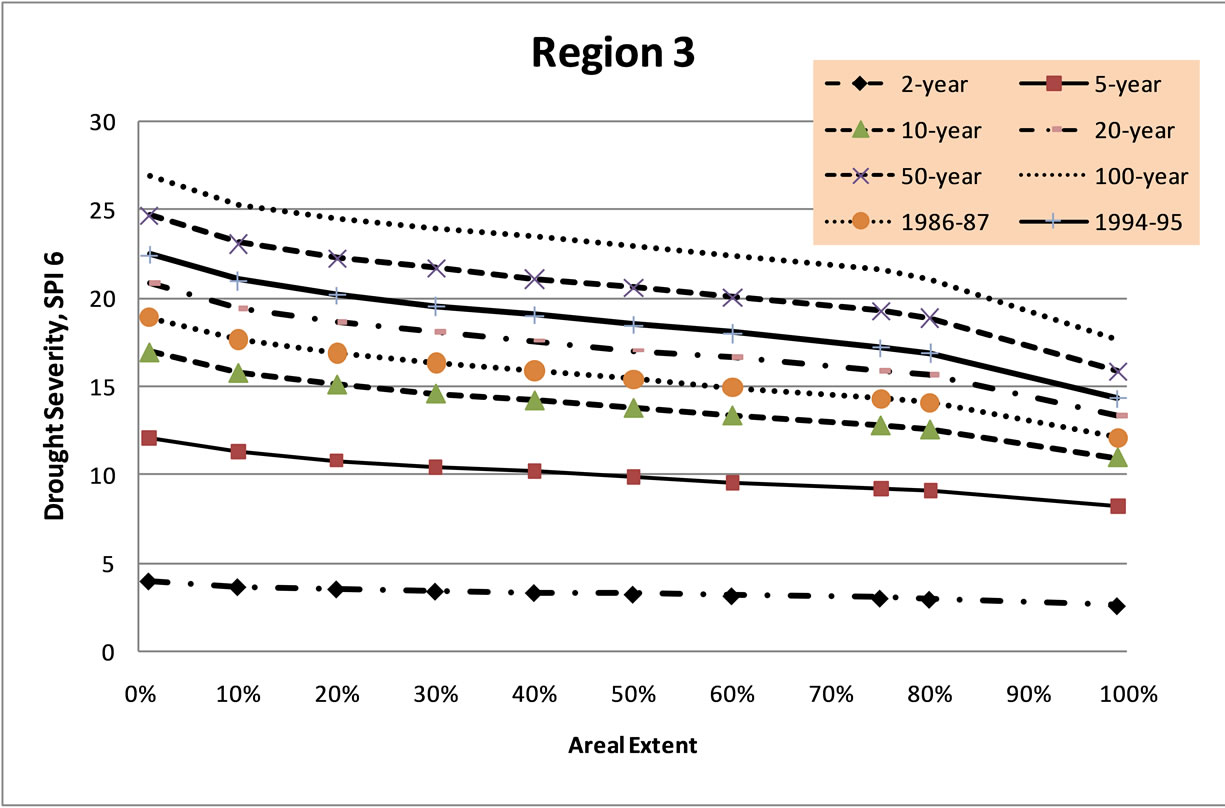
Figure 3. SAF curves of SPI 6 for Region 3 of the Limpopo River Basin.
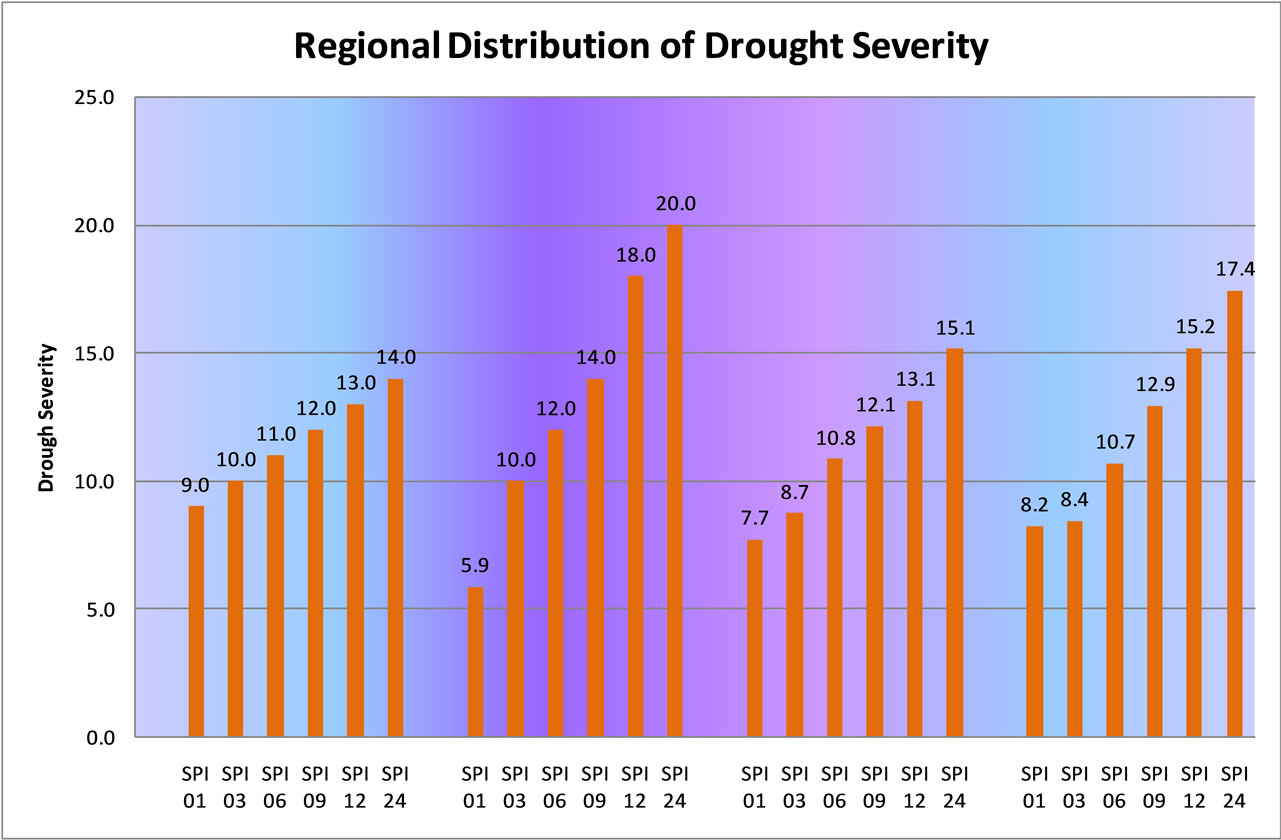
Figure 4. Aggregated mean regional distribution of drought severity computed for different aggregation time scales.
As illustrated, the droughts corresponding to the short-, mediumand long-term periods are of great importance for devising different water resource management strategies in the different regions. In this case, the SeverityArea-Frequency analysis for each homogeneous region corresponding to the short-, mediumand long-term drought shows that when there occurs a severe drought, the drought events may have impacts on the entire Limpopo River Basin.
5. Acknowledgements
The authors through WATERnet acknowledge the DEWFORA project (Improved Drought Early Warning and FORecasting to strengthen preparedness and adaptation to droughts in Africa), a collaborative Project funded under the EU Seventh Framework Programme (EU-FP- 7).
REFERENCES
- A. Loukas and L. Vasiliades, “Probabilistic Analysis of Drought Spatiotemporal Characteristics in Thessaly Region, Greece,” Natural Hazards and Earth Systems Science, Vol. 4, 2004, pp. 719-731. http://dx.doi.org/10.5194/nhess-4-719-2004
- American Meteorological Society, “Statement on Meteorological Drought,” Bulletin of the American Meteorological Society, Vol. 85, 2004, pp. 771-773.
- D. A. Wilhite and M. H. Glantz, “Understanding the Drought Phenomenon: The Role of Definitions,” Water International, Vol. 10, 1985, pp. 111-120. http://dx.doi.org/10.1080/02508068508686328
- J. A. Dracup, K. S. Lee and E. G. Paulson Jr., “On the Definition of Droughts,” Water Resources Research, Vol. 16, 1982, pp. 297-302. http://dx.doi.org/10.1029/WR016i002p00297
- W. C. Palmer, “Meteorological Drought,” Weather Bureau Research Paper, Vol. 45, US Weather Bureau, Washington DC, 1965, pp. 1-58.
- M. T. Ayvaz, H. Karahan and M. M. Aral, “Aquifer Parameter and Zone Structure Estimation Using Kernel-Based Fuzzy c-Means Clustering and Genetic Algorithm,” Journal of Hydrology, Vol. 343, 2007, pp. 240-253. http://dx.doi.org/10.1016/j.jhydrol.2007.06.018
- Q. Zhang, C.-Y. Xu, M. Gemmer, Y. D. Chen and C. Liu, “Changing Properties of Precipitation Concentration in the Pearl River Basin, China,” Stochastic Environmental Research and Risk Assessment, Vol. 23, 2009, pp. 377- 385. http://dx.doi.org/10.1007/s00477-008-0225-7
- S. Sadri and D. H. Burn, “A Fuzzy C-Means Approach for Regionalization Using a Bivariate Homogeneity and Discordancy Approach,” Journal of Hydrology, Vol. 401, 2011, pp. 231-239. http://dx.doi.org/10.1016/j.jhydrol.2011.02.027
- Q. Zhang, M. Xiao and X. Chen, “Regional Evaluations of the Meteorological Drought Characteristics across the Pearl River Basin, China,” American Journal of Climate Change, Vol. 1, 2012, pp. 48-55. ‘http://dx.doi.org/10.4236/ajcc.2012.11005
- V. M. Yevjevich, “An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts,” Hydrological Papers, Vol. 23, Colorado State University Fort, Collins, 1967. http://dx.doi.org/10.1016/j.jhydrol.2009.11.013

