Journal of Biomedical Science and Engineering
Vol.7 No.8(2014), Article
ID:47354,10
pages
DOI:10.4236/jbise.2014.78057
The “Overlapping Equilibria” Effect in the Processes of the Electrolytic Dissociation of Weak Multibasic Organic Acids
Elene Kvaratskhelia, Ramaz Kvaratskhelia, Rusudan Kurtanidze
R. Agladze Institute of Inorganic Chemistry and Electrochemistry, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
Email: elicko@mail.ru, ekvarats@yahoo.com, rkvaratskhelia@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 30 May 2014; accepted 14 June 2014
ABSTRACT
The “overlapping equilibria” effect observed in the processes of electrolytic dissociation of many weak multibasic organic acids determines the character of these processes. In this communication, the degree of “overlapping equilibria” in case of weak dibasic organic acids is quantitatively characterized by the values of “partial” degree of dissociation for second step and ratio of the concentrations of dianion and monoanion. It has been shown that these dissociation parameters are directly connected with the values of the second dissociation constant. It has been also shown that the contribution of third dissociation step in the “overlapping equilibria” effect is especially appreciable in case of penta and hexabasic weak organic acids causing the double “overlapping” phenomenon.
Keywords:Dissociation Constant, Dissociation Degree, “Overlapping Equilibria” Effect, Weak Organic Acids

1. Introduction
Organic acids and specifically weak multibasic organic acids play the great role in the existence of living organisms and in everyday life of humankind. Many multibasic organic acids are widely used in medicine, pharmacology, organic synthesis, food and cosmetic industry, analytical chemistry and many other branches. Oxaloacetic, citric, isocitric, cis-aconitic, oxalosuccinic, α-ketoglutaric, succinic, L-malic and fumaric acids participate in the complex fermentative process (the cycle of tricarboxylic acids or Krebs cycle); with the aid of this process in vital organisms, the oxidation of the main intermediate products of the cleavage of carbohydrates, fats and proteins is near completion.
The wide use of above-mentioned acids in many branches causes a great interest to their chemical behavior because their ability for reactions in various areas, the effects connected with the peculiarities of their solutions form the basis of use of these acids in the various fields. For example, an analysis of the electrolytic dissociation processes of weak multibasic organic acids gives an opportunity for conclusions about the peculiarities of formation of the hydrogen ions concentration in their solutions; this is important for the discussion of the peculiarities and possibility of the various chemical processes proceeding in these solutions.
In this communication, the effect of “overlapping equilibria” which determines the chemical behaviour (and, in particular, the peculiarities of the electrolytic dissociation) of weak multibasic organic acids is considered and analyzed.
2. Results and Discussion
2.1. The Effect of “Overlapping Equilibria” and Methods of Its Investigation
It is well known in the literature that an analysis of the processes of electrolytic dissociation of weak multibasic organic acids is complicated by participating of two or more dissociation steps in the formation of total hydrogen ions concentration in the acid solution. When this occurs the process is said to be overlapping. The analysis of such cases demands the use of iterative techniques, a powerful weapon in the more complex (overlapping two or more dissociation steps) situations. As a rule, the “overlapping equilibria” effect is explained in the literature by the closeness of the dissociation constant values of the adjacent steps. But the results of our investigations convince us that this explanation is not only one-sided but erroneous.
The suggested by us original method for a calculation of the main parameters of the complex processes of electrolytic dissociation of weak multibasic organic acids with the “overlapping equilibria” effect [1] -[3] was used for the investigation of these processes for a big amount of such acids with the various basicities in their dilute solutions [4] -[7] . The general mass action equations suggested by us for m dissociation step of weak multibasic organic acid HnA with the close values of dissociation constants of separate steps is written as follows:
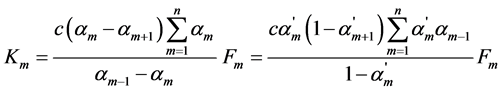 (1)
(1)
where Km is the thermodynamic dissociation constant of m step, αm, αm+1 and αm−1 are the usual degrees of dissociation of corresponding steps (they are equal to the ratio of the number of moles of H+ ions formed in a given dissociation step to the total number of moles of acid), 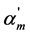 ,
, 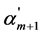 and
and  are the corresponding “partial” degrees of dissociation (they are equal to the ratio of the number of moles of anion dissociated at a given step to the number of moles of this anion formed in the previous step; for first step the concepts of usual and “partial” degrees of dissociation coincide), c is a total concentration of acid, Fm is the quotient of the activity coefficients for m step:
are the corresponding “partial” degrees of dissociation (they are equal to the ratio of the number of moles of anion dissociated at a given step to the number of moles of this anion formed in the previous step; for first step the concepts of usual and “partial” degrees of dissociation coincide), c is a total concentration of acid, Fm is the quotient of the activity coefficients for m step:
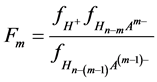 (2)
(2)
The values of the activity coefficients can be approximated by the Debye-Huckel equation:
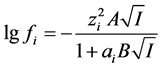 (3)
(3)
where ai is the cation-anion distance of closestapproach, A and B are constants depending on the properties of water at giventemperature, zi is the charge of ion. The ionicstrength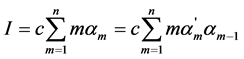 . The usual and “partial” degrees of dissociation may be evaluated successively by iterative solution of the quadratic equations obtained from Equation (1) for the adjacent dissociation steps of weak organic acids with any basicity [1] -[7] . The values of the degrees of dissociation may be used for a calculation of the concentrations of the hydrogen ions, all anions and undissociated acids.
. The usual and “partial” degrees of dissociation may be evaluated successively by iterative solution of the quadratic equations obtained from Equation (1) for the adjacent dissociation steps of weak organic acids with any basicity [1] -[7] . The values of the degrees of dissociation may be used for a calculation of the concentrations of the hydrogen ions, all anions and undissociated acids.
The degree of “overlapping equilibria” may be also characterized by the values of the different dissociation parameters connected with the second dissociation step: the contribution of this step to the formation of the hydrogen ions concentration [H+] (denoted by us before as x2 [1] [2] ), the concentration of dianion [A2−] (the values of these two parameters are equal), the ratio of the concentrations of dianion and monoanion [A2−]/[HA–], the regular dissociation degree of second step α2 and the “partial” degree of this step 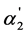 (this term was suggested by us before [3] ). These parameters are connected by the following dependences:
(this term was suggested by us before [3] ). These parameters are connected by the following dependences:
 (4)
(4)
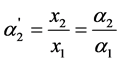 (5)
(5)
 (6)
(6)
2.2. The Weak Dibasic Organic Acids
In Table 1, the values of the ratio of the first and second dissociation constants K1/K2, the ratio of the concentrations of dianion and monoanion [A2−]/[HA–] and the “partial” degree of dissociation for second step  are presented for 57 weak dibasic organic acids (the values of the dissociation constants were taken from [8] -[12] ). The analysis of the data of Table 1 testifies that any convincing dependence between the K1/K2, values and the [A2−]/[HA–] and
are presented for 57 weak dibasic organic acids (the values of the dissociation constants were taken from [8] -[12] ). The analysis of the data of Table 1 testifies that any convincing dependence between the K1/K2, values and the [A2−]/[HA–] and 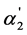 parameters which quantitatively characterize the degree of “overlapping equilibria” is absent. One can see from Table 1 that the values of [A2−]/[HA–] which are equal to or exceed unity (and the
parameters which quantitatively characterize the degree of “overlapping equilibria” is absent. One can see from Table 1 that the values of [A2−]/[HA–] which are equal to or exceed unity (and the 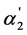 values which are equal to or exceed 0.5) are observed only for the first 11 acids. It is necessary to note that the K2 values for these acids have the order 10−4 - 10−3; for other acids presented in Table 1, these values have the order 10−6 - 10−5. Consequently, we can conclude that the condition [A2−] ≥ [HA–] is observed in the interval of the K2 values 10−4 - 10−3 only (without any dependence on the K1/K2 values). This fact convincingly confirms that the degree of “overlapping equilibria” depends on the K2 values and does not connect with the closeness of the K1 and K2 values.
values which are equal to or exceed 0.5) are observed only for the first 11 acids. It is necessary to note that the K2 values for these acids have the order 10−4 - 10−3; for other acids presented in Table 1, these values have the order 10−6 - 10−5. Consequently, we can conclude that the condition [A2−] ≥ [HA–] is observed in the interval of the K2 values 10−4 - 10−3 only (without any dependence on the K1/K2 values). This fact convincingly confirms that the degree of “overlapping equilibria” depends on the K2 values and does not connect with the closeness of the K1 and K2 values.
In Figure 1 and Figure 2, the dependence of the [A2−]/[HA–] and 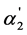 values on the K2 values is shown for the weak dibasic organic acids with the K2 values 10−4 - 10−3. Taking into account that these acids have the high α1 values, the quantity of
values on the K2 values is shown for the weak dibasic organic acids with the K2 values 10−4 - 10−3. Taking into account that these acids have the high α1 values, the quantity of 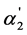 is very close to the value of the regular dissociation degree of second step α2. It is also necessary to note that the dependence of [A2−] and x2 on K2 are analogous to the dependence of
is very close to the value of the regular dissociation degree of second step α2. It is also necessary to note that the dependence of [A2−] and x2 on K2 are analogous to the dependence of 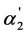 and α2 on K2 (according to the Equation (4)). The same dependence is also observed for x2/x1 (according to the Equation (5)).
and α2 on K2 (according to the Equation (4)). The same dependence is also observed for x2/x1 (according to the Equation (5)).
Taking into account the mass action equation for the second dissociation step:
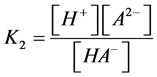 (7)
(7)
We may conclude that the linear dependences between the [A2−]/[HA–] and K2 values shown in Figure 1 correspond to the following equation:
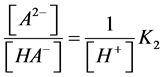 (8)
(8)
With the aid of this Equation we can explain the fact of the intense “overlapping equilibria” effect in the interval of K2 values 10–4 - 10–3. This Equation shows that the [A2−]/[HA–] value equal to unity is achieved (under the acid concentration c = 0.0001 mol·dm–3 when the [H+] value is also close to 0.0001 mol·dm–3) when K2 = 10–4. It is clear that with the further increase of the K2 value the [A2−]/[HA–] quantity will also appreciably rise. When the concentration of acid increases, the “overlapping equilibria” effect weakens, but the [A2−]/[HA–] values remain sufficiently high (Figure 1).
The dependence of 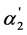 on K2 shown in Figure 2 also characterizes the “overlapping equilibria” effect. One can see from Figure 2 that an increase of the K2 values causes the sharp rise of the
on K2 shown in Figure 2 also characterizes the “overlapping equilibria” effect. One can see from Figure 2 that an increase of the K2 values causes the sharp rise of the 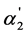 values for all shown acid concentration quantities. These dependences may be described by following equation:
values for all shown acid concentration quantities. These dependences may be described by following equation:
Table 1. The values of the ratio of first and second dissociation constants, ratio of the concentrations of dianion and monoanion and the “partial” dissociation degrees of weak dibasic organic acids with the “overlapping equilibria” effect (c = 0.0001 mol·dm–3).
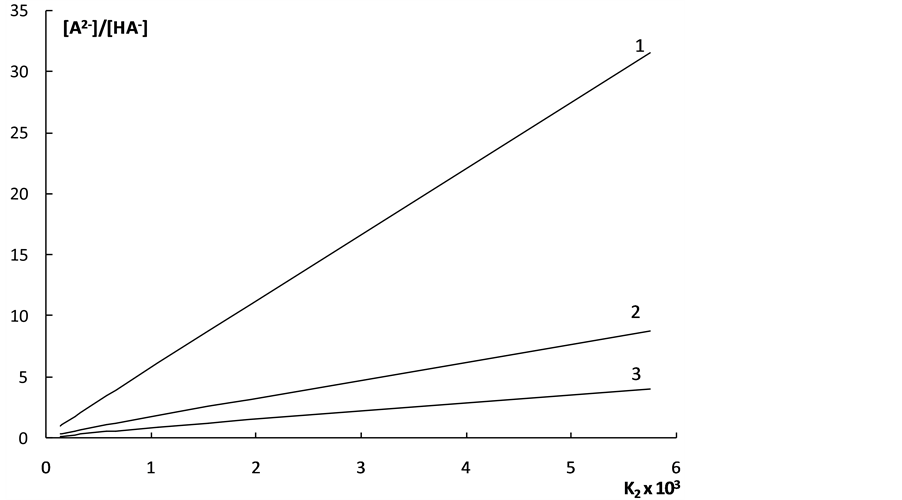
Figure 1. The dependence of the ratio of the concentrations of dianion and monoanion on the K2 values for weak dibasic organic acids. 1 - c = 0.0001 mol·dm–3; 2 - c = 0.0004 mol·dm–3; 3 - c = 0.001 mol·dm–3.
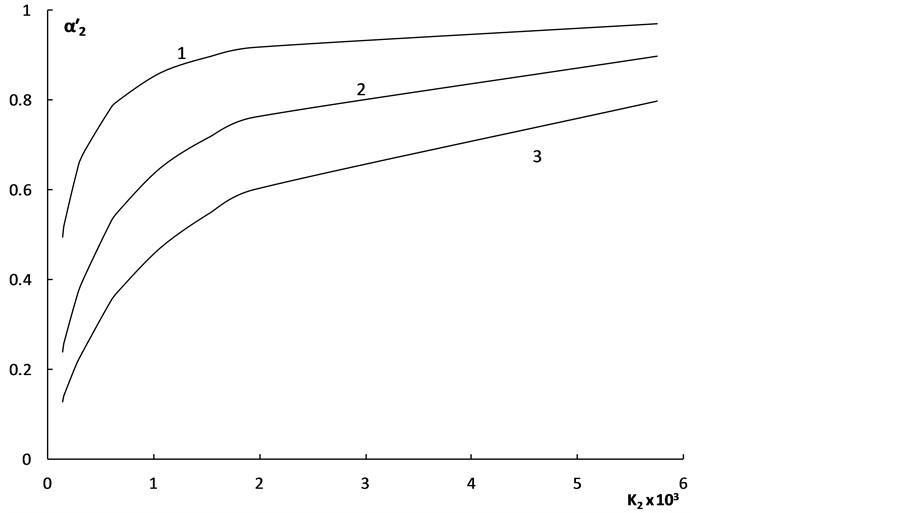
Figure 2. The dependence of the “partial” degrees of dissociation for second step on the K2 values for weak dibasic organic acids. 1 - c = 0.0001 mol·dm–3; 2 - c = 0.0004 mol·dm–3; 3 - c = 0.001 mol·dm–3.
 (9)
(9)
This equation shows that, when c = 0.0001 mol·dm–3, the  value equal to 0.5 is achieved, when K2 = 10–4.
value equal to 0.5 is achieved, when K2 = 10–4.
We can conclude that an interval of the K2 values 10–4 - 10–3 may be named as the region of strong “overlapping equilibria”.
Two main dissociation parameters characterizing the degree of the “overlapping equilibria” effect are connected with each other by the Equation (6). This dependency is shown in Figure 3. One can see from the Equation (6) and Figure 3 that the [A2−]/[HA–] value equal to unity is achieved when 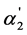 = 0.5.
= 0.5.
In case of weak dibasic organic acids with the K2 values order 10−6 - 10−5 is also observed the linear dependence described by Equation (8). As the 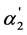 values in this interval of K2 are appreciably less than 0.5, the [A2−]/[HA–] values are also less than 1. This interval of the K2 values may be named as the region of weak “overlapping equilibria” effect.
values in this interval of K2 are appreciably less than 0.5, the [A2−]/[HA–] values are also less than 1. This interval of the K2 values may be named as the region of weak “overlapping equilibria” effect.
In Table 2, the intervals of the K2 values corresponding to the different degrees of the “overlapping equilibria” effect are presented.
2.3. The Weak Multibasic Organic Acids
The “overlapping equilibria” effect is also observed in the processes of electrolytic dissociation of weak multibasic organic acids. In this case this effect has some specific peculiarities which will be considered below. In Table 3 and Table 4 the various dissociation parameters for weak tri, tetra, penta and hexabasic organic acids are presented. In Figure 4 and Figure 5 the dependences of the ratio of the anions concentrations and 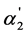 on the K2 values are shown (the dissociation constants values were taken from [9] ).
on the K2 values are shown (the dissociation constants values were taken from [9] ).
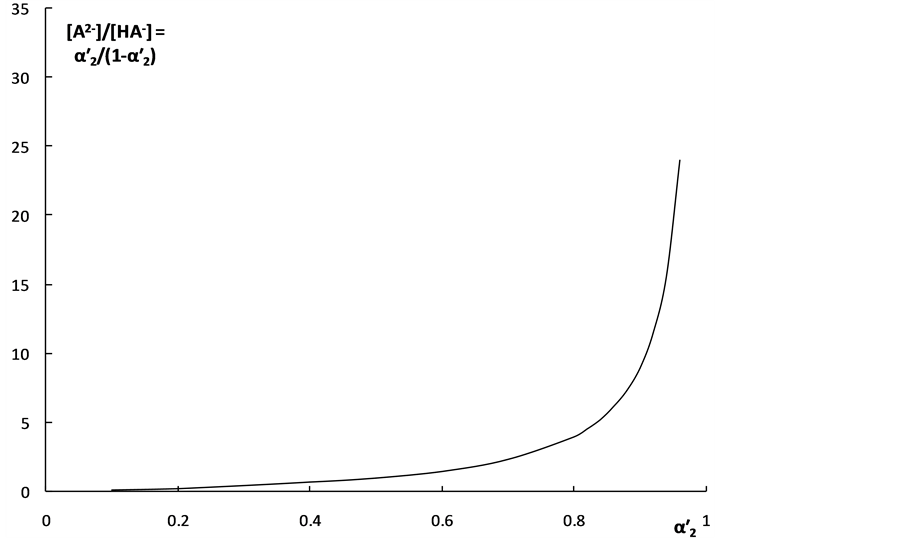
Figure 3. The dependence of the ratio of the concentrations of dianion and monoanion on the “partial” degrees of dissociation for second step for weak dibasic organic acids. c = 0.0001 mol·dm–3.
Table 2. The intervals of the degree of the “overlapping equilibria” effect in the dilute solutions of weak dibasic organic acids (c = 0.0001 mol·dm–3).
Table 3. The values of the ratio of the dissociation constants for different steps, ratio of the concentrations of dianion and monoanion, trianion and dianion and the “partial” dissociation degrees for second and third steps of weak tri and tetrabasic organic acids with the “overlapping equilibria” effect (c = 0.0001 mol·dm–3).
Table 4. The values of the dissociation parameters for weak penta and hexabasic organic acids with the “overlapping equilibria” effect (c = 0.0001 mol·dm–3).
One can see from the data presented in tables that there is not the clear dependence between the values of the parameters which determine the degree of “overlapping equilibria” (the ratios of the concentrations of various anions and the “partial” degrees of dissociation) and the values of the ratios of the dissociation constants of adjacent steps. At the same time one can see from Figure 4 and Figure 5 that the functional dependence exists between the values of these parameters and the K2 values. It is interesting to note that the linear dependence between the [A2−]/[HA–] values and K2 observed in case of dibasic acids (Figure 1) is preserved for tri and tetrabasic acids only at the lesser K2 values; with the further rise of the latters this dependence is deflected from linearity (Figure 4). This phenomenon is connected with the following circumstances. The [A2−]/[HA–] value for dibasic acids is expressed by the following equation:
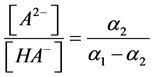 (9)
(9)
and for tri and tetrabasic acids as follows:
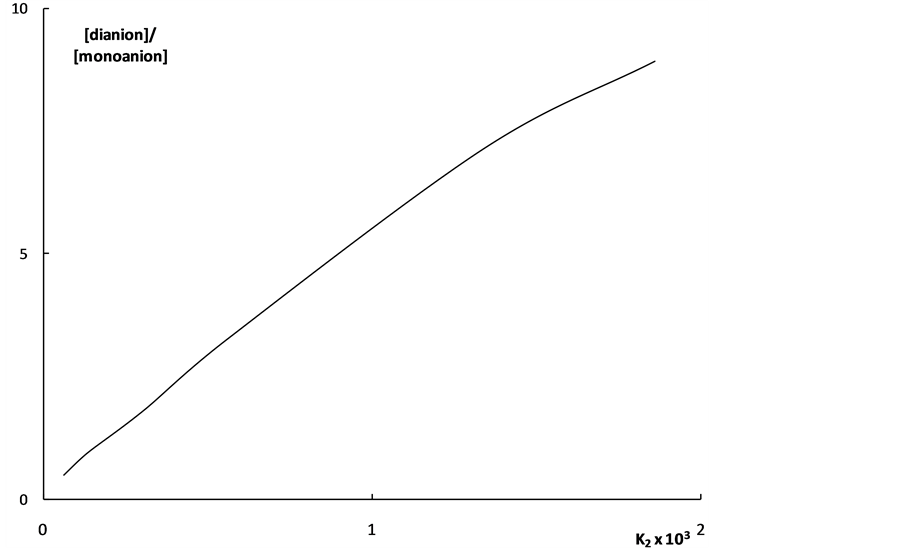
Figure 4. The dependence of the ratio of the anions concentrations on the K2 values for weakmultibasic organic acids. c = 0.0001 mol·dm–3.
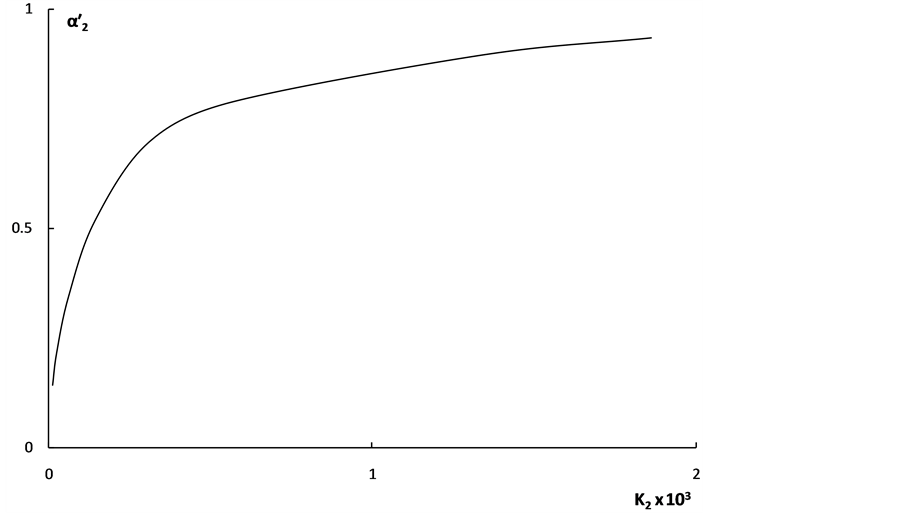
Figure 5. The dependence of the “partial” degrees of dissociation for second step on the K2 values for weak multibasic organic acids. c = 0.0001 mol·dm–3.
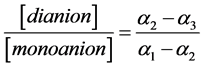 (10)
(10)
Under the small K2 values the K3 and α3 values are also small and the α3 quantity in the Equation (6) may be neglected; in these conditions the Equation (10) becomes analogous to the Equation (6). With the rise of the K2 values the K3 and α3 values also increase and the dependence between the ratio of the concentrations of dianion and monoanion is deflected from linearity.
The data presented in Table 3 testify that in case of weak tri and tetrabasic organic acids third dissociation step does not appreciably contribute to the “overlapping equilibria” effect. This fact is confirmed by the small values of the ratio of the concentrations of trianion and dianion and “partial” degree of dissociation for third step. One can see from Table 3 that these values at the small K3 values are very close to each other. Taking into account the following expression:
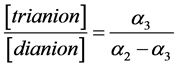 (11)
(11)
and the very small α3 values, the Equation (11) may be presented as follows:
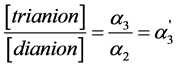 (12)
(12)
The different picture is observed in case of weak organic acids with highest acidity. One can see from Table 4 that in case of benzenepentacarboxylic acid the values of the ratio of the trianion and dianion and the 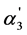 quantity achieve 0.55and 0.36, respectively. This fact testifies about the appreciable contribution of third step in the “overlapping equilibria” effect which is connected with the sufficiently high K3 value (1.1·10−4). At the same time the contribution of forth step in the above mentioned effect is negligible.
quantity achieve 0.55and 0.36, respectively. This fact testifies about the appreciable contribution of third step in the “overlapping equilibria” effect which is connected with the sufficiently high K3 value (1.1·10−4). At the same time the contribution of forth step in the above mentioned effect is negligible.
Even more clearly the “overlapping equilibria” effect is observed in case of hexabasicmellitic acid. Thanks to the higher K3 value (4·10−4) the quantity of the ratio of trianion and dianion concentrations achieves 1.75; that is, the trianion concentration exceeds the concentrations of dianion and monoanion (the ratio [H4A2−]/[H5A–] is equal to 25.94 despite the high value of the K1/K2 ratio). The 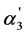 value also achieves the high quantity: 0.645. Thus, in this case takes place the double “overlapping equilibria” effect when two dissociation steps contribute to this phenomenon.
value also achieves the high quantity: 0.645. Thus, in this case takes place the double “overlapping equilibria” effect when two dissociation steps contribute to this phenomenon.
3. Conclusion
If the “overlapping equilibria” effect is observed in the processes of electrolytic dissociation of weak multibasic organic acid HnA, the degree of this phenomenon is determined by the dissociation parameters of the responsible m dissociation step and is not directly connected with the Km−1/Km value. These dissociation parameters are the ratio of the concentrations of anions:
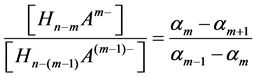
and the “partial” degree of dissociation for m step α′m. The interconnection between these dissociation parameters may be presented as follows:
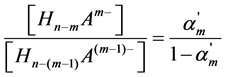
This conclusion is confirmed by the results of the thorough analysis of the processes of dissociation of 57 weak dibasic organic acids and 11 weak organic acids with the higher acidity.
References
- Kvaratskhelia, E. and Kvaratskhelia, R. (2007) The Degrees of Dissociation of Weak Multibasic Organic Acids. Journal of Solution Chemistry, 36, 787-792. http://dx.doi.org/10.1007/s10953-007-9147-0
- Kvaratskhelia, E. and Kvaratskhelia, R. (2010) The Determination of Acidity of the Dilute Solutions of Weak Multi-basic Organic Acids. Journal of Biomedical Science and Engineering, 3, 484-487. http://dx.doi.org/10.4236/jbise.2010.35067
- Kvaratskhelia, E. and Kvaratskhelia, R. (2009) The “Partial” Degrees of Dissociation of Weak Multibasic Organic Acids. Journal of Solution Chemistry, 38, 345-349.
- Kvaratskhelia, E. and Kvaratskhelia, R. (2008) The Electrolytic Dissociation of Mellitic Acid. Journal of Solution Chemistry, 37, 1063-1070. http://dx.doi.org/10.1007/s10953-008-9292-0
- Kvaratskhelia, E., Kvaratskhelia, R. and Kurtanidze, R. (2013) The Regularities of Electrolytic Dissociation of Weak Dibasic and Tribasic Organic Wine Acids. Journal of Applied Solution Chemistry and Modeling, 2, 158-164.
- Kvaratskhelia, E. and Kvaratskhelia, R. (2013) The Electrolytic Dissociation of Thio Derivatives of Dicarboxylic Acids. In: Taylor, J.C., Ed., Advances in Chemistry Research, Volume 17, Nova Science Publishers, New York, 111-124.
- Kvaratskhelia, E. and Kvaratskhelia, R. (2014) The Electrolytic Dissociation of Alkyl and Aryl Derivatives of Malonic Acid. In: Taylor, J.C., Ed., Advances in Chemistry Research, Volume 20, Nova Science Publishers, New York, 134-148.
- Lide, D.R. (2001) CRC Handbook of Chemistry and Physics. 81st Edition, CRC Press, Boca Raton, Ann Arbor, London, Tokyo.
- Dean, J.A. (1999) Lange’s Handbook of Chemistry. 15th Edition, McGraw-Hill, Inc., St. Lous.
- Brande, E.A. and Nachod, F.C. (1955) Determination of Organic Structures by Physical Methods. Academic Press, New York.
- Schwartz, L.M. and Howard, L.O. (1970) Aqueous Dissociation of Squaric Acid. The Journal of Physical Chemistry, 74, 4374-4377. http://dx.doi.org/10.1021/j100719a013
- Schwartz, L.M., Gelb, R.I. and Yardley, J.O. (1975) Aqueous Dissociation of Croconic Acid. The Journal of Physical Chemistry, 79, 2246-2251. http://dx.doi.org/10.1021/j100588a009


