Journal of Biomedical Science and Engineering
Vol.6 No.1(2013), Article ID:27458,8 pages DOI:10.4236/jbise.2013.61012
Review on lumped parameter method for modeling the blood flow in systemic arteries
![]()
1Department of Physics, University of Gjirokastra, Gjirokastra, Albania
2Department of Physics, University of Tirana, Tirana, Albania
3Department of Biomedicine and Prevention, University “Tor Vergata”, Rome, Italy
Email: ikokalari@uogj.edu.al
Received 17 November 2012; revised 20 December 2012; accepted 28 December 2012
Keywords: Fluid Dynamics; Mathematical Modelling; Cardiovascular System; Arterial Tree; Lumped Parameter Models
ABSTRACT
The cardiovascular system is characterized by complex interactions between various control mechanisms and physiological processes. Different approaches are used to provide better diagnostics and physiological understanding, cardiac prosthesis and medical planning. The mathematical description and modelling of the human cardiovascular system plays nowadays an important role in the comprehension of the genesis and development of cardiovascular disorders by providing computer based simulation of dynamic processes in this system. This paper aims to give an overview on lumped parameter models that have been developed by many researchers all over the world, to simulate the blood flow in systemic arteries. Surveying various references we make a review of different approaches to arterial tree modelling and discuss on the applications of such models.
1. INTRODUCTION
The main causes of deaths in industrial countries are cardiovascular diseases [1]. Also, it is in the most productive age in which the people are affected by such diseases. The cardiovascular system (CVS) serves as a transporting vehicle for the nutrients, gases and waste to and from the cells, as well as for the heat through blood convection [2]. It consists of heart (with its four chambers and four valves); systemic circulation (blood vessels in the body); pulmonary circulation (blood vessels in the lungs); nervous and biochemical regulators (which modify the vessels’ parameters in order to regulate the blood flow rate and pressure in the organs in accordance with the actual demand). In this system various organs or mechanisms, such as kidneys, endocrine and nervous systems, respiration, metabolism, physical exercise, etc., may influence as well [2]. These mechanisms act in different time intervals [3]. Even though the majority of the research regarding the physiological systems is based on experiments on animals, these have their limitations [4]. Understanding the complex interactions and physiological functions of the CVS is not easy, but the use of modern technology is a helpful tool for this. Recent progress in imaging technology, as well as more powerful and less expensive computers, has open greater possibilities for developing more sophisticated modeling methods of CVS. A better insight can be attained by a structured analysis of the models which describe this system, organizing the knowledge and the experimental observations in temporal and spatial order [5]. Furthermore, a computer-based simulation of dynamic processes in the CVS could be applied in numerous tasks [6].
This paper describes some categories and methods of modeling the CVS, aiming to present a review of different levels of modeling. Finally, the application fields of the investigated approaches are discussed as well as their advantages and disadvantages.
The flow of blood in the CVS obeys to the conservation laws described by their respective equations. The description of dynamical models, part of whom is the CVS, is usually done by a set of differential equations. Depending on the scope of its use and the accuracy requested by the model, the proper dimensions are selected, from zeroto three-dimensional. The amount of information given about the inner state of the system distinguishes three kinds of mathematical modeling methods [5]:
• White box method describes the internal structure of the system and the characteristics of transition from inputs to outputs. In this method all the parameters and variables of the system are determined as well as their relationship. A serious restraint of this method is the enormous amount of processes and interactions that play a role in the body.
• Black box method considers only the transition characteristics, which means only the relationship between the input and output of a system, without providing any deeper information regarding the internal structure. A limitation of this method is its simplicity and the fact that they disregard the nonlinearities and specific disturbances.
• Grey box method, which combines the two abovementioned methods, uses the knowledge on the internal structure of the system to define the internal structure of the model.
The CVS can be regarded as a wide hydraulic network under the action of a pulsatile pump. Different behaviour can be observed at various locations of the closed loop. The 0D models (named lumped parameter models) consider as uniform the distribution of fundamental variables (pressure, volume and flow rate) in every single compartment (organ, blood vessel, etc.) of the model, in every moment of time. The models of higher dimensions account for the spatial variation of these parameters, as illustrated in Figure 1.
The 0D models that represent the main components of the system, (vasculature compartments and the heart with its valves), are appropriate for the study of global distribution of the pressure, flow rate and blood volume, for specific physiological conditions. The spatial distribution of the parameters can be approximated by setting up the so called multi-compartments models, every compartment of which is supposed to be homogenous and described by a lumped parameter model.
The 1D models, where the wave transport effect is easily represented, describe the variation of the velocity of flow through the length of the blood vessel. The 2D models are appropriate to use when the radial changes of the flow velocity in a tube with axial symmetry are requested. The use of 3D models is needed for the complex description of the blood flow in bifurcations of the vessels, through heart valves, inside ventricles, etc. The 1D, 2D and 3D (distributed parameter models) and lumped models of the venous system are not investigated in this review. Table 1 compares some of the applications of
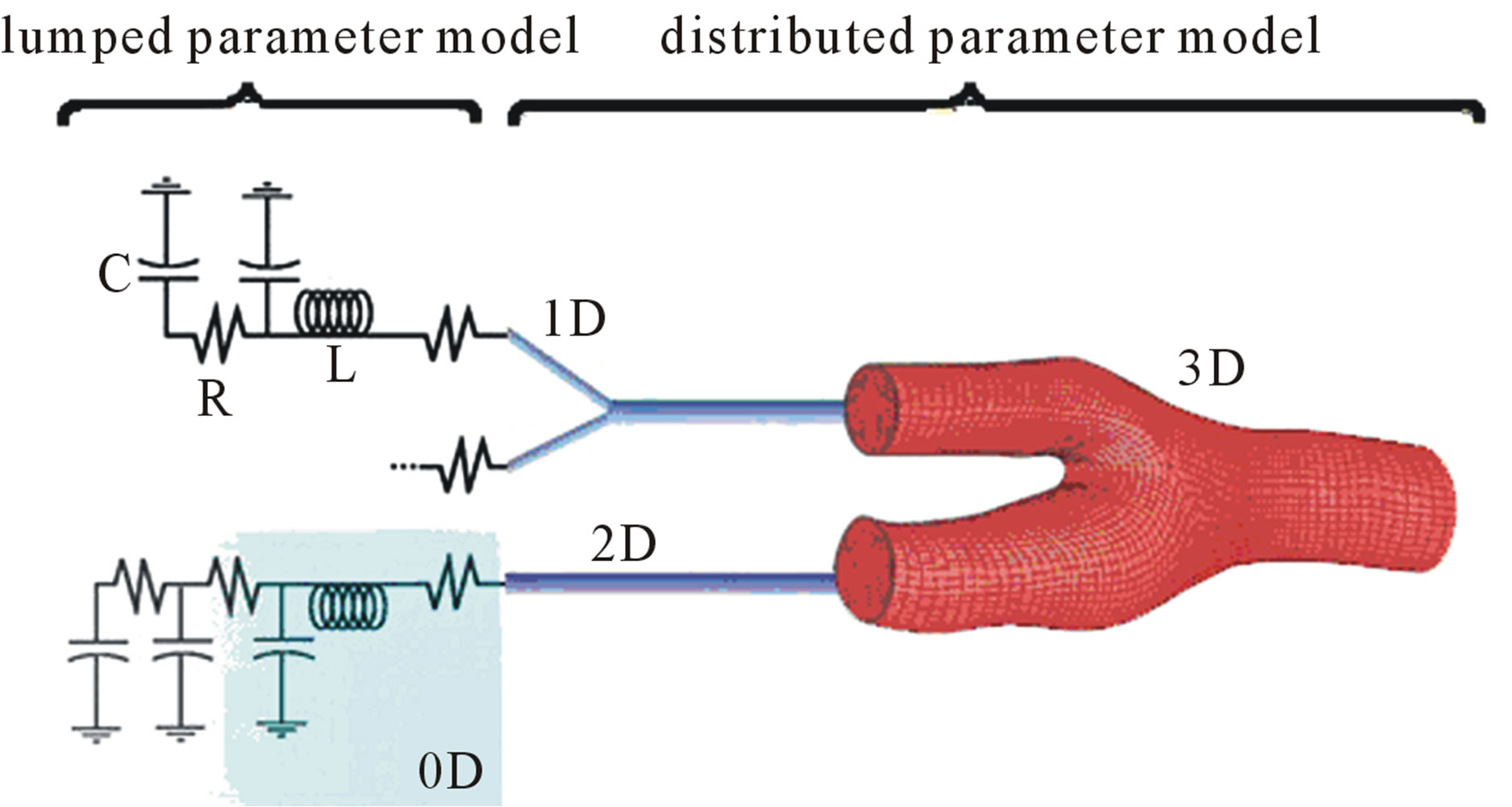
Figure 1. Schematic representation of decoupling by segmental dimension reduction.
Table 1. Comparison of modelling techniques for the study of cardiovascular dynamics.

different kind of models.
2. METHODOLOGY
The collection of relevant papers is done from March 2010 till January 2012, mainly making use of PubMed, HubMed, Pubget, Sciverse (Sciencedirect and Scopus) databases. The keywords used for searching were: cardiovascular system, cardiovascular modelling, arterial tree modelling, Windkessel, lumped parameter models, mathematical modelling and simulation.
Out of more than 250 collected papers regarding the CVS modelling and simulation, about 40 are selected for this review. The repetitive and similar studies were excluded. The papers treating the human circulation dynamics as well as those treating systemic arterial tree modeling and its computer simulation were included as references of this review.
3. DISCUSSIONS
Models are a helpful tool to understand the functionality of a real system by simplifying it. The modeling methods and their product should always be evaluated according to their applications [5]. The two most important applications of the physiological processes simulation are: the design of new medical devices (e.g. [6,7]) and, collecting more information about the complex functioning of these systems with many variables (e.g. [3,8-10]). A better understanding of CVS leads toward more effective and less expensive medical treatment. On the other side, the simulation of the CVS may serve as a testing and training platform for the medicine students (e.g. [8,11]) and their impact in reducing the experiments on animals is significant.
The easy inclusion of the frequent improvements to an existing model is another important aspect. Of the same importance is the model validation, which consists in evaluating the accuracy of the assumptions through comparison of experimental data with those simulated.
In 0D models that simulate the global hemodynamics of the CVS, is applied the analogy between the blood flow in the systemic arteries and the current in an electric circuit. The analogy starts at the left ventricle where the blood pressure varies from a low (nearly zero) to a high (approximately 120 mmHg), then continues into the aorta and into the systemic arteries, where the pressure variation is significantly lower because of the elasticity of the large systemic arteries. The gradient of the blood pressure in arterial tree pushes the blood against the hydraulic impedance like the gradient of the voltage in an electric circuit pushes the current against the electric impedance.
The total loss due to friction, the capacitance of the vessels due to their elasticity and the inertia of blood represent the hydraulic impedance like the electric impedance is represented by the capacitance, resistance and inductance of the circuit. The flow of blood is described by the equation of continuity for the mass conservation, by the Poiseuille’s law for the steady flow and by the Navier-Stokes equation for the non-steady state. Analogically, the current in a circuit is described by Kirchhoff’s laws, Ohm’s law and the line transmission equation for the voltage-current relation for high frequencies. Hence, as shown in Table 2, the friction due to viscosity, the inertia of the flow, the capacitance of the vessel, the blood pressure and the flow rate, can be respectively described by the resistance R, inductance L, capacitance C, voltage and the current in an electric circuit. As consequence the methods used for the study of these circuits can be used to analyse the cardiovascular dynamics too. Milišić and Quarteroni [12] proved that 0D models describe the vessel with a set of two ordinary differential equations (Eq.1) for each compartment, (which represent the mass and momentum conservation), added by one algebraic equilibrium equation (which relates the volume of the compartment with the pressure in it).
Table 2. The quantities which characterize the fluid dynamics and their electrical analogues.

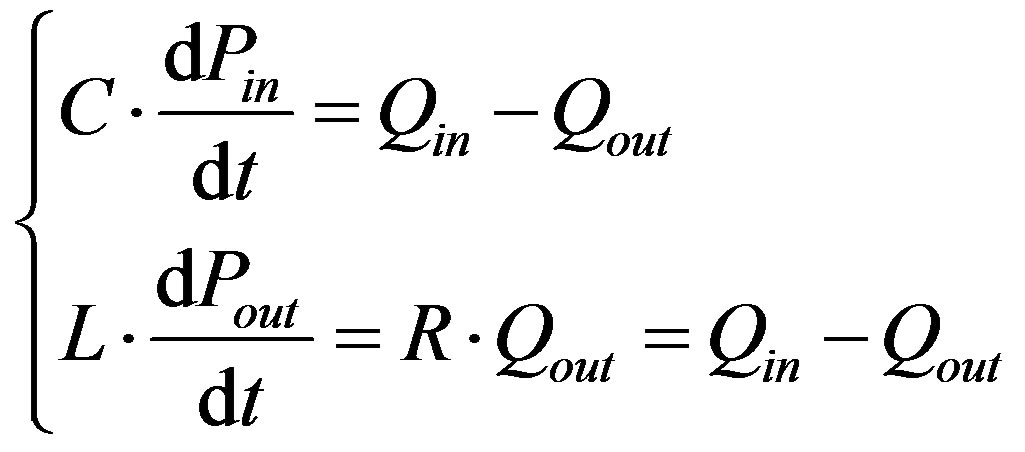 (1)
(1)
The models of the arterial tree, in which the left ventricle and the right atrium represent the boundary conditions, have evolved by becoming more complex with the addition of elements that describe specific physiological or physical phenomena. A considerable number of 0D models are developed to simulate the arterial system, starting with the simple Windkessel (WK) models that consider the veins as deposits in zero pressure and the whole arterial network as a single capacitor in parallel with a single resistor. An important milestone in this development was Guyton’s comprehensive model [3] which specifically describes the majority of arterial bifurcations as well as some hormonal control mechanisms. The 0D models can be categorized as single-compartment models and multi-compartments models.
3.1. Single-Compartment Models
There are numerous models of the CVS that have been extensively studied in recent years. It is a set of mathematical equations between some of the variables of the system, mainly blood pressures and flows that describe these models. These variables interrelate by a set of parameters (blood viscosity, vessel diameter, vessel wall elasticity, etc.) which are difficult or even impossible to be directly measured. An average value reasonably fitted to the experimental data is generally given to the various parameters.
Grodins [13] was the first to start the global dynamic modeling of the CVS. Since then, mathematical modeling has become a prerequisite for hemodynamics analysis, in tandem with the experimental approach. The whole arterial network is described by a single combination resistor-inductor-capacitor (RLC). Hales in 1733 [14] was the first to put forward such model, named Windkessel, suggesting that the pressure variations are related to the large arteries elasticity. This theory was quantitatively formulated later by Frank in 1899 [15], who described the hemodynamics of arterial network in terms of compliance and resistance.
Fank’s model (Figure 2(a)) comprises a capacitor C (which describes the depository properties of large arteries) connected in parallel with a resistor (which describes the dissipative nature of peripheral vessels). This 2-element WK, which describes the pressure decay in aorta during diastole, is still in use today to evaluate the total arterial capacity when the aortic pressure and peripheral resistance are known. This model ignores the veins, which are described as zero pressure far fields.
The compliance of the large arteries acts as the WK (air kettle). The resistance to blood flow in the systemic arterial network is mainly found in the resistance vessels: the smallest arteries and the arterioles. It is not possible the strict division of compliant (conduit) arteries and resistance vessels. This is because resistive vessels have some compliance as well and, large, compliant arteries have small resistive properties.
The 2-element WK model shows the important impact in the load on the heart of both: total arterial compliance as well as peripheral resistance (the resistance of the entire systemic vascular bed). As this model describes the whole arterial tree, in terms of a pressure-flow relation at its entrance by two parameters that have physiological meaning, it is not possible to study phenomena, such as wave travel and wave reflections, which take place inside this network. Even though this model is not able to describe the high frequency components that are associated with the reflections of the pressure in the arterial network, it represents quite well the afterload on the heart. On the other hand, it explains aortic pressure decay in diastole, but fells short in systole. Therefore characteristic impedance was introduced as a third element of the WK model.
In 1954, Wetterer [16] showed the quantitative discrepancies between the pressure measured in systole and the one predicted by the 2-element WK, but he did not explain the cause of this. The developments towards more powerful computing capabilities together with the
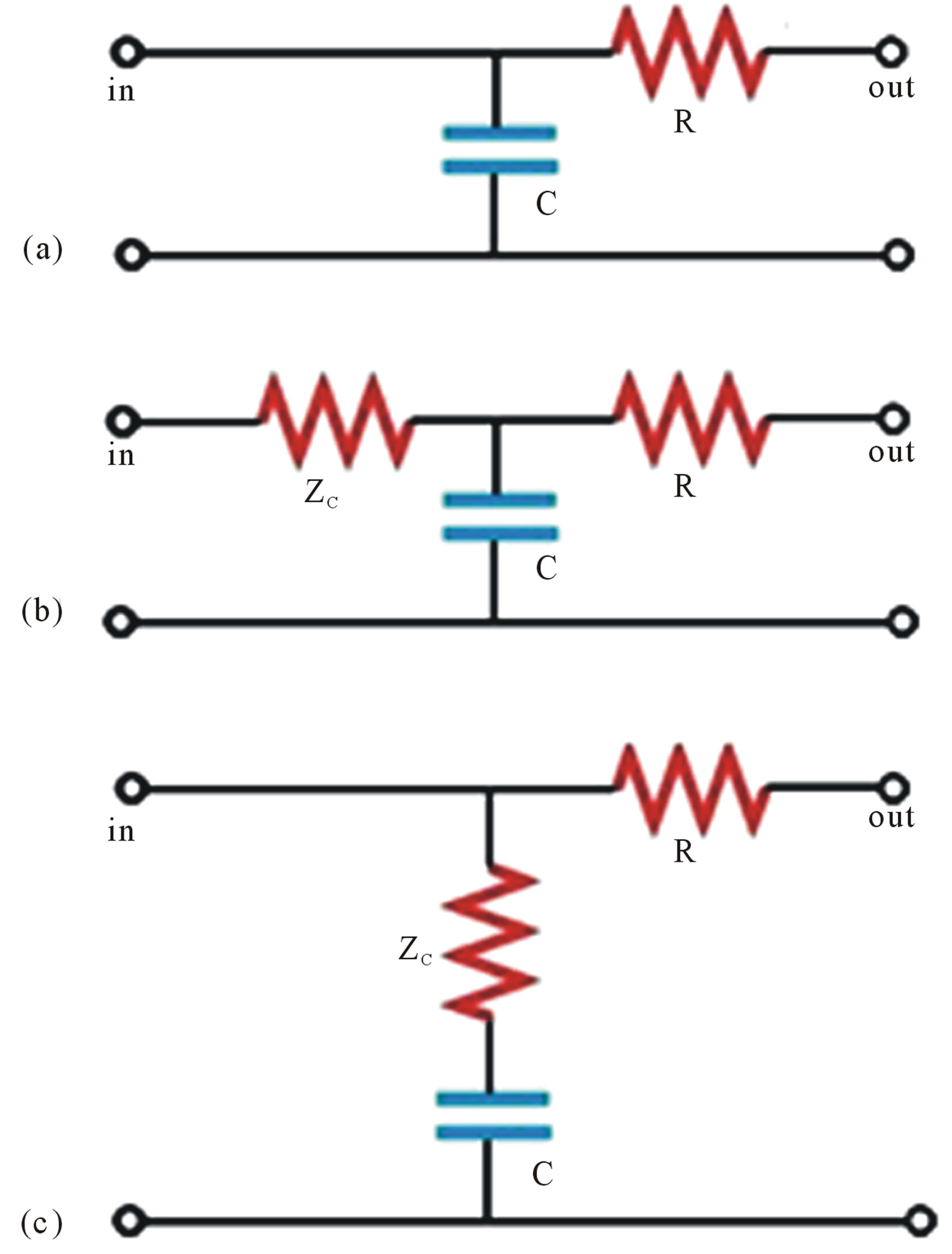
Figure 2. (a) 2-element WK model [15]; (b) 3-element WK by Westerhof et al. [18]; (c) 3-element WK by Buratini et al. [22].
practical measurement of aortic flow made possible the calculation of the input impedance [17]. It was found that the input impedance modulus at higher frequencies was equal to the characteristic impedance of the proximal aorta. This led to the addition of aortic characteristic impedance to the 2-element WK.
The so called Westkessel model was developed by Westerhof et al. [18], who inserted an additional resistor ZC (Figure 2(b)), which represents the aortic characteristic impedance of the arterial tree. Characteristic impedance links this 3-element WK and wave aspects of the arterial system, described in [18,19], to transmission phenomena. The total resistance gives the total resistance of the systemic vascular network in the abovementioned R-C model, while the capacitor C gives the depository properties of the arterial network due to the blood vessels’ elasticity [19]. The characteristic impedance is represented as a resistor (since it has the same dimensions as a resistor), but it should be emphasized that it is not a resistance and should be interpreted in terms of oscillatory phenomena.
By analyzing the flow and the aortic pressure during diastole, when the 2-element and 3-element WK behave similarly, Wang et al. [20] proved that the addition of the characteristic impedance to the 2-element WK is necessary to describe flow and pressure throughout the entire cardiac cycle.
In vivo studies have shown that despite its simplicity, this 3-element WK model significantly improved the simulation of the high frequency components by predicting accurately the systolic and diastolic aortic pressure, the pumped blood volume by the left ventricle and stroke work [21]. Even though this model is largely used in CVS simulations, the same studies have shown that it does not give a realistic waveform of aortic pressure and underestimates the mean arterial pressure and the maximal aortic flow rate [21].
Another configuration of the Westkessel model is developed by Buratini et al. [22]. This describes the arterial features by putting a small resistor ZC in series to the capacitor C. The elements ZC and C connected in such way, describe the elasto-viscous features of the vessel’s walls, differing from the configuration introduced by Westerhof [18], cited above, where the ZC describes the wave reflection during the flow. Even though these two 3-element WK models are equivalent in a certain level, it still remains the discussion of the priority of wave reflection against the elasto-viscous properties of the vessel walls in the arterial characteristics.
In order to increase the model’s accuracy in describing the impedance of the blood vessels and decrease the errors in the low frequencies range, Stergiopulos [23] added an inductive element L (Figure 3(a)) which describes the inertial effect of the blood flow, introducing so the 4-element WK. This fourth element represents the total arterial inertance (the sum of all inertances in the arterial segments) [23]. The use of total arterial inertance corrects the behavior of the input impedance in low frequencies where the 3-element WK is inaccurate.
Another configuration (Figure 3(b)) with the inductive element is studied by Grant in [24], Burattini in [25,26], or others [27,28]. This series inertance affects the arterial input impedance only at high frequencies and not at low frequencies.
Figure 4 plots the measured aortic input impedance together with the impedances predicted by the 2-, 3- and 4-element WK models. The 2-element WK clearly falls short, especially in the high frequencies range. The 3-element WK is less accurate at very low frequencies. The more elements are added in a model; more difficult it becomes to identify its parameters. The addition of a single element in the 4-element WK brings forward much more difficulties than in the 2- and 3-element WK.
With the purpose to further improve the systemic vessels tree models, Jager et al. [29] have added other resistive and inductive elements (Figure 5) to simulate the impedance of the laminar flow (the sleeve effect), but this model is not further explored by other researchers because of its high complexity.
The above mentioned models describe mainly the characteristics of the flow and pressure in aorta and in the arteries where the pressure pulses in the venous side are not significant. But, in the case of the coronary and pulmonary circulation, the pulses of the pressure in veins play an important role [30]. Hence, adding other R, L, and C elements enables the description of the flow characteristics in veins, introducing so the 5- and 6-element models.
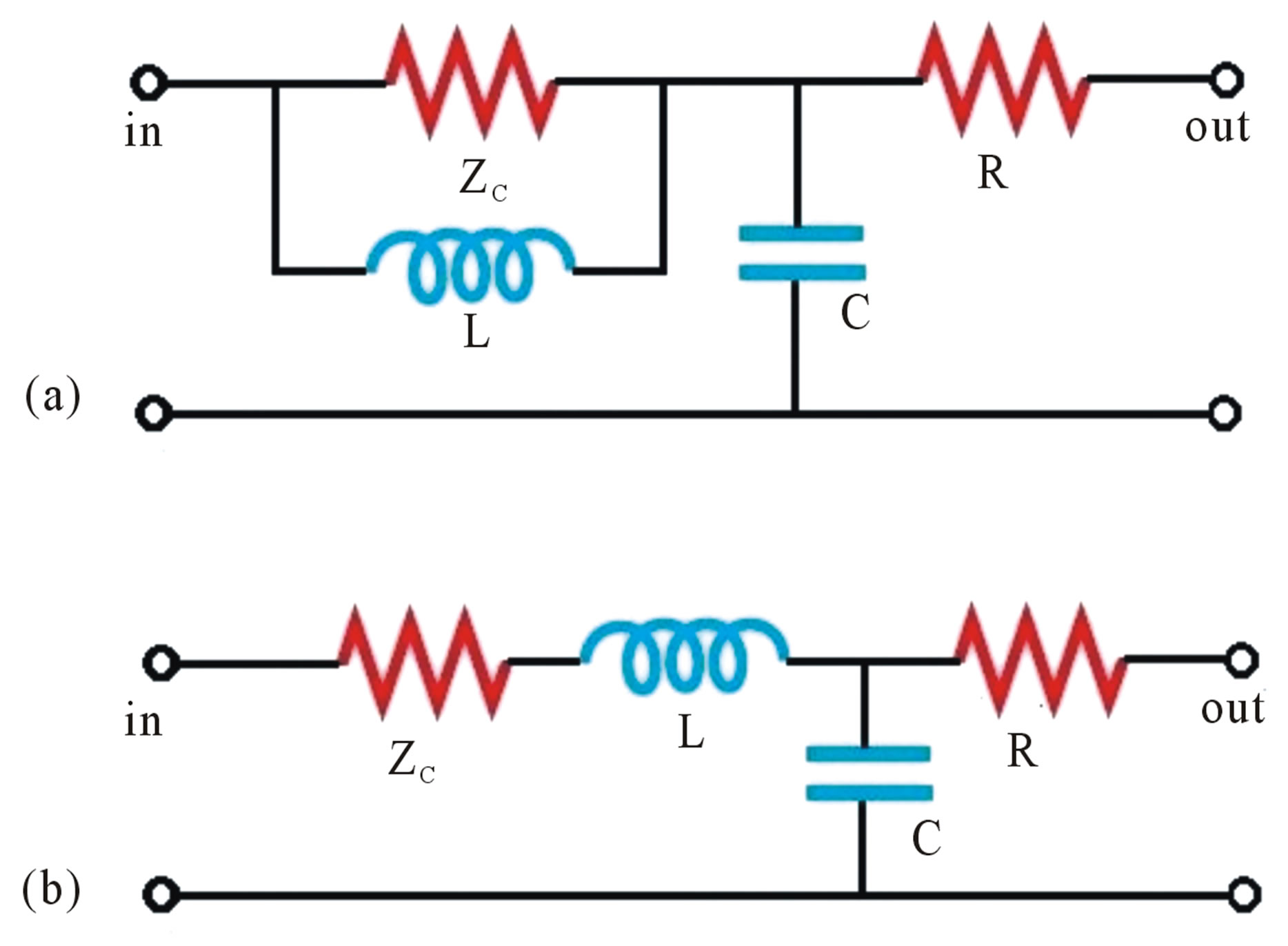
Figure 3. (a) 4-element WK by Stergiopulos et al. [23]; (b) 4-element WK by Grant et al. [24].
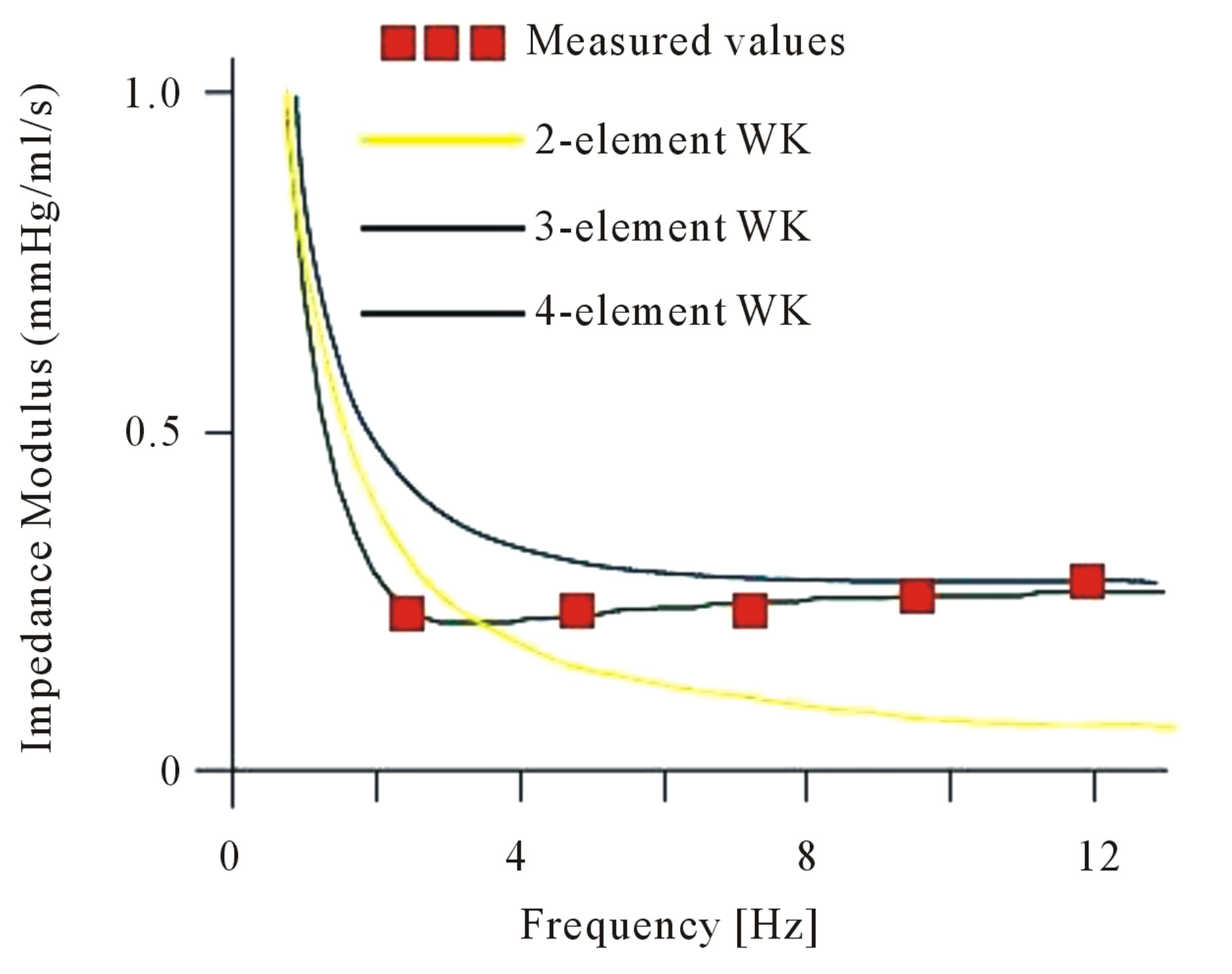
Figure 4. Comparison of measured and predicted input impedances (adapted from [17, p. 176]).
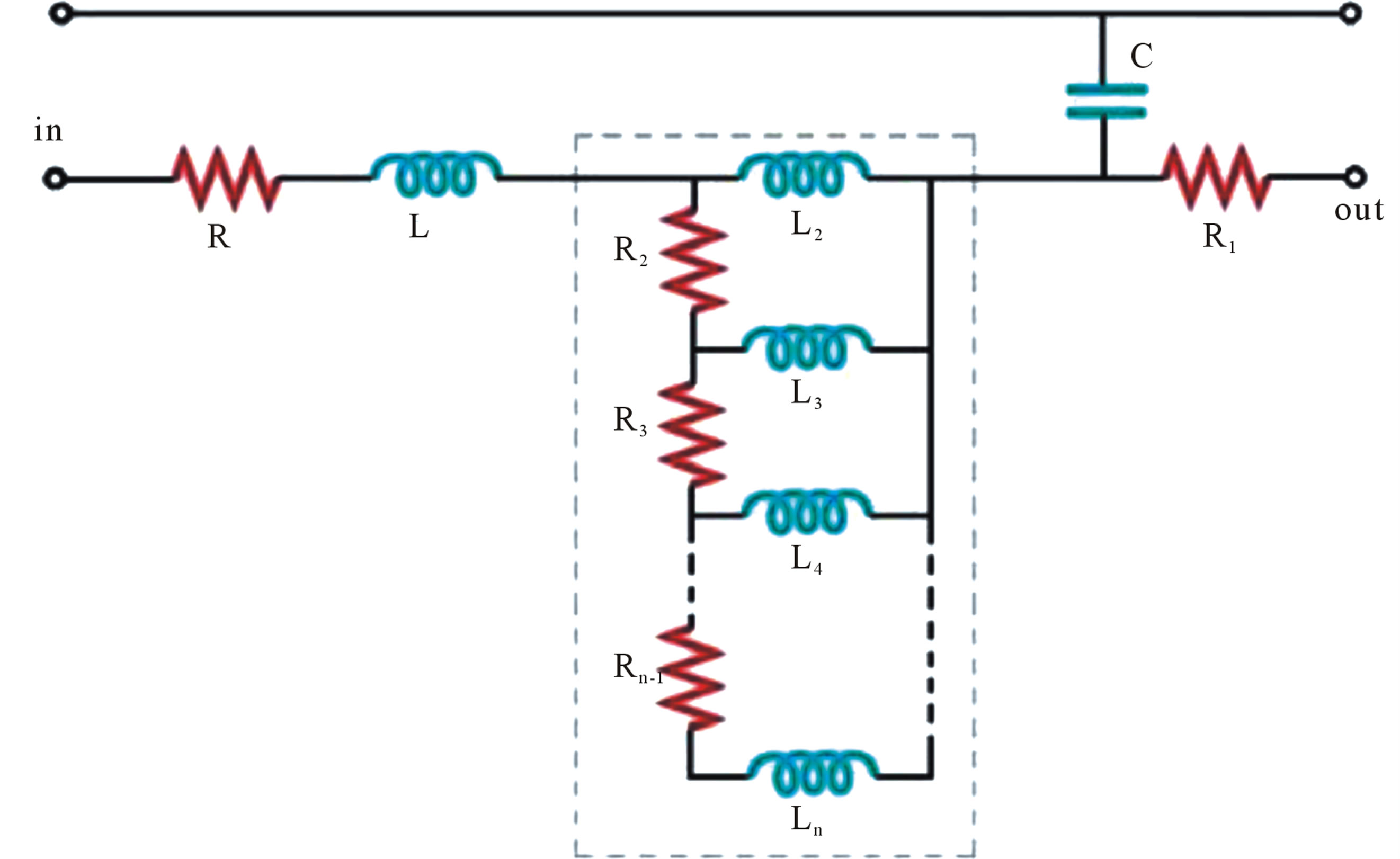
Figure 5. Electrical circuit representing the laminar oscillatory flow impedance in a straight circular tube. The corrective network, enclosed by broken lines, accounts for the sleeve effect (adopted from [29]).
The in vivo studies of Frasch et al. [30] have shown that the 5-element model offers a better description of the dynamics of blood microcirculation and, the 6-element models better describe the contribute of the venous system in the systemic circulation, compared with the 2-, 3- and 4-element WK.
3.2. Multi-Compartments Model
The multi-compartments models are developed to correct the inability of the single-compartment models to calculate the flow and the pressure in different segments of the vessel since they treat the systemic tree as a single block. In the multi-compartments models, the systemic circulation is partitioned in a number of segments (compartments), each described by a combination RLC according to the local characteristics of the vessel. These compartments are combined to create the whole model of the whole arterial network (e.g. Figure 6).
The systemic circulation can be divided, depending on the specific purpose of its use and the accuracy requested by the model, to provide details about a certain area, while the other segments can be put together by using less sophisticated elements. Such flexibility in the model setup is a powerful and helpful tool for the cardiovascular simulations.
Generally, the characteristics of the segments of the vessels are different from those of the whole system. In [12,31] there is a detailed description of the four typical appropriate configurations for the segments of the blood vessels, whose names and schemes are given by Figure 7.
4. CONCLUSIONS
The CVS is very complex and too many questions about it are still with no answer. This review investigates the arterial 0D published models and makes a portrayal of their development and applications.
The mathematical modeling is a powerful tool for deepening the understanding of the CVS functionality and for improving the medical equipment technology. At the same time it offers a promising method of assisting in the non-invasive diagnostics and in the training of the cardio-surgeons. Mathematical models of the CVS vary significantly in their complexity and their objectives. They range from the simple WK model, such as [21], to complex representations of the vascular network, such as [32], or even finite element models of many degrees of freedom. The lumped parameter models enable global representation of the flow in systemic arterial network. Hence the WK enlarges its applicability on the whole cardiovascular dynamics studies.
A model cannot be named “bad” or “good”, but its quality should be evaluated depending on the concrete purpose of its use. All models have different uses or goals, but they all share the common goal of understanding non-invasively the CVS function. The development of a trustful model includes the abstraction of a real system, experimental simulation, the comparison of the simulation data with the real system and the reduction of the eventual inconsistencies.
Many researchers model the systemic vasculature in segments which represent the various blood vessels (capillaries and veins, arterioles, arteries and aorta), (e.g. [33-36]). Since the flow in aorta and in the arteries (which are elastic) is pulsatile, it should be considered the combination RLC of the three elements. As in arterioles and capillaries (with relatively rigid walls) the flow is steady and the friction is dominant, a resistive element is enough. The inertial effect is ignored in veins (because they have great capacity and the flow is relatively steady), by making so the RC combination good enough to represent the flow characteristics. Some multi-compartments models, such as [6,9,37-43], describe the distribution of the pressure and the flow characteristics in each bifurcation of the vessels. Models of this complexity, like [32] and [39,40], even though describe accurately the system; introduce practical difficulties in defining the exact values for most of the parameters.
In this review the main aspects and use of the WK are discussed. This lumped parameter model can be used for the systemic arterial system and the pulmonary arterial bed of all mammals [44]. As limitations of WK model of the arterial system we mention its incapability to study the wave transmission phenomena, the changes in the blood flow distributions, the effects of local vascular changes, etc. [44].
Researches devoted to complex simulations which

Figure 6. Example of multi-compartment model (ao: aorta; at: arteries; al: arterioles; cp: capilaries; vn: veins).
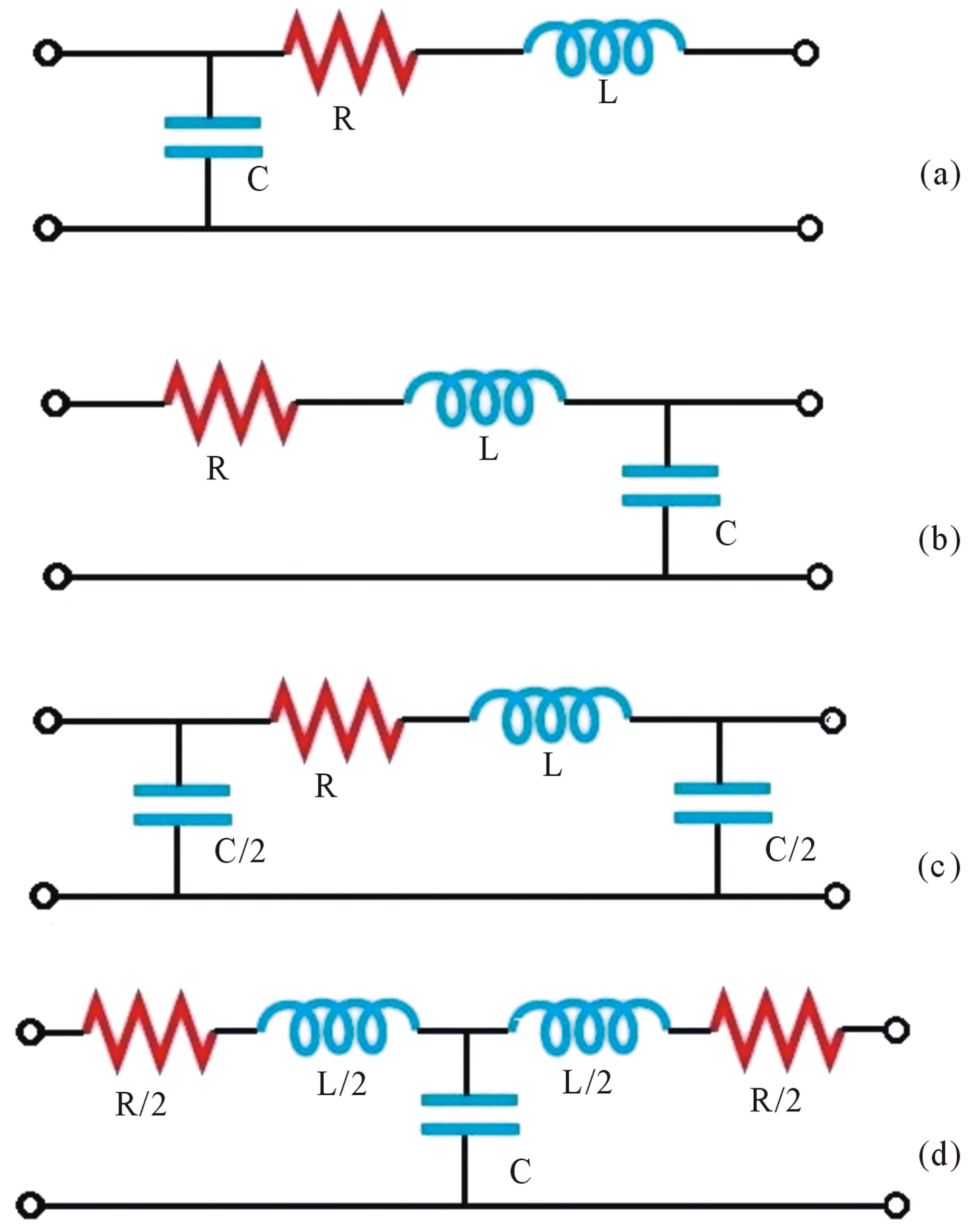
Figure 7. Typical configurations for blood vessel segments, used as blocks in the multi-compartments models (a) L element (b) Inverted L element (c) π element (d) T element.
provide many details on the CVS are quite expensive (in terms of human resources), but such details not always are needed. Hence, less detailed models have demonstrated to be more useful as they provide useful information at a reasonable computational cost.
Deeper studies of the interactions of the CVS with the respiratory, nervous and digestive systems, will lead towards development of more integral models. So far, the 0D models are largely used in the clinical diagnostics and treatment, but maybe it’s time that in collaboration with the medical community these models become personalized according to the specific physiological and pathological conditions of the patients.
REFERENCES
- WHO Fact Sheet No. 317, (2011). www.who.int/mediacentre/factsheets/fs317
- Guyton, A.C. and Hall, J.E. (2006) Textbook of medical physiology. 11th Edition., Elsevier Saunders, Philadelphia.
- Guyton, A.C., Coleman, T.G. and Granger, H.J. (1972) Circulation: Overall regulation. Annual Review of Physiology, 34, 13-44. doi:10.1146/annurev.ph.34.030172.000305
- Wu, X.M. (1994) Modeling and simulation of cardiovascular circulation system: Status and prospect. Sciencepaper Online, 2, 112-116.
- Cellier, F.E. and Kofman, E. (2006) Continuous system simulation. Springer-Science, New York.
- Werner, J., Böhringer, D. and Hexamer, M. (2002) Simulation and Prediction of cardiotherapeutical phenomena from a pulsatile model coupled to the guyton circulation model. IEEE Transaction on Biomedical Engineering, 49, 430-439. doi:10.1109/10.995681
- Simanski, O., Kähler, R., Schubert, A., Janda, M., Bajorat, J., Hofmockel, R. and Lampe, B.P. (2008) Proceedings of the 17th IFAC World Congress. In: Chung, M.J., Misra, P. and Shim, H., Eds, The International Federation of Automatic Control, Seoul, 9601-9606.
- Coleman, T.G. and Randall, J.E. (1983) HUMAN: A comprehensive physiological model. Physiologist, 26, 15- 21.
- Lu, K., Clark, J.W., Ghorbel, F.H., Ware, D.L. and Bidani, A. (2001) A human cardiopulmonary system model applied to the analysis of the Valsalva maneuver. American Journal of Physiology—Heart and Circulatory Physiology, 281, 2661-2679.
- Magosso, E., Biavati, V. and Ursino, M. (2001) Role of the baroreflex in cardiovascular instability: A modeling study. Cardiovascular Engineering, 1, 101-115. doi:10.1023/A:1012574513589
- Abram, S.R., Hodnett, B.L., Summers, R.L., Coleman, T.G. and Hester, R.L. (2007) Quantitative circulatory physiology: An integrative mathematical model of human physiology for medical education. Advances in Physiology Education, 31, 202-210. doi:10.1152/advan.00114.2006
- Milišić, V. and Quarteroni, A. (2004) Analysis of lumped parameter models for blood flow simulations and their relation with 1D models. Mathematical Modeling and Numerical Analysis, 38, 613-632. doi:10.1051/m2an:2004036
- Grodins, F.S. (1959) Integrative cardiovascular physiology: A mathematical synthesis of cardiac and blood vessel hemodynamics. Quarterly Review of Biology, 34, 93- 116. doi:10.1086/402631
- Hales, S. (1733) Statistical essays: Containing haemostaticks, or an account of some hydraulick and hydrostatical experiments on the blood and blood-vessels of animals, etc. 2, Innys & Manby, London.
- Frank, O. (1899) Die grundform des arterielen pulses erste abhandlung: Mathematische analyse. Zeitschrift für Biologie, 37, 483-526.
- Wetterer, E. (1954) Flow and pressure in the arterial system, their hemodynamic relationship, and the principles of their measurement. Minnesota Medicine, 37, 77-86.
- Westerhof, N., Stergiopulos, N. and Noble, I.M. (2010) Snapshots of hemodynamics an aid for clinical research and graduate education. 2nd Edition, Springer, New York. doi:10.1007/978-1-4419-6363-5
- Westerhof, N., Bosman, F., DeVries, C.J. and Noordergraaf, A. (1969) Analogue studies of the human systemic arterial tree. Journal of Biomechanics, 2, 121-208. doi:10.1016/0021-9290(69)90024-4
- Westerhof, N., Elzinga, G. and Sipkema, P. (1971) An artificial arterial system for pumping hearts. Journal of Applied Physiology, 31, 776-778.
- Wang, J.J., O’Brien, A.B., Shrive, N.G., Parker, K.H. and Tyberg, J.V. (2003) Time-domain representation of ventricular-arterial coupling as a Windkessel and wave system. American Journal of Physiology—Heart and Circulatory Physiology, 284, 1358-1368.
- Burkhoff, D., Alexander, J. and Schipke, J. (1988) Assessment of windkessel as a model of aortic input impedance. American Journal of Physiology—Heart and Circulatory Physiology, 255, 742-753.
- Burattini, R. and Natalucci, S. (1998) Complex and frequency-dependent compliance of viscoelastic Windkessel resolves contradictions in elastic Windkessels. Medical Engineering & Physics, 20, 502-514. doi:10.1016/S1350-4533(98)00055-1
- Stergiopulos, N., Westerhof, B.E. and Westerhof, N. (1992) Total arterial inertance as the fourth element of the Windkessel model. American Journal of Physiology— Heart and Circulatory Physiology, 276, 81-88.
- Grant, B.J.B. and Paradowski, L.J. (1987) Characterization of pulmonary arterial input impedance with lumped parameter models. American Journal of Physiology— Heart and Circulatory Physiology, 252, 585-593.
- Burattini, R. and Gnudi, R. (1982) Computer identification of models for the arterial tree input impedance: Comparison between two new simple models and first experimental results. Medical and Biological Engineering and Computing, 20, 134-144. doi:10.1007/BF02441348
- Burattini, R. and Di Salvia, P.O. (2007) Development of systemic arterial mechanical properties from infancy to adulthood interpreted by four-element Windkessel models. Journal of Applied Physiology, 103, 66-79. doi:10.1152/japplphysiol.00664.2006
- Kolh, P., D’Orio, V., Bernard, L., Gerard, P., Gommes, C. and Limet, R. (2000) Increased aortic compliance maintains left ventricular performance at lower energetic cost. European Journal Cardio-Thoracic Surgery, 17, 272-278. doi:10.1016/S1010-7940(00)00341-9
- Sharp, K.M., Pantalos, G.M., Minich, L., Tani, L.Y., McGough, E.C. and Hawkins, J.A. (2000) Aortic input impedance in infants and children. Journal of Applied Physiology, 88, 2227-2239.
- Rager, G.N., Westerhof, N. and Noordergraaf, A. (1965) Oscillatory flow impedance in electrical analog of arterial system: Representation of sleeve effect and non-newtonian properties of blood. Circulation Research, 16, 121- 133. doi:10.1161/01.RES.16.2.121
- Frasch, H.F., Kresh, Y.J. and Noordergraaf, A. (1996) Two-port analysis of microcirculation: An extension of windkessel. American Journal of Physiology—Heart and Circulatory Physiology, 270, 376-385.
- Formaggia, L. and Veneziani, A. (2003) Reduced and multiscale models for the human CVS. Technical Report, PoliMI, Milan.
- Avolio, A.P. (1980) Multi-branched model of the human arterial system. Medical and Biological Engineering and Computing, 18, 709-718. doi:10.1007/BF02441895
- Beyar, R., Hausknecht, M.J., Halperin, H.R., Yin, F.C. and Weisfeldt, M.L. (1987) Interaction between cardiac chambers and thoracic pressure in intact circulation. American Journal of Physiology—Heart and Circulatory Physiology, 253, 1240-1252.
- Santamore, W.P. and Burkhoff, D. (1991) Hemodynamic consequences of ventricular interaction as assessed by model analysis. American Journal of Physiology—Heart and Circulatory Physiology, 260, 146-157.
- Ursino, M. (1998) Interaction between carotid baroregulation and the pulsating heart: A mathematical model. American Journal of Physiology—Heart and Circulatory Physiology, 275, 1733-1747.
- Žáček, M. and Krause, E. (1996) Numerical simulation of the blood flow in the human CVS. Journal of Biomechanics, 29, 13-20. doi:10.1016/0021-9290(95)00027-5
- Chen, S., Zhang, S., Gong, Y., Dai, K., Sui, M., Yu, Y. and Ning, G. (2008) The role of the autonomic nervous system in hypertension: A bond graph model study. Physiological Measurement, 29, 473-495. doi:10.1088/0967-3334/29/4/005
- Heldt, T., Shim, E.B., Kamm, R.D. and Mark, R.G. (2002) Computational modeling of cardiovascular response to orthostatic stress. Journal of Applied Physiology, 92, 1239- 1254.
- Noordergraaf, A., Verdouw, P.D. and Boom, H.B.K. (1963) The use of an analog computer in a circulation model. Progress in Cardiovascular Diseases, 5, 419-439. doi:10.1016/S0033-0620(63)80009-2
- O’Rourke, M.F. and Avolio, A.P. (1980) Pulsatile flow and pressure in human systemic arteries. Studies in man and in a multibranched model of the human systemic arterial tree. Circulation Research, 46, 363-372. doi:10.1161/01.RES.46.3.363
- Olansen, J.B., Clark, J.W., Khoury, D., Ghorbel, F.H. and Bidani, A. (2000) A closed-loop model of the canina cvs that includes ventricular interaction. Computer and Biomedical Research, 33, 260-295. doi:10.1006/cbmr.2000.1543
- Ursino, M. and Magosso, E. (2003) Role of short-term cardiovascular regulation in heart period variability: A model study. American Journal of Physiology—Heart and Circulatory Physiology, 284, 1479-1493.
- Ursino, M. (1999) A mathematical model of the carotid baroregulation in pulsating conditions. IEEE Transactions on Biomedical Engineering, 46, 382-392. doi:10.1109/10.752935
- Westerhof, N., Lankhaar, J.W. and Westerhof, B.E. (2009) The arterial Windkessel. Medical and Biological Engineering and Computing, 47, 131-141. doi:10.1007/s11517-008-0359-2

