Journal of Geographic Information System
Vol.06 No.05(2014), Article ID:51133,12 pages
10.4236/jgis.2014.65047
Spatial and Temporal Evolution of the Static Water Level of the Cuauhtemoc Aquifer during the Years 1973, 1991 and 2000: A Geographical Approach
Luis C. Alatorre1*, Rolando E. Díaz2*, Sonia Miramontes1, Luis C. Bravo1, Erick Sánchez1
1División Multidisciplinaria de la UACJ en Cuauhtémoc, Universidad Autónoma de Ciudad Juárez, Chihuahua, México
2El Colegio de Sonora, Calle Obregón #54, Col. Centro, Hermosillo, México
Email: *luis.alatorre@uacj.mx, *rdiaz@colson.edu.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 August 2014; revised 20 September 2014; accepted 15 October 2014
ABSTRACT
In hydrogeology it is of great interest to examine the temporal and spatial evolution of aquifers. There are different ways of modeling an aquifer: physical models, models based on analog and mathematical techniques. Usually, mathematical techniques involve complex operations difficult to understand for some people, such as differential or partial equations. In contrast, our method requires only a basic knowledge of geometry and trigonometry. Moreover, it is only necessary to know the static level of the aquifer at three different dates. Of course, the results may be limited compared to those that use advanced mathematical methods; however, our method provides a first approximation to determine the behavior of the aquifer through time. Overall, our results allowed us to follow the evolution of the aquifer in detail of various areas of increased extraction and in which removal has been increasing, but also of areas with a considerable recharge during the study period.
Keywords:
Hydrogeology, Spatial and Temporal Evolution, Static Water Level, Cuauhtemoc Aquifer, Chihuahua, Mexico

1. Introduction
The amount of water available in the world is approximately 1.386 million cubic kilometers (km3), of which only 2.5% is fresh water. Most of the freshwater (68.7%) is concentrated as ice in glaciers and mountain regions, 29.9% is stored in aquifers, and only 0.26% is found in lakes, reservoirs and rivers [1] . Looking at the amount of fresh water available in terms of global runoff, it is important to consider that the amount of water stored in all the world’s rivers is 2000 km3, much less than the annual extraction of 3800 km3 [2] . In the last decades, it has been acknowledged that there is a global crisis in terms of the quantity and quality of freshwater. In general terms, population and economic growth have been the major factors leading to this situation. The global report, World Water Vision: Making Water Everybody’s Business, estimates that 20% of the world population has no access to potable water and 50% has no access to adequate sanitation [3] .
According to Shiklomanov (1998), around 10,000,000 km3 of fresh water are stored in aquifers. Groundwater is used by about two billion people worldwide, with an annual extraction of between 600 and 700 km3, which is approximately 20% of all the fresh water consumed worldwide [1] [4] . Among the various economic activities, agriculture is the largest consumer of water worldwide (70%), followed by industry (20%) and households (10%) [4] . In global terms, surface water is by far the most important source of supply. However, this panorama is different in many areas of the world, as groundwater is substituting surface water as the primary and preferred source of water; in South Asia, for example, groundwater supplies approximately 50% of the irrigation water [5] . It is also recognized that groundwater has become the main source of water resources for urban centers through- out the world [6] [7] .
In Mexico in 2010, about 37% of the total volume of water licensed for consumptive uses, that is, uses that consume water in the activity itself, comes from groundwater [8] . The main use of grouped water in Mexico is agricultural, which includes agriculture, aquaculture, livestock, and other activities; the licensed volume is about 61,800 million cubic meters per year (m3∙year−1), of which 33.8% is extracted from groundwater [9] . On the other hand, of the 11,400 million m3∙year−1 licensed nationwide for urban public and domestic uses, 62.2% comes from groundwater [9] .
According to the National Water Commission (CONAGUA), of the 653 aquifers in Mexico, 32 were overexploited in 1975, that is to say, more water was being extracted from those 32 aquifers than it was recharged [9] . In 1985, there were 80 overexploited aquifers, while by December 31, 2009, 100 aquifers were being overexploited; 50.6% of all groundwater used nationally was extracted from those aquifers. It is a disturbing fact that more than half of the groundwater used in Mexico comes from overexploited aquifers, but even more alarming is that, according to the National Water Commission [9] , the agricultural use of grouped groundwater has increased 23.2% from 2001 to 2009, and urban public and domestic use of groundwater has increased 30.3% in the same period.
In addition, the overexploitation of aquifers causes several environmental impacts, such as the phenomenon of soil salinity and the presence of brackish groundwater. According to CONAGUA (2011), by of the end 201031 aquifers had been identified in which there was presence of saline soils and brackish water, mainly located in the Baja California peninsula and the Mexican highlands. In addition, 18 coastal aquifers across the country presented saltwater intrusion.
Most of the overexploited aquifers or with saline intrusion are located in northern and central Mexico [9] . This situation can be explained by the differences in the spatial distribution of surface water and the country’s population, as described below.
Mexico, located between 32˚ and 14˚ degrees north latitude and 118 and 86˚ west longitude, is a country with very heterogeneous conditions of temperature and pluvial precipitation. Mexico has a continental surface of 1,959,248 square kilometers (km2), with a predominantly arid or semi-arid climate in the north and center, and sub-humid and humid in the south and southeast. Thus, while in the north, on the border with the United States of America, annual precipitation is below 500 millimeters (mm), in the south-southeast of the country it is possible to find values above 2000 mm per year [9] .
Besides this variety of physical aspects, Mexico has considerable regional demographic disparities. The Mexican population of nearly 112 million [10] , has quadrupled in the past 60 years. In recent decades, the largest population and economic growth has occurred in areas with low pluvial precipitation. Seventy-seven percent of the population lives in the arid or semiarid regions of central and northern Mexico, where there is only 31% of the renewable water. In contrast, southern and southeastern Mexico has 69% of the renewable water, but only 23% of the national population [9] .
These asymmetries exert a geographically differentiated pressure on groundwater resources, and explain a problem that is most noticeable in north-central Mexico [11] . Of the 100 already overexploited aquifers nationwide in 2009, 72 are located in the states of Sonora, Chihuahua, Baja California, Baja California Sur, Coahuila, Durango, Nuevo Leon, Guanajuato, Puebla, San Luis Potosi, Zacatecas, Estado de Mexico and Queretaro [8] . These entities are located in north-central Mexico and, in geographical terms, correspond mostly to the arid and semi-arid regions of the country. In regions where the availability of surface water is low, aquifers play a major role, as they are sometimes the only source of water for human consumption and the development of economic activities.
Mathematical models have greatly evolved in recent decades and have become a very good tool for the support of decision-making related to the sustainable and efficient management of water resources, since they allow simulating the temporal evolution (past, present, future) of the static levels of aquifers, and evaluating a growing number of scenarios: 1) increase in the number of extraction wells; 2) effects of climate change on precipitation; 3) effects of changes in the rates of natural and artificial recharge; 4) effect of new policies for the administration of water resources, and so on [12] -[19] . There are three basic types of models that have been used in hydrogeology, physical, analog and mathematical, the mathematical or digital models being the more commonly used today; these models use numerical methods to solve the differential equation of groundwater movement, flexibility being their main advantage. However, the main disadvantage of trying to implement these types of models is the large amount of data required, while in most cases the only information available is specific measures of static levels in wells.
One of the main objectives pursued by the study of aquifers is to understand the temporal and spatial evolution of the depth of static water levels, which is a first step to begin to understand the historical behavior of groundwater. Data from punctual measurements of static water levels in extraction wells can be highly relevant information. By complementing this information with interpolation methods, it is possible to obtain the spatial distribution of groundwater levels for each of the dates on which the data were recorded; this, in turn, will reveal the temporal and spatial variations in the depth of the static levels. Currently, many robust interpolation methods have been used to determine the spatial distribution of groundwater levels in aquifers, and many have been discussed in the literature [20] -[23] . In general, there are numerous interpolation methods, but no model yields optimal results in all cases of study; therefore, the best interpolation method depends on the characteristics of the data and the geographic conditions. The implementation of these interpolation methods in geographic information systems (GIS) has been an important tool in the analysis of data points from static water levels of aquifers in different study regions [24] -[33] . For example, to understand the temporal and spatial variations of groundwater depth in the Minquin Oasis, in the Shiyang river basin, were used the records of the static water levels of 48 observation wells for the period 1981-2003, which allowed them to compare different interpolation methods [33] . It should be noted that a temporal analysis of the spatial evolution of groundwater levels was done in our study, considering each of the maps predicted by the interpolation method in dependently, which certainly limited the potential to integrate information with geometrical and trigonometrical mathematical methods.
Therefore, the overall objective of this study was to develop a new methodology based on point data of static water levels and interpolation methods, to obtain and integrate spatially distributed information of static water levels in different periods (years) that allow us to understand the dynamics of groundwater levels (recharge vs discharge). Thus, the specific objectives were: 1) selection and application of an interpolation method that allows us to determine the optimal spatial distribution of groundwater levels for each of the recorded years (1973, 1991 and 2000) in order to better analyze the temporal and spatial variations of those levels; 2) once the values of the static water levels of the aquifer and their distribution were obtained, we determined the exchange rate, in meters per year, of the periods 1973-1991 and 1991-2000, using geometrical and trigonometrical mathematical methods. Our results confirmed that excessive groundwater extraction is causing a serious reduction of groundwater static levels in the study area.
2. Study Area
As study area, we selected the aquifer recharge area of the Laguna de Bustillos basin, mostly contained within the city of Cuauhtémoc, Chihuahua. It lies between the coordinates 28˚13'19'' and 28˚59'35'' N, and 106˚34'39'' and 107˚10'33'' W (Figure 1), with a total area of 2.035 km2. According to the National Water Commission

Figure 1. Delimitation of the area of the aquifer: (a) General location of the Cuauhtémoc aquifer; (b) Border of the Cuauhtémoc aquifer considered for the study.
(2010), the location has an annual precipitation of 415.7 mm, with a semi-dry temperate climate and an average annual temperature of 14.6˚C - 38˚C throughout the year.
It is a plain irregularly enclosed by the mountains of Pedernales, San Juan, Salitrera, Chuchupate, Sierra Azul and Rebote, where the only contribution of water comes from rain. Across this surface, the existing dynamic has led to an overexploitation of water resources, as 569.4 Mm3 are extracted annually and used in the following manner: 92.7% for agricultural use, 4% for urban use, and 3.3% for livestock activities. Given a natural recharge of 115 Mm3 annually, the resource is extracted at a greater rate than it is recharged.
The Cuauhtémoc aquifer is located in the endorheic basin that forms the Cuauhtémoc Valley. This valley has an average elevation of 2000 meters above sea level, and is surrounded on the north, east, west and south by a set of peaks averaging 2400 m above sea level, with some peaks reaching up to 2600 m. These elevations are formed by extrusive igneous rocks, ignimbrites, rhyolites, dacites, dacitic tuffs, and esites and basalts, while the valley lowlands are made up of continental sedimentary layers-conglomerates, lacustrine deposits, foothill and alluvial deposits of the Tertiary and more recent periods [34] .
The flanks of the valley include elevations formed by basaltic and esites and basalts, which, having very low permeability, constitute barriers against the flow of water to neigh boring basins. The oldest rocks in the area correspond to fluidal rhyolites from the Tertiary that usually make up the core of mountains and hills, and some highlands in the SW part of the valley. They are essentially impervious to water and thus favor storm water runoff towards the plains and foothills. It is in the latter that the highest rates of infiltration occur [35] .
CONAGUA (1991) indicates that the Bustillos aquifer behaves as a free aquifer. There is a single regional aquifer in the valley, and its recharge is provided by the infiltration of rainwater into the rock fractures and faults that delimit the valley. There are also recharge sources in the permeable sediments that surround the valley, and along the major streams that cross and empty into the Bustillos lagoon. The recharge comes mainly from rainwater falling into the basin, and at the date of publication of the reports, there was no evidence of water coming from neighboring basins.
If the map of equal elevation of the static levels is taken as reference, the groundwater flow network indicates that all elevations surrounding the valley contribute to the aquifer. Due to the presence of different levels of permeability, the contributions are different from one elevation system to another (right margin and left margin of the valley), but, in general, they seem considerably lower west and southwest of Cuauhtémoc city, where the stratigraphy and impermeability of the substrate do not favor the infiltration of rain [34] .
Groundwater flow follows different directions: north-central, south-central, from east to center and west to the center [36] . Originally, the flow converged in the Lagoon area, but due to the pumping effect it is now concentrated southwest of it [35] . Converge in the portion bounded to the year 2002 for the equipotential 2070 m.s.n.m.
Apparently, the Bustillos lagoon is indicative of the static water level of the aquifer. CONAGUA (1991) indicates that a portion of the flow goes through beneath the ground and out of the basin through a fault system with a northwest-southeast direction; one of the faults crosses the lagoon longitudinally. There is no mention about measurements, but it is suggested that this flow is considerably less than evaporation and pumping, which are the main groundwater discharges.
3. Data and Methodology
3.1. Collection and Debugging of the Database
A Digital Elevation Model (DEM) corresponding to the state of Chihuahua was obtained from the official website of the United States Geological Survey (USGS), with a spatial resolution of 90 m; to ensure that all pixels were hydrologically connected, we used a hole-filling algorithm [37] . Once the DEM was corrected, we proceeded to evaluate the static water levels as accurately as possible, ignoring anomalous values, that is to say, values above the DEM.
The isolines of static water levels in the aquifer basin belonging to Laguna de Bustillos were digitized using images from geohydrological studies done by the National Water Commission in the years 1973, 1991 and 2000 (Figure 2). Once digitized, the vertices of each isoline were extracted in order to assess some of the methods of the Geostatistical interpolation analysis module contained in the ArcGIS 9.3 software.
3.2. Interpolation Methods
In many natural phenomena, we observe certain regularity in the manner in which they occur, which allows us to induce the behavior of a phenomenon in situations that we have not measured directly. In the mathematics of numerical analysis, estimating new points based on the knowledge of a discrete set of points is termed interpolation. For example, in engineering and other sciences, it is frequent to have a certain number of points obtained by sampling or from an experiment and try to build a function that fits them in order to predict the spatial distribution and the values of the points for which there is no data. As such, interpolation methods can be used to estimate unknown values from the data of a geographical point such as elevations, precipitation, chemical concentrations, noise levels and more.
Thus, from the vertices obtained from digitized isolines of the static water levels of the aquifer of Laguna deBustillos (Figure 2), we proceeded to interpolate the static water levels of 1973 using the Geostatistical Analisys module in the ArcGIS 9.3 software and the following methods: 1) Inverse Distance Weighted (IDW); 2) Global polynomial interpolation; 3) Local polynomial interpolation; 4) Radial Basis Function (RBF). There are several radial basis function methods: completely regularized spline, spline with tension, multiquadratic, multiquadratic inverse and thin plate spline; each of these techniques allows us to interpolate an optimal smoothing level for the surface to be predicted, depending, to a large degree, on the mean square error, which should be as close to zero as possible; the last radial basis function method is Ordinary Kriging. Once we obtained the predictions from each of these techniques for the year 1973, the prediction errors were evaluated and the optimal method for generating a distribution map for the years1991 and 2000 was determined; this map is the one that best represents the spatial distribution of the static water levels in the aquifer of the Laguna de Bustillos basin.
3.3. Correlation between Periods
Once we had the value of the static water level of the aquifer for each pixel in the grid at the three different dates, the following formula was used to determine the exchange rate, in meters per year, of each period.
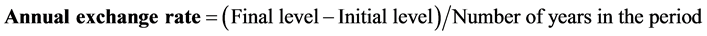
Something that is very important to analyze in the behavior of an aquifer is how it has developed over time. This work argues that this can be achieved by analyzing the correlation between the exchange rate of two pe- riods. The values were already normalized by the annual exchange rate for each period so that the data is comparable. For this study, we plotted the annual exchange rate of period X, or the more recent period, on the x-axis


Figure 2. Static water level curves for the years: (a) 1973; (b) 1991; and (c) 2000.
of a Cartesian plane, and the annual exchange rate of period Y, or the period immediately before the most recent, on the y-axis.
If the annual exchange rate of period X is equal to that of period Y, that is, the discharge or recharge trend of the aquifer is the same between periods, the relationship between the two periods would be given by a straight line whose equation is x = y, or, put another way, x − y = 0 (see Figure 3). Due to the limited number of likely sets of values (x, y) that satisfy the equation (the exchange rate of period X must be equal to that of period of Y), we propose a tolerance variation, changing a line through an area determined by two lines. For example, if we consider that 1 m/year would be an adequate tolerance level to determine whether the annual exchange of the two periods is significant or not, the limits of this tolerance would be given by the equations x − y =1 and x − y = −1 (see Figure 3).
Finally, in our analysis we intended to divide the annual exchange rate of period X, or the most recent period, to differentiate between one type of behavior and another. This is because period X provides the latest diagnosis of the situation of the aquifer. Continuing with the example of 1 m/year, the division would be made graphically
Figure 3. Correlation between periods.
depending on whether the annual exchange rate of period X is greater or less than ± 1 m/year. These new boundaries are represented in Figure 3 as the equations x = 1 and x = −1.
The inclusion of these limits (equations) results in 11 classifications, listed in red in Figure 3 and described below:
1) Exchange rate greater than 1 m/year in period X and a difference greater than 1 m/year between period X and period Y (x > 1 & x − y > 1).
2) Exchange rate greater than 1 m/year in period X and a difference less or equal to 1 m/year and greater than or equal to −1 m/year between period X and period Y (x > 1 & x − y ≤ 1 & x − y ≥ −1).
3) Exchange rate greater than 1 m/year in period X and a difference less than −1 m/year between period X and period Y (x > 1 & x − y < −1).
4) Exchange rate greater than 0 and less or equal to 1 m/year in period X and a difference greater than 1 m/year between period X and period Y (x > 0 & x ≤ 1 & x − y > 1).
5) Exchange rate greater than 0 and less or equal to 1 m/year in period X and a difference less than −1 m/year between period X and period Y (x > 0 & x ≤ 1 & x − y < −1).
6) Exchange rate less than −1 m/year in period X and a difference less than −1 m/year between period X and period Y (x < −1 & x − y < −1).
7) Exchange rate less than −1 m/year in period X and a difference less or equal to 1 m/year and greater or equal to −1 m/year between period X and period Y (x < −1 & x − y ≤ 1 & x − y ≥ −1).
8) Exchange rate less than −1 m/year in period X and a difference greater than 1 m/year between period X and period Y (x < −1 & x − y > 1).
9) Exchange rate less than 0 and greater or equal to −1 m/year in period X and a difference less than −1 m/year between period X and period Y (x < 0 & x ≥ −1 & x − y < −1).
10) Exchange rate less than 0 and greater or equal to −1 m/year in period X and a difference greater than 1 m/year between period X and period Y (x < 0 & x ≥ −1 & x − y > 1).
11) Exchange rate greater or equal to −1 and less or equal to 1 m/year in period X and a difference greater or equal to −1 and less or equal to 1 m/year between period X and period Y (x ≥ −1 & x ≤ 1 & x − y ≥ −1 & x − y ≤ 1).
4. Results
4.1. Interpolations with Geostatistical Analysis
Using values representing static aquifer levels of the Laguna de Bustillos basin, it was possible to compare different methods of interpolation and select the most optimal in terms of prediction errors, that is, mean and mean square errors.
There are various works, such as Aguilar et al. [38] , Kravchenko and Bullock [39] , Kravchenko [40] and Schloeder et al. [41] , that do not intend to establish a definitive method, but seek to compare and determine the most optimal for the case studied. Thus, Table 1 shows the parameters used in the 9 methods of interpolation for the static water level values of the year 1973. In this case, the kernel function indicates a variant of the methods of interpolation, generally very similar to each other. The difference lies in the amount of data that is necessary to introduce to execute such method; the value of p is derived from that data, calculated from a whole group of formulas that are inherent to each procedure.
To find the predicted values by mean of the interpolation methods, one sector was selected by a search form, except for the Ordinary Kriging method which four search sectors were chosen. Another key parameter consists in defining the number of search neighbors; 15 were selected in most cases for all values to carry out the prediction process. In addition, the optimizer parameter determined by GIS was used in all cases in order to reduce the prediction errors.
The regularized spline radial basic function method showed more optimal values, with a mean square error of 1245 and an average error −0.017. Once we determined the interpolation method that best predicts the values of the static water level of the year 1973, the remaining years (1991 and 2000) were interpolated. The summary of the prediction errors for each year is shown in Table 2, and the results of these interpolations are shown in Figure 4. The results for each of the interpolated years show that the prediction errors obtained are acceptable in terms of order of magnitude, whereby these maps of spatial distribution of the static water level are also acceptable (Table 2).
Table 1. Parameters used for the different methods of interpolation and prediction errors.
Table 2. Prediction errors for the three years evaluated by the method of local polynomial interpolation.


Figure 4. Interpolation of the static water level from the geostatistical regularized spline method for each recorded year: (a) 1973; (b) 1991; and (c) 2000.
4.2. Correlation between Periods
If we distribute the values of each pixel across the map according to the classification by periods proposed in Figure 5 and Figure 6, we obtain the following geographical distribution.
Adapting the description provided in the methodology section to the evolution of the levels of aquifer discharge or recharge, we elaborated the following explanation of the classes:
1) Discharge greater than 1 m/year in the period 91-00 and an increase greater than 1 m/year in 91-00 compared to 73-91 (high discharge with a high increase).
2) Discharge greater than 1 m/year in the period 91-00 and an increase or decrease of −1 to 1 m/year in 91-00 compared to 73-91 (high discharge with a low increase or decrease).
3) Discharge greater than 1 m/year in the period 91-00 and a decrease greater than −1 m/year in 91-00 compared to 73-91 (high discharge with a high decrease).
4) Discharge under 1 m/year in 91-00 and an increase greater than 1 m/year in 91-00 compared to 73-91 (low discharge with a high increase).
Figure 5. Correlation between periods of the Cuauhtémoc aquifer.
Figure 6. Classification of the static water levels.
5) Discharge under 1 m/year in 01-00 with a decrease greater than −1 m/year in 91-00 compared to 73-91 (low discharge with a high decrease).
6) Recharge greater than −1 m/year in 91-00 and a decrease greater than −1 m/year in 91-00 compared to 73- 91 (high recharge with a high decrease).
7) Recharge greater than −1 m/year in 91-00 and an increase or decrease of −1 to 1 m/year in 91-00 compared to 73-91 (high recharge with a low increase or decrease).
8) Recharge greater than −1 m/year in 91-00 and an increase greater than 1 m/year in 91-00 compared to 73- 91 (high recharge with a high increase).
9) Recharge below −1 m/year in 91-00 and a decrease greater than −1 m/year in 91-00 compared to 73-91 (low recharge with a high decrease).
10) Recharge below −1 m/year in 91-00 and an increase greater than 1 m/year in 91-00 compared to 73-91 (low recharge with a high increase).
11) Discharge or recharge between −1 and 1 m/year in 91-00 and an increase or decrease between −1 to 1 m/year in 91-00 compared to 73-91 (low recharge or discharge with a low increase or decrease).
5. Conclusions
As shown in the last chapter, the methodology used in this work requires only to know the static water level of the aquifer at three different dates. Of course, the results may be limited compared to those produced by advanced mathematical methods; however, our method provides an approximation to determine the behavior of the aquifer through time.
As can be seen in the map of Figure 6, this method allows us to distinguish in detail the evolution of the aquifer in various areas. For example, the first classification, high discharge with a high increase of 1 m/year, used as an example in this study, corresponds to areas with higher extraction and where extraction has been increasing (red). Furthermore, class 6 would be the area where there is a considerable recharge, even an increasing one. Note that there are no values for Classes 3 and 8.
Acknowledgements
This research was financially supported by the project “Urban Sustainability: Geospatial Analysis of the Interaction of Water and Land Use in the Peri-Urban Area of Cuauhtémoc, Chihuahua, México”, funded by PROMEP, Secretariat of Public Education, México. The support of the Inter-American Institute for Global Change Research (IAI, project CRN3056, which is supported by the US National Science Foundation grant GEO-1128040). This work would not have been possible without the collaboration of each of the co-authors.
References
- Shiklomanov, I. (1998) World Water Resources: Modern Assessment and Outlook for 21st Century. Federal Service of Rusia for Hidrometorology & Environment Monitoring State, Hidrological Institute, San Petesburgo.
- Oki, T. and Kanae, S. (2006) Global Hydrological Cycles and World Water Resources. Science, 313, 1068-1072.
- Cosgrove, W.J. and Rijsberman, F.R. (2000) World Water Vision: Making Water Everybody’s Business. Earthscan Publications Ltd., London.
- Struckmeier, M., Rubin, Y. and Jones, J.A. (2005) Groundwater-Reservoir for a Thirsty Planet? Planet Earth, International Union of Geological Sciences y United Nations Educational Scientific and Cultural Organisation, Leiden.
- Giordano, M. and Villholth, K.G. (2007) The Agricultural Groundwater Revolution: Setting the Stage. In: Giordano, M. and Villholth, K.G., Eds., The Agricultural Groundwater Revolution: Opportunities and Threats to Development, Cromwell Press, International Water Management Institute, Colombo, 1-4.
- Burke, J. and Moench, M. (2000) Groundwater and Society: Resources, Tensions and Opportunities. Naciones Unidas, Nueva York.
- Shah, T., Burke, J. and Villholth, K.G. (2007) Groundwater: A Global Assessment of Scale and Significance. In: Molden, D., Ed., Water for Food, Water for Life: A Comprehensive Assessment of Water Management in Agriculture, International Water Management Institute, Londres: Earthscan, Colombo, 395-423.
- CONAGUA (2011) Atlas del Agua en México. SEMARNAT-Gobierno Federal, 142 p.
- CONAGUA (2011) Estadísticas del Agua en México. Comisión Nacional del Agua. www.conagua.gob.mx
- INEGI (2010) XII Censo general de Población y vivienda. Instituto Nacional de Geografía y Estadística.
- Marin, L.E. (2002) Perspectives on Mexican Ground Water Resources. Groundwater, 40, 570-571. http://dx.doi.org/10.1111/j.1745-6584.2002.tb02542.x
- Bauer, P., Gumbricht, T. and Kinzelbach, W. (2006) A Regional Coupled Surface Water/Groundwater Model of the Okavango Delta, Botswana. Water Resources Research, 42, Article ID: W04403. http://dx.doi.org/10.1029/2005WR004234
- Carroll, R.W.H., Pohll, G.M. and Hershey, R.L. (2009) An Unconfined Groundwater Model of the Death Valley Regional Flow System and a Comparison to Its Confined Predecessor. Journal of Hydrology, 373, 316-328. http://dx.doi.org/10.1016/j.jhydrol.2009.05.006
- Refsgaard, J.C., Højberg, A.L., Møller, I., Hansen, M. and Søndergaard, V. (2010) Groundwater Modeling in Integrated Water Resources Management―Visions for 2020. Ground Water, 48, 633-648. http://dx.doi.org/10.1111/j.1745-6584.2009.00634.x
- Maxwell, R.M. and Kollet, S.J. (2008) Interdependence of Groundwater Dynamics and Land-Energy Feedbacks under Climate Change. Nature Geoscience, 1, 665-669. http://dx.doi.org/10.1038/ngeo315
- Scibek, J., Allen, D.M., Cannon, A.J. and Whitfield, P.H. (2007) Groundwater-Surface Water Interaction under Scena- rios of Climate Change Using a High-Resolution Transient Groundwater Model. Journal of Hydrology, 333, 165-181. http://dx.doi.org/10.1016/j.jhydrol.2006.08.005
- D’Agnese, F.A., Faunt, C.C., Hill, M.C. and Keith-Turner, A. (1999) Death Valley Regional Ground-Water Flow Model Calibration Using Optimal Parameter Estimation Methods and Geoscientific Information Systems. Advances in Water Resources, 22, 777-790. http://dx.doi.org/10.1016/S0309-1708(98)00053-0
- Gustafson, G., Gylling, B. and Selroos, J.O. (2009) The Äspö Task Force on Groundwater Flow and Transport of Solutes: Bridging the Gap between Site Characterization and Performance Assessment for Radioactive Waste Disposal in Fractured Rocks. Hydrogeology Journal, 17, 1031-1033. http://dx.doi.org/10.1007/s10040-008-0419-6
- Tiedeman, C.R., Hill, M.C., D’Agnese, F.A. and Faunt, C.C. (2003) Methods for Using Groundwater Model Predictions to Guide Hydrogeologic Data Collection, with Application to the Death Valley Regional Groundwater Flow System. Water Resources Research, 39, 1010. http://dx.doi.org/10.1029/2001WR001255
- Caruso, C. and Quarta, F. (1998) Interpolation Methods Comparison. Computers and Mathematics with Applications, 35, 109-126. http://dx.doi.org/10.1016/S0898-1221(98)00101-1
- Li, X.Y., Song, D.M. and Xiao, D.N. (2005) The Variability of Groundwater Mineralization in Minqin Oasis. Acta Geographica Sinica, 60, 319-327.
- Theodossiou, N. and Latinopoulos, P. (2006) Evaluation and Optimisation of Groundwater Observation Networks Using the Kriging Methodology. Environmental Modelling and Software, 21, 991-1000. http://dx.doi.org/10.1016/j.envsoft.2005.05.001
- Theodossiou, N. and Latinopoulos, P. (2007) Evaluation and Optimisation of Groundwater Observation Networks Using the Kriging Methodology. Environmental Modelling and Software, 22, 414. http://dx.doi.org/10.1016/j.envsoft.2006.07.001
- Hutchinson, M.F. (1995) Interpolating Mean Rainfall Using Thin Plate Smoothing Splines. International Journal of Geographical Information Systems, 9, 385-403. http://dx.doi.org/10.1080/02693799508902045
- Collins, F.C. (1996) A Comparison of Spatial Interpolation Techniques in Temperature Estimation. Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling, Santa Barbara, 21-26 January 1996.
- Feng, J.M., Zhao, T.B. and Hang, Y.J. (2004) Intercomparison of Spatial Interpolation Based on Observed Precipitation Data. Climatic and Environmental Research, 9, 261-277.
- Fang, S.M., Qian, Z.T. and Li, Y.P. (2005) Comparison of Four Precipitation Spatial Interpolation Methods in Gansu. Journal of Arid Land Resources and Environment, 19, 47-50.
- Li, J., You, S.C. and Huang, J.F. (2006) Spatial Interpolation Method and Spatial Distribution Characteristics of Monthly Mean Temperature in China during 1961-2000. Ecology and Environment, 15, 109-114.
- Kenneth, K.E. (1996) Conceptualization and Characterization of Groundwater Systems Using Geographic Information Systems. Engineering Geology, 42, 111-118.
- Wang, J.L., Sun, J.S. and Zhang, J.Y. (2004) Crop Water Requirement Isoline Based on GIS and Geostatistics. Transactions of the CSAE, 20, 51-54.
- Wei, J.H., Wang, G.Q., Li, C.J. and Shao, J.L. (2003) Recent Advances Associated with GIS. Groundwater Resources Research, 2, 94-98.
- Xu, Y.Q. and Cai, Y.L. (2005) GIS-Based Analysis on Spatial-Temporal Change of Groundwater Level in the Hebei Plain. Acta Scientiarum Naturalium Universitatis Pekinensis, 41, 265-272.
- Sun, Y., Kang, S., Li, F. and Zhang, L. (2009) Comparison of Interpolation Methods for Depth to Groundwater and Its Temporaland Spatial Variations in the Minqin Oasis of Northwest China. Environmental Modelling and Software, 24, 1163-1170. http://dx.doi.org/10.1016/j.envsoft.2009.03.009
- CONAGUA (1991) Actualización del estudio geohidrológico, políticas de operación y proyecto de manejo del acuífero del Valle de Cuauhtémoc Chihuahua, Comisión Nacional del Agua. Contrato CNA-GRN-90-009, 186 p.
- CONAGUA (2000) Cuantificación de la extracción de agua subterránea en el acuífero de Cuauhtémoc Chihuahua, Comisión Nacional del Agua. Contrato GAS-011-PRO-2000. Tomo 1. 414 p.
- CONAGUA (2002) Determinación de la disponibilidad del agua en el acuífero de Cuauhtémoc. Estado de Chihuahua, México, D.F. ftp://ftp.conagua.gob.mx/SISI1610100117809/DR_0805-cuauhtemoc.pdf
- Planchon, O. and Darboux, F. (2001) A Fast, Simple and Versatile Algorithm to Fill the Depressions of Digital Elevation Models. Catena, 46, 159-176. http://dx.doi.org/10.1016/S0341-8162(01)00164-3
- Aguilar-Torres, M.A., Carvajal-Ramírez, F., Aguilar-Torres, F.J. and Agüera, F. (2001) Evaluación de diferentes técnicas de interpolación espacial para la generación de modelos digitales de elevación del terreno agrícola. Mapping, 74, 72-88.
- Kravchenko, A. and Bullock, D. (1999) A Comparative Study of Interpolation Methods for Mapping Soil Properties. Agronomy Journal, 91, 393-400. http://dx.doi.org/10.2134/agronj1999.00021962009100030007x
- Kravchenko, A.N. (2003) Influence of Spatial Structure on Accuracy of Interpolation Methods. Soil Science Society of America Journal, 67, 1564-1571. http://dx.doi.org/10.2136/sssaj2003.1564
- Schloeder, C.A., Zimmerman, N.E. and Jacobs, M.J. (2001) Comparison of Methods for Interpolating Soil Properties Using Limited Data. Soil Science Society of America Journal, 65, 470-479. http://dx.doi.org/10.2136/sssaj2001.652470x
NOTES

*Corresponding authors.





