Natural Science
Vol.5 No.9(2013), Article ID:36493,13 pages DOI:10.4236/ns.2013.59128
Analysis of non-linear reaction-diffusion processes with Michaelis-Menten kinetics by a new Homotopy perturbation method
![]()
1Government Higher Secondary School, Madurai, India; 2Department of Mathematics, The Madura College, Madurai, India *Corresponding Author: raj_sms@rediffmail.com
Copyright © 2013 Devaraj Shanthi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 18 June 2013; revised 18 July 2013; accepted 25 July 2013
Keywords: Oxygen Diffusion; Michaelis-Menten; Non-Linear Differential Equations; New Homotopy Perturbation Method; Numerical Simulation
ABSTRACT
This paper demonstrates the approximate analytical solution to a non-linear singular two-point boundary-value problem which describes oxygen diffusion in a planar cell. The model is based on diffusion equation containing a non-linear term related to Michaelis-Menten kinetics of enzymatic reaction. Approximate analytical expression of concentration of oxygen is derived using new Homotopy perturbation method for various boundary conditions. The validity of the obtained solutions is verified by the numerical results.
1. INTRODUCTION
Pharmacological and physiological experiments are being increasingly performed on thin vital tissue preparations known as slices. Oxygen diffusion for spherical cells in tissue preparations with Michaelis-Menten kinetics is developed by Bassom [1]. Rashevsky [2] modeled the kinetics for oxygen uptake by piecewise linear functions. Lin [3] argued that this supposed Michaelis-Menten [4] kinetics form would be a far more appropriate model. Lin’s [3] results were recomputed by McElwain [5]. Hiltmann et al. [6] proved that this Michaelis-Menten model for spherical cells possesses exactly one solution. This unique solution can only be precisely determined by recourse to numerical procedures, but useful lower and upper bounds on this true solution were given by Anderson et al. [7] and these were improved further by sharp polynomial approximations derived by Asaithambi et al. [8,9].
Finally Bassom et al. [1] mention that modern experiments in both biology and medicine use tissue slices to simulate hypoxia, that is a situation in which the tissue exhibits low oxygen consumption. Bassom et al. [1] consider a Michaelis-Menten uptake in a tissue slice and to provide both theoretical (limiting cases) and numerical analyses of the resulting equations. The purpose of this paper is to derive the approximate analytical expressions of concentration of oxygen for all values of the dimensionless parameters using new Homotopy perturbation method.
2. MATHEMATICAL FORMULATION OF THE PROBLEM
It is convenient to begin by considering a tissue slice within a Cartesian coordinate system which is aligned so that the slice in the 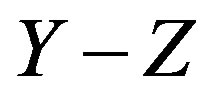 plane with the X-axis normal to the slice (Figure 1). For simplicity, the slice is assumed of infinite extent in the
plane with the X-axis normal to the slice (Figure 1). For simplicity, the slice is assumed of infinite extent in the 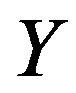 and
and  directions so
directions so
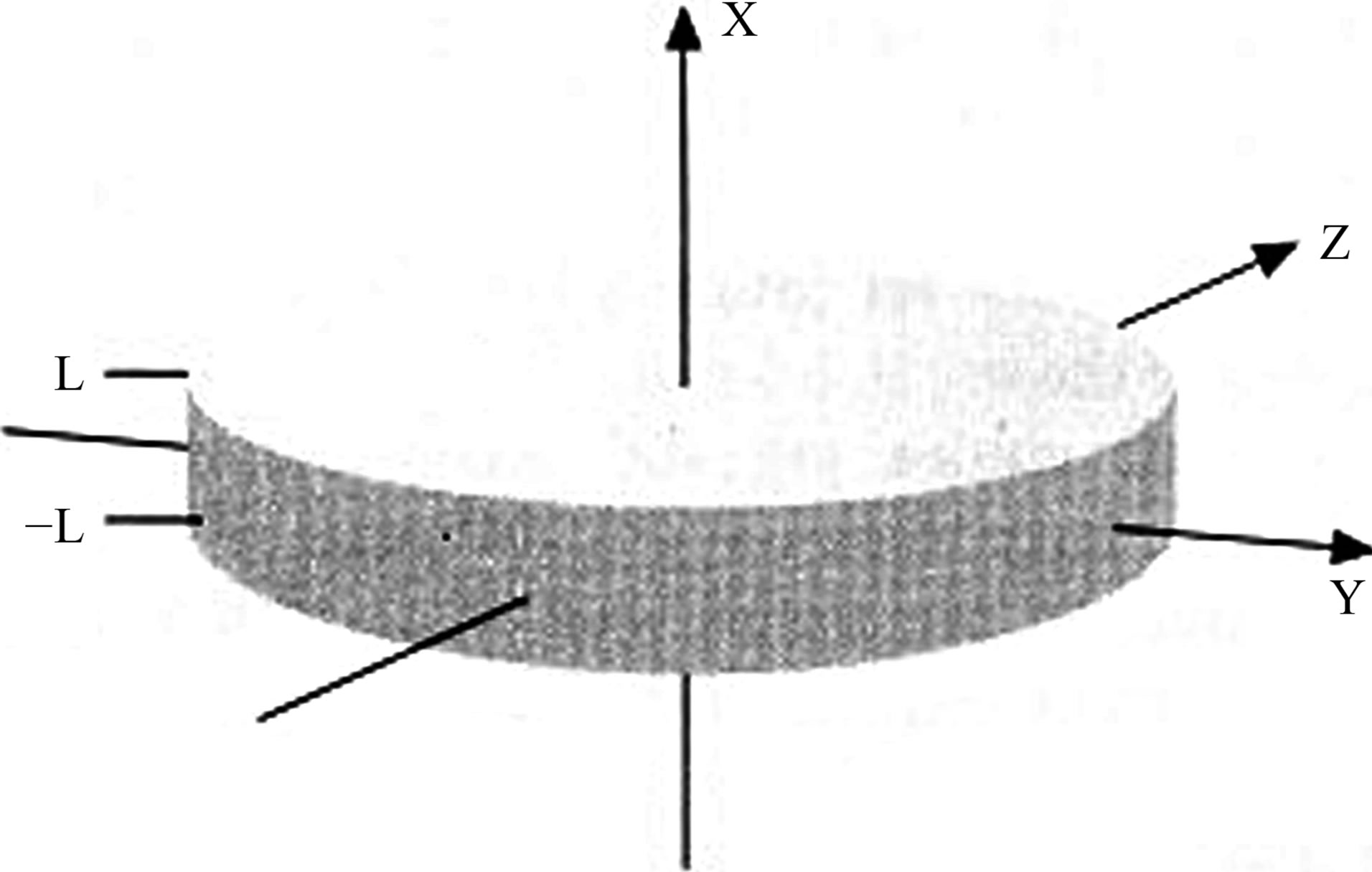
Figure 1. The geometry of the tissue slice and co-ordinate system.
that edges effects need not be considered. The slice is also taken to lie with in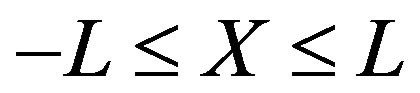 ,so that the surrounding oxygen bath lies above the slice where
,so that the surrounding oxygen bath lies above the slice where  and below it with
and below it with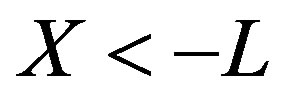 . If
. If 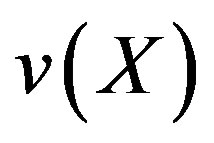 denote the oxygen concentration in the tissue then, by Fick’s law of diffusion, the uptake equation for the steady state is
denote the oxygen concentration in the tissue then, by Fick’s law of diffusion, the uptake equation for the steady state is
 (1)
(1)
where 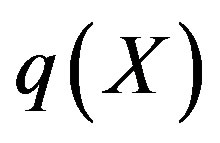 is the oxygen consumption rate which is non linear term in oxygen concentration. D is the constant diffusion coefficient for the tissue.
is the oxygen consumption rate which is non linear term in oxygen concentration. D is the constant diffusion coefficient for the tissue.
3. ANALYTICAL EXPRESSION OF CONCENTRATION OF OXYGEN USING NEW HOMOGOPY PERTURBATION METHOD
Linear and non-linear phenomena are of fundamental importance in various fields of science and engineering. Most models of real life problems are still very difficult to solve. Therefore, approximate analytical solutions such as Homotopy perturbation method (HPM) [10-23] were introduced. This method is the most effective and convenient ones for both linear and non-linear equations. Perturbation method is based on assuming a small parameter. The majority of non-linear problems, especially those having strong non-linearity, have no small parameters at all and the approximate solutions obtained by the perturbation methods, in most cases, are valid only for small values of the small parameter. Generally, the perturbation solutions are uniformly valid as long as a scientific system parameter is small. However, we cannot rely fully on the approximations, because there is no criterion on which the small parameter should exists. Thus, it is essential to check the validity of the approximations numerically and/or experimentally. To overcome these difficulties, HPM have been proposed recently.
Recently, many authors have applied the Homotopy perturbation method (HPM) to solve the non-linear boundary value problem in physics and engineering sciences [10-13]. Recently this method is also used to solve some of the non-linear problem in physical sciences [14-16]. This method is a combination of Homotopy in topology and classic perturbation techniques. Ji-Huan He used to solve the Lighthill equation [14], the Diffusion equation [15] and the Blasius equation [16,17]. The HPM is unique in its applicability, accuracy and efficiency. The HPM [18-23] uses the imbedding parameter p as a small parameter, and only a few iterations are needed to search for an asymptotic solution. The law of mass action of oxygen uptake leads to the following non-linear equations
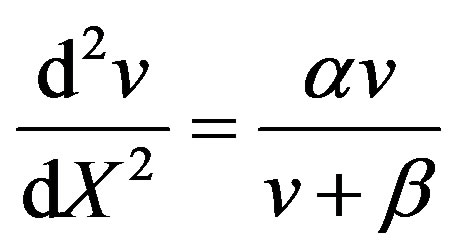 (2)
(2)
with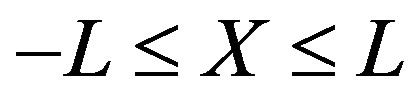 ,
, 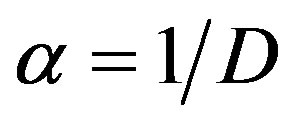 and β denote the Michaelis-Menten constant. The corresponding boundary condition is
and β denote the Michaelis-Menten constant. The corresponding boundary condition is
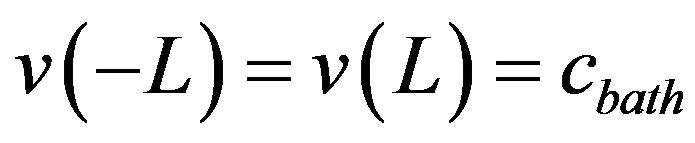 (3)
(3)
This boundary conditions reflect the fact that at the edges of the tissue the oxygen concentration matches that within the solution surrounding the preparation. By introducing the following dimensionless parameters
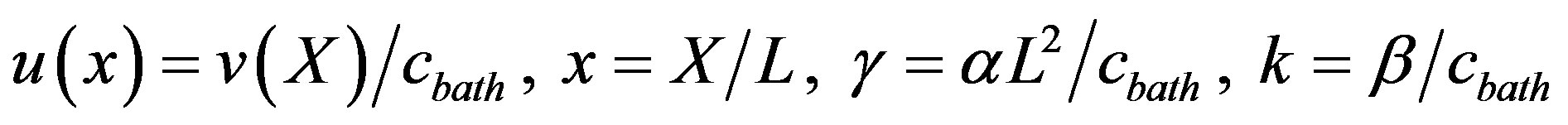 (4)
(4)
Eq.2 and the boundary conditions Eq.3 can be represented in the dimensionless form as follows:
Case (1)
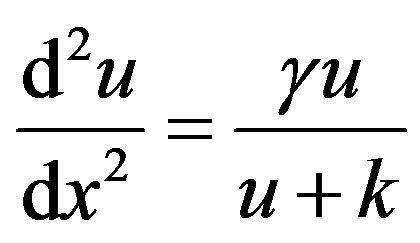 (5)
(5)
with the boundary conditions
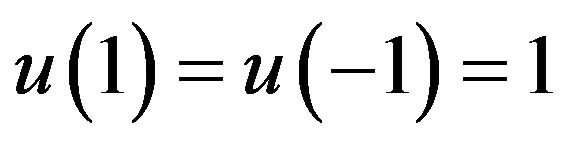 (6)
(6)
The basic concept of general Homotopy perturbation method is given in Appendix A. This problem is solved using new approach in Homotopy perturbation method (Appendix B). Using new Homotopy perturbation method [24], the approximate analytical solution of Eq.5 for the boundary condition Eq.6 is
 (7)
(7)
where the constant
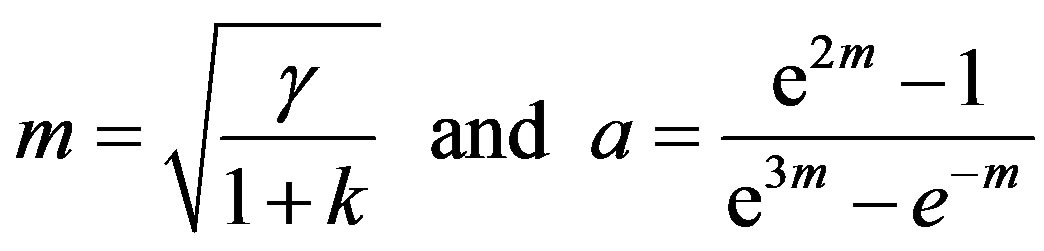 (8)
(8)
Case (2)
Here we consider the mass balance equation and the boundary conditions as follows:
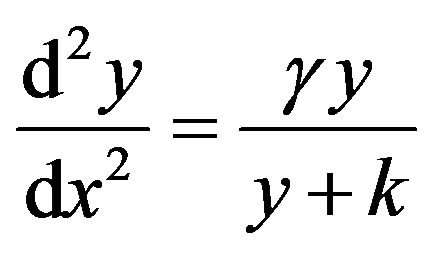 (9)
(9)
Now the boundary condition becomes
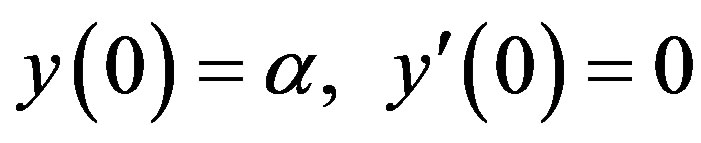 (10)
(10)
where 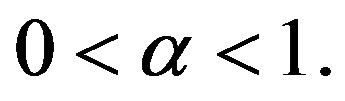 The approximate analytical solution of Eqs.9 and 10 using new Homotopy perturbation method (Appendix C) [24] is
The approximate analytical solution of Eqs.9 and 10 using new Homotopy perturbation method (Appendix C) [24] is
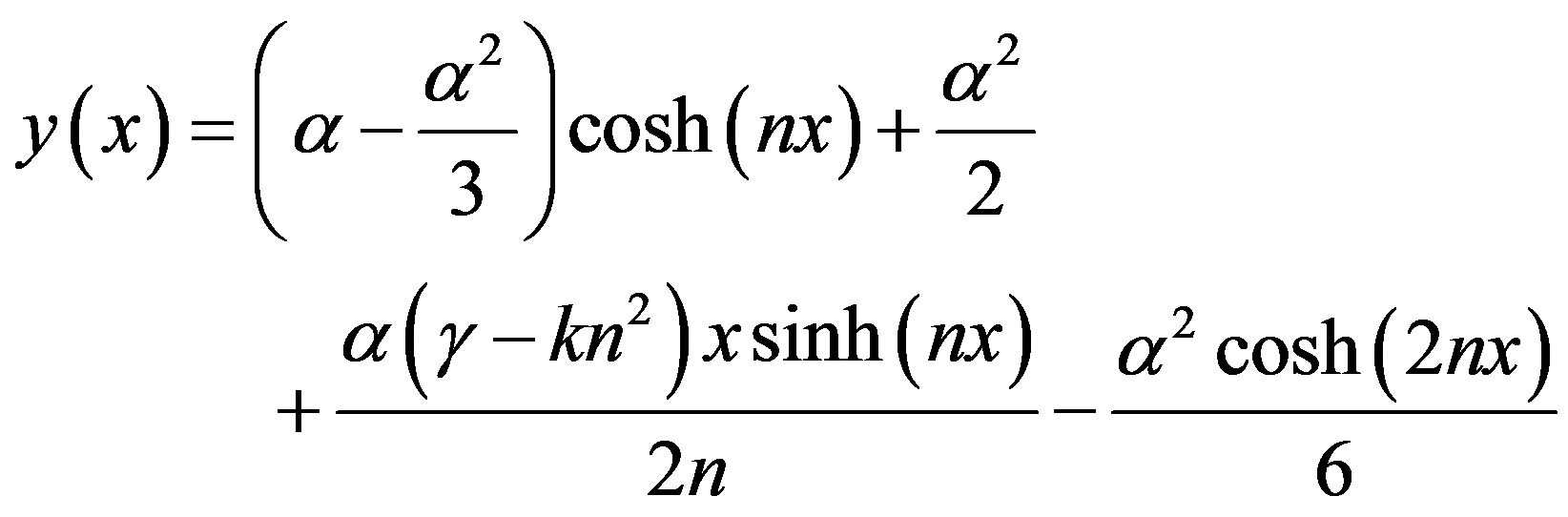 (11)
(11)
where
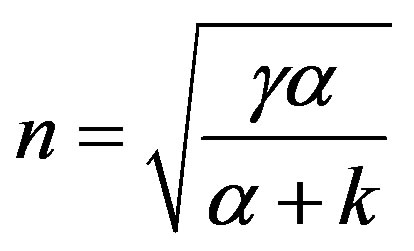 (12)
(12)
Case (3)
Now the non-linear boundary value problem is in the following form:
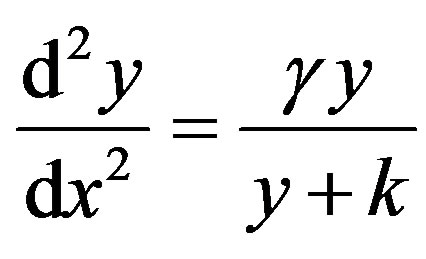 (13)
(13)
The boundary conditions is
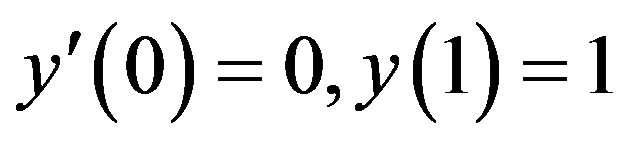 (14)
(14)
The approximate analytical solution of Eqs.13 and 14 is (Appendix D)
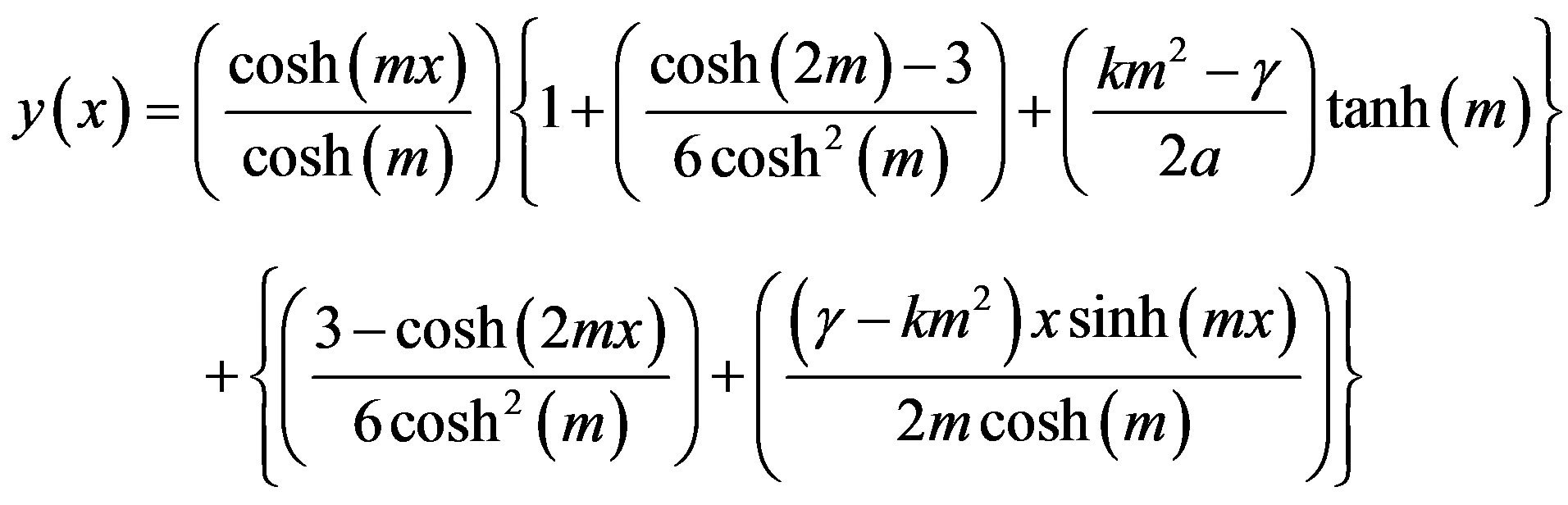 (15)
(15)
The corresponding effectiveness factor for this case is given by Eq.16, where m is defined by Eq.8.
4. NUMERICAL SIMULATION
In order to find the accuracy of our analytical method, the non-linear ordinary differential Eqs.5, 6, 9, 10, 13 and 14 are also solved by numerical methods. The function bvp4c in Matlab/Scilab software which is a function of solving non-linear boundary value problems for ordinary differential equations are used to solve these equations numerically. Our analytical results are compared with numerical simulations in Figures 2-11 and it gives a satisfactory agreement. The Matlab/Scilab program is also given in Appendix E.
5. RESULTS AND DISCUSSIONS
Figures 2 and 3 are the dimensionless concentration u(x) versus the dimensionless distance x. From Figure 2, it is inferred that the dimensionless concentration u(x) increases, when the dimensionless parameter k increases. From Figure 3, it is clear that, the dimensionless concentration u(x) decreases when the dimensionless parameter γ increases.
Diagarms for case (1)
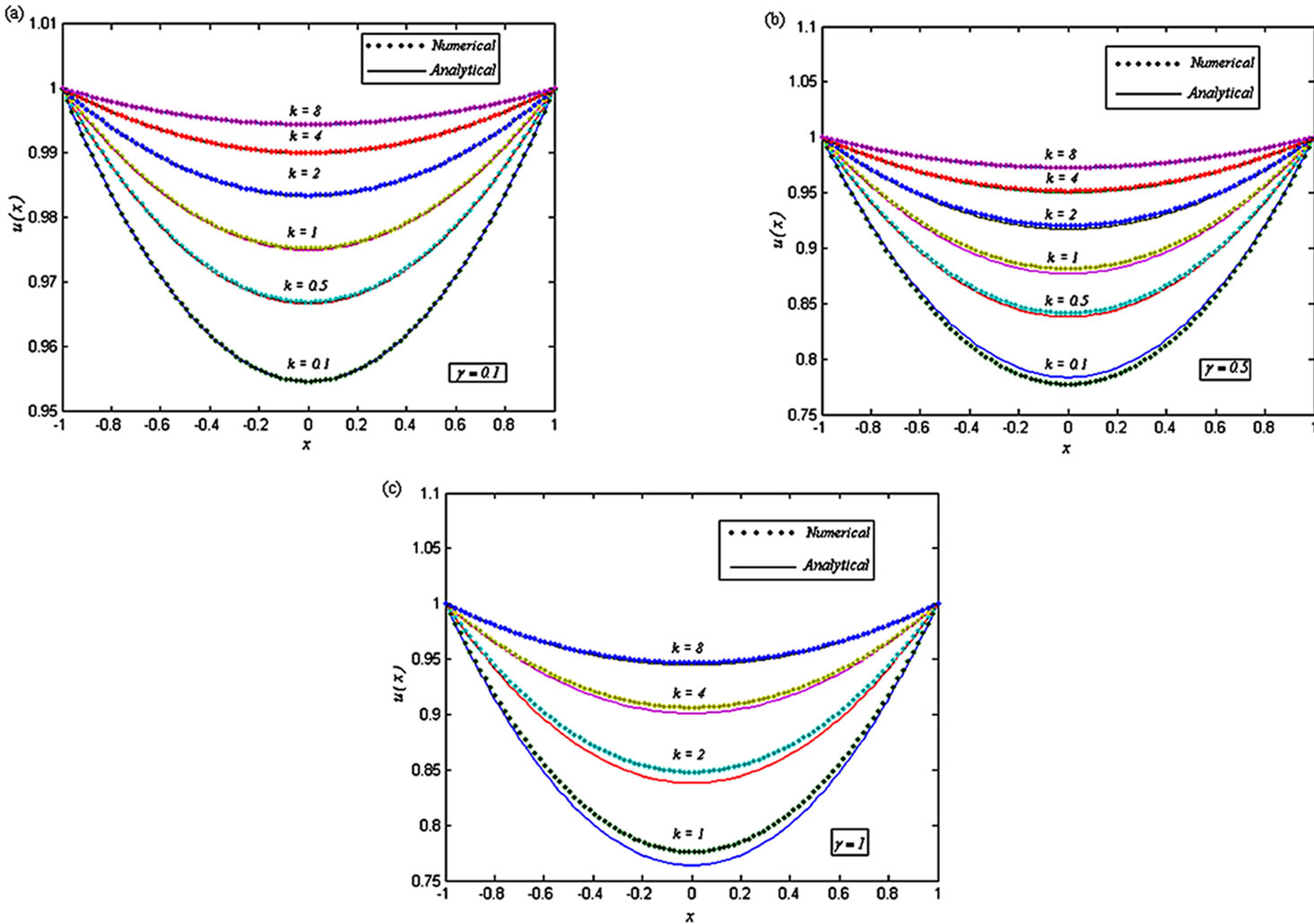
Figure 2. Dimensionless concentration of oxygen u(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters γ and k, when (a) γ = 0.1 and k = 0.1, 0.5, 1, 2, 4 and 8; (b) γ = 0.5 and k = 0.1, 0.5, 1, 2, 4 and 8; (c) γ = 1 and k = 0.1, 0.5, 1, 2, 4 and 8.
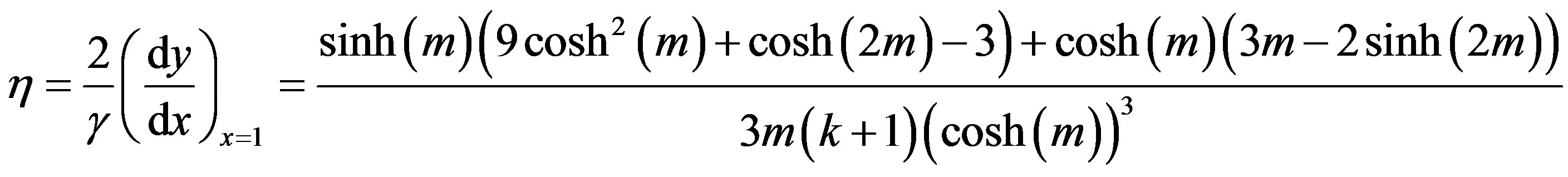 (16)
(16)
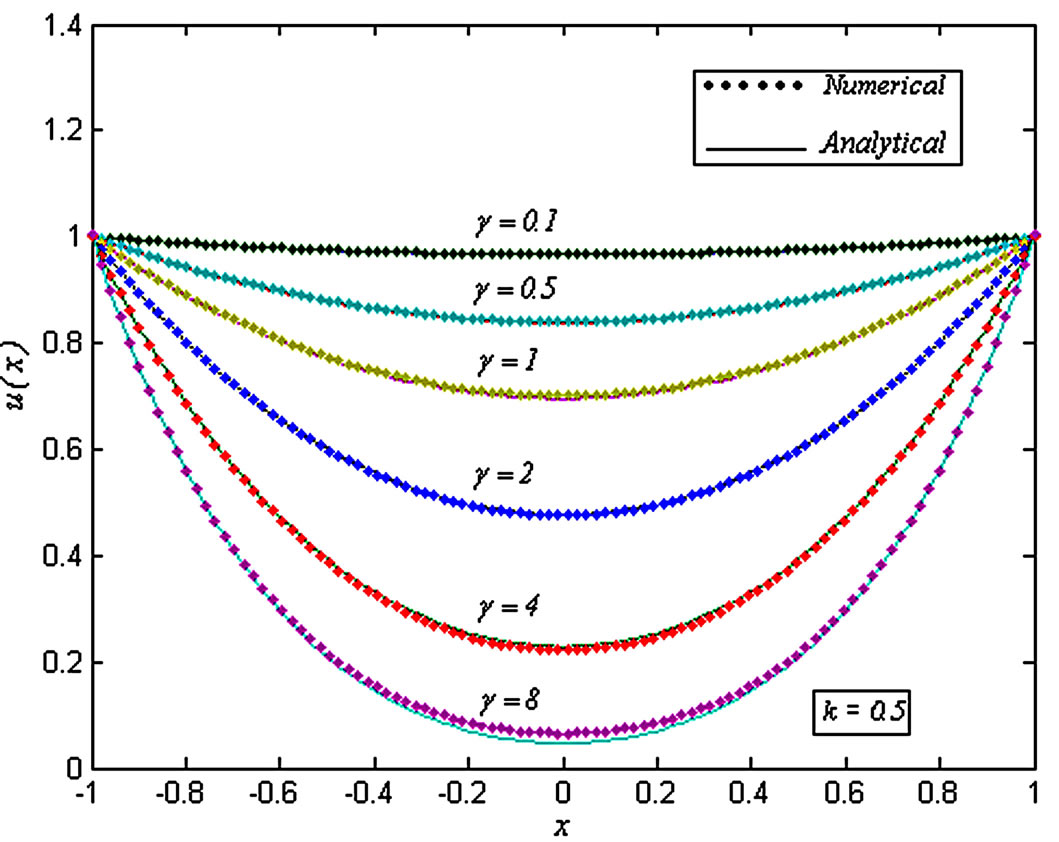
Figure 3. Dimensionless concentration of oxygen u(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters γ and k, when k = 0.5 and γ = 0.1, 0.5, 1, 2, 4 and 8.
Diagarms for case (2)

Figure 4. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) α = 0.1, γ = 0.1 and k = 0.1, 0.5, 1, 2, 4 and 8; (b) α = 0.1, γ = 0.5 and k = 0.1, 0.5, 1, 2, 4 and 8; (c) α = 0.1, γ = 1 and k = 0.1, 0.5, 1, 2, 4 and 8.
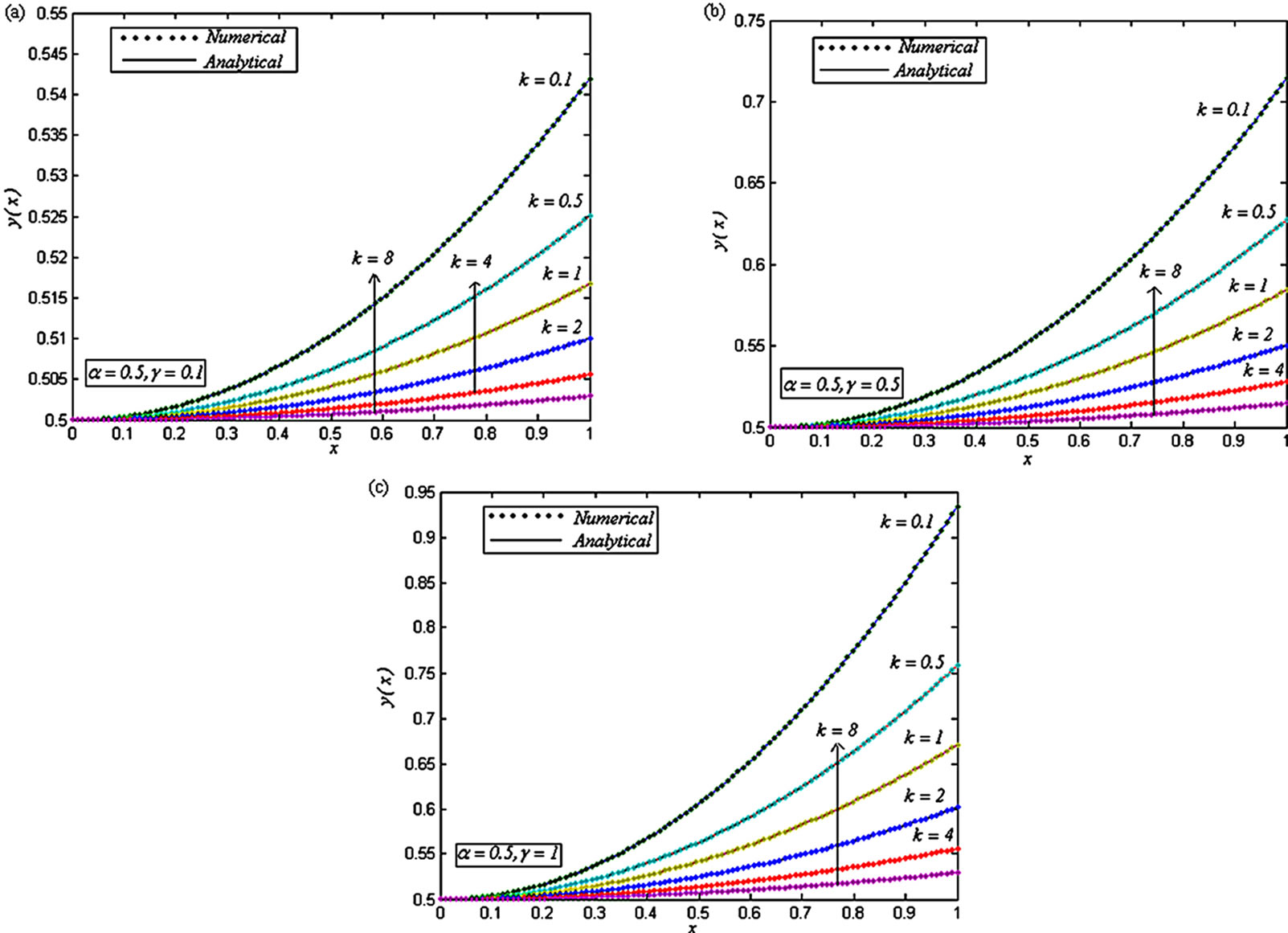
Figure 5. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) α = 0.5, γ = 0.1 and k = 0.1, 0.5, 1, 2, 4 and 8; (b) α = 0.5, γ = 0.5 and k = 0.1, 0.5, 1, 2, 4 and 8; (c) α = 0.5, γ = 1 and k = 0.1, 0.5, 1, 2, 4 and 8.
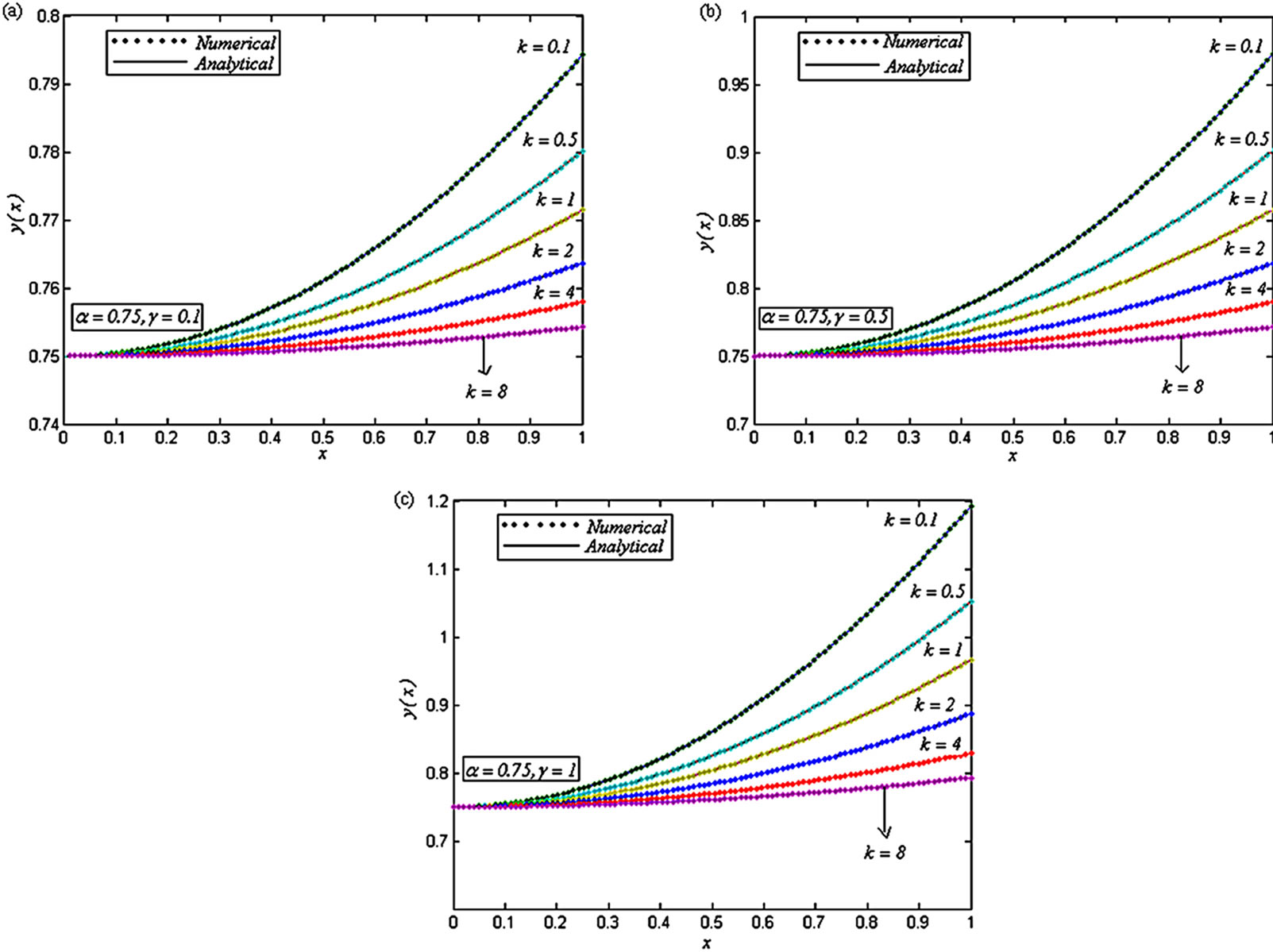
Figure 6. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) α = 0.75, γ = 0.1 and k = 0.1, 0.5, 1, 2, 4 and 8; (b) α = 0.75, γ = 0.5 and k = 0.1, 0.5, 1, 2, 4 and 8; (c) α = 0.75, γ = 1 and k = 0.1, 0.5, 1, 2, 4 and 8.
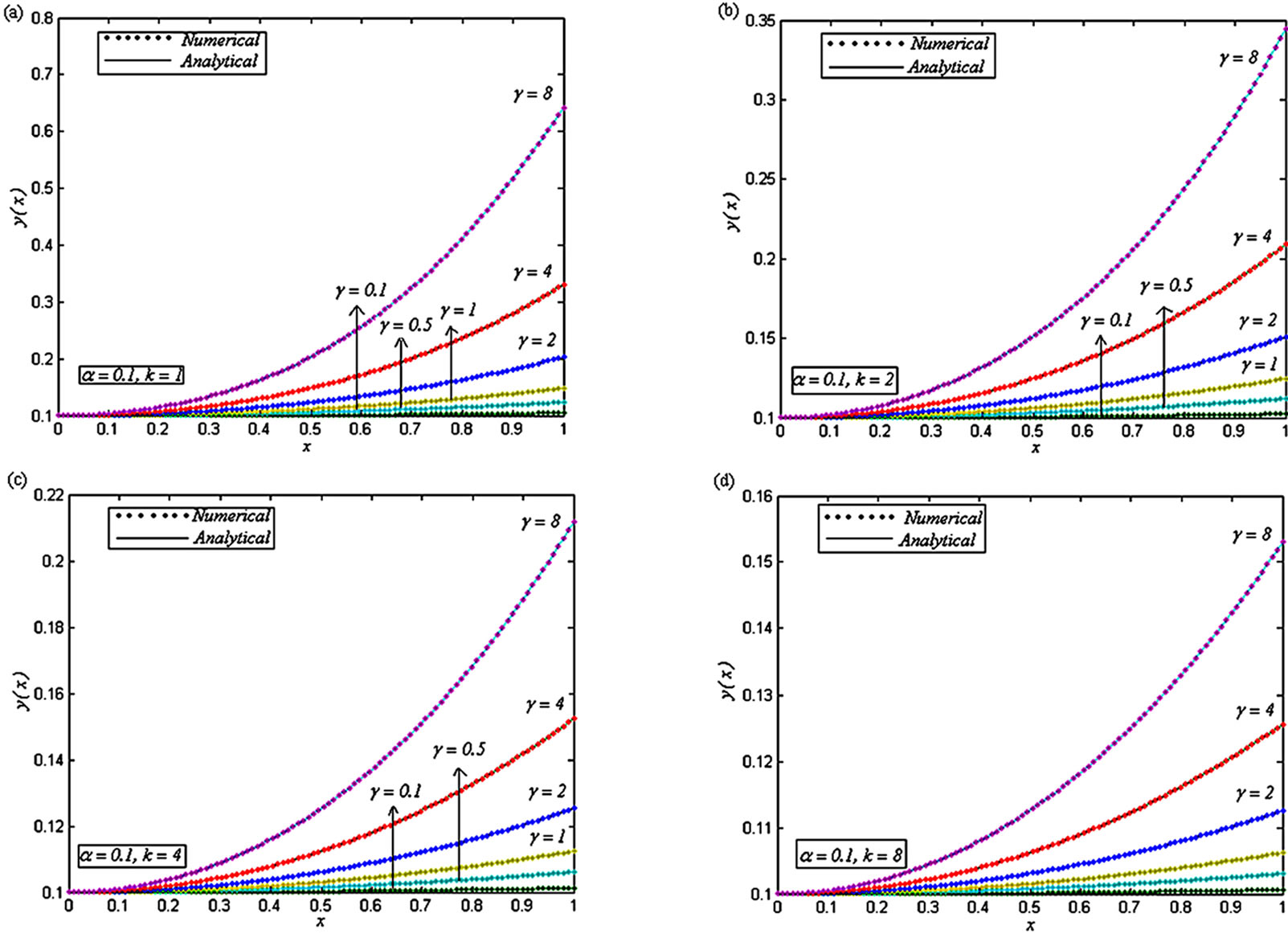
Figure 7. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) α = 0.1, k = 1 and γ = 0.1, 0.5, 1, 2, 4 and 8; (b) α = 0.1, k = 2 and γ = 0.1, 0.5, 1, 2, 4 and 8; (c) α = 0.1, k = 4 and γ = 0.1, 0.5, 1, 2, 4 and 8.

Figure 8. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) α = 0.3, k = 2 and γ = 0.1, 0.5, 1, 2, 4 and 8; (b) α = 0.3, k = 4 and γ = 0.1, 0.5, 1, 2, 4 and 8; (c) α = 0.3, k = 8 and γ = 0.1, 0.5, 1, 2, 4 and 8.
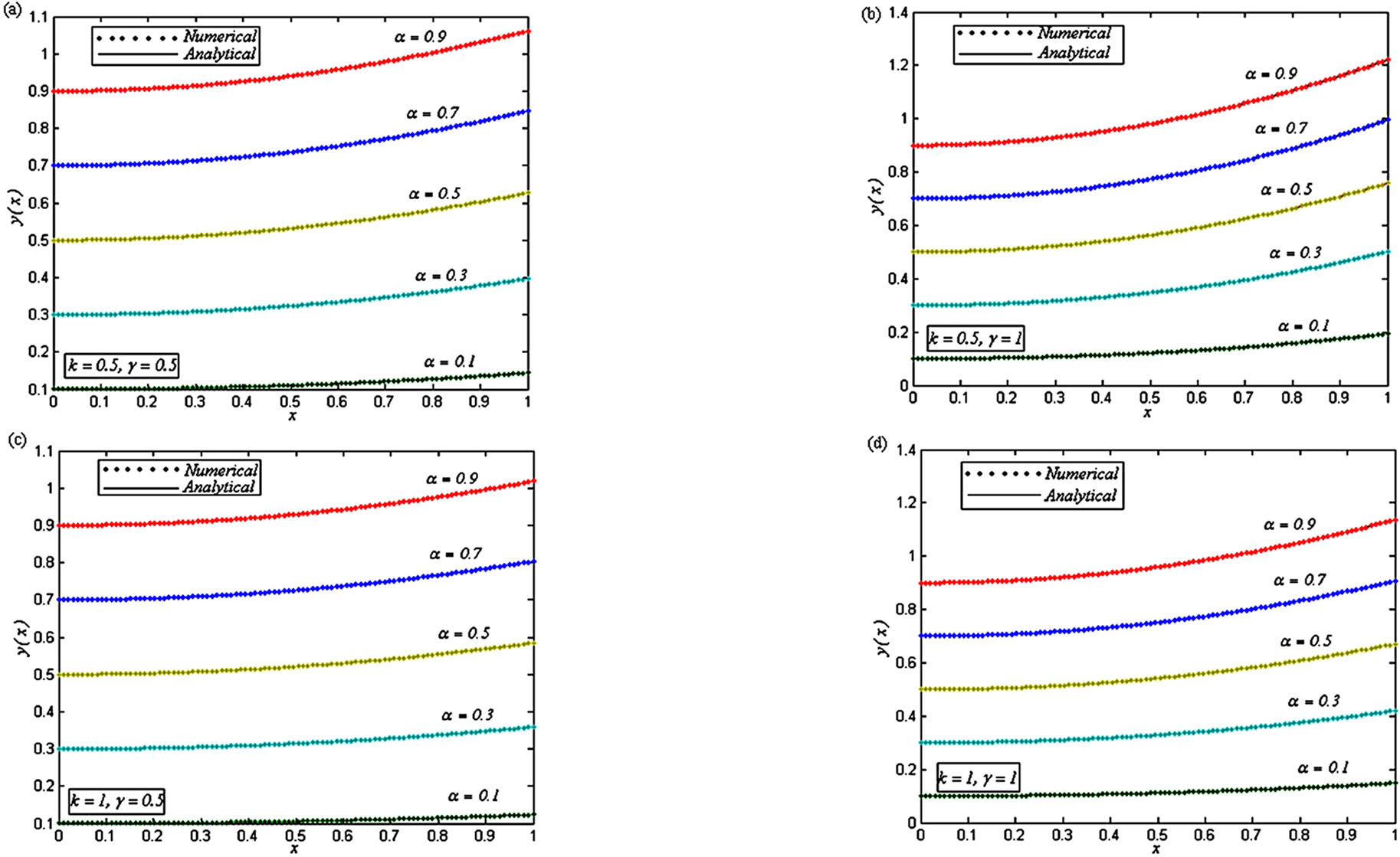
Figure 9. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters α, γ and k, when (a) k = 0.5, γ = 5 and α = 0.1, 0.3, 0.5, 0.7 and 0.9; (b) k = 0.5, γ = 1 and α = 0.1, 0.3, 0.5, 0.7 and 0.9; (c) k = 1, γ = 0.5 and α = 0.1, 0.3, 0.5, 0.7 and 0.9; (d) k = 1, γ = 1 and α= 0.1, 0.3, 0.5, 0.7 and 0.9.
Diagarms for case (3)
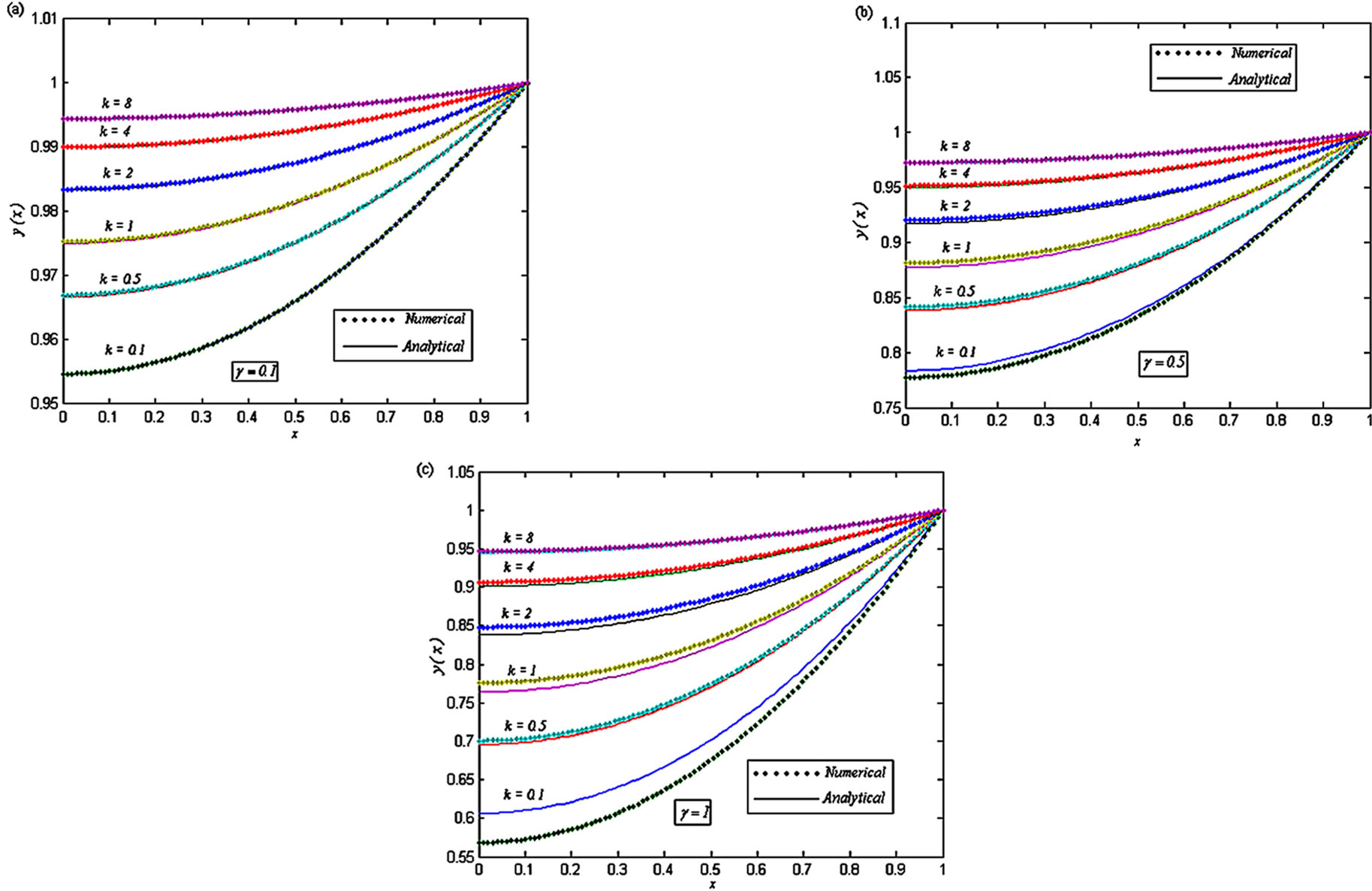
Figure 10. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters γ and k, when (a) γ = 0.1 and k = 0.1, 0.5, 1, 2, 4 and 8; (b) γ = 0.5 and k = 0.1, 0.5, 1, 2, 4 and 8; (c) γ = 1 and k = 0.1, 0.5, 1, 2, 4 and 8.
Figures 4-9 are the dimensionless concentrations y(x) versus the dimensionless distance x From Figures 4-6, it is noted that the dimensionless concentration y(x) decreases, when dimensionless parameter k increases. From these figures, it is evident that when α increases, the dimensionless concentrations y(x) also increases. From Figures 7 and 8, we infer that the dimensionless concentrations y(x) increases, when the dimensionless parameter γ increases. From these figures, it is noted that when α increases, the dimensionless concentrations y(x) also increases. From Figure 9, we infer that, the dimensionless concentrations y(x) increases, when the dimensionless parameter α increases.
Figures 10 and 11 are the dimensionless concentrations y(x) versus, the dimensionless distance x From Figure 10, it is noted that the dimensionless concentrations y(x) increases, when the dimensionless parameter k increases and γ decreases. Figure 12 is the effectiveness
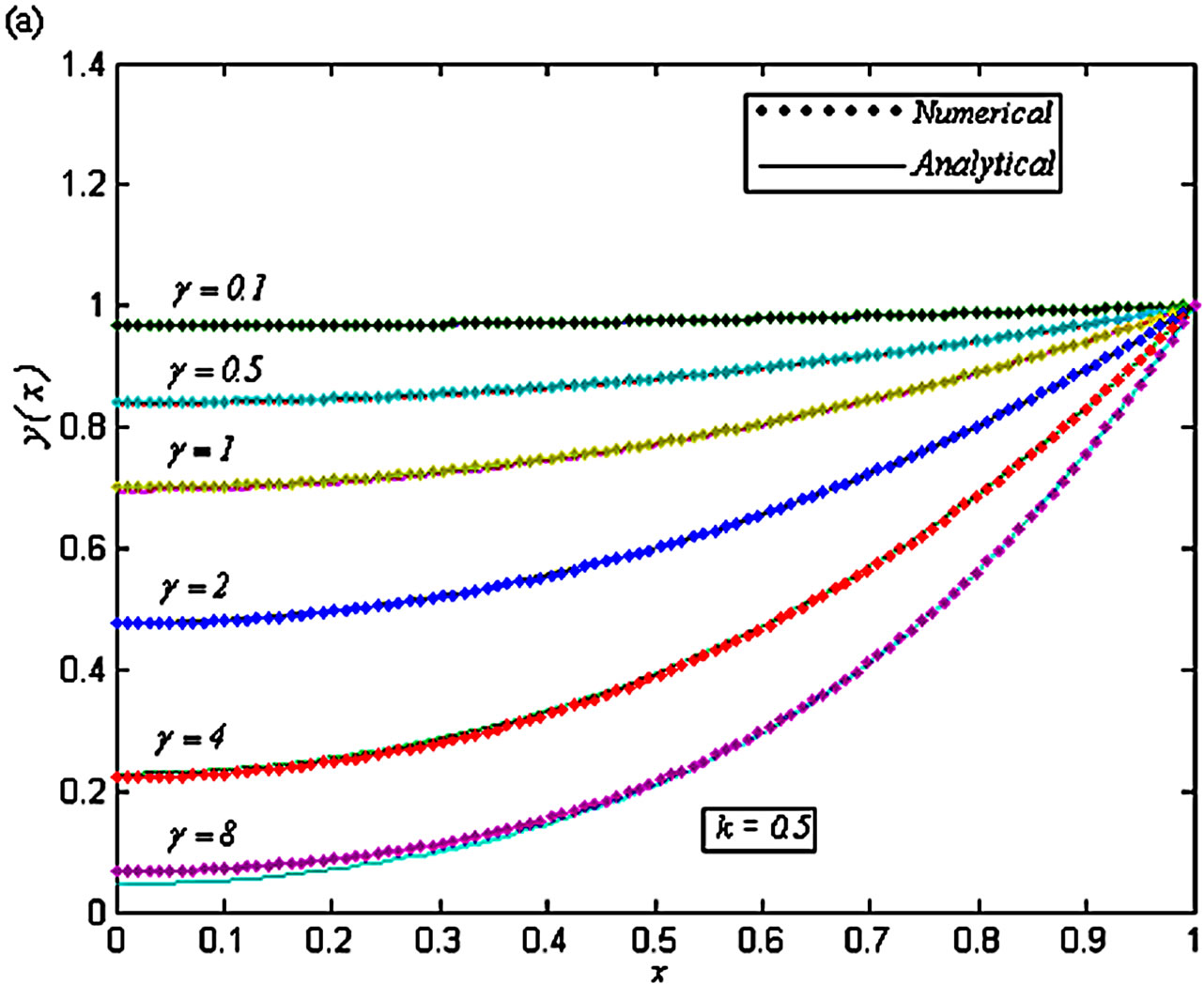
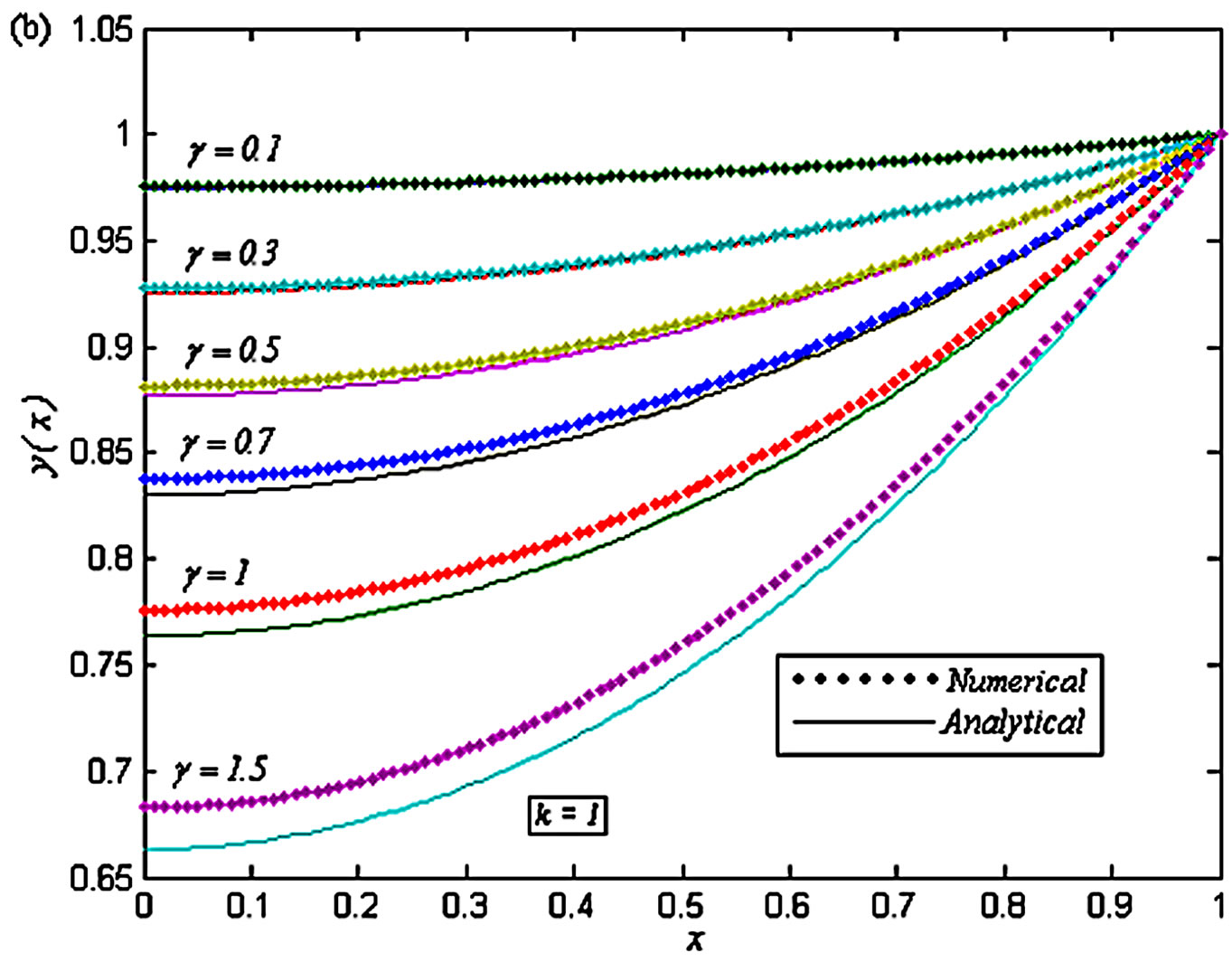
Figure 11. Dimensionless concentration of oxygen y(x) versus the dimensionless distance x for various values of the dimensionless reaction parameters γ and k, when (a) k = 0.5 and γ = 0.1, 0.5, 1, 2, 4 and 8; (b) k = 1 and γ = 0.1, 0.3, 0.5, 0.7, 1 and 1.5.
Diagram for effectiveness factors for case (3)
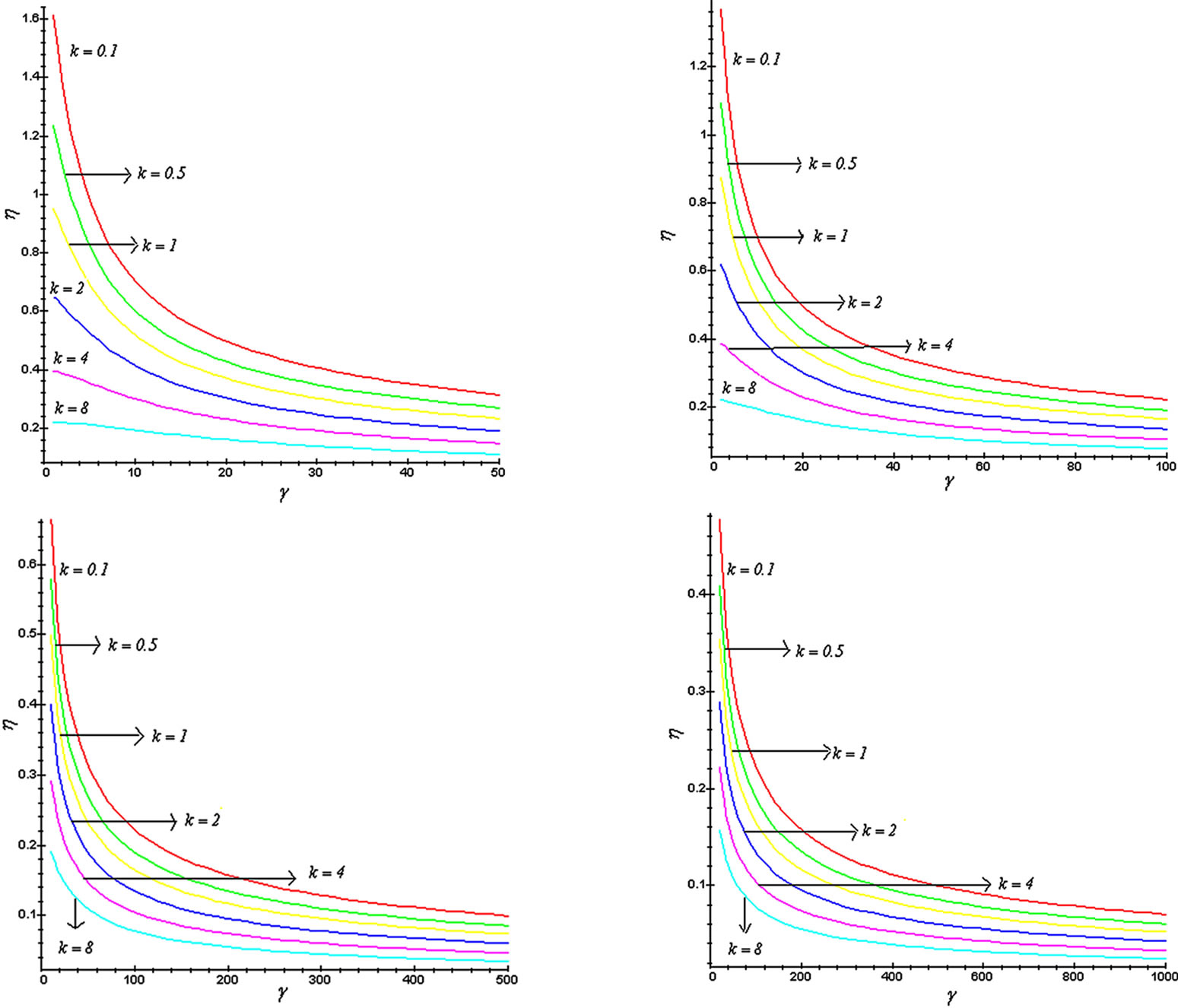
Figure 12. The effectiveness factor η versus the dimensionless parameter γ can be calculated using the Eq. 16, when k = 0.1, 0.5, 1, 2, 4 and 8.
factors versus the dimensionless parameter γ. From this figure, it is evident that the effectiveness factors decreases when the dimensionless parameter k increases and it reaches steady state value when γ = 200.
6. CONCLUSION
In this article, we have been interested in the analysis of non-linear reaction-diffusion equations with Michaelis-Menten kinetics. The non-linear boundary value problem with Michaelis-Menten kinetics has been solved analytically and numerically. Analytical expressions of the concentrations can be derived by using the new Homotopy perturbation method (NHPM). The primary result of this work is simple and approximate expressions of the concentrations for all values of the dimensionless parameters k, γ and α. This method is extremely simple and it is also a promising method to solve other nonlinear equations.
7. ACKNOWLEDGEMENTS
This work is supported by the University Grant Commission (UGC) Minor project No: F. MRP-4122/12 (MRP/UGC-SERO), Hyderabad, Government of India. The authors are thankful to Shri. S. Natanagopal, Secretary, The Madura College Board and Dr. R. Murali, Principal, The Madura College (Autonomous), Madurai, Tamil Nadu, India for their constant encouragement.
REFERENCES
- Bassom, A.P., Ilchmann, A. and Vob, H. (1997) Oxygen diffusion in tissue preparations with Michaelis-Menten kinetics. Journal of Theoretical Biology, 185, 119-127. doi:10.1006/jtbi.1996.0298
- Rashevsky, N. (1960) Mathematical biophysics. Dover, New York.
- Lin, S.H. (1976) Oxygen diffusion in a spherical cell with non-linear oxygen uptake kinetics. Journal of Theoretical Biology, 60, 449-457. doi:10.1016/0022-5193(76)90071-0
- Michaelis, L. and Menten, M. (1913) Die kinetic der inver tinwirkung. Biochemische Zeitschrift, 49, 333-369.
- McElwain, D.L.S. (1978) A re-examination of oxygen diffusion in a spherical cell with Michaelis-Menten oxygen uptake kinetics. Journal of Theoretical Biology, 71, 255-263. doi:10.1016/0022-5193(78)90270-9
- Hiltmann, P. and Lory, P. (1983) On oxygen diffusion in a spherical cell with Michaelis-Menten uptake kinetics. Bulletin of Mathematical Biology, 45, 661-664.
- Anderson, N. and Arthurs, A.M. (1985) Analytical bound ing functions for diffusion problems with MichaelisMentenkinetics. Bulletin of Mathematical Biology, 47, 145-153.
- Asaithambi, N.S. and Garner, J.B. (1989) Point wise solution bounds for a class of singular diffusion problems in physiology. Applied Mathematics and Computation, 30, 215-222. doi:10.1016/0096-3003(89)90053-2
- Asaithambi, N.S. and Garner, J.B. (1992) Taylor series solutions of a class of diffusion problems in physiology. Mathematics and Computers in Simulation, 34, 563-570. doi:10.1016/0378-4754(92)90042-F
- Ghori, Q.K., Ahmed, M. and Siddiqui, A.M. (2007) Application of Homotopy perturbation method to squeezing flow of a Newtonian fluid. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 179- 184. doi:10.1515/IJNSNS.2007.8.2.179
- Ozis, T. and Yildirim, A. (2007) A comparative study of He’s Homotopy perturbation method for determining frequency-amplitude relation of a nonlinear oscillator with discontinuities. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 243-248. doi:10.1515/IJNSNS.2007.8.2.243
- Li, S.J. and Liu, X.Y. (2006) An Improved approach to non-linear dynamical system identification using PID neural networks. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 177-182. doi:10.1515/IJNSNS.2006.7.2.177
- Mousa, M.M., Ragab, S.F. and Nturforsch, Z. (2008) Application of the Homotopy perturbation method to linear and non-linear Schrödinger equations. Zeitschrift für Naturforschung, 63, 140-144.
- He, J.H. (1999) Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262. doi:10.1016/S0045-7825(99)00018-3
- He, J.H. (2003) Homotopy perturbation method: A new non-linear analytical technique. Applied Mathematics and Computation, 135, 73-79. doi:10.1016/S0096-3003(01)00312-5
- He, J.H. (2003) A simple perturbation approach to Blasius equation. Applied Mathematics and Computation, 140, 217-222. doi:10.1016/S0096-3003(02)00189-3
- Ariel, P.D. (2010) Alternative approaches to construction of Homotopy perturbation algorithms. Nonlinear Science Letters A, 1, 43-52.
- Loghambal, S. and Rajendran, L. (2010) Mathematical modeling of diffusion and kinetics of amperometric immobilized enzyme electrodes. Electrochimica Acta, 55, 5230-5238. doi:10.1016/j.electacta.2010.04.050
- Meena, A. and Rajendran, L. (2010) Mathematical modeling of amperometric and potentiometric biosensors and system of non-linear equations—Homotopy perturbation approach. Journal of Electroanalytical Chemistry, 644, 50-59. doi:10.1016/j.jelechem.2010.03.027
- Anitha, S., Subbiah, A., Subramaniam, S. and Rajendran, L. (2011) Analytical solution of amperometric enzymatic reactions based on Homotopy perturbation method. Electrochimica Acta, 56, 3345-3352. doi:10.1016/j.electacta.2011.01.014
- Ananthaswamy, V. and Rajendran, L. (2012) Analytical solution of two-point non-linear boundary value problems in a porous catalyst particles. International Journal of Mathematical Archive, 3, 810-821.
- Ananthaswamy, V. and Rajendran, L. (2012) Analytical solutions of some two-point non-linear elliptic boundary value problems. Applied Mathematics, 3, 2012, 1044- 1058. doi:10.4236/am.2012.39154
- Ananthaswamy, V. and Rajendran, L. (2012) Analytical solution of non-isothermal diffusion-reaction processes and effectiveness factors. ISRN Physical Chemistry, 2012, 1-14.
- Rajendran, L. and Anitha, S. (2013) Comments on analytical solution of amperometric enzymatic reactions based on Homotopy perturbation method” by Ji-Huan He, LuFeng Mo. Electrochimica Acta, 102, 474-476. doi:10.1016/j.electacta.2013.03.163
APPENDIX A
Basic concept of the Homotopy perturbation method [10-24]
To explain this method, let us consider the following function:
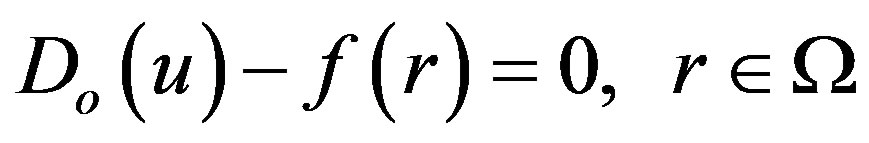 (A1)
(A1)
with the boundary conditions of
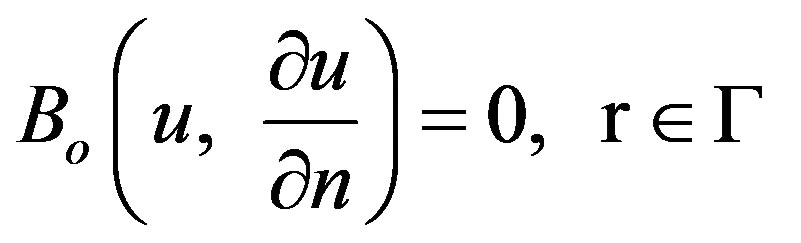 (A2)
(A2)
where 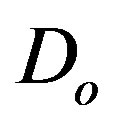 is a general differential operator,
is a general differential operator,  is a boundary operator,
is a boundary operator, 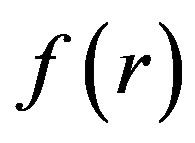 is a known analytical function and
is a known analytical function and 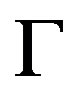 is the boundary of the domain
is the boundary of the domain . In general, the operator
. In general, the operator 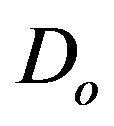 can be divided into a linear part
can be divided into a linear part 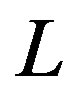 and a non-linear part
and a non-linear part . Eq.A1 can therefore be written as
. Eq.A1 can therefore be written as
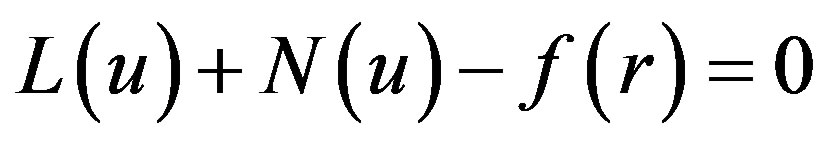 (A3)
(A3)
By the Homotopy technique, we construct a Homotopy 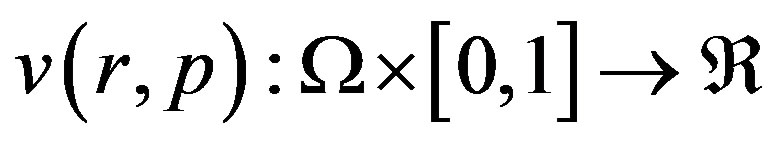 that satisfies
that satisfies
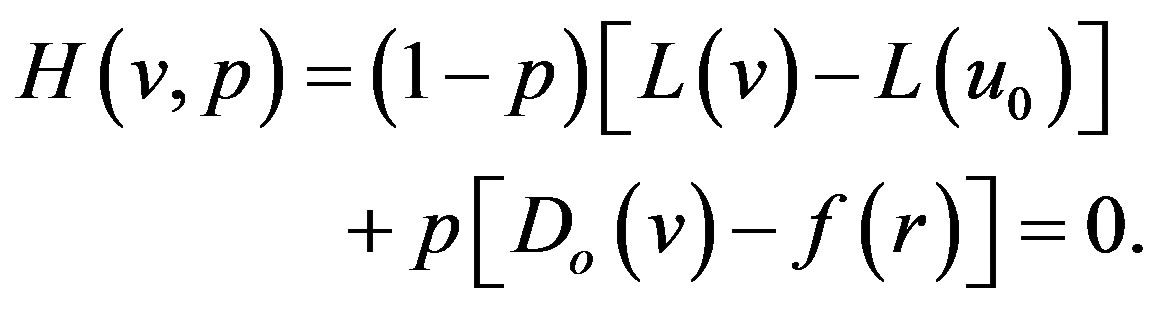 (A4)
(A4)
 (A5)
(A5)
where 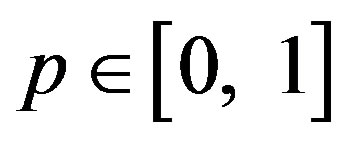 is an embedding parameter, and
is an embedding parameter, and  is an initial approximation of Eq.A1 that satisfies the boundary conditions. From Eqs.A4 and A5, we have
is an initial approximation of Eq.A1 that satisfies the boundary conditions. From Eqs.A4 and A5, we have
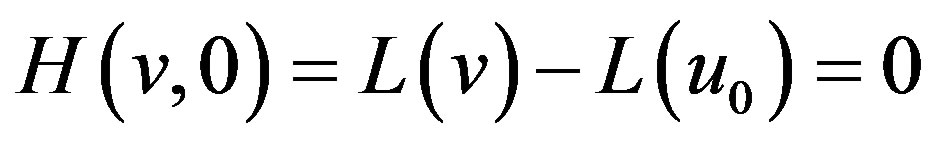 (A6)
(A6)
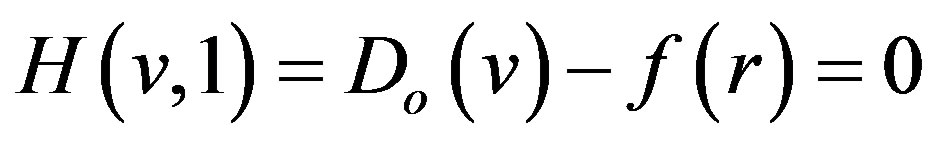 (A7)
(A7)
When p = 0, Eqs.A4 and A5 become linear equations. When p = 1, they become non-linear equations. The process of changing p from zero to unity is that of  to
to . We first use the embedding parameter
. We first use the embedding parameter 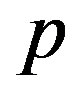 as a “small parameter” and assume that the solutions of Eqs.A4 and A5 can be written as a power series in
as a “small parameter” and assume that the solutions of Eqs.A4 and A5 can be written as a power series in :
:
 (A8)
(A8)
Setting  results in the approximate solution of Eq.A1 is
results in the approximate solution of Eq.A1 is
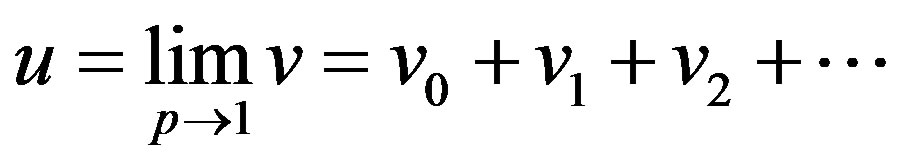 (A9)
(A9)
This is the basic idea of the HPM.
APPENDIX B
Solution of non-linear Eqs.5 and 6 using NHPM
In this Appendix, we indicate how Eq.7 in this paper is derived. To find the solution of Eqs.5 and 6 for case (1), we construct the new Homotopy as follows [24]:
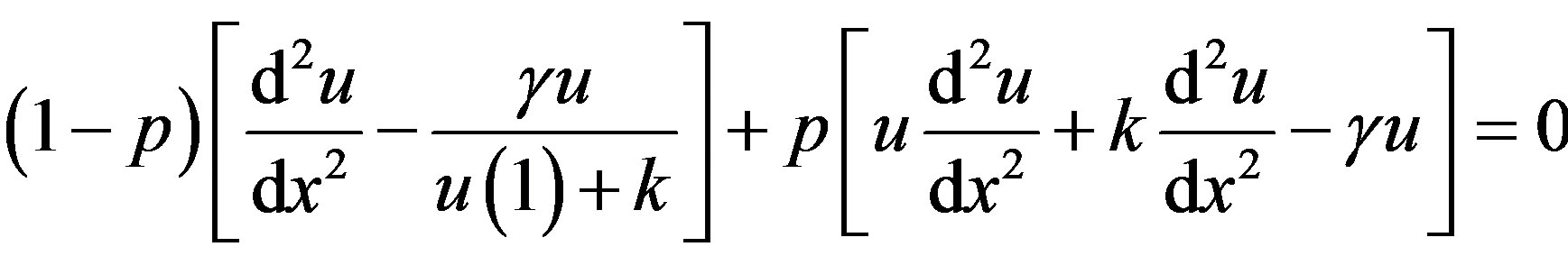 (B1)
(B1)
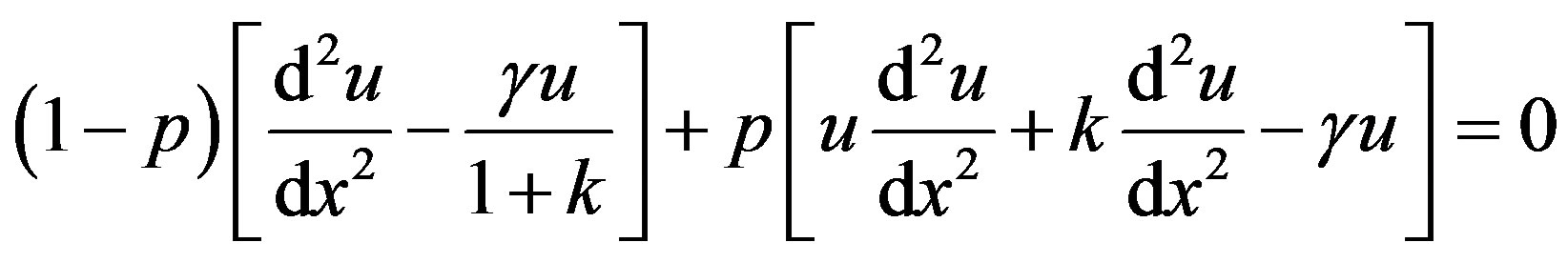 (B2)
(B2)
The analytical solution of Eq.B2 is
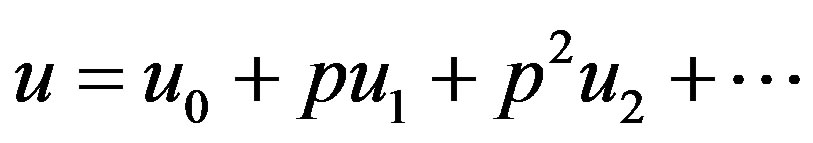 (B3)
(B3)
Substituting Eqs.B3 into Eq.B2 we get
 (B4)
(B4)
Comparing the coefficients of like powers of p in Eq.B4 we get
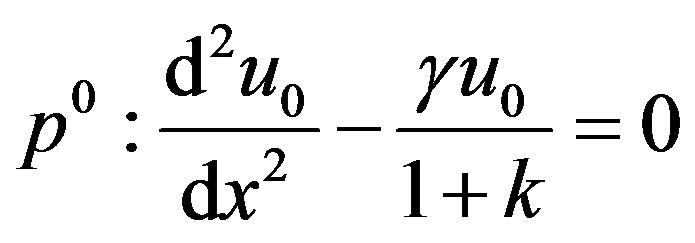 (B5)
(B5)
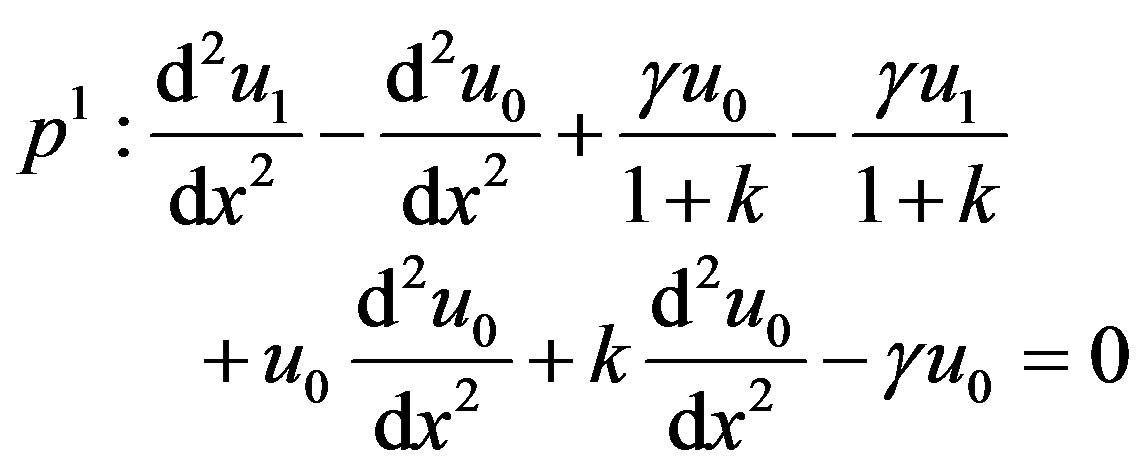 (B.6)
(B.6)
The initial approximations is as follows
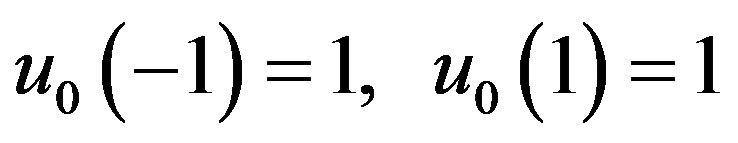 (B7)
(B7)
 (B8)
(B8)
Solving the Eqs.B5 and B6 and using the boundary conditions Eqs.B7 and B8, we obtain the following results:
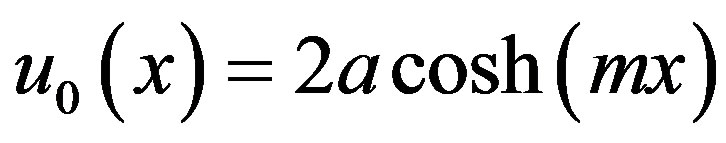 (B9)
(B9)
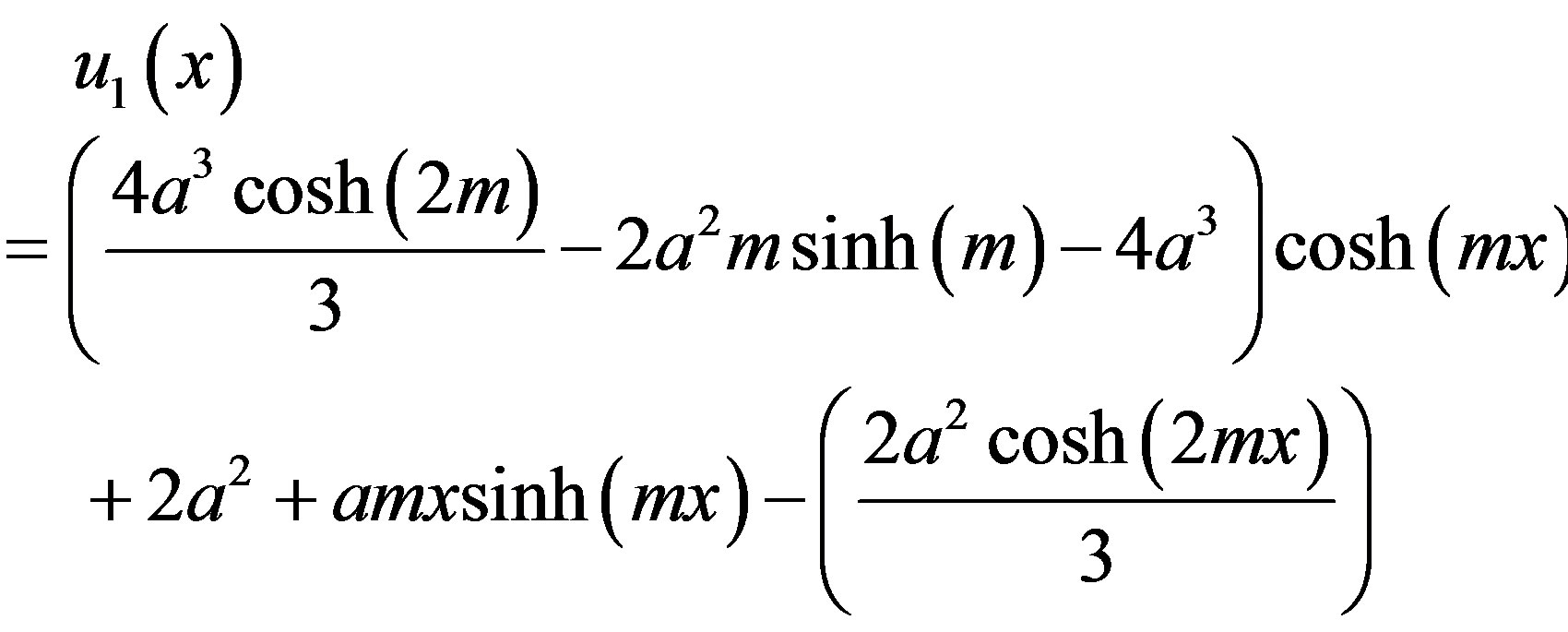 (B10)
(B10)
where 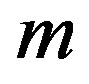 and
and  are defined in the text Eq.8. According to the HPM, we can conclude that
are defined in the text Eq.8. According to the HPM, we can conclude that
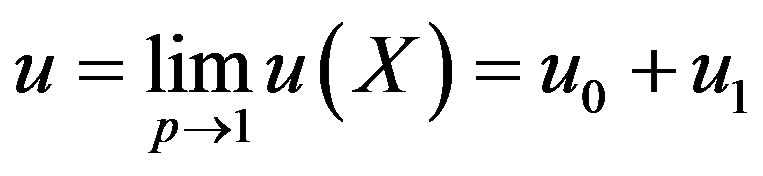 (B11)
(B11)
After putting the Eqs.B9 and B10 into an Eq.B11, we obtain the solutions in the text Eq.7.
APPENDIX C
Solution of non-linear Eqs.9 and 10 using NHPM [24]
In this Appendix, we indicate how Eq.11 in this paper is derived. To find the solution of Eqs.9 and 10 for case (2), we construct the new Homotopy as follows [24]:
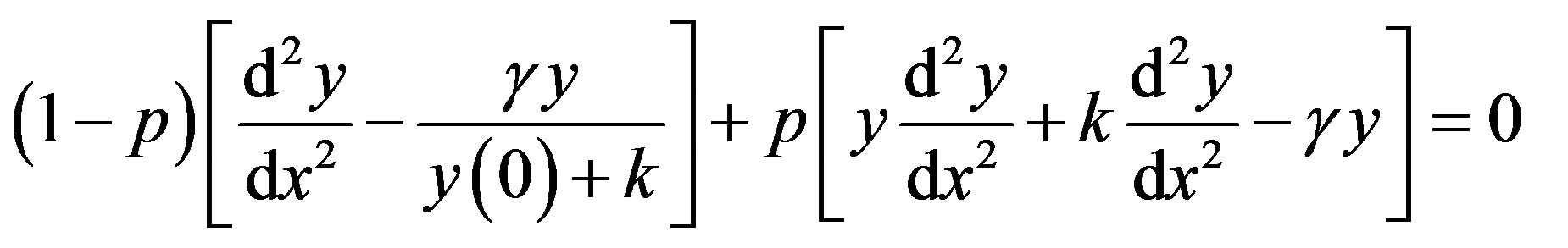 (C1)
(C1)
 (C2)
(C2)
The analytical solution of Eq.C2 is
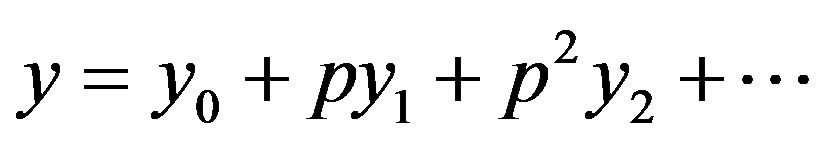 (C3)
(C3)
Substituting Eqs.C3 into Eq.C2, we get
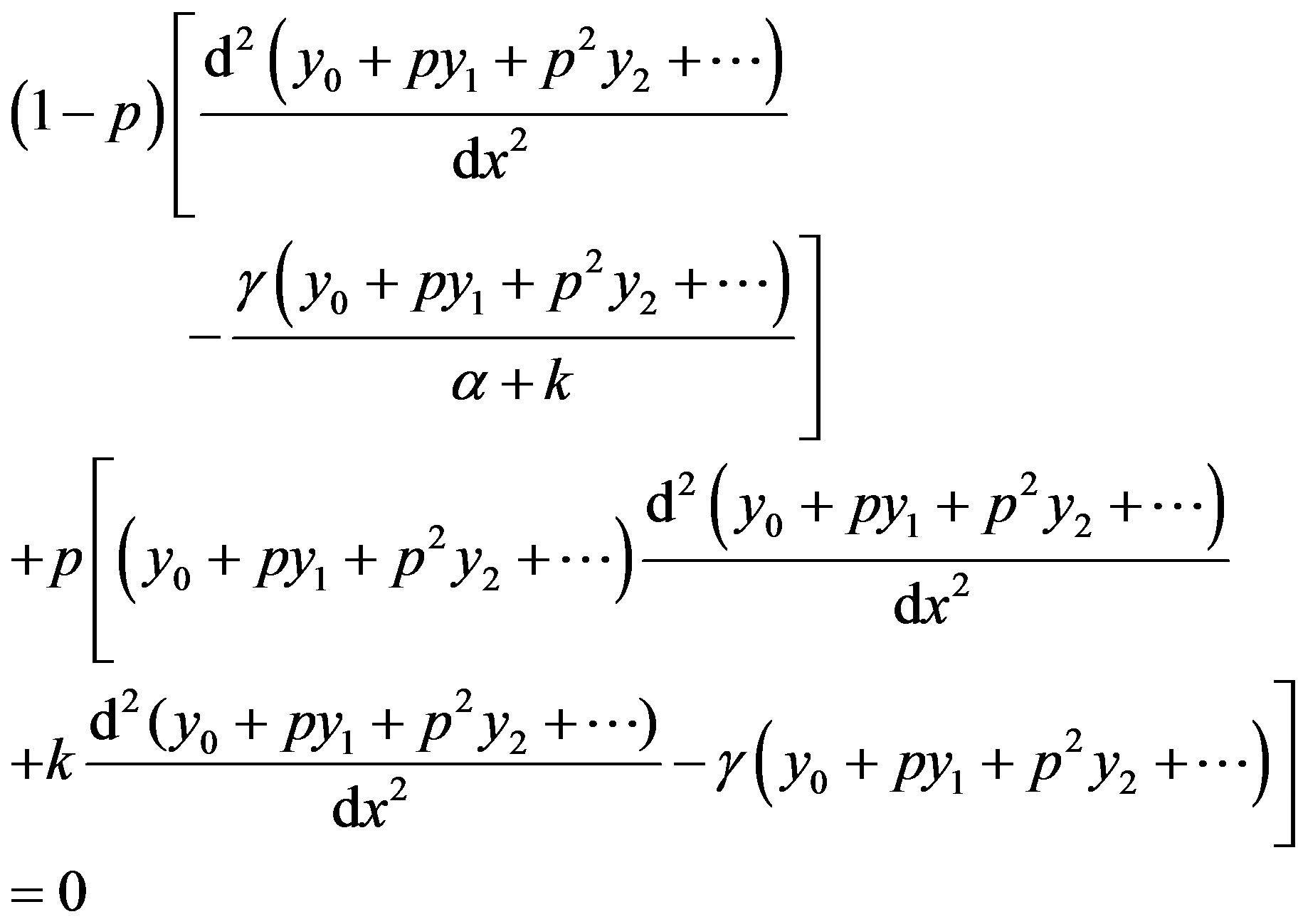 (C4)
(C4)
Comparing the coefficients of like powers of 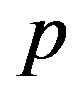 in Eq.C4, we get
in Eq.C4, we get
 (C5)
(C5)
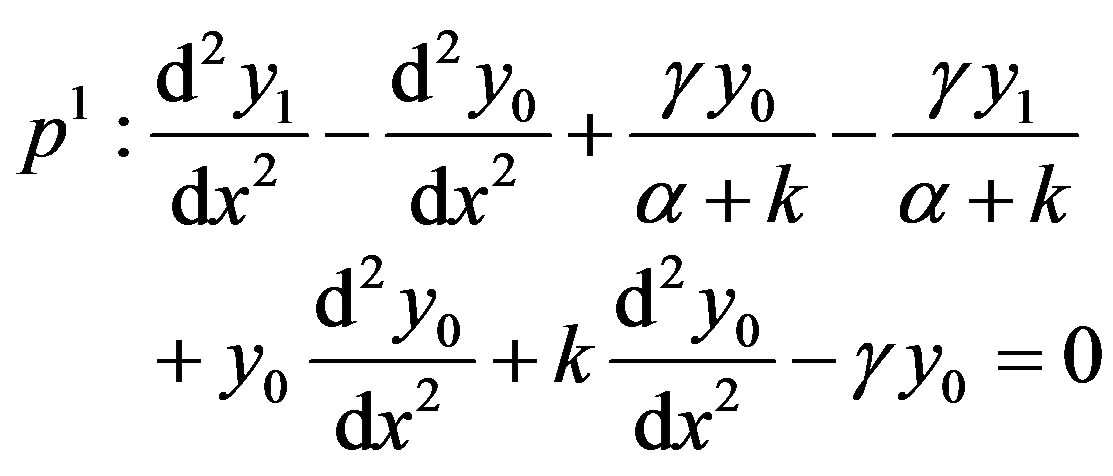 (C6)
(C6)
The initial approximations is as follows
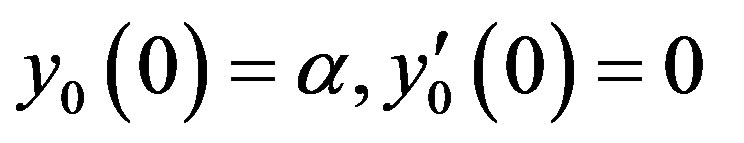 (C7)
(C7)
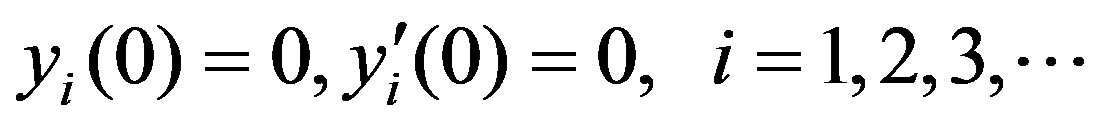 (C8)
(C8)
Solving the Eqs.C5 and C6 and using the boundary conditions Eqs.C7 and C8, we obtain the following results:
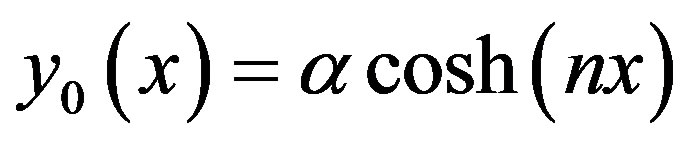 (C9)
(C9)
 (C10)
(C10)
where n is defined in the text Eq.12. According to the HPM, we can conclude that
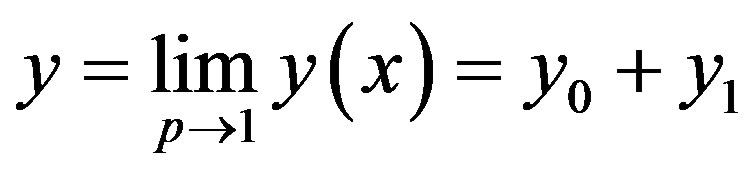 (C11)
(C11)
After putting the Eqs.C9 and C10 into an Eq.C11, we obtain the solutions in the text Eq.11.
APPENDIX D
Solution of non-linear Eqs.13 and 14 using NHPM [24]
In this Appendix, we indicate how Eq.15 in this paper is derived. To find the solution of Eqs.13 and 14 for case (3), we construct the new Homotopy as follows [24]:
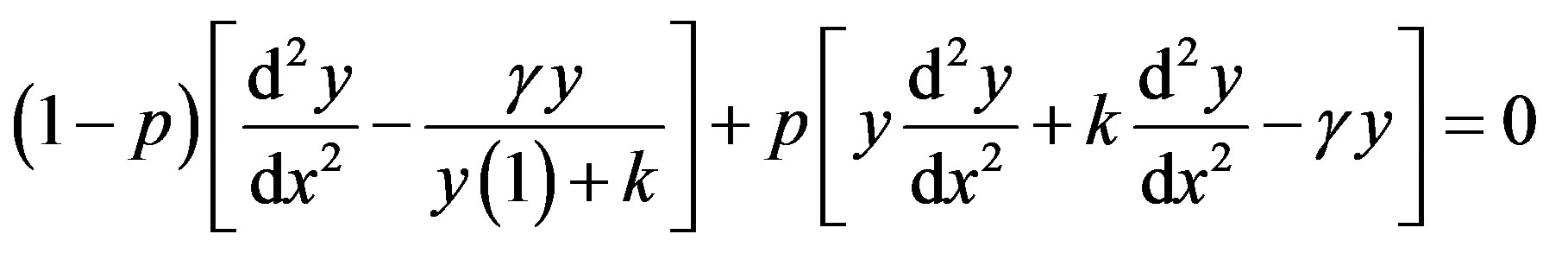 (D1)
(D1)
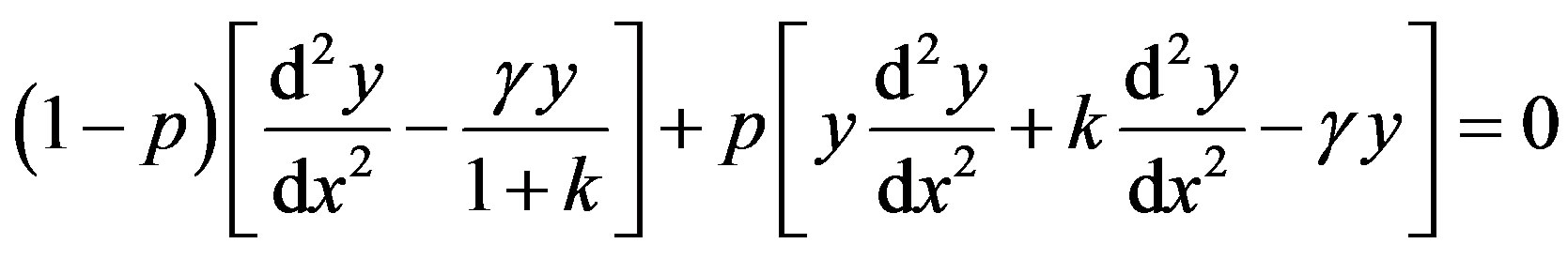 (D2)
(D2)
The analytical solution of Eq.D2 is
 (D3)
(D3)
Substituting Eqs.D3 into D2 we get
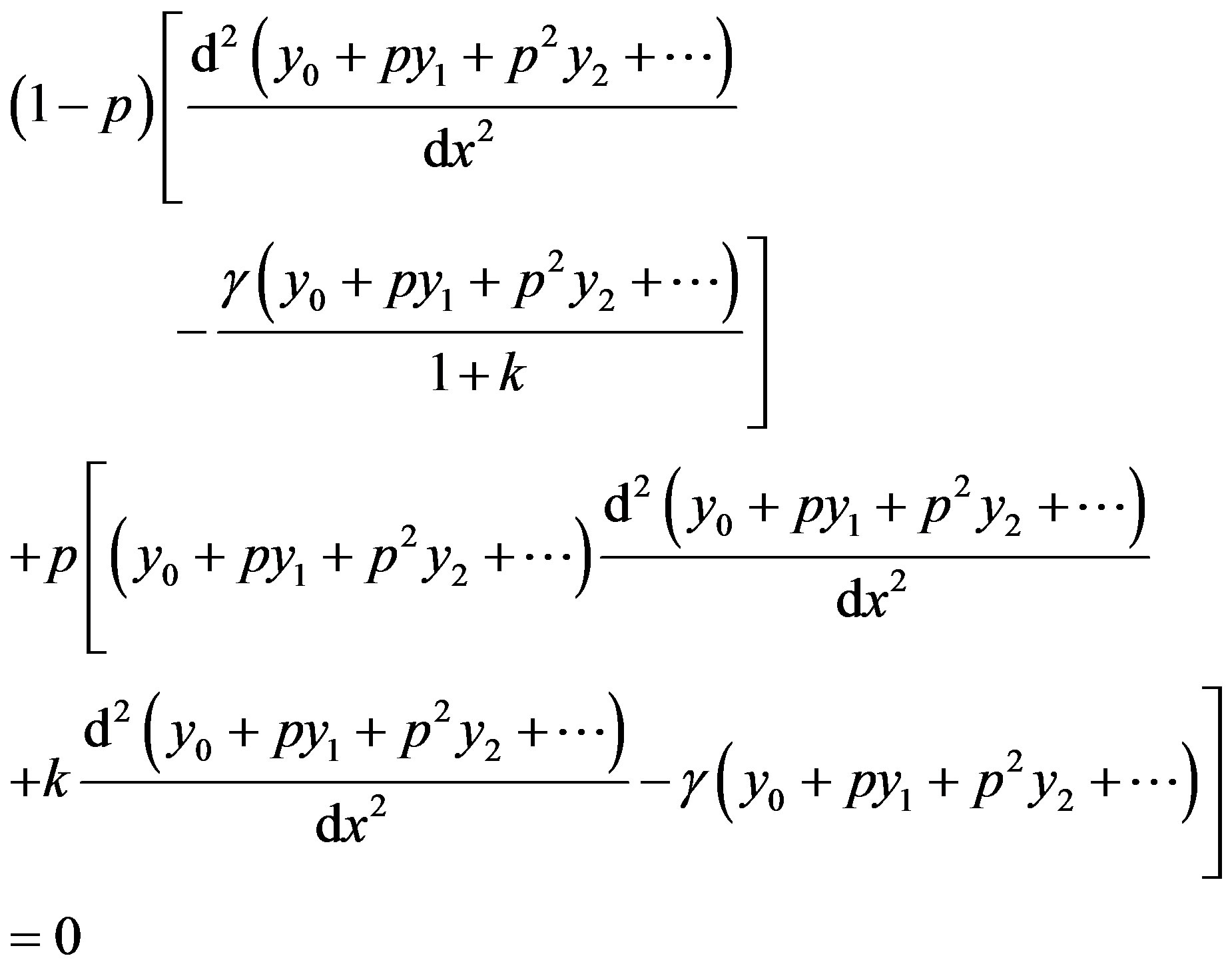 (D4)
(D4)
Comparing the coefficients of like powers of 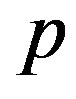 in Eq.D4, we get
in Eq.D4, we get
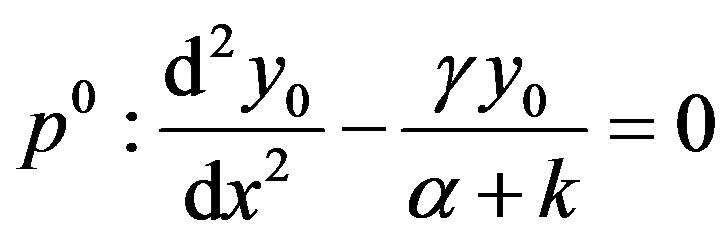 (D5)
(D5)
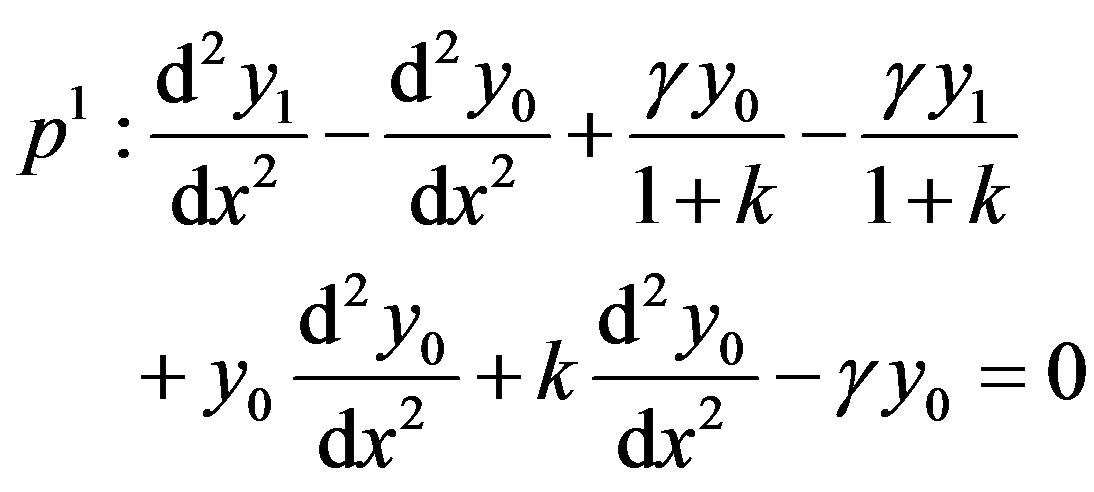 (D6)
(D6)
The initial approximation is as follows:
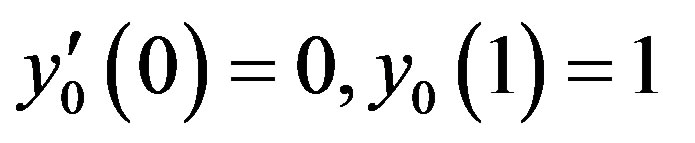 (D7)
(D7)
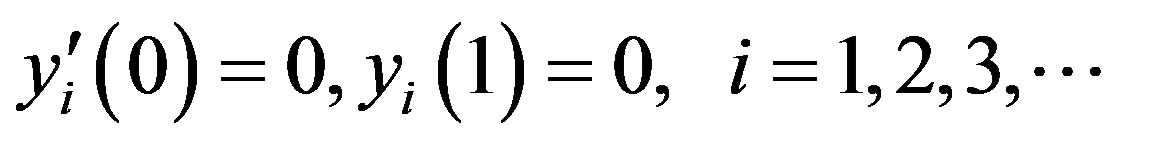 (D8)
(D8)
Solving the Eqs.D5 and D6 and using the boundary conditions Eqs.D7 and D8, we obtain the following results:
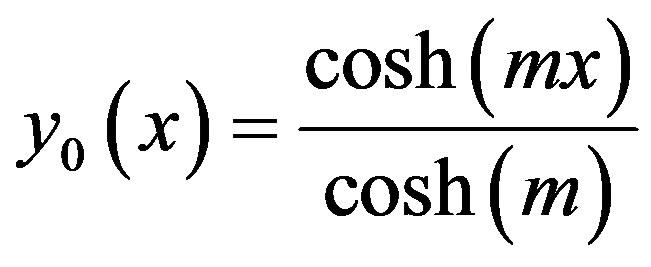 (D9)
(D9)
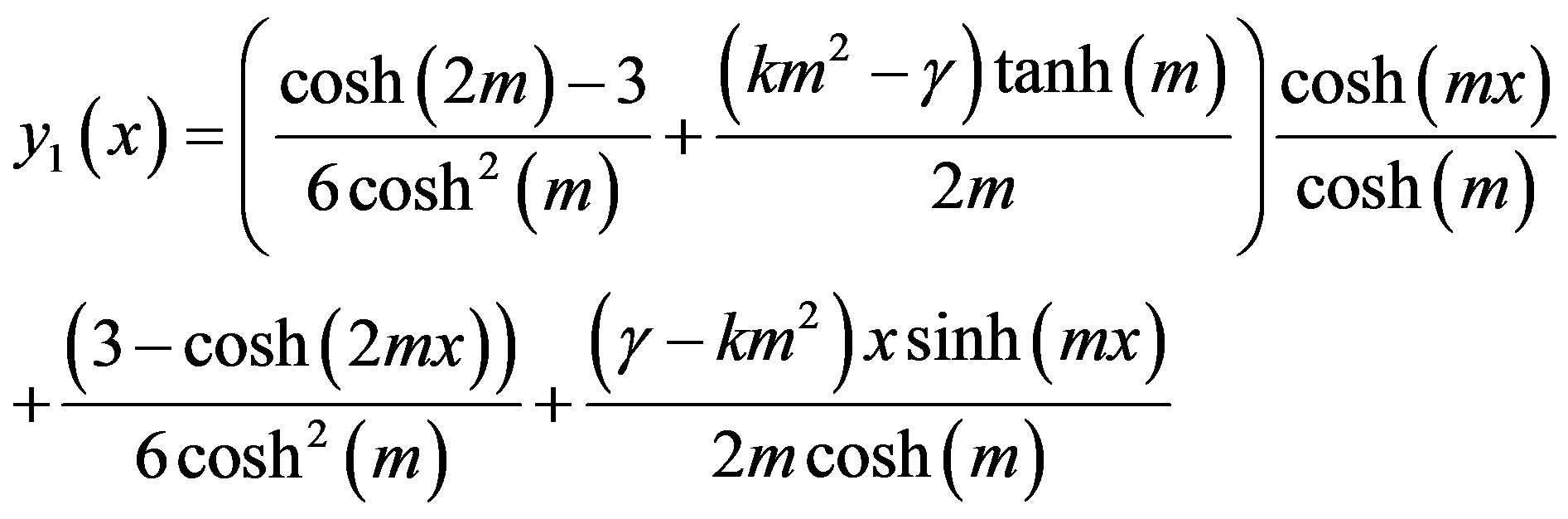 (D10)
(D10)
where m is defined in the text Eq.8. According to the HPM, we can conclude that
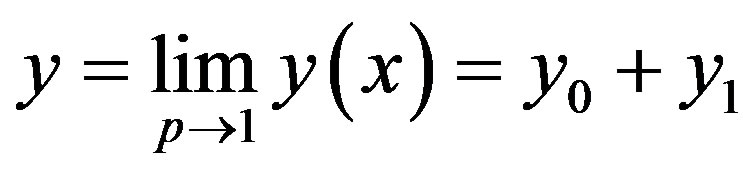 (D11)
(D11)
After putting the Eqs.D9 and D10 into an Eq.D11, we obtain the solutions in the text Eq.15.
APPENDIX E
Matlab/Scilab program to find the numerical solution of non-linear Eqs.5 and 6
function pdex4 m = 0;
x = linspace(-1,1);
t = linspace(0,100);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
figure plot(x,u1(end,:))
title('Solution at t = 2')
xlabel('Distance x')
ylabel('u1 (x,2)')
% -------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c=1;
g=1;
k=4;
f = 1.* DuDx;
F1 =-g*u(1)/(u(1)+k);
s =F1;
% -------------------------------------------------------------
function u0 = pdex4ic(x)
u0 = 1;
% -------------------------------------------------------------
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = ul(1)-1;
ql = 0;
pr = ur(1)-1;
qr = 0;
APPENDIX F
Nomenclature


