Natural Science
Vol.5 No.5(2013), Article ID:32120,9 pages DOI:10.4236/ns.2013.55078
Grand potential formalism of interfacial thermodynamics for critical nucleus
![]()
Institute of Technology and Science, The University of Tokushima, Tokushima, Japan; *Corresponding Author: atsumshimori@tokushima-u.ac.jp
Copyright © 2013 Atsushi Mori, Yoshihisa Suzuki. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 14 March 2013; revised 14 April 2013; accepted 22 April 2013
Keywords: Gibbs Interfacial Thermodynamics; Grad Potential; Interfacial Tension; Work of Nucleus Formation
ABSTRACT
In nucleation theories, the work of formation of a nucleus is often denoted by W = ΔG. This convention misleads that the nucleation should be considered in the isothermal-isobaric system. However, the pressure in the system with a nucleus is no longer uniform due to Laplace’s equation. Instead, the chemical potential is uniform throughout the system for the critical nucleus. Therefore, one can consider the nucleation in the grand ensemble properly. Accordingly, W is found to be the grand potential difference and the interfacial tension is also turned to be an interfacial excess grand potential. This treatment is not entirely new; however, to explicitly treat in the grand potential formalism is for the first time. We have successfully given an overwhelmingly clear description.
1. INTRODUCTION
The work of formation of a nucleus is often written as . It leads one to understand the work of formation of the critical nucleus as a difference of the Gibbs energy. The meaning of the form of the work of formation of a critical nucleus (Equation (4) in the text) becomes, however, clear straightforwardly if we deal the system including a critical nucleus as an isothermal-isochoric open system. The treatment as an isothermal-isobaric closed system brings confusions. The concept of the Gibbs dividing surface is more clearly understood in the isothermal-isochoric open system. As will be stated in the text, the treatments of an isothermal-isochoric open system appeared in literatures already. In this paper, we will give a clearer and direct statement in the grand potential formalism for nucleation, aiming at helping researchers who are not specialists in thermodynamics. In other words, by describing with definite terminologies we will put forward understandings—some terminologies will be for the first time used definitely in this paper.
. It leads one to understand the work of formation of the critical nucleus as a difference of the Gibbs energy. The meaning of the form of the work of formation of a critical nucleus (Equation (4) in the text) becomes, however, clear straightforwardly if we deal the system including a critical nucleus as an isothermal-isochoric open system. The treatment as an isothermal-isobaric closed system brings confusions. The concept of the Gibbs dividing surface is more clearly understood in the isothermal-isochoric open system. As will be stated in the text, the treatments of an isothermal-isochoric open system appeared in literatures already. In this paper, we will give a clearer and direct statement in the grand potential formalism for nucleation, aiming at helping researchers who are not specialists in thermodynamics. In other words, by describing with definite terminologies we will put forward understandings—some terminologies will be for the first time used definitely in this paper.
Gibbs established the interfacial thermodynamic formula for the work of formation of a critical nucleus in 1870s [1]. Since then, this subject was sometimes revisited and developed and/or extended [2-21]. One of true developments may be descriptions for the curvaturedependence of the interfacial tension [4,22-31]; as shall be described in Section 1.2, the interfacial tension  is assumed to be known prior to the calculation of the radius
is assumed to be known prior to the calculation of the radius 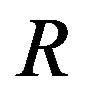 of the nucleus in the Gibbs formula. In other words, Gibbs’ treatment (Section 1.2) alone does work for evaluating the work of formation of the critical cluster if the interfacial tension is independent of the curvature of the interface. Later Tolman’s treatment was extended to the binary system [32]. Clarifying the meaning of the Gibbs dividing surface as done previously [2,3,5,11] and shall be done in Section 1.3 is helpful for general readers to avoid confusions, but not entirely new. Also embodiment of the variation of area
of the nucleus in the Gibbs formula. In other words, Gibbs’ treatment (Section 1.2) alone does work for evaluating the work of formation of the critical cluster if the interfacial tension is independent of the curvature of the interface. Later Tolman’s treatment was extended to the binary system [32]. Clarifying the meaning of the Gibbs dividing surface as done previously [2,3,5,11] and shall be done in Section 1.3 is helpful for general readers to avoid confusions, but not entirely new. Also embodiment of the variation of area  by defining the conical system with the solid angle
by defining the conical system with the solid angle  around the center of the nucleus, such as done previously [2, 3,5,9,11,21], is, indeed, very helpful for ones who need rigorous arguments, but also not entirely new.
around the center of the nucleus, such as done previously [2, 3,5,9,11,21], is, indeed, very helpful for ones who need rigorous arguments, but also not entirely new.
Throughout this paper we restrict ourselves to the case of spherical interfaces for simplicity and for the sake of avoiding complexity for better understanding. For example, two principal curvatures appear in general; this may bring confusion. Also, for the same sake we limit ourselves to unary cases. Also, for the same sake we omit the structure of both two phases; if at least one of the coexisting phases is crystalline, the interfacial tension becomes, strictly speaking, crystallographic orientation dependent.
1.1. Issue
One of purposes of the thermodynamics of nucleation is to calculate the reversible work of formation of a critical nucleus of a stable phase in an undercooled parent phase [1]. Through this work,  , one can obtain the steady-state nucleation rate as
, one can obtain the steady-state nucleation rate as  with
with  being the temperature multiplied by Boltzmann’s constant. Not only in textbooks [34-36] but also in advanced research papers [14,37-45] the following expression (or essentially equivalent one) is seen for the work of formation of a critical nucleus:
being the temperature multiplied by Boltzmann’s constant. Not only in textbooks [34-36] but also in advanced research papers [14,37-45] the following expression (or essentially equivalent one) is seen for the work of formation of a critical nucleus:
 (1)
(1)
where  is the difference between the chemical potentials of the nucleating phase (
is the difference between the chemical potentials of the nucleating phase ( phase) and the parent phase (
phase) and the parent phase ( phase). The direct interpretation of Equation (1) is as follows. Limiting ourselves to the case that the molecular volumes (volumes per molecule) of the
phase). The direct interpretation of Equation (1) is as follows. Limiting ourselves to the case that the molecular volumes (volumes per molecule) of the  and
and  phases are equal1, let us denote the molecular volume
phases are equal1, let us denote the molecular volume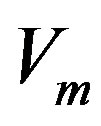 . Hereafter, the subscript
. Hereafter, the subscript  indicates the molecular quantities. Then, the quantity
indicates the molecular quantities. Then, the quantity 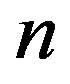 is defined as the number of molecule consisting the nucleus, which is equal to
is defined as the number of molecule consisting the nucleus, which is equal to  with
with 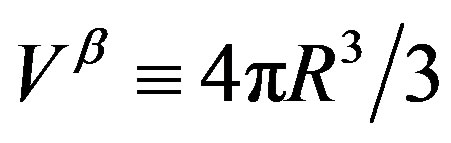 being the volume of the nucleus. The first term in Equation (1) is the volume term, which is the reversible work associated with the transformation from the
being the volume of the nucleus. The first term in Equation (1) is the volume term, which is the reversible work associated with the transformation from the  phase to the
phase to the 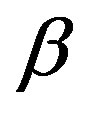 phase of
phase of 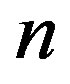 molecules. The second term in Equation (1) is the surface term, which is the reversible work to form a surface of area
molecules. The second term in Equation (1) is the surface term, which is the reversible work to form a surface of area . Here,
. Here,  is the radius of the nucleus; the rigorous definition of
is the radius of the nucleus; the rigorous definition of  will be given later. Remembering that the chemical potential is equal to the molecular Gibbs energy, the expression of
will be given later. Remembering that the chemical potential is equal to the molecular Gibbs energy, the expression of 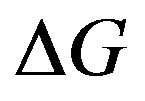 seems at apparent appropriate. The question arises whether the expression of Equation (1) is only valid for the case that no volume change is associated with the
seems at apparent appropriate. The question arises whether the expression of Equation (1) is only valid for the case that no volume change is associated with the  phase transition or not. Exact expression for the reversible work
phase transition or not. Exact expression for the reversible work 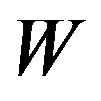 was already given and the approximation which reduces the exact expression to Equation (1) was derived [11]. Also the expression of
was already given and the approximation which reduces the exact expression to Equation (1) was derived [11]. Also the expression of  makes one understood at apparent that the interfacial tension
makes one understood at apparent that the interfacial tension 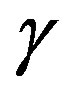 is defined as the superficial interfacial Gibbs energy; also exact expression for
is defined as the superficial interfacial Gibbs energy; also exact expression for 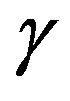 was already given [7,11]. Unfortunately, the previous derivations were not so transparent. A clearer interpretation will be given in this paper in a framework of the grand potential formalism. This paper aims at leading the readers to a clear understanding of the work of formation of a nucleus and solving the misunderstanding. The meaning of the interfacial free energy (or the interfacial tension)
was already given [7,11]. Unfortunately, the previous derivations were not so transparent. A clearer interpretation will be given in this paper in a framework of the grand potential formalism. This paper aims at leading the readers to a clear understanding of the work of formation of a nucleus and solving the misunderstanding. The meaning of the interfacial free energy (or the interfacial tension)  becomes also clear; the interfacial tesion
becomes also clear; the interfacial tesion  can be understood as the superficial grand potential [3-5,9,11,12].
can be understood as the superficial grand potential [3-5,9,11,12].
1.2. Gibbs Interfacial Thermodynamics
To review the Gibbs’ formalism for evaluating W is not only heuristic but also ingredient for understanding the thermodynamic “ensemble” appropriate for the system of nucleation. In other words, due to this one can find why the grand potential formalism is appropriate; that is, constant  condition is imposed. It is sufficient to limit ourselves to the unary case; formulation for the multi-component system is seen, for example, in a previous paper [46].
condition is imposed. It is sufficient to limit ourselves to the unary case; formulation for the multi-component system is seen, for example, in a previous paper [46].
Consider a spherical nucleus of the  phase in an undercooled
phase in an undercooled  phase of the chemical potential
phase of the chemical potential  at the temperature
at the temperature  The chemical potential
The chemical potential 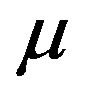 and temperature
and temperature 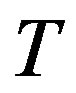 are regarded as those of the reservoir. Along with the isothermal condition, for the critical nucleus one can regard a cluster of the
are regarded as those of the reservoir. Along with the isothermal condition, for the critical nucleus one can regard a cluster of the  phase is in equilibrium with the
phase is in equilibrium with the 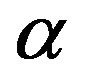 phase with respect to the material transport. One can select
phase with respect to the material transport. One can select  as independent variables specifying the total system with
as independent variables specifying the total system with  being the volume of the total system. The following is the procedure of the calculation of the work of formation of a critical nucleus.
being the volume of the total system. The following is the procedure of the calculation of the work of formation of a critical nucleus.
1) The pressure of the  phase is determined by the equilibrium equation with respect to the materials transport, i.e.
phase is determined by the equilibrium equation with respect to the materials transport, i.e.
 (2)
(2)
2) Presuming the interfacial tension  as known, the radius
as known, the radius  is determined by Laplace’s equation,
is determined by Laplace’s equation,
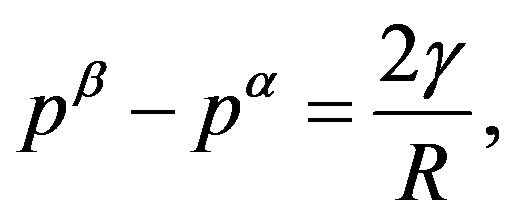 (3)
(3)
where 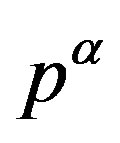 is the pressure of the
is the pressure of the 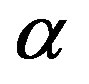 phase corresponding to
phase corresponding to .
.
3) The work of formation of the critical nucleus of radius R is calculated by
 (4)
(4)
We note that eliminating  using Laplace’s equation (Equation (3)), Equation (4) is rewritten into
using Laplace’s equation (Equation (3)), Equation (4) is rewritten into
 (5)
(5)
We should note that the work of formation of a critical nucleus consists of two terms; as has been mentioned the first term is the volume term and, in tern, the second term is the surface term. The first term in Equation (4) is the work to replace the  phase of volume
phase of volume  with the
with the 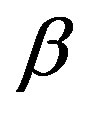 phase. The second term,
phase. The second term,  , is understood as the work associated with the formation of area
, is understood as the work associated with the formation of area  of the surface free energy
of the surface free energy 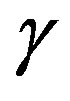 per unit area. In other words, in writing the work of formation of the critical nucleus we divide the process of nucleus formation into two. One is to form a hypothetical nucleus of the
per unit area. In other words, in writing the work of formation of the critical nucleus we divide the process of nucleus formation into two. One is to form a hypothetical nucleus of the  phase possessing the bulk properties throughout the entire volume
phase possessing the bulk properties throughout the entire volume 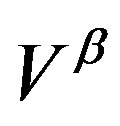 in the parent
in the parent  phase. The other is regarded to that to form a actual structure of the interface.
phase. The other is regarded to that to form a actual structure of the interface.
1.3. Gibbs Dividing Surface and Surface of Tension
For the first one of the two works of formation of a critical nucleus, the mathematical surface of radius 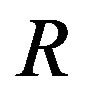 is a key concept. This surface is called the Gibbs dividing surface. Owing to introducing the dividing surface one can divide the work of formation of a nucleus into two. The volume term is the work of formation of a hypothetical cluster as illustrated in Figure 1. The surface term of the form of
is a key concept. This surface is called the Gibbs dividing surface. Owing to introducing the dividing surface one can divide the work of formation of a nucleus into two. The volume term is the work of formation of a hypothetical cluster as illustrated in Figure 1. The surface term of the form of 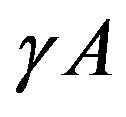 is, however, not very general; this form is valid only for the surface of tension, which will be explained later. The general form includes a curvature-dependent term [7]. There are varieties of choices of the dividing surface. Most straightforward one is the equimolar surface; the total numbers of molecules of the hypothetical system and the real one are the same thereby. The dividing surface introduced in Section 1.2 is called the surface of tension as mentioned there. By this choice, the coefficient
is, however, not very general; this form is valid only for the surface of tension, which will be explained later. The general form includes a curvature-dependent term [7]. There are varieties of choices of the dividing surface. Most straightforward one is the equimolar surface; the total numbers of molecules of the hypothetical system and the real one are the same thereby. The dividing surface introduced in Section 1.2 is called the surface of tension as mentioned there. By this choice, the coefficient 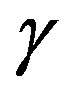 appears in the surface term in the work of formation of a critical nucleus coincides with the interfacial tension. The definition of the surface of tension is implicit; the choice so that the curvature-dependent term vanishes is the definition. For the choice of the surface of tension, Laplace’s equation (Equation (3)) holds; Laplace’s equation is the equation of the mechanical balance at the
appears in the surface term in the work of formation of a critical nucleus coincides with the interfacial tension. The definition of the surface of tension is implicit; the choice so that the curvature-dependent term vanishes is the definition. For the choice of the surface of tension, Laplace’s equation (Equation (3)) holds; Laplace’s equation is the equation of the mechanical balance at the
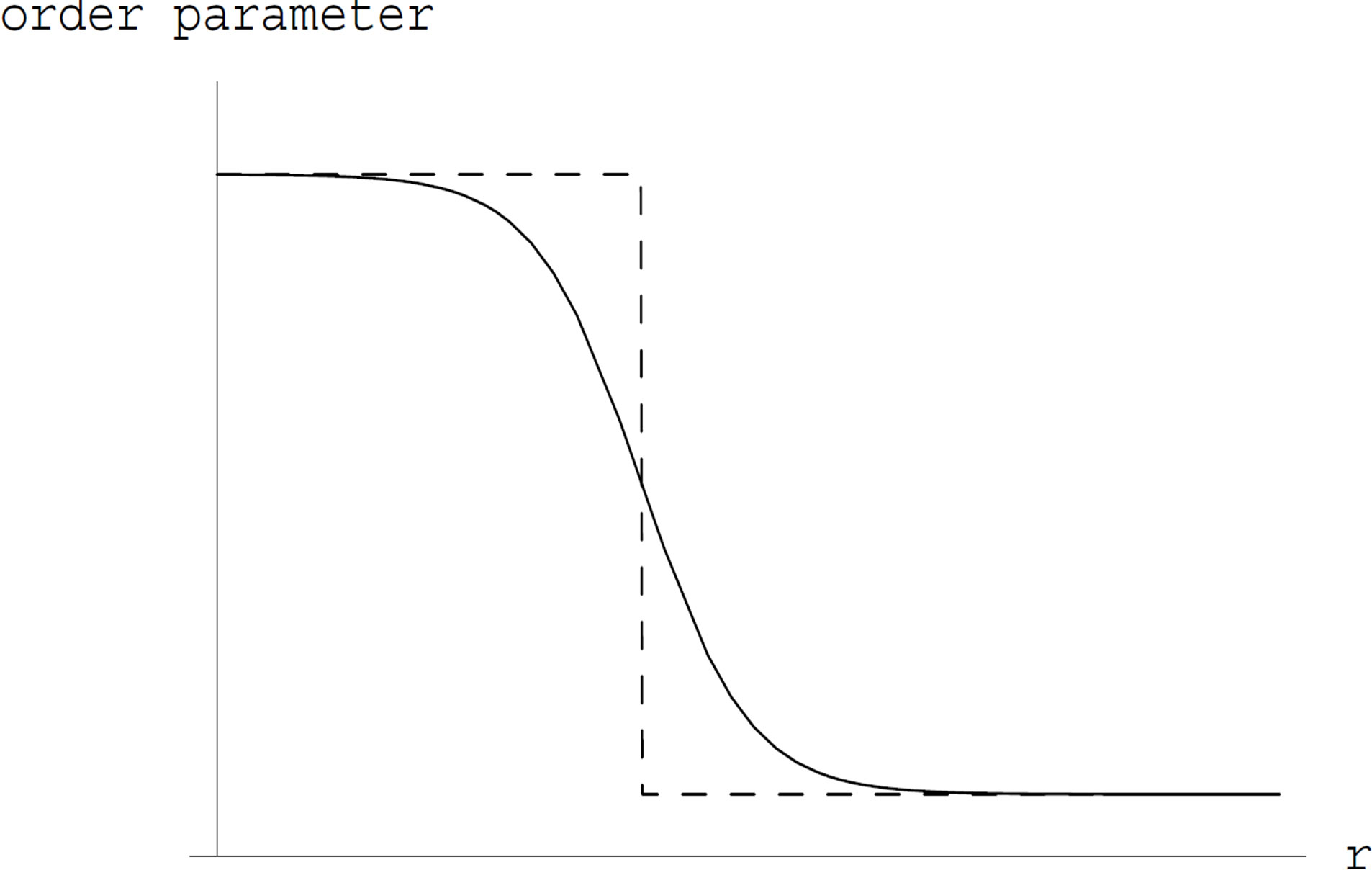
Figure 1. A schematic illustration of the profile of the order parameter (the density in, e.g., vapor-liquid case) with the horizontal axis indicating the distance from the center of the nucleus. In general, the order parameter varies between two bulk values gradually. Dashed lines indicate the hypothetical system, in which inside the dividing surface, indicated by a vertical dashed line, is occupied with a bulk β phase and outside with a bulk α phase.
curved interface possessing the mechanical tension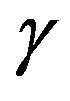 . Therefore, the interfacial free energy
. Therefore, the interfacial free energy 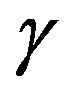 is called the interfacial tension.
is called the interfacial tension.
2. WORK OF FORMATION OF CRITICAL NUCLEUS
Sometimes very unnatural variables are specified [2,11]. That is, the internal energy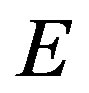 , the entropy
, the entropy , and the amount of substances are selected as independent variable. The mass as well as the number of molecule can be employed as the amount of substances. Nevertheless, Nishioka [11,13] derived a correct conclusion that
, and the amount of substances are selected as independent variable. The mass as well as the number of molecule can be employed as the amount of substances. Nevertheless, Nishioka [11,13] derived a correct conclusion that  is equal to the superficial grand potential through an entangled argument.
is equal to the superficial grand potential through an entangled argument.
As pointed in Section 1.2 the chemical potential throughout the system is uniform. Along with the fact that the system is considered as isothermal, it is appropriate to select the temperature 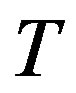 and the chemical potential
and the chemical potential  as independent variables. In this case, because at least one extensive variable is necessary for complete description, the total system volume
as independent variables. In this case, because at least one extensive variable is necessary for complete description, the total system volume  must be, in general, selected as one of the independent variables. We note that the uniformity of the chemical potential was already pointed out [2]; the treatment there was, however, not fully satisfactory.
must be, in general, selected as one of the independent variables. We note that the uniformity of the chemical potential was already pointed out [2]; the treatment there was, however, not fully satisfactory.
2.1. Isothermal-Isochoric Open System and Grand Potential
As mentioned above the temperature and the chemical potential are uniform throughout the system. One can regard that the system is exposed to the isobaric reserver because if the chemical potential and the temperature are kept constant, the corresponding pressure, which is a function of  and
and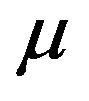 , is also constant. In Figure 2 we illustrate an isobaric closed system and an isochoric open system; whereas in the former the system size changes after the nucleation, in the latter the system size is unchanged thereafter. Therefore, we should take into NPT v.s. μVT N, P, T μ(P, T), V,T
, is also constant. In Figure 2 we illustrate an isobaric closed system and an isochoric open system; whereas in the former the system size changes after the nucleation, in the latter the system size is unchanged thereafter. Therefore, we should take into NPT v.s. μVT N, P, T μ(P, T), V,T
 (a) (b)
(a) (b)
Figure 2. Comparison of the isobaric closed system and the isochoric open system before and after the nucleation. For clarity we assume that the nucleating phase is more condensed than the parent phase. In the isobaric case the total volume varies due to the nucleation. Accordingly, to figure out the work of formation of the nucleus in the isobaric system is somewhat complicated.
account the change of the total volume in calculation of the work of formation of a nucleus for the former case. This is somewhat complicated. Hence, it is convenient to treat the system as isothermal-isochoric open one. Of course, two ways of description are both correct. The reversible work calculated as the Gibbs energy difference should coincide to that calculated as the grand potential difference. Indeed, a consideration with confusions led to the correct answer [33]. Unfortunately, in [33] the volume term and the surface term had been intertwined with each other; the form of Equation (5) has been eventually obtained.
At least in Japan, a thermodynamics class does not teach the grand potential systematically. One can, however, obtain isochoric open system by Legendre transformation of the isothermal-isochoric closed system, i.e., the independent variable is transformed from the amount of substances to the chemical potential to obtain this system [47]. The thermodynamic potential is obtained from the Helmholtz energy F by extracting 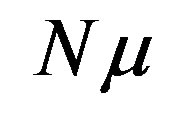 (remember that
(remember that  is thermodynamic conjugate variable to
is thermodynamic conjugate variable to ); that is,
); that is,
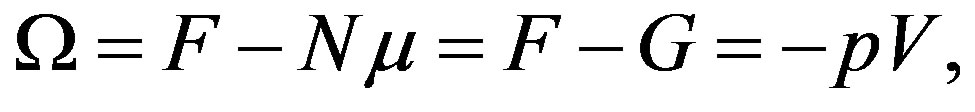 (6)
(6)
where 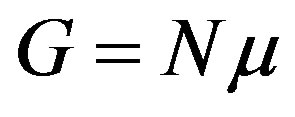 is the Gibbs energy. To reach to the last expression we have used the definition
is the Gibbs energy. To reach to the last expression we have used the definition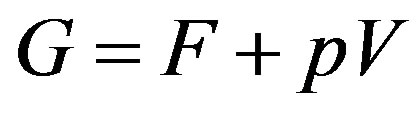 . One may be familiar with this form in the grand canonical ensemble (
. One may be familiar with this form in the grand canonical ensemble ( ensemble) through the bridging relation in this ensemble [48]. The thermodynamic potential Ω is the grand potential. We note that the grand potential (or merely the symbol
ensemble) through the bridging relation in this ensemble [48]. The thermodynamic potential Ω is the grand potential. We note that the grand potential (or merely the symbol ) already appeared in a thermodynamic expression for the interface in literatures[20,25,28,31,42,49-51] and a textbook [48]. In addition, the grand potential
) already appeared in a thermodynamic expression for the interface in literatures[20,25,28,31,42,49-51] and a textbook [48]. In addition, the grand potential  may be familiar in the fields of the density-functional theory.
may be familiar in the fields of the density-functional theory.
By virtue of the last expression of Equation (6), we obtain the volume term of the work of formation of a critical nucleus, as the grand potential difference between the system including the hypothetical nucleus and the homogeneous  phase, as
phase, as
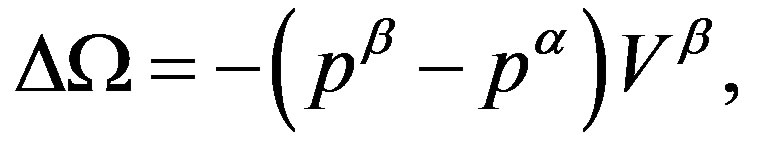 (7)
(7)
where  and
and 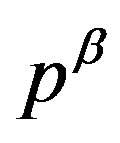 are the pressures of respective bulk phases; even though there is no bulk part of the
are the pressures of respective bulk phases; even though there is no bulk part of the  phase in reality such as for a small nucleus, the pressure
phase in reality such as for a small nucleus, the pressure 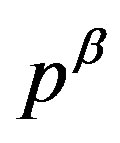 is well defined (through Equation (2)). Due to the positive interfacial tension between the
is well defined (through Equation (2)). Due to the positive interfacial tension between the 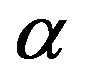 and
and  phases, the pressure
phases, the pressure  of the phase inside the dividing surface is greater than
of the phase inside the dividing surface is greater than  (thermodynamic derivation of this relation will be given in Section 2.2). In this way, we have the first term in Equation (4), which is negative and corresponding to the volume bulk term in Equation (1).
(thermodynamic derivation of this relation will be given in Section 2.2). In this way, we have the first term in Equation (4), which is negative and corresponding to the volume bulk term in Equation (1).
2.2. Work of Formation of Critical Nucleus
As argued up to now, we know that the work of formation of a critical nucleus is composed of the volume term, which is corresponding to the first term in Equation (1) and given by Equation (7), and the surface term, which is corresponding to the second term in Equation (1). If the equilibrium with respect to the materials transport holds between the parent phase and the nucleus, the pressure inside the nucleus,  , is obtained by solving
, is obtained by solving
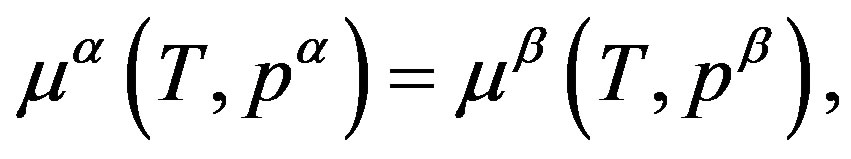 (8)
(8)
which corresponds to Equation (2) and consistent to the isothermal open system (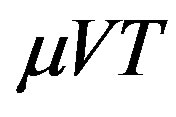 ensemble). Because the
ensemble). Because the 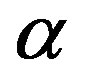 phase is metastable and the
phase is metastable and the 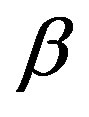 phase is the stable phase; that is,
phase is the stable phase; that is,
 (9)
(9)
holds, one can derive . Recalling the GibbsDuhem relation
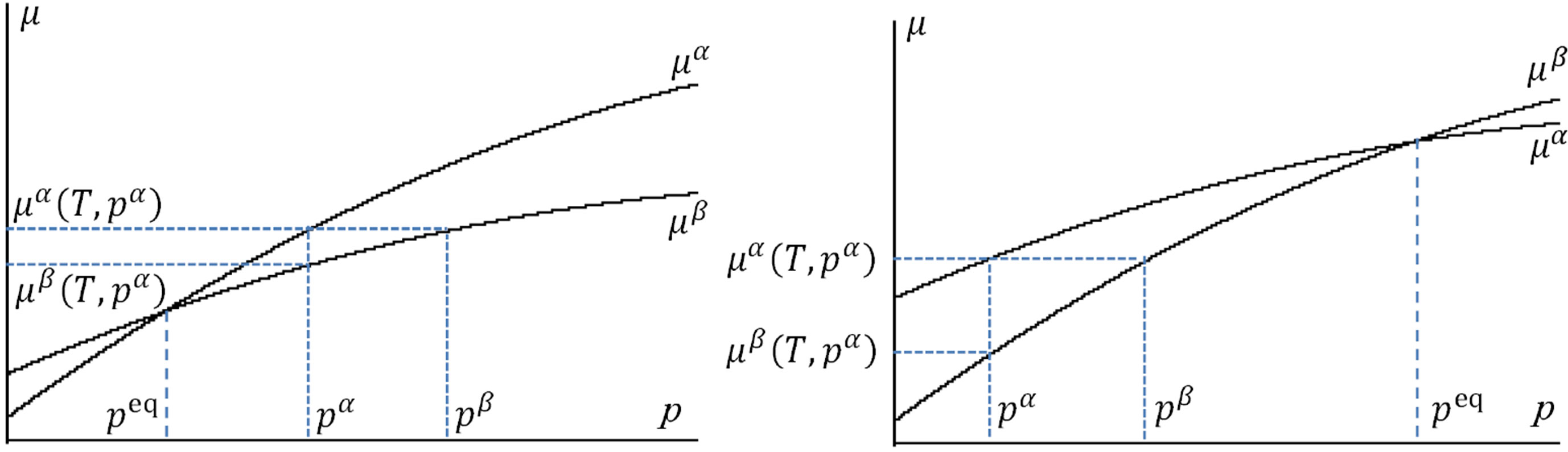
. Recalling the GibbsDuhem relation , we draw schematically the chemical potentials as functions of the pressure in Figure 3; the larger the slope is, the larger the molecular volume
, we draw schematically the chemical potentials as functions of the pressure in Figure 3; the larger the slope is, the larger the molecular volume  is. In Figure 3(a), we illustrate
is. In Figure 3(a), we illustrate  and
and 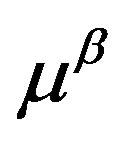 for a normal case
for a normal case . Because the
. Because the  phase is metastable (Equation (9)), the location of
phase is metastable (Equation (9)), the location of  is in the side
is in the side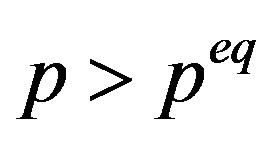 . Therefore, from Equation (8) one can find the location of
. Therefore, from Equation (8) one can find the location of 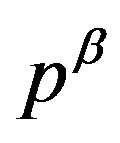 as illustrated in Figure 3(a). An illustration for an abnormal case
as illustrated in Figure 3(a). An illustration for an abnormal case  such as the case of water-ice phase transition is given in Figure 3(b). The interpretation is logically the same.
such as the case of water-ice phase transition is given in Figure 3(b). The interpretation is logically the same.
 (a) (b)
(a) (b)
Figure 3. The 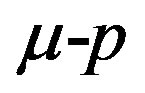 relations are plotted for (a) a normal case
relations are plotted for (a) a normal case  and (b) an abnormal case
and (b) an abnormal case . Therefrom, one can confirm inequality
. Therefrom, one can confirm inequality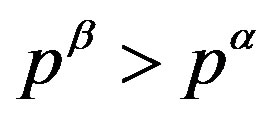 .
.
In this way, the negativity of the volume term is understood. The criterion for the dividing surface has not been given yet. The surface term, in general, take a form [7,9,11]
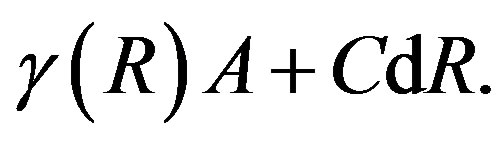 (10)
(10)
Here, 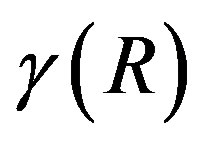 denotes that this coefficient depends on the criterion for the dividing surface. The surface of tension is defined by
denotes that this coefficient depends on the criterion for the dividing surface. The surface of tension is defined by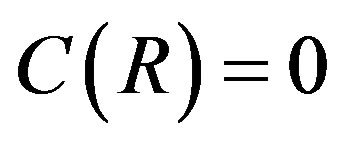 . Only for this choice of
. Only for this choice of , the coefficient
, the coefficient  coincide with the interfacial tension. In other words, the surface term consist of, in general, the interfacial area dependent term and the curvature dependent term. The surface of tension is defined for which the curvature dependent term vanishes. We note that
coincide with the interfacial tension. In other words, the surface term consist of, in general, the interfacial area dependent term and the curvature dependent term. The surface of tension is defined for which the curvature dependent term vanishes. We note that 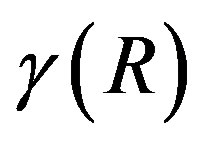 takes the minimum for the surface of tension [7].
takes the minimum for the surface of tension [7].
In this way, we have obtained Equation (4) for the work of formation of a critical nucleus. We give a note here. The work for the formation of the critical nucleus takes, however, the same value if the physical condition is unchanged; that is, it is not dependent on the criterion of the dividing surface. Therefrom, one can derive the relation between the general 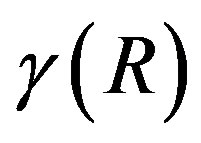 and the interfacial tension. This was done by Kondo [7].
and the interfacial tension. This was done by Kondo [7].
Noting  and
and , let us solve the equation that the derivative with respect to
, let us solve the equation that the derivative with respect to 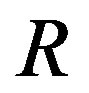 of Equation (4) vanishes. By a simple calculation we have Laplace’s equation (Equation (3)). This is a mechanical balance equation. Namely, in a case that two phases are coexisting via an interface of a curvature radius
of Equation (4) vanishes. By a simple calculation we have Laplace’s equation (Equation (3)). This is a mechanical balance equation. Namely, in a case that two phases are coexisting via an interface of a curvature radius  with an interrfacial tension
with an interrfacial tension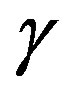 , the force acting from the inside of the interface due to the pressure
, the force acting from the inside of the interface due to the pressure 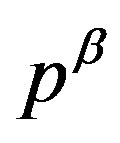 balances with the composed force of the force due to the outside pressure
balances with the composed force of the force due to the outside pressure 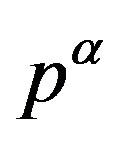 and that due to the interfacial tension (corresponding to
and that due to the interfacial tension (corresponding to ). The quantity
). The quantity 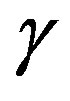 defined as the interfacial free energy per unit area of the interface is, if one chooses the surface of tension as the dividing surface, coincides with the mechanical interfacial tension. Readers can readily confirm the coincidence between the unit of the energy per area and the tension.
defined as the interfacial free energy per unit area of the interface is, if one chooses the surface of tension as the dividing surface, coincides with the mechanical interfacial tension. Readers can readily confirm the coincidence between the unit of the energy per area and the tension.
Now, let us derive the form of the first term in Equation (1), following Nishioka and Kusaka [13]. We start with the relation
 (11)
(11)
which is nothing other than the Gibbs-Duhem relation for the isothermal case. We consider a case that an incompressible  phase nucleus is nucleated in the
phase nucleus is nucleated in the 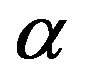 phase. Let us integrate Equation (11) for the
phase. Let us integrate Equation (11) for the  phase for
phase for  from
from 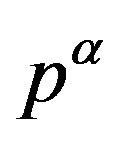 to
to .
.
 (12)
(12)
Eliminating 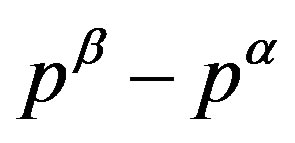 in Equation (4) using the equation derived by dividing Equation (12), we have an equation corresponding to Equation (1):
in Equation (4) using the equation derived by dividing Equation (12), we have an equation corresponding to Equation (1):
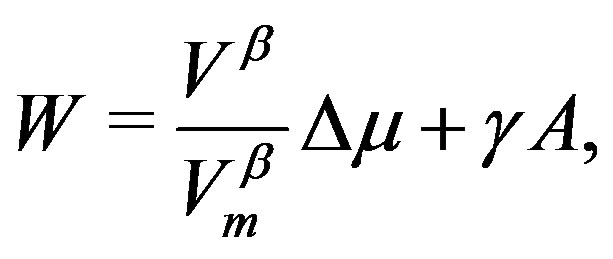 (13)
(13)
where
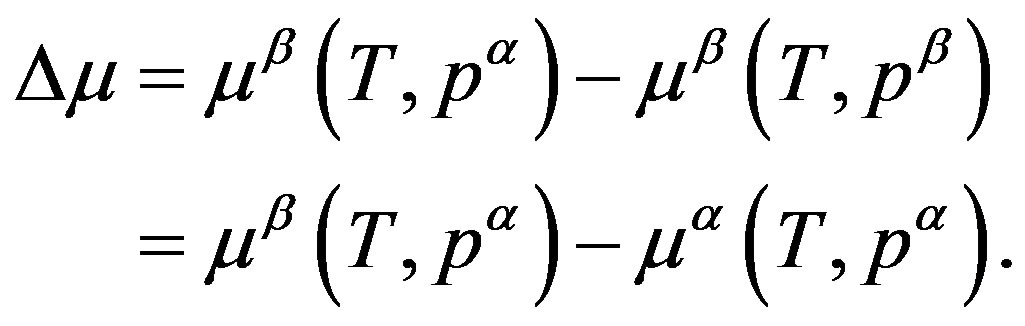 (14)
(14)
To reach to the last expression, Equation (8) has been used. One can integrate Equation (11) for the  phase to obtain the form of Equation (1) in a case that the
phase to obtain the form of Equation (1) in a case that the  phase is incompressible. This is, however, not the present concern. It should be noted that for a case that no volume change is associated with the
phase is incompressible. This is, however, not the present concern. It should be noted that for a case that no volume change is associated with the 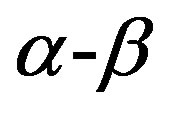 phase transition, a form far form Equation (1) is obtained [52], although in this case one has intuitively
phase transition, a form far form Equation (1) is obtained [52], although in this case one has intuitively  with
with  .
.
3. GIBBS ADSORPTION ISOTHERM
In this section, we derive the Gibbs adsorption isotherm
 (15)
(15)
where 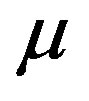 represents the chemical potential of the materials reservoir, which is equal to
represents the chemical potential of the materials reservoir, which is equal to , and
, and  is the superficial number density per unit area of the interface, sometimes referred to as the excess number density or the interfacial adsorption quantity. A rigorous definition of
is the superficial number density per unit area of the interface, sometimes referred to as the excess number density or the interfacial adsorption quantity. A rigorous definition of  will be given later.
will be given later.
3.1. Conical System and Superficial Quantities
We define the system as a spherical cone as illustrated in Figure 4. In this definition, there are two variables describing the extent of the system; through the solid angle  we can apply Euler’s theorem for the homogeneous equation. Unlike previous papers [9,11,13], we define the system as open with the chemical potential
we can apply Euler’s theorem for the homogeneous equation. Unlike previous papers [9,11,13], we define the system as open with the chemical potential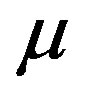 . In those papers, the arguments were started with selecting the entropy
. In those papers, the arguments were started with selecting the entropy , the number of molecule
, the number of molecule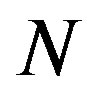 , the radius
, the radius , and the solid angle
, and the solid angle  as independent variables. However, the argument becomes simplified with the selection of independent variables
as independent variables. However, the argument becomes simplified with the selection of independent variables 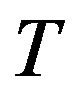 and
and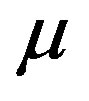 , instead of
, instead of 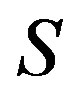 and
and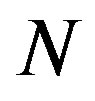 . We note that
. We note that 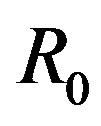 is selected enough larger than
is selected enough larger than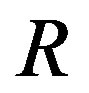 .
.
For the hypothetical system, because of the bulk properties, the following fundamental equations (Gibbs relations) hold for two parts of the system:
 (16)
(16)
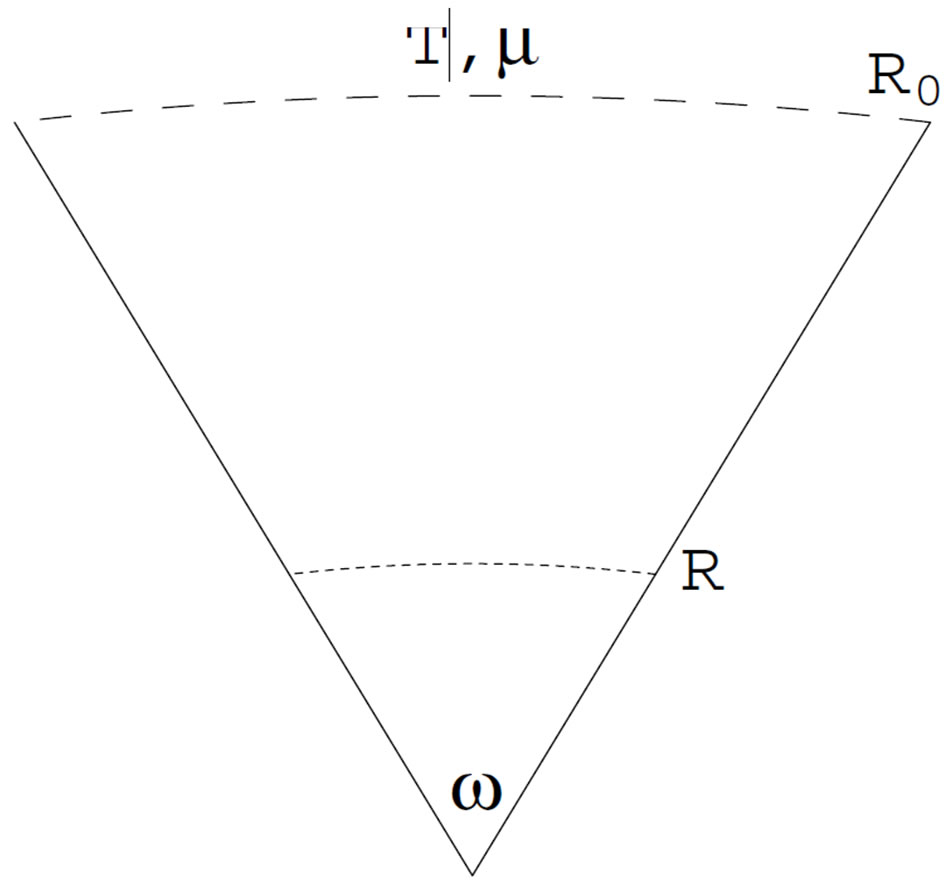
Figure 4. Conical system with the solid angle ω around the center of the nucleus. The system is defined as isochoric with the solid angle ω and the radius R0. The system is exposed to the reservoir of the temperature T and the chemical potential μ.
Here, according to a convention  is used to represent the internal energy. This equation is rewritten in terms of the grand potentials
is used to represent the internal energy. This equation is rewritten in terms of the grand potentials  as
as
 (17)
(17)
Those equations hold for both systems with the solid angle  and the entire sphere
and the entire sphere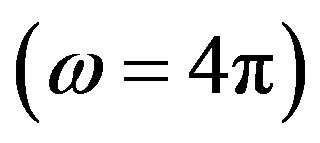 . In those expressions
. In those expressions
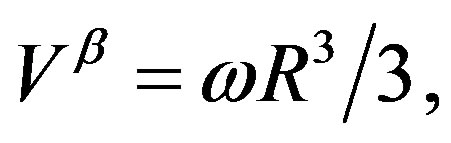 (18)
(18)
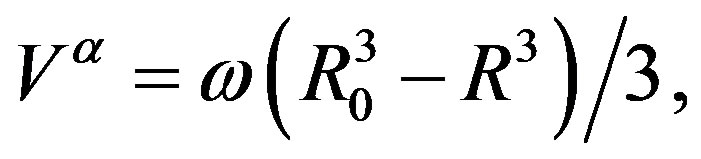 (19)
(19)
and we should note that  and
and  are independent variables.
are independent variables.
Let us denote quantities for the entire spherical system by symbols with a superscript  and those for the system with the solid angle
and those for the system with the solid angle  by symbols without a superscript. For a while, let us consider again a general dividing surface. Denoting the contribution due to the nucleus by…, the fundamental equation
by symbols without a superscript. For a while, let us consider again a general dividing surface. Denoting the contribution due to the nucleus by…, the fundamental equation
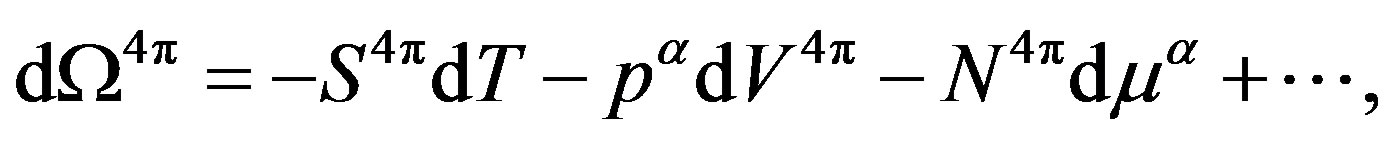 (20)
(20)
holds. Here,  and because the
and because the 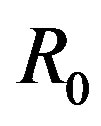 is an independent variable,
is an independent variable,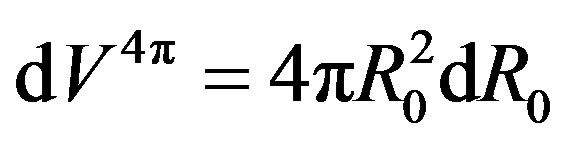 . Let us rewrite Equation (20) using
. Let us rewrite Equation (20) using 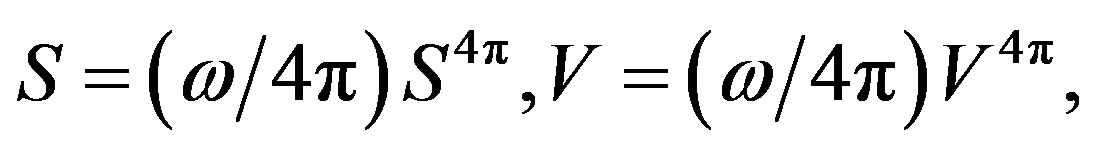 and
and
 . Because
. Because 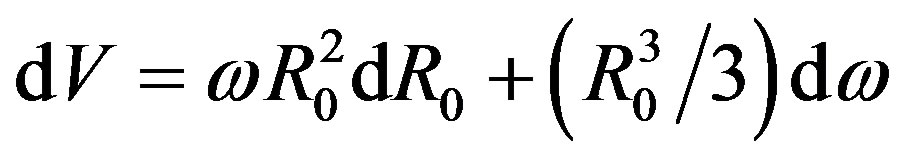 (from
(from ), we have
), we have
 (21)
(21)
Here, we express the contribution of the nucleus by introducing the coefficient  defined by
defined by
 (22)
(22)
as previously done [2,3,5,9,11,13]. In those previous papers, the expression in the square brackets was given.
Differentiating 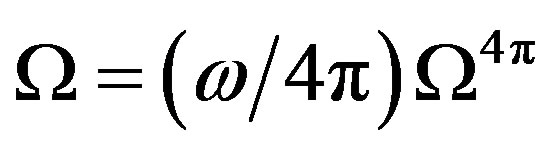 and using Equation (20), we have
and using Equation (20), we have
 (23)
(23)
By comparing Equations (21) and (23), we obtain
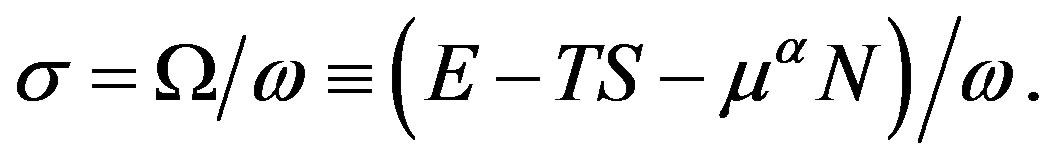 (24)
(24)
In previous papers [2,3,5,9,11,13], the last expression was given, despite that the mid expression is conceptually meaningful. This equation is the equation obtained from the relation on the basis of the fact that when the solid angle is multiplied by , the grand potential
, the grand potential
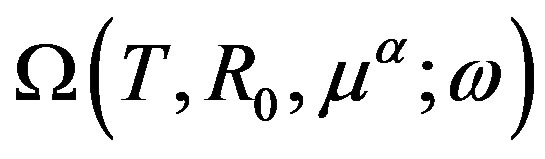 is transformed as
is transformed as
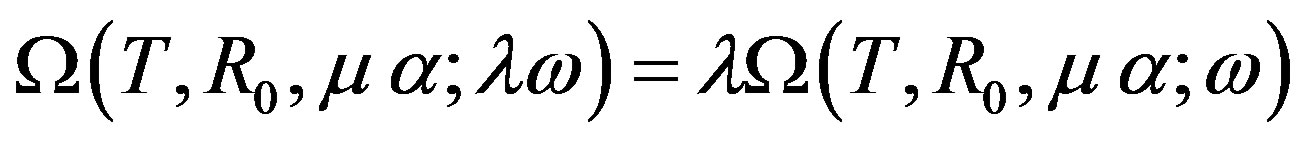
(Euler’s theorem). We note that Nishioka [11] derived the same equation by applying Euler’s theorem to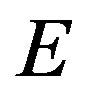 .
.
3.2. Interfacial Tension
In Equation (21), existence of  is due to the nucleus. Therefore, one can write
is due to the nucleus. Therefore, one can write
 (25)
(25)
(pay attention on the independent variables). The first two terms are of the hypothetical system defined in Section 3.1. The last two terms are for forming interfacial structure after the formation of the hypothetical system. As mentioned above, we note that a term depending on the derivative of the curvature radius, 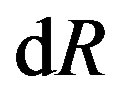 , appears. This term, also as mentioned above, vanishes if the surface of tension is taken as the dividing surface.
, appears. This term, also as mentioned above, vanishes if the surface of tension is taken as the dividing surface.
Let us go forward the argument by taking the surface of tension as the dividing surface. Using the equation obtained by putting 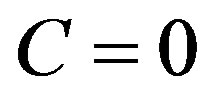 in Equation (25), we rewrite Equation (21) into
in Equation (25), we rewrite Equation (21) into
 (26)
(26)
The fundamental equation for the hypothetical system is just the addition of both of Equation (17):
 (27)
(27)
Subtracting Equation (27) from Equation (26), we have the fundamental equation for the superficial grand potential :
:
 (28)
(28)
where  and
and  are, respectively, the superficial entropy and the superficial number of molecules. In this equation
are, respectively, the superficial entropy and the superficial number of molecules. In this equation 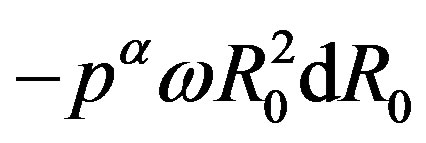 has been eliminated because the state of the interface is independent of the selection of
has been eliminated because the state of the interface is independent of the selection of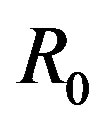 ; in other words,
; in other words,  has been fixed at the position
has been fixed at the position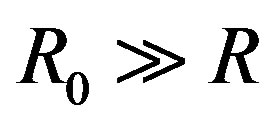 .
.
Euler’s relation obtained from the fact that  is transformed as
is transformed as 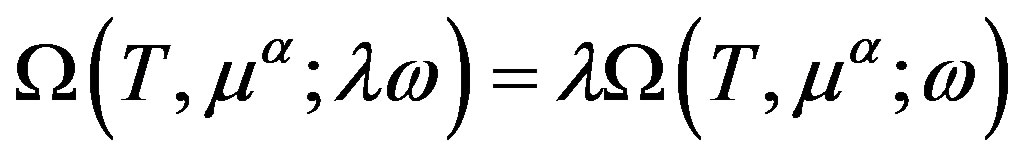 when
when  is multiplied by
is multiplied by  as
as  is
is
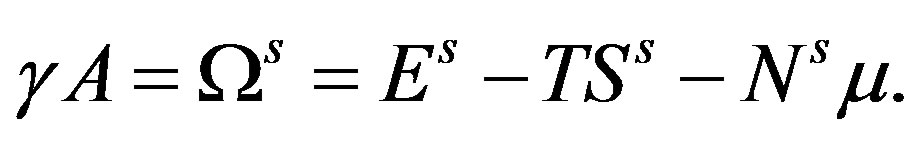 (29)
(29)
To derive this equation, one can use the same method to derive Equation (24). From Equation (29), the interfacial tension  is revealed to be the superficial grand potential per unit area of the interface. Introducing the superficial quantities per unit area of the interface,
is revealed to be the superficial grand potential per unit area of the interface. Introducing the superficial quantities per unit area of the interface, 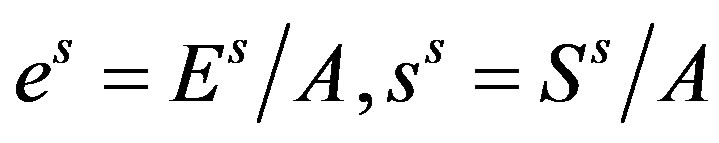 , and
, and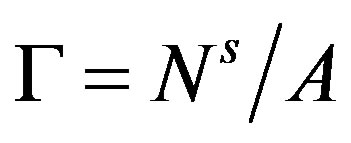 , we have
, we have
 (30)
(30)
The last expressions in Equations (29) and (30) have already be given in previous papers [3,4,5,9,11-13,15,20, 21,31]. In those papers, except for [12,20,21,31]—Rusanov et al. [20] explicitly stated, however, the word of the superficial grand potential did not appear.
3.3. Gibbs-Duhem Relation for Interface
A general way to obtain the Gibbs-Duhem relation is to take differential of Euler’s relation and subtract the fundamental equation. For the interface, the same procedure is possible; we can have the Gibbs-Duhem relation for the interface
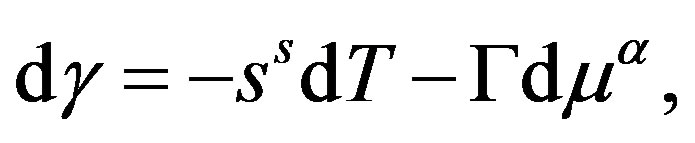 (31)
(31)
by taking differential of Equation (29) and subtract the first equation of Equation (28) and dividing by . We can, also, obtain Equation (31) by direct differentiation of Equation (30) and using the fundamental equation for
. We can, also, obtain Equation (31) by direct differentiation of Equation (30) and using the fundamental equation for . From Equation (31) we have Equation (15) or
. From Equation (31) we have Equation (15) or 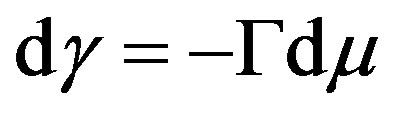
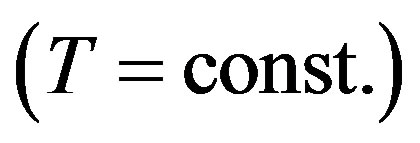 . This is the Gibbs adsorption isotherm.
. This is the Gibbs adsorption isotherm.
4. SUMMARY
We have given a grand potential formalism for the interfacial thermodynamics. It is revealed that the work of formation of a critical nucleus is equal to the grand potential difference. This makes a point of view clearer overwhelmingly than regarding the work of formation of the nucleus as the Gibbs energy difference. Also, the interfacial tension is revealed to be defined as the superficial grand potential per unit area of the interface. Although equivalent form was given previously [3-5,9,11, 13], this paper has explicitly closed up the grand potential property for the first time.
5. ACKNOWLEDGEMENTS
This paper is base on a lecture [in Japanese] at the 35th research meeting on the crystal growth (Toronkai) held by Japanese Association for Crystal Growth on Sept. 7-9, 2011 at Shimotsuma, Japan.
REFERENCES
- Gibbs, J.W. (1993) The scientific papers of J. Willard Gibbs, thermodynamics. Ox Bow, Woodbridge.
- Tolman, R.C. (1948) Consideration of the Gibbs theory of surface tension. The Journal of Chemical Physics, 16, 758-774. doi:10.1063/1.1746994
- Hill, T.L. (1951) On Gibbs theory of surface tension. The Journal of Chemical Physics, 19, 1203-1203. doi:10.1063/1.1748502
- Buff, F.P. (1951) The spherical interface. I. Thermodynamics. The Journal of Chemical Physics, 19, 1591-1594. doi:10.1063/1.1748127
- Hill, T.L. (1952) Statistical thermodynamics of the transition region between two phases. I. Thermodynamics and quasi-thermodynamics. Journal of Physical Chemistry, 56, 525-531. doi:10.1021/j150496a027
- Kondo, S. (1955) A statistical-mechanical thory of surface tension of curved surface layer I. Journal of the Physical Society of Japan, 10, 381-386. doi:10.1143/JPSJ.10.381
- Kondo, S. (1956) Thermodynamical fundamental equation for spherical interface. The Journal of Chemical Physics, 25, 662-669. doi:10.1063/1.1743024
- Plesner, I.W. (1964) Statistical thermodynamics of spherical droplets. The Journal of Chemical Physics, 40, 1510- 1517. doi:10.1063/1.1725355
- Nishioka, K. (1977) Thermodynamics of a liquid microcluster. Physical Review A, 16, 2143-2152. doi:10.1103/PhysRevA.16.2143
- Wilemski, G. (1984) Composition of the critical nucleus in multicomponent vapor nucleation. Journal of Chemical Physics, 80, 1370-1372. doi:10.1063/1.446822
- Nishioka, K. (1987) Thermodynamics formalism for a liquid microcluster in vapor. Physical Review A, 36, 4845- 4851. doi:10.1103/PhysRevA.36.4845
- Voorhees, P.W. and Johnson, W.C. (1989) The thermodynamics of a coherent interface. The Journal of Chemical Physics, 90, 2793-2801. doi:10.1063/1.455928
- Nishioka, K. and Kusaka, I. (1992) Thermodynamics formulas of liquid phase nucleation form vapor in multicomponent systems. The Journal of Chemical Physics, 96, 5370-5376. doi:10.1063/1.462721
- Oxtoby, D.W. and Kashchiev, D. (1994) A general relation between the nucleation work and the size of the nucleus in multicomponent nucleation. The Journal of Chemical Physics, 100, 7665-7671. doi:10.1063/1.466859
- Debeneditti, P.G. and Reiss, H. (1998) Reversible work of formation of an embryo of a new phase within a uniform macroscopic mother phase. The Journal of Chemical Physics, 108, 5498-5505. doi:10.1063/1.475938
- Laaksonen, A., McGraw, R. and Vehkamäki, H. (1999) Liquid-drop formalism and free-energy surface in binary homogeneous nucleation theory. The Journal of Chemical Physics, 111, 2019-2027. doi:10.1063/1.479470
- Kashchiev, D. (2003) Thermodynamically consistent description of the work to form a nucleus of any size. The Journal of Chemical Physics, 118, 1837-1851. doi:10.1063/1.1531614
- Schmelzer, J.W.P., Baidakov, V.G. and Boltachev, G.S. (2003) Kinetics of boiling in binary liquid-gas solutions: Comparison of different approaches. The Journal of Chemical Physics, 119, 6166-6183. doi:10.1063/1.1602066
- Kashchiev, D. (2004) Multicomponent nucleation: Thermodynamically consistent description of the nucleation work. The Journal of Chemical Physics, 120, 3749-3758. doi:10.1063/1.1643711
- Rusanov, A.I., Shchekin, A.K. and Tatyanenko, D.V. (2009) Grand potential in thermodynamics of solid bodies and surfaces. The Journal of Chemical Physics, 131, 161104. doi:10.1063/1.3254324
- Corti, D.S., Kerr, K.J. and Torabi, K. (2011) On the interfacial thermodynamics of nanoscale droplets and bubbles. The Journal of Chemical Physics, 135, 024701. doi:10.1063/1.3609274
- Tolman, R.C. (1949) The effect of droplet size on surface tension. The Journal of Chemical Physics, 17, 333-337. doi:10.1063/1.1747247
- Koenig, F.O. (1950) On the thermodynamic relation between surface tension and curvature. The Journal of Chemical Physics, 18, 449-459. doi:10.1063/1.1747660
- Buff, F.P. and Kirkood, J.G. (1950) Remarks on the surface tension of small droplets. The Journal of Chemical Physics, 18, 991-992. doi:10.1063/1.1747829
- Buff, F.P. (1955) Spherical interface. II. Molecular theory. The Journal of Chemical Physics, 23, 419-427. doi:10.1063/1.1742005
- Bogdan, A. (1997) Thermodynamics of the curvature effect on ice surface tension and nucleation theory. The Journal of Chemical Physics, 106, 1921-1929. doi:10.1063/1.473329
- McGraw, R. and Laaksonen, A. (1997) Interfacial curvature free energy, the Kelvin relation, and vapor-liquid nucleation rate. The Journal of Chemical Physics, 106, 5284-5287. doi:10.1063/1.473527
- Koga, K., Zeng, X.C. and Shchekin, A.K. (1998) Validity of Tolman’s equation: How large should a droplet be? The Journal of Chemical Physics, 109, 4063-4070. doi:10.1063/1.477006
- Bartell, L.S. (2001) Tolman’s δ, surface curvature, compressibility effects, and free energy of drops. Journal of Physical Chemistry B, 105, 11615-11618. doi:10.1021/jp011028f
- Blokhuis, E.M. and Kuipers, J. (2006) Thermodynamic expressions for the Tolman length. The Journal of Chemical Physics, 124, 074701. doi:10.1063/1.2167642
- Tröster, A., Ottel, M., Block, B., Virnau, J.P. and Binder, K. (2012) Numerical approaches to determine the inter facial tension of curved interface from free energy calculations. The Journal of Chemical Physics, 136, 064709. doi:10.1063/1.3685221
- Nishioka, K., Tomino, H., Kusaka, I. and Takai, T. (1989) Curvature dependence of the interfacial tension in binary nucleation. Physical Review A, 39, 772-782. doi:10.1103/PhysRevA.39.772
- Yang, A.J.-M. (1983) Free energy for the heterogeneous systems with spherical interfaces. The Journal of Chemical Physics, 79, 6289-6293. doi:10.1063/1.445734
- Mutaftschiev, B. (1993) Nucleation theory. In: Hurle, D.T.J., Ed., Handbook of Crystal Growth, Part 1a, Chapter 4, Elsevier, Amsterdam.
- Saito, Y. (1996) Statistical physics of crystal growth. World Scientific, Singapore.
- Markov, I.V. (2003) Crystal growth for beginners: Fundamentals of nucleation, crystal growth and epitaxy. 2nd Edition, World Scientific, Singapore. doi:10.1142/9789812796899
- Doyle, G.J. (1961) Self-nucleation in the sulfuric acidwater system. The Journal of Chemical Physics, 35, 795- 799. doi:10.1063/1.1701218
- Kashchiev, D. (1982) On the relation between nucleation work, nucleus size, and nucleation rate. The Journal of Chemical Physics, 76, 5098-5102. doi:10.1063/1.442808
- Laaksonen, A., Kulmala, M. and Wanger, P.E. (1993) On the cluster compositions in the classical binary nucleation theory. The Journal of Chemical Physics, 99, 6832- 6835. doi:10.1063/1.465827
- Vilsanen, Y. and Strey, R. (1994) Homogeneous nucleation rates for n-butanol. The Journal of Chemical Physics, 101, 7835-7843. doi:10.1063/1.468208
- Schmelzer, J.W.P., Schmelzer Jr., J. and Gutzow, I.S. (2000) Reconciling Gibbs and van der Waals: A new approach to nucleation theory. The Journal of Chemical Physics, 112, 3820-3831. doi:10.1063/1.481595
- Bowels, R.K., Reguera, D., Djikaev, Y. and Reiss, H. (2001) A theorem for inhomogeneous systems: The generalization of the nucleation theorem. The Journal of Chemical Physics, 115, 1853-1866.
- Auer, S. and Frenkel, D. (2001) Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature, 409, 1020-1023. doi:10.1038/35059035
- Gasser, S., Weeks, E.R., Schofield, A., Pusey, P.N. and Weitz, D.A. (2001) Real-space imaging of nucleation and growth in colloidal crystallization. Science, 292, 258-262. doi:10.1126/science.1058457
- Kawasaki, T. and Tanaka, H. (2010) Formation of a crystal nucleation from liquid. Proceedings of the National Academy of Sciences of the United States of America, 107, 14036-14041.
- Nishioka, K., Mori, A., Takano, K.J., Kaishita, Y. and Narimatsu, S. (1999) Pressure-dependence of the interfacial tension of a critical nucleus in the binary-ideal solution. Journal of Crystal Growth, 200, 592-598. doi:10.1016/S0022-0248(98)01391-8
- Callen, H.B. (1985) Thermodynamics and an introduction to thermostatistics. 2nd Edition, Wiley, New York.
- Landau, L.D. and Lifshitz, E.M. (1989) Statistical physics. 3rd Edition, Pt. 1, Pergamon, Oxford.
- Yang, A.J.-M. (1985) The thermodynamical stability of the heterogeneous system with a spherical interface. The Journal of Chemical Physics, 82, 2082-2085. doi:10.1063/1.448344
- Barrett, J. (1999) First-order correction to classical nucleation theory: A density functional approach. The Journal of Chemical Physics, 111, 5938-5946. doi:10.1063/1.479889
- Hurbý, J., Labetski, D.G. and van Dongen, M.E.H. (2007) Gradient theory computation of the radius-dependent surface tension and nucleation rate for n-nonane clusters. The Journal of Chemical Physics, 127, 164720. doi:10.1063/1.2799515
- Mori, A. and Suzuki, Y. (2013) Vanishing linear term in chemical potential difference in volume term of work of critical nucleus formation for phase transition without volume change. Journal of Crystal Growth, 375, 16-19. doi:10.1016/j.jcrysgro.2013.04.005
NOTES
1A slight consideration reveals that we are not limited to the case that no volume change is associated with the phase transition. If there is a volume change, one should account for effect of the total volume change in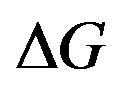 . In the main text, it is written that this situation is somewhat confusing. Naively thinking may impede going forward and result in going around three positions (Equations (3)-(5) of [33]).
. In the main text, it is written that this situation is somewhat confusing. Naively thinking may impede going forward and result in going around three positions (Equations (3)-(5) of [33]).

