Engineering
Vol. 4 No. 10 (2012) , Article ID: 23355 , 4 pages DOI:10.4236/eng.2012.410087
Assessing Sprinkler Irrigation Performance Using Field Evaluations at the Medjerda Lower Valley of Tunisia
1Institut National de Recherches en Génie Rural, Eaux et Forêts, University of Carthage, Tunis, Tunisia
2High Institute of Environmental Science and Technology, University of Carthage, Tunis, Tunisia
3Department Soil and Water, Estación Experimental de Aula Dei, Consejo Superior de Investigaciones Cientificas, Zaragoza, Spain
Email: yacoubi.samir@iresa.agrinet.tn, slatni.adel@iresa.agrinet.tn, khemaies.zayani@isste.rnu.tn, enrique.playan@eead.csic.es
Received July 13, 2012; revised August 11, 2012; accepted August 25, 2012
Keywords: Sprinkler Irrigation; Uniformity; Wind Drift and Evaporation Losses; Wind Speed; Pressure Head
ABSTRACT
Irrigation uniformity and wind drift and evaporation losses (WDEL) are major concerns for the design and management of sprinkler irrigation systems under arid or semi-arid conditions. Field trials were carried out to assess irrigation uniformity and WDEL under various wind velocities, sprinkler spacings and operating pressure heads. Based on experimental data, a frequency analysis was performed to infer the occurrence probability of a given uniformity coefficient (UC). In addition, statistical regressions were used to model WDEL as a function of different climatic variables. Increasing the operating pressure head improved uniformity at low wind speeds. It was shown that UC has been severely impaired at wind speeds above 4 m/s. In the prevailing wind conditions, the frequency analysis showed that a sprinkler spacing of 12 m × 12 m provided the best uniformity. In the local conditions, it is recommended to stop irrigation when wind velocity exceeds 4 m/s. Moreover, it was shown that wind speed and relative humidity were the main significant variables influencing WDEL.
1. Introduction
Arid and semi-arid regions are characterized by an acute imbalance between rainfall and evapotranspiration. The tough competition between the water demands of agricultural, industrial and urban water sectors is becoming a serious concern [1]. It is against this backdrop that the improvement of on-farm irrigation efficiency is becoming a must: it permits to conserve water and better valorizes it. This objective may be achieved by using pressurized irrigation systems. It is worth emphasizing that sprinkler irrigation is practiced over 32% of the irrigated acreage in Tunisia. In the lower valley of Medjerda (located at northern Tunisia), near 27,000 ha of irrigated land is supplied by canals. Surface irrigation is by far the most common irrigation method in the region [2]. The high cost of switching from surface to pressurized irrigation systems currently limits the adoption of modern irrigation systems in the study area [3]. Slatni et al. [4], Zairi et al. [5] and AHT-Group/SCET [6] showed that irrigation systems in the region are characterized by low irrigation efficiency due to the lack of farmers’ skills and inappropriate irrigation scheduling. A strategy for improving irrigation efficiency at the Medjerda lower valley has been approved by Tunisian public authorities [7]. Likewise, about 4500 ha are currently being converted from surface to pressurized irrigation systems.
When properly designed and managed, sprinkler irrigation produces high uniformity, reduces water supply and protects farmer’s income. Pereira [8] stressed that on-farm sprinkler irrigation performance depends on wind speed, pressure head variation, nozzle diameter and shape, sprinkler layout and spacing, soil infiltration and farmer skills. Unfortunately, a limited number of studies have been devoted to assess the impact of hydraulic and climatic factors on sprinkler irrigation performance under Tunisian conditions. Field evaluations are required to calibrate sprinkler irrigation simulation models recently developed for predicting irrigation performance under various operating and environmental conditions. Therefore, field trials are essential in upgrading on-farm sprinkler irrigation design and management.
According to Keller and Bliesner [9], distribution uniformity, wind drift and evaporation losses determine sprinkler irrigation performance. Burt et al. [10] reported that pressure head variation at the hydrant, sprinkler design, spacing and layout, as well as climate conditions, are critical sources of heterogeneity in water application under sprinkler irrigation. Out of these, wind speed is the most uncontrollable factor, and has the greatest impact on distribution uniformity. Wind disrupts the trajectory of raindrops and induces droplet evaporation, therefore enhancing wind drift and evaporation losses (WDEL). According to Vories et al. [11], ignoring wind speed and direction in sprinkler design leads to the underestimation of the peak flows and the required capacity of the irrigation system. Highly variable wind speed disfavors the reliable design and management of sprinkler irrigation systems [12]. Zapata et al. [13] presented a method to estimate the fraction of suitable time for irrigation operation. This method was adapted to the design of collective sprinkler irrigation networks in windy areas, guaranteeing maximum on-farm performance through the use of a historical wind speed database and a ballistic solid-set irrigation simulation model. The operating pressure head determines sprinkler discharge, wetted diameter, drop diameter and hence irrigation uniformity [14]. Kincaid et al. [15] reported that nozzle diameter and operating pressure head determined drop diameter. Among the series of drops emitted by a sprinkler, the smallest drop diameter influences WDEL, while the largest one determines soil surface compaction. In the literature, values of WDEL have been reported ranging between 2% and 50% [16]. This variability is due to climatic and hydraulic conditions prevailing at the experimental sites. Indeed, it has been reported that WDEL is dependent on relative humidity, air temperature, wind speed, pressure head at the nozzle, drop diameter and riser height [17]. In arid and semi-arid areas, Yazar [18] showed that WDEL may represent an important fraction of the supplied water. Yacoubi et al. [19] found that WDEL amounted to 24% of annual water depth applied to tomato crops in northern Tunisia. Using simulation models, these authors emphasized the interest of nocturnal irrigation to reduce water losses, improve irrigation uniformity and sustain crop yield. The identification of factors influencing WDEL is crucial inasmuch as they determine the water stewardship strategy. Playán et al. [16] demonstrated how wise management of sprinkler irrigation systems can lead to the reduction of WDEL and to significant water conservation.
This study intends to elucidate the combined effect of the abovementioned factors on irrigation uniformity and WDEL. Experiments were carried out under combinations of operating pressure, sprinkler spacing and climatic conditions to assess the local influence of each factor on irrigation performance. Experimental data were used to infer the occurrence probability of a given distribution uniformity and to identify practices leading to adequate on-farm irrigation performance standards for the Medjerda lower valley region.
2. Material and Methods
2.1. Characterization of the Field Experiments
Trials were carried out at the experimental station of INRGREF in the lower valley of the Medjerda in northeast Tunisia. The region is characterized by a Mediterranean semi-arid climate with a mild winter and hot and dry summer. Annual evapotranspiration and average rainfall amount to 1112 and 440 mm, respectively. Field trials were designed in accordance with local sprinkler irrigation practices, namely the range of operating pressure heads and the sprinkler spacing. The overwhelming majority of irrigated parcels in the area has a small size, and use hand-move laterals under moderate pressure head. This technique doesn’t require high technical skills and properly valorizes water resources and local manpower.
The impact sprinklers used in this research were IR30, manufactured by Irriline (Vancouver, Canada). Sprinklers were equipped with circular nozzles (4.4 mm in diameter) set up at 1 m height and 27˚ as trajectory angle. Three sprinklers’ spacings were analyzed in this research: 12 m × 12 m, 12 m × 18 m and 18 m × 18 m. Nozzle pressures of 200, 300 and 400 kPa were experimented. Table 1 summarizes the main hydraulic characteristics of used sprinklers.
2.2. Irrigation Uniformity
The evaluation of irrigation uniformity was performed at the plot scale on bare soil. For the sake of convenience, three plots were set up with the abovementioned spacings. Plots were separated 24 m to avoid interferences. Inside each plot, a battery of rain gauges was set up on a square grid of 3 m × 3 m, in accordance with ISO standard 7749/2 [20] and Merriam and Keller [21]. Rain gauges were made out of plastic, and had an open diameter of 79 mm and a height of 240 mm. Consequently 16, 24 and 36 rain gauges were used in plots with spacings 12 m × 12 m, 12 m × 18 m and 18 m × 18 m, respectively. Gauges were mounted on plastic supports, so that the upper part of the gauge was placed at 0.50 m above the soil surface.

Table 1. Hydraulic characteristics of used sprinkler as determined in laboratory conditions.
All experiments lasted for 2 hours. A total of 264 field trials were performed.
The water depths collected in the rain gauges were used to infer the uniformity coefficient, UC (%) as defined by Christiansen [22]:
 (1)
(1)
where hm, hi and n refer to the average water depth within the plot, the collected water depths in the rain gauges and the number of rain gauges, respectively.
A meteorological station, installed at the edge of the field provided the climatic parameters, viz. wind speed, wind direction (both at 2 m height), air temperature and relative humidity, at a 15 min interval.
2.3. Frequency Analysis of Distribution Uniformity
A frequency analysis was performed on the water depths collected in the rain gauges at the pressure heads of 200 and 300 kPa. The pressure of 400 kPa was not used for this purpose, since the number of experiments at high wind speed was limited. The recorded average wind speed was within 0.05 and 6.5 m/s. The frequency analysis provides the probability of occurrence of certain uniformity according to wind speed for the different sprinkler spacing and pressures. Three probability distribution laws were assessed: normal, log-normal and Weibull. The density functions of these laws are:
Normal law:
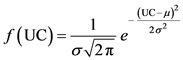 (2)
(2)
Log-normal law:
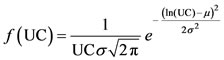 (3)
(3)
Weibull law:
 (4)
(4)
where m and σ are the average and the standard deviation of UCi values (for the normal law) and log(UCi) values (for the log-normal law), respectively. Likewise, b and l are shape and scale factors: b > 0 and l > 0.
The distribution function F of UC values was used to calculate the probability of occurrence of a given uniformity as follows:
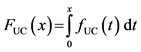 (5)
(5)
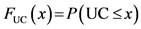 (6)
(6)
The adequacy of these laws can be assessed using the  and Kolmogorov-Smirnov tests with 5% as level of significance. Dagnelie [23] stated that agreement is not unanimous regarding the application of
and Kolmogorov-Smirnov tests with 5% as level of significance. Dagnelie [23] stated that agreement is not unanimous regarding the application of 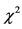 test if the number of observations is insufficient. For this reason, the following parameters are often used to assess the adequacy of a given distribution law:
test if the number of observations is insufficient. For this reason, the following parameters are often used to assess the adequacy of a given distribution law:
Bias:
 (7)
(7)
Mean Absolute Error:
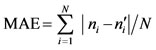 (8)
(8)
Mean Square Error:
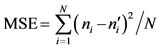 (9)
(9)
where N, ni and  are the number of observations, the observed and the theoretical number of UC data, respectively. The law which best fits the recorded data is the one minimizing the abovementioned parameters.
are the number of observations, the observed and the theoretical number of UC data, respectively. The law which best fits the recorded data is the one minimizing the abovementioned parameters.
2.4. WDEL Evaluation
WDEL measurements were performed at the 12 m × 12 m spacing during April-August, 2009.
WDEL was estimated as:
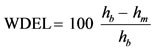 (10)
(10)
where hb and hm are the supplied and the average measured water depths, respectively. The supplied water depth was determined by:
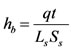 (11)
(11)
where q is the sprinkler discharge, t the duration of the test, Ls the spacing between adjacent laterals and Ss the spacing between two consecutive sprinklers. Thus, estimated WDEL represents the amount of water discharged by the sprinklers which does not reach the crop canopy. The effect of individual climatic parameters on WDEL at pressure heads of 200 and 300 kPa was analyzed through simple linear regression. Multiple linear and stepwise regressions were then performed for proper prediction of WDEL using the regression models presented in Table 2. In this table, W, RH, (es − ed) and T refer to the wind speed, relative humidity, vapor pressure deficit and air temperature, respectively.
The analysis was carried out using the XLSTAT software, version 17. Following Tarjuelo et al. [24], three

Table 2. Multiple linear and stepwise regression models used for modeling WEDL.
wind speed classes were considered: 0 - 2 m/s (low wind speed), 2 - 4 m/s (moderate wind speed) and high wind speed (W ≥ 4 m/s). A frequency analysis was performed using hourly data of a time series covering the period 1998-2008. Results are summarized in Table 3, showing that moderate wind speeds are the most frequent in the area, while high speeds have a probability of occurrence of about 20%.
3. Results and Discussion
3.1. Uniformity Analysis
Table 4 summarizes the core statistics of UC data obtained with the three sprinkler spacings, the three operating pressure heads and the three prevailing wind speed classes. In the table, N, UCm and CV refer to the number of field trials, the mean uniformity coefficient and the coefficient of variation.
3.1.1. Effect of Pressure on Uniformity
For the same wind class, Table 4 shows that UC increases with the pressure head. However, this improvement should be balanced against the increase in energy consumption. Conversely, for the same pressure head, UC decreases as wind speed increases. A threshold value of UC less than 75% has often been used to indicate unsatisfactory uniformity, as is often the case of sprinkler irrigation at high wind speeds [9]. Likewise, Table 4 shows that the increase in pressure head from 200 to 400 kPa improves UC at low and moderate wind speeds. This effect was clear for 12 m × 18 m and 18 m × 18 m spacing, the effect on the spacing 12 m × 12 m being less evident. Increasing the pressure head from 200 to 300 kPa showed a less discernible impact at moderate wind speeds. These results bolster those of Tarjuelo et al. [25] who stated that increasing pressure improves UC only in the presence of low wind speeds.
3.1.2. Effect of Spacing on Uniformity
The frequency analysis showed that UC exceeds 80% in 60%, 46% and 25% of cases for the spacings of 12 m × 12 m, 12 m × 18 m and 18 m × 18 m, respectively.
Thus, 12 m × 12 m would be the only spacing producing UC greater than the threshold of 75% in most cases. Examination of Table 4 shows that small sprinkler spac-

Table 3. Distribution of the relative frequency of wind speed.
ings improved UC for all pressure heads and wind speed classes. Similar findings were reported by Moazed et al. [26] and Tarjuelo et al. [25]. At wind speeds lower than 4 m/s, the spacing 12 m × 12 m provided the highest values of UC (76.6% ≤ UC ≤ 86.1%) for the entire pressure head range. This result corroborates the findings of Tarjuelo et al. [24], who showed that the 12 m × 12 m spacing produced the maximum uniformity for a wide range of wind speeds.
By cons, at low wind speeds the 12 m × 18 m spacing produced UC values greater than 75% for the entire range of pressure heads. This result is due to the alignment of the sprinklers with respect to the dominant wind direction. Similar results were reported by Vories and Von Bernuth [27]. The combination of 18 m × 18 m spacing and 200 kPa pressure head should be avoided for all wind speeds because of the poor sprinkler overlap. Using rotating sprinklers operated at low pressure heads (100 - 250 kPa), Sahoo et al. [28] obtained results discouraging the use of large sprinkler spacings. Likewise, the combination of 12 m × 18 m spacing and 300 kPa pressure is only prescribed at low wind speeds.
3.1.3. Effect of Wind Speed on Uniformity
Experimental results show a consistent decrease of uniformity with increasing wind speed (Table 4) in all spacings and pressures. Uniformity was significantly affected by wind speeds higher than 4 m/s, regardless of the spacing. For wind speeds below 4.4 m/s, a pressure head of 400 kPa produced the highest UC values in all spacings. Wind effect on UC can be appreciated for speeds higher than 2 m/s. Similar results were reported by Kincaid [29] who stated that UC dwindles when the wind speed exceeds 2.2 m/s for the spacings 12 m × 12 m, 12 m × 15 m and 12 m × 18 m. Under pressures of 200 and 300 kPa, a wind speed of 4 m/s stands as a threshold beyond which irrigation should be cut-off, since UC values would fall below 75%.
3.2. Modeling the Distribution of UC
Experiments performed at 400 kPa were not considered in this analysis given the small variability in wind speed. In order to obtain a sufficiently large data set, data obtained at 200 and 300 kPa for a given sprinkler spacing were pooled. The analysis was also performed for fixed operating pressure head and variable sprinkler spacing. Based on  and Kolmogorov-Smirnov tests at a probability value of 5% and minimum values of Bias, MAE and MSE, the Weibull law is the best suited to fit ex-
and Kolmogorov-Smirnov tests at a probability value of 5% and minimum values of Bias, MAE and MSE, the Weibull law is the best suited to fit ex-
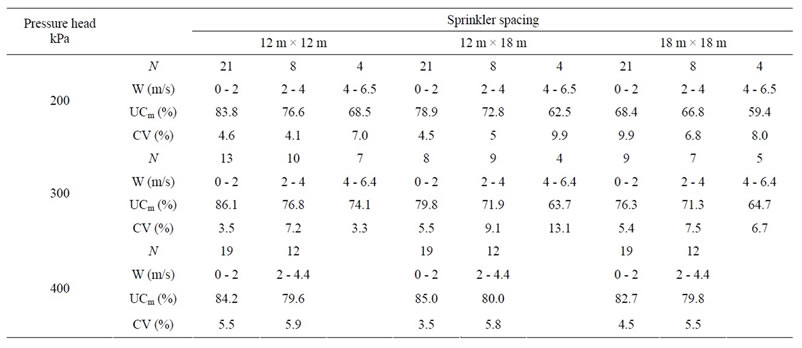
Table 4. Effect of wind speed and sprinkler spacing on UC at different pressure heads.
perimental data for each spacing. When results were separated according to the operating pressure head, Weibull law provided the best fit for 200 kPa, while normal law provided the best fit for 300 kPa. The optimum parameters are reported in Table 5 for the three wind speed ranges.
Table 6 summarizes the occurrence probabilities corresponding to the acceptable distribution uniformity (Keller and Bliesner, 1990).
Indeed, these authors considered that UC equal to 75% and 80% are deemed to be relatively low and satisfactory, respectively. Spacings 12 m × 18 m and 18 m × 18 m should be avoided in the local conditions since the probability to obtain UC higher than 75% is relatively small (less than 68% for wind speed higher than 4 m/s). In the prevalent wind conditions, the 12 m × 12 m spacing provides the best water distribution inasmuch as the occurrence probability is higher than 90% and 69% for UC values of 75% and 80 %, respectively. Under low wind speeds, results show that fair uniformity can be achieved by the 12 m × 18 m spacing (probability of 88% for UC higher than 75%) while the 18 m × 18 m spacing produces the lowest irrigation uniformity (probability of 30% for UC higher than 75%).
Figure 1 shows that the cumulative distribution functions are virtually coalescing at 200 kPa and are well distinguishable at 300 kPa. For a pressure head of 200 kPa, Figure 1 shows that the probability to obtain UC in exceess of 75% drops from 66% to 58% in passing from the interval 0 - 2 to 0 - 4 m/s. Conversely, the pressure head of 300 kPa produces a clearer drop in probability (22.6%) for the same ranges of wind speed.
Figures 2(a) exhibits a clear effect of pressure head on UC at low wind speeds. However, when the wind speed exceeds 2 m/s, the effect of pressure head on UC fades (Figure 2(b)). Under calm weather, the probability that UC lies within 80% and 90% is 37% for a pressure head of 200 kPa (Figure 2(a)). The same probability increases to 52% when the pressure head is 300 kPa. For wind speeds below 4 m/s, Figure 2(b) shows that the increase of probability when the pressure head increases from 200 to 300 kPa is very moderate (31% and 32%).
3.3. WDEL Analysis
Tables 7 and 8 present basic statistics for the climatic factors controlling WDEL at 200 and 300 kPa (respectively) on the basis of thirty experimental trials. Field trials performed at a pressure head of 200 kPa correspond to more stern climatic conditions in terms of air temperature and vapor pressure deficit than those carried out at 300 kPa. Notwithstanding similar average losses for 200 and 300 kPa, the corresponding CV values were quite different Figures 3(a)-(d) illustrate the effect of individual climatic parameters on WDEL at 300 kPa. Wind speed was the most explicative variable, followed by relative humidity. Vapor pressure deficit and air temperature were the less relevant variables.
The parameters of the regression models are summarized in Table 9. Model (2b) produced the best results with wind speed and relative humidity as input variables. Based on field evaluations under semiarid conditions, Seginer et al. [30] showed that WDEL generated by a single sprinkler operating at a pressure head of 300 kPa were related to wind speed and the wet-bulb depression.
Figure 4 displays measured versus predicted WDEL. The regression line is virtually identical to the first bisector, which upholds the accuracy of the model.
Figures 5(a)-(d) show the effect of isolated climatic
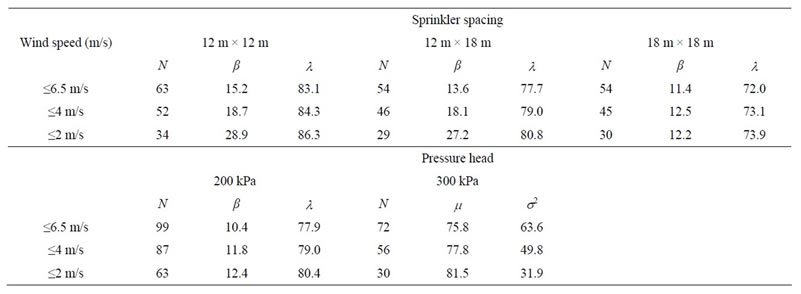
Table 5. Fitting parameters of the Weibull and normal laws.

Table 6. Occurrence probability UC > 80% and UC > 75%.
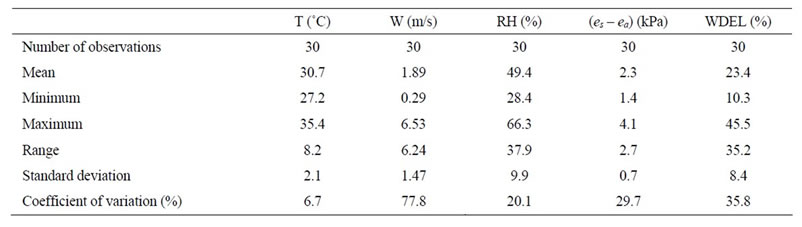
Table 7. Basic statistics of climatic factors controlling WDEL at 200 kPa.
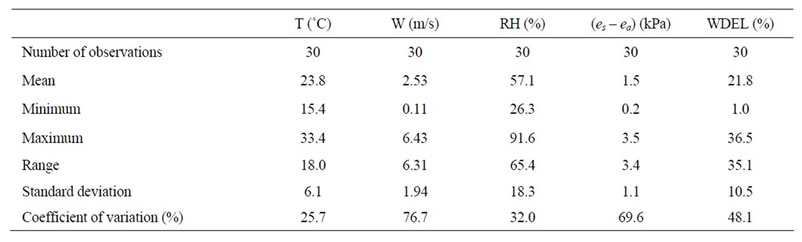
Table 8. Basic statistics of climatic factors controlling WDEL at 300 kPa.

Table 9. Parameters of the multiple linear and the stepwise regression models at 300 kPa.

Figure 1. Effect of wind speed on cumulative distribution function at 200 kPa and 300 kPa.
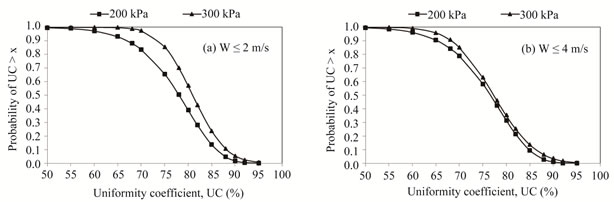
Figure 2. Effect of pressure head on cumulative distribution function for fixed wind speed: (a) W < 2 m/s and (b) W < 4 m/s.
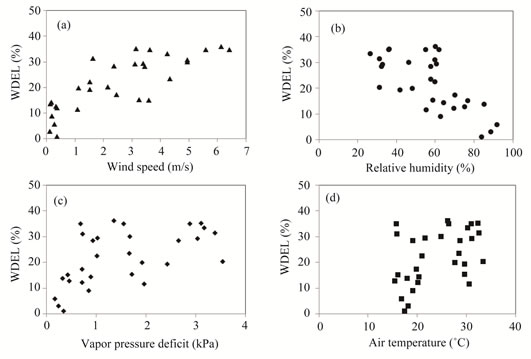
Figure 3. WDEL as function of wind speed, relative humidity, vapor pressure deficit and air temperature at 300 kPa.

Figure 4. Measured vs predicted WDEL at 300 kPa.
parameters on WDEL at 200 kPa. Apart from wind speed, other climatic parameters showed no significant effect on WDEL (5% level). Regression parameters are summarized in Table 10. WDEL could only be explained by wind speed. Edling [31] showed that small droplets evaporate faster than large ones. According to Keller and Bliesner [9], decreasing the pressure head increases the drop diameter and therefore reduces the water-air contact area per unit of water mass. This result upholds the finding of Montero et al. [32], who showed that drop diameter, measured by optical spectropluviometer, increased as pressure head decreased. Consequently, large drops contribute less than small ones in alleviating the atmospheric evaporation demand [33].
Figure 6 exhibits a fair agreement between measured and predicted WDEL. The regression line is virtually identical to the first bisector, which upholds the accuracy of the model. The non-zero intercept in the regression line of the model WDEL = a·W + b suggests prominent water losses even under calm weather (14.95%). This result is at odds of the statement that wind speed is the only significant factor determining WDEL. Consequently, this model should be used with watchfulness at very low wind speed.
4. Conclusion
Field trials were carried out to assess irrigation uniformity under three sprinkler spacings and three operating pressure heads. Increasing pressure from 200 to 400 kPa improved UC at low wind speeds (W < 2 m/s). This improvement is less distinguishable for wind speeds in the interval of 2 - 4 m/s. For pressures in the range of 200 - 400 kPa and wind speeds below 4 m/s, the 12 m × 12 m spacing produced the highest UC values. The ill-effect of wind on UC was clear for speeds higher than 2 m/s. Water distribution was largely distorted by wind speeds higher than 4 m/s. For a given sprinkler spacing, the Weibull law was the most suitable to fit lumped experimental UC data obtained at 200 and 300 kPa. Similarly, the normal and Weibull laws were the best suited to model UC data obtained at 300 and 200 kPa separately. In the prevalent wind conditions, 12 m × 12 m spacing provided the best water distribution since the probability of UC higher than 80% exceeded 69%. Likewise, for the 12 m × 18 m and 18 m × 18 m spacings, the probability
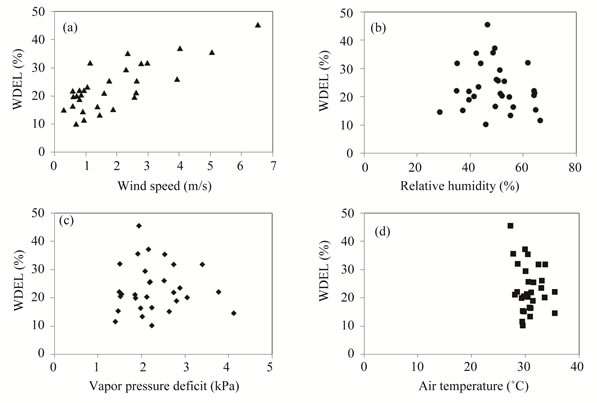
Figure 5. WDEL as function of wind speed, relative humidity, vapor pressure deficit and air temperature at 200 kPa.

Table 10. Parameters of the multiple linear and the stepwise regression models at 200 kPa.
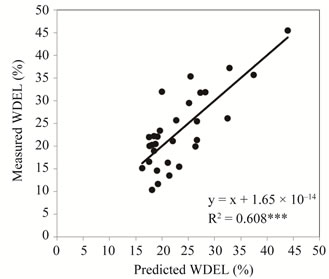
Figure 6. Measured versus predicted WDEL at 200 kPa.
of UC higher than 75% was less than 68% for wind speeds higher than 4 m/s. Under these circumstances, it is recommended to cut-off sprinkler irrigation. It was shown that wind drift and evaporation losses are dependent on the prevalent hydraulic and climatic conditions. Operating at 300 kPa, WDEL was conditioned by wind speed and relative humidity; operating at 200 kPa WDEL was only conditioned by wind speed. Using wind speed as the only variable for calculating WDEL under 200 kPa pressure head should be taken cautiously since it may overestimate WDEL under very low wind speeds. These results may be used as guidelines for designing and managing sprinkler irrigation systems in the Medjerda lower valley and in other irrigated areas where operating and climatic conditions could be similar.
5. Acknowledgements
The authors are thankful to the INRGREF for the valuable support of this research.
REFERENCES
- M. Abu-Zeid and A. Hamdy, “Coping with Water Scarcity in the Arab World,” The 3rd International Conference on Water Resources and Arid Environments and the 1st Arab Water Forum, 2008, p. 26. http://www.icwrae-psipw.org/images/stories/2008/Water/1.pdf
- HYDROPLAN/SCET-Tunisie, “Etude du Projet de Modernisation des Périmetres Publics Irrigués de la Basse Vallée de la Medjerda. Phase 1: Analyse de la Situation Actuelle,” Tunis, 2002, p. 196.
- M. Rebai and A. Zairi, “Les Périmètres Irrigués de la Basse Vallée de la MEDJERDA: Problématiques et Perspectives,” 2006. http://www.eau-sirma.net/les_rencontres/marrakech-29-31-mai-2006-maroc/les-actes
- A. Slatni, J. C. Mailhol, A. Zairi, G. Château and T. Ajmi, “Analyse et Diagnostic de la Pratique de l’Irrigation Localisée dans les Périmètres Publics Irrigués de la Basse Vallée de la Medjerda en Tunisie,” Actes du séminaire Euro-Méditerranéen “La Modernisation de l’Agriculture Irriguée”, Tome1, IAV Hassan II, Rabat-Institus, Rabat, 2004, pp. 112-122.
- A. Zairi, A. Slatni, J. C. Mailhol, R. Boubaker, H. El Amami, M. Ben Ayed and M. Rebai, “AnalyseDiagnostic de l’Irrigation de Surface dans les Périmètres Publics Irrigués de la Basse Vallée de la Medjerda,” Numéro Spécial des Annales de l’INRGREF, Actes du Séminaire “Economie de l’eau en irrigation”, Hammamet, 2000, pp. 10-26.
- AHT-Group/SCET Tunisie, “Projet de Modernisation des Périmètres Publics Irrigués de la Basse Vallée de la Medjerda. Analyse Diagnostic des Equipements d’Irrigation,” Tunis, 2009, p. 52.
- R. Al Atiri, “Les Efforts de Modernisation de l’Agriculture Irriguée en Tunisie,” 2004. http://www.wademed.net/ Articles/005DGGRO.pdf
- L. S. Pereira, “Higher Performances through Combined Improvements in Irrigation Methods and Scheduling: A Discussion,” Agricultural Water Management, Vol. 40, No. 2, 1999, pp. 153-169. doi:10.1016/S0378-3774(98)00118-8
- J. Keller and R. D. Bliesner, “Sprinkler and Trickle Irrigation,” Van Nostrand Reinhold, New York, 1990.
- C. M. Burt, A. J. Clemmens, T. S. Strelkoff, K. H. Solomon, R. D. Bliesner, L. A. Hardy, T. A. Howell and D. E. Eisenhauer, “Irrigation Performance Measures: Efficiency and Uniformity,” Journal of Irrigation and Drainage Engineering, Vol. 123, No. 6, 1997, pp. 423-442. doi:10.1061/(ASCE)0733-9437(1997)123:6(423)
- E. D. Vories, R. D. Von Bernuth and R. H. Mickelson, “Simulating Sprinkler Performance in Wind,” Journal of Irrigation and Drainage Engineering, Vol. 113, No. 1, 1987, pp. 119-130. doi:10.1061/(ASCE)0733-9437(1987)113:1(119)
- F. Dechmi, E. Playán, J. Cavero, J. M. Faci and A. Martínez-Cob, “Wind Effects on Solid Set Sprinkler Irrigation Depth Yield of Maize,” Irrigation Science, Vol. 22, No. 2, 2003, pp. 67-77. doi:10.1007/s00271-003-0071-9
- N. Zapata, E. Playan, A. Martinez-Cob, I. Sanchez, J. M. Faci and S. Lecina, “From On-Farm Solid-Set Sprinkler Irrigation Design to Collective Irrigation Network Design in Windy Areas,” Agricultural Water Management, Vol. 87, No. 2, 2007, pp. 187-199. doi:10.1016/j.agwat.2006.06.018
- N. Lamaddalena, U. Fratino and A. Daccache, “On-Farm Sprinkler Irrigation Performance as Affected by the Distribution System,” Biosystems Engineering, Vol. 96, No. 1, 2007, pp. 99-109. doi:10.1016/j.biosystemseng.2006.09.002
- D. C. Kincaid, K. H. Solomon and J. C. Oliphant, “Drop Size Distributions for Irrigation Sprinklers,” Transactions of the ASAE, Vol. 39, No. 3, 1996, pp. 839-845.
- E. Playán, R. Salvador, J. M. Faci, N. Zapata, A. Martínez-Cob and I. Sánchez, “Day and Night Wind Drift and Evaporation Losses in Sprinkler Solid-Sets and Moving Laterals,” Agricultural Water Management, Vol. 76, No. 3, 2005, pp. 139-159. doi:10.1016/j.agwat.2005.01.015
- J. M. Tarjuelo, J. F. Ortega, J. Montero and J. A. de Juan, “Modelling Evaporation and Drift Losses in Irrigation with Medium Size Impact Sprinklers under Semi-Arid Conditions,” Agricultural Water Management, Vol. 43, No. 3, 2000, pp. 263-284. doi:10.1016/S0378-3774(99)00066-9
- A. Yazar, “Evaporation and Drift Losses from Sprinkler Irrigation Systems under Various Operating Conditions,” Agricultural Water Management, Vol. 8, No. 4, 1984, pp. 439-449. doi:10.1016/0378-3774(84)90070-2
- S. Yacoubi, K. Zayani, N. Zapata, A. Zairi, A. Slatni, R. Salvador and E. Playán, “Day and Night Time Sprinkler Irrigated Tomato: Irrigation Performance and Crop Yield,” Biosystems Engineering, Vol. 107, No. 1, 2010, pp. 25-35. doi:10.1016/j.biosystemseng.2010.06.009
- ISO Standard 7749/2, “Agricultural Irrigation Equipment. Rotating Sprinklers. Part 2. Uniformity of Distribution and Test Methods,” Geneva, 1990.
- J. L. Merriam and J. Keller, “Farm Irrigation System Evaluation: A Guide for Management,” Utah State University, Logan, 1978.
- J. E. Christiansen, “Irrigation by Sprinkling,” California Agricultural Experiment Station Bulletin 670, University of California, Berkeley, 1942.
- P. Dagnelie, “Théorie et Méthodes Statistiques. Applications Agronomiques. Vol. 2,” Les Presses Agronomiques de Gembloux, Gembloux, 1978.
- J. M. Tarjuelo, J. Montero, P. A. Carion, F. T. Honroubia and M. A. Calvo, “Irrigation Uniformity with Medium Size Sprinklers. Part II: Influence of Wind and Other Factors on Water Distribution,” Transactions of the ASAE, Vol. 42, No. 3, 1999, pp. 677-689.
- J. M. Tarjuelo, J. Montero, F. T. Honroubia, J. Ortiz and J. F. Ortega, “Analysis of Uniformity of Sprinkler Irrigation in Semi-Arid Area,” Agricultural Water Management, Vol. 40, No. 2, 1999, pp. 315-331. doi:10.1016/S0378-3774(99)00006-2
- H. Moazed, A. Bavi, S. Boroomand-Nasab, A. Naseri and M. Albaji, “Effects of Climatric and Hydraulic Parameters on Water Uniformity Coefficient in Solid Set Systems,” Journal of Applied Sciences, Vol. 10, No. 16, 2010, pp. 1792-1796. doi:10.3923/jas.2010.1792.1796
- E. Vories and R. D. von Bernuth, “Single Nozzle Sprinkler Performance in Wind,” Transactions of the ASAE, Vol. 29, No. 5, 1986, pp. 1325-1330.
- N. Sahoo, P. L. Pradhan, N. K. Anumala and M. K. Ghosal, “Uniform Water Distribution from Low Pressure Rotating Sprinklers,” The CIGR Ejournal, Manuscript LW 08014, Vol. X, 2008, p. 10. http://www.cigrjournal.org/index.php/Ejounral/article/viewFile/1231/1088
- D. C. Kincaid, “Minimizing Energy Requirements for Sprinkler Laterals,” ASAE Paper No. 84-2585, St. Joseph, 1984.
- I. Seginer, D. Kantz and D. Nir, “The Distortion by Wind of the Distribution Patterns of Single Sprinklers,” Agricultural Water Management, Vol. 19, No. 4, 1991, pp. 341-359. doi:10.1016/0378-3774(91)90026-F
- R. Elding, “Kinetic Energy, Evaporation and Wind Drift of Droplets from Low Pressure Irrigation Nozzles,” Transactions of the ASAE, Vol. 28, No. 5, 1985, pp. 1543-1550.
- J. Montero, J. M. Tarjuelo and P. Carrion, “Sprinkler Droplet Size Distribution Measured with an Optical Spectropluviometer,” Irrigation Science, Vol. 22, No. 2, 2003, pp. 47-56. doi:10.1007/s00271-003-0069-3
- D. L. Martin, D. C. Kincaid and W. M. Lyle, “Design and Operation of Sprinkler Systems,” In: Glenn J. Hoffman, Ed., Design and Operation of Farm Irrigation Systems, American Society of Agricultural and Biological Engineers, St. Joseph, 2007, pp. 557-631.

