Engineering
Vol. 3 No. 9 (2011) , Article ID: 7336 , 10 pages DOI:10.4236/eng.2011.39117
Exergy Analysis of Single Array Wind Farm Using Wake Effects
School of Mechanical and Building Sciences, VIT University Chennai Campus, Chennai, India
E-mail: jeya2k@yahoo.com, cpkarthikeyan@vit.ac.in, anand_samuel@hotmail.com
Received July 1, 2011; revised August 12, 2011; accepted August 22, 2011
Keywords: Wake Effect, Energy Efficiency, Exergy Efficiency, Wind Farms and Wind Turbines
ABSTRACT
The influence of wake parameters on the exergy analysis of single array wind farm is studied in this paper. Key parameters which influence wake effects in a wind farm are wind velocity, tip speed ratio, number of blades, rotor speed, rotor diameter and hub height. Three different models namely power, wake and exergy model were used in estimating the exergy efficiency of the single array wind farm. Even though it is ideal for wind farms to fix the wind turbines in rows and columns the conditions of the site may not always be conducive for it. Hence analysis has been done keeping the wind turbines at random in a row and the effect of positioning on the performance is analyzed. Energy and exergy efficiency calculations were made for different cases by varying the positions of wind turbines in the single array wind farm. Standard relations were used in estimating the energy deficit in the wind farm due to wake effects. The wake effects were found to have an aggregated influence on the energy production of the wind farm, which results from the changes in the key parameters mentioned above. Potential areas for reducing energy losses by proper location and selection of turbines based on rating are highlighted. The influence of individual parameters contributing to the wake effect were analyzed and discussed in detail.
1. Introduction
Generation of power using wind turbine is cost effective compared to other resources, but if not done properly can influence potential energy losses. India is one among the five countries having high installed capacity of wind turbines. The state of Tamil Nadu contributes about half of the total installed capacity in India. Muppandal region has the distinction of having one of the largest concentrations of wind turbines at a single location with an aggregate wind power capacity of 540 MWe. The deficit in energy production of any wind farm is characterized by wake effects influenced by the turbines. The turbine positioned upstream in the wind direction influences the wind speed at turbine locations on its downwind (lee) side [1]. This shadowing effect from upstream turbines on other turbines further downstream is referred to as the wake effect. Wind turbines extract energy from the wind and downstream there will be a wake from the wind turbine, where wind speed is reduced.
To analyze the influence of wake on exergy efficiency, parameters such as wind velocity, tip speed ratio, number of blades, rotor speed, rotor diameter and hub height are to be analyzed. Performance studies of wind farms are rarely reported in literature when compared to studies related to individual wind turbines. When placing multiple turbines in a wind farm due to space constraints, wake decay effects are to be considered. The upwind turbines alter the wind pattern for the downwind turbines because of the high turbulence around the turbines downstream. If turbines are placed very near to one another in the direction of the wind, the total power generated is often reduced. Energy and exergy losses in a wind farm can be identified using energy and exergy analysis.
2. Studies on Wind Farm
Wind farms or wind parks are locally concentrated groups of wind turbines that are electrically and commercially tied together. The location of wind farm site and the position of wind turbines have an influence on the wind farm output. Kaminski (1987) conducted a study on wind farm efficiency optimization [2]. Optimal spacing between wind turbines to maximize instantaneous power from a one-line array of machines to be placed in a line parallel to constant wind direction was formulated using nonlinear optimization techniques.
Diveux (2001) did optimization study for a single turbine by changing principal parameters such as diameter of rotor, hub height, and rotor speed to minimize cost per unit generation [3]. The behavior of the system components was coupled using a non-linear technique, technical and economical aspects of the complete system design were taken into account in the optimization problem. The annual electrical energy cost was estimated using a cost model for the wind turbine rotor, nacelle and tower. Performance evaluation was done using an energy output model which envelopes power coefficient of the rotor, CP, Wei-bull parameters k and c and power law coefficient a of the wind profile. The optimal values of the parameters were determined using genetic algorithms, which appear to be efficient for such a problem.
Square wind farm array was considered for the layout optimization analysis [4,5]. In this approach a statistical and mathematical method called ‘Monte Carlo simulation method’ was used. Optimization was made by the mean of maximum energy production and minimum cost installation criteria. As a test case, a square site was subdivided into 100 square cells of possible turbine locations and as a result, the optimal arrangements of the wind turbines in the wind park were found. Aytun Ozturk and Bryan Norman (2004) discussed the optimized layout of wind turbine in a square array using greedy heuristics approach [6]. Generator placement which maximizes profit was found by product of the cost efficiency of the generators and the total power output from the wind farm.
Christopher Koroneos (2003) applied exergy analysis to renewable energy sources including wind power [7]. The actual use of wind energy from the existing available energy was discussed. A new approach to application of wind energy by using compressed air power to some extent instead of electricity was put forward by Jia et al. (2004). Results of investigations on the application of high-pressure compressed air for pressure reduction led to conclusion that pressure reduction with, expander is better than the throttle regulator in energy saving [8].
Thermodynamic aspects of renewables for sustainable development were investigated by Dincer and Rosen (2007). In this article, possible future energy-utilization patterns and related environmental impacts, potential solutions to current environmental problems, energy efficiency, renewable energy technologies and their relations to sustainable development, and how the principles of thermodynamics via exergy can be beneficially used to evaluate energy systems and technologies as well as environmental impacts were discussed [9].
Dincer and Cengel (2001) introduced Second Law efficiency, referring to the exergy efficiency and studied its use in assessing the efficiency and energy utilization [10]. Ahmat Duran et al. (2006) investigated energy and exergy characteristics of wind energy. A case study on a 100-kW wind generating system for 21 climatic stations in the province of Ontario, Canada was performed [11]. New energy and exergy efficiency maps of the wind energy generating system were introduced to provide a common basis for regional assessments and interpretations. The results showed that aerial differences between energy and exergy efficiencies were approximately 20% - 24% at low wind speeds and approximately 10% - 15% at high wind speeds Onder Ozgener (2007) formulated energy and exergy efficiency for the single wind turbine system [12]. Exergy, exergy destruction rates, exergy efficiencies and other properties at various wind velocities were analyzed. Many of the literature discussed the velocity deficiency of downward wind turbine wind farm due to wake effect and proposed various models to calculate the losses in wind array. Array efficiency has been calculated by various researchers. But very few literatures are available on the exergy efficiency of wind turbine based on wake effects. Exergy analysis is an accurate method to analyze actual input and available output power of wind farm thermodynamically. Here an attempt is being made to study the energy and exergy efficiency of wind farm using energy deficit caused by wake effects. The deficit in the energy is estimated using wake parameters and models for power, wake and exergy.
3. Exergy Efficiency of Wind Farm
Exergy efficiency calculations need adequate knowledge on the actual output power developed by all the turbines in the wind farm and theoretical maximum power produced by each turbine. The influence of variables on exergy efficiency can be analyzed with the help of thermodynamic parameters, aerodynamic parameters and site parameters. The influence of aerodynamic parameters (wake effects) on the exergy analysis of single array wind farm is studied using three realistic models namely the power, wake and exergy model.
3.1. Power Model
The power model describes the method used for estimating the available power and the power extracted by the wind turbines in the wind farm. The pressure up to an elevation of 5000 m was calculated from Equation (1) [13]
 (1)
(1)
The density of dry air was calculated using the ideal gas law Equation (2),
 (2)
(2)
The available power can be determined form the amount of air passing through the rotor of wind turbine per unit time. Mass flow rate of the air stream touching the rotor surface (A) was estimated using relation (3)
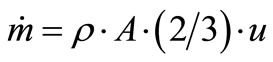 (3)
(3)
Exergy of kinetic energy is found using the relation,
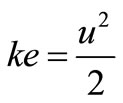 (4)
(4)
Available power is found using the relation,
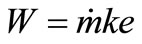 (5)
(5)
Equation (5) gives the maximum power available in the wind. But practically wind turbine extracts only 20% - 40% of energy of the wind; the mechanical power developed by the wind turbine in such situations can be estimated using Equation (6),
 (6)
(6)
The maximum power coefficient Cp of turbine was determined as a function of tip speed ratio (λ), number of blades (Nb) [3].
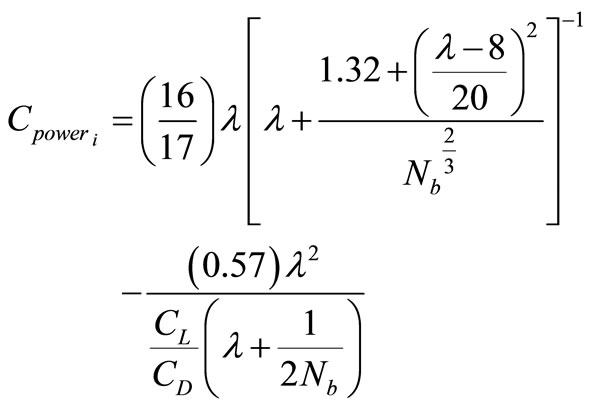 (7)
(7)
Power coefficient of turbine Cp will be less if the number of blades is less at the same tip speed ratio. Wind farms for electrical power production use two or three blades, most two blade wind turbines use a higher tip speed ratio than three bladed turbines to maintain same power coefficient. Based on the study carried out by Burton (2001) it was found that maximum achievable theoretical power was possible with 3 blades [14].
Tip speed ratio can be expressed in terms of tip speed and free stream wind velocity
 (8)
(8)
A single equation relating electrical power output and wind power input is given in Equation (9).
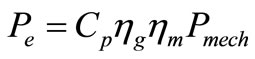 (9)
(9)
Assumptions made in the study are 1) generator efficiency and gear box efficiency for the rated speed were taken as constants for the calculations 2) Cp values change with respect to tip speed ratio and number of blades and 3) model is applicable for a single turbine which will be applied for each turbine and the total power can be estimated. Power losses due to wake deficit losses, availability losses and transmission losses are considered in the next subsection.
3.2. Wake Model for Single Array Wind Farm
Energy deficit from the wind farm due to wake effect is considered in the wake model. The wake model is used to determine the variation of incident wind speeds on each wind turbine within a wind farm. Calculation of deficit in energy due to wake effects is done by a systematic approach where each turbine is considered in turn in order of increasing axial downstream displacement. Wake is initially modeled by the incident wind speed and tip speed ratio with respect to the first wind turbine. The effect of this wake on all the turbines downstream is then be modeled.
Wind flows from left to right (Figure 1) at the speed u0 and hits the turbine whose rotor radius is rr. At the distance X, the wind speed is u and the wake radius is r1.
 (10)
(10)
Equation (10) is used if velocities of the downstream turbines are affected by the upstream turbines [13].
Equation (11) defines the dimensional scalar which determines how quickly the wake expands with distance,
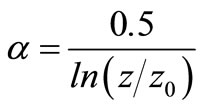 (11)
(11)
where z is the hub height of the turbine generating the wake and z0 is a constant called surface roughness, which depends on the terrain characteristics.
Let i be the position of the turbine that generates the wake, Equation (12) defines the wind speed at j,
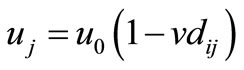 (12)
(12)
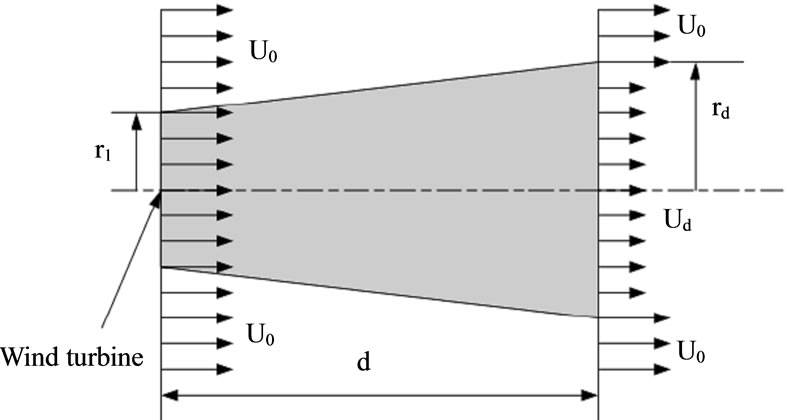
Figure 1. simple wind turbine flow model.
where, u0 is the free stream velocity and vdij is the velocity deficit induced on position i by the wake generated by j. vdij can be calculated from
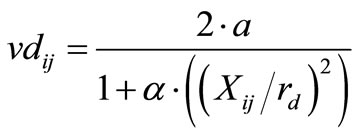 (13)
(13)
The term in the numerator is called axial induction factor and is given by
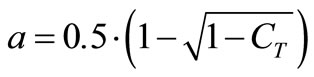 (14)
(14)
The term in the denominator is called downstream rotor radius and is given by the equation
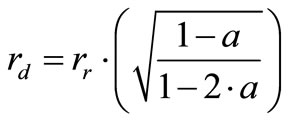 (15)
(15)
The term Xij is the distance between positions i and j.
The model assumes that the kinetic energy deficit of interacting wakes is equal to the sum of the energy deficits of the individual wakes (indicated by subscripts 1 and 2).
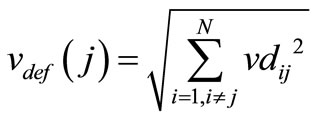 (16)
(16)
For a wind farm involving N wind turbines placed in a pre-defined configuration, the wind farm efficiency for a specific wind speed u and calculated onset wind velocities is given by the following equation
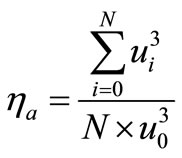 (17)
(17)
where,
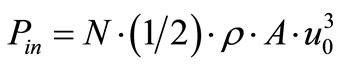 (18)
(18)
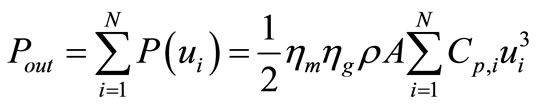 (19)
(19)
where, ui is the resultant velocity of the turbine.
3.3. Exergy Model
Exergy analysis broadly indicates the locations of energy degradation in a process or system. The results of the analysis can therefore lead to improved operation. Exergy analysis can also quantify the quality of energy in a waste stream. The main aim of exergy analysis in this article is to identify meaningful (exergy) efficiencies and the causes and magnitudes of exergy losses. The exergy of a matter flow is defined as the maximum work that can be acquired when the air flows from state (T2, P2) to the ambient state (T1, P1). Temperature difference has been considered to be negligible in the present work. Flow work for all the turbines in the wind farm is expressed as exergy input [12].
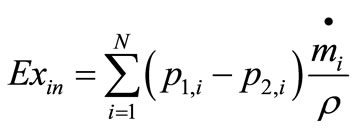 (20)
(20)
The generated electrical power from the wind turbines is considered as the exergy output of the wind farm. The actual power generation from the wind farm depends on the frequency of the wind pattern for the specific site. The generally used model for electrical power extracted from wind energy Pe,av is given by Abdel Hamid (2009) [15]. Pe,av is assumed to vary as u between cut-in (uc) and rated wind speeds (ur).
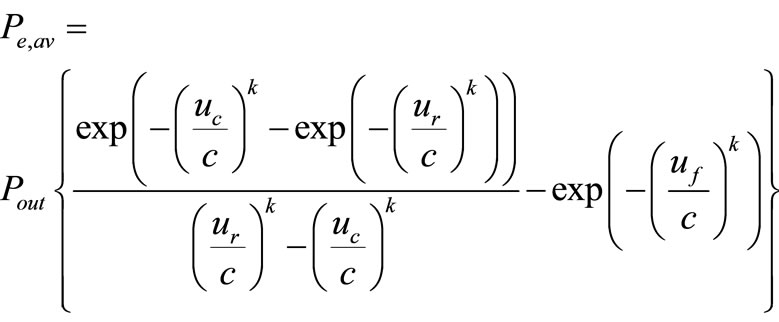 (21)
(21)
Then,
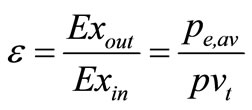 (22)
(22)
Exergy efficiency stresses that both internal losses and external irreversibility’s need to be dealt with to improve efficiency. In many cases the internal irreversibility’s are more significant and more difficult to deal with. The following formula is depicted here to quantify exergy destruction.
 (23)
(23)
Power model and the wake model are used to derive the energy and exergy efficiencies. Equations (10) to (19) are used to calculate the energy efficiency of the wind farm. Equations (20) to (23) are used to calculate the exergy efficiency of the wind farm.
4. Parametric Studies of a Single Array Wind Farm
For the study, a single column of wind farm with 10 possible turbine locations was considered. The width and height of each cell is equal to five rotor diameters 5 D or 200 m each. The total height of the array equals 50 D with turbines placed exactly in the center of each cell. The 5 D × 5 D square grid size in the vertical and horizontal directions is taken from the study carried out by Grady (2005) [5].
Figure 2 shows the single column layout of the array of dimension 50 D × 5 D. Four different combinations of
Figure 2. Single column layouts.
the turbines in the single column array were attempted as shown in Figure 3. The dark boxes in Figure 3 indicate the location of wind turbines, Case A represents a single column layout of turbines which are located in the 1st, 4th, 7th and 10th cells of the column. Similarly Case B, C and D, have turbines located at 1st, 2nd, 3rd, 4th cells; 1st, 3rd, 5th, 7th cells and 1st, 2nd, 9th, 10th cells respectively.
Single Column Array with Four Turbines
In recent literatures [16-22], the choice and number of principal parameters considered for parametric study of wind farms were made purely on design constraints. But, in this study parameters influencing the wake decay effects were directly considered. Six principal parameters considered in the study are: 1) Rotation speed of the rotor, n; 2) Number of blades Nb; 3) Rotor diameter D; 4) Hub height H; 5) Change in velocity u0; 6) Distance between adjacent wind turbine for wind farm layout X. Table 1 shows the range of parameters which influence the wake decay effect of wind turbines in wind farms. The aim of the wind farm analysis is to find the best combination of these parameters for Case A, B, C and D location patterns. The best of the combination was formulated based on the amount of wake and its decay effect.

Figure 3. Single column layout Case A: 1,4,7,10; Case B: 1,2,3,4; Case C: 1,3,5,7; Case D: 1,2,9,10.
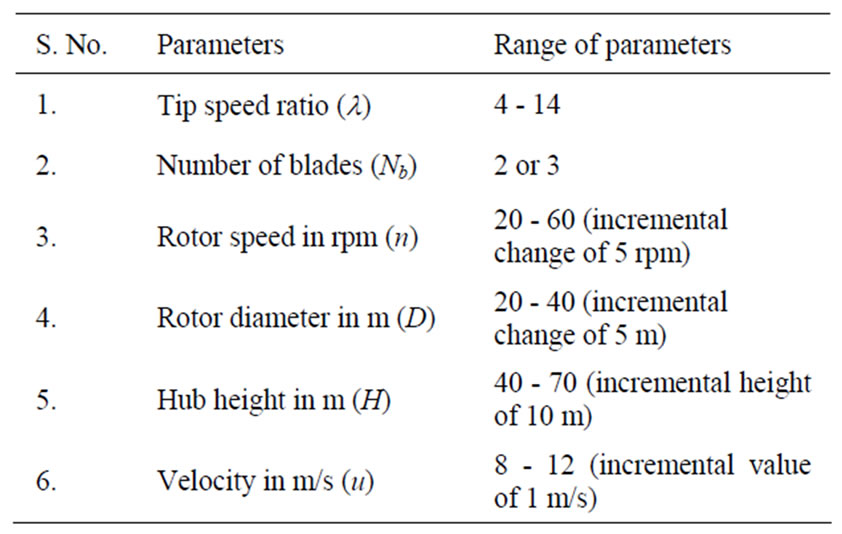
Table 1. Variation of principal parameters used in the study.
5. Influence of Wake Parameters on Wind Farm Efficiency
Using the equations quoted in section 3, energy and exergy efficiency was calculated for different cases. Variation of exergy and energy efficiency with respect to different wake related parameters are reported in this section. Table 1 shows the list of parameters related to wake effects in a wind farm. Wind turbines in parks are usually spaced at least 5 rotor diameter distances from one another in order to avoid turbulence around the turbines downstream. The ultimate objective of the wake study is to understand and minimize turbulence so that the influence of the turbine upstream of the wind direction is not felt by the turbines located on the downwind side. Minimum turbulence in the wind parks allows maximum energy extraction from the free wind at a nominal speed.
5.1. Effect of Tip Speed on Energy and Exergy Efficiency
Energy efficiency versus tip speed ratios for all the four cases are shown in Figure 4. By varying the tip speed ratio from 4 to 14, it was found that the efficiency increased initially and after reaching the peak, resulted in a negative slope. Wind speed up to some critical values extracted power from the wind after which, on account of the wakes the trend got reversed. A maximum efficiency of 44.5% was noticed for Case A positioning. Case B positioning registered the lowest peak efficiency of 38.5 %. Huge kinetic energy deficit due to wakes formed downstream of the turbines was the influencing factor. Since the turbines were placed very close to each other the wakes highly influence the next turbine in the row.
As shown in Figure 3, an equal gap of 10 D was assumed between wind generators in Case A, where as the gap was very less in Case B. In case B, the wake effects resulted in a lesser efficiency of the farm. Kinetic energy
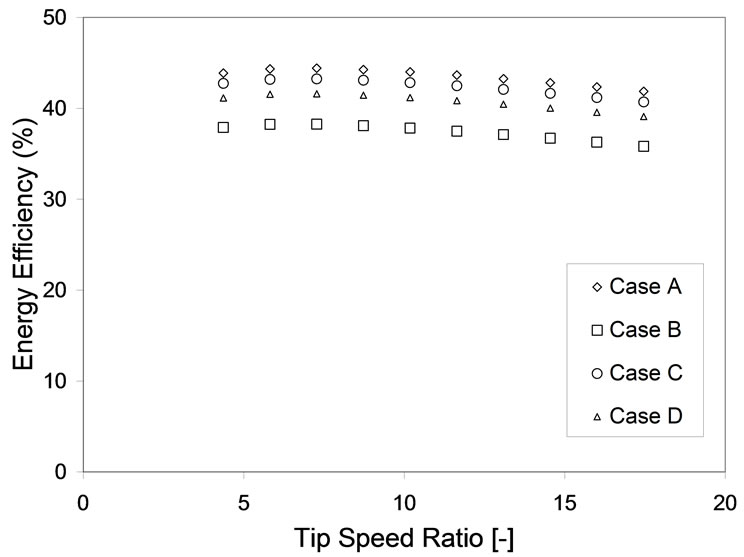
Figure 4. Energy efficiency for various tip speed ratio.
deficits due to wakes downstream of turbines resulted in huge loss of power available in the wind. For Case C and D again the same judgment can be noticed. In Case D, the gap was more between first 2 and last 2 wind turbines, the efficiency was found to be more compared to Case C. When the tip speed ratio was increased beyond 6, the reduction in exergy efficiency registered was found to be high. However the positioning of wind turbines does not influence the exergy efficiency of the wind farm by much (Figure 5). Energy efficiency seems to slightly more affected by wakes than Exergy efficiency. The amount of energy and exergy available in the wind are less at high tip speed ratios.
5.2. Effect of Number of Blades on Exergy Efficiency
Normally the number of blades used for wind turbines in the wind farm is two or three for the electrical power generation. More the number of blades less the tip speed ratio, hence less the energy and exergy efficiencies. Instability is a factor to be considered with the turbines having less number of blades, specially two bladed turbines. The impact of number of blades on energy and

Figure 5. Exergy efficiency for various tip speed ratio.
exergy efficiency was studied using case studies. Two different cases were considered, case1: three bladed turbines were considered and case 2: two bladed turbines were considered. Figure 6 shows the comparison of energy efficiencies for 4 Cases A, B, C and D.
The loss is in energy efficiency by opting a two bladed system is only 1.5%, but the instability of the system as a whole is a dominant factor in the overall performance.
Figures 7 and 8 show the comparison of exergy efficiencies for two and three bladed systems. The case with three blades has a better efficiency by a margin of 1% (Negligible). In terms of the number of blades there was not much energy and exergy efficiency improvement. The amount of wake generated by the three bladed turbines are more at higher tip speed ratio than the two bladed turbines, but the instability involved in two bladed turbines is a critical factor. The maximum energy and exergy efficiencies were also analyzed for the same rotor speed (n = 28 rpm). Figures 8 and 9 show the effect of number of blades on the energy and exergy efficiencies respectively. Three bladed turbines show better energy and exergy efficiencies, as shown in Figure 7. Three bladed turbines had better results than two bladed turbines by an energy efficiency margin of 2 %. For exergy

Figure 6. Energy efficiency for various rotor speeds, Nb = 3.
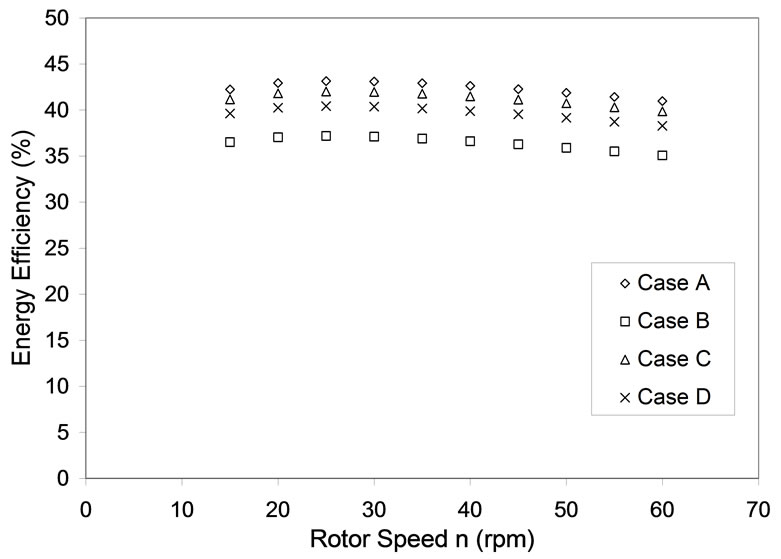
Figure 7. Energy efficiency for various rotor speeds, Nb = 2.
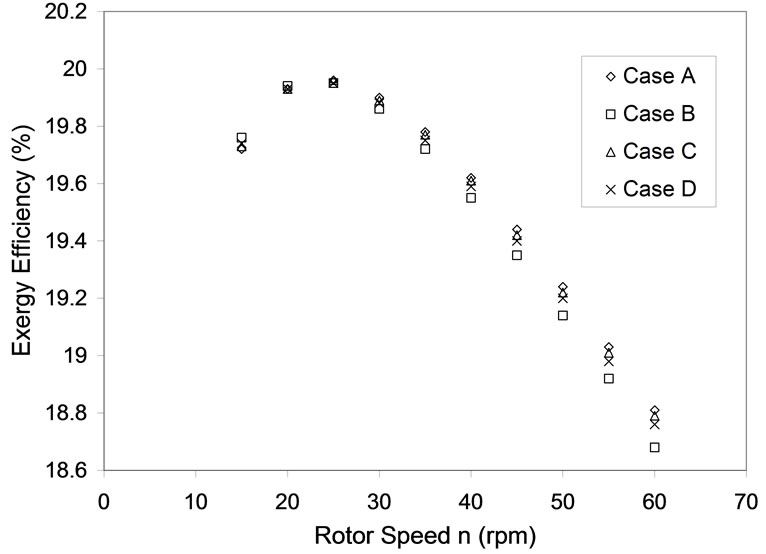
Figure 8. Exergy efficiency for various rotor speeds, Nb = 3.
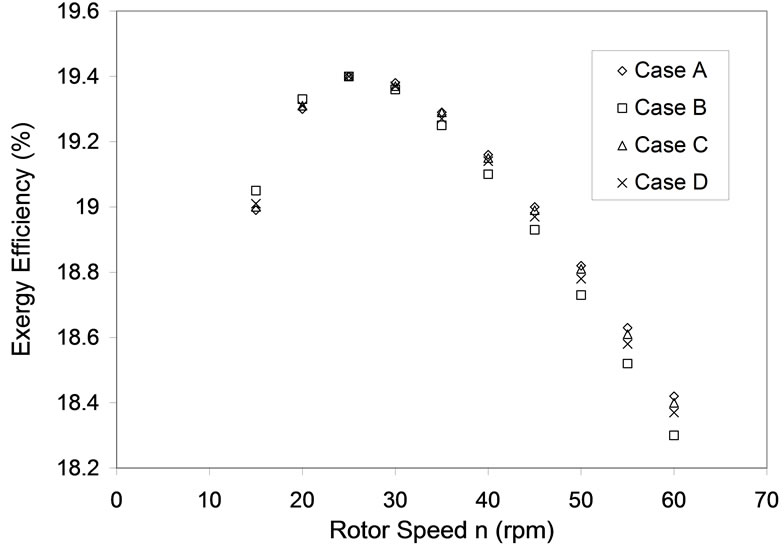
Figure 9. Exergy efficiency for various rotor speeds, Nb = 2.
efficiency, the margin of improvement was only 1%.
Figures 6, 7, 8 and 9 show the variation of energy and exergy efficiency for three and two bladed turbines. Three bladed turbines outclassed two bladed turbines both in terms of energy and exergy efficiencies. The betterment in energy and exergy efficiencies was found to be marginal 2% and 1% respectively. Comparing all the four Cases A, B, C and D it was found that there was not much difference in the energy efficiencies for two and three bladed systems. Exergy efficiencies plotted for two and three bladed systems in Figures 9 and 8 respectively show there is a significant difference in the amount of available power in the wind. Case A had the maximum energy efficiency when compared to all other case on account of the spacing between turbines and the minimum wake effects in the farm. Case C and Case D followed Case A in their list of performances with Case B being the least in its performance.
5.3. Effect of Diameter and Hub Height Variation on Exergy Efficiency
The diameter of the rotor and hub height of the turbines was varied in the calculation of the exergy and exergy efficiencies. The variation in the diameter was made with incremental values of 10 m. Equation 24 was used in estimating the changes in hub height with respect to the changes in diameter. Figures 10, 11, 12 and 13 show the respective results. In order to meet the technical, environmental and physical constraints of the farm the following relation was used.
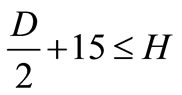 (24)
(24)
From the analysis, it is observed that increase in diameter value increases the exergy efficiency up to a certain point after which the efficiency values drop. More the diameter, more the energy and exergy efficiencies since the amount of wakes and turbulence are less when compared to smaller turbines. More the diameter more is the space required for placement of wind turbines based on thumb rules like 3D or 5D.
5.4. Effect of Free Stream Velocity Variation on Exergy Efficiency
In this section, energy and exergy efficiency results were
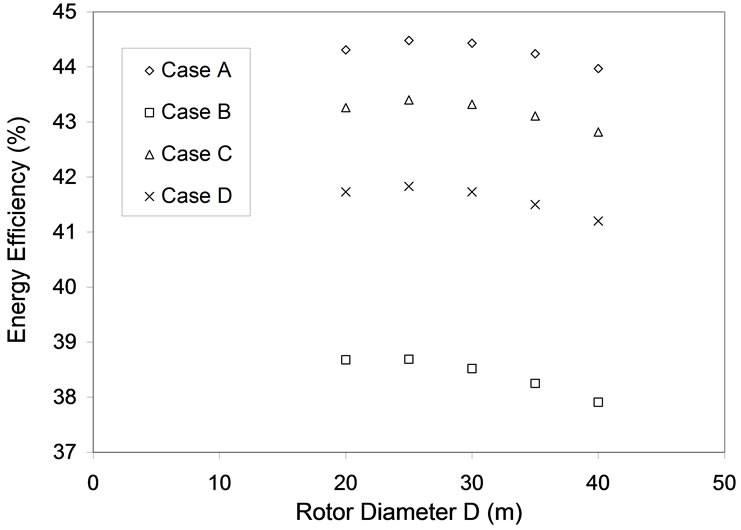
Figure 10. Effect of layout on energy for various rotor diameters.
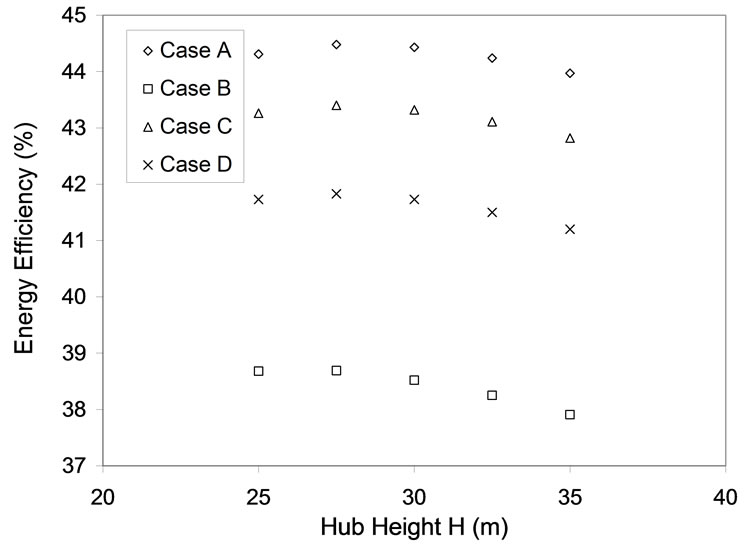
Figure 11. Effect of layout on energy for various hub heights.

Figure 12. Effect of layout on exergy for various rotor diameters.
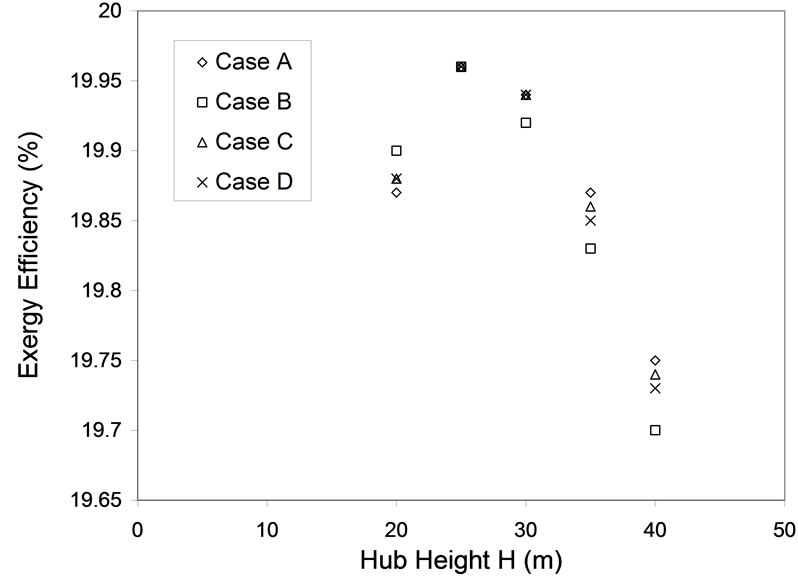
Figure 13. Exergy efficiency for various hub heights.
obtained by varying wind speeds. These speeds have a very strong influence on the wind farm performances. Design wind speed is a characteristic of the blade shape and is linked to the aerodynamic phenomena that occur at the blade profile level. High design wind speeds was found to produce better results, but the speeds were often linked to the site properties. Typical site data were taken into consideration for calculation of wind speeds.
Free stream velocities have a high impact on wind turbines located close to each other. Exergy efficiencies of farms were found to increase with free stream velocity as shown in Figure 15.
If the velocity is increased drastically, the pressure difference on each wind turbine gets increased which increases the exergy input. The energy efficiency increases with increasing velocity but the increase is very small as shown in Figure 14. In all the studies the combination of 1, 4, 7 and 10 (Case A) proves to be a better option than all the other cases.
6. Conclusions
Wake effects in wind farms were studied using energy

Figure 14. Effect of layout on energy for various free stream velocity.
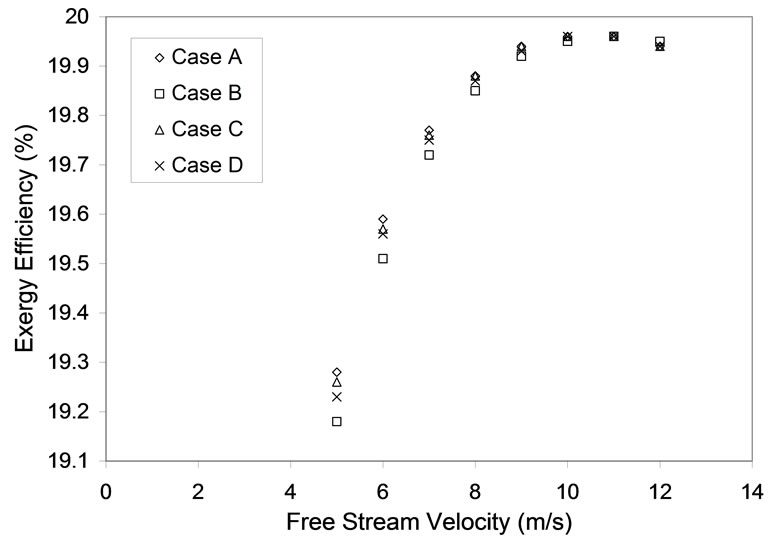
Figure 15. Exergy efficiency for various free stream velocity.
and exergy efficiencies by varying turbine parameters like tip speed ratio, rotor speed, number of blades, hub height, diameter and free stream velocity. Tip speed ratios for case of wind farms with high wake effects were found to influence exergy and energy efficiencies in a significant way. Kinetic energy deficits due to wakes downstream of turbines resulted in loss of power available in the wind leading to lesser efficiencies of the farm.
Rotor speeds had the same trend as tip speed ratio for cases with high wake effects. Although three bladed turbines produced higher wake effects in comparison to two bladed turbines, exergy efficiency of three bladed turbines was much higher. On account of this factor, three bladed turbines had higher energy efficiencies when compared to two bladed turbines. Rotor diameter and hub height had the most significant influences on energy and exergy efficiencies for cases with high wake effects when compared to all other turbine parameters.
Case A, which had uniform and sufficient distance (10 D) between wind turbines proved to the best in terms of energy and exergy efficiency for different values of turbine parameters. Case C and Case D had an optimal performance on account of wake effects. Case B proved to be the worst of all on account of severe wake effects. The distance between two adjacent wind turbines is a critical factor in the wake decay effect and hence the power generation. Free stream velocity although being a site parameter of the farms, play a major role in wake decay effects along with the distance between turbines.
7. REFERENCES
- F. Koch, M. Gresch, F. Shewarega, I. Erlich and U. Bachmann, “Consideration of Wind Farm Wake Effect in Power System Dynamic Simulation,” IEEE Power Tech Conference, Russia, 2005.
- F. C. Kaminski and R. H. Kirchhoff, L.-J. Sheu, “Optimal Spacing of Wind Turbines in a Wind Energy Power Plant,” Solar Energy, Vol. 39, No. 6, 1987, pp. 467-471. doi:10.1016/0038-092X(87)90053-3
- T. Diveux, P. Sebastian, D. Bernard and J. R. Puiggali, “Horizontal Axis Wind Turbine Systems: Optimization Using Genetic Algorithms,” Wind Energy, Vol. 4, No. 4, 2002. pp. 151-171. doi:10.1002/we.51
- G. Mossetti, C. Poloni and B. Diviacco ‘Optimization of Wind Turbine Positioning in Large Wind Farms By Means of Genetic Algorithm’ Journal of Wind Engineering and Industrial Aerodynamics, Vol. 51, No. 1, 1997, pp. 105-116. doi:10.1016/0167-6105(94)90080-9
- S. A. Grady, M. Y. Hussaini and M. M. Abdullah, “Placement of Wind Turbines Using Genetic Algorithms,” Renewable Energy, Vol. 30, No. 2, 2005, pp. 259-270. doi:10.1016/j.renene.2004.05.007
- U. A. Ozturk and B. A. Norman, “Heuristic Methods for Wind Energy Conversion System Positioning,” Electric Power Systems Research, Vol. 7, No. 3, 2004, pp. 179- 185. doi:10.1016/j.epsr.2003.12.006
- C. Koroneos, T. spachos and N. Moussiopulos, “Exergy Analysis of Renewable Energy Sources,” Renewable Energy, Vol. 28, No. 2, 2003, pp. 295-310. doi:10.1016/S0960-1481(01)00125-2
- G. Z. Jia, X. Y. Wang and G. M. Wu, “Investigation on Wind Energy-Compressed Air Power System,” Journal of Zhejiang University Science, Vol. 5, No. 3, 2004, pp. 290-295. doi:10.1631/jzus.2004.0290
- I. Dincer and M. A. Rosen, “Exergy: Energy, Environment and Sustainable Development,” Elsevier Publication, Amsterdam, 2007.
- I. Dincer and Y. A. Cengel, “Energy, Entropy and Exergy Concepts and Their Roles in Thermal Engineering,” Entropy, Vol. 3, No. 3, 2001, pp. 116-149.
- A. D. Sahin, I. Dincer and M. A. Rosen, “Thermodynamic Analysis of Wind Energy,” International Journal of Energy Research, Vol. 30, No. 8, 2006, pp. 553-566. doi:10.1002/er.1163
- O. Ozgener and L. Ozgener, “Exergy and Reliability Analysis of Wind Turbine Systems: A Case Study,” Renewable and Sustainable Energy Reviews, Vol. 11, No. 8, 2007, pp. 1811-1826.
- J. F. Manwell, J. G. McGowan and A. L. Rogers, “Wind Energy Explained: Theory, Design and Application,” Wiley, Chichester, 2002,
- T. Burton, D. Sharpe, N. Jenkins and E. Bossanyi, “Wind Energy Handbook,” Wiley, Chichester,2001.
- R. H Abdel-Hamid, M. A. Abu Adma, A. A. Fahmy and S. F. A. Samed, “New Technique for Identifying Optimal Generating Units Parametes for Wind Energy Plant,” East-West Economic Corridor, Marseille, 2009.
- A. Ahmadi and M. A. Ahayaei, “Exergy Analysis of Wind Turbine,” International Journal of Exergy, Vol. 6, No. 4, 2009, pp. 457-476. doi:10.1504/IJEX.2009.026672
- A. D. Sahin, I. Dincer and M. A. Rosen, “New Spatio-Temporal Wind Exergy Maps,” Journal Energy Resource. Technology, Vol. 128, No. 3, 2006, pp. 194- 201.
- A. Mirandola and A. Stoppers, “A Viable Approach to the Optimization of Energy Systems,” International Journal of Thermodynamics, Vol. 6, No. 4, 2003, pp. 157-167.
- C. Koroneos and E. Katopodi, “Exergy Analysis of the Wind Power Hydrogen and Electricity Production,” East-West Economic Corridor, Athens, 2006.
- M. Lewis-Beck, A. Bryman and T. F. Liao, “The Sage Encyclopedia of Social Science Research Methods,” Sage Publications, Thousand Oaks, 2004.
- M. L. Neelis, H. J. Van der Kooi and J. J. C. Greeings, “Exegetics Life Cycle Analysis of Hydrogen Production and Storage Systems for Automotive Applications,” International Journal of Hydrogen Energy, Vol. 29, 2004, pp. 537-545.
- G. Xydis, C. Koroneos and M. Loizidou, “Exergy Analysis in a Wind Speed Prognostic Model as a Wind Farm Siting Selection Tool: A Case Study in Southern Greece,” Applied Energy, Vol. 86, No. 11, pp. 2411-2420. doi:10.1016/j.apenergy.2009.03.017
Nomenclature
a - axial induction factor (-)
A - swept area of the turbine (m2)
c - scale factor (m/s)
Cp - maximum power coefficient (dimensionless)
Ct - thrust coefficient (-)
D - diameter of the wind turbine (m)
Exdest - exergy destruction (kW)
Exin - exergy input (kW)
Exout - exergy out (kW)
k - shape factor (-)
K - wake decay constant (-)
H - hub height (m)
۠m - mass flow rate (kg/s)
ke - kinetic energy (kJ)
p1 - inlet pressure of the turbine (kPa)
p2 - outlet pressure of the turbine (kPa)
Pmech - mechanical power of wind turbine (kW)
Pin - power input (kW)
Pout - power output (kW)
N - number of turbines (-)
n - rotor speed (rpm)
Nb - number of blades (-)
rd - rotor diameter (m)
r1 - wake radius (m)
Tatm - atmospheric temperature (K)
u1 - undisturbed wind velocity (m/s)
u2 - velocity at the inlet of the turbine (m/s)
u3 - velocity at the outlet of the turbine (m/s)
u4- velocity at the far wake of wind turbine (m/s)
u0 - free stream velocity (m/s)
uresultant - resultant velocity (m/s)
uc - cut in wind speed (m/s)
ur - rated wind speed (m/s)
uf - furling wind speed (m/s)
Wu - flow work for the individual turbine (kW)
W - available work (kW)
X - Distance between the adjacent winds turbines (m)
η - energy efficiency (-)
ηm - mechanical efficiency (-)
ηe - electrical efficiency (-)
ε - exergy efficiency (-)
ρ - air density (kg/m3)
λ - tip speed ratio (-)
ω - angular velocity (rad/s)
α - entrainment constant(-)

