Intelligent Control and Automation
Vol. 3 No. 4 (2012) , Article ID: 24888 , 9 pages DOI:10.4236/ica.2012.34044
A Hybrid System Approach for High Consumption Industrial Furnace Control
Department of Automation and System Engineering, Faculty of Electrical Engineering and Information Technologies, Ss. Cyril and Methodius University, Skopje, Macedonia
Email: goranst@feit.ukim.edu.mk
Received August 8, 2012; revised September 8, 2012; accepted September 16, 2012
Keywords: Hybrid Control; Industrial Furnace; Predictive Control
ABSTRACT
In this paper we describe a hybrid system approach for high consumption industrial furnace control. The problem is observed in systematic way starting from the need for modeling this system as hybrid. For description of this behavior we use the Hybrid System Description Language. After that, we design an optimal controller for the furnace and we simulate and compare the controller with other relevant predictive controllers. We have shown that using the hybrid approach for control of industrial furnaces leads to significant improvement of the control system performances.
1. Introduction
Processes and plant constructions of thermal systems and industrial furnaces, kilns and ovens in particular, have been subject to both scientific and technological research for long time [1] . This is mainly due to the process complexity of energy conversion and transfer into thermal systems, however, their control and supervision have recently become topics of extensive research.
The overall control task is to drive the process to the desired thermodynamic equilibrium and to regulate the temperature profile through the plant. In industrial operating environment, technical control specifications involve goal and task description of aims and procedures of supervision functions. From the general systems theoretical standpoint, it is the thermal systems where it became apparent that controlled processes in the real-world plants constitute a non-separable, unique interplay of the three fundamental natural quantities: energy, mass and information.
From control point of view, in thermal systems the essential impact occurs due to time delay and natural I/O operating modes. These modes interact with the controlling infrastructure in the process real-time, provide the way the complexity of sensor-actuator problem be properly resolved by natural ordering of I/O modes and respective input-output variable pairing [2,3].
In this paper we present a hybrid model for a high consumption industrial furnace that should represent the real plant more accurately. On the basis of this model, we will design controller(s) that will lead to increasing of the control system performance.
The paper is organized as follows. At the beginning we explain the principles of hybrid systems and we elaborate on the need of using hybrid modeling for control of high consumption industrial furnaces. In the third section we present linearized model of the furnace and we derive hybrid model for designing of the predictive controller that is explained in section four. In section five the simulation results are presented. At the end we give concluding remarks and possible future work.
2. The Need for Hybrid Model for High Consumption Industrial Furnace
A hybrid system denotes in general a system composed of two unlike components. A hybrid control system is a control system with both continuous and binary/integer signals. Such a system generates a mixture of continuous and discrete signals, which take values in a continuum (such as the real numbers ) and a finite set (such as a, b, c), respectively.
) and a finite set (such as a, b, c), respectively.
In the last decade several modeling formalisms have been developed to describe hybrid systems. One of the most popular and widely used is the class of discrete hybrid automata (DHA) introduced in [4] . DHA result from the interconnection of a finite state machine (FSM), which is the discrete dynamics of the hybrid system, with a switched affine system (SAS), which is the continuous dynamics, see Figure 1. as presented in [5] .
The information exchange of the two basic elements of the hybrid automaton is based on the event generator (EG) and the mode selector (MS). The EG is responsible for activating the logic variables based on the continuous

Figure 1. Discrete time hybrid automata.
state and input signals. These logic events and other exogenous logic inputs affect the logic states of the FSM. After that the MS combines all the logic variables to choose the “mode” of the continuous dynamics of the SAS. Continuous dynamics are expressed as linear affine difference equations.
Industrial furnaces are usually represented in control science as nonlinear mathematical models. In order to simplify the model of the furnace in the near surrounding of the operating point, researchers usually use linearization. Nevertheless, it is not unusual for a system to have more than one operating points so linearization must be done in all of them. On the other hand, these systems are usually subject to logic and integer variables inputs (furnace empty/full; door open/closed; line speed: 1, 2, 3, or 4; and so on). In these cases, there are several possible solutions:
a). Linearization in one operating point and neglecting the logic and integer variables. In this case the designer of the control system should carefully choose one operating point to linearize the plant, and design the controller as robust as possible. For the integer and logic variables the most common value must be assumed. Reduced efficiency of the controller is expected due to the neglecting of the variables and when the operating point is different from the one of linearization.
b). Hybrid approach. Here the designer should model the system in one of the popular hybrid modeling languages, and design a controller for the hybrid model. This approach is very similar to the Switching control, but in addition it allows the user to incorporate logical rules in the mode selection of the system, as we have previously described. In order to implement hybrid multi model system, the nonlinear function, must be linearized in several operating points before the hybrid approach is implemented.
c). Nonlinear control techniques. These techniques are the method that can achieve best control performance if no logic and integer variables are involved in the system. Additionally, nonlinear control is too demanding in means of computational power, and in other cases this kind of design is not feasible. That is why this method is rarely implemented in industry.
We can summarize that the furnace has complex model that consists of continuous dynamics over different segments and integer/boolean logic variables that significantly affect the transfer function. That is why a hybrid approach for modeling of the furnace is the most appropriate choice. As one of the possible representations, the authors in [6] have proposed a class of hybrid systems definition of the form of Equations -.

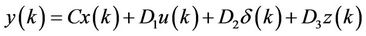

where 
is the state vector, 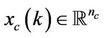 and
and 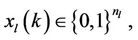 the output vector is
the output vector is
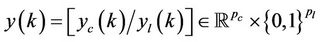
and the input vector is
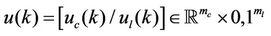 ,
,
 and
and 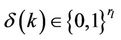 are auxiliary variables.
are auxiliary variables.  and
and  denote real constant matrices,
denote real constant matrices, 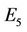 is real vector,
is real vector,  , and
, and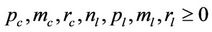 . Without loss of generality, we assumed that the continuous components of a mixed-integer vector are always the first. Inequalities must be interpreted component wise. Systems that can be described by model - are called Mixed Logical Dynamical (MLD) systems.
. Without loss of generality, we assumed that the continuous components of a mixed-integer vector are always the first. Inequalities must be interpreted component wise. Systems that can be described by model - are called Mixed Logical Dynamical (MLD) systems.
In this paper we will elaborate the hybrid system design approach in modeling and control of high consumption industrial furnace. The operating point of the furnace depends on the temperature profile that we want to achieve. The most used temperature profile in this furnace is when we need to regulate the temperature near 1000˚ Celsius. Nevertheless, if we want to use the furnace for heating other types of pipes, we need to stabilize the output temperature to different operating points e.g. 500, 700 or 1200 degrees etc. Additionally there are several discrete parameters that significantly influence the furnace behavior. The state that represents the presence of pipe in each of the furnace zones has great impact on the coefficients for the increase/decrease of the temperature in the respective zone. Also the state of the doors (open/closed) at the beginning and at the end of the furnace impacts the cooling of the furnace.
3. Model of the Furnace
In our previous work, we have presented different types of model predictive control implemented on linearized models of industrial furnaces [7,8]. In order to elaborate our results we are going to compare our work with previous related work. In this section we present the linearized model of the furnace and the discrete time hybrid model.
3.1. Continuous Time Model
The modeling of an industrial furnace is not an easy task. That is why, in this paper we decided to use the previous work [3] where a complete identification of a high consumption industrial furnace in the factory “FZC 11 Oktomvri” in Kumanovo, in the Republic of Macedonia has been done.
Structural, non-parametric and parameter identification has been carried out using step and PRBS (PseudoRandom Binary Sequence) response techniques in the operational environment of the plant as well as the derivation of equivalent state realization. With regard to heating regulation, furnace process is represented by its 3 × 3 system model. The families of 3 × 3 models have 9 controlled and 9 disturbing transfer paths in the steady and transient states. The structural model of the furnace is depicted in Figure 2.
Experiments involved the recorded outputs (special thermocouples): temperature changes in the three zones in response to input signal change solely in one of the zones. Firstly, only the burners at the first zone were excited and data for the temperatures in all three zones is collected; the temperature  and the corresponding fuel flow Qi for each input-output process channel (transfer path) were recorded.
and the corresponding fuel flow Qi for each input-output process channel (transfer path) were recorded.
After collecting the data, the parameter modeling of

Figure 2. Diagram of the conceptual MIMO system model for gas-fired furnace in FZC “11 Oktomvri”.
the furnace was conducted and the system’s state space model presented in Equations and was derived. This model represents a linearization of the furnace model near the operating point.


where  is the state vector of the system, y is the output vector of the system and the values of matrix A are defined in Equation , the values of matrix B are defined in Equation , and the values of matrices C and D are defined in Equation .
is the state vector of the system, y is the output vector of the system and the values of matrix A are defined in Equation , the values of matrix B are defined in Equation , and the values of matrices C and D are defined in Equation .


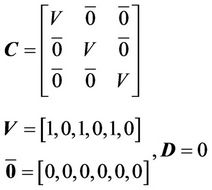
The time constants are T1 = 6.22 min and T2 = 0.7 min.
3.2. Discrete Time Hybrid Model
Before we introduce the hybrid model we need to elaborate the furnace dynamics. In this paper we are dealing with 3-input 3-output gas fired furnace. The maximum temperature that can be achieved is 1300˚ Celsius when operating at full power (the valves for the burners are opened 100%). The model for the temperature is discrete and it is represented with the Equations -.





where  = 1.195;
= 1.195; 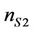 = 0.6232;
= 0.6232; 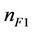 = 0.07968;
= 0.07968; 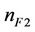 = 0.04155;
= 0.04155;  = 0.01245;
= 0.01245;  = 0.006492.
= 0.006492. 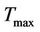 represents the maximum temperature that can be achieved in this furnace and is equal to 1300˚ Celsius. Signals
represents the maximum temperature that can be achieved in this furnace and is equal to 1300˚ Celsius. Signals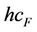 ,
, 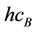 and
and 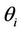 are logic signals that can change their value according to the process dynamics and represent disturbances of the system. The outdoor temperature around the furnace
are logic signals that can change their value according to the process dynamics and represent disturbances of the system. The outdoor temperature around the furnace 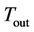 is continuous state disturbance to this system.
is continuous state disturbance to this system.
It is obvious that the system is both discrete and nonlinear by nature but cannot be implemented as a discrete control system because of the logical conditions in the transfer function and the interconnection between the states and variables that combine a non-affine set for synthesis of the control system.
In order to overcome this problem we are going to propose 2 solutions.
a). The model could be linearized near the best-fit operating point, and after that to be represented as a hybrid system, by decomposing this model to sections according to the logic rules.
b). The model will be divided into several sections and linearized in each of them. In this way we will derive a multi-model of the furnace that can be later decomposed to more section according to the logic rules. This way we will have more complex model and controller, but improvements in the results are expected.
Both of the solution will be compared between each other, and with a standard MPC controller on a linearized model of the furnace.
4. Controller Synthesis
Model Predictive Control (MPC) has become the accepted standard for complex constrained multi variable control problems in the process industries. Here at each sampling time, starting at the current state, an open-loop optimal control problem is solved over a finite horizon [9] . Only the first computed control value in the sequence is implemented. At the next time step the computation is repeated starting from the new state and over a shifted horizon, leading to a moving horizon policy [10] .
Controlling a system means to calculate input signals in a manner that when the calculated sequence is applied to the system it will eliminate the difference between the referent signal and the measured output of the system. In this paper we will compare three different MPC techniques to a highly complex nonlinear model of an Industrial furnace. As mentioned in the previous section the controllers to be compared are linear MPC, hybrid MPC on a model linearized in one operating point, and hybrid multi-model MPC.
The optimization problem of linear MPC is known for a long time and it is not a subject of this paper. The reader can find detailed explanations on MPC in [11] , [12] and many other books. Regarding the hybrid optimization problem, it should be of the form
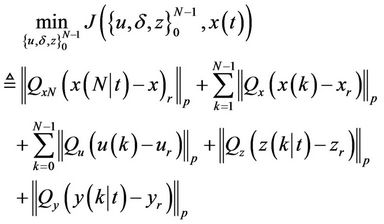

where the explanation of the elements is the same as in Equations -.
We use the Hybrid Toolbox for Matlab [13] as a design tool for the controller for the high consumption industrial furnace. This toolbox can work with several different types of hybrid system models (e.g. Mixed Logical Dynamical Systems, Piecewise Affine Systems and Discrete-time Hybrid Automata) and presents a formal mathematical equivalence between these models. We use HYSDEL to represent the model of the furnace.
In order to achieve better results we have divided the temperature domain of the furnace in five sections as presented here:
 ;
;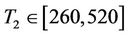
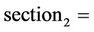 ;
;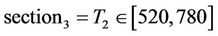 ;
;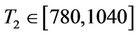
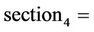 ;
;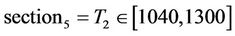 .
.
For each of the section a linearized model for the furnace was derived near the midpoint of the respective section (e.g. for section4 the model was linearized near T2 = 910˚ Celsius).
MLD hybrid model generated from the HYSDEL file for the multi-model linearized problem has 25 continuous states, 9 inputs (4 continuous, 5 binary) and 3 continuous outputs. The HYSDEL model has 22 continuous auxiliary and 15 binary auxiliary variables. The optimization problem to be solved has 118 mixed-integer linear inequalities. The sampling time of the system is 0.5 minutes. If comparison to the hybrid model of the furnace linearized in one operating point whose HYSDEL representation has only 38 mixed-integer linear inequalities, it is obvious that the complexity of the optimization problem is significantly increased with the introduction of multi-model linearization. This affects the computation time of the optimization algorithm and favors the one point linearization method for implementation if it has satisfactory behavior.
5. Simulation Results
To verify the hybrid approach for control of high consumption industrial furnace the authors have conducted series of simulations. The Disturbance signals from the front and the back door, and the timing of the pipe entering in the first zone of the furnace are graphically represented on Figure 3. On Figure 3 the logic variable for pipes entering zone 1 is resented. The logic variables for zone 2 and 3 have deterministic dependence on this value with fixed delay. In reality this delay is represented through the line speed of the conveyor driving the pipes in the furnace, but this is to be done in near future. During this simulation a fixed delay time of 10 minutes between zones is adopted. During the simulation the continuous disturbance signal  has value of 15˚ Celsius.
has value of 15˚ Celsius.
The main results are presented on Figures 4-6 where the temperatures in the respective zones of the furnace are presented long with the reference signal. The control signals applied to the three control valves respective are presented on Figures 7-9.
From the presented results it is obvious that introduceing the hybrid control approach for high consumption industrial furnace improves the quality of the control. The controller leads the system faster to the referent setpoint and the steady state error is acceptable. The hybrid MPC—one linearized model method, has also satisfactory results. Nevertheless we must point out that the tracking of the referent trajectory is best when it is near the linearization point (s), and as the referent trajectory moves from this point we have bigger error in the control algorithm. This is more expressed in the hybrid controller with only linearization point, which is linearized near 800˚ degrees. In this case it is obvious that output tracks the reference without any problem near this region, but if we have work plans that require a lot of temperature
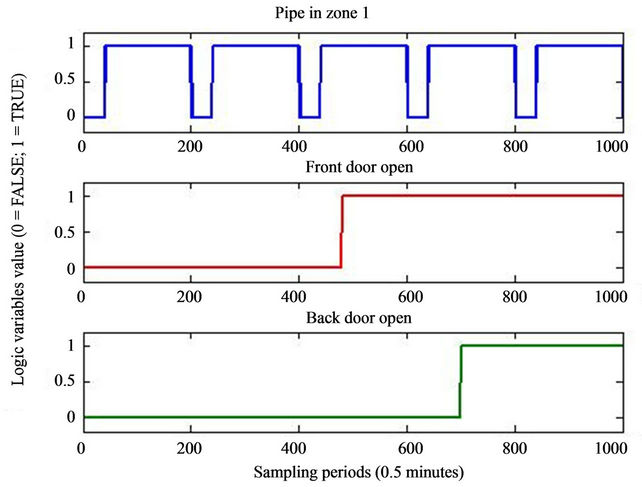
Figure 3. Timing of the logic variable disturbances of the furnace during the simulation.
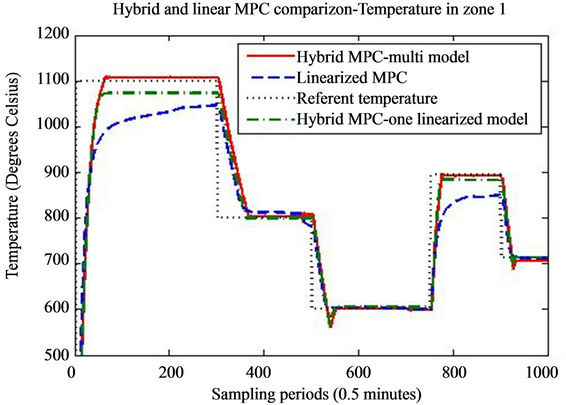
Figure 4. Temperature in the first zone of the furnace during the simulation.
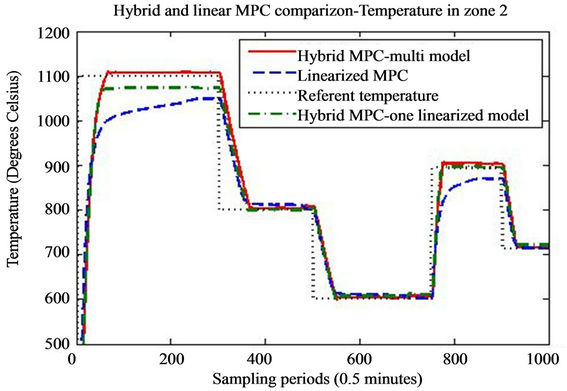
Figure 5. Temperature in the second zone of the furnace during the simulation.
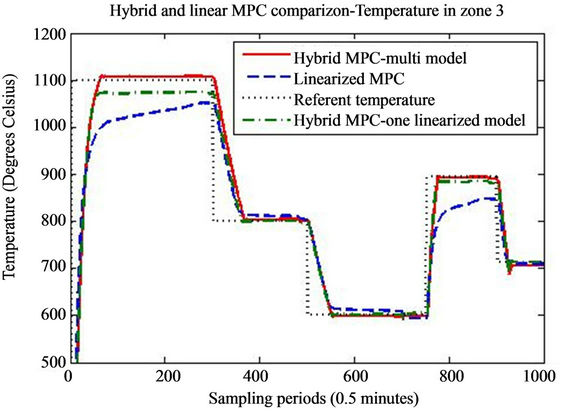
Figure 6. Temperature in the third zone of the furnace during the simulation.
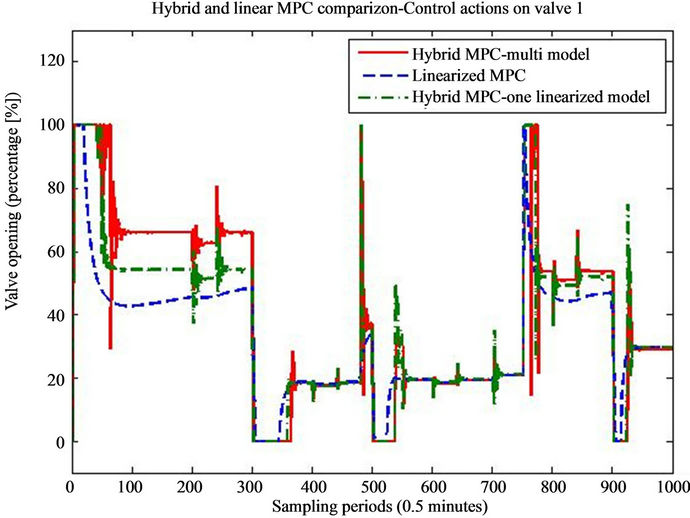
Figure 7. Valve openings on the first valve of the furnace during the simulation.
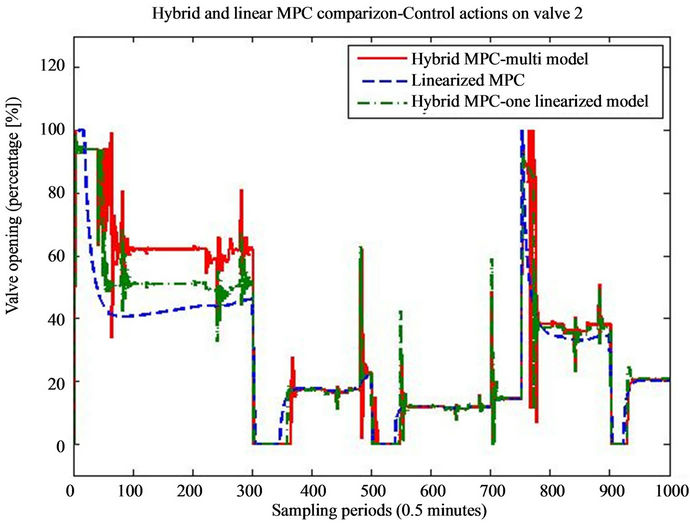
Figure 8. Valve openings on the second valve of the furnace during the simulation.
changes throughout the temperature domain of the furnace, the multi-model hybrid approach is to be considered. The previous remark, regarding the performance of the controller near the linearization point also stands for the multi-model hybrid approach. The difference here is that we have several models and the difference between the set-point and the active model cannot be very big. Logically if we introduce more models linearized in different operating point we will increase the performance of the controller, but also we will increase the complexity and the time necessary to perform the optimization.
Regarding the control signals, on all three figures (Figures 7-9) we can note that the hybrid controllers have fast reaction time to the disturbances. When there is new pipe entering in the one of the zones of the furnace, the control signal in the respective zone, acts towards
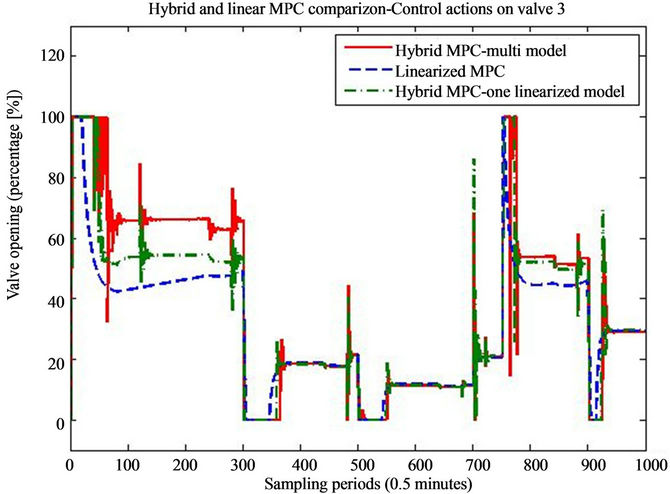
Figure 9. Valve openings on the third valve of the furnace during the simulation.
stabilization of the temperature. Also we can note that when the furnace is operating near 800˚ degrees, all three controller generate the same control value, but if we move far from this central linearization point, the calculated values for the control action differ a lot.
6. Conclusions
In this paper, a hybrid model of the high consumption industrial furnace in the factory “FZC 11 Oktomvri” in Kumanovo, R. Macedonia was presented. This approach resulted with significant improvements regarding to the linearized model that have been used before. Also we have shown that increasing the complexity of the model is not always necessary and depends on the specifics of the problem.
The new model incorporates the logic signals that act as disturbances to the furnace (new pipe entering in the zone, opening of the back and the front cooling door). Also in order to improve the performance of the furnace, multi point linearization was implemented on five characteristic points in the temperature domain. These results are confirmed with the presented simulation results.
We are also currently working to extend the results of this paper towards implementation of the line speed control of the furnace in the model and practical implementtation of the controller to the furnace.
7. Acknowledgements
This work was partially supported by the Faculty of Electrical Engineering and Information Technologies in Skopje, project: DEPAMPC—Development of Probability Algorithms for Model Predictive Control.
REFERENCES
- J. Rhine and R. Tucker, “Modelling of Gas-Fired Furnaces and Boilers,” McGraw-Hill, Boston, 1991.
- G. Dimirovski, A. Dourado, N. Gough, B. Ribeiro, M. Stankovski, I. Ting and E. Tulunay, “On Learning Control in Industrial Furnaces and Boilers,” Proceedings of the IEEE International Symposium on Intelligence Control, Patras, 17-19 July 2000, pp. 67-72.
- M. Stankovski, “Non-Conventional Control of Industrial Energy Processes in Large Heating Furnaces,” Ph.D. Dissertation, Ss. Cyril and Methodius University, Skopje, 1997.
- F. Torrisi and A. Bemporad, “HYSDEL—A Tool for Generating Computational Hybrid Models for Analysis and Synthesis Problems,” IEEE Transactions on Control Systems Technology, Vol. 12, 2004, pp. 235-249. doi:10.1109/TCST.2004.824309
- A. Bemporad, S. Di Cairano and N. Giorgetti, “Model Predictive Control of Hybrid Systems with Applications to Supply Chain Management,” Congress of ANIPLA Associazione Nazionale per LAutomazione, Napoli, 23-24 November 2005, pp. 1-15.
- A. Bemporad and M. Morari, “Control of Systems Integrating Logic, Dynamics, and Constraints,” Automatica, Vol. 35, No. 3, 1999, pp. 407-427. doi:10.1016/S0005-1098(98)00178-2
- G. Stojanovski, M. Stankovski and G. Dimirovski, “Multiple-Model Model Predictive Control for High Consumption Industrial Furnaces,” Facta Universitatis Series: Automatic Control and Robotics, Vol. 9, No. 1, 2010, pp. 131-139.
- G. Stojanovski and M. Stankovski, “Advanced Industrial Control Using Fuzzy-Model Predictive Control on a Tunnel Klin Brick Production,” Proceedings of the 18th World Congress, The International Federation of Automatic Control, Milano 2011, pp. 10733-10738.
- A. Bemporad, W. Heemels and B. De Schutter, “On Hybrid Systems and Closed-Loop MPC Systems,” IEEE Transactions on Automatic Control, Vol. 47, No. 5, 2002, pp. 863-869. doi:10.1109/TAC.2002.1000287
- D. Q. Mayne, J. B. Rawlings, C. V. Rao and P. O. M. Scokaert, “Constrained Model Predictive Control: Stability and Optimality,” Automatica, Vol. 36, No. 6, 200, pp. 789-814. doi:10.1016/S0005-1098(99)00214-9
- E. Camacho and C. Bordons, “Model Predictive Control,” Springer-Verlag, London, 2004.
- J. Maciejowski, “Predictive Control with Constraints,” Prentice Hall, Upper Saddle River, 2002.
- A. Bemporad, “Hybrid Toolbox—User Guide,” 2004. http://cse.lab.imtlucca.it/ bemporad/hybrid/toolbox

