Circuits and Systems
Vol.07 No.04(2016), Article ID:65998,15 pages
10.4236/cs.2016.74026
Hybrid Neuro Fuzzy Controller for Automatic Generation Control of Multi Area Deregulated Power System
Baghya Shree Solaiappan1*, Nagappan Kamaraj2
1Department of Electrical and Electronics Engineering, Anna University-University College of Engineering, Dindigul, India
2Department of Electrical and Electronics Engineering, Thiagarajar College of Engineering, Madurai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 February 2016; accepted 24 April 2016; published 27 April 2016
ABSTRACT
This paper is intended in investigating the Automatic Generation Control (AGC) problem of a deregulated power system using Adaptive Neuro Fuzzy controller. Here, three area control structure of Hydro-Thermal generation has been considered for different contracted scenarios under diverse operating conditions with non-linearities such as Generation Rate Constraint (GRC) and Backlash. In each control area, the effects of the feasible contracts are treated as a set of new input signals in a modified traditional dynamical model. The key benefit of this strategy is its high insensitivity to large load changes and disturbances in the presence of plant parameter discrepancy and system nonlinearities. This newly developed scheme leads to a flexible controller with a simple structure that is easy to realize and consequently it can be constructive for the real world power system. The results of the proposed controller are evaluated with the Hybrid Particle Swarm Optimisation (HCPSO), Real Coded Genetic Algorithm (RCGA) and Artificial Neural Network (ANN) controllers to illustrate its robustness.
Keywords:
AGC, ANFIS, ANN, Deregulated Power System, HCPSO, RCGA

1. Introduction
Nowadays, soft computing techniques and Artificial Intelligence plays a major role in all kinds of fields. Here, Adaptive Neuro Fuzzy Inference system (ANFIS) approach is applied to power system problem so as to regulate the power flow. The escalation in size and convolution of electric power industry along with increase in power demand has necessitated the use of intelligent systems that combine knowledge, techniques and methodologies from various sources for the real-time control of power systems.
The electric power trade at present is largely in the hands of Vertically Integrated Utilities (VIU) which possess generation, transmission and distribution systems facilitates to supply power to the customer at regulated tariff. The major revolutionize that has arisen be the emergence of Independent Power Producer (IPP) that can sell power to VIU. Given the present situation, it is generally agreed that the first step in deregulation will be to separate the generation of power from the transmission and distribution, thus putting all the generation on the same footing as the IPP. In an interconnected power system, a sudden load perturbation in any area causes the deviation of frequencies of all the areas and also in the tie-line powers. This has to be corrected to ensure the generation and distribution of electric power with good quality. This is accomplished by Automatic Generation Control (AGC). The main objectives of AGC [1] [2] are to be maintained the desired MegaWatt output and the nominal frequency in an interconnected power system besides maintaining the net interchange of power between control areas at predetermined values. The AGC task is carried out through the error signal produced during generation and net interchange between the areas (i.e.,) Area Control Error (ACE) [3] .
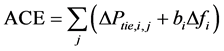 (1)
(1)
where 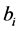 be the frequency bias coefficient of the ith area,
be the frequency bias coefficient of the ith area, 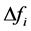 be the frequency error of the ith area,
be the frequency error of the ith area, 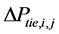 be the tie line power flow error between ith area and jth area.
be the tie line power flow error between ith area and jth area.
With the restructuring of electric utilities, AGC requirements should be expanded to include the planning functions necessary to ensure the resources needed for AGC implementation are within the functional requirements. So most of the methods that may be proposed must have a good ability to track the contracted or un-contracted demands and can be used in a practical environment. A lot of studies have been made about AGC in a restructured power industry over last decades. These studies try to modify the conventional LFC system [4] to take into account the effect of bilateral contracts on the dynamics [5] and improve the dynamical transient response of the system under competitive conditions [6] - [8] . This paper proposes a control scheme that guarantees a minimum transient deviation and ensures zero steady state error. The stabilization of frequency oscillations in an interconnected power system [9] becomes challenging when implements in the future competitive environment. Consequently advanced economic, high efficiency and improved control schemes [10] [11] are required to ensure the power system reliability. The conventional load-frequency controller may no longer be able to attenuate the large frequency oscillation due to the slow response of the governor [12] [13] . A number of control strategies have been employed in the design of load frequency controllers in order to achieve better dynamic performance [13] [14] . Among the various types of load frequency controllers, the most widely employed is the conventional proportional integral (PI) controller [13] - [15] . Conventional controller is simple for implementation but takes more time and gives large frequency deviation. A number of state feedback controllers based on linear optimal control theory have been proposed to achieve enhanced performance [16] [17] . Fixed gain controllers are designed at nominal operating conditions and fail to provide best control performance over a wide range of operating conditions [18] . Subsequently, to keep system performance near its optimum, it is desirable to track the operating conditions and use updated parameters to compute the control. Adaptive controllers with self-adjusting gain settings have been proposed for LFC [17] [19] - [22] .
There has also been considerable research work attempting to propose better AGC systems based on modern control theory [16] , neural network [23] - [27] fuzzy system theory [19] and reinforcement learning [26] . Recent study confirms that ANFIS approach has also been applied to hydrothermal system [28] - [30] . All research during the earlier period in the area of AGC narrates interconnected two equal area thermal system and petite attention has been paid to AGC of unequal multi area systems [31] . Most of ancient time works have been centred in the region of the design of governor secondary controllers, and design of governor primary control loop. Apparently no literature has discussed AGC performance subject to simultaneous small step load perturbations in all area or the application of ANFIS technique to a multi-area power system.
In this paper, an effort has been made to apply ANFIS controller for the automatic generation control for the three area hydro-thermal restructured power system in consideration with GRC and backlash.
2. System Analyzed
In this multi source generating system, there are three control areas in which each areas has different combinations of GENCOs and DISCOs as shown in Figure 11. Area 1 comprises of three GENCOs with thermal power system of reheat and hydro turbine combinations and two DISCOs, Area 2 comprises of two GENCOs with hydro and thermal (reheat turbine) combination and one DISCO, Area 3 consists of two GENCOs with hydro and thermal (reheat turbine) combination and two DISCOs as shown in Figure 2.
In this restructured environment, any GENCO in one area may supply DISCOs in the same area as well as DISCOs in other areas. In other words, for restructured system having several GENCOs and DISCOs, any DISCO may contract with any GENCO in another control area independently by Bilateral Transaction. The transactions should be made through an independent system operator (ISO). The primary intention of ISO is to control many ancillary services, one of which is AGC. In open access scenario, any DISCO has the freedom to purchase MW power at competitive price from different GENCOs, which may or may not have contract with the same area as the DISCO. The contracts of GENCOs and DISCOs described by “DISCO participation matrix” (DPM). The DPM for the nth area power system is as follows:
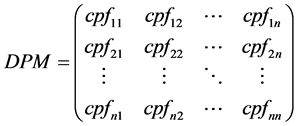 (2)
(2)
In DPM, the number of rows is equal to the number of GENCOs and the number of columns is equal to the number of DISCOs in the system. Any entry of this matrix is a fraction of total load power contracted by a DISCO towards a GENCO [24] . The sum of total entries in a column corresponds to one DISCO be equal to one
(i.e.,) 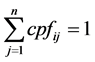
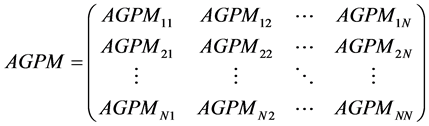 (3)
(3)
where, 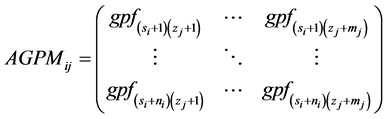
Figure 1. Three area restructured power system.
Figure 2. Three area multi source power system structure.
For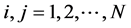 , and
, and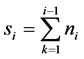 ;
;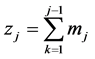 ;
;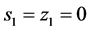 . Where,
. Where, 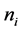 and
and 
GENCOs and DISCOs in area i. The gpfij refer to generation participation factor and shows the participation aspect of GENCOi in total load following the requirement of DISCOj based on the possible contract.
The Augmented Generation Participation Matrix (AGPM), which depicts (3) the effective participation of DISCO with various GENCOs in all the areas with nonlinearities. The Sum of all entries in each column of AGPM is unity. To demonstrate the effectiveness of the modeling strategy and proposed control design, a three control area power system is considered with nonlinearities. While there are many GENCOs in each area, the ACE signal has to be distributed among them due to their ACE participation factor in the AGC task.
The scheduled contracted power exchange is given [13] :

Disturbance in ith area,
where,
Area Interface for ith area,

Scheduled power tie line power flow deviation,





where
where 

In a power system having steam plants, power generation can change only at a specified maximum rate. The structure for ith area in the presence of GRC is shown in Figure 3. A typical value of the generation rate constraint (GRC) for thermal unit is 3%/min, i.e., GRC for the thermal system is 


Governor Dead band is none other than the total quantity of a sustained speed change when there is no resulting change. Though, the speed governor characteristics are nonlinear they are approximated for linear analysis. The limiting value of governor dead band is 0.06% [26] . One of the effects of governor dead band is to raise the obvious steady state speed regulation, R. Turbine-Governor Dead bands are found due to backlash in the linkage
Figure 3. Control structure for ith area with GRC.
connecting the piston to the camshaft [23] . Backlash is the nonlinearity which causes governor dead band and tends to produce continuous sinusoidal oscillations with a natural period of about 2 secs.
3. ANFIS Approach
The Hybrid combination of neural and fuzzy is considered to be an adaptive network, which has no synaptic weights, however they have adaptive and non-adaptive nodes. The adaptive network can be simply transformed to neural network architecture with classical feed forward topology. This proposed network is functioning very similar to adaptive network simulator of Takagi-Sugeno’s fuzzy controllers. This adaptive network is operationally comparable to a fuzzy inference system (FIS). ANFIS adjusts the entire parameters using back propagation gradient descent and least squares type of method for non-linear and linear parameters, respectively by the provided set of input/ output data [23] [28] . The fuzzy reasoning is expressed as Rule 1: If x is A1 and y is B1, then
Figure 4 shows a 2-input, type-3 ANFIS with 9 rules. Three membership functions are associated with each input, so the input space is partitioned into 9 fuzzy subspaces, each of which is governed by fuzzy if-then rules. The premise part of a rule defines a fuzzy subspace, while the consequent part specifies the output within this fuzzy subspace. The node functions in the same layer are of the same function family as described below. Layer 1 is the input layer. Neurons in this layer simply pass external crisp signals to Layer 2. Layer 2 is the fuzzification layer. Neurons in this layer perform fuzzification based on Gaussian membership function. If x be the input to node i, and 



Layer 5 is the defuzzification layer. Each neuron in this layer is connected to the respective normalisation neuron, and also receives initial inputs, x and y. The weighted average defuzzification method is employed here, it is shaped by weighting each membership function in the output by its respective maximum membership value.
Figure 4. ANFIS structure.
Layer 6 is represented by a single summation neuron. This neuron calculates the sum of outputs of all defuzzification neurons and produces the overall ANFIS output, z.
The Multi Layer Perceptron (MLP) structure model of ANN is exercised for AGC of three unequal area Hydro-Thermal system. Examinations has confirmed that ANNs have a broad number of application in the power engineering due to many virtues [29] [30] such as capability of synthesize multifaceted and discernible planning, briskness due to parallel mechanism, robustness and fault forbearance.
In this article, ANFIS controller in MATLAB/Simulink, which is an advance adaptive control configuration of ANN, has been proposed. The proposed ANN controller uses back propagation through-time algorithm. The back-propagation technique is an iterative method employing the gradient decent algorithm for minimizing the minimum square error between the actual output and the objective for each pattern in the training. Then update the network weights in a recursive algorithm starting from the output layer and working backward to the first hidden layer. The learning process of ANFIS system acquires the semantically properties of the underlying fuzzy system into account. The ANFIS system consists of the components of a conventional fuzzy system except that computation at every phase is carried out by a layer of hidden neurons and the neural network’s learning capacity is offered to boost the system knowledge.
ANFIS Controller Design
This ANFIS controller make use of Sugeno-type fuzzy inference system (FIS) controller, with the parameters surrounded by the FIS determined by the neural-network back propagation method. The ANFIS controller is designed by taking ACE and its derivative (d(ACE)/dt) as the inputs. The output stabilizing signal is worked out by using the fuzzy membership functions depending on these variables. ANFIS-Editor is used for realizing the system and for putting into practice. The fuzzy controller employs 49 rules and 7 membership functions in each variable to resolve output.
The procedure for designing ANFIS controller in MATLAB Simulink is as follows:
1) Sketch the Simulink model with fuzzy controller and simulate it with the specified rule base.
2) Collect the training data while simulating the model.
3) The two inputs, i.e., ACE and d(ACE)/dt and the output signal provides the training data.
4) Use anfisedit to generate the ANFIS.fis file.
5) Stack the training data composed in Step 2 and create the FIS with Gaussian membership function.
6) Train the collected data with generate FIS up to a particular no. of Epochs.
7) Save the FIS. This FIS file is the Neuro-Fuzzy enhanced ANFIS file.
4. Simulation Results and Discussion
The AGC problem of three area deregulated power system is considered here with the non-linearities. Hybrid combinations of Neuro and fuzzy is used as a controller to evaluate frequency and tie-line responses of multi source power system. The simulations are carried out for the possible electricity contracts and also for large demand variations using HCPSO, RCGA, ANN controllers and the results were compared. Table 1 depicts tie line power deviations for all the scenarios using the various controllers. The values show that the tie line power exchange between the areas, ANFIS controller reaches the exact exchange of power between the areas with minimum deviations compared to other controllers. Table 2 shows the comparison of GENCO power deviation for the three scenarios with theoretical and the simulated values by Equation (10). In this ANFIS accomplish its controller task perfectly in getting the same value as it gains in theoretical calculation. The plant parameters for three area deregulated power system used for modeling the control structure is presented in Table 3. The results illustrate that proposed controller proves good dynamic performance over the others in terms of settling time, overshoot and undershoot (Table 4 and Table 5).
4.1. Scenario 1 Poolco Based Transactions
In this scenario, GENCOs take part only in the load pursuing the control of their areas. The transaction among DISCOs and available GENCOs is being simulated based on the following AGPM by Equation (3). The variations in tie line power flows and frequency is shown in Figure 5 and Figure 6 and the values are depicted in Table 4 and Table 5. The figures show that ANFIS controller secure the steady state deviation (Marked as Black colour) with minimum settling time and reduced overshoot and undershoot.
Table 1. Tie line power deviation (pu MW).
Table 2. GENCO power deviations in pu Mw.
Table 3. Power system plant and control parameters.
Table 4. Tie line power deviation with respect to response characteristics.
Table 5. Frequency deviation with respect to response characteristics.
4.2. Scenario 2 Synthesis of Poolco and Bilateral Based Transactions
In this case, DISCOs have the liberty to deal with any of the GENCOs within or with other areas. The AGC assignment accomplished through the following AGPM. The inconsistency based on this transaction is shown in Figure 7 and Figure 8 prevailing to frequency and tie line power deviations (Table 4 and Table 5). The simulated characteristics illustrate that in this case also ANFIS provides better performance in reaching its steady state.
Figure 5. Frequency deviation for scenario 1.
Figure 6. Tie line power deviation for scenario 1.
Figure 7. Frequency deviation for scenario 2.
Figure 8. Tie line power deviation for scenario 2.
4.3. Scenario 3 Contract Violation
In this scenario, the DISCOs may defy the contracts by demanding more power than that stated in the contract. This excessive power is revealed as a located load of that area (un- contracted demand). This case has been carried out for various demand condition such as 10%, 20% and 30% which is depicted in Table 6 and Table 7. In all the load disturbances cases, ANFIS gains a good performance measures. The intention of this scenario is to test the effectiveness of the proposed controller against the uncertainties and sudden large load disturbances in the presence of GRC and backlash. Figure 9 and Figure 10 show the 10% rise in demand (presented in Table 4 and Table 5) of discos in all the three areas. The characteristics thus derived demonstrate that ANFIS is being a best one to provide the steady state deviations with minimum overhooot, undershoot and also it settles quickly compared to other controllers.
Table 6. Tie line power deviation for load change.
Table 7. Frequency deviation for load change.
Figure 9. Frequency deviation for scenario 3.
Figure 10. Tie line power deviation for scenario 3.
The Deviation in tie line power flows for these possible contracts are presented in Table 4. The results thus obtained through simulation depicts that the proposed ANFIS controller holds good performance as compared to RCGA, HCPSO and ANN controllers for all possible contracts and for wide range of load disturbances.
5. Conclusion
Adaptive Neuro Fuzzy approach is employed to AGC problem in deregulated power system. The proposed controller proves its capability in organizing the different areas of deregulated power system in the presence of non- linearites. This controller achieves reliability over tracking frequency and tie line power deviations for a wide range of load disturbances and system uncertainties. The simulation result carves out its robust performance with reduced overshoot, undershoot and settling time while compared to RCGA, HCPSO and ANN controllers. The Artificial Intelligence has bench marked its effectiveness in Automatic Generation Control and it is best suitable for real time power system to get online coordination for the deregulated environment.
Cite this paper
Baghya Shree Solaiappan,Nagappan Kamaraj, (2016) Hybrid Neuro Fuzzy Controller for Automatic Generation Control of Multi Area Deregulated Power System. Circuits and Systems,07,292-306. doi: 10.4236/cs.2016.74026
References
- 1. Bevrani, H., Mitani, Y. and Tsuji, K. (2004) Robust Decentralized AGC in a Restructured Power System. Energy Conversion and Management, 45, 2297-2312.
http://dx.doi.org/10.1016/j.enconman.2003.11.018 - 2. Ibrabeem, P.K. and Kothari, D.P. (2005) Recent Philosophies of Automatic Generation Control Strategies in Power Systems. IEEE Transactions on Power Systems, 20, 346-357.
http://dx.doi.org/10.1109/TPWRS.2004.840438 - 3. Elgerd, O.I. (1971) Electric Energy Systems Theory. McGraw-Hill, New York, 315-389.
- 4. Yousef, M.Z., Jain, P.K. and Mohamed, E.A. (2003) A Robust Power System Stabilizer Configuration Using Artificial Neural Network Based on Linear Optimal Control. Canadian Conference Electrical and Computer Engineering, 1, 569-573.
- 5. Bevrani, H., Mitani, Y., Tsuji, K. and Bevrani, H. (2005) Bilateral Based Robust Load Frequency Control. Energy Conversion and Management, 46, 1129-1146.
http://dx.doi.org/10.1016/j.enconman.2004.06.024 - 6. Menniti, D., Pinnarelli, A. and Scordino, N. (2004) Using a FACTS Device Controlled by a Decentralized Control Law to Damp the Transient Frequency Deviation in a Deregulated Electric Power System. Electric Power Systems Research, 72, 289-298.
http://dx.doi.org/10.1016/j.epsr.2004.04.013 - 7. Tan, W. and Xu, Z. (2009) Robust Analysis and Design of Load Frequency Controller for Power Systems. Electric Power Systems Research, 79, 846-853.
http://dx.doi.org/10.1016/j.epsr.2008.11.005 - 8. Shayeghi, H., Shayanfar, H.A. and Jalili, A. (2009) Load Frequency Control Strategies: A State of-the-Art Survey for the Researcher. Energy Conversion and Management, 50, 344-353.
http://dx.doi.org/10.1016/j.enconman.2008.09.014 - 9. Kirchmayer, L.K. (1959) Economic Control of Interconnected Systems. Wiley, New York.
- 10. Bhatt, P., Roy, R. and Ghoshal, S. (2010) Optimized Multi Area AGC Simulation in Restructured Power Systems. International Journal of Electrical Power & Energy Systems, 32, 311-322.
http://dx.doi.org/10.1016/j.ijepes.2009.09.002 - 11. Rakhshani, E. and Sadeh, J. (2010) Practical Viewpoints on Load Frequency Control Problem in a Deregulated Power System. Energy Conversion and Management, 51, 1148-1156.
http://dx.doi.org/10.1016/j.enconman.2009.12.024 - 12. Abraham, R.J., Das, D. and Patra, A. (2011) Load Following in a Bilateral Market with Local Controllers. International Journal of Electrical Power & Energy Systems, 33, 1648-1657.
http://dx.doi.org/10.1016/j.ijepes.2011.06.033 - 13. Tan, W. (2011) Decentralized Load Frequency Controller Analysis and Tuning for Multi-Area Power Systems. Energy Conversion and Management, 52, 2015-2023.
http://dx.doi.org/10.1016/j.enconman.2010.12.011 - 14. Ansarian, M., Shakouri, H., Nazarzadeh, G.J. and Sadeghzadeh, S.M. (2006) A Novel Neuro Optimal Approach for LFC Decentralized Design in Multi-Area Power System. 2006 IEEE International Power and Energy Conference, Putra Jaya, 28-29 November 2006, 167-172.
http://dx.doi.org/10.1109/pecon.2006.346640 - 15. Ram, P. and Jha, A.N. (2010) Automatic Generation Control of Interconnected Hydrothermal System in Deregulated Environment Considering Generation Rate Constraints. 2010 International Conference on Industrial Electronics, Control & Robotics (IECR), Orissa, 27-29 December 2010, 148-159.
http://dx.doi.org/10.1109/IECR.2010.5720143 - 16. Khuntia, S.R. and Panda, S. (2010) Comparative Study of Different Controllers for Automatic Generation Control of an Interconnected Hydro-Thermal System with Generation Rate Constraints. 2010 International Conference on Industrial Electronics, Control & Robotics (IECR), Orissa, 27-29 December 2010, 243-246.
http://dx.doi.org/10.1109/iecr.2010.5720151 - 17. Tan, W. (2010) Unified Tuning of PID Load Frequency Controller for Power Systems via IMC. IEEE Transactions on Power Systems, 25, 341-350.
http://dx.doi.org/10.1109/TPWRS.2009.2036463 - 18. Ghoshal, S.P. and Goswami, S.K. (2003) Application of GA Based Optimal Integral Gains in Fuzzy Based Active Power-Frequency Control of Non-Reheat and Reheat Thermal Generating Systems. Electric Power Systems Research, 67, 79-88.
http://dx.doi.org/10.1016/S0378-7796(03)00087-7 - 19. Tan, W. (2009) Tuning of PID Load Frequency Controller for Power Systems. Energy Conversion and Management, 50, 1465-1472.
http://dx.doi.org/10.1016/j.enconman.2009.02.024 - 20. Gomez, A.F., Delgado, M. and Vila, M.A. (1999) About the Use of Fuzzy Clustering Techniques for Fuzzy Model Identification. Fuzzy Sets and Systems, 106, 179-188.
http://dx.doi.org/10.1016/S0165-0114(97)00276-5 - 21. Shayeghi, H., Shayanfar, H.A. and Jalili, A. (2006) Multi-Stage Fuzzy PID Power System Automatic Generation Controller in Deregulated Environments. Energy Conversion and Management, 47, 2829-2845.
http://dx.doi.org/10.1016/j.enconman.2006.03.031 - 22. Shayeghi, H. and Shayanfar, H.A. (2006) Decentralized Robust AGC Based on Structured Singular Values. Journal of Electrical Engineering, 57, 305-317.
- 23. Demiroren, A. and Zeynelgil, H.L. (2007) GA Application to Optimization of AGC in Three Area Power System after Deregulation. International Journal of Electrical Power & Energy Systems, 29, 230-240.
http://dx.doi.org/10.1016/j.ijepes.2006.07.005 - 24. Wu, Q.H., Hogg, B.W. and Irwin, G.W. (1992) A Neural Network Regulator for Turbo Generator. IEEE Transactions on Neural Networks, 3, 95-100.
http://dx.doi.org/10.1109/72.105421 - 25. Beaufays, F., Magid, Y.A. and Widrow, B. (1994) Application of Neural Network to Load Frequency Control in Power System. IEEE Transactions on Neural Networks, 7, 183-194.
http://dx.doi.org/10.1016/0893-6080(94)90067-1 - 26. Chaturvedi, D.K., Satsangi, P.S. and Kalra, P.K. (1999) Load Frequency Control: A Generalized Neural Network Approach. International Journal of Electrical Power & Energy Systems, 21, 405-415.
http://dx.doi.org/10.1016/S0142-0615(99)00010-1 - 27. Zeynelgil, H.L., Demiroren, A. and Sengor, N.S. (2002) The Application of ANN Technique to Automatic Generation Control for Multi-Area Power System. International Journal of Electrical Power & Energy Systems, 24, 345-354.
http://dx.doi.org/10.1016/S0142-0615(01)00049-7 - 28. Hosseini, S.H. and Etemadi, A.H. (2008) Adaptive Neuro-Fuzzy Inference System Based Automatic Generation Control. Electric Power Systems Research, 78, 1230-1239.
http://dx.doi.org/10.1016/j.epsr.2007.10.007 - 29. Rao, C.S. (2010) Adaptive Neuro-Fuzzy Based Inference System for Load Frequency Control of Hydrothermal System under Deregulated Environment. International Journal of Engineering Science and Technology, 2, 6954-6962.
- 30. Rojas, I., Bernier, J.L., Rodriguez-Alvarez, R. and Prieto, Z. (2010) What Are the Main Functional Blocks Involved in the Design of Adaptive Neuro-Fuzzy Inference Systems. Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, 6, 551-556.
http://dx.doi.org/10.1109/ijcnn.2000.859453 - 31. Ramey, D.G. and Skooglund, J.W. (1970) Detailed Hydro Governor Representation for System Stability Studies. IEEE Transactions on Power Apparatus and Systems, PAS-89, 106-112.
http://dx.doi.org/10.1109/TPAS.1970.292676
Nomenclature
i subscript referred to area
F Area frequency
Ptie tie line power flow
PT turbine power
PV governor valve position
PC governor set point
ACE area control error
cpf contract participation factor
gpf generation participation factor
KP subsystem equivalent gain constant
TP subsystem equivalent time constant
TT turbine time constant
TG governor time constant
R droop characteristic
B frequency bias
FD Frequency Deviation
Tij tieline synchronizing coefficient between areas i&j
Pd area load disturbance
PLji contracted demand of DISCO j in area i
PULji un-contracted demand of DISCO j in area i
PM,ji power generation of GENCO j in area i
PLoc total local demand


GRC Generation Rate Constraint
DPM Disco Participation Matrix
NOTES
1In the Figure 1 G1, G2, G3 represents the Gencos in the control area and D1, D2 represents their corresponding Discos.




















