ABSTRACT

Whereas the human body requires a vast numbers of atoms to maintain its intricate anatomical functions, we assert that the human brain requires “something extra” to carry out its higher mental and emotional functions. Recently, neuroscientists are beginning to suspect brain cells are not fast enough, or intricate enough, to correlate complex spatiotemporal information into cognitive understanding. They conclude that spacetime fields may be necessary to assist the brain during neurological processing―in much the same way magnetic and electric fields are essential for the propagation of light. This “something extra,” we argue, is spacetime itself―where structures in the brain, called facilitators (somewhat like Descartes pineal gland), have evolved biologically in such a way, so as to be able to store and retrieve spacetime quanta for the formation and generation of consciousness and memory. In this way, cognition is not a thing complete. Rather it is emergent, and accumulates as discretized spacetime quanta in the brain so rapidly, we perceive our own awareness to be continuous, events spontaneous. In this paper, we consider spacetime to be a field (like all quantum fields), which can be excited into quanta particles called gravitons. We then apply this quanta excitation to help explain the brain’s cognitive processes. If the brain has indeed evolved to interact with discretized spacetime, then with the advent of improved functional imaging equipment, we might be able to map detailed correlations between neural processes, conscious experience and spacetime. In so doing, it might be possible to learn more about the fundamental workings of spacetime itself.

Keywords:

Neuroscience, Consciousness, Memory, Brain Communication, Spacetime, Spacetime Quanta, Gravitons, Time, Quanta, General Relativity, Relativized Quantum Physics (RQP)

1. Introduction

How does the brain access, store and processes memory? And where inside the mind does consciousness and self-awareness derive its source? Instead of trying to answer these and other types of cognitive questions by mapping data collected from functional MRI, electroencephalography and magnetoencephalography, into the larger topographies of the brain [1] [2] ―we take a more fundamental approach. We begin with the assumption that cognition, in its fullest sense―that of perception, comprehension, remembering, awareness, and much more―is made up of discretized spacetime elements that are created during brain interaction with spacetime. For this to occur, we propose that specialized structures in the brain, called facilitators, have evolved over millions of years to perform their own unique and complex functions, which have the unique ability to excite the spacetime field into energetic, n-valued quanta for the purposes of creating various aspects of cognition [3] . This quanta is purely gravitational in nature [4] ; not an electromagnetic phenomenon.

According to their unique adaptation, facilitators (for instance in the brain’s frontal lobe) perform a secondary function to gather and assemble the n-valued quanta into various spacetime patterns necessary for the higher mental proce- sses―to include memory, consciousness, personality, abstract reasoning, and much more [5] [6] [7] . Facilitators not only generate and organize spacetime quanta, they rapidly communicate amongst all other facilitators in the brain [8] [9] [10] [11] . In this way, one might think of cognition as a kind of dynamic mist filling the interstices of our particulate brain. The function of the brain is to bring into existence consciousness and memory by forming the mist into unique mental spacetime structures, and to provide maintenance to the higher mental functions by either adding new quanta elements to the mind, or removing and rearranging old spacetime elements―in so doing, bringing greater complexity to the human mind for the purposes of retrieving memories, or expressing feelings and ideas…all that comprises the entirety of each human soul¹. This is why we experience self-awareness―know only our self, and not the consciousness of another―be it human, animal or machine―although some quantum tunneling may occur from this cognitive mist (demarcated by our cranium) into the larger spacetime.

2. The Journey

To vividly understand what is being presented here, let’s take an imaginary journey into the human brain―a mental and emotive organ that runs on about 12 watts of power―a fifth of the wattage required to light up a standard 60 watt light bulb [12] [13] . During our voyage, let’s say we are gifted with scientific prowess and the extraordinary ability to shrink down to the size of an atom, and even smaller. Moreover we are able to do so without any loss of our cognitive abilities. Let such diminishment increase the sensitivity of our eyes to all frequency ranges of electromagnetic radiation―sensitive enough to distinguish between single photons of light.

Off we go shrinking into the human brain―the most complex object in the known universe―an intricate network of specialized cells called neurons that process and transmit information through electrical and chemical signals―and possibly through photons. Together, with their supportive glial cells, they form the bulk of our sinuous brain [14] [15] [16] [17] [18] . The tinier we diminish, the more the brain appears to magnify. Down we shrink inside the brain to the size of an atom. Correspondingly, the brain expands outwardly until it appears to be a collection of molecules and then individual atoms; each bobbing gently within the dark spaces of the mind.

Like bees swarming around their atomic hive, electrons jump probabilities during emission and absorption of various quanta of color. Mesmerized by the blizzard of light-fantasia, and hoping to discover the secrets of the mind, onward we glide closer toward the myriad of scintillations. But we have made the mistake of trying to perceive the origin of consciousness in the same way early astronomers tried to understand the workings of the universe―by observing luminous moons, planets, and light-giving-stars, and not on the more influential and large-scale gravitational darkness of spacetime. No wonder it has taken us so long to discover dark matter and dark energy―and still we know not what they are. Nor for that matter, the constituent parts and basis for contemplation. Could it be their emergent property is one in the same?

Meandering about sparking brain atoms, we search for the formative answers to consciousness. But nothing here seems to provide solutions to those cognitive mysteries we are seeking. And so deeper we delve into the unknown nebula. The smaller we shrink, the greater brain atoms separate, until they are further apart from us, than Earth is to the Sun.

All has grown murky quiet. We have entered a lonely dark microcosm; a silent sea without reference―except for the internal one each of us carries our whole life through. What was once a solid, sinuous, three-pound-brain, has become hollow dark space―a four-dimensional opaque ocean made of nothing-shadows. Only the glimmer of distant brain-atoms tells us something else exists here―other than: “I think therefore I am.” For the longest while we stare out into the enormity of an empty brain; a dark place where time is counted only by our tiny nervous heartbeats.

“What does it all mean?” We ask, to no one there. “And how do shadows create colorful dreams, speak the language of culture, conceive of mathematics and physics, evoke song and dance, and choose amongst countless alternatives, when all the brain is but nothing emptiness?”

We are like the sea captain lost amongst a vast, dark ocean at night. With sails slack, the crew is on the verge of mutiny. Seeking eternal answers, the captain looks up into the nighttide sky for guiding reassurance.

“There!” Shouts the captain, pointing between parting storm clouds. Above, the north star Polaris appears. At the same moment a brisk breeze makes full the sails. The crew cheers in jubilation. All hope is restored as they sail toward their port-of-call.

But we are not upon some vast, dark Earthly sea, instead we are lost within the darkness of the mind. We feel afraid and lonely. All hope and faith dissipates. “It means naught,” we whisper to our self; we are defeated. It is at that last instance of losing our mind, we glimpse something meaningful and encouraging―not a guiding star, but the recognition of the interconnectedness between spacetime and the corporeal brain.

“Could it be…,” we muse, “that the brain is interdependent with spacetime―a mutual necessity to generate consciousness and freewill? Just as much as spacetime mutually depends on the physical mind to do the same? Yes” we whisper with joyful certainty.

3. Cognition

Before we proceed with developing a mathematical framework capable of generating n-valued quanta―necessary to build-up higher cognitive processes in the spacetime brain, it is essential to first establish a physical theory for the mind; one in which our calculations will have real, substantiated meaning. This of course will be of no easy undertaking, simply because our personal and cultural beliefs will tend to misguide us away from establishing a legitimate basis of query; or from asking meaningful questions [19] [20] [21] [22] . This is particularly true when the subject and ideas are so completely foreign to anything we know, or have previously experienced, and so we inevitably fall back upon our childhood teachings―and often do so unknowingly.

In such unfamiliar situations even well-trained scientists and educated scholars bring unintended prejudices into the scientific mix. This is why it is necessary to first develop a genuine and correct physical frame of reference and theory, before presupposing the mathematics for any phenomena being investigated. Otherwise we will falter and arrive at degenerate conclusions and meaningless equations and numbers. Without a well-thought out physical theory, we will have no assured way of interpreting the data registered on our scientific instruments. Finally, without a basis for interpreting the mind, and its various states of consciousness, all questions will tend to devolve into to existential ones, such as:

“Do I have a soul?” “Where will I go when I die?” “Will I recognize my family when I pass on?”

In sum total, without a methodology to correct our prejudicial thoughts and conclusions, we will be left in a deep state of conflict between our personal beliefs―with its forever truths, and that of science―with its facts forever changing as evidence requires [23] [24] [25] [26] .

Where does this leave us at developing a theory for consciousness and the higher mental processes [27] ? It seems prudent to begin with someone who has scientifically studied cognition―yet maintains a poetic vision of our existence. Someone to best put into words the paradoxical mysteries that bridge the miracle of consciousness with the hard data accumulated during measurements of the brain and its cognitive processes. Someone like neuroscientist David Eagleman, who during an interview published in Scientific American, stated [28] :

“Consider that whole beautiful world around you, with all its colors and sounds and smells and textures. Your brain is not directly experiencing any of that. Instead, your brain is locked in a vault of silence and darkness inside your skull. All it ever experiences are electrochemical signals coursing around through its massive jungle of neurons. Those signals are all it has to work with and nothing more. From these signals it extracts patterns, assigns meaning to them, and creates your subjective experience of the outside world. Your reality is running entirely in a dark theater. Our conscious experience of the outside world is one of the great mysteries of neuroscience: not only do we not have a theory to explain how private subjective experiences emerge from a network of cells, we currently aren’t even certain what such a theory would look like.”

In closing this section, to be clear―we are not saying existential questions are void of merit. Nor are we asserting the soul does, or does-not, exist. On-the- other-hand, neither are we accepting any theological or philosophical teachings that avow science will always be incapable of comprehending the sublime-mind. What we are suggesting is:

If ever we are to comprehend the underlying processes generating our phenomenal experiences, or those processes associated with becoming aware―we are aware; or the workings of the mind-brain that makes it possible for us to suddenly realize our mortality―and in that instant a kind of unreality pervades our thinking, causing us to reach out for deeper meaning… Then, it is essential to first determine, not only a theoretical approach to the mind-brain, but a physically based one as well. In this way, and only in this way, may we incrementally gain insight into the workings of cognition. Only then may we legitimately propose existential questions that are free of the tainting of our own prejudgments―the kind of questions that have meaning in regards to the world we emerged into at birth―one seemingly not of our own choosing or design. Only in a physically based theory will we have hope of gradually being able to answer those existential questions, as to whether the human soul is eternal or ephemeral.

4. Bridging Philosophy into Science

In some sense, the science of neurology began with the father of modern philosophy, René Descartes (1596-1650)―when he asserted the pineal gland (located near the middle of the brain) is where thoughts are formed, and also where the soul is most closely linked to the body [29] . Surprisingly, medical writings on this pinecone-shaped-gland have existed for more than 2000 years―e.g. the Greek physician Herophilus [30] . Of all the various philosophies concerning the mind and body, it was the advent of Descartes’ philosophy that initiated a modern interpretation of the mind and brain. As Valeriy Sbitnev writes [31] :

“Descartes was the first to bind the mind with consciousness and self- awareness and distinguished this from the brain, which houses intelligence. The main assumption was that consciousness, like a non-material ephemeral cloud, is outside the brain and is detected by a special organ called the pineal gland.”

Even today, Cartesian dualism between mind and body continues to inspire: philosophers; neurologists; physicists; psychologists; theologians and others [32] [33] . Each struggles with their own unique way of answering how an immaterial mind can have causal effects on a physical brain, and how a corporeal brain can affect an unlocatable, impalpable mind―except as Descartes proposed, through some vague interaction of the mind with the brain’s physical pineal gland [34] .

In this paper we intend to continue with Descartes’ mind-body philosophy. However, instead of arguing for an immaterial mind, we will argue the case that the mind is not some other worldly composition as first suspected by Plato (from the world of Forms), and Descartes’ mind-body, but rather comprised of discretized spacetime―a kind of non-substance, or at least an in-between substance, that actually exists in its own unique way, and which can be measured both scientifically and cognitively.

5. Developing Cognitive Science

During the nineteenth century great advances were being made in the neurological sciences by such notable individuals as: Paul Broca (1824-1880)―who investigated the frontal lobes of the brain; Ivan Pavlov (1849-1936)―who studied involuntary reflex action; and neurophysiologist and Nobel Laurate Sir Charles Sherrington (1857-1952)―who wrote extensively on the brain and central nervous system―(“The integrative action of the nervous system”) [35] [36] . Sherrington’s remarkable insight was to step back from the details of neurology and present a “grand panorama of nervous systems….” [37] . In his book, “Man on his Nature,” he refers to the “enchanted loom” as a figurative description of the brain at work―which appears as one of the more eloquent and beautiful passages on the workings of the physical mind [38] [39] :

“…enchanted loom where millions of flashing shuttles weave a dissolving pattern, always a meaningful pattern, though never an abiding one. Its commanding presence orders sensation, movement, thought, a lifetime of memory and dream.”

Moving forward through history―many new inroads (and roadblocks) were made into the mind-body problem. Even so, everyone remained perplexed as to how those attributes we associate with the mind, functioned in relationship to the brain. A restricted example of this is expressed by Emanuel Diamant [40] :

“However, despite extended and extensive research efforts, which encompass many exploration fields, the underlying fundamentals and operational principles of visual information processing in human brain remain unknown. We still are unable to figure out where and how along the path from eyes to the cortex the sensory input perceived by the retina is converted into a meaningful object representation, which can be consciously manipulated by the brain. Studying the vast literature considering the various aspects of brain information processing, I was surprised to learn that the respected scholarly discussion is totally indifferent to the basic keynote question: ‘What is information?’ in general or ‘What is visual information?’ in particular.”

Almost concurrently, through the application of science we begin to get glimpses into solving the mind-body problem. As theoretical physicist Giuseppe Vitiello writes in his own vital way [41] :

“This vivid physical picture of the brain mesoscopic activity was confirming to me what Hiroomi Umezawa, one of the fathers of modern quantum field theory, was meaning by saying that [42] : ‘In any material in condensed matter physics any particular information is carried by certain ordered pattern maintained by certain long range correlation mediated by massless quanta. It looked to me that this is the only way to memorize some information; memory is a printed pattern of order supported by long range correlations.’ The key words here are ‘widespread cooperation’ supporting ‘patterned synchronized oscillations’ and ‘ordered pattern’ maintained by certain long range correlation…. The interesting point in Umezawa’s many-body model for the brain is that two main ingredients appear there together: the notion of ‘field’ introduced by Lashley in his puzzling dilemma and the notion of ‘coherence’, intrinsic to the laser theory inspiring Pribram view. Both these notions are basic ones in the QFT (quantum field theory) dynamics generating ordered patterns, but not in neuroscience, and in general in biology and biochemistry, where the atomistic view of assembling little pieces together has been prevailing on the search of the microscopic dynamical laws ruling their cooperative behavior so that the mesoscopic and macroscopic functioning of the system could emerge. One must have the courage of a Lashley and of a Pribram to dare to introduce the field concept and the wave notion of coherence. This is why, when listening Walter Freeman talking of dynamical widespread cooperation supporting patterned synchronized oscillations, it was clear to me that he is one of those few people who dare to open new paths in the forest.”

Many of the boldfaced ideas above, are not only fundamental to quantum field theory, they will serve to guide us toward a spacetime quanta approach in solving some of the mind-body problems.

Five years later, and sharing a similar sentiment as Giuseppe Vitiello, Stuart R. Hameroff, Travis J. A. Craddock and Jack A. Tuszynski, expressed [43] :

“However no specific brain area houses consciousness; neural activity in a given area may be non-conscious at one moment, and correspond with consciousness at another. What causes the transition? …Another shortcoming of conventional approaches is that neurons and synapses are considered as simple switches, whereas real biological cells are far more complex. For example single cell organisms such as Paramecium swim, avoid obstacles and predators, learn, find food and mate, all without possessing a single synapse. …Inspired by the application of quantum theoretical methods to the study of the brain and other biological structures scientists began to investigate brain functioning from the microscopic level of quantum physics. Perhaps the first attempt to describe the brain using the terminology of quantum physics was made by Ricciardi & Umezawa (1967) [44] .”

Probably the most prominent physicist to apply quantum physics to consciousness, is Sir Roger Penrose. Along with anesthesiologist Stuart Hameroff, they developed a quantum mechanical model for the mind-brain, wherein consciousness was argued to reside within tiny structures in the brain called microtubules [45] ―the nanometer range of manufacturing awareness, which they referred to as “Orchestrated Objective Reduction Theory” (OR). Sometime thereafter, Penrose attempted to extend OR into quantum gravity―and did so knowing full well that quantum gravity was inherently problematic and incomplete―as they themselves confirm in their own words [46] :

“Current ideas of quantum gravity normally refer, instead, to some sort of physical scheme that is to be formulated within the bounds of standard quantum field theory―although no particular such theory, among the multitude that has so far been put forward, has gained anything approaching universal acceptance, nor has any of them found a fully consistent, satisfactory formulation.”

One of the most confounding problems for quantum physics, let alone its inclusion of gravity, is the notion of “time” (not to mention the unphysical infinities that pop up during quantum physics calculations) [47] - [52] . The reason for temporal confusion is that relativistic time―called proper time, is tangled with space, to form spacetime. More than that, relativistic time as been verified experimentally for near a century. So there is little doubt that relativistic time is the correct interpretation of time, and not the classical time or operator time of quantum physics [53] . This fact alone, should have told us to formulate a cognitive quanta theory―not from quantum physics, but from the only other fundamental theory remaining―that of general relativity. At most, quantum physics should be limited to a subset of general relativity―just as Newtonian gravity is. And not the other-way-around, as so many prominent physicists believe [54] [55] . This misdirected attitude is reflected in the writings of one of the most important physicists―a gentlemen-scholar and Nobel Laurate, Steven Weinberg [56] :

“…quantum field theory has become the most widely accepted conceptual and mathematical framework for attacks on the fundamental problems of physics. If something like a set of ultimate laws of nature were to be discovered in the next few years (an eventuality by no means expected), these laws would probably have to be expressed in the language of quantum field theory.”

Because Weinberg is one of the founding contributors to the Standard Model of Particle physics, and that this theory is commonly held to be the only one providing insight into the fundamental structure of matter, as-well-as to three of the four fundamental forces, few dare to challenge it. There is an almost unshakeable faith in the Standard Model, even though it cannot answer many disconcerting questions. For example it omits the fundamental force of gravity; does not explain dark matter or dark energy― which comprises most of the universe; It cannot explain what happened to antimatter in the universe after the Big Bang; It does not fully explain the origin of mass or neutrino oscillations.

For these and other shortcoming reasons, and that we are proposing a spacetime quanta approach to consciousness, and that Einstein has a way of becoming right―including with his greatest blunder, the cosmological constant―which currently is opening up new scientific vistas, we now turn away from the Standard Model, and toward the theory general relativity to help provide understanding into consciousness in relationship to the brain [57] .

6. Evolution and the Mind-Brain

Because physics alone cannot address the more complex biological functions so readily, and that our theory hypothesizes specialized structures in the brain, which have evolved to facilitate quanta through excitation of the spacetime field, to which these structures then gather the quanta in the formation and maintenance of the mind, we necessarily adjoin the biological theory of Darwinian evolution to our general relativistic quanta approach (RQP). However, since all things that manifest in nature have an underlying reality, and that the founding theory we will be applying in this paper is that of general relativity, we assume the impetus behind evolution itself, arises from the microscopic properties of spacetime. Though it is not the objective of this paper to thoroughly develop this idea, nevertheless we offer the briefest of explanations for the adaptive force behind the theory evolution―which turns out to be elementally the same as that giving rise to consciousness [58] .

In terms of largescale evolution and consciousness Noble Laurate and neurophysiologists, Sir John Carew Eccles [59] writes:

“In Darwinian evolution, consciousness would have occurred initially some 200 million years ago in relation to the primitive cerebral cortices of evolving mammals. It would give global experiences of a surrounding world for guiding behavior beyond what is given by the unconscious operation of sensory cortical areas per se. So conscious experiences would give mammals evolutionary advantage over the reptiles, which lack a neocortex giving consciousness.”

In this regard, let us imagine planet Earth long before life had appeared on land or sea; long before oxygen-blue-filled-skies existed overhead. At this time chemical structures floated and bobbed about ancient white-wave-crested seas. An era of immense storms that terrorized the oceans with gigantic swells and bolts of lightning thundering down into the mighty lifeless, but chemically charged waters. Far below in the calm murkiness something profoundly original was about to occur, either by chance, or from some complex casual reason. One of these chemical structures was altered ever so slightly. This was no ordinary chemical change, nor one yet of Darwinian adaptation. For the first time on Earth, this sea bearing molecule had, in some way, been altered in a unique way―to excite the tiniest foundations of spacetime itself. The result, creation of spacetime quanta energy.

Inadvertently, this was to provide the chemical structure with an energetic advantage to all other atoms and chemical structures in this vast sea. And as we now know, energy is everything when it comes to causing change. Unwittingly with this energetic advantage, this first chemical structure could rearrange itself into evermore complex chemical structures, to split off as a kind of chemical birth. There it is, the first structural components that would eventually lead to consciousness and life, and kind of “willtron;” a package of impetus for Darwinian evolution.

Over the eons these chemical structures developed new methods of interacting with spacetime to produce an ever more abundance of spacetime quanta. Chemical structures that did not undergo this type of adaptive change, remained as brine―it may be, but maybe not necessarily so, that organic compounds are the most conducive kind at producing spacetime quanta―the process from which all forms of consciousness and life eventually emerge; or it might have been the first chemical structure to do so, was organic.

As eons withered away, and new ones sprung up, during this forever expanse, such chemical structures had long since evolved into very efficient facilitators―ones located throughout the brain. It was the time of the human and these specialized brain facilitators had evolved―linked to a central nervous system [60] . Overall, these specialized structures in the brain, together with the central nervous system, function synergistically in several ways:

a) To convert information received through the five senses, and carried along via the central nervous system, to the facilitators;

b) Facilitators then code this information into vibrations (like an old-time recording needle into vinyl) for the purposes of exciting spacetime field (permeating throughout the physical brain);

c) As with all quanta fields, upon being excited, the spacetime field also produces quanta, but in the form of n-valued excited gravitons;

d) The other function of these various brain facilitators is to gather and arrange n-valued quanta―gravitons, for the maintenance and development of mind, so the body can react to the changing conditions occurring in the external world relative to the body-mind;

e) Since the mind is functionally non-linear (as is the theory of general relativity we apply here), it can also react physically to its own internal contemplations.

f) Because the mind-body is comprised of organized discretized bits of spacetime―which is linked directly to its own spacetime field―then the vast cognitive processes required for reasoning, memory and consciousness, are able to be accomplished at unimaginable rapidity. This could not happen if only neuron junctions, brain matter or atoms were involved; the processes would simply be to slow.

g) Collectively, the components of brain, with their: specialized facilitators, central nervous system with its five senses, and their association with a discretized spacetime constructed mind, synergistically create consciousness, store and retrieve a lifetime of memories, and give us free will―we are not just input response as are computers.

Now that we have a physical-spacetime basis for cognition, we may begin to address those existential implications: For example, we may address the eternal question of what happens when we die? From our physical theory we can now say―when we die, so too does the brain’s link to our conscious mind. Lights out! Yet…who’s to say whether or not our discretized, spacetime-consciousness may, or may not, wander out of the brain into the celestial heavens, whereupon it might link to other conscious states; furthermore, to witness such heavenly wonders―or not. For now, I prefer a good night sleep.

7. Edging toward the Specifics

As we have already indicated, it will be with a gravitational spacetime quanta (RQP) that we will attempt to unlock some of the founding mysteries associated with the mind-body problem. To formulate such a gravitational approach would be an impossible undertaking―had it not been for the efforts of physicist Markus Fierz and Nobel Laurate Wolfgang Pauli. Together, they laid the ground work for what has become known as, massive gravity. They initiated their work on a quantum gravity as far back as 1939 [61] [62] [63] [64] . Though there were problems with such an approach [65] [66] , and they could not complete their intended work, thereafter a number of prominent researchers worked hard to resolve these concerns [67] - [74] . The two main problems with such an approach is: the physical interpretation of time, and those nonphysical infinities that annoyingly flare-up during perturbative calculations. As Nobel Laurate Gerard ‘t Hooft elucidates [75] :

“Perturbation expansions with respect to small coupling constants are often looked upon as ugly but necessary tools, and repeatedly physicists attempt to avoid them altogether.” ‘t Hooft then goes on to say, however “…Many of our cherished particle theories can only be defined perturbatively.”

From our point of view, this adherence to perturbations is the main reason why quantum gravity has failed to date. It starts off by creating its own infinities, ends up with infinities, and then everyone looks agog asking each other every time, “What are we doing wrong, o’l chap?” As Maud Jaccard, et al, states in regards to perturbative massive gravity [76] :

“…in general the solutions of the truncated theory are spurious and do not converge to solutions of the full non-local theory as the order of the expansion N → ∞.”

In gravitational agreement, Thanu Padmanabhan concludes [52] :

“The Lagrangian describing classical gravity, treated as a function of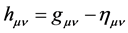, is not perturbatively renormalizable; in fact, there does not exist any simple redefinition of the field variables which will lead to a perturbatively renormalizable theory. So the most straight forward approach, based on the belief that nature will continue to be kind to us, is blocked. The miracle fails.”

To avoid such unmanageable series expansions, our assumption is to instead build a spacetime metric 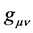describing the interaction of microscopic spacetime with vacuum energy―each mutually affecting the other. This is more than a hypothetical approach. Its idea is based on first principle―on the foundational principle of general relativity: matter-energy dynamically affects spacetime, and the dynamics of spacetime affect matter energy. From this idea, we will argue―not only is it unnecessary to expand the spacetime metric 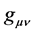for weak gravitational fields, as is always done, it is not physically real. No longer will we perturbate the associated Lagrangian―meaning the Lagrangian representing microscopic spacetime, will now have a fixed number of terms, and that the metric will have only one term. More importantly this will lead to an exact finite termed solution to Einstein’s general relativistic wave equation―free of those annoying infinities, and one that naturally and remarkably exhibits the essential spacetime quanta needed to begin to solve the mind-body problem.

As a side note: In general relativity the spacetime metric 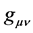is everything. All the mathematical structures of general relativity are built upon the spacetime metric―the cornerstone to describing, not only the mathematical dynamics of spacetime, but the emergence of discretized consciousness. For instance the Christoffel symbols 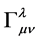are built upon the metric:

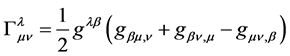; and it are these Christoffel symbols which in turn form the Riemann Curvature tensor:

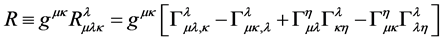
In this way the entire general relativistic wave equation is constructed entirely from tensor metric:

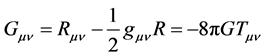(1)

where 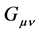is the Einstein Tensor expressing the spacetime curvature in General Relativity, and 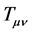is the energy momentum Tensor. G is the gravitational constant.

Once we have constructed the metric from strong physical principles in microscopic spacetime and firm mathematics, we are then free to act upon this tensor structure with the general relativistic wave equation to produce an energy momentum tensor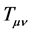. What we discovered by via general relativistic calculations (which was not presupposed, but which manifested free of any preconceived ideas of what the energy momentum tensor should turn out to be)―is that the resulting energy momentum tensor expressed a quantum description of spacetime. That is to say, the spacetime field showed it was capable of being excited into n-valued energetic states―exhibited by all quanta fields. Hence quanta gravity was expressed naturally through the covariant, general relativistic equations―relevant to any coordinate frame. In literature, the spacetime quanta particles are referred to as gravitons. What this implies, is that the spacetime field behaves like a quantum field (one in which evolution is simply the impetus to seek energetic advantages―via the production spacetime quanta). This same process eventually led to the emergence of consciousness―an interplay of facilitators forming discretized spacetime within the interstices of the material brain―analogous to bees constructing a hexagonal honeycomb.

Upon constructing the spacetime metric in microscopic spacetime, through a straight-forward general relativistic calculation, we will compute for the energy momentum tensor. At that point we will be able to check if such a spacetime approach to spacetime, is valid both mathematically and physically. If so, then we have a contender for a physical theory, which we may then apply toward a theory for consciousness.

The question that arises, is there such a method of validating the energy- momentum tensor and so metric. The answer is yes―and it relies on the principle of conservation of energy―to which all of founding physics ultimately relies. In mathematical terms, we must show the general relativistic wave equation, based on our constructed spacetime metric, is divergenceless:

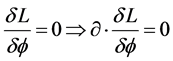(2)

Here, L represents the Lagrangian for gravity interacting with any chosen massless elementary particles. The expression on the left indicates a variation on the Lagrangian with respect to the particle field ϕ. Variation ultimately produces the wave equation, from which much important physical information is subsequently be determined. The mathematical expression on the right, represents the divergence of the wave equations (calculated from the left expression). This equation is equivalent to taking the divergence on the energy momentum tensor, which turns out to be particle interaction terms with gravity.

Our approach then, is to consider the microscopic level of spacetime―and show it is there that n-valued gravitons, can and do arise from the spacetime field. And it is this spacetime quanta we will apply to building a theory for the conscious mind. This will be the first step in solving the mind-body problem proposed by Descartes [77] .

In the next few sections we provide the necessary details in developing a general relativistic approach that produces n-valued spacetime quanta through the development of the spacetime metric. We refer to this approach as: Relativized Quantum Physics (RQP).

8. Spacetime Metric Considerations

In this section we construct the spacetime metric. Historically, there are several possible starting points. The one most commonly applied for weak gravitational fields (flat spacetime) by Einstein [78] [79] , and by quantum gravity physicist [73] [80] [81] , is to linearly expand the spacetime metric 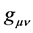as follows:

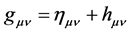(3)

where is the Minkowski metric for flat spacetime, and represents the graviton particle field. Such a metric expansion was known to Einstein for weak gravitational fields―linearized gravity, but not in a way leading to quantum field theory. Also where represents the graviton particle field―which would come later in the 1930’s with interpretations and development by Wolfgang Pauli and Markus Fierz [67] . In 1952 Suraj Gupta writes a seminal paper in this direction, to the Proceedings of the Physical Society:

“The quantization of the complete gravitational field is carried out by extending the work of an earlier paper. The main obstacles in the quantization of Einstein’s field are overcome by expressing the field quantities in the Riemannian space as expansions in the flat space, and then splitting the gravitational field into the linear and the non-linear parts. The linear part of the gravitational field is regarded as the free gravitational field, while the non-linearity is treated as a direct interaction between the gravitons. This treatment is quite general, but it suffers from the usual limitations of the perturbation method.” [82]

Following the work of Gupta, sometime in the 1960’s, Richard Feynman took up this longstanding approach, to try and develop a form of quantum gravity compatible with general relativity. Feynman began with the gravitational free- field―meaning gravity is only interacting with itself, and not with any other particle. He then formed all possible combinations of the graviton particle h_μν interacting with itself, forming an infinite expansion of higher ordered terms. However, since this is the condition for a weak gravitational field, he legitimately dropped all higher ordered terms above third order. Even so, he was left with too many terms to generate general relativity from a particle field approach. To solve the problem―as to which terms represented nature, and which did not―Feynman applied an analogous methodology, as to that which James Clerk Maxwell applied for the electromagnetic fields equations, leading to the discover the composition of light [83] . Specifically, what Feynman did was to construct a Lagrangian for pure gravity, by writing out all possible terms up to second and third order, to which he required the following condition holds:

(4)

By solving this equation, Feynman was able to eliminate the erroneous terms and sift out the correct terms to reproduce Einstein’s geometric gravitational field equation for free fields expanded up to third order [73] , from a graviton particle perspective first envisioned by Fierz and Pauli back in 1939.

Over the next two decades, this approach was further developed to include massless elementary particles interacting with the gravitational field [treating gravity as a spin-2 graviton particle h_μν]. It was John Fang who put this approach into its final and complete form, for both curved and flat spacetime, and also to all orders of the series expansion [84] . Fang’s approach is referred to the consistency formulation, later amended to the Maxwell-Fang Consistency Condition (MFCC) in honor of Maxwell who first conceived of this field approach.

In terms of the consistency formulation for general relativity interacting with any massless particle, Equation (2) (which we adhere to), must satisfy the condition:

(5)

where is the Einstein Tensor and is the energy momentum Tensor. It is this condition we apply to the massless gravitational field interacting with vacuum energy, which subsequently reveals massless gravitons can be excited in a natural and straightforward way, to yield n-valued massive gravitons emerging from the excited microscopic spacetime field.

9. Developing the Spacetime Metric for n-Valued Spacetime Quanta

Let us now consider a volume of spacetime―one that represents the most prevalent shape of universe [85] ―that of flat spacetime described by Minkowski spacetime metric. Let us further consider the tiniest level of microscopic spacetime, where vacuum energy fluctuates chaotically about [86] [87] . By the principle of general relativity, vacuum energy fluctuations will dynamically affect spacetime. Thus we conclude in this tiny region of spacetime, may no longer be represented by the Minkowski metric [88] :

(6)

Following the early lead of quantum fields (e.g. QED [89] [90] ), we assume the gravitational field must undergo periodic oscillations to produce quanta in the form of simple harmonic motion―that is they act like tiny harmonic oscillators in response to the chaotic vacuum fluctuations. Under a general relativistic approach, this spacetime motion must be reflected in the spacetime metric [91] . Let us then construct such a spacetime metric representing microscopic spacetime oscillations.

Because general relativity is a classical theory, we begin construction of the metric with the classical Lagrangian representing a vibrating system of particles about a point of equilibrium. The coordinate solution to the Lagrangian equation has the form of normal coordinates [92] given by:

(7)

Assuming these coordinates quasi-describe graviton oscillations, by the principle of equivalence, let the general relativistic coordinate system experience accelerations expressed by preceding equation. Joining these ideas together allows us to construct a basis for the general relativistic coordinate system, from the aforementioned normal coordinates [93] [94] ; moreover it allows us to compute the modified flat spacetime metric (representing oscillating gravitons):

(8)

We now introduce the natural number “n” as is done to such oscillatory systems (e.g. quantum particle in a box):

(9)

Introduction of this n natural number expression, is reinforced and developed without prejudgment, subsequent to the energy momentum calculation and upon relating the covariant energy momentum tensor to its contravariant form, as discussed below in more detail. For a more complete development of this section refer to [4] .

In general, the previous metric equation can take on various n-values, implying gravitons might vibrate at any rate. However, since much of spacetime is basically flat, we assume the most likely n-value state will have values of either 0 or 1 states. An n-value equal to zero returns spacetime to pure Minkowski, meaning gravitons will attain zero-mass-energy―i.e. at its nodal points. This is required to build a massless theory of gravity. After it is constructed we assume nature allows for higher n-values―implying massive or energetic gravitons. For example, in regions of spacetime near, or even inside a galactic center, n-value will greatly increase. Finally, using Einstein’s summing conventions, our modified Minkowski metric allows to immediately compute the spacetime interval for the oscillating gravitons:

(10)

10. Energy Momentum Tensor for Gravitational Quanta

Let us now calculate our energy momentum tensor from the constructed spacetime metric, by inserting it into Einstein Tensor. After taking numerous derivatives, nevertheless a straightforward calculation, the energy momentum tensor turns out to have only diagonal components that resemble a perfect fluid. Upon closer inspection, the tensor has the form of rotational kinetic energy. Which is what we expect given that we modeled the spacetime metric on oscillating gravitons. The energy momentum tensor was calculated to be:

(11)

With that being said, we can arrange the energy momentum tensor into an oscillating energy from:

(12)

where “” represents a constant matrix, which allows us to write the energy momentum tensor in a generalized rotational or vibrational kinetic energy form. Stepping back and reflecting, it shows that an oscillating spacetime metric results in a vibrational energy momentum tensor. This is as it should be, since by general relativistic principle, spacetime affects matter-energy. Said another way, this result supports our premise about the oscillating nature of microscopic spacetime:

(13)

Before closing this section, we point out the covariant and contravariant energy momentum tensors transformation as:

(14)

This shows these energy momentum tensors―acting on the same point in spacetime, undergo cyclic phasing from real to imaginary energies―and at certain values, becomes zero (nodes). Analogous to standing waves, indicates spacetime can be excited from its fundamental frequency:

(15)

We mention that the covariant and contravariant energy momentum tensors are conserved:

(16)

By the consistency condition this implies our approach is mathematically correct gravitationally [80] [84] , in as much as James Clerk Maxwell analogous approach applied to the electromagnetic equations were shown to be inconsistent, but after Maxwell added a single term to Amperes’ law they became consistent and revealed the composition of light for the first time in human history.

Finally we write out the spacetime quanta energy levels describing elemental units for memory and conscious emergence during brain and spacetime interactions.

(17)

where, , and where is the graviton angular frequency [91] :

(18)

11. Science of Memory

In the year 1922, physicist Leó Szilárd wrote his doctoral thesis on memory, as related the Second Law of Thermodynamics―and in particular on Maxwell’s Demon [95] [96] [97] . Szilárd began with James Clerk Maxwell’s question he had asked some 50 years prior: Can the Second Law be statistically violated?

However, upon showing the second law could be violated statistically, to preserve the fundamental second law, Szilárd proposed something quite remarkable―the idea that entropy and memory were equivalent. Though many, if not most, consider Claude Shannon the originator of information theory [98] , and even though Shannon deserves much credit, a growing number of people consider Szilárd to hold that honor.

Over the next hundred and fifty years, many scientific luminaries tried to answer Maxwell’s question. They include: W. Thomson (Lord Kelvin) [99] ; J. Poincare [100] ; M. Planck [101] ; L. Szilárd [102] [103] ; J. von Neumann [104] ; G. Gamow [105] ; M. Born [106] ; N. Wiener [107] ; D. Bohm [108] ; L. Brillouin [109] ; M. N. Saha [110] ; R. Feynman [111] ; Bell [112] ; K. R. Popper [113] ; C. H. Bennett [114] ; S. W. Hawking [115] ; R. Landauer [116] ; R. Penrose [117] ; W. J. Christensen Jr. [97] [118] and others.

Szilárd approach is really a statistical quanta approach relating memory to the Second Law of Thermodynamics. Moreover, it was Richard Tolman who substantiated entropy with general relativity [119] . Between Szilárd and Tolman, we have a substantive means to affirm our assumption, that spacetime can manifest quanta memory, in association with conscious choice, and that spacetime is thus able to act as a storage substrate in the developmental processes of cognition.

We now define spacetime entropy that we directly associate with quanta memory and consciousness:

(19)

where S_c is the entropy for consciousness; dQ is a small change in heat energy; T is the constant temperature of the system or constant within infinitesimal intervals; T⁰⁰ is the time component of the energy momentum tensor calculated previously and finally dV is the small volume element.

By defining α to be:

(20)

The entropy as related to cognition is given by:

(21)

where V is the volume under consideration, T is the constant temperature of the system, and ΔQ is the amount of heat energy absorbed or emitted by the brain during an amount of cognitive processes.

12. Conclusions

Cogito ergo sum―How is this possible? We have argued the human brain evolved over millions of years, and did so, in such a way, that it gradually learned to exploit these dynamical features of spacetime field that can be excited into quanta called gravitons. If the brain has indeed evolved to interact discretely with spacetime, then with current and future functional imaging equipment (revealing comprehensive correlations between neural processes and the landscapes of conscious experience), it would not only tell us more about the emergence of consciousness, it would also provide a unique tool for the investigation of the elements and processes of microscopic spacetime―its quanta, emergence of fundamental particles.

In closing, the mathematical relationship of memory and consciousness to entropy (contained within the volume of the brain) is given by:

(22)

where the brain is approximated to be of constant temperature, V is the volume of the brain, ΔQ is the amount of heat absorbed or emitted by the brain system, and:

(23)

Spacetime has another essential property for cognition―that of an amazingly quick processing speed, because it is not limited to the bumping of information between neuronal junctions during cognition.

Summing up―Brain matter is not so much a locational repository for memory, nor for our ever-changing conscious states that reside between the interstices of brain matter―as much as it is a composite of various facilitators that interact with microscopic spacetime to produce and maintain our rapidly shifting mind, which interprets through the brain, the external world, the body it resides in, and awareness of its conscious self. Cogito ergo sum.

Acknowledgements

My deepest appreciation goes out to Philip Goodchild [120] , a scholar with a sense of good humor and the dignity to respect another seeking answers to the mystery we have awoken into. To Arianna Vecchio, whose research will lead to great understandings in neuroscience, and helping those who suffer due to no fault of their own [121] .

Cite this paper

Christensen Jr., W.J. (2017) God Is a Porcupine―Brain, Consciousness and Spacetime Physics. Jour- nal of Modern Physics, 8, 1294-1318. https://doi.org/10.4236/jmp.2017.88084

References

NOTES

¹Personal correspondence with Noam Chomsky, who expressed interest in these ideas on memory and consciousness, and awaits to read more.