Received 22 October 2015; accepted 18 January 2016; published 22 January 2016

ABSTRACT

A metallic disk with strong spin orbit interaction is investigated. The finite disk geometry introduces a confining potential. Due to the strong spin-orbit interaction and confining potential the metal disk is described by an effective one-dimensional model with a harmonic potential. The harmonic potential gives rise to classical turning points. As a result, open boundary conditions must be used. We bosonize the model and obtain chiral Bosons for each spin on the edge of the disk. When the filling fraction is reduced to 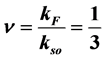the electron-electron interactions are studied by using the Jordan Wigner phase for composite fermions which give rise to a Luttinger liquid. When the metallic disk is in the proximity with a superconductor, a Fractional Topological Insulator is obtained. An experimental realization is proposed. We show that by tunning the chemical potential we control the classical turning points for which a Fractional Topological Insulator is realized.

Keywords:

Spin-Orbit, Chiral Bosons, Chains, Metallic Disk, Topological Insulators

1. Introduction

The presence of the spin-orbit interaction in confined geometries gives rise to a Topological Insulator (T.I.). Following ref. [1] one maps the spin-orbit interaction to a spin dependent magnetic field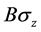. As a result, the non interacting electrons are mapped to two effective Quantum Hall problems, for each species of spin. When the electron density is tuned to an integer Landau filling 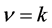(for each spin) the ground state is made up of two decoupled spin species which form an integer Quantum Hall state with opposite chiralities. When k is odd

the system is a TI and when k is even we have a trivial insulator. When 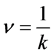the presence of electron-electron interaction for each species of spin gives rise to a Fractional Topological Insulator (F.T.I.).

Using the proposal for the Fractional Quantum Hall, which is built on an array of quantum wires [2] , the authors [3] [4] have shown that by fine tuning the spin orbit interaction for a configuration of coupled chains a Topological Insulator (T.I.) emerges. When the filling factor is such that it corresponds to composite Fermions, a Fractional Topological Insulator (F.T.I.) has been introduced in ref. [3] . It has been shown that for a model of coupled chains in the y direction the spin orbit interaction can be gauged away resulting in twisted boundary conditions for which a F.T.I. was obtained.

The purpose of this paper is to demonstate that a two-dimensional metallic disk with spin-orbit interaction and electron electron interaction gives rise either to a Topological Insulator or Fractional Topological when the disk is in the proximity to a superconductor. We bosonize [5] [6] the model in the limit of strong spin orbit interactions and geometrical confinement. We find that the edge of the disk is equivalent to a one-dimensional model with a harmonic potential. We obtain a chiral Bosonic model [7] and show that a T.I. emerges for the

filling factor.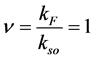

For the filling factor 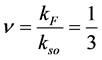we use the composite electrons method [8] [9] and show that the composite Jordan Wigner phase [10] gives rise to an interacting one-dimensional model in the Bosonic form. We obtain a Luttinger liquid with the Luttinger parameter 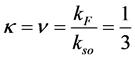which is the proximity to a super- conductor, then we obtain a F.T.I.

An experimental verification is proposed. We show that the F.T.I. is obtained by tunning the chemical potential, the interactions and the radius of the disk.

The plan of the paper is as follows. In Section 2 we present the spin-orbit interactions in metals. In Section 2.1 and 2.2 we review the model introduced in ref. [3] . We find it advantageous to use open boundary conditions and study the model in the framework of Bosonization. In Section 3.1 we introduce our new model. We consider a metallic disk with srong spin orbit interaction and confinement. In Section 3.2 we study the metallic disk with

strong spin orbit interactions and confinement for the filling factor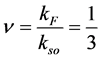. Using the composite Fermion

method we obtain a Luttinger liquid which in the proximity with a superconductor represents a F.T.I. At the end of this section we consider the experimental realization of the model. Section 4 is devoted to conclusions.

2. The Spin Orbit in Two Dimensions in the Presence of a Confining Potential

The Hamiltonian for a two dimensional metal in the presence of a parabolic confining potential is given by:

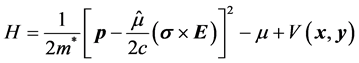(1)

Using the confining potential 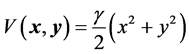we obtain the electric fiel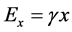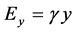d:, and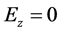. We introduce a fictitious magnetic field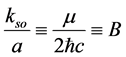. As a result the Hamiltonian in Equation (1) is a function of the spin orbit momentum 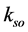and takes the form:

(2)

a is the lattice constant and, are the gauge fields.

2.1. The Emerging Topological Insulator for a Two-Dimensional Model Periodic in the y Direction with the Filling Factor for a System of Coupled Chains

In this section we will review the model introduced in ref. [3] . We find essential to modify the model and use open boundary conditions. This modification is important for avoiding complications caused by the twist introduced by the spin-orbit interaction. The open boundary conditions impose a constraint on the Bosonic fields (the right and left Bosonic field are not independent).

For the remaining part we will bosonize [7] the model given in ref. [3] using the open boundary conditions. We will use open boundary conditions also for the metalic disk (see Sections 3.1-3.2) The methodology for both model will be same, therefore we find it necessary to present the details of the Bosonization method (for open boundary conditions). The model considered in ref. [3] is as follows: In the y direction we have N chains with the tunneling matrix element t. The confining potential obeys, for and for . We will assume open boundary conditions in the x direction. In the y direction the

confined potential is effectively zero for and for (N are the number of chains). We will use the conditions and.

(3)

is the one dimensional model for each chain and describes the tunneling between the chains. The confining potential enforces the open boundary conditions.

(4)

The open boundary conditions avoid the twist.

(5)

As a result the Hamiltonian is transformed,

Next we use the mapping for introduced by [3] [11] . This parametrization removes the oscillating phase for certain channels and therefore gaps are opened.

In the next step we bosonize the model for the filling factor using the electronic density and the Bosonic phase for each chain (is the chemical potential, is the Fermi momentum and is the spin orbit strength).

(6)

, are anti commuting Klein factors [10] [12] [13] .

Due to the boundary conditions the left and right movers are not independent. The Bosonic representation of the Fermion field is given in terms of the right movers. The left movers are given by.

(7)

We define a new chiral (right moving) Fermi field for and for. This implies that the chiral Fermionic field obeys. is

periodic in the domain (the domain has bee enlarged to). Using the step function we write the representation of the chiral field.

(8)

We find:

(9)

The bulk is gaped and only four chiral modes remain gapless,

(10)

The chiral edge Hamiltonian is given by,:

(11)

Using the proximity to a superconductor with the pairing field we can gap out the edges (the bulk states are gaped) without breaking time reversal symmetry.

(12)

In the presence of a magnet which breaks reversal-symmetry the spectrum will also be gaped out [11] .

2.2. The Fractional Topological Insulator for the Filling Factor

Next we will consider the model at the filling factor. We use composite Fermions in one dimensions and Bosonize the model around (we mention that in one dimensions we can Bosonize around any odd number of Fermi momentum). In this section we will show how the method of composite Fermions works in one dimensions.

According to Equation (6) a composite Fermions is obtained whenever an even number of Jordan Wigner phases is attached to a Fermion. If describes an electrons, a composite fermions is obtained by modifying the Jordan Wigner phase to. As a result one observes that the Bosonic representation for the composite fermions with is obtained for. As a result the Bosonization is invariant under the fermi momentum and filling factor mapping: and. Following the steps given in Equation (6) for the filling factor we find:

(13)

Repeating the formulation given in Equations (7)-(8) we have

(14)

In the next step we use the relation and obtain similar expressions to Equations (8)-(12). The bulk is gaped and only four chiral modes remain gapless

(15)

The chiral edge Hamiltonian is given by,:

(16)

Using the relation imposed by the open boundary conditions with only one independent Bosonic field we have:

(17)

We build from and non-chiral Bosonic fields,:

(18)

(19)

This shows that model is a Luttinger liquid with the parameter. When the chains are in the

proximity with a superconductor we add to the Luttinger liquid Hamiltonian in Equation (19) the pairing part given in Equation (12) (second line in Equation (12)). As result the model of the coupled chains in proximity to a superconductor gives rise to a F.T.I.. Following ref. [3] the F.T.I. is identified with the help of the Josephson periodicity which measure the degeneracy of the ground state.

3. The Metallic Disk in the Presence of the Spin Orbit Interaction―A Realization of a Topological Insulator

In this section we present our model. it was shown that in strong magnetic we can use the limit of large magnetic field study the physics of electrons in strong magnetic fields [14] . we Using the analogy with the strong magnetic field we propose to study the spin -orbit interaction in the limit. As a result a one dimensional model in a confining potential emerges. For a parabolic potential with the condition we find a constrained Hamiltonian,

In the limit we obtain. The two dimensional parabolic potential is replaced by a one dimensional model with a parabolic potential.

3.1. A Realization of a Topological Insulator for the Metallic Disk at Filling Factor

In the second quantized formulation we find:

(20)

Due to the constrained the potential is replaced by a one dimensional model. The coordinate y acts as the momentum, and only x remains the x coordinate. We find:

(21)

In the second line of Equation (21) we have used the constraint relation which emerges from the strong spin-orbit interaction, This result is interpreted as a second class constrained [15] [16] The one dimensional effective model given in Equation (21) with the potential allows to introduce a space dependent Fermi momentum, , where are the classically turning

points. We can map this problem to the edge of the disk. We introduce the angular variables for the edge (is the angular variable for the edge which is a function of the original coordinate x). The mapping between the space dependent Fermi momentum and the angular variable is given by the function:

The turning point causes the vanishing of the field. For this reason we must use open boundary conditions. As a result we Bosonize in terms of a single mover.

(22)

The Fermi momentum is a function of the chemical potential instead of two Fermi points the Fermi momentum is x dependent. The vanishing points give rise to the effective edge for the disk. is given by,

Due to the fact that the Fermi momentum is x dependent we that Fermi velocity is also space dependent,

In the next step we obtain the Bosonic representation for the metallic disk.

(23)

represents the Hamiltonian for the upper half disk and is the Hamiltonian for the lower half. Due to the turning points we have the relations:

(24)

Using the boundary conditions given in Equation (24) we obtain for Equation (23) the representation:

(25)

Next we map the problem to the edge of the disk. We find from the mapping the relation. The term is replaced by the derivative on the boundary of the disk.

(26)

We express the Hamiltonian in Equation (25) in terms of the chiral Fermions on the boundary of the disk. We have the mapping and find:

(27)

Nest we consider the proximity effect of a superconductor with the pairing field. As a result of the pairing field a superconducting gap is open on the edges. As a results the Hamiltonian with the pairing field gives rise to the Bosonized form of the T.I. Hamiltonian:

(28)

3.2. The Metallic Disk in the Presence of the Spin Orbit Interaction―A Composite Fermion Formulation for a F.T.I.

For particular densities the composite fermions construction introduced by [8] can be used. In one dimensions the Jordan Wigner construction allows to obtain composite Fermions. Repeating the procedure of a space dependent Fermi momentum introduced in Section 3.1 we find that the turning points depends on the chemical potential,. By changing the chemical potential to, we obtain. The turning points decreases to.

The construction of the composite fermions leaves the position of the turning point invariant. The Jordan Wigner construction is based on the fact that both Jordan Wigner representations and describe a Fermion. The first representation represents an interacting Fermion model with the filling factor. The second one represents a non interacting Fermion model with the filling factor 1. For the chemical potential, the composite Fermion with the momentum will obey the relation. For we obtain giving the same turning point.

For this case we repeat the formulation given in Equation (13). We replace and with the chiral bosons,. Due to the boundary conditions at the points we use the relations. We introduce and

(29)

We employ the mapping to the edge of the disk. When we a superconductor is in the proximity of the disk the paring field will generate a gap

(30)

We introduce the fields:

(31)

measures the charge density which is conjugated to. We map the Bosonic fields and to the edge of the disk:,. The Bosonic form of the Hamiltonian in Equation (29) reveals the Luttinger liquid structures with the interacting parameter,. As a result the charge sector represents an F.T.I..

(32)

Comparing the results in Equation (31) with the one given in Equation (27) we notice that and the pairing operator is replaced by the symmetric form,. As a result the

Josephson current will be different for the two cases. The use of the zero mode operators given in ref. [10] [17] can reveal the Josephson periodicity of the degenerate ground state.

When the superconductor is replaced by a magnetic system a gap on the edge of the disk via spin-flipping backscattering will appear. In this case the Josephson charge current will be replaced by a Josephson spin current [3] .

The experimental verification is done by measuring the Josephson current between the metallic disk and the superconductor which will show different results for the T.I. and the F.T.I.

The experimental question is how to drive the disk to be either a T.I. or F.T.I. Our results show that for the two cases we have different turning points, for a T.I. and for a F.T.I. The physical radius of the disk R determines what state can be obtained. When the radius R obeys the T.I. and the F.T.I. are possible. We will have a coherent or a mixture of the two phases. In order observe a single phase we have to chose the radius to satisfy. For this case the phase with is not possible ( the ring radius is shorter then the turning point ), from the other-hand the F.T.I. with is possible to observe.

4. Conclusions

In the first part of this paper we have presented the Bosonization for the model introduced in ref. [3] . We have found that it is essential to use open boundary conditions. This results are obtained by using chiral Bosonization. The Fractional case has been obtained with the help of the Jordan Wigner transformation for composite Fermions.

In the second part we propose a new model for a Fractional Topological Insulator. We consider a metallic disk, and take advantage of the strong spin orbit interaction in the presence of a parabolic potential. We map the problem to an one-dimensional model with a harmonic potential. On the edge of the disk we find a chiral fermion model which in the proximity to a superconductor gives rise to a Fractional Topological Insulator when the radius of the disk is tuned to be larger than the fractional turning point.

The mapping to the one dimension allows showing that the Fractional Topological Insulator emerges as an effective Luttinger liquid model for the filling factor.

A possible experimental realization of the model is suggested based on tunning of the chemical potential and the radius of the disk.

Cite this paper

D.Schmeltzer, (2016) Fractional Topological Insulators—A Bosonization Approach. Journal of Modern Physics,07,118-128. doi: 10.4236/jmp.2016.71012

References