Received 9 October 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT

The main aim of this paper is to explain why the Weinberg-Salam angle in the electro-weak gauge group satisfies. We study the gauge potentials of the electro-weak gauge group from our wave equation for electron + neutrino. These potentials are space-time vectors whose components are amongst the tensor densities without derivative built from the three chiral spinors of the wave. The 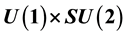gauge invariance allows us to identify the four potential space-time vectors of the electro-weak gauge to four of the nine possible vectors. One and only one of the nine derived bivector fields is the massless electromagnetic field. Putting back the four potentials linked to the spinor wave into the wave equation we get simplified equations. From the properties of the second-order wave equation we obtain the Weinberg-Salam angle. We discuss the implications of the simplified equations, obtained without second quantification, on mass, charge and gauge invariance. Chiral gauge, electric gauge and weak gauge are simply linked.

Keywords:

Invariance Group, Dirac Equation, Chirality, Electron, Neutrino, Electro-Weak Gauge, Gauge Bosons, Photon, Weinberg-Salam Angle

1. Introduction

L. de Broglie found [1] the wave associated to the movement of any particle in 1924. P. A. M. Dirac found his wave equation in 1928 [2] . L. de Broglie and his students considered this wave equation as the true wave equation of the electron, not the Schrödinger equation, because it was relativistic; it gave the spin 1/2 property; it gave the true results for the spectroscopy of light. The solutions in the H atom case were calculated immediately by C. G. Darwin [3] . All awaited results were obtained: the true number of energy levels, all quantum numbers compatible with the spin 1/2. L. de Broglie published his work on the Dirac equation in 1934 [4] ; next he studied the photon and he obtained a quantum wave for the photon from two spinors [5] [6] . Our article follows the method initiated there. This theory of light was not successful at this time, because the photon conserved the mass of the spinor wave, and this mass broke the gauge symmetry. We shall see that these defects are avoided here, because we start from a wave equation where the mass term is compatible with the gauge symmetry. Next the gauge theory of weak interactions was brought closer electromagnetism by the Weinberg-Salam model [7] and G. Lochak built the theory of a leptonic magnetic monopole [8] -[10] . From this magnetic monopole he got an extension of de Broglie’s theory of light [11] - [13] .

We previously have obtained a wave equation for a pair electron + neutrino [14] and we have generalized this equation as a wave equation for all objects of the first generation, electron, neutrino, quarks u and d with three states of color each, and their antiparticles [15] . This wave equation is form invariant under the 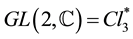group of invertible elements in the Clifford algebra of space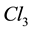. It has a mass term and nevertheless it is gauge invariant under the 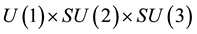gauge group of the standard model, in a way that gives automatically the insensitivity of the electron and its neutrino to strong interactions. The first consequence of this is a separation of the wave equation into a lepton part and a quark part. If the quark part is cancelled the wave is reduced to the electron + neutrino case, gauge invariant under the group of electro-weak interactions. If the neutrino wave is cancelled the wave equation is reduced to an equation for the electron alone which has the Dirac equation as linear approximation [16] -[21] . Since the wave equation has not lost its mass term it is easy to account for inertia and gravitation [22] [23] . We shall follow notations and results explained there, and a first chapter explains the three Clifford algebras needed by the standard model. Since we study here only electro-weak interactions we shall need only two of these three algebras, the 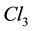algebra of space and the 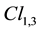algebra of space-time. Following de Broglie’s idea, we have previously studied, in Chapter 4 of [23] a way to construct by anti-symmetrical product the quantum wave of a photon from two spinor waves. The electromagnetic potential is a space-time vector and the electromagnetic field is a space-time bivector 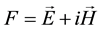satisfying:

(1.1)

where 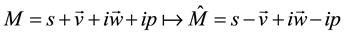is the main automorphism of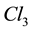; 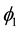and 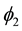are two Dirac spinors. This gives for the dilation D defined from any element:

(1.2)

This is the awaited transformation, because the electromagnetic potential moves with the charges and must then be a contravariant space-time vector, while the electromagnetic field of two photons and must transform as each photon field, and this is the case if the electromagnetic field F of a system of two photons is. With the link that we always use between the space algebra and the space-time algebra:

(1.3)

and

(1.4)

we get a potential which changes sign when we exchange the indexes:

(1.5)

(is the reverse of). Since our wave equation has a mass term containing a which is itself a complicated function of the spinor wave it is impossible to get the very beautiful electromagnetism of L. de Broglie from two different spinor waves, and we must use the same wave. But if we use in Equation (1.5) the electromagnetic field disappears! Nevertheless we have another possibility, using the same if, the charge conjugate of. In the standard model of quantum physics, the charge conjugate of

(1.6)

where e is the wave of the electron; n is the wave of the electronic neutrino; p is the wave of the positron and a, the wave of the anti-neutrino, satisfies:

(1.7)

Therefore searching for anti-symmetrical products with and its charge conjugate is equivalent to searching anti-symmetrical products with alone.

2. Tensor Densities without Derivative

The quantum wave of the pair electron + neutrino is a function of space and time into the space-time algebra [23] :

(2.1)

where is the right Weyl spinor of the electron, is the left Weyl spinor of the electron and is the left Weyl spinor of the electronic neutrino. In the standard model there is no right neutrino. We have explained that this experimental rule gives usually an invertible ( [23] , Sec. 6.4).

Therefore, with the 12 real parameters of the wave, tensor densities without derivative are available, and we shall review them here. With the D dilation of Equation (1.2) we use

(2.2)

Under the dilation D the wave is transformed with only one M not two like x or:

(2.3)

We shall use also

(2.4)

Each chiral spinor L, R and n allows us to get tensor densities, forming a space-time vector and a space-time bivector:

(2.5)

The, are covariant space-time vectors, satisfying and while the are bivectors satisfying and. Since these bivectors transform under D differently from the gauge fields, they cannot be used directly to get these gauge fields. On the contrary the are similar to the potentials of the gauge interaction. With each pair, and we get 16 tensor densities forming one general even term in space-time (8 components) and one general odd term (also 8 components). We shall use:

(2.6)

We get:

(2.7)

Next we shall use for the odd terms in space-time:

(2.8)

3. The Wave Equation

A double link exists between the wave equation and its Lagrangian density because the wave equation is obtained from the Lagrangian density by variational calculus and, this is new, the Lagrangian density is exactly the scalar part of the invariant wave equation ( [23] , Sec. B.3):

(3.1)

This means that when we write the wave equation with R, L and n or when we use the variational calculus to get the wave equation, we encounter the same equations which read in the R case:

(3.2)

Next the L spinor satisfies:

(3.3)

And the n spinor satisfies:

(3.4)

4. Derivative

In de Broglie’s work on light [5] [6] the electromagnetic field and the electromagnetic space-time vector A such as are physical quantities which can be obtained from the spinor waves. F is a bivector and A is a contravariant vector. All laws of electromagnetism are form invariant under (see [18] and [23] chapter 4). In the dilation defined in (1.2) A and F become

(4.1)

The tensor densities of the Dirac theory have been intensively studied by L. de Broglie [4] and his students, especially O. Costa de Beauregard [24] and T. Takabayasi [25] . With the mathematical tool of Clifford algebra they have been also studied by D. Hestenes [26] [27] , R. Boudet [28] [29] and one of us [30] . The problem with these tensors comes from the non-commutativity of the multiplication in space and space-time algebra, coming from the dimension 3 of space:

(4.2)

A solution must exist to this problem. First, since Feynman graphs act equally for fermions and bosons, the dynamics of both fermions and bosons must come from same laws. Now we know that the Lagrangian mechanism, for all fermions, comes from the real part of the wave equation. None meta-physical principle rules that physical laws necessary come from a Lagrangian density. Then the dynamics of bosons must also come directly from the wave equation of fermions, and only from this wave equation. Now every user of Feynman graphs thinks that all this theory results from a unique Lagrangian density, giving not only the dynamics of the fermion wave, but also the dynamics of the gauge bosons. But the link between boson fields and potential terms is not deduced from the Lagrangian density, it is postulated as definition of the potentials, or to get a simplified second-order equation, or to follow the rules of the gauge group. In the lone electromagnetic domain two links

are used between potential and field: in de Broglie’s electromagnetism, and in

classical electromagnetism. How must we choose? None of these two different derivatives comes from a Lagrangian density. Then we must consider only a derivative using the spinor wave equation. Naming the derivative of A we shall use in space-time algebra:

(4.3)

For instance with

(4.4)

we get

(4.5)

Therefore if we set two awaited properties are satisfied: is a bivector in space-time, because and transforms under the dilation D defined in (1.2) as follows

(4.6)

which means that transforms as a gauge field.

5. Gauge Fields

We name the bivector derivative of the space-time vector:

(5.1)

From we get

(5.2)

and using (3.2) we have

(5.3)

With (2.6) and since

(5.4)

is the form of the exterior product of the space-time algebra in space algebra, we get

(5.5)

Next we get

(5.6)

Similarly we get

(5.7)

Now we let

(5.8)

This vector satisfies

(5.9)

and we get

(5.10)

This, with (1.7), gives

(5.11)

This vector is then similar to the space-time potential built by L. de Broglie in his electromagnetic field of the photon, and in the work of G. Lochak [11] - [13] and one of us [18] (see also [23] , Chapter 4). And we remark that with our wave equation we get the photon without mass term, because:

(5.12)

A detailed study of the nine space-time vectors available from the 78 tensor densities without derivative shows that this field is the only field without mass term. Since the photon is moving at the limit velocity, we know that its mass is null, then we may identify A to the electromagnetic potential and F to the electromagnetic field. This means that these tensors are both quantum quantities and classical quantities. The electromagnetic field F is exactly the bivector with real components of pre-quantum optics. Moreover the zero proper mass of the photon does not need a symmetry breaking of the gauge, it is perfectly compatible with the gauge symmetry. The main difference from classical physics is the double aspect of each gauge boson, made of a space-time vector potential and of its derivative which is a space-time bivector.

The previous calculation of and shows the necessity to study also and. We get

(5.13)

(5.14)

6. Gauge Invariance

We have explained [17] [19] [23] how the electro-weak gauge reads in the Clifford algebra. The part of the gauge uses a B potential which is a space-time vector and the gauge transformation reads

(6.1)

which gives

(6.2)

Then B may be any linear combination of, , , and. But, , and are excluded, because they are changed in the gauge transformation. Next for the gauge group we have

(6.3)

For the group generated by we have

(6.4)

which gives

(6.5)

while the gauge transformation of the wave gives

(6.6)

This implies that the identification, is possible. For the group generated by we have

(6.7)

which gives

(6.8)

while the gauge transformation of the wave gives

(6.9)

The gauge derivative of the wave equation for electron + neutrino is then compatible with the identification:

(6.10)

7. Simplified Wave Equations and Weinberg-Salam Angle

The Weinberg-Salam angle and the are so defined:

(7.1)

From this definition results:

(7.2)

We have seen that is required by the null mass of the photon. We have just obtained, then this allows us to identify:

(7.3)

Now the knowledge of the gauge potentials B, , and allows us to simplify the wave equations. In (3.3) we have:

(7.4)

We get also

(7.5)

Next for the wave equation of R we use

(7.6)

and we get

(7.7)

At the second order we get:

(7.8)

We get a similar relation with and these two terms are the only ones if. The second order wave equation coming from the Dirac equation (and the same comes from the Schrödinger equation) has no term which should couple directly mass and charge. It is then necessary that:

(7.9)

This means: first that the standard model of quantum mechanics, where too many parameters are available, has now one of these parameters fixed. Secondly this comfort the identification that we have made between gauge potentials and space-time vectors linked to the spinor wave. It is also possible to get the value of from the calculation of. These two calculations do not need to consider n, because the second order equation coming from the Dirac wave equation accounts only the electromagnetic part of the electro-weak gauge.

We get also

(7.10)

And we also have:

(7.11)

We then get for the neutrino part of the wave:

(7.12)

which gives with (3.4) and (7.11)

(7.13)

There are many simplifications in our previous calculations, for instance (5.12) becomes

(7.14)

The electromagnetic field appears as second behind the space-time vectors. From the beginning of quantum mechanics the potential terms are in the wave equations, the electromagnetic field is only used as coming from the potential space-time vector.

Now if we follow T. Socroun [31] who incorporates the constants into the potentials we use:

(7.15)

Then Equations (5.8), (6.10) and (7.11) imply the simple equality:

(7.16)

The electromagnetic boson is then the sum of the chiral boson and of the weak boson. This is

the key to understand the operator, equivalent in the initial Weinberg-Salam model to the weak isospin: in a gauge transformation of the part of the electro-weak gauge group the gauge transformation reads:

(7.17)

and we have

(7.18)

The gauge appears then as composed, in any order, of an electric gauge and a weak gauge:

(7.19)

This is true only with and could be a departure to get. The projector or the weak isospin are then a direct consequence of the structure of the lepton wave.

8. Concluding Remarks

The parameter has been experimentally found near. Since this value was not issued from the calcula- tions by approximation used in the standard model of quantum physics, an explanation has been studied in a frame containing both the electro-weak gauge and the group of chromodynamics. These theories known as great unified models were able to get the value, but they predicted a disintegration of the proton which was never observed. Then the problem of this value was not solved. Our calculation respects all known properties of the quantum wave included in this standard model, but we do not use the second quantification. The wave considered here is the initial wave of L. De Broglie, a physical wave propagating in space and time with spin 1/2 property. This wave is fully relativistic, since the group used in the Dirac theory is a subgroup of the group of form invariance, made of all invertible elements of the space algebra.

The theory of light built by L. de Broglie was able to account for the photon of A. Einstein, but his construction started from the linear Dirac equation, so his photon had a mass which was never observed. And this mass term was breaking the gauge symmetry. The problem of the mass was also present in the Weinberg-Salam model of electro-weak interactions. The electron and the neutrino of this model have lost mass. Since it was necessary somewhere to account for the mass of the electron, a complicated mechanism of spontaneous symmetry breaking was invented. Even if the Higgs boson is now observed, this symmetry breaking is not able to reduce the too great number of parameters of the standard model.

Actually the symmetry breaking is useless in the frame developed here, based on a wave equation with mass term which is both form invariant (then relativistic) and fully gauge invariant under the gauge group of the standard model. Since the group of form invariance is greater there are new strains and less freedom: it is the reason of our ability to calculate a parameter like, free in the frame of the linear quantum mechanics, non-free with our non-linear wave equation or of our ability to link weak gauge and electromagnetic gauge in (7.19). Even if the gauge group is made of two different groups, the electro-weak gauge is a completely unified frame, since the gauge is totally linked to the electric and gauges.

The simplified wave Equations (7.10) and (7.13) give also a new understanding of mass and charge. The mass term of the Dirac equation links the derivative of the left wave to the right wave and vice-versa. Why? The reason comes from the structure of the wave, with left and right spinors in a different column, and from the transformation under a dilation of the derivative:

(8.1)

Then must apply to, not X, and. This term explains the necessary presence

of the which is transformed by. Since there are 3 such terms this introduces

a degree of freedom which shall give the 3-dimensional gauge group. But then the for instance which transforms into cannot be directly linked to which transforms into:

(8.2)

We have a factor which must be compensated. This may be done by two ways: where m and bring each a factor or by q alone which brings a factor (see [23] , Sec 4.1.2). The form (7.10) (7.13) of the wave equation is not free, but is constrained by the group of form invariance. All this cannot be deducted from the usual field theory which arbitrarily supposes. The greater group of invariance brings not only new strains but also a better understanding of physical laws.

Cite this paper

ClaudeDaviau,JacquesBertrand, (2015) Electro-Weak Gauge, Weinberg-Salam Angle. Journal of Modern Physics,06,2080-2092. doi: 10.4236/jmp.2015.614215

References