Received 21 July 2015; accepted 18 August 2015; published 21 August 2015

ABSTRACT

The energy emitted by an electron in course of its transition between two quantum levels can be considered as a dissipated energy. This energy is obtained within a definite interval of time. The problem of the size of the time interval necessary for transitions is examined both on the ground of the quantum approach as well as classical electrodynamics. It is found that in fact the emission time approaches the time interval connected with acceleration of a classical velocity of the electron particle from one of its quantum levels to a neighbouring one.

Keywords:

Dissipated Energy and Time Intervals of the Quantum Transitions, Electron Acceleration in Simple Quantum Systems Considered as a Test of the Theory

1. Introduction. Planck’s Approach to an Electron Transition and Its Difficulty

The phenomenon of the electron transitions between quantum levels is basic for the quantum theory. In fact the theory began by a fit of the transition energy of a set of oscillators to the intensity of the emission spectrum of the black body examined with respect to its dependence on the body temperature [1] [2] . A success of Planck was based on discovery that the energy of the oscillators is regularly a multiple

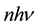(1)

of the same expression

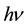(2)

where 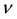is the oscillator frequency and 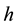is the Planck constant.

In a further development of the theory the result of (2) has been extended to any transition energy between two quantum levels, not necessarily those belonging to the oscillator. In effect the formula

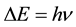(3)

couples the energy interval

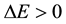(4)

with the frequency 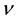of the electromagnetic wave characteristic for any transition between two different quantum levels.

However an important lack of the theory which remained in it was the problem of the time interval

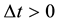(5)

necessary for the process of the energy change 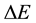entering (3). In accordance with the statistical background of the energy spectrum of the black-body radiation the problem of 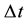has not been examined for an individual transition between separate quantum levels, but approached on the basis of a probabilistic analysis of the population number of the quantum states forming the interval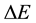. This kind of reasoning, characteristic already for the old quantum theory [3] [4] , has been consequently prolongated and extended in case of quantum mechanics; see e.g. [1] [5] -[7] .

The aim of the present paper is to examine the problem of the transition time

(6)

on the ground of a non-probabilistic (non-statistical) approach. Therefore formally the task becomes rather opposite to a treatment which has been usually applied. Only the emission rate of energy 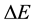between two neighbouring quantum states is mainly considered. The obtained result is that and 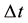should satisfy the equation

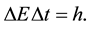(7)

Formally (7) is much similar to the well-known Heisenberg principle of uncertainty for energy and time [8] which is

(8)

But the interval entering (8) is not necessarily limited to entering (3). Another remark concerning (8) is of a more principal character: in (7) there is no uncertainty concerning for a given. A different situation does exist in the case of (8). In fact (8) gives the relation

(9)

so may assume an infinite spectrum of values for some constant.

Physical and philosophical implications of (9) have been discussed on many occasions, see e.g. [9] [10] . An important philosophical implication of (9) was to point out an indeterministic character of the relation between and. But in several further studies [11] -[13] , the validity of (8) has been objected on the basis of various reasons. In effect in numerous textbooks (see e.g. [7] [14] ), the relation (8) has been neglected at all.

2. Quanta of the Dissipated Energy and Intervals of Time Necessary to Produce Them

In the first step, the aim of the formalism developed in the present paper is to demonstrate that for an electron transition can be a defined quantity similar to and. To this purpose the is referred to the dissipation energy which accompanies the electron transition by the equation:

(10)

Evidently occuring in the transition seems to be of a typically emissive character. In short we assume that the emission of should not be necessarily of a radiation character dictated by (3), but can materialize also in the form of. Consequencies of such assumption are illustrated on three examples concerning respectively the hydrogen atom, a particle enclosed in the potential box and the harmonic oscillator. In Section 3 the results of the present Section are applied in calculating the electron acceleration produced in course of the quantum transitions performed in the mentioned three systems.

The energy differences

(11)

between two neighbouring quantum states having the indices

(12)

are mainly considered. We have

(13)

for the hydrogen atom [15] ,

(14)

for a free particle having mass enclosed in a one-dimensional potential box of length [16] , and

(15)

for the harmonic oscillator having the frequency.

The time periods of the electron particle circulation on the orbits are defined by a physical character of each of the above systems. They are

(16)

for the case of electron in the hydrogen atom occupying the state [15] ,

(17)

for the particle of mass m being in state n in the potential box because of the relation between energy and velocity equal to

and

(18)

for all states of the harmonic oscillator.

A characteristic property of expressions (13)-(18) is that

(13a)

holds for the atomic orbit of the hydrogen [see (13)],

(14a)

for a free particle (free electron) in state in the box [see (14)], and

(15a)

for the harmonic oscillator [see (15) and (18)]. A common feature of (13a)-(15a) is that

(19)

If we note that the resistance connected with any of transitions examined above can be defined by the ratio

(20)

where is a potential and is a current intensity given by the electron particle of charge, so

(21)

we obtain

(22)

In the last step in (22) the result of (19) is taken into account.

The in (22) is equal to the well-known quantum of resistance examined experimentally in the planar free- electron structures [16] [17] ; some theoretical results connected with are presented in [18] -[20] .

Let the dissipation heat of the quantum emission process satisfy the Joule-Lenz equation [21] [22]

(23)

By putting

(24)

[see (10)] we obtain from (21)-(24) the following relation

(25)

which gives

(26)

But because of (19) the formula (26) can be transformed into

(27)

which implies that

(28)

In effect of (28) the relation (26) can be presented in a more familiar form:

(29)

cf. here (7).

A comparison of the time rate of energy emission calculated according to the method presented above with the quantum-mechanical method is done in [23] .

3. A Check of the Theory: Acceleration of Electrons Obtained in Effect of Their Quantum Transitions

The physics of the test is much similar to that entering the Tolman experiment [22] . The point is that the change of the electron energy in course of its transition between the quantum levels is accompanied by a change of the velocity which the electron has along its path. For example in the hydrogen atom the emission of energy from some level to level is associated with an increase of the tangential velocity along the orbit. Let us assume that the expense of energy connected with acceleration is approximately equal to the emission energy. In this case

(30)

where the time of emission is also a time of the acceleration. Consequently the length of the electron path covered in course of acceleration should approach that obtained during the electron circulation; see (28). In effect instead of (30) we should have a transformed relation

(30a)

where is the path travelled in course of. The calculations of (30a) effectuated for the quantum systems examined in Section 3 are presented below. They seem to confirm the validity of (30a). The absolute value of is taken in (30a) in order to make this formula applicable to both positive and negative cases of acceleration; see [22] .

Beginning with the hydrogen atom we have in the formula (13), the velocity in state is [15]

(31)

(31a)

(31b)

is given in (16), and

(32)

is the nth orbit radius [15] . A substitution of parameters (13) and (32) into the left-hand side of (30a) gives the following expression

(33)

On the other side, a substitution of the absolute value of given in (31a) and the results of (31b) and (16) give for the right-hand side of (30a) the formula

(34)

Evidently both expressions (33) and (34) are equal:

A similar operation can be repeated for the electron in the potential box. Here [see (17) and equation below of it] the velocity

(35)

so

(36)

The time period in state n is that given in (17) and

(37)

for any state n. Therefore the left-hand side of (30a) becomes

(38)

and the right-hand side is

(39)

In effect we obtain

which is a similar property to that calculated above in the case of the hydrogen atom.

The case of the harmonic oscillator is rather different than that of the electron in the hydrogen atom or the potential box because the velocity ceases to be a constant number within the oscillation time period T: it changes gradually from zero value at the turning points of the oscillator to a maximal absolute value at the central point of the oscillator motion which is represented by the Hamiltonian:

(40)

where k is the force constant. In consequence the formalism described in (30) and (30a) is applied solely to the velocity acceleration at a single point

(41)

The electron velocity in state n and point (41) is obtained from the formula

(42)

where is the oscillator energy in state n. This gives

(43)

By considering solely the positive sign in (43) the increment of velocity due to the change of the quantum state becomes

(44)

The length is

(45)

where―the amplitude of the oscillator―is coupled to the oscillator energy in state n by the formula

(46)

so

(47)

In effect the left-hand side of Equation (30a) becomes

(48)

and the right-hand side of (30a) is

(49)

In consequence we obtain an approximate equality of both sides of (30a) represented by the relation

but not precisely the relation

4. Semiclassical Approach to the Dissipated Energy and Transition Time Deduced from the Ohm’s Law

An approach to the Joule-Lenz dissipation energy and its transition time can be done also on a semiclassical basis. First we note that the effective electric field which gives the Ohm relation with the electric current on the orbit n, viz.

(50)

where is a constant, should satisfy the relation [22]

(51)

Here is the electromotive force and is the radius of the Bohr orbit n. Evidently

(52)

where is the time period of the electron circulation on the orbit. The potential V entering R according to the formula

(53)

can be provided by the energy difference between some excited orbit state emitting the energy and a stationary state n for which the circular electron motion is examined:

(54)

The efficiency of the Joule-Lenz heat within a time interval is given by the formula

(55)

where is a transversal cross-section of the nth orbit conductor

(56)

is the radius of the electron particle [22]

(57)

and is the conductor length

(58)

Since (see [22] )

(59)

we obtain because of (55) the following result

(60)

By assuming that

[see (10)] the formula (60) yields evidently the result

(61)

obtained in (28).

5. Energy Emission and Its Time in the Case of

In preceding sections the case of the neighbouring quantum states and n has been mainly considered. An opposite situation is the case of

(62)

For example for the hydrogen atom the situation (62) implies

(63)

see (13) where is replaced by an almost infinite number. The formula (63) is times larger than (13) and for we have

(64)

Assuming that the end state of the energy emission has the index the time interval of the emission becomes [see (16)]

(65)

The length of the electron path covered within the time period is

(66)

see (32).

Our aim is to check the validity of the formula (30a) for the case of the emission from the state. In this case the absolute value of the electron velocity change between and is

(67)

We substitute on the left-hand side of (30a) the quantities and respectively from (64) and (66) so

(68)

On the right-hand side of (30a) a substitution of calculated from the formula (67) should be done together with the time expression for given in (65). We obtain the acceleration expression

(69)

We find that the left-side of (30a) presented in (68) differs from the right-hand side presented in (69) solely by a factor of 2:

It is easy to demonstrate that a particle in the potential box and the harmonic oscillator submitted to the check given by the Equation (30a) do not satisfy this equation. For an electron in the potential box the energy coming from a transition between the state and state is approximately proportional to [the left side of (30a)], whereas the velocity change entering the right-hand side of (30a) is solely proportional to n. A similar discrepancy between the both sides of (30a) occurs for the harmonic oscillator. Here the transition energy between and is approximately proportional to n but the velocity change in the central point of the oscillator is approximately proportional only to the square root of n.

It should be noted that for the transition in the hydrogen atom the product of [see (64)] and [see (65)] gives

(70)

This result is different from a similar product calculated in the case on [see (29)] solely by the factor of 1/2.

6. Poynting’s Vector in the Hydrogen Atom and the Emission Time

We define [21] [22] [24]

(71)

as Poynting’s vector. The time rate of the loss of energy is [24]

(72)

A well-known formal asymmetry of the Bohr model of the hydrogen atom is the presence of the electric field strength

(73)

in the orbit plane for any quantum state n, but this presence is combined with the absence of a similar magnetic field strength. In fact are also present in the hydrogen atom if we note that the electron is circulating along the orbit n having the radius [see (32)] with the velocity [see (31)]. In effect we obtain the relation

(74)

[given in (16)] which supplies the frequency

(74a)

With the electron circulating with frequency (74a) is associated the field strength according to the well- known formula [25] :

(75)

In effect

(76)

which is the size of a vector normal to the orbit plane.

A substitution of and into the expression (71) gives for the absolute value of the Poynting’s vector the expression

(77)

Since and are numbers constant in time, the time derivative of the expressions and composed of these vectors being on the right-hand side of (72) should vanish. There remains solely the surface integral of the Poynting vector value given in (77). This is a toroidal surface which encloses the electron orbit as the torus axis. Approximately the torus surface becomes equal to a surface of a thin cylinder having its axis length of the size

(78)

On the other side, the cross-section of the toroidal cylinder is dictated by the radius (see e.g. [22] )

(79)

of the electron particle which moves along the orbit. In effect the toroidal surface is approximated by the product of (78) and the circumference of the cross-section of the torus cylinder which is

(80)

The value of the Poynting vector for a thin electron orbit can be assumed as a constant number given in (77), therefore a non-vanishing term on the right of (72) becomes equal to

(81)

This is a product of (77), (78) and (80). In effect the Equation (72) has the form

(82)

Since the emitted energy in course of the electron transition between levels and n is [see (13)]

the emission time for that energy is

(83)

where the term taken in brackets is that calculated in (82).

The result of (83) should be compared with that given by the quantum-mechanical formula (29). This gives

(84)

which is a number larger by the factor of

(85)

than that of (83).

This is an expected situation because the emission rate described by the Poynting vector is not restricted to a single transition from level to level n [a limitation which exists in calculations leading to (84)] but concerns emission from n to any level below n.

It seems of interest to demonstrate that in the hydrogen atom can be obtained with the aid of the Biot- Savart law [21] [22] . For a constant current intensity along the nth orbit, we have from the Biot-Savart law

(86)

The current along the orbit is defined by the formula

(87)

where

(88)

is the volume occupied by the electron particle and

(89)

is the cross-section area of both of the volume and the electron orbit.

Since the integral of leads to result proportional to, and is a constant applied in (32), we obtain from (86) and (87):

(90)

which is a formula identical to that given in (76).

7. Summary and Comments

In his derivation of the formula (3) applied in the present paper, Einstein [4] has pointed out that statistical considerations supplemented by classical physics were necessary to obtain that formula. In effect no insight to an individual transition time of a particle between two quantum levels has been done. The aim of the paper was to bridge this gap.

The first step demonstrates that instead of (3) the Joule-Lenz dissipation energy can be applied [see (10) and (24)]. This yields an estimate of the emission time involved in an individual electron transition process; see Section 2.

The obtained in the formalism were checked by using them to calculate the electron velocity accelerated in effect of the quantum transitions. Beyond of a quantum theory a semiclassical approach based on electrodynamics is also developed in order to derive the formula for; see Section 4.

It has been demonstrated that for the acceleration formula (30)-(30a) is satisfied perfectly well for the electron in the hydrogen atom and electron particle in the potential box, and with a good accuracy when the acceleration of the central point of the oscillator is examined; see Section 3.

A good fit of to the formulae of Section 3 implies that in course of the electron transition its velocity, considered for example for the hydrogen atom, changes rather smoothly from that in state, viz.

(91)

to the velocity in state n, viz.

(92)

A separate study of in the hydrogen atom has been done with the aid of the Poynting vector; see Section 6.

A similar agreement of emission time and acceleration time is present also for in the case of the hydrogen atom, but ceases to hold for the electron motion in the potential box and harmonic oscillator; see Section 5.

The only condition imposed on the applied formalism is that the electron states considered in a system are periodic in time. This property can be coupled rather easily with the idea of the electron orbit, for example that introduced by Bohr in the model of the hydrogen atom. In this case the electron remaining in a quantum stationary state is circulating incessibly along an orbit of a definite size within a definite constant period of time [15] .

In general the use of the orbit idea is well known in the whole domain of the atomic, molecular and solid-state physics [26] . For solids the idea became widely applied as soon as Bloch proposed to describe the electron wave functions with the aid of combinations of the atomic orbitals spread over all atoms building up regularly a given crystal sample [27] . Such combinations, classified according to the quantum parameter, are also orbits which can be repeated unlimitedly in time. The time period required by the packet to perform a travel across the crystal volume is therefore

(93)

where is the electron wave packet velocity; L is the edge length defining the volume size of the elementary crystal cube equal to; and the coefficient is a constant not much larger than unity.

The Bloch model, especially of a one-dimensional crystal, is much similar to the model based on the standing-like wave functions characteristic for the electron particles enclosed in a potential box discussed in the present paper; see e.g. [28] .

Cite this paper

StanisƚawOlszewski, (2015) Non-Probabilistic Approach to the Time of Energy Emission in Small Quantum Systems. Journal of Modern Physics,06,1277-1288. doi: 10.4236/jmp.2015.69133

References