Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57673,16 pages
10.4236/jmp.2015.67100
Relation between FQHE Plateau Width and Valley Energy
Shosuke Sasaki
Center for Advanced High Magnetic Field Science, Graduate School of Science, Osaka University, Osaka, Japan
Email: sasaki@mag.ahmf.sci.osaka-u.ac.jp, zazensou@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 May 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
We have investigated the Fractional Quantum Hall Effect (FQHE) on the fundamental Hamiltonian with the Coulomb interactions between normal electrons without any quasi particle. The electron pairs placed in the Landau orbitals can transfer to many empty orbitals. The number of the quantum transitions decreases discontinuously when the filling factor n deviates from the specific fractional number of n0. The discontinuous decreasing produces the energy valley at the specific filling factors n0 = 2/3, 4/5, 3/5, 4/7, 3/7, 2/5, 1/3 and so on. The diagonal elements of the total Hamiltonian and the number of the quantum transitions give the total energy of the FQH states. The energy per electron has the discontinuous spectrum depending on the filling factor n. We obtain the function form of the energy per electron in the quantum Hall system. Then the theoretical Hall resistance curve is calculated near several filling factors. Therein the quantum Hall plateaus are derived from the energy valleys. The depths of the energy valleys are compared with the widths of the quantum Hall plateaus appearing in the experimental data of the Hall resistance. Our theoretical results are in good agreement with the experimental results.
Keywords:
Fractional Quantum Hall Effect, 2D Electron System, Quantum Theory, Hall Resistance

1. Introduction
The quantum Hall effect is derived by the total Hamiltonian
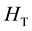 of a many-electron system which is composed of the single electron Hamiltonian
of a many-electron system which is composed of the single electron Hamiltonian
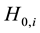 of the i-th electron and the Coulomb interaction between electrons as follows:
of the i-th electron and the Coulomb interaction between electrons as follows:
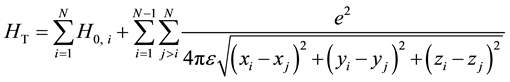 (1)
(1)
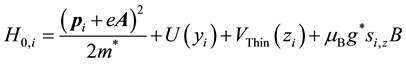 (2)
(2)
where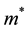 , e,
, e,
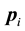 and N are the effective mass, the elementary charge, the momentum and the total number of electrons. Therein
and N are the effective mass, the elementary charge, the momentum and the total number of electrons. Therein
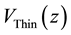 indicates the potential of the z-direction which confines the electrons to an ultra- thin conducting layer. Also
indicates the potential of the z-direction which confines the electrons to an ultra- thin conducting layer. Also
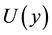 is the electric potential along the Hall voltage (y-direction). The vector potential,
is the electric potential along the Hall voltage (y-direction). The vector potential,
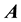 , has the components,
, has the components,
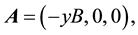 (3)
(3)
where B is the strength of the magnetic field. The last term of Equation (2) indicates the Zeeman energy where
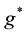 is the effective g-factor,
is the effective g-factor,
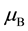 is the Bohr magneton
is the Bohr magneton
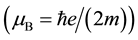 and
and
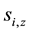 is the z-component of the i-th electron spin operator. The details have been explained in the previous papers [1] -[14] . When the Coulomb interaction between electrons is ignored in the quasi-2D electron system, the Hamiltonian of the single electron is exactly diagonalized same as in the Landau solution. At a filling factor
is the z-component of the i-th electron spin operator. The details have been explained in the previous papers [1] -[14] . When the Coulomb interaction between electrons is ignored in the quasi-2D electron system, the Hamiltonian of the single electron is exactly diagonalized same as in the Landau solution. At a filling factor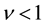 , all the electrons are placed in the Landau orbitals with the Landau level number
, all the electrons are placed in the Landau orbitals with the Landau level number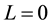 . The residual Landau orbitals (
. The residual Landau orbitals (



We define two symbols W and C which are the expectation values of


Then all the electron pairs placed in the nearest Landau orbitals can transfer to all the empty orbitals at the specific filling factors








The total energy of the quantum Hall system is the sum of W (expectation value of

2. Expectation Value of the Total Hamiltonian and Its n-Dependence
We describe the expectation value of the total Hamiltonian


where









Figure 1 shows one of the experimental data [16] . The upper figure indicates the Hall resistance








We next examine the microscopic charge-distribution in more details. Figure 2 shows the electron configuration with a minimum classical-Coulomb-energy at






The classical Coulomb energy between the pair (A, C) is weakened by the screening (shielding) effect of electron B. Also the classical Coulomb energy between the pair (A, D) is weakened by the screening effect of electrons B and C. Accordingly the n-dependence of the classical Coulomb energy mainly comes from the first nearest and the second nearest pairs. The number of the more distant pairs (third, fourth, fifth and so on) are enormous many. The total number of electron pairs is
Figure 1. Hall resistance RH and diagonal resistance R in ultrahigh- mobility device in [16] .
Figure 2. Electron configuration with the minimum classical Coulomb energy at
energies) may be approximated by the macroscopic Coulomb energy

(Case of
We can ignore the boundary effect in both ends for a macroscopic electron-number N. Then the number of the first nearest pairs is equal to






Next we estimate the classical Coulomb energy for n = 3/5, 4/7, 5/7 where the electron-configurations with the minimum classical Coulomb energy are shown in Figures 3-5.
(Case of




(Case of




(Case of




(Any case of
We calculate the classical Coulomb energy for a general case of










Figure 3. Electron configuration with the minimum classical Coulomb energy at
Figure 4. Electron configuration with the minimum classical Coulomb energy at
Figure 5. Electron configuration with the minimum classical Coulomb energy at
This equation is expressed by using


From Equations (4) and (10) the expectation value of the total Hamiltonian is obtained as

The single electron eigenenergy


where



We put together the constant parts as follows;

Therein f is the constant value as


where

The function W depends linearly upon







3. n-Dependence of the Total Energy
We already calculated the energy of electron pairs placed in the nearest orbitals by employing the perturbation calculation in the previous papers [1] - [13] . The exact








