Journal of Modern Physics
Vol.06 No.03(2015), Article ID:54303,7 pages
10.4236/jmp.2015.63035
The Interacting Generalized Ricci Dark Energy Model in Non-Flat Universe
Masashi Suwa*, Koji Kobayashi, Hisashi Oshima
School of Pharmacy, Nihon University, Chiba, Japan
Email: *suwa.masashi@nihon-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
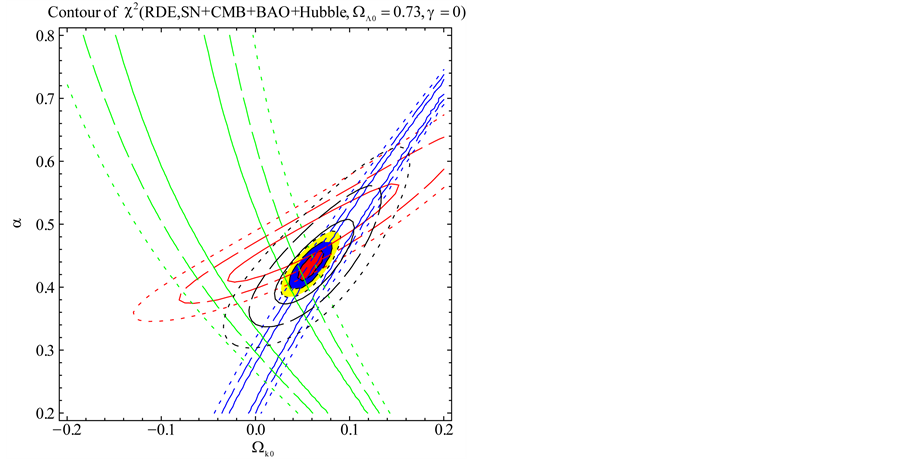
We extend our previous analysis and consider the interacting holographic Ricci dark energy (IRDE) model in non-flat universe. We study astrophysical constraints on this model using the recent observations including the type Ia supernovae (SNIa), the baryon acoustic oscillation (BAO), the cosmic microwave background (CMB) anisotropy, and the Hubble parameter. It is shown that the allowed parameter range for the fractional energy density of the curvature is 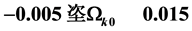 in the presence of the interactions between dark energy and matter. Without the interaction, the flat universe is observationally disfavored in this model.
in the presence of the interactions between dark energy and matter. Without the interaction, the flat universe is observationally disfavored in this model.
Keywords:
Dark Energy, Ricci, Non-Flat

1. Introduction
The current astrophysical observations of the Type Ia supernovae (SNIa) [1] [2] , the cosmic microwave background (CMB) [3] -[10] and the large scale structure (LSS) [11] have revealed that the expansion of our universe is accelerated [1] [2] . This indicates that there exists some unknown energy, called dark energy, to realize the accelerated expansion. The simplest interpretation of dark energy is the cosmological constant. However, this model requires an incredible fine-tuning, since the observed cosmological constant is extremely small compared to the fundamental Planck scale . Also, this model suffers from the cosmic coincidence problem: why the cosmological constant and matter have comparable energy density today even though their time evolution is so different.
. Also, this model suffers from the cosmic coincidence problem: why the cosmological constant and matter have comparable energy density today even though their time evolution is so different.
Among various attempts to solve these problems, we focus on the holographic dark energy (HDE) models [12] motivated by the holographic principle of quantum gravity [13] -[16] . Requiring that the total vacuum energy of a system with size L would not exceed the mass of the black hole of the same size, the dark energy density is proposed as
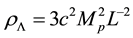 (1)
(1)
where c is a dimensionless parameter,  is the reduced Planck mass. As for the size L, which is regarded as an IR cutoff, various possibilities are discussed in literatures, such as the Hubble parameter L−1 = H [12] , the future event horizon
is the reduced Planck mass. As for the size L, which is regarded as an IR cutoff, various possibilities are discussed in literatures, such as the Hubble parameter L−1 = H [12] , the future event horizon 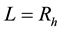 [12] , the age of our universe L = T [17] , and the Ricci scalar curvature
[12] , the age of our universe L = T [17] , and the Ricci scalar curvature  [18] . With a reasonable choice of L, Equation (1) naturally explains the observed value
[18] . With a reasonable choice of L, Equation (1) naturally explains the observed value 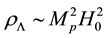 (
( is the present Hubble parameter). In our previous work [19] , we studied the Ricci dark energy (RDE) model with
is the present Hubble parameter). In our previous work [19] , we studied the Ricci dark energy (RDE) model with  by introducing an interaction between dark energy and matter. It was shown that a nonvanishing interaction rate
by introducing an interaction between dark energy and matter. It was shown that a nonvanishing interaction rate 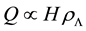 is favored by the observations [19] .
is favored by the observations [19] .
In this paper, we extend our previous analysis, and consider the interacting RDE (IRDE) model in non-flat universe. This paper is organized as follows. In Section 2, we describe the generalized IRDE model in non-flat universe, and obtain analytic expressions for cosmic time evolution. In Section 3, we discuss the observational constraints on this model. We summarize our results in Section 4.
2. The Interacting Ricci Dark Energy Model
We study the interaction Ricci Dark Energy (IRDE) model in non-flat universe. The Friedmann-Robertson- Walker metric non-flat univrerse is given by
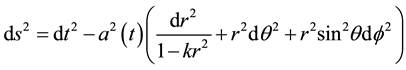 (2)
(2)
where k = 1, 0, −1 for closed, flat, and open geometries. The Friedmann Equation in non-flat univrerse takes the form
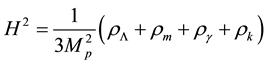 (3)
(3)
where  and
and 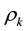 represent energy density of dark energy, matter, radiation and curvature, respectively, and
represent energy density of dark energy, matter, radiation and curvature, respectively, and 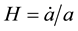 is the Hubble parameter.
is the Hubble parameter.
We generalize the energy density of the Ricci dark energy as
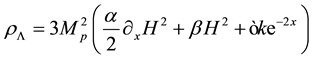 (4)
(4)
where α, b and 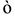


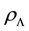
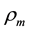
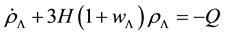

We adopt the interaction rate given by
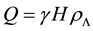
where 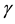
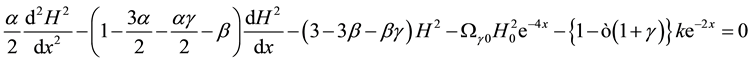
The solution to Equation (8) is given by
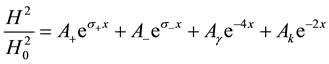
where
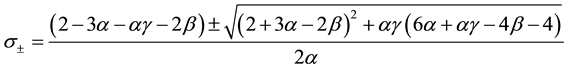
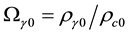

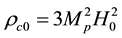
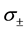
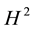
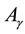
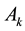

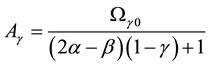
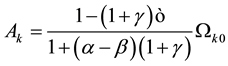
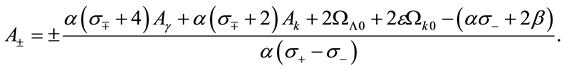
In the case of
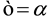
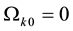
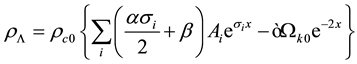
where
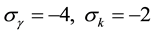
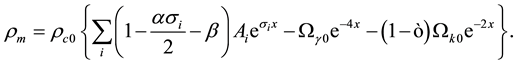
To derive the Equation of state parameter 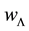
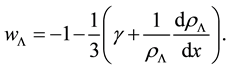
3. Observational Constraints
In this section, we discuss cosmological constraints on the IRDE model in the non-flat universe 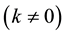
The luminosity distance in the non-flat universe can be written as
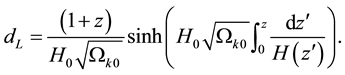
The SNIa observations measure the distance modulus μ of a supernova and its redshift z. The distance modulus is given by
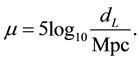
We use the Union data set of 580 SNIa [41] [42] to obtain limits on the relevant parameters α, γ and 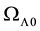
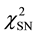
The CMB shift parameter R is given by
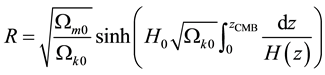
where 

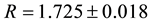
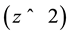
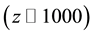
Signatures of the baryon acoustic oscillation (BAO) are provided by the observations of large-scale galaxy clustering. The BAO parameter A is defined by
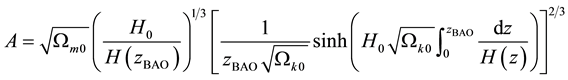
where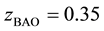
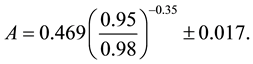
The BAO constraints are obtained by minimizing 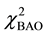
The Hubble parameter constraints are given by minimizing
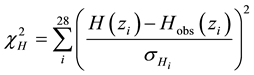
where 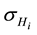

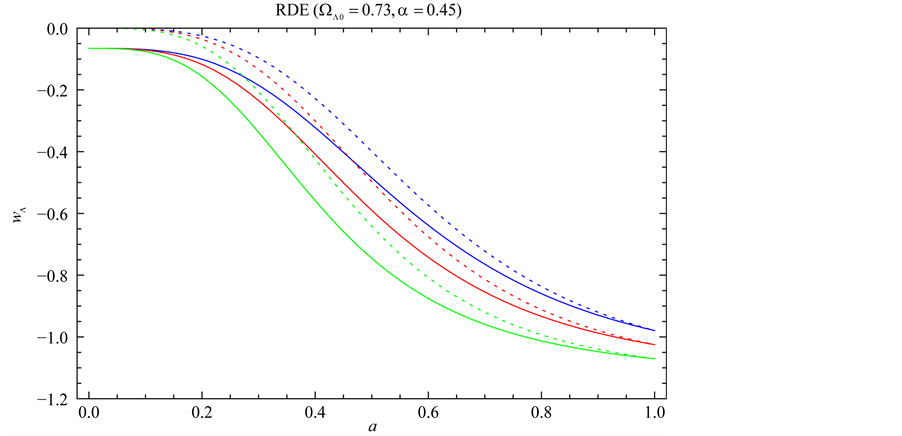
In Figure 1, we plot the Equation of state parameter 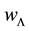

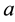
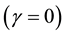

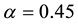
Figure 1. Plot of 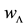
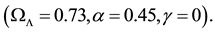
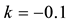
value 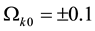
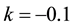
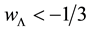
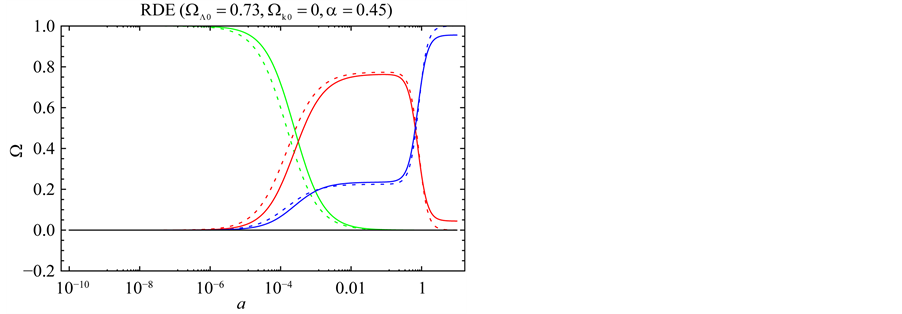
In Figure 3, we plot the evolution of the energy density fractions Ω for radiation (green), matter (red) and dark energy (blue) for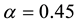
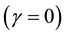
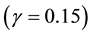
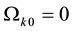
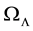



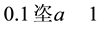
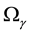
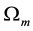
4. Conclusion
We have considered the IRDE model in the non-flat universe. We have derived the analytic solutions for the
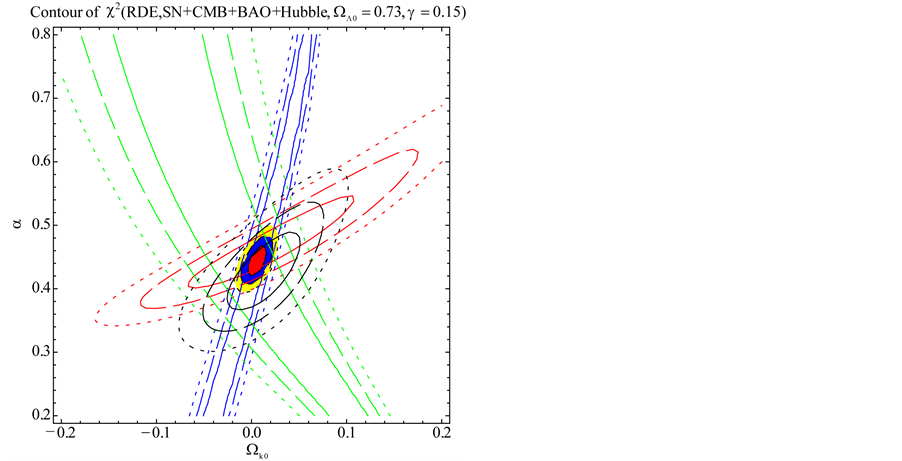
Figure 2. The probability contours for SNIa (red), CMB (blue), BAO (green) and Hubble (black) observations in the 
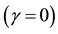
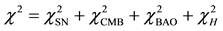

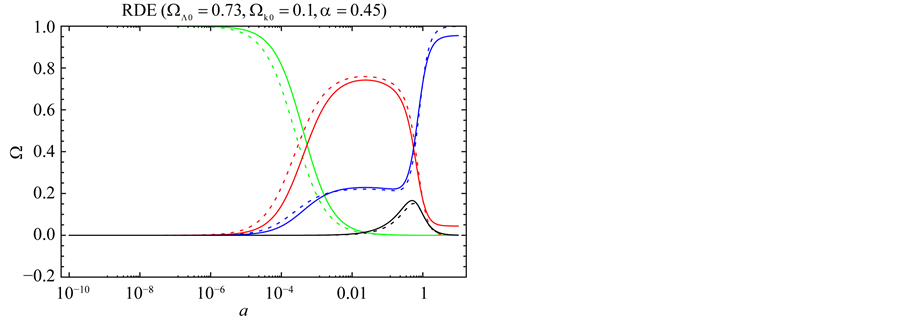
Figure 3. Plot of Ω versus a for RDE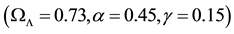
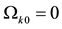
Hubble parameter (9), the dark energy density (14) and matter energy density (15). We have also studied astrophysical constraints on this model using the recent observations including SNIa, BAO, CMB anisotropy, and the Hubble parameter. We have shown that the allowed parameter range for the fractional energy density of the curvature is 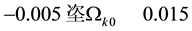
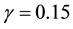

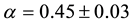
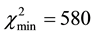
Acknowledgements
We would like to thank T. Nihei for his valuable discussion, helpful advice and reading the manuscript.
References
- Riess, A.G., et al. (1998) The Astronomical Journal, 116, 1009. http://dx.doi.org/10.1086/300499
- Perlmutter, S., et al. (1999) The Astronomical Journal, 517, 565. http://dx.doi.org/10.1086/307221
- Bennet, C.L., et al. (2003) The Astronomical Journal, 148, 1. http://dx.doi.org/10.1086/377253
- Spergel, D.N., et al. (2003) The Astronomical Journal, 148, 175. http://dx.doi.org/10.1086/377226
- Spergel, D.N., et al. (2007) The Astronomical Journal, 170, 377. http://dx.doi.org/10.1086/513700
- Page, L., et al. (2007) The Astronomical Journal, 170, 335. http://dx.doi.org/10.1086/513699
- Hinshaw, G., et al. (2007) The Astronomical Journal, 170, 263. http://dx.doi.org/10.1086/513698
- Komatsu, E., et al. (2009) The Astronomical Journal, 180, 330. http://dx.doi.org/10.1088/0067-0049/180/2/330
- Komatsu, E., et al. (2011) The Astronomical Journal, 192, 18. http://dx.doi.org/10.1088/0067-0049/192/2/18
- Hinshaw, G., Larson, D., Komatsu, E., Spergel, D.N., Bennett, C.L., Dunkley, J., Nolta, M.R., Halpern, M., et al. arXiv:1212.5226 [astro-ph.CO].
- Eisenstein, D.J., Zehavi, I., Hogg, D.W., Scoccimarro, R., Blanton, M.R., Nichol, R.C., et al. (2005) Astrophysical Journal, 633, 560-574. http://dx.doi.org/10.1086/466512
- Li, M. (2004) Physics Letters B, 603, 1-5. http://dx.doi.org/10.1016/j.physletb.2004.10.014
- ’t Hooft, G. arXiv:gr-qc/9310026.
- Susskind, L. (1995) Journal of Mathematical Physics, 36, 6377. http://dx.doi.org/10.1063/1.531249
- Maldacena, J.M. (1998) Advances in Theoretical and Mathematical Physics, 2, 231-252.
- Fischler, W. and Susskind, L. (1998) arXiv:hep-th/9806039.
- Cai, R.G. (2007) Physics Letters B, 657, 228-231. http://dx.doi.org/10.1016/j.physletb.2007.09.061
- Gao, C., Wu, F., Chen, X. and Shen, Y.G. (2009) Physical Review D, 79, Article ID: 043511. http://dx.doi.org/10.1103/PhysRevD.79.043511
- Suwa, M. and Nihei, T. (2010) Physical Review D, 81, Article ID: 023519. http://dx.doi.org/10.1103/PhysRevD.81.023519
- Wang, B., Lin, C.Y. and Abdalla, E. (2006) Physics Letters B, 637, 357-361. http://dx.doi.org/10.1016/j.physletb.2006.04.009
- Berger, M.S. and Shojaei, H. (2006) Physical Review D, 74, Article ID: 043530. http://dx.doi.org/10.1103/PhysRevD.74.043530
- Setare, M.R. (2006) Physics Letters B, 642, 1-4. http://dx.doi.org/10.1016/j.physletb.2006.09.027
- Setare, M.R. (2007) [hep-th/0701242].
- Wu, Q., Gong, Y., Wang, A. and Alcaniz, J.S. (2008) Physics Letters B, 659, 34-39. http://dx.doi.org/10.1016/j.physletb.2007.10.061
- Feng, C., Wang, B., Gong, Y. and Su, R.K. (2007) [arXiv:astro-ph/0706.4033].
- Karwan, K. (2008) [arXiv:astro-ph/0801.1755].
- Horvat, R. (2004) Physical Review D, 70, Article ID: 087301. http://dx.doi.org/10.1103/PhysRevD.70.087301
- Pavon, D. and Zimdahl, W. (2005) Physics Letters B, 628, 206-210. http://dx.doi.org/10.1016/j.physletb.2005.08.134
- Guberina, B., Horvat, R. and Nikolic, H. (2007) JCAP, 0701, 012.
- Zhang, X. and Wu, F.Q. (2005) Physical Review D, 72, Article ID: 043524. http://dx.doi.org/10.1103/PhysRevD.72.043524
- Chang, Z., Wu, F.Q. and Zhang, X. (2006) Physics Letters B, 633, 14-18. http://dx.doi.org/10.1016/j.physletb.2005.10.095
- Zhang, X. and Wu, F.Q. (2007) Physical Review D, 76, Article ID: 023502. http://dx.doi.org/10.1103/PhysRevD.76.023502
- Zhang, X. (2005) International Journal of Modern Physics D, 14, 1597. http://dx.doi.org/10.1142/S0218271805007243
- Setare, M.R., Zhang, J. and Zhang, X. (2007) JCAP, 0703, 007.
- Zhang, J., Zhang, X. and Liu, H. (2008) Physics Letters B, 659, 26-33. http://dx.doi.org/10.1016/j.physletb.2007.10.086
- Zhang, X. (2007) Physics Letters B, 648, 1-7. http://dx.doi.org/10.1016/j.physletb.2007.02.069
- Zhang, X. (2006) Physical Review D, 74, Article ID: 103505. http://dx.doi.org/10.1103/PhysRevD.74.103505
- Zhang, J., Zhang, X. and Liu, H. (2007) Physics Letters B, 651, 84-88. http://dx.doi.org/10.1016/j.physletb.2007.06.019
- Ma, Y. and Zhang, X. (2008) Physics Letters B, 661, 239-245. http://dx.doi.org/10.1016/j.physletb.2008.02.028
- Zhang, J., Zhang, X. and Liu, H. (2007) European Physical Journal C, 52, 693-699. http://dx.doi.org/10.1140/epjc/s10052-007-0408-2
- Kowalski, M., Rubin, D., Aldering, G., Agostinho, R.J., Amadon, A., Amanullah, R., et al. (2008) Astrophysical Journal, 686, 749-778. [arXiv:astro-ph/0804.4142] http://dx.doi.org/10.1086/589937
- Suzuki, N., Rubin, D., Lidman, C., Aldering, G., Amanullah, R., Barbary, K., et al. (2012) Astrophysical Journal, 746, 85. http://dx.doi.org/10.1088/0004-637X/746/1/85
- Nesseris, S. and Perivolaropoulos, L. (2005) Physical Review D, 72, Article ID: 123519. http://dx.doi.org/10.1103/PhysRevD.72.123519
- Perivolaropoulos, L. (2005) Physical Review D, 71, Article ID: 063503. http://dx.doi.org/10.1103/PhysRevD.71.063503
- Nesseris, S. and Perivolaropoulos, L. (2007) [arXiv:astro-ph/0612653].
- Pietro, E.D. and Claeskens, J.F. (2003) Monthly Notices of the Royal Astronomical Society, 341, 1299-1310. http://dx.doi.org/10.1046/j.1365-8711.2003.06508.x
- Simon, J., Verde, L. and Jimenez, R. (2005) Physical Review D, 71, Article ID: 123001. http://dx.doi.org/10.1103/PhysRevD.71.123001
- Gaztañaga, E., Cabré, A. and Hui, L. (2009) Monthly Notices of the Royal Astronomical Society, 399, 1663-1680. http://dx.doi.org/10.1111/j.1365-2966.2009.15405.x
- Stern, D., et al. (2010) JCAP, 1002, 008.
- Moresco, M., et al. (2012) Journal of Cosmology and Astroparticle Physics, 8, 6.
- Busca, N.G., Delubac, T., Rich, J., Bailey, S., Font-Ribera, A., Kirkby, D., et al. [arXiv:astro-ph/1211.2616].
- Farooq, O., Mania, D. and Ratra, B. [arXiv:astrp-ph/1308.0834].
NOTES
*Corresponding author.