Journal of Modern Physics
Vol.05 No.16(2014), Article ID:51065,13 pages
10.4236/jmp.2014.516167
Prediction and Derivation of the Higgs Boson from the Neutron and Properties of Hydrogen Demonstrating Relationships with Planck’s Time, the Down Quark, and the Fine Structure Constant
Donald William Chakeres
Department of Radiology, The Ohio State University, Columbus, OH, USA
Email: donald.chakeres@osumc.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 August 2014; revised 18 September 2014; accepted 12 October 2014
ABSTRACT
A high accuracy Higgs boson, H0, is an important physical constant. The Higgs boson is associated with the property of mass related to broken symmetry in the Standard Model. The H0 mass cannot be derived by the Standard Model. The goal of this work is to derive and predict the mass of H0 from the subatomic data of the frequency equivalents of the neutron, electron, Bohr radius, and the ionization energy of hydrogen. H0’s close relationships to the fine structure constant, α, the down quark, and Planck time, tP are demonstrated. The methods of the harmonic neutron hypothesis introduced in 2009 were utilized. It assumes that the fundamental constants as frequency equivalents represent a classic unified harmonic system where each physical constant is associated with a classic harmonic integer fraction. It has been demonstrated that the sum exponent of a harmonic integer fraction, and a small derived linear δ value of the annhilation frequency of the neutron, vn, 2.2718591 × 1023 Hz, (vns) as a dimensionless coupling constant represent many physical constants as frequency equivalents. This is a natural unit system. The harmonic integer fraction series is 1/±n, and 1 ± 1/n for n equals 1 to ∞. The H0 is empirically and logically is associated with harmonic fractions, 1/11 and 1 + 1/11. α−1 is associated with 11. α−1 is a free space scaling constant for the electromagnetic force so it is logical that 11 should also have a pair, but for a free space mass constant. Also there should be a harmonic faction pair for the down quark, 1 − 1/11, just as there is pairing of the up quark, 1 − 1/10, and top quark, 1 + 1/10. The harmonic neutron hypothesis has published a method deriving a high accuracy Planck time, tP from the same limited subatomic data. The δ line for H0 should be closely associated with tP since they both are related to mass. The preferred derived value related to tP2 is 125.596808 GeV/c2. A less attractive derived value is 125.120961 GeV/c2 from the weak force factors only. The experimental CMS and Atlas value ranges are 125.03+0.26+0.13−0.27−0.15 and 125.36±0.37±0.18 GeV/c2. Empirically the H0 δ line is closely related to the same factors of the tP δ line, but with inverse sign of the slope. The H0 completes the paring of a free space constant for mass, the down quark, and an inverse sign δ line factors with tP. It is possible to accurately derive the mass of H0 from subatomic physical data. The model demonstrates that H0 is closely associated with α, the down quark, and tP. This prediction can be scrutinized in the future to see if it is accurate. The model has already published accurate predictions of the masses of the quarks.
Keywords:
Higgs Boson, Neutron, Unificaiton Model, Down Quark, Fine Structure Constant, Planck Time, Gravity

1. Introduction
The Higgs boson, H0, is one of the current research hotspots in Particle Physics research [1] -[6] . The Higgs boson is a neutral, positive parity, no color charge, and zero spin elemental boson. All particles get their mass properties from interacting with the Higgs boson. The Standard Model and electroweak theory do not predict the mass of the Higgs boson. Higgs and others in the 1960s proposed that the symmetry of the Standard Model had to be broken for an unusual type of field to exist throughout space that would give certain particles mass properties. The existence of the Higgs boson was confirmed at CERN on 4 July 2012. According to the Standard Model with broken symmetry a “vacuum” is filled with a condensate of Higgs particles where other particles continuously collide with Higgs bosons as they travel. The stronger the interaction with the Higgs condensate the more massive a particle becomes. Mass is proportional to coupling with the Higgs boson.
A precise Higgs boson is an important physical constant, but cannot be highly accurately measured. The experimental CMS and Atlas value ranges are 125.03+0.26+0.13−0.27−0.15 and 125.36±0.37±0.18 GeV/c2. The goal of this work is to derive and predict a high accuracy H0 from solely subatomic data: the neutron, n, electron, e, Bohr radius, α0, and the ionization energy of hydrogen, the Rydberg constant, R. The derived value is 125.596808 GeV/c2.
The prediction and derivation of H0 is done utilizing a purely computational method introduced in 2009 referred to as the harmonic neutron hypothesis [7] -[13] . In a US copyrighted document from September of 2006 “The imaginary number neutron symphony” the author Donald Chakeres predicted “It is logical to assume that the lower bound of the Higgs boson should be defined by the interception of the qf value for the inverse down quark (qf 12/11) and the complex conjugate slope of the weak kinetic line (Figure 3)” [13] . This quantum fraction prediction for H0 has been proven to be true. In 2009 the quarks were predicted to be associated with a specific line, bem [10] . This has been proven to be true. In 2013 the model predicted the masses of the quarks utilizing identical computational methods starting only with the physical data of vn and the ionization energy of the electron in hydrogen. The derivations have been shown to be accurate on comparison to 2014 experimental data that were not available in 2013, Table 1 [10] . Therefore, this model is valid and has already made important predictions. The same may be true for the H0.
The main hypothesis is that the fundamental constants as frequency equivalents represent a classic unified harmonic fraction system, Tables 1-3, Figure 1. The annihilation frequency of the neutron, vn, 2.27185908 × 1023 Hz, as a dimensionless coupling constant (vns) is the fundamental frequency/coupling constant. It was assumed that the gravitational binding energy of the electron in hydrogen would be as equally important to the gravitational force as the ionization energy of hydrogen is to electromagnetic force. The genesis of the hypothesis was based on the empiric observation that there is an integer exponent relationship between the gravitational binding energy of the electron in hydrogen, the energy of Planck’s constant with a frequency of 1 Hz, and the energy equivalent of the neutron. When these are evaluated as frequency equivalents this has properties of classic quantum spectra. This property is that the possible energy levels are defined a simple integer equation and a natural physical unit. Two times the frequency equivalent of gravitational binding energy of the electron in hydrogen, 2 ´ 2.90024 ´ 10−24 is 5.80048466 ´ 10−24 Hz. The frequency equivalent of Planck’s constant, h, is 1 Hz.
Table 1. Comparison of the predicted harmonic neutron hypothesis quark masses from 2013 and experimental data from 2014.
Table 1 lists the experimental mass values for the quarks and their ranges in 2013, the 2013 harmonic neutron hypothesis predictions, and the reported experimental values from 2014 [10] . The derived values accurately predicted the experimental data in advance of its publication except for the strange quark supporting the hypothesis. This was related to assigning the qf to be 29/30 while the correct qf is apparently 27/28. The quarks were predicted to be associated with the bem lines in 2005, 2009 and 2013 [7] [10] [13] . The same may well be true for the H0.
Table 2. Example of the integer exponents and associated frequencies of a harmonic exponential system with a vf of 100.
Table 2 is a chart of the n, harmonic exponents, n, v, and derived vf values for an integer exponential harmonic system described in this model. To simplify the math a fundamental frequency of vf of 100 is utilized. Note that if a single frequency and its integer are known the whole matrix can be derived.
Table 3. Example of the harmonic fraction exponents and frequencies of a harmonic exponential system with a vf of 100.
Table 3 is a chart of the n, harmonic fraction exponents, 1/±n, v, and derived vf values for an exponential harmonic fraction system described in this model. To simplify the math a fundamental frequency of vf of 100 is utilized. Note that if a single frequency and its harmonic fraction are known the whole matrix can be derived.
vn Hz is 2.2718591 × 1023 Hz. The vns reciprocal is 4.4016815 ´ 10−24. All three are separated by a ratio of vns. Each of these represent unit values of the forces for gravitational force, electromagnetic, and strong forces. Two times the frequency equivalent of gravitational binding energy of the electron in hydrogen times vns equals 1.3178. 1 Hz for h times vns equals vn Hz. The 2 factor in the gravitational binding energy arises from the fact it is a kinetic energy. Looking at the ratio coupling constant relationships these represent the consecutive integer exponent series of −1, 0, and 1: (vns)n Hz. This is a discrete quantum relationship that is similar to classic spectra where a physical constant is utilized in a consecutive integer series function that defines a series of discrete associated possibilities, harmonics.
This discrete exponential integer relationship has classic harmonic fraction properties when evaluated on a 2 dimensional plane, Figure 1. This plane is referred to as the universal harmonic exponent plane. An integer series of n equals 0 to ±∞ is plotted with the x and y axes equal n. This is an orthogonal array of discrete points all equally spaced. The point (0, 0) is associated with a v, frequency, of 1. The other points represent discrete integers exponents of the fundamental frequency of the system (vf)n. The points running diagonally from the left upper margin down to right are all identity points of the same value, The points (1, −1), (0, 0), and (−1, 1) all have an orthogonal sum of 0. This sum is a classic vector property. An equal orthogonal sum distance from the (0, 0) point represents a fixed ratio in the linear domain. This is a discrete system so an orthogonal sum distance of 1 from (0, 0) is a diamond pattern, not a circle. This is the most basic pattern in the model (see Figure 4 of the 2009 paper [7] ). For example, a line connecting the points (0, 1) and (1, 0) is associated with an orthogonal vector sum of 1. The system is not continuous though just like any harmonic system. The pattern is related solely on integers and harmonic integer fractions. In this model the only valid discrete possible points are along lines intersecting two integer points. Analysis of the interception points of the integer lines represents the classic harmonic fraction series, Figure 1. This is the origin of the harmonic fraction properties, but in an exponential system. The actual axes of the physical system represent the harmonic fractions series on the x axis. The y axis follows identical patterns, but their unit values are not 1, but in the range of 10−3 for δs.
Under routine circumstances if one has a physical constant its value can be utilized in standard equations, but it is isolated and does not inherently predict other logically associated values. In a harmonic system if the frequency and the harmonic fraction are simultaneously known then it is possible to derive an infinite number of other harmonics including the fundamental frequency. This harmonic mathematical character is how it is possible to derive physical constants from no standard physical data of the entity in question. This is not a new or radical concept for quantum spectra. The fundamental constants in many aspects do represent a classic quantum spectra. A good example is the Moselely’s law. If one knows the ionization energy of hydrogen then it is possible to predict all of the ionization energies of other elements if their number of protons are known despite the absence of physical measurements.
The hydrogen and the neutron subatomic data scale the whole universal harmonic 2D system, but these specific individual hydrogen values were not directly used in the H0 derivation. The annihilation frequency of the neutron was used directly in all of the calculations though. It is inappropriate to view this as a derivation from standard product ratio relationships of these subatomic entities to cosmologic ones. This derivation is a direct one independent of any actual physical measure of H0, but based purely on harmonic fraction properties. This is the unique aspect of this model that both quantum and cosmologic physical constants are accurately scaled simultaneously on a unified geometric 2 dimensional vector universal harmonic plane through simple linear relationships. The Standard Model fails in this goal. This is the significance of this method. There are no actual data from CERN measurements utilized.
The model is based on classic physical, mathematical, and quantum properties including: a fundamental frequency, vf, a consecutive integer series, harmonic integer fractions, 1 ± 1/n and 1/±n for n = 1 to ∞, discrete values associated with each quantum integer, natural unit system where the speed of light, charge, Planck’s constant, and the exponent of the neutron are all 1, an exponential distribution of energy over time, dimensionless coupling constants, standard vector properties for computations on a 2 dimensional plane, standard proportionality constants, but analyzed as exponential equivalents, these are linear on the 2D plane, resonance, prime number properties, discrete quantum values, and symmetry.
The model is not in conflict with the Standard Model, but is a supplement that excels at the scaling ratios between entities evaluated. The calculations are valid since all of the routine experimental values are used, but as frequency or exponent equivalents of base vns. The difference of two exponent points on the 2D universal harmonic exponent plane represents a standard proportionally constant in the linear domain. Two points define a line and a slope. These transformations do not alter any of the results. The frequency equivalent values can be converted to the identical values of the standard units and visa versa.
The harmonic neutron hypothesis has demonstrated that harmonic integer fraction exponents, plus small derived δds from the properties of hydrogen exponents of annihilation frequency of the neutron, vn, 2.271859078 × 1023 Hz, (vns) as a dimensionless coupling constant represent other physical constants as frequency equivalents [7] -[12] . The δds are defined by lines related to simple sums and differences of the δk lines defined by the electron, Bohr radius, and the ionization energy of hydrogen points. The known exponents, exp δks, are the loge of the physical constant frequency equivalent divided by the loge of vns. The derived exponents are referred to as expd. This is a classic exponential base transformation. The known or derived exponent minus its harmonic fraction is δd or k, derived or known. The differences between the known or derived exponents and the harmonic fractions are very small. The harmonic fraction pattern is empirically a usually obvious, see Table 2 from the 2009 paper [7] .
The δs are a mathematical imperative, and make the system much more complicated to understand. They “shim” all of the individual exponents of the constants to a common resonance of vn Hz. There are four product ratio relationships of α, e, α0, and R as frequency equivalents [11] . These associate specific known numbers with specific known integer fractions. For example 2 is associated with the integer fraction of 10/1155. This is associated with its fundamental frequency of 2(1155/10) which is 5.8744 × 1034. Each of these specific number- quantum fraction pairs are associated with a different fundamental frequency. The solution to bring all of the fundamental constants into resonance with vn or any single fundamental frequency is to add small δ values to their integer fractions. These δk values for each known entity can be calculated if the harmonic faction is known and the frequency equivalent of the constant. These calculated δ values from known physical constants are referred to as δk. The δ can also be derived from a δd line defined by the properties of hydrogen. These derived values are referred to as δd to avoid confusion of the origin of the specific δ. The actual δd are defined by the δd line and an associated quantum fraction value. Physical entities defined by a common proportionality constant have a common δ line property. The known constants spontaneously fall on δ lines since they are related to a common proportionality constant relationship. The δk and d values represent natural units just as vns does. This is how it is possible to make exact predictions of physical constant value without direct measurements.
Review of the known exponent show that they are all nearly identical to one of the harmonic fraction series [7] . For example, the harmonic fraction of the Bohr radius is 4/5, and it known exponent is 0.80291631 which is only 1/1000’s from 0.8. This pattern is repeated for all of the studied constants. It is more difficult to assign the principal quantum numbers when they are large unless the value of the constant is known with high precision. For the small ones below 14 it is usually not a problem because they are very widely spaced. This predictive power of the method is possible since the model is a classic harmonic system where other physical constant values can be derived from the harmonic fraction series and the fundamental frequency, Tables 1-3. The Rydberb series and Planck’s equation are examples of this type of system. Each harmonic fraction, integer can be associated with a discrete harmonic and physical constant. An example analogous to this method is if one knows the wave length of a single hydrogen spectral line and the associated n1, and n2 then the complete infinite wavelength series including the Rydberg constant can be derived with no other physical data. This is exactly similar to this method. The common fundamental frequency in this model is vn.
The harmonic neutron hypothesis has derived a high accuracy Planck time, tP, gravitation constant, G, the quarks, leptons, running fine structure constant, α−1 at Z, and the kinetic energy lost in neutron beta decay [7] - [13] . All of the derivations are done utilizing only four physical values as frequency equivalents: vns, the electron, ve, Bohr radius, vα0, the Rydberg constant, vR, which is associated with the ionization energy of hydrogen. δd are derived from logical δk lines since the slopes and intercepts are related to the electron, Bohr radius, and the ionization energy of hydrogen points. These fundamental constants represent the harmonic fractions including the entities, harmonic fractions, and exponents: n, 1, 1; e, 6/7, 0.86023062; α0, 4/5, 0.80291631; and R, 2/3, 0.66436554.
These data are plotted on a 2 dimensional universal harmonic plane, Figures 1-4. The x axis is the harmonic fraction minus 1. This −1 factor centers the neutron at the (0, 0) point, and is equivalent to dividing each constant’s frequency equivalent by vn. These represent coupling constants. The y axis is the known or derived exponentk or d of vns minus the harmonic fraction, the small δs are in the range of 10−3. These points are exactly equivalent to their standard unit values as exponents of vns for the known or derived physical constants so there is no possible manipulation of the known or derived data.
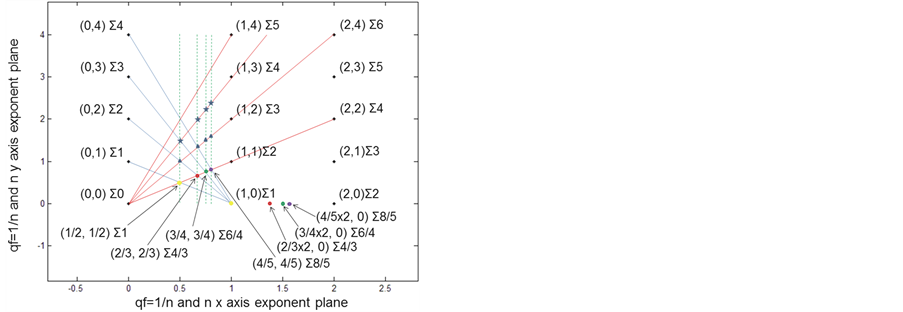
Figure 1 . An example of a generalized universal harmonic exponential 2D plane with integer unit values and its property as a 1/n and 1±1/n series geometric exponent calculator.
Figure 1 plots a 2D consecutive integer orthogonal array representing discrete exponent points, vfn. The point (0, 0) is associated with a frequency of 1, vf0. All other points represent the orthogonal sum of their x and y axis locations, shown as Σ values to the right of their x, y coordinates. The frequency associated with those points is vfΣ. The ratio between any two integer points on a vertical or horizontal axis is vf. Note that running from the upper left to the lower right the Σ values are identities. The line connecting points (0, 1) and (1, 0) all add to 1. This is not a continuous number system, but identical to harmonic systems that are discrete and related to integers and integer fractions. This is a classic quantum characteristic. An equal ratio relationship from the (0, 0) point is a diamond pattern. This is identical to the published pattern for the fundamental constants, Figure 4 from the 2009 paper [7] . The only valid discrete points can fall at the intersections of lines connecting two integer points. These are the only possible unit based points. The red lines all arise from (0, 0) and radiate to the integer points of (1, n). The blue lines all start at point (1, 0) and radiate to integer points (0, n). Let us focus on the red line connecting (0, 0) and (1, 1) and the intersection points of the blue lines. The points (0, 0) and (1, 1) are separated by an orthogonal distance of 2 so their ratio equals vf2 or vf−2 depending on the direction of the vector. This universal harmonic plane has classic vector properties. Note that each blue line intercepts the red line at classic harmonic fraction values only. The sums of the orthogonal distances shown as the yellow, red, green and purple circles are valid points. Also note that their Σ values simultaneously represent the identical harmonic fractions for a vf2 fundamental frequency, ½ × 2, ¾ × 2, 4/5 × 2. These all fall on the x axis. Other possible valid values are seen on the lines connecting (0, 0) and (1, 2); and (0, 0) and (1, 3) as blue triangles and blue stars. This is the identical pattern seen with the quarks in Figure 2 from the 2013 paper [10] . The harmonic fraction properties arise not from the classic properties of integer divisions of a string, but from the integer properties of a 2D integer based exponent plane.
Figure 2 . A universal harmonic exponential 2D plot of the points for the n, h, e, α0, and R, and the wk, em, and H0δd lines demonstrating their relationships.
Figure 2. This is a universal harmonic exponent plot. The x axis equals the qfs minus 1. The y axis is the difference between the known or derived exponents and their qfs, δd or k. The previously published points related to h, n, e, R, α0 are plotted [7] . These are identical to those points in FIG of the 2011 paper [8] . These points define three lines. e and α0 define the wk line with slope of awk and y intercept of bwk (blue solid line). The em line is defined by h and R (red solid line) with a slope of bem and a y intercept of bem. The black line defines H0d line. The H0d slope is the sum of 2 × bwk − awk + bem for the tP2 derivation. The H0d line related to the tP2 derivation is defined by two points, (−1, −(bwk − awk)) and (0, bwk + bem). At x axis 12/11-1, 1/11, the known lower and upper H0k points are plotted as blue and red dots, δk. The derived tP2 H0d point is centered at the black dot, δd. The experimental values are nearly identical to the derived value. The tP2 related derived H0d equals 125.596808 GeV/c2. The experimental CMS and Atlas value ranges are 125.03+0.26+0.13−0.27−0.15 and 125.36±0.37±0.18 GeV/c2. Figure 3 and Figure 4 are close up and distant views of the same data
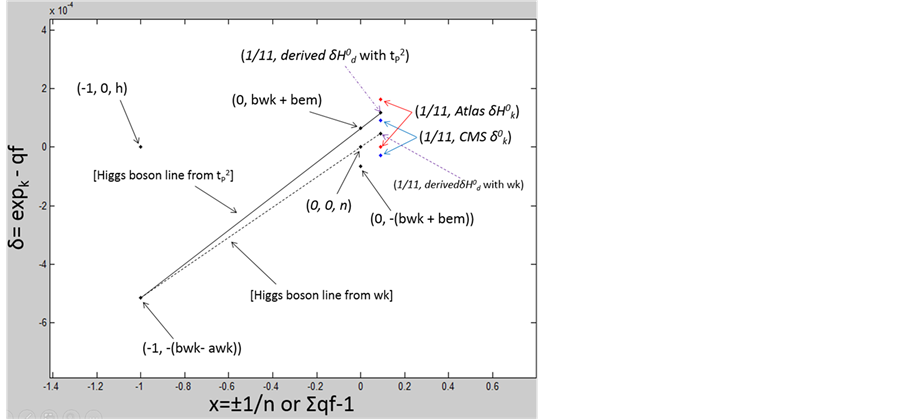
Figure 3 . A close up view of the universal harmonic exponential 2D plot of the points for the known experimental ranges of H0 δk points, and the predicted H0 points and H0 δd lines.
Figure 3. This is a universal harmonic exponent plot. The x axis equals the qfs minus 1. The y axis is the difference between the known or derived exponents and their qfs, δk or d. This is a detail view of the H0d line compared to Figure 2. The solid black line defines the preferred H0d line related to tP2. The H0d slope is the sum of 2 × bwk − awk + bem. The H0d line is defined by two points, (−1, −(bwk − awk)) and (0, bwk + bem). The dash dot purple arrow points to that specific derivation point. The dashed black line is the H0 d line related to the points (−1, bwk − awk) and (0, 0) which is related to the purely wk derivation. The dashed arrow points to that specific derivation. At x axis 12/11-1, 1/11, the known lower and upper H0k points for both the CMS and Atlas data are plotted as blue dots for CMS and red dots for Atlas, δk. The experimental values fall just outside of the derived values. The derived tP2 H0d equals 125.596808 GeV/c2. The experimental CMS and Atlas value ranges are 125.03+0.26+0.13−0.27−0.15 and 125.36±0.37±0.18 GeV/c2. The end points of the H0d line at x −1 and 0 are related to the inverses of the wk line and the tP2 line points
Figure 4 . An expanded view of the universal harmonic exponential 2D plot of the predicted H0 point and H0 δd line showing its close relationship to the tP2 δk line..
Figure 4. This is a universal harmonic exponent plot. The x axis equals the qfs minus 1. The y axis is the difference between the known and/or derived exponents and their qfs, δk or d. This is an expanded view of the H0d from tP2 (solid green), tP2d (dashed green), wk (solid red), em (dashed red), and ±(bwk + bem) lines (purple solid and dashed). tP2 in this plot is dimensionless. Its actual units are s2 not Hz. The H0d line can be defined by two points, [0, (bwk + bem)] and [−163/35, −163/35 × (bwk − awk) − 128/35 × (bwk + bem)]. The slope of the H0d line is bwk minus the slope of the tP2d line, 2xbem – awk + bem. The tP2d green dashed line has an inverse, but symmetric pattern. It is defined by the points [0, −(bwk + bem)] and [−163/35, −163/35 × awk +128/35 × (bwk + bem)]. The absolute δ distance from (−163/35, 0) to the y intercept of the H0d line at x equals −163/35 is identical to the δd distance from [−163/35, −163/35 × (bwk)] to the y intercept of the tP2d line at x equals −163/35. The sum of the −(bwk + bem) line and a line from (0, 0) to −163/35 × (bwk-awk) equals the H0d line. The sum of the +(bwk + bem) line and a line from (0, 0) to −163/35 × awk equals the tP2d line.
The ratio of two physical constant frequency equivalents can represent proportionality constant. For example the ratio of the ionization energy of hydrogen and the electron frequency equivalents is identical to Coulombs constant in the frequency domain. On the 2 dimensional harmonic fraction minus 1 δ exponent plane, the universal harmonic plane, proportionality constants represent the sum orthogonal distances along the x and y axes. This is a classic vector property. Therefore, a line connecting two points on the universal harmonic plane represents a common proportionally constant. For example the distance between two points is (integer fraction + δ). Assuming that the input of proportionality constant equation equals the constant itself then the output is the constant squared. The square of the proportionality constant in the exponent domain is (2 × integer fraction + 2 × δ). This defines a line. The slope of that line scales the proportionality constant. Some physical constants such as gravity are defined by more than two factors so the associated δ line represents a more complicated composite, but still defined by a single line, and single proportionally constant. There physical constants that are related to a common proportionality constant spontaneously and naturally fall on lines on the universal harmonic plane. This is how it is possible to derive related constants if the δ line is known.
From these hydrogen points two force lines have been defined. The weak kinetic, wk, line is logically associated with e and α0. The harmonic fraction possibilities on this line have been shown to be related to weak force and kinetic entities such as the leptons, W, and Z. The kinetic energy lost in the neutron beta decay process points fall on this line, Figure 1 of the 2011 paper [8] . The slope is referred to as awk, and y intercept as bwk.
From the points for Planck’s constant with a frequency of 1, and R the electromagnetic, the em line is defined. Its harmonic possibilities on that line are logically associated with electromagnetic entities including quarks and mesons. These points are the bem derived δds. The slope and y intercept both equal bem. The top, bottom, and charm quarks all fall on the line defined by slope −bem and y intercept bem, Figure 2 of the 2013 paper [10] .
Other physical constant’s harmonic fractions represent logical product values of two quantum numbers, another classic property of harmonic system. This is not a property of standard quantum spectra. This pattern is classic in many other harmonic systems. Utilizing these harmonic fractions and lines defining the δd line values for different forces other constants are derived to high accuracy including the quarks. Associated physical constants fall on a common δd force line.
Starting with these four subatomic points tP2 was derived from the slopes and intercepts of the em and wk line in a similar fashion as the quarks [9] . In the frequency domain, tP2 is identical to the Newtonian gravitational constant. The product of tP2 times the frequency equivalents of two masses and the frequency equivalent of their separation distance is the frequency equivalent of the energy of the system just like the standard equation. The tP2 harmonic fraction is the sum of the harmonic fractions defining the binding energy of the electron in hydrogen and includes: the e, 6/7, α0, 4/5, proton, an exponent of slightly less than 1, and the gravitational binding energy of electron with an exponent slightly less than −1. This is the exponent equivalent of the standard gravitational equation for energy. The actual derivation of tP2 did not utilize any of these specific subatomic points just as the method utilized here to derive H0 did not utilize specific hydrogen points. It is assumed that the line defining H0 is a sum of the slopes and y intercepts of two lines previously published similar to the line defining tP and G. It is also assumed that there is a close relationship between tP2 and H0 lines since both are related to the property of mass and gravity. In fact the slope of the H0 line is bwk minus the slope of tP2 line. The y intercept of the H0 line is the inverse of the tP2 line.
There should be a universal field fundamental physical constant related to the principal quantum number +11 and harmonic fractions of 1/11 and 12/11. This represents H0. 11 is a very unique prime of the harmonic neutron hypothesis since it is the highest prime number that is necessary to define the down quark and therefore all of the components of the neutron [7] [10] . The principal quantum number −11 is associated with the down quark, qf 10/11. 11 is also associated with the charm and bottom quarks [10] [12] . There is a similar inverse sign pair principal quantum number relationship of the up and top quarks. Their respective principal quantum numbers are −10 and +10, and integer fractions of −1/10 and 9/10 for the up quark, and +1/10 and 11/10 for the top quark.
11 is also associated with the exponent of α−1 that represents a universal electromagnetic field constant. 1/11 is the harmonic fraction associated with α−1. There should be a paired universal field constant that is associated with mass and gravity. It is logically hypothesized that it is the H0. A high accuracy H0 should be derivable from vns, the H0 line, and its harmonic fractions values of 1/11, 12/11 which is demonstrated here.
In the harmonic neutron hypothesis, physical constants are assumed to be derivable from four previously published values, vns, and slopes and y intercepts of two lines, which are derived from points associated with the e, α0, and R. Starting with these data, only H0 is accurately derived beyond it experimental accuracy similar to previously derived for tP, and the quarks. It is not typical to derive nuclear, high energy collider, gravitational, astronomy constants from these types of initial sub-atomic data. This model is not in conflict with the Standard Model or astronomy methods. This method is accurate, valid, and complimentary. It is an innovative scaling supplement. This model succeeds where the Standard Model fails.
2. Methods and Results
Tables 1-3 are examples of the mathematical pattern of an exponential harmonic fraction matrix and are similar to this model’s system. The fundamental frequency, vf, in this example is 100. It is difficult to imagine this system in base vn. Note that the system is extremely defined and integrated identically in concept to the Rydberg series. Knowing one frequency and its harmonic fraction allows for derivation of all of the other values. For example, if the known frequency is 21.5443 and its harmonic fraction is 2/3 then 21.54433/2 must be the vf. That equals 100, and therefore all of the other harmonic can be derived. Table 1 represents the integer exponents, Table 2 the harmonic fractions, and Table 3 the partial harmonic fractions.
The harmonic neutron hypothesis states that the fundamental constants as frequency equivalents are related to the annihilation frequency of the neutron, vn, 2.271859078 × 1023 Hz, relative error of 2.2 × 10−8 as a dimensionless number, vns [3] -[6] . The floating point (the number of accurate digits) is based on known experimental data for the subatomic data, of approximately 5 × 10−8. For H0 the relative error is much higher, 6 × 10−3. All of the known fundamental constants are converted to frequency equivalents, vk. The masses are converted by multiplying by c2 (speed of light squared) then dividing by h (Planck’s constant). The distances are converted by dividing the wavelength into c. Energies in Joules are converted by dividing by h. The eV value for the neutron is 939.565378(21) × 106. Hz is converted to eV by multiplying by the constant, 4.1356675 × 10−15 eV/Hz. eV was converted to Hz by multiplying by the constant 2.4179893 × 1014 Hz/eV. All of the data for the fundamental constants were obtained from the websites (http://physics.nist.gov/cuu/Constants/ and www.wikipedia.org. The NIST site http://physics.nist.gov/cuu/Constants/energy.html has an online physical unit converter that can be used for these types of calculations so the values used in the model are all standard conversions. Some of the values have slightly changed since the original paper since the values for the fundamental constants have been updated since 2009. The differences are not significant. Frequency is inherently dimensionless. Frequency represent cycles per second in the time domain, and in the distance domain equals the wave velocity times one unit time divided by the circumference of a circle defining one cycle. Therefore, frequency is also a distance divided by a distance, and therefore dimensionless.
The harmonic neutron hypothesis assumes that harmonic integer fraction exponents of vns are the degenerate, not split by δ, values in a symmetric pattern, not the frequency values themselves. vns is raised to exponents of a consecutive harmonic quantum fraction (qf) series 1 ± 1/n for the principal quantum numbers n = 1 to ∞ represents many of the degenerate exponent values of the fundamental constants, Equation (1). The degenerate ratios of the constant’s frequency and vns represent vns raised to qfs, harmonic quantum fraction exponents of 1/±n for n = 1 to ∞, Equation (2). The exponents of known entities are the ratio of the loge of the vk divided by the loge of vns, Equation (3), Figures 2-4. The qf are plotted at qf-1, x axis location since they are related to the ratio of the known frequency and vn Hz, Equation (2).
 (1)
(1)
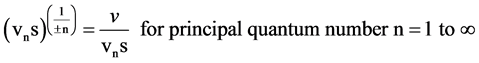 (2)
(2)
 (3)
(3)
vns raised to its known exponent, expk, equals it frequency equivalent of a physical constant, Equation (4). The δ values can be viewed as shifting the fundamental frequency for a specific physical constant slightly away from vn, Figure 1, Equations (4), (5). The known frequency equivalent of a fundamental constant is vk. The known vk is vns raised to the sum of the qf and the δk. The derived vd is vns raised to the derived exponentd. The derived δd is a linear function of the qf. The derived vd is vns raised to the δd line points at x equals 0, and x equals −1 and related to the qf, Equations (4), (5). δd values change with the qf. This is an alternate form to define any line. There are small derivable δd values that “shim” the degenerate qf to their exact exponent values, and bring all of the constants to a common fundamental frequency of vn, Equation (5). δ is the known exponent minus the qf, Equation (5). Some force δ lines can be derived since they commonly represent simple sums and differences of the slopes and y intercepts of the wk and em lines, bwk, awk, and bem, as in the H0d δ line.
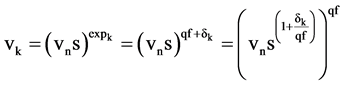
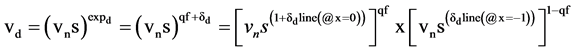 (4)
(4)
 (5)
(5)
Each fundamental constant is plotted and transformed on to the universal harmonic plane Figures 2-4. The harmonic fraction exponent minus 1 is the x axis value, Equation (6). The closet qf to the known exponent is its associated qf. The y axis is δ, Equation (5).
 (6)
(6)
The slopes and intercepts of two lines have been published and were derived from the properties of hydrogen and the neutron, Table 4, Figures 2-4. One line is related to weak kinetic, wk and entities, which is referred to as the wk line, Equations (7), (8). These fall on the harmonic fractions qf locations. This is defined by the points for the mass of the e, (−1/7, δe) and the Bohr radius α0, (−1/5, δα0). The slope is awk, 3.0003642866 × 10−3 and the y-intercept is bwk, 3.5163832934 × 10−3. Their respective principal numbers are 7 and 5, qfs 6/7, 4/5, and x axis values of −1/7 and −1/5. The frequency equivalent of the α0, vα0, is 5.665256398 × 1018 Hz; expα0 is 0.80291631044. The qf is 4/5 and its δ is 2.916310436 × 10−3. The frequency equivalent of the e, ve, is 1.23558996 × 1020 Hz; expe is 8.602306169. The qf is 6/7 and its δ is 3.087759823 ×10−3.
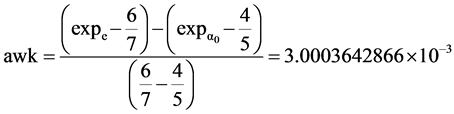 (7)
(7)
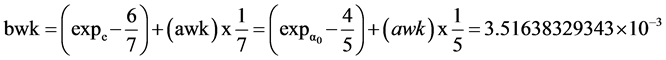 (8)
(8)
Table 4. Example of the partial harmonic fraction exponents and frequencies of a harmonic exponential system with a vf of 100.
Table 4 is a chart of the n, the partial fraction exponents, 1 ± 1/n, v, and derived vf values for an exponential harmonic partial fraction system, described in this model. To simplify the math a fundamental frequency of vf of 100 is utilized. In this case the partials can be two different values (n ± 1)/n. Note that if a single frequency and its harmonic fraction are known the whole matrix can be derived.
The electromagnetic, em, line is defined by the points for Planck’s constant, (−1, 0) and R (−1/3, δR), Figure 1, Equation (9). This is the second line that was previously published. It slope and y intercept, bem, are identical and equal −3.4516836 × 10−3. This line is related to the principal quantum number 3, qf, 2/3. The ionization energy of hydrogen is related to the Rydberg constant, R. The frequency equivalent of the hydrogen ionization energy, vR, is 3.28984196 × 1015 Hz; expR is 6.6436554435. The qf is 2/3 and its δ is −2.301122316 ×10−3. The line formed from the qf-1, δ point for Planck’s constant (h) is plotted at (–1, 0) by definition (Figures 2-4). The frequency of Planck’s constant is 1 Hz.
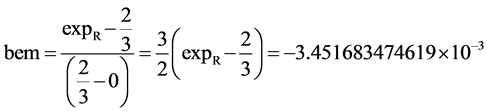
The mean experimental values for H0 were evaluated as frequency and exponent equivalents Table 5, Equations (3), (5). The experimental CMS and Atlas value ranges are 125.03+0.26+0.13−0.27−0.15 and 125.36±0.37±0.18 GeV/c2. The known upper and lower CMS and Atlas bounds δk, vk, expk are listed in Table 5. Empirically, this must be a harmonic fraction as hypothesized for H0, 12/11. These are plotted on the universal harmonic plane at x axis value of 12/11-1, 1/11, Figures 2-4.
The slope for the H0d line should be a simple sum of the y intercepts and slope of bwk, awk, and bem composite similar to the tP2 line, Equation (10). The slope should logically be a sum of all three factors unifying the weak and electromagnetic forces into one. The possible δd lines for H0d are empirically obvious by plotting the known H0 δk at +1/11, Figures 2-4. Lines going from the point (−1, −(bwk − awk)) to either the (0, 0) or (0, bwk + bem) points both go through the H0 known point range. The preferred logical point is (0, bwk + bem) since it is related to the inverse of the tP2 point. The other cosmology constants such as the Hubble constant and the cosmic background microwave radiation both fall on the tP2 line. The alternate possible point (0, 0) would imply that H0 is related solely to the weak kinetic, wk, force. This is believed to be less likely and less conceptually attractive.
In the tP2 case, the derived H0d slope is related to the sum of the difference between bwk and awk, plus the sum of bwk and bem, Equation (11) The H0d line related to tP2 derived slope can be described as the difference between the weak and electromagnetic force lines. The H0d line slope also equals bwk minus the slope of the tP2d line, Equation (11), Table 6. The actual line equation is y equals 5.8071882562 ´ 10−4 times (qf-1) plus 6.4699818816 × 10−5.
The tP2 related derived slope of the derived H0d line is 5.80718825 ´ 10−4, Equation (11). The tP2 related derived δH0d at x axis position 1/11 is 1.174924393 ´ 10−4, Equation (12). The tP2 related derived exponent of H0d is the sum of 12/11 and δH0d is 1.091026583, Equation (13). The frequency equivalent of the derived H0d is 3.03691744 ´ 1025 Hz, Equation (14). The derived H0d GeV/c2 mass equivalent is 125.596808 ´ GeV/c2, Equation (15).
The alternate wk related derived H0d is associated with a slope of bwk-awk, 5.1601801504 ´ 10−4. The δk is 4.691081880 ´ 10−5. The expk is 1.0909560017. The vk is 3.0254115 ´ 1025. The eV equivalent is 125.120961 GeV/c2. Though this does fall in the range of both experimental ranges this is believed not to be the true value
Table 5. List of natural unit values used for the derived/predicted calculations for H0 and tP2.
Table 5 lists the published values of vns, and the slopes and intercepts of the wk and em lines used for the derivation of H0. See Equations (7)-(9). All of these values have a relative error of approximately 5 × 10−8.
Table 6. Comparison of known experimental upper and lower bounds of the CMS and ATLAS H0 data and the harmonic neutron hypothesis predictions.
Table 6 compares the known and derived H0k and d range of GeV/c2, Hz, δk and d, and exponentsk and d. The experimental ranges for both the CMS and Atlas data are shown. The derived value has a relative error of approximately 5 × 10−8. The predicted values are related to both the line associated with tP2 and the one with the wk only. The tP2 derived values are assumed to be most valid and likely. See Equations (11)-(15).
for the conceptual reason that the Higgs boson should not be just a weak force constant. Previous miss assignments have been done though.
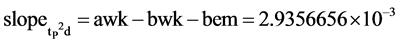
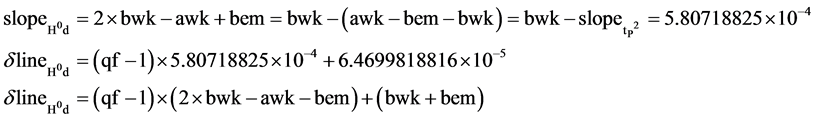
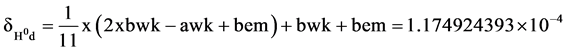

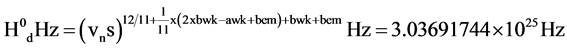
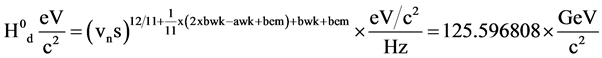
There is a symmetric inverse relationship of the H0d and the tP2d lines, Figure 3, Figure 4. The points defining their right margin, y intercepts, at x equals 0 are respectively ±(bwk + bem). The left margins can be defined at to the same x axis value, −163/35 as tP2. The extension of the H0d line δ shows an inverse symmetric relationship with the tP2 point to a point defined by (−163/35, −163/35 × bwk). The H0d line δ value equals −2.6397901 ´ 10−3 at x equals −163/35. This δd also equals (−163/35) × (bwk − awk) + (−128/35) × (bwk + bem). The difference between the δd (−163/35 × bwk), −1.6376300 ´ 10−2, and the tP2 δd, −1.3736514 ´ 10−2, is 2.6397901 ´ 10−3.
3. Discussion
A robust model that scales from quantum to cosmic physical constants does not exist [14] . The Standard Model fails. An important unique aspect of the harmonic neutron hypothesis is that it does resolve some of these limitations by analyzing the scaling relationships between the physical constants as a classic unified harmonic system. Derivation of an accurate H0 supports the validity of the model. There are no high energy data utilized. The initial data utilized for all of the calculations are subatomic data. These data are translated into a unified harmonic system from which many specific harmonic could be derived. There can be one harmonic for each consecutive integer. An analogy is Planck’s equation of energy, Planck’s constant and frequency. The only possible frequencies are integers. If one knows the energy and its corresponding quantum number then all of them can be derived including Planck’s constant independent of any other physical data. Derivation of H0 is the identical situation. The H0d δ line, harmonic fraction, and vn, fundamental frequency, are known. Any physical constant could be derived if these data are known.
A high accuracy H0 is an important physical constant for physics. The experimental data are moderately accurate [1] -[6] . This method demonstrates a simple, logical, and an accurate method since it is based on high resolution subatomic quantum values, as well as established harmonic neutron hypothesis methods. It also explains H0 precise logical origin and unification with other fundamental constants including the neutron, hydrogen, tP, the down quark, α, the weak and electromagnetic forces.
The principal quantum number 11 is very important and unique in the harmonic neutron hypothesis. The down quark is associated with the principal quantum number of −11 and the harmonic fractions −1/11, x axis location, and 10/11, qf. The principal quantum number of H0 is +11 and the associated harmonic fractions are +1/11, x axis location, and 12/11, qf. These are symmetric harmonic fraction pairs. This follows the identical harmonic fraction pattern for the up and top quarks [10] . These demonstrate harmonic fraction and geometric symmetry on the qf-1, δ exponent plane.
From analysis of the qf from the product ratio relationships of the e, R, and α0, α−1 is related to the principal quantum number 11, qf 1/11. vns raised to the exponent 1/11 equals 132.83343, the degenerate α−1 value. The reciprocal α’s δ is 5.7916812 ´ 10−4. α−1 equals 137.035999. The ratio frequency equivalents of the neutron divided into derived H0 is 133.6754. This is almost equal to α−1 and (vns)1/11. The differences are related to their δ values. α represents a force field scaling constant of free space for the electromagnetic force. H0 has a similar role, but unifies mass and gravity. α−1 is 1/11 above h, qf 0, which is the unit value for electromagnetic phenomena. H0 is 1/11 above the unit value for mass, qf 1, in the hypothesis.
The slope of the H0 line is defined by the inverses of two previously defined points important in the harmonic neutron hypothesis. One is the inverse of the left side end of the wk line at x axis −1 [7] . The wk line is defined by the point (−1, bwk − awk). The left side end of the H0d line is defined by its inverse, (−1, − (bwk − awk)). The right side end of the tP2d line is (0, −(bwk + bem)) [9] . The right side end of the H0d line is (0, bwk + bem). The slope of the tP2d line is the sum of awk − bwk − bem. The slope of the H0d line is 2 × bwk – awk + bem. bwk minus the slope of tP2 also equals the slope of the H0d line, therefore they are closely related in an inverse fashion, Equation 11. This demonstrates the relationship of the weak and electromagnetic forces to the H0d line. The H0d line literally represents the difference between the weak and electromagnetic force lines. Inertia and mass are literally what the differences between matter and electromagnetic energy are.
The δds for the H0d and tP2d lines are inverse symmetric pairs. At x equals 0 they are (bwk + bem) and –(bwk + bem). For the H0d line at x equals −163/35 they are (−163/35) × (bwk − awk) + (−128/35) × (bwk + bem) below δd zero and the same absolute distance above the −163/35 × bwk. It is logical that H0d and tP2d should be closely related. They are both related to mass and gravity. Inverse relationships as this are common in physics in general and the harmonic neutron hypothesis. The Rydberg series and Moseley’s law are exponential inverses as well.
Some have stated that the model is conjecture. The exponent and frequency values used in the calculations are transformed from the standard units, and the results can be converted back to standard units. All of the standard physics equations are maintained, but translated into exponential ones. It is impossible to manipulate the results since all of the components are fixed by valid physical values previously published, and harmonic fractions are integer fractions that cannot be altered. A perspective of the fundamental constants as a unified harmonic system is what is new and powerful. The logic and calculations are innovative, but represent classic valid physics and mathematics.
Some raise the issue that these findings are coincidence. The four subatomic entities used in the derivation, the slope and y intercept of the lines, and the methods used are all from the previous papers. These papers also derived the fundamental constants of the quarks, lepton, mesons, and the kinetic energy of neutron beta decay. This is a very restrictive system where the harmonic fractions have to be logical and mathematically related, the δd lines have to logical and derived from solely the three previously published slope and y intercept values, and the actual physical value points have to fall on the these lines.
In this specific derivation the only variables are the harmonic fraction, and the slope and y intercept of the H0 d line. The choice of 12/11 as the harmonic fraction is logical since 11 is the most unique integer of the hypothesis and associated with free space field constants of the electromagnetic force. There should be a pair representing a free space constant for mass and gravity. This obviously represents the H0. The slope and y intercept of the H0 line empirically are obvious. The also represent exact inverse values related to tP2d that was previously published. Any change in any of these factors leads to huge changes in the derived value. The H0 is one of many constants demonstrated to follow this same pattern. Following is a list of the physical entities and their documented harmonic fractions: Planck time squared, −163/35; cosmic background microwave radiations, CMB, 1/2; Hubble constant, −3/4; h, 0; n, 1; kinetic energy lost in the neutron beta decay process, ½; hydrogen ionization energy, 2/3; kinetic energy lost in the neutron beta decay process, 3/4; Bohr radius, 5/6; kinetic energy lost in the neutron beta decay process, 5/6; electron, 6/7; kinetic energy lost in the neutron beta decay process,7/8; up quark, 9/10; top quark, 11/10; down quark, 10/11; fine structure constant, 1/11; Higgs boson, 12/11; α−1, 1/11; W, 13/12; Z, 13/12; muon, 23/24; pion+, pion0, 27/28; strange quark, 29/30; bottom quark, 33/32; kaon0, 83/84; kaon+, 84/85; Tau, 84/83; charm quark, 109/110.
4. Conclusion
The harmonic neutron hypothesis is able to scale from quantum to cosmologic physical constants. This is done on a 2D universal harmonic plane that is indirectly scaled by the subatomic data. The calculations are made from the structure of the 2D universal harmonic plane not individual subatomic points. It has powerful predictive value exceeding the Standard Model since the physical constants are paired with a classic harmonic fraction. This allows for derivation of physical constants independent of any specific experimental data. This is a classic property of all quantum spectra so this is not a radical new concept. H0 can be derived/predicted from subatomic data only. H0d is logically and mathematically related to α−1, tP2, the down quark, and the differences between weak and electromagnetic forces. The derived H0d can be evaluated in the future to see if this is an accurate prediction. This derivation supports the validity of the neutron harmonic hypothesis that now includes some of the most important astronomy and quantum physical constants: the leptons, quarks, tP, H0, and G. All are defined utilizing solely vns and the published values for the four points of the n, e, R, α0, and the slopes and intercepts of the em and wk lines.
Acknowledgements
I would like to thank Tom Budinger PHD for his sage advice, support, and help. I would also like to thank Richard White MD for his support of this work.
References
- Higgs, P.W, (1964) Physical Review Letters, 13, 508-509. http://dx.doi.org/10.1103/PhysRevLett.13.508
- Iso, S. (2013) What Can We Learn from the 126 GeV Higgs Boson for the Planck Scale Physics Hierarchy Problem and the Stability of the Vacuum? arXiv:1304.0293
- Gherghetta, T., von Harling, B., Medina, A.D. and Schmidt, M.A. (2013) The Scale-Invariant NMSSM and the 126 GeV Higgs Boson. arXiv:1212.5243v2
- Carena, M., Beringer, J., et al., Particle Data Group (2012, 2013) Physical Review D, D86, Article ID: 010001. (2012 and 2013 Partial Update for the 2014 Edition).
- CMS Collaboration (2012) Physics Letters B, 716, 30-61. arXiv:1207.7235. Bibcode:2012PhLB..716...30C. http://dx.doi.org/10.1016/j.physletb.2012.08.021
- ATLAS Collaboration (2012) Physics Letters B, 716, 1-29. arXiv:1207.7214. Bibcode:2012PhLB..716....1A. http://dx.doi.org/10.1016/j.physletb.2012.08.020
- Chakeres, D.W. (2009) Particle Physics Insights, 2, 1-20.
- Chakeres, D.W. (2011) Particle Physics Insights, 4, 19-23. http://dx.doi.org/10.4137/PPI.S7961
- Chakeres, D.W. (2011) Particle Physics Insights, 4, 25-31. http://dx.doi.org/10.4137/PPI.S8241
- Chakeres, D.W. (2013) Particle Physics Insights, 6, 1-7. http://dx.doi.org/10.4137/PPI.S12390
- Chakeres, D.W. (2011) Particle Physics Insights, 4, 33-38. http://dx.doi.org/10.4137/PPI.S8269
- Chakeres, D.W. (2012) The Harmonic Neutron Hypothesis: Alpha and the Annihilation Frequency Equivalent of the Neutron Are Sufficient to Derive the Effective Fine Structure Constant at Z American Physical Society Poster.
- Chakeres, D.W. (2006) The Imaginary Number Neutron Symphony. US Copyright, TXu1-295-777.
- Lykken, J. and Spiropulu, M. (2014) Scientific American, 310, 34-39. http://dx.doi.org/10.1038/scientificamerican0514-34