Journal of Modern Physics
Vol.05 No.17(2014), Article ID:51913,4 pages
10.4236/jmp.2014.517190
Self Organised Criticality in Dilute Lattice
Ajanta Bhowal Acharyya
Department of Physics, Lady Brabourne College, Calcutta, India
Email: ajanta.bhowal@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; revised 18 October 2014; accepted 8 November 2014
ABSTRACT
The variation of  in BTW model in presence of holes (dissipative sites) has been studied. The value of
in BTW model in presence of holes (dissipative sites) has been studied. The value of 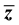 decreases as the fraction of number of holes increases. Interestingly, it is observed that the variation of the rate of change of
decreases as the fraction of number of holes increases. Interestingly, it is observed that the variation of the rate of change of 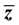 with the fraction of number of holes is different for the two different types of distribution of holes over the lattice. When the holes are randomly distributed over the lattice then the dissipation is more compared to that of the case when the holes are present in the form of a single compact cluster with same fraction. The value of
with the fraction of number of holes is different for the two different types of distribution of holes over the lattice. When the holes are randomly distributed over the lattice then the dissipation is more compared to that of the case when the holes are present in the form of a single compact cluster with same fraction. The value of 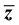 is less in the first case than that observed in the second case.
is less in the first case than that observed in the second case.
Keywords:
BTW Model, Self Organised Criticality

1. Introduction
There exists some extended driven dissipative systems in nature which show self-organised criticality (SOC). This phenomena of SOC is characterised by spontaneous evolution into a steady state which shows long-range spatial and temporal correlations. The simple lattice automata model of sandpile which shows this SOC beha- viour is introduced by Bak, Tang and Wiesenfeld (BTW) [1] . The steady state dynamics of the model shows a power law in the probability distributions for the occurence of the relaxation (avalanches) clusters of a certain size, area, lifetime, etc. Extensive work has been done so far to study the properties of the model in the steady SOC state [2] - [9] .
Dissipative sandpile model has also been studied recently. However, it is in question whether the SOC state is reached by dissipative model. Manna, Kiss and Kertesz [10] studied a sandpile model in presence of dissipation. In this model, the dissipation of a grain is considered during a relaxing event in a probabilistic manner. The numerical results showed that the system reaches a subcritical state, with a characteristic size of the avalanches depending inversely on the probability of dissipation. On the other hand, Manna et al. [11] studied the directed dissipative sandpile model in two dimensions with observation that the long time steady state is critical. Malcai et al. [12] studied the dissipative sandpile model (with closed boundary) and found that the scaling properties were in the universality class of the stochastic Abelian model with conservative dynamics and open boundaries. Najafi et al. [13] studied the statistics of avalanches and the wave frontiers in dissipative Abelian sandpile model.
2. The Model and Simulation
The BTW model is a lattice automata model which shows some important properties of the dynamics of the system, evolving spontaneously towards a critical state. We consider a two dimensional square lattice of size  with some holes on it. Out of these
with some holes on it. Out of these 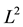 sites, a particular fraction of sites are chosen randomly as hole. If any particle falls on any one of these holes, the particle will dissipate through the hole.
sites, a particular fraction of sites are chosen randomly as hole. If any particle falls on any one of these holes, the particle will dissipate through the hole.
The model can be described in the following way: At each site 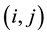 of the lattice, a variable (so called height)
of the lattice, a variable (so called height)  is associated which can take positive integer values. The height variable associated with the hole-sites remains zero for all time. In every time step, one particle is added to a randomly chosen site according to
is associated which can take positive integer values. The height variable associated with the hole-sites remains zero for all time. In every time step, one particle is added to a randomly chosen site according to
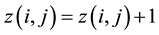 (1)
(1)
If, at any site the height variable exceeds a critical value  (i.e., if
(i.e., if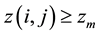 ), then that site becomes unstable and it relaxes by a toppling. As an unstable site topples, the value of the height variable, of that site is decreased by 4 units and that, of each of the four of its neighbouring sites increased by unity (local conservation), i.e.,
), then that site becomes unstable and it relaxes by a toppling. As an unstable site topples, the value of the height variable, of that site is decreased by 4 units and that, of each of the four of its neighbouring sites increased by unity (local conservation), i.e.,
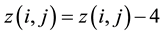 (2)
(2)
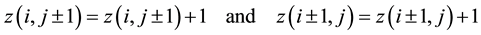 (3)
(3)
for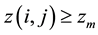 . Each boundary site is attached to an additional site which acts as a sink. We use here the open boundary conditions so that the system can also dissipate through the boundary. In our simulation, we have taken
. Each boundary site is attached to an additional site which acts as a sink. We use here the open boundary conditions so that the system can also dissipate through the boundary. In our simulation, we have taken . In this paper, the system can not only dissipate through the boundary but also through holes present on the lattice.
. In this paper, the system can not only dissipate through the boundary but also through holes present on the lattice.
Now, we allow the system to evolve under the BTW dynamics (following Equations (1)-(3)) starting from an initial condition with all the sites having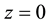 . As in the case of BTW model, here also the average height variable first increases and ultimately it reaches a steady value.
. As in the case of BTW model, here also the average height variable first increases and ultimately it reaches a steady value.
In this paper, we have studied how this steady value changes with the fraction of holes 
3. Results
In our simulation, we first studied the variation of average height variable 
Figure 1 shows this variation when the holes are situated randomly on the lattice, for a fixed system size 



From Figure 1 and Figure 2, it is observed that the value of the average height variable 

We also studied the distribution of avalanche size in BTW model with holes(randomly scattered) for
When the holes are created, randomly on the lattice, with a finite probability, then there will be a small fluctuation in the number of holes 


Figure 1. The time varitions of 

Figure 2. The time variations of 
And the average value of fraction of holes is calculated using the relation



Whereas in the second case, when the holes are in the form of a square shaped cluster, we have taken the time average of the average value of height variable, for a particular size of the cluster (i.e., for a particular fraction of the holes in the cluster). The variation of average value of height variables with the fraction of holes is studied in both the cases.
It is interesting that the value of average height variable decreases with different rate as the fraction of holes increases in the two cases. Figure 4 shows the variation of the value of average height variable with the fraction of holes for two different arrangement of holes for
4. Summary
The self-organised criticality is studied in a dilute square lattice by using lattice automata (BTW) model. The
Figure 3. Log-Log plot of the unnormalized distributions of avalanche size for BTW model and BTW model with holes (randomly scattered) for two different values of the fraction of holes.
Figure 4. Variation of time average of 






dilution in the lattice is created in two different ways. The i) randomly distributed and ii) regular clustered with same fraction of dilution. The diluted site retains the value zero of the BTW automaton throughout the dynamics towards the self organisation of critical state. Hence, the dilution acts like the points of dissipation in the lattice. The average value of the BTW automaton is observed to take different values for two different kinds of the arrangements of the dilution. It is found that in the intermediate range of the dilution, for random distribution of holes, the average value of the automaton is less than that for regular clustered distribution. Eventually, both types of distribution provide the same value of average of automaton for very low and high fraction of dilution.
Acknowledgements
The author would like to acknowledge the computational facility provided by UGC, DST-FIST, UG/PG Com- puter laboratory of Lady Brabourne college. She would also like to thank P. K. Mahanty for useful comments and S. Samui for help in the preparation of figures.
References
- Bak, P., Tang, C. and Wiesenfeld, K. (1987) Physical Review Letters, 59, 381-384. Bak, P., Tang, C. and Wiesenfeld, K. (1988) Physical Review A, 38, 364. http://dx.doi.org/10.1103/PhysRevA.38.364
- Dhar, D. (1990) Physical Review Letters, 64, 1613-1616. Majumder, S.N. and Dhar, D. (1991) Journal of Physics A, 24, L357.
- Ivashkevich, E.V. (1994) Journal of Physics A, 27, 3643-3653. Priezzhev, V.B. (1994) Journal of Statistical Physics, 74, 955-979.
- Priezzhev, V.B., Ktitarev, D.V. and Ivashkevich, E.V. (1996) Physical Review Letters, 76, 2093-2096. http://dx.doi.org/10.1103/PhysRevLett.76.2093
- Benhur, A. and Biham, O. (1996) Physical Review E, 53, R1317-R1320. http://dx.doi.org/10.1103/PhysRevE.53.R1317
- Lubek, S. and Usadel, K.D. (1997) Physical Review E, 55, 4095. http://dx.doi.org/10.1103/PhysRevE.55.4095
- Ivashkevich, E.V., Ktitarev, D.V. and Priezzhev, V.B. (1994) Journal of Physics A, 27, L585. http://dx.doi.org/10.1088/0305-4470/27/16/004
- Pietronero, L., Vespignani, A. and Zapperi, S. (1994) Physical Review Letters, 72, 1690. Ivashkevich, E.V. (1996) Physical Review Letters, 76, 3368-3371.
- Bhowal, A. (1997) Physica A, 247, 327-330. http://dx.doi.org/10.1016/S0378-4371(97)00369-5
- Manna, S.S., Kiss, L.B. and Kertesz, J. (1990) Journal of Statistical Physics, 61, 923-932. http://dx.doi.org/10.1007/BF01027312
- Manna, S.S., Chakrabarti, A.D. and Cafiero, R. (1999) Physical Review E, 60, R5005. http://dx.doi.org/10.1103/PhysRevE.60.R5005
- Malcai, O., Shilo, Y. and Biham, O. (2006) Physical Review E, 73, Article ID: 056125. http://dx.doi.org/10.1103/PhysRevE.73.056125
- Najafi, M.N., Araghi, S.M. and Rouhani, S. (2012) Physical Review E, 85, Article ID: 051104. http://dx.doi.org/10.1103/PhysRevE.85.051104






