Journal of Modern Physics
Vol.05 No.15(2014), Article ID:50147,12 pages
10.4236/jmp.2014.515151
Describing Chaos of Continuous Time System Using Bounded Space Curve
Binghua Huang1*, Yafen Wei2, Ying Huang2, Yongqing Liang1
1Electrical Engineering School of Guangxi University, Nanning, China
2Information Engineering School of Jimei University, Xiamen, China
Email: *gxuhbh@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 June 2014; revised 19 July 2014; accepted 12 August 2014
ABSTRACT
The qualitative solutions of dynamical system expressed with nonlinear differential equation can be divided into two categories. One is that the motion of phase point may approach infinite or stable equilibrium point eventually. Neither periodic excited source nor self-excited oscillation exists in such nonlinear dynamic circuits, so its solution cannot be treated as the synthesis of multi- harmonic. And the other is that the endless vibration of phase point is limited within certain range, moreover possesses character of sustained oscillation, namely the bounded nonlinear oscillation. It can persistently and repeatedly vibration after dynamic variable entering into steady state; moreover the motion of phase point will not approach infinite at last; system has not stable equilibrium point. The motional trajectory can be described by a bounded space curve. So far, the curve cannot be represented by concretely explicit parametric form in math. It cannot be expressed analytically by human. The chaos is a most universally common form of bounded nonlinear oscillation. A number of chaotic systems, such as Lorenz equation, Chua’s circuit and lossless system in modern times are some examples among thousands of chaotic equations. In this work, basic properties related to the bounded space curve will be comprehensively summarized by analyzing these examples.
Keywords:
Nonlinear Oscillation, Lorenz Equation, Chaos, Chua’s Circuit, Lossless Circuit, Space Curve

1. Introduction
1.1. State Description of Nonlinear Dynamic System
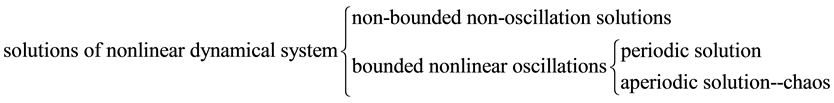
The solutions of nonlinear dynamic system can be classified as indicated above.
The motional form of particle or charge in nonlinear dynamic system can be described by state equation. Its solution can be represented by phase portrait. The motional trajectory of phase point in 3-dimensions phase space can be expressed by a space curve. Its parametric forms and other expressions of intersection surface are shown in (1). The motional trajectory denoted by (1) can be divided into two categories. First, the motional trajectory will tend to be infinite or return to stable equilibrium point at last. For example, the parametric equation of circular helix is shown in (2). It is a space curve denoted by rectangular coordinates. The trajectory of the space curve approaches infinite. It is not bounded.
 (1)
(1)
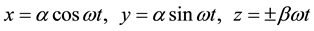 (2)
(2)
Second, the motional form of phase point will neither tend to be infinite, nor return to stable equilibrium point at last (or system has not stable equilibrium point), but always wander endlessly within definite range of phase space belong to bounded oscillation solution.
The bounded oscillation solution can also be divided into two categories. One is periodic oscillation or constant periodic oscillation. This kind of oscillation can be expressed as Fourier series. Another one is called non- constant periodic oscillation or aperiodic oscillation for short. Dynamic variable in such oscillation will keep oscillating continuously at last without determination period, or its period is infinitely or sufficiently long. Although the orbit in phase portrait is always without repetition, the sustained oscillation with infinite or sufficient length is deterministic. Such a phenomenon is called orbital chaos of continuous time system.
1.2. Birth of Chaos Regarding Academic Term
The birth of modern chaos theory or the source of term chaos is not consistent in different literatures. The Lorenz is father of chaos or raise of Lorenz equation in 1963 is the first precedent of studying chaos theory [1] . Above opinion has been supported in many literatures. In a lot of other literatures, however, it is considered that the term―chaos was imported firstly in Li-Yorke Theorem put forward by Li Tianyan and Yorke. When they proposed Period Three Implies Chaos and published it in American Mathematical Monthly in 1975, technical term chaos was used for the first time in history of mathematics and science. Since then definition of chaos was truly imported into mathematics, so this should be treated as real birth of chaos theory of mathematics. Moreover, Lorenz equation is just a model of chaos born in continuous time system, while chaos theory put forward by Li-Yorke includes concept of discrete chaos (e.g. the famous Logistic map). The theorem gives more extensive meaning to the term chaos. Objectively and fairly, the Ukrainian mathematician, Sharkovsky also made contribution to scientific theory of chaos. The some results proved by Sharkovsky are more general than Li-Yorke Theorem as early as in 1964.
2. Chaos Is Most Universally Common Form of Bounded Oscillation Solution
2.1. Describing Chaos Using Bounded Space Curve
Continuously, chaotic oscillation is the most universally motional form of phase point in multi-dimensions phase space. It has characteristics of mis-convergence, mis-divergence and aperiodicity during observation interval. Its Fourier transformation exists. Human can only conclude differential equations constraining such kind of chaotic function, can only cognize its general expression as shown in (1), where 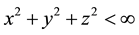 when
when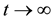 , it is bounded to differ from (2). Obviously, chaos as a kind of bounded nonlinear function displayed in phase portrait is much more complicate compared with (2). Its extent of complex can enough be believed. This space curve cannot be represented by concretely explicit parametric form in math. It cannot be expressed analytically by human. It exists no in math manuals. In other words, chaotic function has not concretely explicit math expression. It only has phase portrait. However, this kind of chaotic function extensively exists in natural science. Describing the motional trajectory of phase point using bounded space curve, chaotic functions which are not introduced in math manual are universal, while some functions introduced in math manual are special. These functions which have concretely possessed explicit math expression are specific.
, it is bounded to differ from (2). Obviously, chaos as a kind of bounded nonlinear function displayed in phase portrait is much more complicate compared with (2). Its extent of complex can enough be believed. This space curve cannot be represented by concretely explicit parametric form in math. It cannot be expressed analytically by human. It exists no in math manuals. In other words, chaotic function has not concretely explicit math expression. It only has phase portrait. However, this kind of chaotic function extensively exists in natural science. Describing the motional trajectory of phase point using bounded space curve, chaotic functions which are not introduced in math manual are universal, while some functions introduced in math manual are special. These functions which have concretely possessed explicit math expression are specific.
2.2. The Complexity Is Common Phenomenon Instead of Singular
Modern chaos theory covers everything, and chaos can be found in every subject area. Although it is complicated, it is the most common phenomenon with universality in the nature. In the past, the nature recognized by human is limited in simple situations. For example, only two situations, divergence and convergence were studied in discrete iterative map previously. When a kind of sequence is found, that is neither divergent nor convergent, humanity considered singular and special in past. It is unilateral that the humanity hardly realizes objective truth of the nature. In fact, the sequence of neither divergent nor convergent is universal phenomenon in the nature, while the divergent and convergent sequences are two simplest special situations. Taking the Lorenz equation, Chua circuit and lossless circuit as typical examples, this paper analyzes and studies orbital chaos in continuous time system to illustrate the basic properties of continuous chaos.
Chaos is a popular form of oscillation solution (the orbit will never repeat during observation), while its degenerated forms, namely periodic orbit and limit cycle are special forms of oscillation solution, both of which are generally called oscillation solution. In other words, it is a very ordinary and common that character and patterns of non-linear oscillation solution displayed in phase portrait are extremely complex. But the complicacy cannot explain the chaos is singular.
In last century, the era when chaos theory was first published, chaos was considered as a singular attractor in a lot of literatures. Human may absolutely ask an inversive question in recognition of objective truth in the nature. Why can the phase point persistently repeat original motional orbit? Why is it so strange?
People can also make a completely opposite conclusion: The motional trajectory of phase point will neither diverge to be infinite nor converge to stable limit cycle. The phase point which freely and arbitrarily wanders in phase space (non-random but deterministic) is ordinary and universal motional form. The constant periodic oscillation which continuously repeats original orbit is an individual and special motion form.
So far, half a century has passed since Lorenz first discovered chaos in 1963. Appearance of chaos system doesn’t shake the basic theory of differential equation and doesn’t get rid of constraint of all subject theories and scientific laws in natural science. No matter how it changes, however, establishing state equations can not violate regulars and laws of various subject theories. Chaotic phase portrait can be plotted, only when it is supported by differential equation theory and numerical simulation technique. So what are its singularities on earth?
2.3. The Extensiveness of Chaotic Function
Nowadays, new chaos systems spring up constantly. New chaos and deformation put forward in various literatures make a great innovative contribution to development of chaos theory [2] -[6] . The chaos can be correctly recognized and applied, only when generality character is concluded and abstracted from these literatures. Based on the original equation of chaos, some non-linear items are added. With such addition, if new stable equilibrium point will never appear in the system and ideal character will also never appear in the system, phase point will never tend to be infinite. Then, it is inevitable that another chaos or super-chaos system will be created. Various non-linear chaos systems will be put forward in succession (frequency occurrence in recent literatures) with deep study and practical engineering application of chaos in the near future. And such tendency will develop rapidly.
It is not difficult to create a chaos system with nonlinear function, as long as chaotic phase portrait created with numerical simulation are new or deformed diagrams, then a new chaotic function is certainly constituted. When a circuit contains three or above dynamic variables, for example, Chua’s and Colpitts circuit can create various chaotic equations [7] -[9] . Just like there are a lot of non-linear functions in mathematics, certainly, there also is a great deal of chaotic function in various subject areas. After development for a certain time, a great amount of chaos or super-chaos systems will be built up in near future. Then present chaos systems in a small number will become very ordinary, including Lorenz equation. This equation will become a common example among thousands of non-linear oscillation equation without any unique character. However, contribution of Lorenz is still indelible because he is the first one to put forward this kind of phenomenon.
3. Multiple Kinds of Chua’s Circuit Deformation and Butterfly Effect
Various kinds of Chua’s circuit family show the deformed equations can be created in a very extensive range
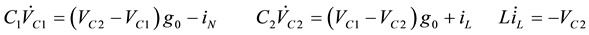 ( 3a )
( 3a )
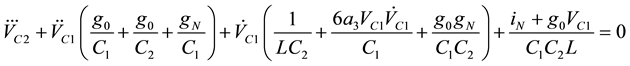 (3b)
(3b)
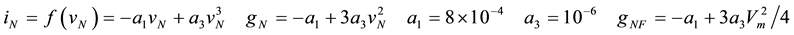 ( 4a )
( 4a )
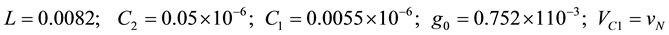 (4b)
(4b)
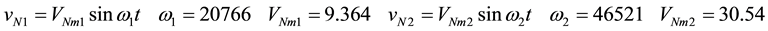 (5)
(5)
Example 1: The first kind of Chua’s circuit deformation has two different oscillation characters, which means there also is butterfly effect in it. The circuit is shown in Figure 1, and its equation is shown in (3). Its parameters after deformation are shown in (4), where 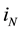 denotes current of voltage-controlled nonlinear device
denotes current of voltage-controlled nonlinear device , the
, the 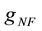 denotes equivalent first harmonic conductance. The (3) is found by harmonic balance principle. Two sets of fundamental wave solution
denotes equivalent first harmonic conductance. The (3) is found by harmonic balance principle. Two sets of fundamental wave solution 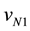 and
and 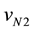 can be determined with power balance theory or fundamental wave analysis method. The corresponding two fundamental wave voltage amplitudes and two frequencies are shown in (5), which are consistent with the data in [10] . In the solution, the voltage
can be determined with power balance theory or fundamental wave analysis method. The corresponding two fundamental wave voltage amplitudes and two frequencies are shown in (5), which are consistent with the data in [10] . In the solution, the voltage 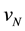 of entering into nonlinear device
of entering into nonlinear device 






We draw a phase portrait of Chua’s circuit and take phase points in the last one percent to represent the curve described after entering into steady state. Figure 2 shows that there are two different oscillation characters for different network parameters.
Figure 1. Chua’s circuit.

Figure 2. The first kind of Chua’s circuit deformation horizontal is Vc1 and vertical is Vc2. (a)

The 


When
is formed as a limit cycle as shown in phase portrait Figure 2(b). At this time, only one frequency component has self-oscillation capability for its satisfaction of power balance. Therefore, only limit cycle will be generated shown in Figure 2(b). The operation of Program chua73/70.nb shows only one real solution satisfying equation balance.
When parameter 





Example 2: The second kind of Chua’s circuit deformation. Two non-linear items will be added in



The data in (6) and (7) is consistent with the data in [11] ; the Figure 3 is consistent with the phase diagram9 of four-scroll chaos as shown in [11] .
Example 3: The third kind of Chua’s circuit deformation

A non-linear item

The necessary and sufficient condition for periodic oscillation is that there should and must be only one unique fundamental wave solution. There are two fundamental wave solutions in the second kind of Chua’s circuit deformation; and there is no fundamental wave solution in the third kind. So they are all belong to the condition of aperiodic chaotic oscillation.
Example 4: The fourth kind of Chua’s circuit deformation


Figure 3. The second kind of Chua’s circuit deformation. (a)


Figure 4. Phase portrait of the third kind of deformation.



A non-linear item 

As mentioned above, the sufficient and necessary condition of producing chaos is that there is no unique fundamental wave in this dynamic system. In other words, the solution of equation cannot be represented by means of Fourier series.
4. Chaos Oscillation Generated in Lossless Circuit


Example 5: the Figure 6 is a lossless circuit with voltage controlled non-linear inductance 














It is assumed that 





Figure 5. Phase diagram of the fourth deformation. (a)


Figure 6. Example 5 circuit.
4.1. The Excited Source 

The main harmonic solutions of the (16) can be found by Program Tab1.nb and listed in Table 1. The phase portraits in Figure 7 are drawn from the (16). The change rule of oscillation character can be displayed. When


It is thus obvious that aperiodic chaos is the most universally common oscillation form in non-linear system. When the nonlinear strength of circuit is reduced, its slight non-linearity is almost equal to linearity. Oscillation of system will be degenerated into its special form of periodic state, and closed periodic orbit is represented in phase portrait Figure 7(a). The change rule that phase portraits gradually develops from periodic state to chaotic state can confirm chaotic basic property to be infinite (or sufficient) extension of oscillation period.
In Table 1, the Uhm denotes the amplitude of self-oscillation component; Upm denotes the amplitude of force oscillation component; maxu denotes the maximum of the

4.2. Keeping the Fixed Non-Linear Factor 
The main harmonic solutions of the (16) can be found by Program Table 2 and listed in Table 2. When setting specific value


4.3. The Solution of the Equations (16) Is Described by Bounded Space Curve
The variable 


4.4. Chaotic Boundedness Is Different from Its Attractiveness
Above mentioned two conditions show that if there is sufficient strong non-linearity and excitation in zero-loss system, original oscillation period T will double or undoable extend to sufficient or infinite length with gradual change of system parameter (



Table 1. Example 5 main harmonic solutions



Table 2. Example 5 main harmonic solutions


There is no transient process in the linear zero-loss circuit. It will enter steady state in the first instant when excited source switches on, so does in the non-linear zero-loss circuit. The phase portrait Figure 7 and Figure 8 are not attractor, but bounded space curve. There is a difference between boundedness and attractiveness.
Van der Pol oscillation with variable damping elements is a limit cycle, called attractor. It can attract adjacent orbit leaving limit cycle. This is because there is an energy dissipation element with variable resistance, which is capable of converging orbital changes caused by external disturbance. Its fundamental wave solution of stable state is independent of initial conditions.
Some of chaos are not attractor, for example, chaos generated in zero-loss system is different from chaos system with variable damping. Energy sent by excited source within an excitation period is zero, and the system is



Figure 7. Phase portrait of Table 1, Horizontal means 







not capable of converging changes of energy storage in circuit caused by external disturbance because there is no energy dissipation element. Its trajectory is partially unstable under disturbance in small scope. Its stability in big scope is dependent on limited initial energy storage, which is overall stability. Therefore, chaos oscillation composed with zero-loss circuit is not an attractor, which means that there is distinguish between boundedness and attractiveness in continuous system.
The bounded oscillation solutions include chaotic and periodic state, they can all be sought by using the harmonic analysis and the power balance theorem. The Table 1 and Table 2 are main harmonic component of oscillation solution, it approximate the simulate solution displayed in phase portraits Figure 7 and Figure 8 [14] -[17] .



Figure 8. Phase portrait of Table 2, Horizontal means 








Figure 9. Phase portraits of plane projection of the space curve (17). (a) plot

5. Sixty-Six Plane Phase Portraits of Lorenz Chaos Equation
There are six variables 






According to above-mentioned work, so there are twelve variables in total, when combining them in pairs, sixty-six different plane phase portrait can be drawn from an output of chaos equation. When above-mentioned phase portraits are drawn, parameters and initial values in state equation, as well as all data in system, should keep invariant, version number of simulation software adopted in computer and algorithm, step size, simulate time set in operation, should also be invariant. Then it is shown that sixty-six plane phase portraits will keep completely consistent at any time [18] .
Total sixty-six phase portraits of plane projection are all circumstantial evidence. The mutual relations among twelve variables completely obey mathematic theories and laws including various arithmetical operations, such as sum, product, difference and differential, integral. There is no singular manifestation at all. If the twelve variables are expressed as functions of time 



The chaos is neither random nor seemingly random. Taking Lorenz equation as an example, It shows that these sixty-six plane projection diagram all are uniquely certain and invariant rather than random. If chaos is random, which means chaos signal emitted this time is quite different from the next, the chaos cannot be applied in engineering practice at all. It’s not seemingly random also, the butterfly effect of seemingly random does not exist in phase trajectory composed by set of phase points, but in particular critical point. Random phase point cannot stay and be displayed in the phase portraits. For example, the set of all phase points of unstable limit cycles are seemingly random, which cannot be displayed as an orbit.
6. Conclusions―Basic Properties of Chaos
Selecting properly three dynamic variables in nonlinear systems constitute a three-dimension phase space, the continuous chaos can be described by a bounded space curve. If nonlinear systems contain n > 3 dynamic variables, a n-dimension Euclidean space can be constituted. According to above-mentioned three examples, the characteristics of the bounded space curve can be comprehensively summarized as follow:
1) The solutions of Chua’s circuit and Lorenz equation cannot be constituted by proper harmonic component, while the main basic part of chaotic solution of lossless circuit can be represent by two properly main harmonic components. They are all belong to that there is no unique fundamental wave solution in this dynamic system.
2) Continuous chaos systems exist in the nature universally and commonly. It has not slightest singularity, but it is also very complicate. Chaotic functions are the universal term of variously bounded nonlinear aperiodic oscillation. There are thousands of functions of this kind, rather than limited several examples. Chaotic functions possess character of continuous oscillation. The periodic function is its degenerate forms.
However, the relationship among several variables in nonlinear equations cannot be expressed into concretely explicit formulations. They can only be expressed by using general parametric forms (20) or phase portraits. The 



3) Sensitivity and dependence on initial value, solutions of any differential equation are all dependent on initial value, while the sensitivity is just at some particular points, instead of all the point sets. It is not unique character of chaos. Such sensitivity can also be found in many mathematic equations, even in some linear equations.
4) Certainty of chaos oscillation. There is no inner randomness in chaos oscillation because the numerical simulation solution is unique. Each equation corresponds only to a phase diagram.
5) The simulation time Td must be defined before explaining aperiodicity of chaos.
Chaos has two characteristics, aperiodicity and continuous oscillation, which make it differ from both periodic oscillation and non-oscillation solution. It is a kind of non-linear oscillation equation. If oscillation is aperiodic in certain time of analogic simulation, the system solution will be chaotic. No unique fundamental wave solution can be determined in chaos system family, such as Chua’s circuit, Lorenz system, Chen system, Lu system, Liu system, Qi system, etc., because their solutions cannot be expressed in Fourier series. When aperiodicity of time domain corresponds to spectral continuity of frequency domain, the solution in the system possesses Fourier transformation.
Periodicity or aperiodicity is dependent on the nature of non-linear system itself that is differential equation expressing this system, including its initial conditions. Infinitely or sufficiently long periodic system may exist in the nature. Therefore, the answer to this problem is
We have to consider carefully about the value of Td. Is there any established rule or connotative regulation in academic world for the value in different subject areas? Development history of physics shows the Td may possess different magnitude orders (computing unit may be second or million years). For example, computing unit in circuit, information communication technology may be second, while that in celestial mechanics may be up to hundred years. Therefore, different values of Td should be defined in different subject areas.
Acknowledgements
This work was supported by National Natural Science Foundation of China (60662001).
References
- Lorenz, E.N. (1963) Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, 20, 130-141. http://dx.doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
- Feng, C.-W., Cai, L., Kang, Q. and Zhang, L.-S. (2011) A Novel Three-Dimensional Autonomuos Chaotic System. Acta Physica Sinica, 60, 030503/1-7.
- Tang, L.-r., Li, J. and Fan, B. (2009) A New Three-dimensional Chaotic System and Its Circuit Simulation. Acta Physica Sinica , 58, 785-793.
- Xe, Z., Liu, C.-X. and Yang, T. (2010) Study On A New Chaotic System With Analysis and Circuit Experiment. Acta Physica Sinica, 59, 131-139.
- Liu, Y.-Z., Lin, C.-S. and Wang, Z.-L. (2010) A New Switched Four-Scroll Hyperchaotic System and Its Circuit Implementation. Acta Physica Sinica, 59, 8407-8413.
- Yu, S.-M.,Qiu, S.-S. and Lin, Q.-H. (2003) New Results of Study on Generating Multiple-Scroll Chaotic Attractors. Science in China (Series F), 46, 104-115.
- Chua, L.O., Komuro, M. and Matsumoto, T. (1986) The Double Scroll Family. IEEE Transactions on Circuits and Systems, 33, 1073-1117.
- Kennedy, M.P. (1994) Chaos in the Colpitts Oscillator. IEEE Transactions on Circuits and Systems I, 41, 771-774.
- Maggio, G.M., De Feo, O. and Kennedy, M.P. (1999) Nonlinear Analysis of the Colpitts Oscillator and Applications to Design. IEEE Transactions on Circuits and Systems, 46, 1118-1130.
- Huang, B.-H., Niu, L.-R., Lin, L.-F. and Sun, C.-M. (2007) Fundamental Wave Analysis Based on Power Balance. Acta Electronica Sinica, 35, 1994-1998.
- Huang, B.H., Huang, X.M. and Wei, S.G. (2008) Journal on Communications, 29, 65-70.
- Huang, B.H., Li, G.M. and Wei, Y.F. (2012) Modern Physics, 2, 60-69.
- Huang, B.H., Li, G.M. and Liu, H.J. (2013) Modern Physics, 3, 1-8. http://dx.doi.org/10.12677/MP.2013.31001
- Huang, B.H., Huang, X.M. and Li, H. (2011) Main Components of Harmonic Solutions of Nonlinear Oscillations. International Conference on Electric Information and Control Engineering, ICEICE, Wuhan, 15-17 April 2011, 2307- 2310.
- Huang, B.H., Huang, X.M. and Li, H. (2011) Procedia Engineering, 16, 325-332. http://dx.doi.org/10.1016/j.proeng.2011.08.1091
- Huang, B.-H., Yang, G.-S., Wei, Y.-F. and Huang, Y. (2013) Harmonic Analysis Method Based on Power Balance. Applied Mechanics and Materials, 325-326, Manufacturing Engineering and Process II, 1508-1514
- Huang, B.-H., Yang, G.-S., Wei, Y.-F. and Huang, Y. (2013) Harmonic Analysis Method Based on Power Balance. Applied Mechanics and Materials, 327, Advanced Research on Materials, Applied Mechanics and Design Science, 1508-1514
- Sixty-Six Plane Phase Portraits Are Drawn from Lorenz Equation.
NOTES
*Corresponding author.




















