Journal of Modern Physics
Vol.5 No.12(2014), Article
ID:48202,21
pages
DOI:10.4236/jmp.2014.512117
A New Version of Special Relativity Absorbed the Uncertainty Principle: Its Content as Well as Application and Experimental Test
Dapeng Qian
Public Security Bureau of Yingkou, Yingkou, China
Email: qdpnew@sina.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2014; revised 7 May 2014; accepted 2 June 2014
ABSTRACT
Based on the space spherical symmetry of 3-dimensional and the translational symmetry of time and the uncertainty principle, a 4-dimensional space-time cylinder model of quarks and leptons is established. With this model, equations of the special relativity can be extended more perfectly, thereby achieving a unity of the special relativity and quantum mechanics in deeper level. New equations can not only interpret issues explained by old equations but also solve several important pending problems. For example, a formula to strictly calculate the coefficient ξ of Lorentz invariance violation (LIV) is derived, to above 4 × 1019 eV UHECR protons the calculated |ξ| wang#Bracket## 4.5 × 10−30, although there is the LIV effect it is too weak to change the GZK cutoff, which is consistent with observations of HiRes and Auger; Also, a relation formula between the Hubble constant and several basic constants is derived, thus theoretically calculated H0 = 70.937 km∙s−1∙Mpc−1, which is well consistent with the final observation result of HST Key Project. In addition, an unusual effect predicted by new equations can be experimentally tested in the electron storage ring; a preliminary experiment result has hinted its signs of existence.
Keywsords
Special Relativity, Uncertainty Principle, Cylinder Model with Intrinsic 4-Dimensional Space-Time of Quarks/Leptons, Lorentz Invariance Violation, GZK Cutoff of UHECR, Planck Energy, Hubble Constant, Super-High Energy Electron, Electron Storage Ring

1. Introduction
How to unify the relativity and the quantum mechanics? This is a great problem in physics across the centuries, which has been a concern. Popular view is that, since the establishment of quantum electrodynamics, the unification of special relativity and quantum mechanics has been completed, the remaining work is only to explore the issue of unification of general relativity and quantum mechanics. However, if broadened thinking, it can be found that above view is flawed.
As we all know, from the fundamental sense, the special relativity firstly is a measurement theory about time, space, energy, momentum and so on, i.e. it is a physical framework to theory to do principled rules for all measurement acts. On the other hand, we also know that measurements of these physical quantities must be subject to the insurmountable constraint of one natural law, that is, the Heisenberg uncertainty principle that reflected essential feature of quantum mechanics. So in this sense judgment, the special relativity as a clean measurement theory that utterly disregards uncertainty relation, can not be a complete theory. Thus if taking into account the universality constraint of the uncertainty principle, it is necessary to further improve the special relativity; only completing this work can truly achieve unifying relativity and quantum mechanics.
In fact people already realized that any perfect physical theory regarding space-time not only has the rational core of the relativity also must contain the uncertainty principle and treat it as one of fundamentals of the theory. However, what specific method should be taken to make the uncertainty principle naturally implant into the concept system of special relativity and keep that the overall structure of special relativity is not destroyed? For this problem, the physics must make satisfactory answer.
Now this paper presents a way to solve this problem. First, based upon the uncertainty principle, the time translational symmetry and the 3-dimensional space spherical symmetry, for the elementary particles of the level of quarks and leptons there established a cylinder model with 4-dimensional space-time (PSTC model). Then, used this model, we deduced a series of new equations that are compatible with old equations of special relativity and also fit for the uncertainty principle, thus achieve unifying special relativity and quantum mechanics in deeper level via a way different from the quantum electrodynamics.
New equations which reveal the concepts of space, time, mass, energy etc. have richer connotations, so that can help people to re-understand the essence of some physical phenomena and solve several pending important problems, such as: 1) The new mass equation directly shows the inevitable existence of the Lorentz invariance violation (LIV) and derives a strict formula to calculate the LIV coefficient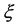 . For energy higher than 4 × 1019 eV UHECR protons, the calculation
. For energy higher than 4 × 1019 eV UHECR protons, the calculation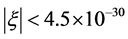 , although there is the LIV effect but
, although there is the LIV effect but 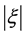 value is too small to change the GZK cutoff, which is consistent with observations of the HiRes [1] and the Auger [2] . 2) It can be proved that the Planck energy is a Lorentz invariant, so for “the observer independence of Planck energy” [3] , that has been regarded as basic principle; its theoretical source is finally found. Also, it is proved that the Planck energy is not the common upper limit of energy of all particles. 3) Using the new equation, a relation formula between the Hubble constant and several basic constants is derived, thereby theoretically calculated H0 = 70.937 km∙s−1∙Mpc−1, which is well consistent with the final measuring result of the HST Key project [4] . Via this relation formula the mystery of Dirac large numbers can also be clarified.
value is too small to change the GZK cutoff, which is consistent with observations of the HiRes [1] and the Auger [2] . 2) It can be proved that the Planck energy is a Lorentz invariant, so for “the observer independence of Planck energy” [3] , that has been regarded as basic principle; its theoretical source is finally found. Also, it is proved that the Planck energy is not the common upper limit of energy of all particles. 3) Using the new equation, a relation formula between the Hubble constant and several basic constants is derived, thereby theoretically calculated H0 = 70.937 km∙s−1∙Mpc−1, which is well consistent with the final measuring result of the HST Key project [4] . Via this relation formula the mystery of Dirac large numbers can also be clarified.
According to an extraordinary effect prophesied by new equations, it is expected that in the electron storage ring RF cavity downstream direction there is an emission of unusual electrons of much higher than the beam energy. It is possible to test the new equations of special relativity by detecting those small probability unusual events. A preliminary experiment was done and its result hinted the signs of emission of super-high energy electrons. To this end I propose an experimental program and called for experimental physicists to exactly complete the interesting exploratory experiment.
This paper is organized as follows. Section 2 describes the cylinder model of intrinsic 4-dimensional spacetime of particles. Section 3 gives new improved equations of special relativity. Section 4 describes that use new equations to solve several important problems. Section 5 proposes an experimental plan to test the prophecy of the new equation. Section 6 gives the conclusion.
2. The Cylinder Model of Instrinsic 4-Dimensional Space-Time of Particles
2.1. Establishment of the Model
Einstein’s idea on space-time was to take the “physical object” as the premise. He said: “Space-time is not necessarily something to which one can ascribe a separate existence, independently of the actual objects of physical reality. Physical objects are not in space, but these objects are spatially extended” [5] . Einstein’s words remind people: the space-time is actually one kind of attributes of physical objects. In order to understand more deeply the space-time, it is necessary to more sufficiently face the object. It has long been known, “the actual objects of physical reality” are in hierarchical structure. In general, between different structural levels the objects could have fundamentally different concept and attributes. On the space-time attributes of the object, if accept the viewpoint of Einstein at his later years, namely the actual space-time must depend on the actual object, we will not be able to rule out such a possibility that the current understanding space-time will only be maintained to certain one very low-level particles. Starting from this assumption, we can further deduce as follows.
• When measuring such a particle, because the uncertain amount of the momentum and the energy can not be infinite, according to the Landau interpretation of the uncertainty principle, then the space uncertain amount and the time interval between twice measuring are impossible to zero. If abandoning the unreasonable infinity of the uncertain amount of momentum and energy, and taking a limited maximum value to replace them respectively, then the uncertain amount of space and the time interval will have the minimum value that are greater than zero. This indicates that in the actual observable sense the particles on this level should have a certain size.
• So-called the particle has “a certain size”, it means that the particle not only has a 3-dimensional space size, also has an intrinsic time size. Thus, according to the space-time unity of the special relativity, such a particle that has the nonzero and finite intrinsic scales of space-time should have an intrinsic 4-dimensional geometric shape.
• Taking into account when the particle is in rest, because there are the 3-dimensional space spherical symmetry and time translation symmetry, then the geometrical shape of particle should be a 4-dimensional cylinder that the timeline is taken as the rotational symmetry axis, and its axial height is the maximum value of the intrinsic time interval of particle.
• According to the above, the space and time of the 4-dimentional cylinder of particles must be the real physical space-time, rather than any formal mathematical space-time, such as the Minkowski space-time etc., so only Euclidean geometry is suitable for it.
• What particles are the final form that maintain the understandable time and space? According to the existing knowledge let us assume that they are particles of the quarks-leptons level. Of course, this is a mandatory assumption, of which correct or not need by testing its derived results later to judge.
Above these can be attributed to a basic postulate:
[Postulate] The particle of quarks-leptons level is not the point particle but Euclid 4-dimensional spacetime cylinder with a certain time interval as its axial height.
This [Postulate] gives the particles the cylinder model with intrinsic 4-dimensional space-time (for short PSTC model). In accordance with the requirements of [Postulate], when the particle is rest relative to the observer, its intrinsic time axis 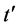 is parallel with the time axis t of the coordinate system of observer, namely there is a zero deflection from the axis
is parallel with the time axis t of the coordinate system of observer, namely there is a zero deflection from the axis 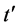 to the axis t; when the particle movement at the light-speed c relative to the observer, there is the maximum deflection angle from the axis
to the axis t; when the particle movement at the light-speed c relative to the observer, there is the maximum deflection angle from the axis 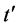 to the axis t. Because the geometry of 4-dimensional cylinder is of Euclid, so in this case the
to the axis t. Because the geometry of 4-dimensional cylinder is of Euclid, so in this case the  axis is orthogonal with the axis t. Therefore, in general, according to [Postulate] and the particle’s 4-dimensional space-time cylinder on
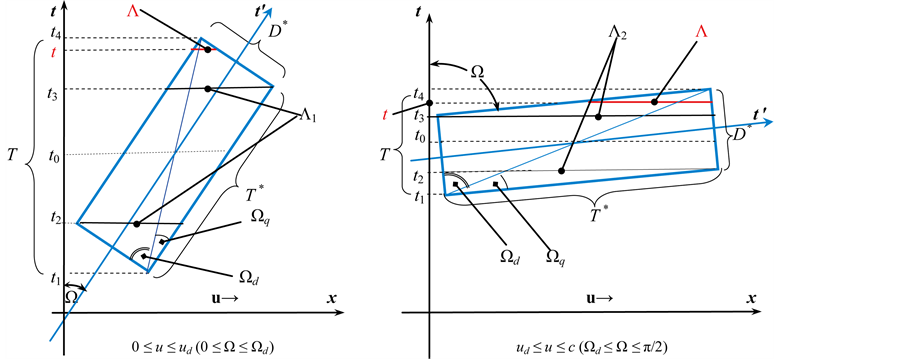
axis is orthogonal with the axis t. Therefore, in general, according to [Postulate] and the particle’s 4-dimensional space-time cylinder on  plane projection (Figure 1), the following two corollaries can directly be derived:
plane projection (Figure 1), the following two corollaries can directly be derived:
[Corollary 1] If a particle is moving at a speed 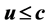 relative to an observer, there is a deflect angle
relative to an observer, there is a deflect angle 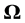 between the intrinsic time axis
between the intrinsic time axis ![]() of particle and the time axis t of coordinates system of observer on the
of particle and the time axis t of coordinates system of observer on the  plane, which
plane, which
 (1)
(1)
[Corollary 2] The shape of particle observed randomly at one moment is a 3-dimensional space crosssection of the 4-dimensional space-time cylinder in the observer’s coordinates-system.
2.2. The Intrinsic Time Height of Particle and the Intrinsic Time-Space Ratio of Particle
Having a nonzero and finite intrinsic time height is the most important feature of the particles 4-dimensional space-time cylinder model. The time height concept comes from the Landau interpretation of the energy-time uncertainty relation [6] , Landau believes that the particle energy E at one moment can be arbitrarily accurately
 (a) (b)
(a) (b)
Figure 1. Projection of the particle’s intrinsic 4-dimensional space-time cylinder on the t-u-t' plane (The velocity u of particle is along the x-axis direction of the coordinate system of observer).
measure, in the uncertainty relation
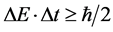 (2)
(2)
 is the difference of two accurate measurement values of energy,
is the difference of two accurate measurement values of energy,  is the time interval between twice measurements. Therefore, in according to the meaning of particle’s intrinsic time height concept defined by the [Postulate], there is obviously:
is the time interval between twice measurements. Therefore, in according to the meaning of particle’s intrinsic time height concept defined by the [Postulate], there is obviously:
[Corollary 3] If an observer successively twice measures a particle but their time interval is less than the particle’s apparent time height, then such measurements is meaningless.
Here the so-called “apparent time height” (denoted by T) is a projection value of the particle 4-dimensional cylinder on the observer’s coordinate system time axis, according to [Corollary 1], T changes with speed u. The axial height of the particle 4-dimensional cylinder defined by the [Postulate] is called the particle’s intrinsic time height (denoted by ), for the same kind particles
), for the same kind particles  is a fixed value, which is a Lorentz invariant. By (1) it can be proved
is a fixed value, which is a Lorentz invariant. By (1) it can be proved
 (3)
(3)
where
 (4)
(4)
 denotes the diameter of particle, the dimensionless constant
denotes the diameter of particle, the dimensionless constant 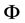 called as the intrinsic time-space ratio of particle is an important parameter describing the intrinsic geometry feature of particle. The value of
called as the intrinsic time-space ratio of particle is an important parameter describing the intrinsic geometry feature of particle. The value of 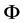 need to use the new special relativity to calculate, which will be elaborated in Section 3.4.1, now in advance the results are given:
need to use the new special relativity to calculate, which will be elaborated in Section 3.4.1, now in advance the results are given:
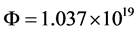 (5)
(5)
In addition, the calculating formula of the particle’s intrinsic time height will in Section 3.4.2 be deduced, now it is also written in advance:
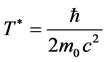 (6)
(6)
(6) show that 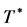 depend on the particle mass
depend on the particle mass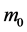 , so different quarks, leptons and so on have different intrinsic time height. For example, the electron’s
, so different quarks, leptons and so on have different intrinsic time height. For example, the electron’s 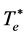 or
or 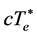 calculation as follows:
calculation as follows:
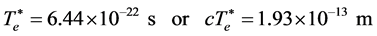 (7)
(7)
Further use of (4) and (5) to calculate the diameter of electron:
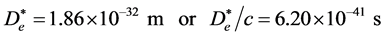 (7’)
(7’)
On high-level composite particles as well as macroscopic objects, because they are the gathering of quarks and leptons in 3-dimensional space, so although their space scales can continue to amplify, their intrinsic time scale remains the intrinsic time height of elementary particles.
The intrinsic time-space ratio of particle is very large value, which shows the serious imbalance between the intrinsic time scale and intrinsic space scale, so saying geometry form of particle is the “4-dimensional cylinder”, rather is a very slender “4-dimensional thorn”.
2.3. The 3-Dimensional Space Cross-Section of the 4-Dimensional Space-Time Cylinder of Particle
The [Corollary 2] points out that the particle’s shape that is randomly observed at one moment is a 3-dimensional space cross-section of the particle’s 4-dimensional space-time cylinder in the coordinates-system of observer. Referring to Figure 1, according to the space rotational symmetry with the velocity u direction as axis, it can be seen that the 3-dimensional space cross-section is the rotational ellipsoid or its section, that is, an ellipsoid crown, an ellipsoid zone as well as the sphere or a cylinder in extreme situations. What specific shape is depends on two factors: 1) the angle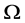 , which is associated with the speed u according to (1); 2) the randomness that a moment of measurement occurs in the time height T. Referring to Figure 1, all types of 3-dimensional space cross-section are listed in Table 1:
, which is associated with the speed u according to (1); 2) the randomness that a moment of measurement occurs in the time height T. Referring to Figure 1, all types of 3-dimensional space cross-section are listed in Table 1:
In Table 1, ![]() denotes the angle between the short side and the diagonal in the rectangle that the particle’s 4-dimensional cylinder is projected on the plane
denotes the angle between the short side and the diagonal in the rectangle that the particle’s 4-dimensional cylinder is projected on the plane  of observer’s coordinate system, the speed corresponding to
of observer’s coordinate system, the speed corresponding to 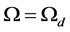 is
is
 (8)
(8)
When 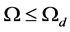 i.e.
i.e. 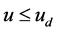 (see Figure 1(a)), for any moment t in time intervals
(see Figure 1(a)), for any moment t in time intervals 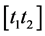 and
and 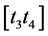 we can define a dimensionless variable
we can define a dimensionless variable![]() :
:
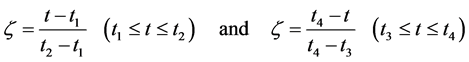 (9)
(9)
Similarly, when  i.e.
i.e. 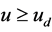 (see Figure 1(b)), for any moment t in time intervals
(see Figure 1(b)), for any moment t in time intervals  and
and  we can also define the dimensionless variable
we can also define the dimensionless variable![]() :
:
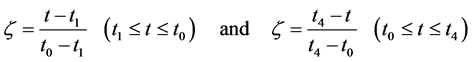 (9’)
(9’)
![]() is called the random fluctuation variable, apparently there is
is called the random fluctuation variable, apparently there is
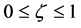 (10)
(10)
According to Figure 1 and (1) (3) (4) (9) (9’) (10), using the elliptic equation to make definite integrals the
Table 1 . The 3-dimensional space cross-sections of the 4-dimensional space-time cylinder of particles.
volume V of 3-dimensional space cross-sections can be gotten:
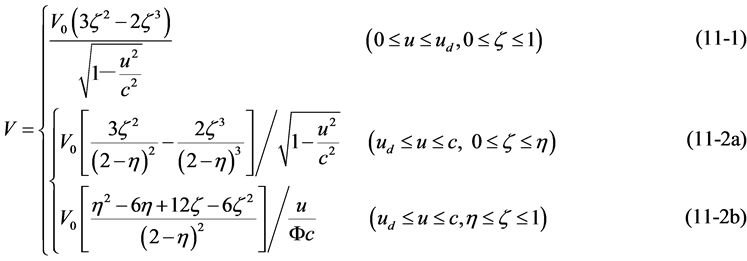
where
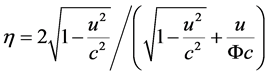 (12)
(12)
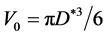 is the volume of 3-dimensional space cross-section of rest particle relative to observer, that is the volume of sphere with diameter as
is the volume of 3-dimensional space cross-section of rest particle relative to observer, that is the volume of sphere with diameter as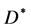 .
.
According to Figure 1 further getting other features of the 3-dimensional space cross-sections as follows:
1) If 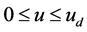 and
and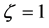 , it is a complete ellipsoid whose minor axis is
, it is a complete ellipsoid whose minor axis is  and long axis is
and long axis is  (especially when
(especially when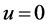 ,
, 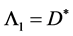 , it becomes a sphere),
, it becomes a sphere),
 (13)
(13)
2) If  but
but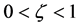 , it is an ellipsoid crown having different height
, it is an ellipsoid crown having different height 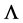 and bottom area S,
and bottom area S,
 (14)
(14)
 (15)
(15)
where  is the area of ellipsoid projection in observer
is the area of ellipsoid projection in observer  coordinate plane.
coordinate plane.
3) If  and
and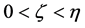 , it is an ellipsoid crown having different height
, it is an ellipsoid crown having different height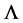 ,
,
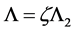 (14’)
(14’)
4) If 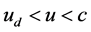 and
and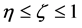 , it is an ellipsoid zone having different end-plane diameters and a same height
, it is an ellipsoid zone having different end-plane diameters and a same height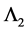 ,
,
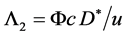 (16)
(16)
5) If![]() , it is a 3-dimensional space cylinder having the same height
, it is a 3-dimensional space cylinder having the same height 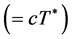 and different diameter D,
and different diameter D,
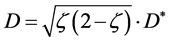 (17)
(17)
6) If , the particle is no observed at this moment.
, the particle is no observed at this moment.
2.4. Advantages of the PSTC Model
To sum up, the differences as well as advantages of the PSTC model compared to other non-point particle models as follows:
1) The basis of establishment of PSTC model is realistic and reliable, it is based upon the spherical symmetry of 3-dimensional space, the translational symmetry of time, the space-time unity of relativity, the Heisenberg uncertainty principle, and its applying objects are quarks and leptons, which all are empirical facts and recognized principle, there are no additional imaginary content.
2) The PSTC model is simple, there is only 4-dimensional space-time, with no additional dimension.
3) For space-time, the PSTC model requires real physical space-time, i.e. Euclidean space-time, rather than any mathematical space-time, such as the Minkowski space-time etc. We know that the Minkowski geometry is one of expression forms of special relativity but has not the substantive contribution to the special relativity.
4) The PSTC model points out that the particles not only has a size of the space, in the time also has a nonzero and finite intrinsic “height”, the ratio of the time height T* to the diameter D*,  , is a large number, which shows the difference between the particle’s intrinsic time scale and space scale.
, is a large number, which shows the difference between the particle’s intrinsic time scale and space scale.
5) The PSTC model can be used to develop the basic theory of physics, such as the development and improvement of special relativity.
3. The New Improved Equations of Special Relativity Based upon the PSTC Model
Using the particle’s intrinsic 4-dimensional space-time cylinder model (PSTC model), a series of new more perfect equations corresponding to old equations of the special relativity are derived. The PSTC model is based on the uncertainty principle, so new equations have reflected the constraint of uncertainty principle. Taking into the applicability and the testability, we first focus on the new mass equation.
3.1. More Perfect New Mass Equation
In accordance with [Postulate], “the amount of mass” included inside the particle of quarks and leptons etc. must uniformly be distributed in the intrinsic 4-dimensional space-time cylinder, and further in accordance with [Corollary 2], the particle’s shape observed at one moment is a 3-dimensional space cross-section of the 4-dimensional cylinder, so the mass m of particle is proportional to the volume V of 3-dimensional cross-section, that is
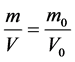 (18)
(18)
where, m0 denotes the rest mass of particle. Then (11) into (18) we obtain the more universal mass equation:
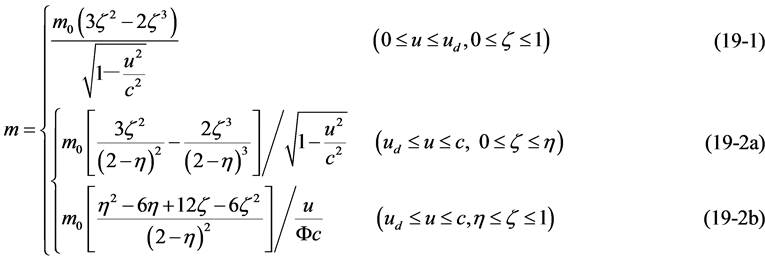
where on the speed 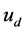 please see (8), on the speed substitution variable
please see (8), on the speed substitution variable  please see (12).
please see (12).
To this equation interpretations and in-depth discussions as follows:
[I] The mass m is not a single variable function of the speed u, it depend on both of the speed u and the random variable![]() . The variable
. The variable ![]() that appears in the derivation process of equation makes the randomness concept automatically enter the relativistic equations.
that appears in the derivation process of equation makes the randomness concept automatically enter the relativistic equations.
[II] When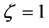 , (19) has the maximum value form
, (19) has the maximum value form
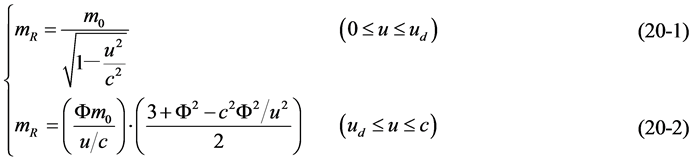
It can be seen that mR depends singly on u. When  (20-1) happens to be the Lorentz-Einstein mass formula (In this case mR and
(20-1) happens to be the Lorentz-Einstein mass formula (In this case mR and 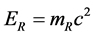 are called Lorentz mass and Lorentz energy). However when
are called Lorentz mass and Lorentz energy). However when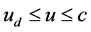 , the maximum form is another (20-2), in particular
, the maximum form is another (20-2), in particular![]() , the mass is not the infinity but a finite maximum value.
, the mass is not the infinity but a finite maximum value.
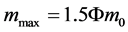 (21)
(21)
Because the new equation eliminates the infinity, so the theoretical suppression of the physical particles moving at light speed will be eliminated. When ![]() the electron’s maximum mass
the electron’s maximum mass
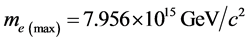 (22)
(22)
[III] Because generally m is a double variable function on u and![]() , even when the particle’s speed is constant, its mass m and its energy
, even when the particle’s speed is constant, its mass m and its energy  still at
still at 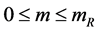 and
and  change with
change with![]() . When
. When![]() ,
,  and
and  , which shows in particles movement there is a strange “high speed but low mass (energy)” effect or HSLM effect for short.
, which shows in particles movement there is a strange “high speed but low mass (energy)” effect or HSLM effect for short.
[IV] With reference to Figure 1(a), it can be proved that when 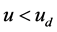 the probability
the probability 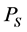 that the particle appears in the HSLM state of
that the particle appears in the HSLM state of 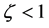 (i.e.
(i.e.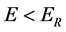 ) is calculated by the following formula
) is calculated by the following formula
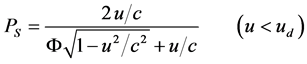 (23)
(23)
Since Lorentz energy  is singly corresponding to the speed
is singly corresponding to the speed![]() , so the probability
, so the probability 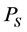 can be calculate by
can be calculate by 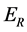 replacing u via (20-1)
replacing u via (20-1)
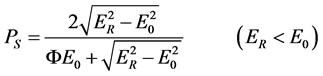 (23’)
(23’)
The formula shows that the higher the particle’s speed u (i.e. the higher the Lorentz energy ER), the greater the possibility appearing in HSLM state. Because 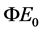 is huge and there is always
is huge and there is always 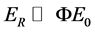 in the current observation, so the probability of particle in HSLM state is very small. Such as the electron’s
in the current observation, so the probability of particle in HSLM state is very small. Such as the electron’s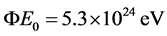 , the probability of different energy electron appearing in HSLM state is shown in the following table (Table 2):
, the probability of different energy electron appearing in HSLM state is shown in the following table (Table 2):
The probability of particle appearing in a neighborhood of ![]()
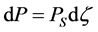 (24)
(24)
However the probability of particle in “normal state” of 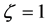 i.e.
i.e.  is
is
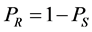 (25)
(25)
Because there is always 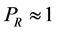 in the current observation range, so
in the current observation range, so 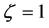 i.e.
i.e.  and
and 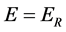 state is most probable, what described by the Lorentz-Einstein mass formula is just the mass-speed relationship in this state.
state is most probable, what described by the Lorentz-Einstein mass formula is just the mass-speed relationship in this state.
[V] It can be seen in Figure 1(b), when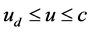 , the probability of particle appearing in each
, the probability of particle appearing in each 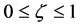 state is all equal, so the particle is in the fluctuation state of the mass and energy. Especially when
state is all equal, so the particle is in the fluctuation state of the mass and energy. Especially when![]() , the following
, the following 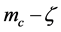 relation is deduced from (19-2b):
relation is deduced from (19-2b):
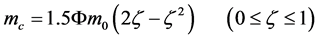 (26)
(26)
when![]() , the projection of the particle’s 4-dimensional spacetime cylinder on the
, the projection of the particle’s 4-dimensional spacetime cylinder on the 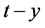 plane and
plane and 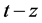 plane of coordinate system of observer is a circle, in which there is the relationship of an arbitrary circumferential angle
plane of coordinate system of observer is a circle, in which there is the relationship of an arbitrary circumferential angle  and
and![]() :
:
![]() (27)
(27)
(27) into (26) and using (21), to obtain
 (28)
(28)
Table 2. The probability Ps of different ER value electron appearing in HSLM state.
which shows that when a particle moving at the light speed, its energy changes proportional to the square of the sinusoidal of phase angle.
[VI] For the mass , according to the
, according to the ![]() state probability to weighted average, we get the mean mass
state probability to weighted average, we get the mean mass
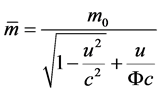 (29)
(29)
The (29) shows:
1) The mean mass  has included overall effects of the variable
has included overall effects of the variable![]() , it is only associated with the speed u and is applicable in the all speed range
, it is only associated with the speed u and is applicable in the all speed range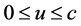 .
.
2) In the “lower energy” state of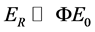 , (29) and the Lorentz-Einstein formula difference is very small.
, (29) and the Lorentz-Einstein formula difference is very small.
3) For composite particles and macroscopic objects, as long as the rest mass 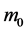 have define, then (29) are generally applicable for physical objects of all levels.
have define, then (29) are generally applicable for physical objects of all levels.
4) The mass/energy of satisfying the conservation law are neither the 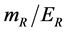 nor the
nor the , but the
, but the![]() .
.
5) (29) multiplied (3) to obtain
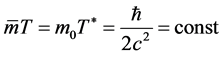 (30)
(30)
That is, the product of the particle’s apparent time height T multiplied by the mean mass is a Lorentz invariant.
6) When 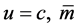 has the maximum
has the maximum
 (31)
(31)
when
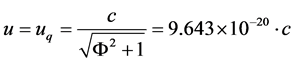 (32)
(32)
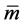 has the minimum value
has the minimum value
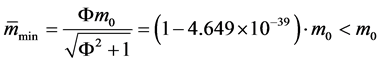 (33)
(33)
It should be noted, according to the PSTC model, only to the particles of level of quarks/leptons the speed ![]() is meaningful, but for composite particles such a speed can not be defined. (32), (33) show that the particle in the lowest energy state is not in absolute motionless but in motion at the tiny speed
is meaningful, but for composite particles such a speed can not be defined. (32), (33) show that the particle in the lowest energy state is not in absolute motionless but in motion at the tiny speed .
.
7) Putting the total mean energy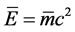 , the mean momentum
, the mean momentum 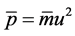 and the rest energy
and the rest energy 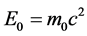 into Equation (29), the new energy-momentum relation formula is obtained as follows
into Equation (29), the new energy-momentum relation formula is obtained as follows
 (34)
(34)
where
 (35)
(35)
Compared with the old energy-momentum relationship
 (36)
(36)
(34) than (36) multi-a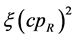 , which indicates that the existence of so-called Lorentz invariance violation (LIV) is an inevitable result of the new special relativity, and the violation coefficient
, which indicates that the existence of so-called Lorentz invariance violation (LIV) is an inevitable result of the new special relativity, and the violation coefficient 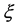 can be directly exactly calculate by (35). Equation (35) shows that the absolute value of LIV coefficient
can be directly exactly calculate by (35). Equation (35) shows that the absolute value of LIV coefficient 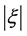 is dependent on the speed u of particle, that is the higher the u the smaller (not the larger!) the
is dependent on the speed u of particle, that is the higher the u the smaller (not the larger!) the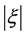 , when
, when 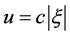 attains the minimum value
attains the minimum value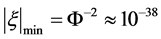 . Table 3 lists LIV coefficients corresponding to different speeds. Of particular note is that if the particle speed is low to
. Table 3 lists LIV coefficients corresponding to different speeds. Of particular note is that if the particle speed is low to 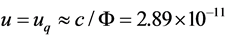 (m/s) = 0.289 (Å/s) then
(m/s) = 0.289 (Å/s) then , (34) becomes the strange form
, (34) becomes the strange form
 (37)
(37)
(37) suggests that people should re-understanding of the “stationary” concept, because such an extreme tiny speed ~0.289 (Å/s) has never been actually observed. About (29) and (34) we will do for a more in-depth discussion in Section 4.
3.2. Improved Lorentz Transformations and Kinematic Formulas
By the ![]() state probability to weighted average
state probability to weighted average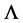 , the maximum average length
, the maximum average length  of the 3-dimensional space cross-sectional in the particle movement direction is got (see Figure 1, Table 1, (13) (14) (14’) (16)). According to the [Postulate],
of the 3-dimensional space cross-sectional in the particle movement direction is got (see Figure 1, Table 1, (13) (14) (14’) (16)). According to the [Postulate],  is the final standard ruler in the length measurement in the particle movement direction. Using
is the final standard ruler in the length measurement in the particle movement direction. Using , the improved Lorentz transformations can be derived:
, the improved Lorentz transformations can be derived:
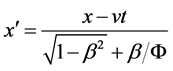 (38-1)
(38-1)
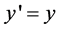 (38-2)
(38-2)
 (38-3)
(38-3)
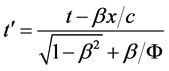 (38-4)
(38-4)
and inverse transforms
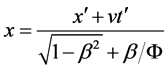 (39-1)
(39-1)
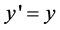 (39-2)
(39-2)
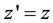 (39-3)
(39-3)
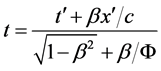 (39-4)
(39-4)
where ![]() is the movement velocity of an inertial
is the movement velocity of an inertial 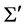 relative to another inertial
relative to another inertial ![]() along the x-axis, and
along the x-axis, and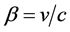 . According to the reasoning mode of the classical theory of special relativity, from the above coordinate transformations it can be further derived that the time dilation
. According to the reasoning mode of the classical theory of special relativity, from the above coordinate transformations it can be further derived that the time dilation  (40)
(40)
the “length contraction” 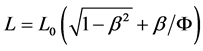 (41)
(41)
the velocity addition law 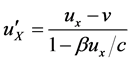 (42)
(42)
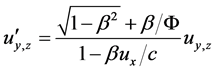 (43)
(43)
and
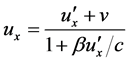 (42’)
(42’)
 (43’)
(43’)
3.3. The Transformation of Physical Quantities and the Covariance of Physics Laws
3.3.1. The Energy and Momentum Transformations between Two Inertial Frames
Defining ,
, 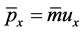 , and then using (29) and (42) (43) it can be proved that
, and then using (29) and (42) (43) it can be proved that
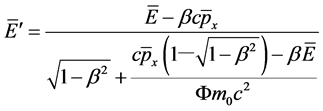 (44)
(44)
 (45)
(45)
3.3.2. Transformation of Electromagnetic Fields and the Covariance of Maxwell Equations
If time and space coordinates are transformed by (38) (39) (38’) (39’), the electromagnetic field are transformed by following (48), then in all inertial reference frames Maxwell’s equations still has the same form,
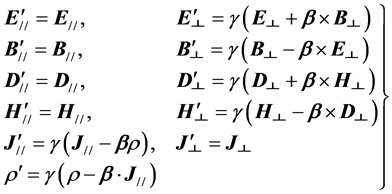 (46)
(46)
where
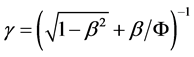 (47)
(47)
It can be seen that the new transform still kept the beautiful symmetry.
3.3.3. The Doppler Effect and the Invariance of Phase Angle
For the monochromatic plane wave![]() , if the space coordinate and time are transformed by (38) (39) respectively, the frequency ω and wave vector k of are transformed by the following equations
, if the space coordinate and time are transformed by (38) (39) respectively, the frequency ω and wave vector k of are transformed by the following equations
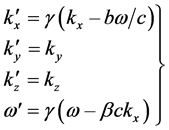 (48)
(48)
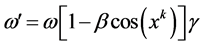 (49)
(49)
where k is in the 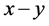 coordinate plane. Then it could be prove that the phase angle transformation between two inertial frames is
coordinate plane. Then it could be prove that the phase angle transformation between two inertial frames is
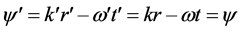 (50)
(50)
so in the new special relativity the phase angle of monochromatic plane wave is still a Lorentz invariant.
3.4. Evaluation of the Particle’s Intrinsic Time-Space Ratio and the Intrinsic Time Height
Using above those results we can design two ideal experiments respectively to evaluate the particle’s intrinsic time-space ratio 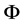 and the particle’s intrinsic time height
and the particle’s intrinsic time height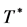 .
.
3.4.1. Evaluation of the Particle’s Intrinsic Time-Space Ratio
The new mass equation indicates that when ![]() there is no the infinity but the finite maximum value of the mass, then let us imagine as follows: In the earliest period of the universe big bang, an “observer” saw that there were newly generated two neutrons to each other separation at the light speed in a same straight line that he was as center, thus the “observer” did first measurement to the two neutrons system. According to (40), the life of neutron moving at light speed is ~1019 times of the rest neutron, which equals ~3 × 1014 years and greatly exceeds the universe age ~1.38 × 1010 years, so the “observer” can still do the second measurement of the two neutrons system. Clearly, the time interval
there is no the infinity but the finite maximum value of the mass, then let us imagine as follows: In the earliest period of the universe big bang, an “observer” saw that there were newly generated two neutrons to each other separation at the light speed in a same straight line that he was as center, thus the “observer” did first measurement to the two neutrons system. According to (40), the life of neutron moving at light speed is ~1019 times of the rest neutron, which equals ~3 × 1014 years and greatly exceeds the universe age ~1.38 × 1010 years, so the “observer” can still do the second measurement of the two neutrons system. Clearly, the time interval 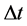 between twice measurements is the maximum of all time intervals, that about equals the universe’s age
between twice measurements is the maximum of all time intervals, that about equals the universe’s age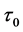 . Substituting
. Substituting 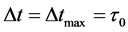 into the uncertainty relation formula
into the uncertainty relation formula
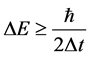 (51)
(51)
to get in twice measurements the minimum value of the uncertain energy
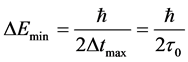 (52)
(52)
However, what is the specific form of energy corresponding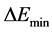 ? In general, the specific form of energy must satisfy two conditions: First, it is physically real; Second, it has the lowest strength. The observer saw that these two neutrons are in the movement at the speed of light, then the average kinetic energy of particle is a very large value, so
? In general, the specific form of energy must satisfy two conditions: First, it is physically real; Second, it has the lowest strength. The observer saw that these two neutrons are in the movement at the speed of light, then the average kinetic energy of particle is a very large value, so  is not about the kinetic energy but a certain kind of potential energy. For two each other distant neutrons, there is only a gravitational potential energy in all kinds of potential energies, and when two neutrons are in the most distant the strength of gravitational potential energy has the minimum value. Therefore, the real
is not about the kinetic energy but a certain kind of potential energy. For two each other distant neutrons, there is only a gravitational potential energy in all kinds of potential energies, and when two neutrons are in the most distant the strength of gravitational potential energy has the minimum value. Therefore, the real  is only the gravitational potential energy when the distance of two neutrons is maximum. Today’s observer sees, the distance between two neutrons is so large that the gravitational field certainly is the weak field, and because their velocity vectors are in a same straight line, so the Newton’s gravity equation can be used to calculate the minimum of gravitational potential energy
is only the gravitational potential energy when the distance of two neutrons is maximum. Today’s observer sees, the distance between two neutrons is so large that the gravitational field certainly is the weak field, and because their velocity vectors are in a same straight line, so the Newton’s gravity equation can be used to calculate the minimum of gravitational potential energy 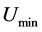 of this two-neutrons system, but the mass substituted into the equation is not the rest mass
of this two-neutrons system, but the mass substituted into the equation is not the rest mass  but
but  given by (31), so
given by (31), so
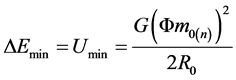 (53)
(53)
In addition, for the expression of the universe age, we require an in-depth analysis. Two neutrons predecessors, i.e. quarks and so on primordial particles, were from a same cosmic singularity starting, the big bang caused they fly at the light speed at that time. If the subsequent expansion of the universe is roughly uniform and isotropic, today’s “observer” and the two neutrons must be on those locations of the great circle shown in Figure 2.
As is known, at different periods the universe expansion speed is variable, so the universe age 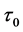 is not equal to the great circle radius
is not equal to the great circle radius 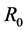 divided by the today’s light speed c, namely
divided by the today’s light speed c, namely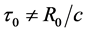 . However, taking into there is always a same light speed at a same period, i.e. on a same great circle, so the universe age should be expressed as the ratio of the quarter of great circle perimeter to the light speed, that is
. However, taking into there is always a same light speed at a same period, i.e. on a same great circle, so the universe age should be expressed as the ratio of the quarter of great circle perimeter to the light speed, that is
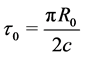 (54)
(54)
(53) (54) into (52), to ultimately get
 (55)
(55)
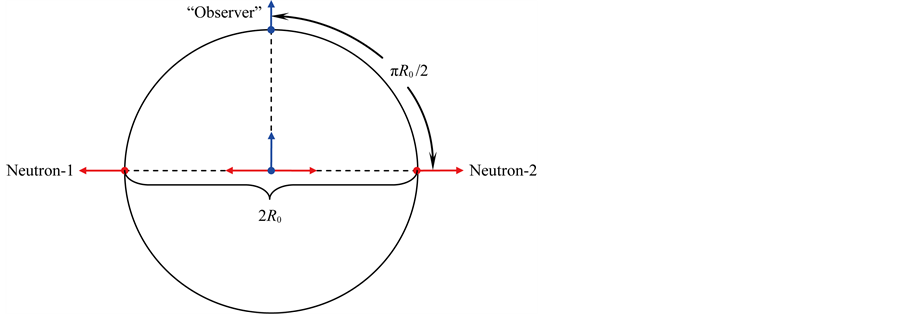
Figure 2. Schematic diagram of the ideal experiment of “two-neutrons”.
All factors of the (55) right side have the known exact value, so  is directly calculated, which has previously been given in (5).
is directly calculated, which has previously been given in (5).
It can be seen that 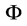 is an important constant that reflects the feature of PSTC model as well as the differences between new equations and old equations of the special relativity.
is an important constant that reflects the feature of PSTC model as well as the differences between new equations and old equations of the special relativity.  value is very large but after all is limited, if it is seen as infinite, new equations will immediately degenerate into old equations. When the speed is not extremely close to the light speed or not extremely close to zero, the difference of the new with the old equations are very small.
value is very large but after all is limited, if it is seen as infinite, new equations will immediately degenerate into old equations. When the speed is not extremely close to the light speed or not extremely close to zero, the difference of the new with the old equations are very small.
Finally it must be noted that the particle that fits this ideal experiment only is the neutron and not any other particles, for the following reasons: So far all astronomical observations and experimental facts show that the weak gravitational source substances satisfying Newton’s gravitation law have all the structural unit with the nucleons as main component, so the real and stable “basic gravitational charge” must be nucleons. In addition, in order to avoid electromagnetic interaction so only the neutron is chosen.
3.4.2. Evaluation of the Particle’s Intrinsic Time Height
We can design another ideal experiment to deduce the formula (6) calculating the particle intrinsic time height. Let us imagine that an observer is measuring the energy of a slow-moving free-particle, such as an electron. He can choose an appropriate way to satisfy always the particle speed 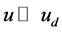 after each measurement, so in twice successive measurements the attainable maximum of uncertainty energy is certainly
after each measurement, so in twice successive measurements the attainable maximum of uncertainty energy is certainly
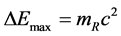 (56)
(56)
which correspond to once occur in 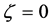 state, another occurs at
state, another occurs at 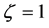 state. (56) into the uncertainty relationship (2), to obtain
state. (56) into the uncertainty relationship (2), to obtain . According to [Corollary 3], the time interval
. According to [Corollary 3], the time interval 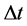 between twice measurements can be sufficiently large but can not be arbitrarily small, so if
between twice measurements can be sufficiently large but can not be arbitrarily small, so if 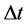 takes the minimum value i.e. the particle’s apparent time height T, then the inequality
takes the minimum value i.e. the particle’s apparent time height T, then the inequality 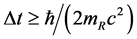 becomes the equality
becomes the equality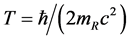 , further (3) (20-1) into which and taking
, further (3) (20-1) into which and taking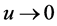 , (6) is got.
, (6) is got.
4. Applying New Special Relativity to Solve Several Problems
4.1. On the Lorentz Invariance Violation and the GZK Suppression of UHECR
About this issue, the new special relativity gives three levels theoretical results which consistent with observations of HiRes and Auger: First, pointed up the existence of Lorentz invariance violation is inevitable and the LIV coefficient 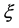 can also be strictly calculated by (35); Second, although existed the LIV effect, for above 4 × 1019 eV UHECR protons the calculated
can also be strictly calculated by (35); Second, although existed the LIV effect, for above 4 × 1019 eV UHECR protons the calculated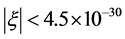 , which indicates that LIV effect too weak to change the GZK cutoff; Third, although existed the GZK suppression not rule out possible appearing a very few random events beyond GZK energy. Now, detailed as follows.
, which indicates that LIV effect too weak to change the GZK cutoff; Third, although existed the GZK suppression not rule out possible appearing a very few random events beyond GZK energy. Now, detailed as follows.
The people have known that the higher than 1018 eV UHECRs, in propagating from the extragalactic sources to the Earth, interact with CMB photons to result in a decline of their energy and flux and finally cause the spectrum suppression at (3 - 6) × 1019 eV, that is the GZK cutoff predicted by Greisen, Zatsepin and Kuzmin in 1960s [7] [8] . However by the 1990s, the AGASA [9] experiment results show an extension of the spectrum beyond the GZK cutoff, so the GZK mechanism based on the special relativity is challenged. For this reason, S. R. Coleman and S. L. Glashow [10] introduced a theory of Lorentz invariance violation (LIV), a tiny correction term  is added into the energy-momentum relationship, namely
is added into the energy-momentum relationship, namely
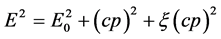 (57)
(57)
Thus, if the coefficient absolute value 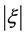 is just as small as ~10−23 enough to eliminate the GZK cutoff. However, in 2008, the HiRes Collaboration announced to confirm the GZK cutoff with a
is just as small as ~10−23 enough to eliminate the GZK cutoff. However, in 2008, the HiRes Collaboration announced to confirm the GZK cutoff with a 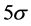 standard deviation [1] and then the Auger collaboration gives the result consistent with HiRes and rejects a single power law spectrum above 4 × 1019 eV with a 6σ standard deviations [2] . Therefore the data of HiRes and Auger can set constraints on the LIV. The current common research way on this problem is from different
standard deviation [1] and then the Auger collaboration gives the result consistent with HiRes and rejects a single power law spectrum above 4 × 1019 eV with a 6σ standard deviations [2] . Therefore the data of HiRes and Auger can set constraints on the LIV. The current common research way on this problem is from different 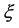 values to calculate the energy spectrum, then comparison with the data of Auger and HiRes thereby find the most fitting
values to calculate the energy spectrum, then comparison with the data of Auger and HiRes thereby find the most fitting  value as the constraint on LIV, obviously this phenomenological study cannot reveal the nature of problem.
value as the constraint on LIV, obviously this phenomenological study cannot reveal the nature of problem.
Here let us use the new Equation (34) of the special relativity to solve this problem. Although (34) and the Coleman-Glashow formula (57) both have the same form (I even deliberately use the same symbol ), their origins and meanings are completely different. A detailed account of (34) characteristics and significance is as follows:
), their origins and meanings are completely different. A detailed account of (34) characteristics and significance is as follows:
1) (34) is derived out from a basic Equation (29) of the new special relativity, so the occurring of 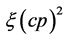 is inevitable, which does not require reluctantly to add. In fact, the existence of so-called Lorentz invariance violation effect is one of inherent features of the new special relativity.
is inevitable, which does not require reluctantly to add. In fact, the existence of so-called Lorentz invariance violation effect is one of inherent features of the new special relativity.
2) The LIV coefficient 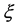 is a function of the speed and has the strict expression i.e. (35), so
is a function of the speed and has the strict expression i.e. (35), so 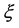 is a theoretical value independently calculated before the experimental observation, not by fitting observation data to adjust.
is a theoretical value independently calculated before the experimental observation, not by fitting observation data to adjust.
3) (29) points out, for all kinds of particle the physical quantity with common upper limit is just the speed i.e. the light speed c (not other physical quantities, e.g., energy). When![]() , the particle energy is not the infinity but a limited maximum (see (31)), so for different particles according to their different rest energy E0 there are different maximal attainable energies (and not different maximal attainable speeds).
, the particle energy is not the infinity but a limited maximum (see (31)), so for different particles according to their different rest energy E0 there are different maximal attainable energies (and not different maximal attainable speeds).
4) (35) shows, the higher the speed u, the smaller (and not the larger!) the coefficient absolute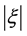 , when
, when ![]() it attains the minimum value
it attains the minimum value .
.
5) When 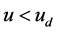 Lorentz energy
Lorentz energy  and speed
and speed ![]() is one to one, so via (20-1)
is one to one, so via (20-1) 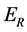 can replace u then (35) is rewritten as
can replace u then (35) is rewritten as
 (58)
(58)
In the energy region , (58) can be simplified to
, (58) can be simplified to
 (58’)
(58’)
For the UHECR spectrum ankle region protons and 56Fe, we use (58’) to specifically calculate the LIV coefficient values and list to Table4
To above 4 × 1019 eV protons, the calculated . By comparison with some fitting calculations [11] [12] , it can be seen, although (34) has expected that there is the Lorentz invariance violation effect, the violation coefficient
. By comparison with some fitting calculations [11] [12] , it can be seen, although (34) has expected that there is the Lorentz invariance violation effect, the violation coefficient 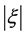 is too small to change the GZK suppression of UHECR spectrum, which is consistent with experimental results that the HiRes collaboration and the Auger collaboration confirm the GZK suppression with a 5σ standard deviation [1] [2] .
is too small to change the GZK suppression of UHECR spectrum, which is consistent with experimental results that the HiRes collaboration and the Auger collaboration confirm the GZK suppression with a 5σ standard deviation [1] [2] .
On the other hand, we know that events beyond GZK energy were also really recorded in cosmic ray observation, in order to explain this phenomenon, it is necessary to use the basic Equation (19-1). As described above, (34) is derived from (29), and (29) is derived from (19). The mass of composite particles is usually embodied as the mean mass 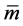 described by (29) that has contained the all influence of the random variables
described by (29) that has contained the all influence of the random variables![]() , however, for the proton as most simple composite particle, when its energy is very high the random variable
, however, for the proton as most simple composite particle, when its energy is very high the random variable ![]() still has some influence, and therefore the high-speed low-energy (HSLM) effect has still a certain degree of performance.
still has some influence, and therefore the high-speed low-energy (HSLM) effect has still a certain degree of performance.
Now let us imagine that a group of beyond the GZK energy protons from an extragalactic source which is more distant than the mean free path fly to the Earth. In this process, a very few of protons could appear in certain HSLM state in some time. Because at the HSLM state the energy and the relative cross-section are both smaller than the normal values, therefore the possibility that the HSLM protons interact with the CMB photons will be smaller than of the normal protons, thereby they can propagate farther than the normal mean free path. If arriving Earth before restored to the normal 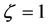 state, then the Earth will receive the over GZK energy event. Of course, such event is very rare. To summarize, although the tiny LIV coefficients
state, then the Earth will receive the over GZK energy event. Of course, such event is very rare. To summarize, although the tiny LIV coefficients 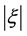 will not change the GZK cutoff, yet not rule out the possibility that a very few of beyond GZK energy protons reach the Earth, moreover, occurring such small probability events beyond GZK energy is random and do not constitute a single power-law spectrum, which are all consistent with Auger observation [2] .
will not change the GZK cutoff, yet not rule out the possibility that a very few of beyond GZK energy protons reach the Earth, moreover, occurring such small probability events beyond GZK energy is random and do not constitute a single power-law spectrum, which are all consistent with Auger observation [2] .
4.2. On the Observer Independence of the Planck Energy and the Doubly Special Relativity
2002, J. Magueijo and L. Smolin modified Einstein’s special relativity and proposed the “doubly special relativity (DSR)”, of which one of four basic principles is the observer independence of the Planck energy [3] . Below we prove that this “basic principle” can be derived by the new special relativity.
Considering a particle at a velocity u moves along the x axis of an inertial frame![]() , its energy and momentum are
, its energy and momentum are  and
and 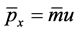 relative to the observer in inertial frame
relative to the observer in inertial frame![]() . In another inertial frame
. In another inertial frame 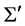 at speed
at speed 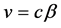 moving along the x axis relative the
moving along the x axis relative the![]() , the particle’s energy
, the particle’s energy 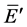 and momentum
and momentum 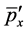 are transformed by (44) (45) respectively. When the particle speed
are transformed by (44) (45) respectively. When the particle speed ![]() relative to the observer of the inertial frame
relative to the observer of the inertial frame![]() , its mass attains the maximum
, its mass attains the maximum 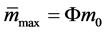 (see (31)), thus its energy and momentum attain also the maximum
(see (31)), thus its energy and momentum attain also the maximum  and
and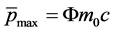 . Putting
. Putting ![]() and
and 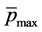 into (44) and (45), the calculations are
into (44) and (45), the calculations are and
and 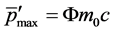 respectively, so whether in the
respectively, so whether in the ![]() or
or 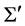 this particle’s energy all attain the maximum value of the same, however, the relative velocity v between two inertial systems has no any impact. The above calculation has proved an important result, that is, when moving at the strict light speed c, each particle can attain its own maximal mean mass
this particle’s energy all attain the maximum value of the same, however, the relative velocity v between two inertial systems has no any impact. The above calculation has proved an important result, that is, when moving at the strict light speed c, each particle can attain its own maximal mean mass 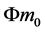 (or energy
(or energy ), which is the invariant independent of the observers.
), which is the invariant independent of the observers.
As a special case, we use (31) and (55) to calculate the maximum value of the mean mass of neutron
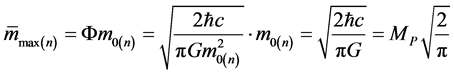 (59)
(59)
where, 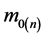 denotes the rest mass of neutron,
denotes the rest mass of neutron, 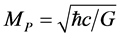 is the Planck mass. (59) shows, the Planck mass (or energy) and the maximum value of the neutron average mass (or energy) both are in the same order of magnitude, their distinguish is only a constant factor
is the Planck mass. (59) shows, the Planck mass (or energy) and the maximum value of the neutron average mass (or energy) both are in the same order of magnitude, their distinguish is only a constant factor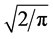 . Because the maximum of neutron mean mass (or energy) is the invariant independent of the observers, so the Planck mass (or energy) also is necessarily the invariant independent of the observers, that is, there is the observer independence of the Planck energy.
. Because the maximum of neutron mean mass (or energy) is the invariant independent of the observers, so the Planck mass (or energy) also is necessarily the invariant independent of the observers, that is, there is the observer independence of the Planck energy.
In addition, we prove that an important formula of DSR can be derived by (29). According to (20-1), letting the Lorentz mass  and the rest mass
and the rest mass 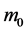 replace the speed ratio
replace the speed ratio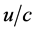 , then (29) is written in the following form
, then (29) is written in the following form
 (60)
(60)
When , it can be simplified to
, it can be simplified to
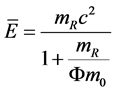 (61)
(61)
At the same speed the mass ratio 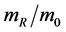 of any kind of particles can be replaced with the neutron’s mass ratio
of any kind of particles can be replaced with the neutron’s mass ratio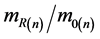 , so
, so
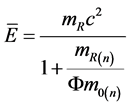 (62)
(62)
According to (59), the Planck mass 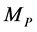 and the neutron’s mean mass maximum
and the neutron’s mean mass maximum 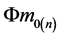 are in the same order of magnitude, their difference is just on a constant factor
are in the same order of magnitude, their difference is just on a constant factor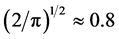 , so
, so 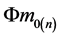 can be substituted by
can be substituted by  to write (29) as
to write (29) as
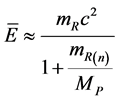 (63)
(63)
It is interesting, the DSR also has such a similar formula [3] , which even is as the highlight [13] .
Now it has been seen that the DSR’s one basic principle and a similar to (63) result all can be proved by the new special relativity. However, this does not mean that my new special relativity and the DSR are the same thing, in essence they are different in not only the theoretical fundamentals but also some typical results. For example, the new special relativity has proved that the Planck energy cannot serve as the common upper limit of the energy of all kinds of particles, and indicate that of importance is not the Planck energy but the parameter 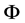 describing the particle’s intrinsic space-time feature. Another example, as described in Section 4.1, the formula (35) calculating LIV coefficient
describing the particle’s intrinsic space-time feature. Another example, as described in Section 4.1, the formula (35) calculating LIV coefficient  point out, the higher the speed, the weaker the LIV effect, thus to prophesy that the GZK cutoff of UHECR will not change. However, in theories of the DSR as well as superstrings, loop quantum gravity and so on there are no such contents.
point out, the higher the speed, the weaker the LIV effect, thus to prophesy that the GZK cutoff of UHECR will not change. However, in theories of the DSR as well as superstrings, loop quantum gravity and so on there are no such contents.
4.3. On the Hubble Constant and the Dirac Large Numbers
4.3.1. A Relation Formula between the Hubble Constant and Several Basic Constants Is Derived, Thus Theoretically Calculated the Hubble Constant H0 = 70.937 km∙s−1∙Mpc−1
(32) (33) show that there is a specific speed ![]() being extremely nearing 0, when
being extremely nearing 0, when![]() , the particle’s mean mass has a minimum value. Let us conceive that in an inertial frame without existence of any force field, there is a free electron moving at the speed
, the particle’s mean mass has a minimum value. Let us conceive that in an inertial frame without existence of any force field, there is a free electron moving at the speed ![]() from the coordinate origin starting. According to Hubble law, the coordinate origin as center and
from the coordinate origin starting. According to Hubble law, the coordinate origin as center and ![]() as radius spherical surface is expanding by the speed
as radius spherical surface is expanding by the speed ![]() along with the universe expansion, where
along with the universe expansion, where
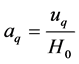 (64)
(64)
Because in the real universe this expansion is inevitable, so even though there is no any external forces, but the electron moving at ![]() can only be confined within the sphere of radius as
can only be confined within the sphere of radius as![]() , that is, the electron is equivalently at the lowest energy
, that is, the electron is equivalently at the lowest energy ![]() of the infinite deep ball square potential well of radius as
of the infinite deep ball square potential well of radius as ![]() [14] ,
[14] ,
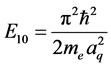 (65)
(65)
where,  denotes the rest mass of electron. On the other hand, because
denotes the rest mass of electron. On the other hand, because ![]() value is very small, so in accordance with the classical mechanics this electron’s kinetic energy is expressed as
value is very small, so in accordance with the classical mechanics this electron’s kinetic energy is expressed as
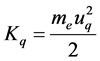 (66)
(66)
Noting (65) is a derived result of the Schrodinger equation, and the energy operator in Schrodinger equation is of corresponding the classical mechanics, so there must be
![]() (67)
(67)
By (32) and (64)-(67) thus obtaining another  expression:
expression:
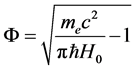 (68)
(68)
According to the magnitude of the “today”  value it can be seen
value it can be seen , so (68) is written as
, so (68) is written as
 (69)
(69)
Here it must be noted that the particle that fits above ideal experiment only is the electron and not any other particles, for the following reasons: 1) According to the PSTC model, only to the particles of quarks/leptons level the speed uq can be defined, so composite particles are rejected; 2) Particles must be in the free state, so only the leptons can be selected; 3) Because neutrinos are always in the oscillation so also are rejected; 4) The life of  lepton and
lepton and ![]() lepton are too short to meet the requirement of a long time and stable movement, so only the electron is qualified.
lepton are too short to meet the requirement of a long time and stable movement, so only the electron is qualified.
Combining (69) with (55), a relationship between the Hubble constant and several basic constants is obtained:
 (70)
(70)
All factors of (70) right side have known accurate values, so we can use this formula to exactly calculated
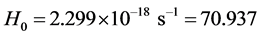 km∙s−1∙Mpc−1 (71)
km∙s−1∙Mpc−1 (71)
(32) (70) into (64) calculated aq = 1.26 × 104 km, so our theoretical value is the “near-place” Hubble constant.
Generally believed that the Hubble law is an empirical law and the Hubble constant is obtained by astronomical observations. However, the theoretical result (70) is derived from a non-point model of microscopic particles, in its deductive process the Hubble law is used but does not involve any astronomically observed quantity (such as the redshift, the luminosity), which indicates that the theoretical value (71) is completely independent to astronomical observation, so its comparison with the measuring value of Hubble constant is a persuasive way to test the new special relativity. It is noted that after long efforts the enough credible observed values of the Hubble constant have been obtained, such as the final measurement result of Hubble space telescope key project [4] for H0 = 72(71) ± 4 ± 7 km∙s−1∙Mpc−1, the exciting is my theoretically calculated value is well consistent with this observed value.
4.3.2. Exposing the Mystery of Dirac Large Numbers
Dirac long noted, there are two approximately equal non-dimensional large numbers,
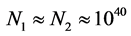 (72)
(72)
N1 is the ratio of the universe Hubble radius to the electron classical radius, N2 is the ratio of the static electricity force to the gravitation between proton and electron. In addition there are a series of large pure numbers, which are roughly equal with integer powers of  respectively, and can all be attributed to a “mysterious numbers relation” pieced together by the dimension and order of magnitude [15]
respectively, and can all be attributed to a “mysterious numbers relation” pieced together by the dimension and order of magnitude [15]
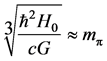 (73)
(73)
or
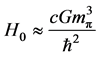 (73’)
(73’)
where  denotes the
denotes the ![]() meson mass. Dirac considered that the correlation between large numbers, in particular the numbers relationship given by (73) is not a meaningless coincidence, but implies there should be a fundamental fact that has not yet been elucidated. In view of this, he proposed the famous large numbers assume that: Any two dimensionless large numbers that appear in nature are related to each other, they are linked by a simple mathematical relationship [16] .
meson mass. Dirac considered that the correlation between large numbers, in particular the numbers relationship given by (73) is not a meaningless coincidence, but implies there should be a fundamental fact that has not yet been elucidated. In view of this, he proposed the famous large numbers assume that: Any two dimensionless large numbers that appear in nature are related to each other, they are linked by a simple mathematical relationship [16] .
The Dirac large numbers problem as a mystery to the people left a deep impression, however, so far on this problem did not achieve breakthroughs. Why exists such a mysterious numbers relation (73)? What is the elusive basic fact hiding at behind those large numbers? Dirac had reward to seek answers the questions has not been deciphered.
It is interesting that in our new special relativity there is also a dimensionless large number of approximately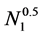 , that is the parameter
, that is the parameter  describing the geometry characteristic of intrinsic spacetime of particle. In particular, we use the new mass equation to logically derive out the strict and exact relationship (70) between the Hubble constant and a number of fundamental constants. Comparing (70) with (73’), it can be seen that (70) as a rigorous theoretical results has done a thorough clarification for the Dirac’s pieced “mystery numbers relation”. Now via (55) (69) (70), we can use
describing the geometry characteristic of intrinsic spacetime of particle. In particular, we use the new mass equation to logically derive out the strict and exact relationship (70) between the Hubble constant and a number of fundamental constants. Comparing (70) with (73’), it can be seen that (70) as a rigorous theoretical results has done a thorough clarification for the Dirac’s pieced “mystery numbers relation”. Now via (55) (69) (70), we can use  as the element to one by one analysis for those bewildering large numbers, for example as follows:
as the element to one by one analysis for those bewildering large numbers, for example as follows:
The ratio of the Hubble radius to the electron classical radius
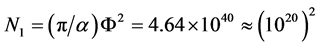
The ratio of the static electricity force to the gravitation between proton and electron
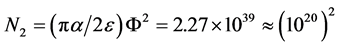
The ratio of the electron classical radius to the Planck length

The ratio of the Planck length to the Schwartzchild radius of proton

The ratio of the Hubble radius to the Schwartzchild radius of proton
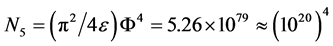
where ![]() denotes the fine structure constant,
denotes the fine structure constant, ![]() denotes the ratio of mass of electron to proton. Above formulas show: 1) Every one of large numbers all contain the factor
denotes the ratio of mass of electron to proton. Above formulas show: 1) Every one of large numbers all contain the factor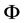 ; 2) The integer powers of
; 2) The integer powers of 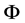 determines the order of magnitude of large numbers; 3) These large numbers are not vague, they have the exact number, their details are determined by dimensionless small numbers
determines the order of magnitude of large numbers; 3) These large numbers are not vague, they have the exact number, their details are determined by dimensionless small numbers .
.
Based on the above analysis it can be considered that the Dirac large numbers principle is a secondary effect, the important thing that hides at behind the relevance of large numbers is the particle’s intrinsic space-time feature described by parameter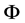 , this should be that Dirac had been looking for but never found the “basic fact”.
, this should be that Dirac had been looking for but never found the “basic fact”.
5. Experimental Test of the New Mass Equation
In Section 3.1 [III], it has been pointed out, the new mass equation predicts that there is a unusual “high speed-low mass (HSLM) effect” in motion of particles. The HSLM effect is very weak, however, in the electron storage rings with high current and long time running we could still observe abnormal phenomenon caused by it, that is, an emission of super-high energy electrons much higher than the beam energy in the RF cavity downstream direction. By detecting such small probability abnormal events we can test the new mass equation. In the NSRL800MeV electron storage ring, I used the lead plates-X films detector to cumulatively detect for a long time, preliminary experiment results hinted the signs of existence of super-high energy electrons [17] . To this end I propose an experimental plan and I hope physicists in large electronic accelerator laboratories to complete this interesting exploratory experiment.
5.1. Experimental Principle
According to (19.1), at a same speed, the mass m of HSLM electron in  state is smaller than the mass
state is smaller than the mass  of normal electrons in
of normal electrons in 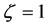 state, i.e.
state, i.e. . In the electron storage ring, so when the beam passes through the accelerating electric field, HSLM electrons in the beam will be accelerated more quickly than normal electrons. If these abnormal electrons return to the most probable
. In the electron storage ring, so when the beam passes through the accelerating electric field, HSLM electrons in the beam will be accelerated more quickly than normal electrons. If these abnormal electrons return to the most probable  state before reaching the deflection magnetic field, their energy
state before reaching the deflection magnetic field, their energy 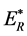 will certainly be higher than the normal electrons energy
will certainly be higher than the normal electrons energy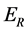 , thereby an abnormal emission of electrons much higher than the beam energy will appear in the RF cavity downstream direction (see Figure 3).
, thereby an abnormal emission of electrons much higher than the beam energy will appear in the RF cavity downstream direction (see Figure 3).
5.2. Characteristics of Super-High Energy Electrons
1) Strength: Using (19-1) (23’) (24) (15) it can be proved that numbers of super-high energy electrons may appear per hour
 (74)
(74)
where,  (MeV) denotes the energy of super-high electron; ER (MeV) denotes the energy of beam; U (MV) denotes the accelerating voltage; I (mA) denotes the average current intensity; E0 (MeV) is the rest energy of electron; e (C) is the electron charge. So in
(MeV) denotes the energy of super-high electron; ER (MeV) denotes the energy of beam; U (MV) denotes the accelerating voltage; I (mA) denotes the average current intensity; E0 (MeV) is the rest energy of electron; e (C) is the electron charge. So in  the numbers of super-high energy electrons may appear per hour
the numbers of super-high energy electrons may appear per hour
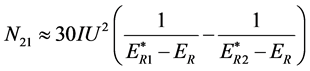 (75)
(75)
In existing electron storage rings, calculated N21 values are all very small, such as, if ER = 2000 MeV, U = 1.5 MV, I = 500 mA, about average 1 hour appearing 1 event of super-high energy electrons of 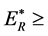 34,000 MeV.
34,000 MeV.
2) Energy-positional distribution: Shown in Figure 3, the extension line of beam in straight section (i.e. the tangent line of beam in deflection section) as the y axis and the bending magnet starting point as the origin point to establish a coordinate system. For different electron storage rings, according to the beam energy, the magnetic field strength and the machine structure parameters, a relation between the energy  of super-high energy electron and the injection point coordinate x at the absorber can be deduced. For example, the electron storage ring in Figure 3, if
of super-high energy electron and the injection point coordinate x at the absorber can be deduced. For example, the electron storage ring in Figure 3, if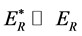 , there is
, there is
 (76)
(76)
where r is the normal bending radius of beam in the bending magnetic field; a is the length of first bending magnetic field; b is the distance between the exit end of first magnetic field and the absorber.
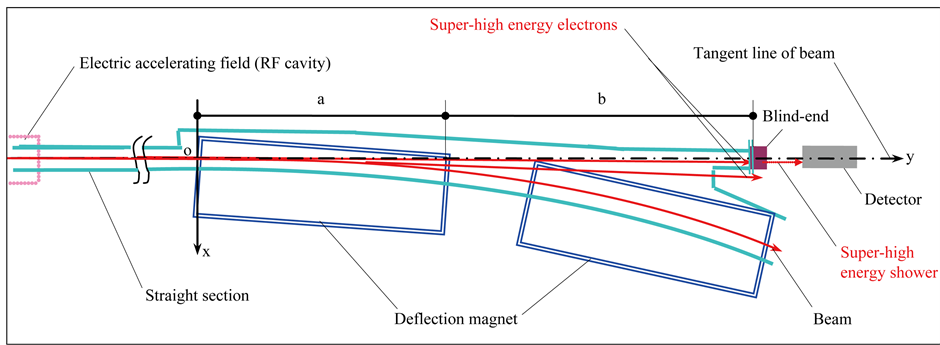
Figure 3. New equations expect that in the electron storage ring RF cavity downstream direction there are small probability events of emission of unusual electrons whose energies are much higher than the beam energy.
5.3. Feasibility of Experiment
The super-high electrons occurring in electron storage rings are very rare, but it is still feasible to detect such small probability events by existing experimental techniques, which because:
1) Electron storage rings have higher current and can run continuously for a long time, so to facilitate the long-term search and cumulative record. And, to many electron storage rings, in the RF cavity downstream direction occurring super-high energy electrons, the beam pipeline of synchrotron radiation are not installed and the vacuum chamber is only closed by the blind end, which facilitate the placement of detector.
2) The sampling electromagnetic calorimeter can be used as a detector, and such detectors are mature technologies. Because the copper blind-end is very thick, the super-high energy electron injects in which will occur electromagnetic cascade shower, so the detector will in fact accept such the secondary particles shower. To the sampling electromagnetic calorimeter, the copper blind-end is equivalent to its front-side absorber. Of course, it is best to place the detector to inside of the vacuum chamber of storage ring. In addition, taking into the residual gas bremsstrahlung along the straight section axis is a main interference, so in order to reduce its impact, the detector should be appropriately off-axis placed.
6. Conclusions
Could the special relativity and the quantum mechanics unify at deeper level via a way different from the quantum electrodynamics? This is a potential big problem which should not be overlooked; In recent years, about whether existing the Lorentz invariance violation has become a hot topic of extensive discussions; Since the superstring theory driven, the way using a non-point particle model to replace the concept of mass point to seek developments of theory has been widely accepted. Under this context, therefore, it is imperative to try to use the basic principles of quantum mechanics, especially the uncertainty principle to further improve the special relativity. This paper is in this direction an independent research and useful contribution.
This work is first based upon the space spherical symmetry of 3-dimensional and the translational symmetry of time, and the uncertainty principle, to establish a 4-dimensional space-time cylinder model of the quarks and leptons. Then, we use this model to deduce a series of new equations that are compatible with old equations of special relativity and also satisfy the uncertainty principle, thereby achieve unifying special relativity and quantum mechanics in basic concepts. New equations which reveal the concepts of space, time, mass, energy etc. have richer connotations, so that can help people to re-understand the essence of some physical phenomena and solve several pending important problems. The results derived by new equations show:
1) The mass is a binary function of speed u and another dimensionless variable . The random variable
. The random variable ![]() that appears in the derivation process of equation makes the concepts of randomness and probability automatically enters the relativistic equations.
that appears in the derivation process of equation makes the concepts of randomness and probability automatically enters the relativistic equations.
2) When ![]() the energy is not the infinity but a finite maximum value
the energy is not the infinity but a finite maximum value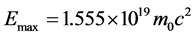 . This result will eliminate the divergence difficult, and lay a foundation for building a new quantum field theory without renormalization.
. This result will eliminate the divergence difficult, and lay a foundation for building a new quantum field theory without renormalization.
3) The violation of Lorentz invariance is inevitable and the LIV coefficient 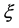 can be strictly calculated. To above 4 × 1019 eV UHECR protons, the calculated
can be strictly calculated. To above 4 × 1019 eV UHECR protons, the calculated , so although there is the LIV effect
, so although there is the LIV effect  is too small to change the GZK cutoff, which is consistent with observations of HiRes and Auger.
is too small to change the GZK cutoff, which is consistent with observations of HiRes and Auger.
4) It is proved that the Planck energy is a Lorentz invariant, so there is certainly “the observer independence of Planck energy”. However it is also proved that the Planck energy isn’t the common upper limit of energy of all kinds of particles.
5) A relation formula between the Hubble constant and several basic constants is derived, thus the theoretical value H0 = 70.937 km∙s−1∙Mpc−1 is obtained, which is well consistent with the final result of observation of HST key project. The mystery of Dirac large numbers can be clarified too by this relation formula.
6) An unusual effect is predicted, and accordingly expected that in the electron storage ring RF cavity downstream direction there is an emission of rare unusual electrons of much higher than the beam energy. New equations can be tested by searching for such small probability events.
References
- HiRes Collaboration (2008) Physical Review Letters, 100, Article ID: 101101. [arXiv:astro-ph/0703099] http://dx.doi.org/10.1103/PhysRevLett.100.101101
- Auger Collaboration (2008) Physical Review Letters, 101, Article ID: 061101. [arXiv:0806.4302] http://dx.doi.org/10.1103/PhysRevLett.101.061101
- Magueijo, J. and Smolin, L. (2002) Physical Review Letters, 88, Article ID: 190403. [arXiv:hep-th/0112090v2] http://dx.doi.org/10.1103/PhysRevLett.88.190403
- Freedman, W.L., Madore, B.F., Gibson, B.K., Ferrarese, L., Kelson, D.D., Sakai, S., et al. (2001) Astrophysical Journal, 553, 47-72. [arXiv:astro-ph/0012376v1]
- Einstein, A. (1955) Relativity: The Special and the General Theory. Note to the Fifteenth Edition, Methuen & Co. Ltd., London.
- Landau, L.D. and Lifschitz, E.M. (1977) The Quantum Mechanics. English Translation, Pergamon.
- Greisen, K. (1966) Physical Review Letters, 16, 748. http://dx.doi.org/10.1103/PhysRevLett.16.748
- Zatsepin, G.T. and Kuzmin, V.A. (1966) Pisma Zh. Eksp. Teor. Fiz., 4, 114-117.
- Takeda, M., Hayashida, N., Honda, K., Inoue, N., Kadota, K., Kakimoto, F., et al. (1998) Physical Review Letters, 81, 1163-1166. [arXiv:astro-ph/9807193] http://dx.doi.org/10.1103/PhysRevLett.81.1163
- Coleman, S. and Glashow, S.L. (1999) Physical Review D, 59, Article ID: 116008. [arXiv:hep-ph/9812418v3] http://dx.doi.org/10.1103/PhysRevD.59.116008
- Scully, S.T. and Stecker, F.W. (2009) Astroparticle Physics, 31, 220-225. [arXiv:0811.2230v4]
- Bi, X.J., Cao, Z., Li, Y. and Yuan, Q. (2009) Physical Review D, 79, Article ID: 083015. [arXiv:astro-ph/0812.0121] http://dx.doi.org/10.1103/PhysRevD.79.083015
- Magueijo, J. (2003) Faster than the Speed of Light. Perseus Publishing, New York.
- Zeng, J.Y. (1981) Quantum Mechanics. Science Press, 209-212.
- Dirac, P.A.M. (1937) Nature, 139, 323. http://dx.doi.org/10.1038/139323a0
- Weinberg, S. (1980) Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (1972). Chinese Translations, Science Press, 724-726.
- Qian, D.P. (2010) Journal of Liaoning University, Natural Sciences Edition, 37, 236-240.


