Journal of Modern Physics
Vol.5 No.8(2014), Article ID:46453,7 pages DOI:10.4236/jmp.2014.58078
Magnetic-Field-Induced Phase Transition and a Possible Quantum Hall Effect in the Quasi-One-Dimensional CDW Organic Conductor HMTSF-TCNQ
Keizo Murata1, Yuhei Fukumoto1, Keiichi Yokogawa1, Woun Kang2, Ryo Takaoka, Ryota Tada1, Hikaru Hirayama1, James S. Brooks3, David Graf3, Harukazu Yoshino1, Takahiko Sasaki4, Reizo Kato5
1Graduate School of Science, Osaka City University, Osaka, Japan
2Department of Physics, Ewha Womans University, Seoul, Korea
3National High Magnetic Field Laboratory/Florida State University, Tallahassee, USA
4Institute for Materials Research, Tohoku University, Sendai, Japan
5RIKEN, Wako, Saitama, Japan
Email: muratak@sci.osaka-cu.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 March 2014; revised 26 April 2014; accepted 21 May 2014
ABSTRACT
In the Temperature-Pressure phase diagram, the quasi-one-dimensional conductor, HMTSF-TCNQ, the ground state at ambient pressure is an insulator of charge density wave (CDW) below 30 K, while it shows a good metallic nature at higher temperature. The CDW insulating state is suppressed by a pressure of 1 GPa, which is considered to be a quantum critical point. Neither at 0 - 0.5 nor 2 GPa but only around this critical point in pressure, field-induced phases appear from 0.2 T through 10 T, where Rxy is almost constant and Rxx is very low. These phenomena are achieved when the magnetic field is applied along the least conducting axis. The behaviors are consistent with a kind of Quantum Hall Effect (QHE). The field-induce phase accompanied by the QHE might be the field-induced CDW (FICDW) similar to that of FISDW, observed in (TMTSF)2X salts. This paper presents the latest result of the Hall effects reviewing the history of the authors’ work on this material from preliminary to the latest ones.
Keywords:Charge Density Wave, Magnetoresistance, Field-Induced CDW, Fermi Surface, Nesting, Quantum Hall Effect

1. Introduction
It is commonly observed that the highly correlated system has an insulating ground state at low pressure in the temperature-pressure phase diagram. And this insulating state is suppressed by increasing pressure or by doping, and such pressure (or doping value) is likely to be “the quantum critical point”. Those insulating states are either magnetic (antiferromagnetic Mott insulator, or spin density wave (SDW)) or non-magnetic (charge density wave (CDW), or charge order (CO)) in either case of organic or inorganic materials. Around the pressure of the quantum critical point, the superconductivity is frequently found.
In the case of the first organic superconductor, (TMTSF)2PF6, the insulating phase is a spin density wave (SDW) below 12 K at ambient pressure. When the SDW is suppressed by a pressure of 0.65 GPa, superconductivity appears [1] . The suppression of SDW by pressure is understood as a recovery of the Fermi surface by denesting with increasing pressure. At the pressure where SDW is suppressed, superconductivity appears in (TMTSF)2PF6. By then applying a magnetic field, superconductivity is suppressed, and successive magneticfield-induced SDW (FISDW) transitions appear, which is schematically shown in Figure 1.
The FISDW is interpreted as the recovery of nesting due to one-dimensionalization by a strong magnetic field. But since this nesting is imperfect, and a resultant small 2D Fermi pocket provides a cascade of phase transitions. But if the imperfect nesting produces just simple robust 2D Fermi surfaces, only Shubnikov de Haas (SdH) oscillations should appear. But if the system can generate a band gap for certain interval of magnetic field, by separating completely filled lower Landau levels and completely empty higher ones, a gain in energy is kept in the electronic states, then the quantum Hall effect (QHE) occurs instead of SdH oscillations. The new type of quantum Hall effect (QHE) [2] is quite different from the conventional QHE seen in GaAlAs.
Since the scenario of the QHE is discussed in terms of nesting of 1D Fermi surface for SDW, it is of great interest to see if the field-induced phase scenario holds for CDW. For this purpose, we studied the quasi-one-dimensional (Q1D) organic conductor, HMTSF-TCNQ, shown in Figure 2, where HMTSF and TCNQ are the abbreviation of hexamethylenetetraselenafulvalene and tetracyanoquinodimethane, respectively. The CDW (TCDW = 30 K at ambient pressure [3] -[5] ) of this crystal is relatively easily suppressed by the pressure of ~1 GPa in agreement with the very old work [6] . (We note that for TTF-TCNQ 10 GPa are required to suppress the CDW phase [7] .) Hence with HMTSF-TCNQ, it is easy to use a simple pressure clamp apparatus in high magnetic fields. Our studies on HMTSF-TCNQ show magnetoresistance (MR) kinks around ~1 GPa, but neither at ambient pressure nor at 2 GPa [8] -[12] . This feature implies that a scenario similar to that of FISDW in (TMTSF)2PF6 holds. We have been very much interested in whether or not the similar scenario holds for CDW.
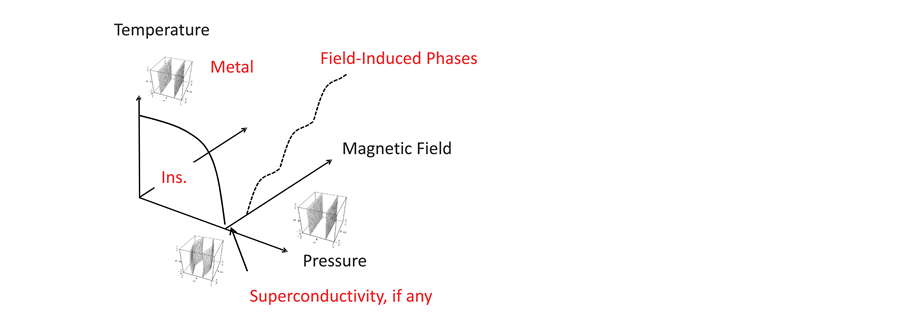
Figure 1. Schematic diagram of a 1D conductor. The insulating phase is either a SDW or CDW. The inset images show pairs of 1D Fermi surfaces in the 1st Brillouin zone. In the case of HMTSF-TCNQ, there are both electron and hole FS (Fermi surface) pairs in the 1st Brillouin zone (but just one pair is shown to avoid busy figure). At Pc and B = 0, two pairs of FS are there, in FI (field-induced) phase one pair of FS and a straw-shaped 2D FS (not shown), and in higher in B, straw-shaped FS disappears by the Landau quantum limit and leaving one pair of 1D FS. Orientation of the magnetic field is parallel to the least conducting axis.
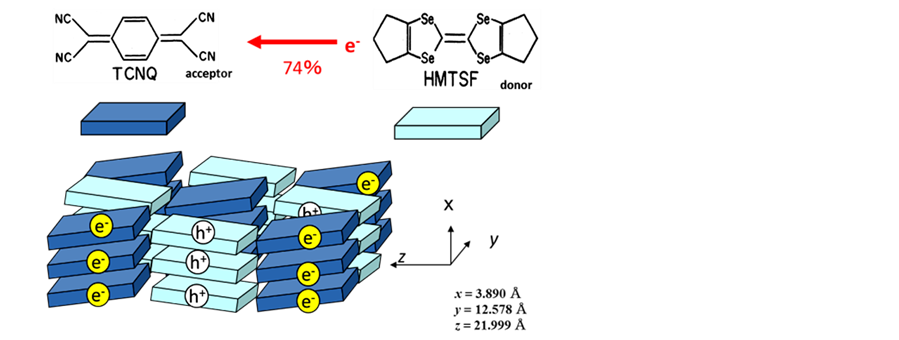
Figure 2. Schematic view of the crystal model of HMTSF-TCNQ. Both HMTSF and TCNQ molecules stack themselves along the 1D-axis. Since the axis indexing for a, b and c is different among the bibliography, to avoid confusion, we adopt the naming of x, y and z axes for the most conducting to the least conducting axes.
It should be noted that until recently it was difficult to obtain high quality crystals of HMTSF-TCNQ, i.e. most of the samples consisted of many small, oriented crystallites mimicking a single crystal morphology. Such crystals had broad Bragg spots, and the signature of the CDW transition in the resistivity was neither sharp nor large. More recently, one of authors (R.K.) succeeded in synthesizing high quality single crystals, and our understanding of the field-induced phase has very much advanced or even renewed as a result. The purpose of this paper is to review the history of the refinement of the data to avoid confusion with preliminary data, together with the recent results on Hall effect, to discuss the magnetic field-induced phase of this material.
A field-induced CDW in a two dimensional conductor was discussed previously for α-(BEDT-TTF)2KHg(SCN)4 and α-(BEDT-TTF)2TlHg(SCN)4 [13] [14] , where 1D and 2D Fermi surfaces coexist even below TCDW where the Fermi-surface reconstructs. In the present case, field-induced phases are indicated by the clear presence of 1D Fermi surfaces and 2D straw-shaped Fermi surfaces.
2. History of Our Study on the Field-Induced Phases in HMTSF-TCNQ
Although the facts that the CDW transition at ambient pressure occurs at 30 K and that the field induced phase transition is observed neither at ambient pressure (or even up to 0.5 GPa) nor at 2 GPa but at around 1 GPa are unchanged, data quality has become very much improved by the refinement of the crystal quality. Having the latest and the most refined measurement, we thought it important and timely to provide a table of figures how the magneto resistance (MR) behavior has improved with the refinement of the crystal quality.
The batch of samples we studied were classified into three stages. Stage I: we started a preliminary study with the samples made in 1970th. Stage II: samples made by the co-author (R.K.) but with unsatisfactory quality with poor Bragg spots. However those samples were produced with the best effort at that time. Stage III: samples by R.K. with a refinement with a new idea of crystal growth. We could obtain samples with sufficiently beautiful Bragg spots. Further all the samples were examined by X-ray before the transport study, and many of the puzzled problems were solved [15] .
Studies in high magnetic field were carried out with the clamp type pressure cell, with samples immersed in the pressure medium Daphne 7373. Electrical contacts were made with 10 μm gold wire and carbon paste sometimes with and sometimes without gold deposit on samples. Four terminal methods were used with ac current from 10 μA to 100 μA. Pressure at low temperature for later works was calibrated against the superconducting transition temperature.
Figure 3(a) is the MR of the sample from Stage I with the pressure of about 1.4 GPa at low temperature (inset pressure value is of 300 K) [8] . The MR of Rxx shows undulations with hysteretic curves, which continued up to the maximum studied field 31 T. Figure 3(b) and Figure 3(c) show the MR of Rxx of the Stage II samples at around 1.3 GPa at low temperature [10] . The smooth undulation in MR observed in the samples of Stage I is
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f)
Figure 3. (a) Magnetoresistance (MR) of Rxx in Stage I. (b) MR of Rxx in Stage II with B//y. (c) MR of Rxx in Stage II with B//z. (d) MR of Rxx in Stage II with B//y at p = 2 GPa. (e) MR of Rzz of Stage III on linear scale, and (f) logarithmic scale. Copyright permission is requested for Ref. [8] for (a), for Ref. [10] for (b), (c), and for Ref. [15] for (e) and (f).
unseen, but instead, kinks are observed. Especially the Figure 3(b) is very reminiscent of the MR of the FISDW in (TMTSF)2ClO4 [16] . However, it was very puzzling that kinks in MR were observed in two directions (i.e. B//y and B//z) although the bending direction of the kinks were opposite. This puzzle was solved by the precise analysis of AMRO (angular dependence of MR oscillations), which was carried out with the samples of Stage III, which will be described later. The conclusion from that is that the FI phase is ruled only by the z-component of the magnetic field [15] , and around 1 GPa, FI phase is seen between 0.2 T and 10 T. The MR of Rzz is shown in Figure 3(e) and Figure 3(f), which show the same data each other but in a linear and logarithmic scale for Rzz. Although it is not fair to compare Rxx for Stages I and II, and Rzz for Stage III, it is possible to detect the anomalous fields in either ways.
The phenomena that have been unchanged from the preliminary to the latest resultsare that: 1) the events occur neither at ambient pressure nor at 2 GPa as shown in Figure 3(d), which proved that the phenomena is specific only around the critical pressure; 2) typical FI phenomena occur between 0.2 T and around 10 T at ~1 GPa; 3) magneto resistance is larger at lower temperature; 4) specific fields are unchanged with temperature between 0.3 K and 4.2 K, where we have intensively surveyed.
The undulating behavior with hysteresis from Stage I samples might be caused by the rounding of sharp kinks with hysteresis observed in Stage II samples. From the results with Stage II samples, we obtain a tentative image that the FI phase is related to three dimensional Fermi pocket since MR anomalies were seen in both (any, as a result) angles of the magnetic field in the y-z plane. However, by examining the Stage III samples, we reached the conclusion that the FI phase is related to two dimensional Fermi pocket, which is of straw-shape whose axis is orienting to the z-direction. The reason for the apparent observation of kinks in both (any, as a result) angles of the magnetic field in the y-z plane was solved by the AMRO (angular dependence of magnetoresistance oscillations) of the Rzz and the precise MR measurement with the sample rotation of high quality samples of Stage III in magnetic field, which will be explained later. The sample rotation was carried out by the rotation of miniature pressure cell in magnetic field.
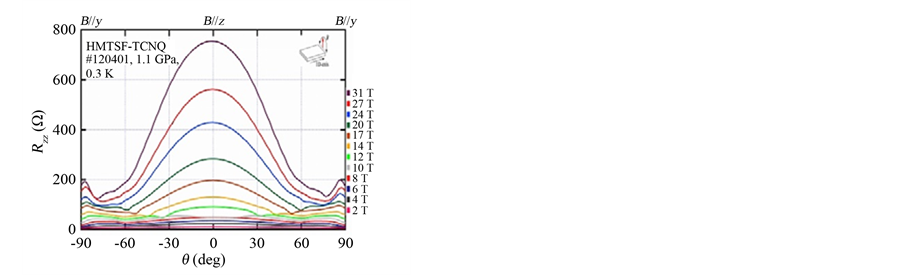
Figure 4(a) shows the AMRO of Rzz rotated in the B//y-z plane in several fields from 2 to 31 T at 0.3 K [15] . One can find easily the region of gigantic MR and its boundary from the region of low MR. By plotting the zcomponent of the boundary fields, it turned out that the transition takes place at Bz = 10 T as shown in Figure 4(b). We carried out the AMRO study in the same way in the B//x-z plane in several fields (not shown). And we obtained the similar results as Figure 4(b). We could conclude that the 10 T transition is ruled by the strawshaped FS. From the result of Figure 3(e) and Figure 3(f) and it extended measurement up to 45 T, we could judge that there is no structure in MR with B//z above 10 T. We conclude then that 10 T is the field of quantum limit of the lowest Landau level [15] .
There is a fine oscillation in the AMRO in Figure 4(a). By analyzing precisely the fine structure, it turned out that there is typical Lebed-Osada oscillations, which demonstrate existence the 1D Fermi surface. Further, Lebed-Osada oscillations exist below and above the 10 T transition. And the Lebed-Osada oscillations are less distinctively pronounced below the 10 T transition [15] . Therefore we established the model that below B//z = 10 T, there is a coexistence of 1D and 2D FS, above 10 T the 1D FS survives and the 2D FS disappears due to the quantum limit of the lowest Landau limit.
Figure 5(a) shows the Rxy of the Stage II sample [12] . And with the Stage III samples, the result has settled to Figure 5(b). What is unchanged all through the stages is that Rxy is linear and negative close from B = 0 to 0.2 T and rather flat nature up to certain field, i.e. 10 T finally. Above 10 T, the result was quite different. This is associated with the clear appearance of 10 T-transition due to the beautiful crystalline nature in the Stage III samples. As shown in Figure 5(c), Rxx is almost zero up to 10 T. Together with the flat nature of Rxy, these phenomena favor the quantum Hall effect. A difficulty is that there is not more than two steps. Maybe it is due to the coexistence of 1D and 2D FS’s.
Summarizing the final results of MR, AMRO and Rxy, present idea for ~1 GPa is the following; for 0 < Bz < 0.2 T two pairs of 1D FS recovered by de-nesting by pressure; for 0.2 T < Bz < 10 T one pair of FS become nested by one-dimension alization by high magnetic field like in (TMTSF)2X salt. However imperfect nesting leaves a straw-shaped 2D FS. Other pair of 1D FS survives. Above 10 T the lowest Landau level at the straw-shaped 2D FS becomes in the state of Landau quantum limit.
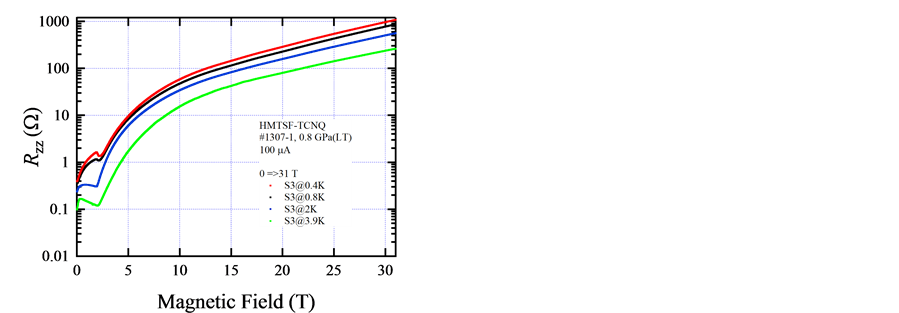
Figure 6 shows the MR measured at lower pressure of ~0.7 GPa. Then the quantum limit transition is reduced from 10 T at 1 GPa to 2 T. At lower pressure, FS should be more 1D-like, i.e. the nesting of the FS might be more easily nested. This means that the FS pocket is smaller at 0.7 GPa than that at 1 GPa, so the Landau quantum limit is more easily achieved at low field of 2 - 3 T.
3. Summary
Back to the original motivation to see if the FI-phase is similar to that in (TMTSF)2X. We have to take note the difference. HMTSF-TCNQ has two pairs of 1D FS. One is of electrons and the other of holes. Charge transfer is 0.74, which is not commensurate at least at ambient pressure. Electron correlation might not be large. Compared with that, (TMTSF)2X has only one 1D FS of holes. Charge transfer is 0.5, SDW is not commensurate but close
 (a)
(a) (b)
(b)
Figure 4. (a) AMRO, taken in the B//y-z plane at 0.3 K at 1.1 GPa. It is obvious that the gigantic MR state is located around B//z, and with its clear boundary; (b) The boundary field is shown to be ruled by the same value (10 T) of the zcomponent of mangetic field. Copyright permission is requested for Ref. [15] .
 (a)
(a) (b)
(b) (c)
(c)
Figure 5. (a) and (b) Rxy taken at ~1 GPa and 0.4 - 0.5 K. (a) Stage II sample; (b) Stage III sample; (c) Rxx of Stage III sample.
 (a)
(a) (b)
(b)
Figure 6. (a) Rzz taken at 0.7 GPa of Stage III samples. 10 T transition (quantum limit) at 1 GPa occurs at 2 T; (b) Quantum limit field is plotted in the B-P phase diagram.
to commensurate [17] . Electron correlation is non-negligible so long as it exhibits SDW. But our conclusion is that in many senses probable FICDW is quite similar to the FISDW of (TMTSF)2X since the scenario of the quantum Hall effect explained for (TMTSF)2X seems to explain the phenomena seen in HMTSF-TCNQ.
Acknowledgements
This work was carried out at the National High Magnetic Field Laboratory at Tallahassee, USA, starting from the preliminary work performed at High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University (Project No. 09H0072, 10H0005, 11H0046).
This work is partially supported JSPS Inst. Prog. for Young Researcher Overseas Visits “Promoting International Young Researchers in Mathematics and Math. Sci. by OCAMI”, and Grant-in-Aid Sci. Res. on Innovative Areas #23110722 from M. Education, and NSF DMR#1005293 (FSU). W. K. was supported by a grant from the National Research Foundation of Korea (NRF), funded by the Korean Government (MSIP) (Nos. 2011-003090 2, 2010-00453 and 2008-0061893). Work at the NHMFL is supported by the NSF DMR#0654118, and by the State of Florida.
To achieve this experiment, the assistance of A. Kiswandhi, S. Benjamin, L. Winter of the Brooks group was indispensable. We appreciate Prof. H. Fujiwara of Osaka Prefecture University for the X-ray examination for selecting high quality crystals.
References
- Jérome, D., Mazaud, A., Ribault, M. and Bechgaard, K. (1980) Journal de Physique Lettres (Paris), 41, 95-98. http://dx.doi.org/10.1051/jphyslet:0198000410409500
- Chaikin, P. (1996) Journal de Physique I, 6, 1875-1898. http://dx.doi.org/10.1051/jp1:1996169
- Phillips, T.E., Kistenmacher, T.J., Bloch, A.N. and Cowan, D.C. (1976) Journal of the Chemical Society, 66, 334-335.
- Bloch, A.N., Cowan, D.O., Bechgaard, K., Pyle, R.E., Banks, R.H. and Poehler, T.O. (1975) Physical Review, 34, 1561-1564.
- Weyl, C., Engler, E.M., Bechgaard, K., Jehanno, D. and Etemad, S. (1976) Solid State Communications, 19, 925-930. http://dx.doi.org/10.1016/0038-1098(76)90688-8
- Jérome, D. and Schulz, H.J. (2002) Advances in Physics, 51, 293-479. http://dx.doi.org/10.1080/00018730110116362
- Yasuzuka, S., Murata, K., Yasuzuka, S., Arimoto, T. and Kato, R. (2007) Journal of the Physical Society of Japan, 76, Article ID: 033701. http://dx.doi.org/10.1143/JPSJ.76.033701
- Murata, K., Yokogawa, K., Brooks, J.S., Kismarahardja, A., Steven, E., Kano, M., Seno, Y., Tamilselvan, N.R., Yoshino, H., Sasaki, T., Jérome, D., Senzier, P., Bechgaard, K., Uruichi, M. and Yakushi, K., (2010) Journal of Physics: Conference Series, 215, Article ID: 012064. http://dx.doi.org/10.1088/1742-6596/215/1/012064
- Murata, K., Yokogawa, K., Brooks, J.S., Kismarahardja, A., Steven, E., Kano, M., Seno, Y., Tamilselvan, N.R., Yoshino, H., Sasaki, T., Jérome, D., Senzier, P., Bechgaard, K., Uruichi, M. and Yakushi, K. (2010) Physica B, 405, S111-S112. http://dx.doi.org/10.1016/j.physb.2010.02.012
- Murata, K., Yokogawa, K., Kobayashi, K., Masuda, K., Sasaki, T., Seno, Y., Tamilselvan, N.R., Yoshino, H., Brooks, J.S., Jérome, D., Bechgaard, K., Uruichi, M., Yakushi, K., Nogami, Y. and Kato, R. (2010) Journal of the Physical Society of Japan, 79, Article ID: 103702. http://dx.doi.org/10.1143/JPSJ.79.103702
- Murata, K., Kang, W., Masuda, K., Kuse, T., Sasaki, T., Yokogawa, K., Yoshino, H., Brooks, J.S., Choi, E.S., Kiswandhi, A. and Kato, R. (2012) Physica B, 407, 1927-1929.
- Murata, K., Kang, W., Masuda, K., Fukumoto, Y., Graf, D., Kiswandhi, A., Choi, E.S., Brooks, J.S., Sasaki, T., Yokogawa, K., Yoshino, H. and Kato, R. (2013) Journal of Low Temperature Physics, 170, 377-382. http://dx.doi.org/10.1007/s10909-012-0799-9
- Kartsovnik, M. and Laukhin, V.N. (1996) Journal de Physique I (France), 6, 1753-1786. http://dx.doi.org/10.1051/jp1:1996187
- Lebed, A.G. (2009) Physical Review Letters, 103, Article ID: 046401. http://dx.doi.org/10.1103/PhysRevLett.103.046401
- Murata, K., Fukumoto, Y., Yokogawa, K., Takaoka, R., Kang, W., Brooks, J.S., Graf, D., Yoshino, H., Sasaki, T. and Kato, R. (2014) Fizika Nizkikh Temperatur (New Achievement of Fermiology, a Memorial Issue for the 60th Year Anniversary of Lifschitz-Kosevich Theory), 40, 477-483. http://fnte.ilt.kharkov.ua/main.php?page=3 Low Temperature Physics, 40, 371-376. http://dx.doi.org/10.1063/1.4869591
- Kajimura, K., Ukahci, H., Tokumoto, M., Murata, K., Ukachi, T., Anzai, H., Ishiguro, T. and Saito, G. (1983) Journal de Physique Archives, 44-C3, 1059-1062.
- Takahashi, T., Maniwa, Y., Kawamura, H. and Saito, G. (1986) Journal of the Physical Society of Japan, 55, 1364-1373. http://dx.doi.org/10.1143/JPSJ.55.1364

