Journal of Modern Physics
Vol.4 No.12(2013), Article ID:41264,5 pages DOI:10.4236/jmp.2013.412202
Investigation the Dimensional Ratio Effect on the Resonant Properties of Piezoelectric Ceramic Disk
1Hue University of Sciences, Hue City, Vietnam
2Institutes of Applied Physics and Scientific Instrument, Vietnamese Academy of Science and Technology, Hanoi, Vietnam
Email: vothanhtungdhkh@gmail.com
Copyright © 2013 Vo Thanh Tung et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 28, 2013; revised October 27, 2013; accepted November 25, 2013
Keywords: BZT-50BCT; PZT Family; Finite Element Modeling; Vibration Mode
ABSTRACT
In this work, the vibration characteristics of a piezoelectric ceramic disk with different dimensional ratio are studied by simulation method. Computational finite element modeling combined with the computational programs has allowed for the prediction of the effect, the change of diameter-to-thickness ratio on the resonant characteristics, the vibration modes as well as comparing the physic properties of piezoceramics. Three types of piezoelectric materials were chosen, piezoelectric materials (PZT) and Pb-free piezoelectric materials Ba(Zr0.2Ti0.8)O3-50(Ba0.7Ca0.3)TiO3(BZT-50BCT), BaTiO3 for research.
1. Introduction
After discovered in 1950 of lead zirconate titanate [Pb(Zr,Ti)O3; PZT] ceramics with their excellent piezoelectric properties, piezoelectric materials are widely used for various applications such as actuators, sensors, sonar transducers, accelerometers, resonator, frequency control devices, filters [1-5] and etc. However, PZT is now facing global restrictions in its usage because of Pb toxicity to the environment and to human body. Therefore, recently, many Pb-free ferroelectric systems, such as Ba(Zr0.2Ti0.8)O3-x(Ba0.7Ca0.3)TiO3 (hereafter abbreviated as BZT-xBCT), (K0.436Na0.5Li0.064)Nb0.92Sb0.08O3... have been reported to compete with PZT family [6].
In practical applications, the piezoelectric ceramics are usually circular, so the vibration characteristics of piezoelectric ceramic disks are important in design and application of devices. Knowledge of the vibration modal shapes and the influence of the material property and geometry are of interest for the further development of novel devices and selection of the appropriate disk geometry for specific applications [7-9]. Moreover, the vibration characteristics of piezoelectric ceramic disks had been studied intensively by many of the researchers [7,10-13]. These characteristics are identified by the resonant response and the resulting modal shapes of the structure. And the resonant mode and frequency of a piezoceramic structure is a function of its geometry and material properties.
The aim of this paper is to analyze the effects of the variation of diameter to thickness (d/t) ratios of ceramic disk on vibration properties of piezoelectric materials. Three types of piezoelectric materials, PZT and Pb-free materials Ba(Zr0.2Ti0.8)O3-50(Ba0.7Ca0.3)TiO3(BZT-50BCT) and BaTiO3 are used for comparison. Furthermore, the paper uses a finite element modeling method to investigate the vibration modes, the resonant frequencies and piezoelectric coefficients of ceramic disks concerning the diameter-to-thickness ratio. Greater knowledge in the relationship between disk dimensions allows for improved material and structure selection with regards to resonating frequencies and structure stability. In addition, from the received results, we analyze and compare the influence of Pb and Pb-free components in material on the properties of piezoceramics in PZT family and Pbfree piezoceramic (BZT-50BCT).
2. Analysis of the Piezoelectric Ceramic Disk
Investigations using computational finite element methods (FEM method) have successfully analyzed the behavior of piezoceramic discs [7,14-17]. In our study, we used a simplified 3-D axis-symmetric model in the FEM of simulation program for design the model geometry. The modeling dimensions of piezoceramic discs with the change of the radius and thickness is illustrated in Figure 1. Accuracy in defining length, diameter and thickness resonant frequency requires a fine mesh. Modeling conducted is meshed of by using the standard meshing tool with the variation of the elements, vertex elements, edge elements and boundary elements belong to the dimension of the ceramic samples (Figure 1).
The understanding of the resonance characteristics of piezoceramic disks can be investigated by visualization modes generated in the structure at resonant frequencies. The two dependant factors to the resonating frequencies diameter (d) and wall thickness (t) were investigated in the FEM model. Models were constructed that explored a change in t with a constant d and a change in d with a constant t. The modeling dimensions of piezoceramic discs with radius ranging from 5.2 mm to 5.5 mm, and thickness ranging from 0.4 mm to 1.5 mm. The (diameter/thickness) ratio of the samples used for the dimensional ratio effect was from 7.25 to 20.16.
The mechanical properties of piezoelectric materials (the relation between stress and strain) can, assuming only small deformation, be described as a linear-elastic material. Each of these sets of the parameters expresses as a mathematical description of the direction and inverse piezoelectric effect, and is sufficient to describe the properties of the material.
By theoretical treatment, the material properties are defined in the stress-charge form, in which the user has to specify the elasticity matrix, coupling matrix, relative permittivity matrix, piezoelectric coefficient matrix and density. The complete set of constants of the pure BaTiO3 and PZT5A transducers shown in Table 1 is taken out from the data libraries of the simulation program. A full set of elastic, piezoelectric, and dielectric parameters for the morphology phase boundary composition of BZT50BCT are measured and calculated by Dezhen Xue and et al., [18] when using a resonance method.
Both sets of mechanical and electrical boundary conditions are used to analyze piezoelectric properties. In terms of the mechanical boundary conditions, the vibrations of all surfaces are free. Based on the electrical boundary conditions, the voltage of the bottom surface of the cantilever beam is set as the common ground. On the other hand, the top surface is set as Terminal/Electrical at the voltage of 0.5 V.
3. Results and Discussion
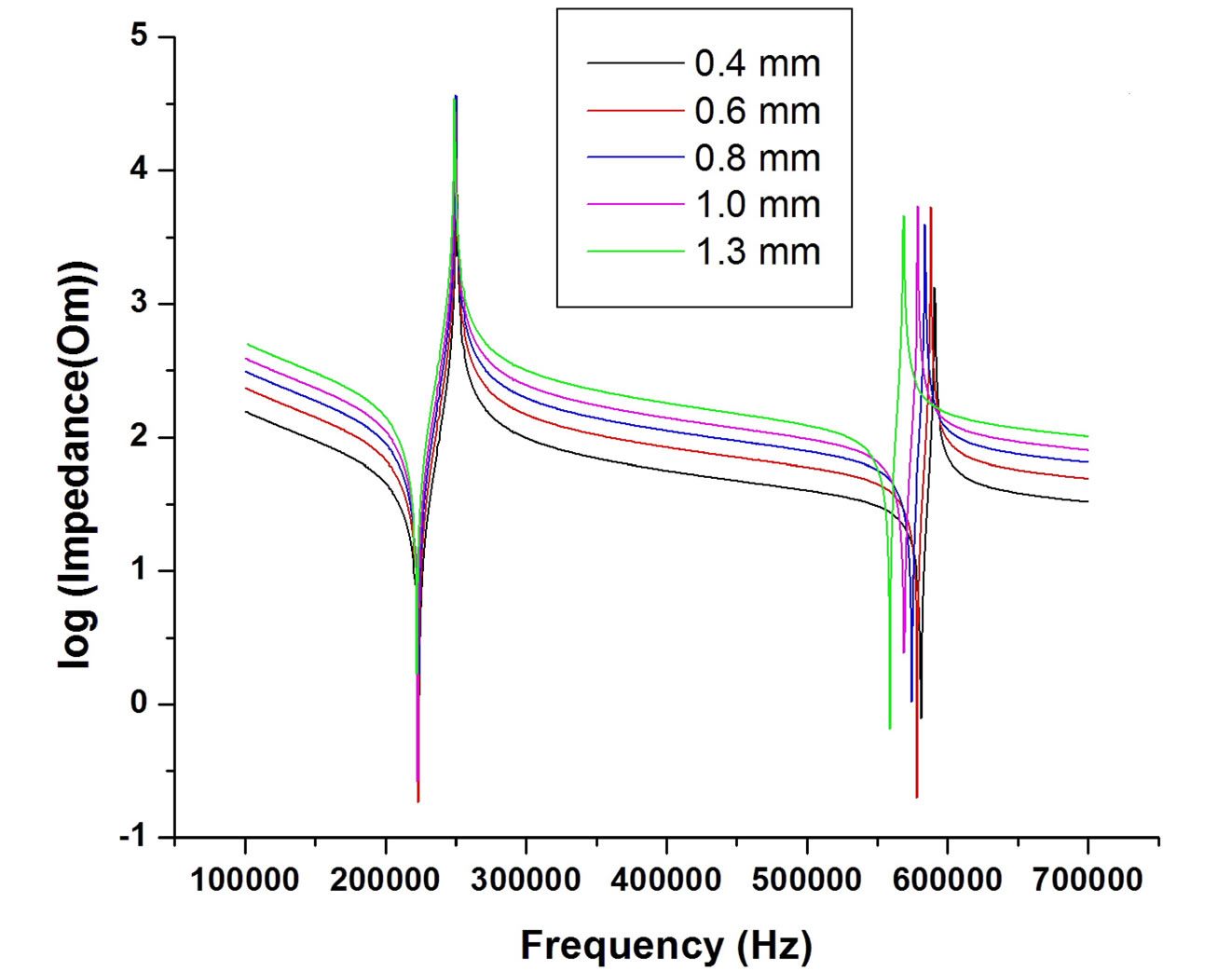
Figures 2(a)-(c) show a comparison the FEM impedance analysis for three ceramic samples PZT, BaTiO3 and BZT-50BCT respectively in the radial vibration mode with respect to the changing thickness and a constant diameter t = 5.5 mm. It is firstly seen that the resonance peaks are presented as near straight vertical lines at the fundamental resonant frequency. The meaning of such phenomenon is that the resonant and anti-resonant frequencies are defined to coincide. Therefore, the planar effective electromechanical coupling factor kp is not changed with the variation of thickness of ceramic samples. In addition, it is observed that the resonant
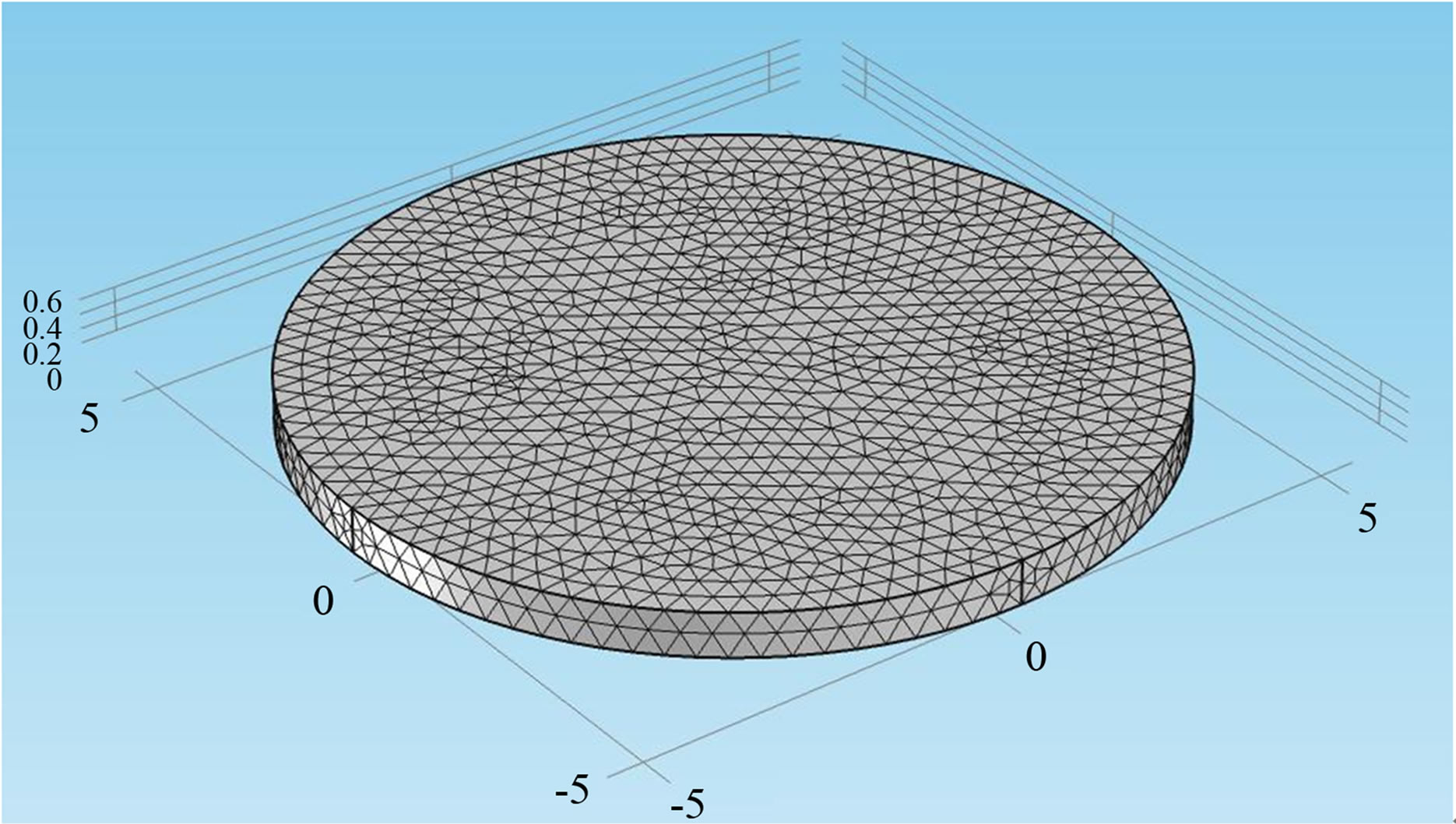
Figure 1. The fully expanded meshed model of the disk ceramic samples.


Table 1. Measured and derived piezoelectric, dielectric and elastic constants of the BZT-50BCT, BaTiO3 and the PZT5A transducer with the density of 7750 kg/m3 [16,17].
frequencies for the second vibration mode of the piezoelectric ceramic disk in the radial vibration mode are separated. Especially, the separation of resonant peaks is specifically expressed when increasing the thickness of samples (the blue curve in Figure 2: thickness at 1.5 mm for PZT, 1.3 mm for BaTiO3, BZT-50 BCT in Figure 1). This means that interaction of the change ratio d/t is observed for the overtone vibration modes, especially when d/t < 10. However, these are seen to be unaffected on the fundamental vibration mode when changing the dimension ratio d/t.
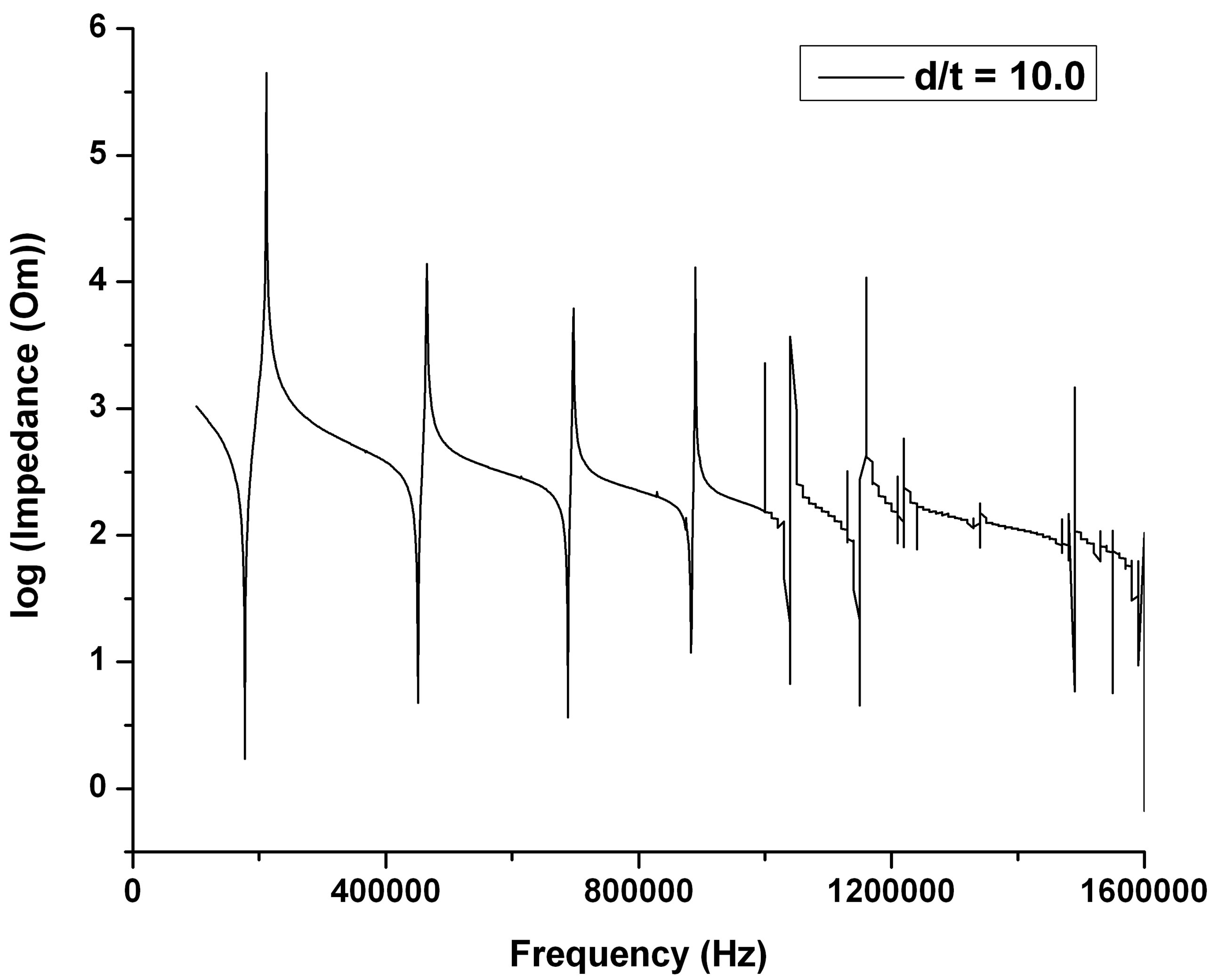
The frequency spectrums of different diameter-tothickness ratio are shown in Figures 3(a)-(f) for PZT and BZT-50BCT samples. The resonant spectrum range varies from 100 kHz to 1600 kHz for PZT ceramics disks (Figures 3(a)-(c)) and from 100 kHz to 2000 kHz for BZT-50BCT samples (Figures 3(d)-(f)).
Figures 3(a)-(c) display the relation between (overtone mode resonant frequency/fundamental resonant frequency) ratio and (diameter/thickness) ratio of PZT samples. The (overtone mode resonant frequency/fundamental resonant frequency) ratio is increased with the decreasing of (diameter/thickness (d/t)) ratio. Besides the fundamental mode, there are five radial vibration overtone modes exist in the measured frequency range for (d/t) = 27.5. When the (d/t) decreased to 15.71, only six radial
 (a)
(a) (b)
(b)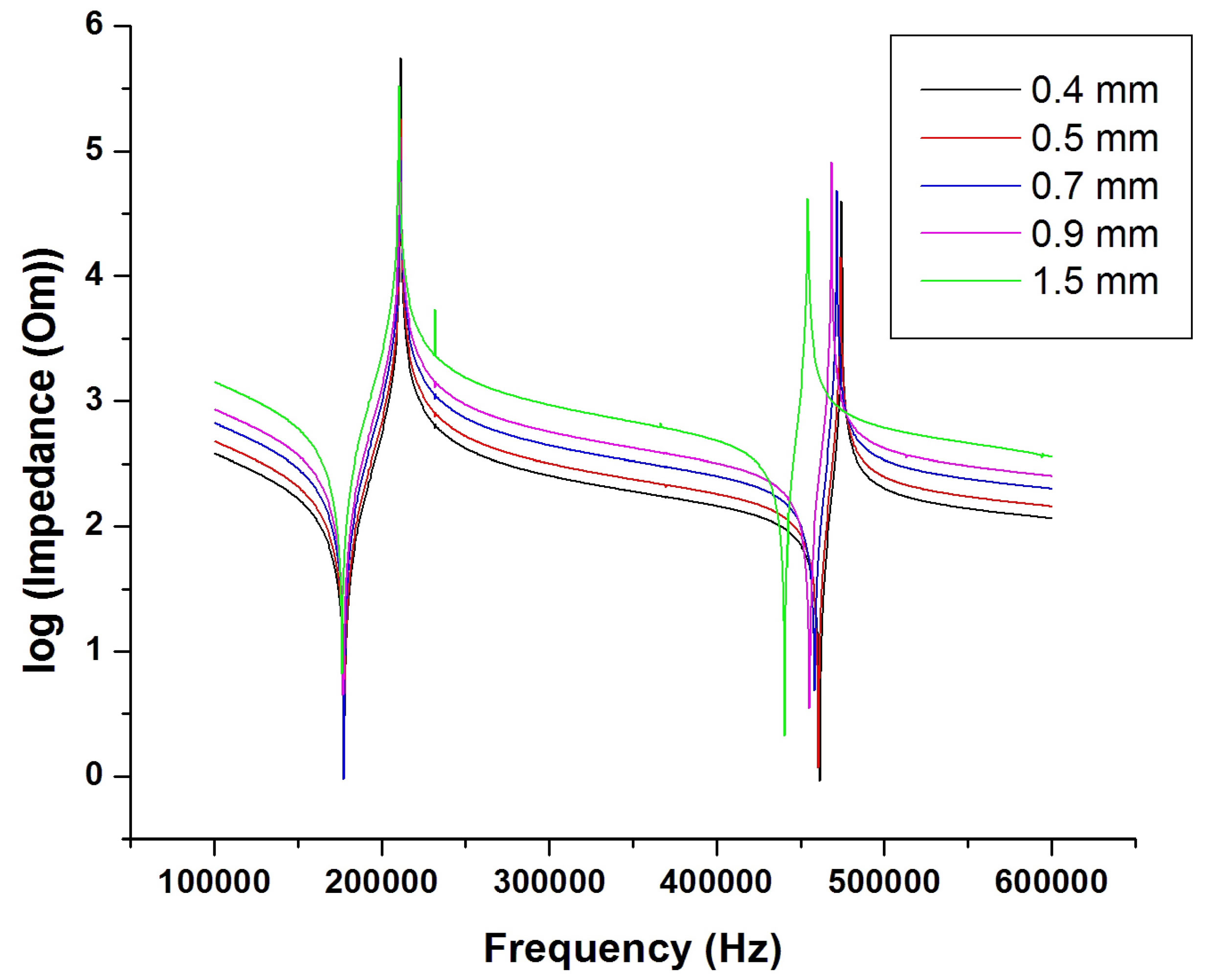 (c)
(c)
Figure 2. The log functions of the variations of impedance on frequency for radial vibration modes with the change of thickness for (a) PZT; (b) BaTiO3 and (c) BZT-50BCT.
 (a)
(a)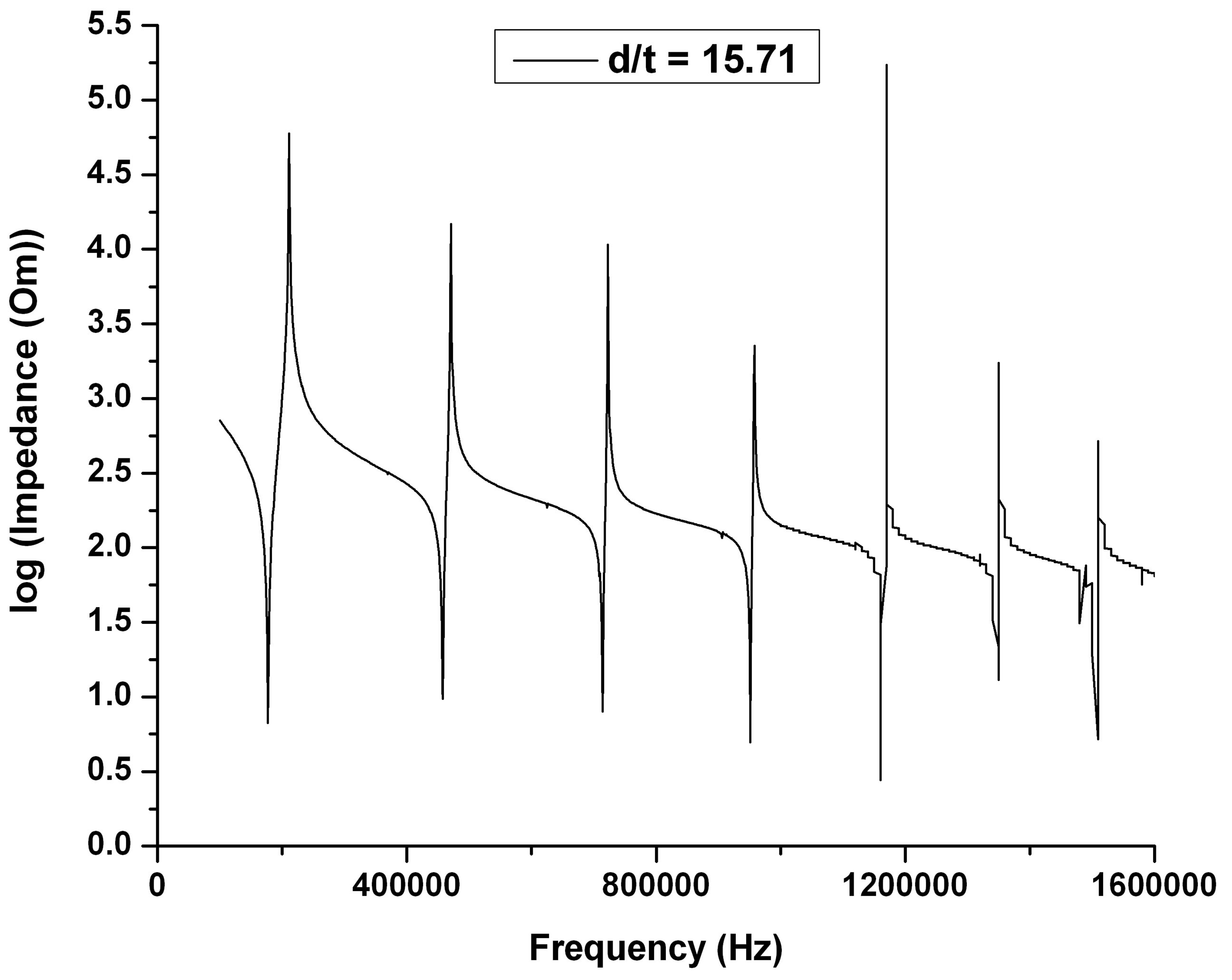 (b)
(b)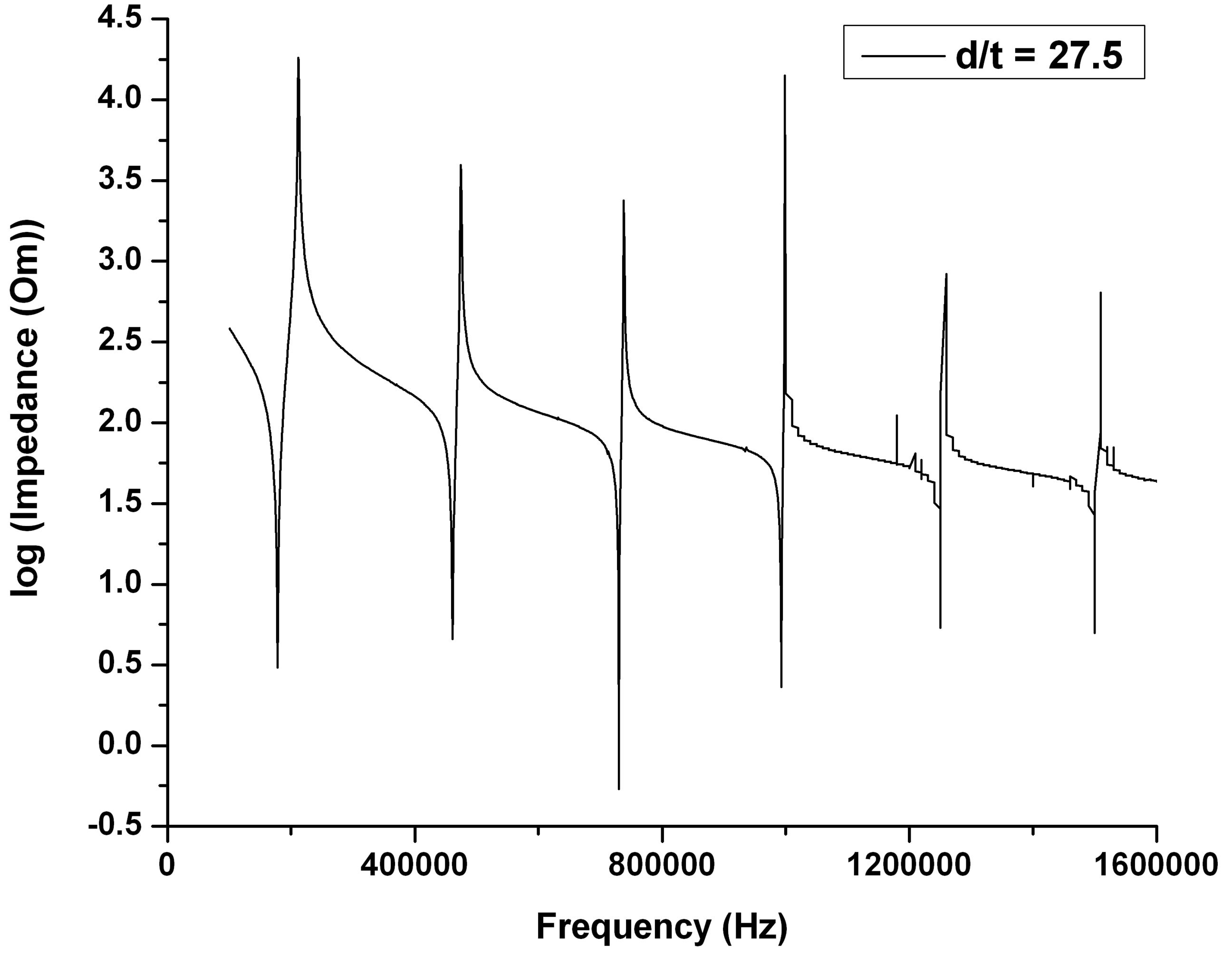 (c)
(c)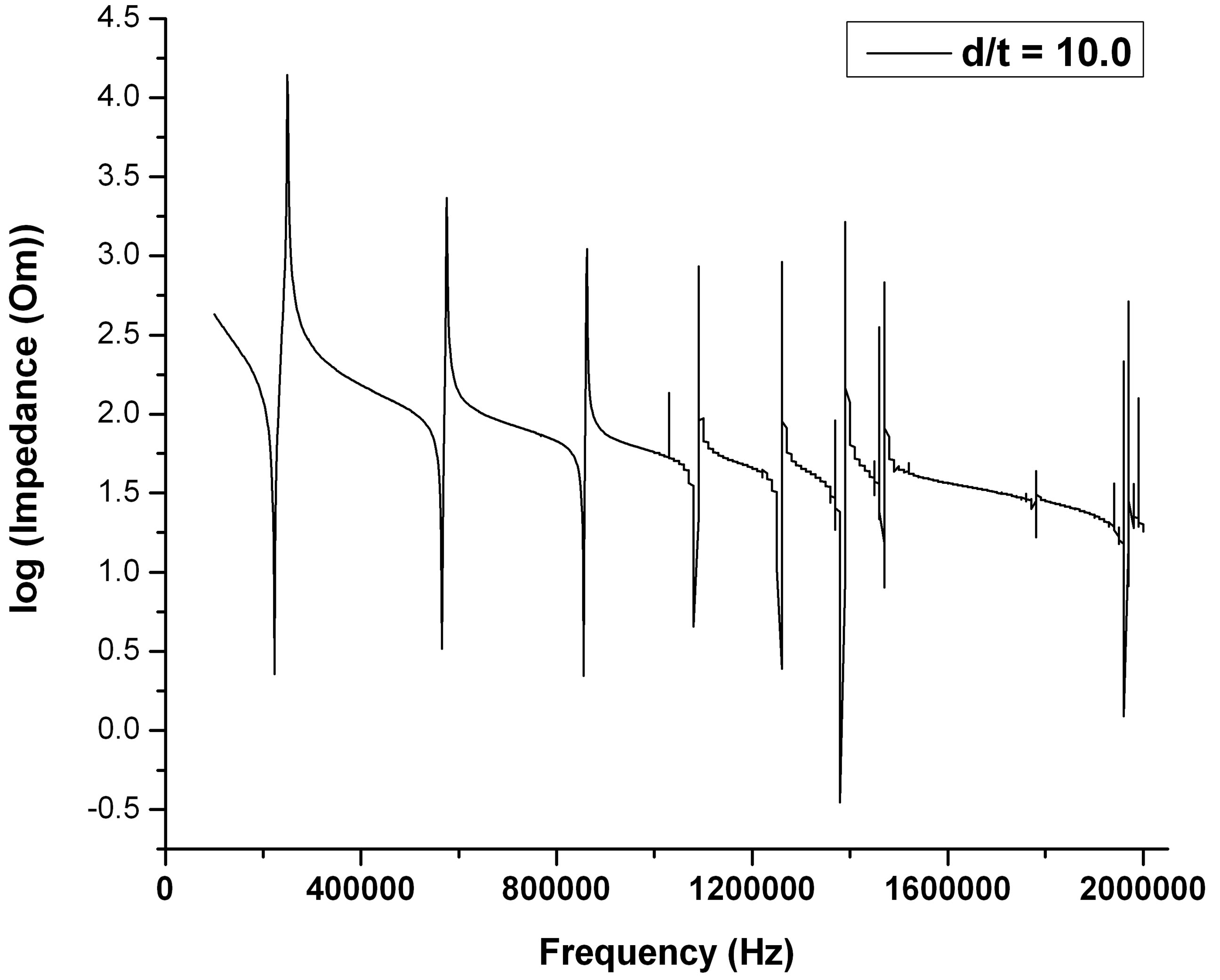 (d)
(d)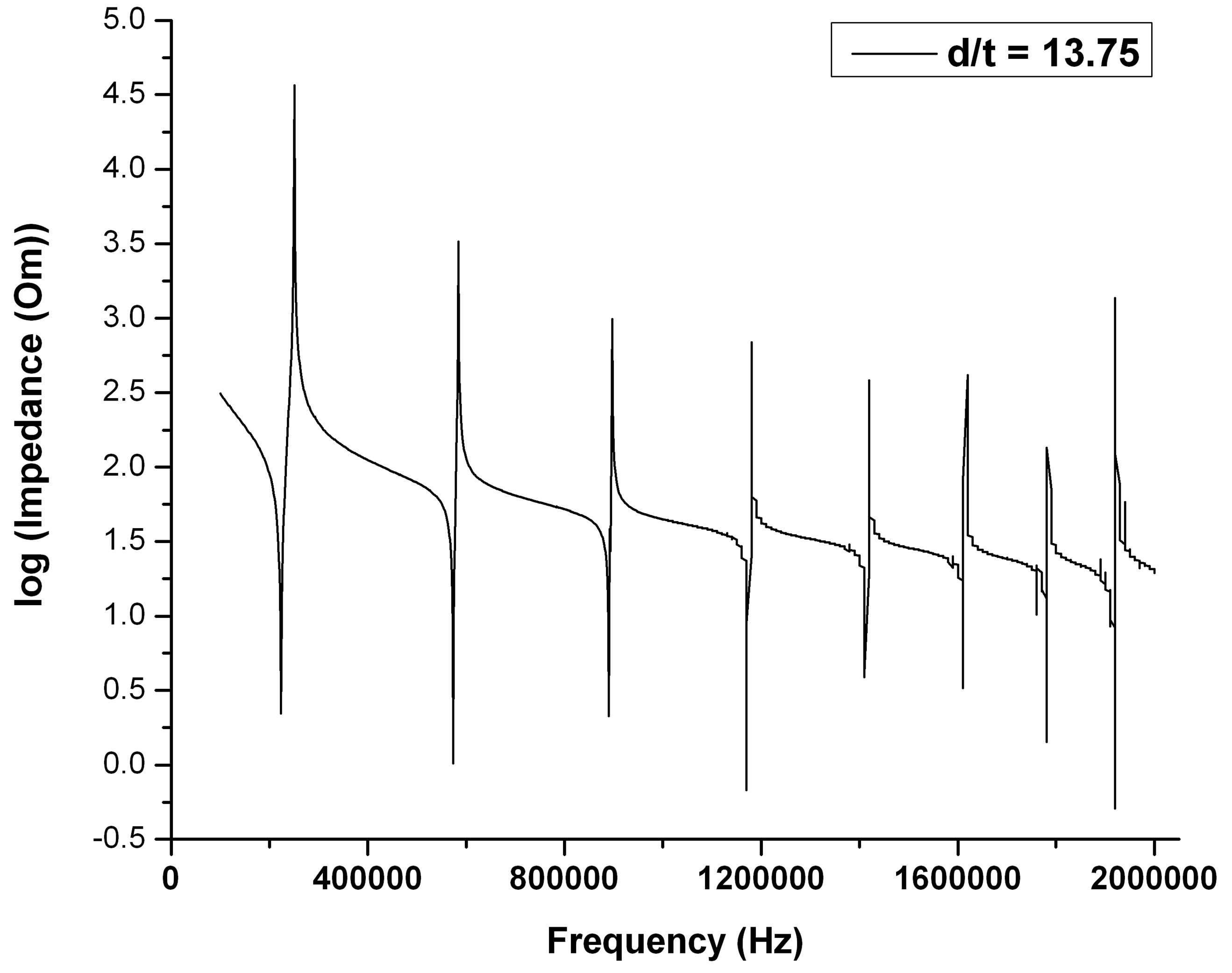 (e)
(e)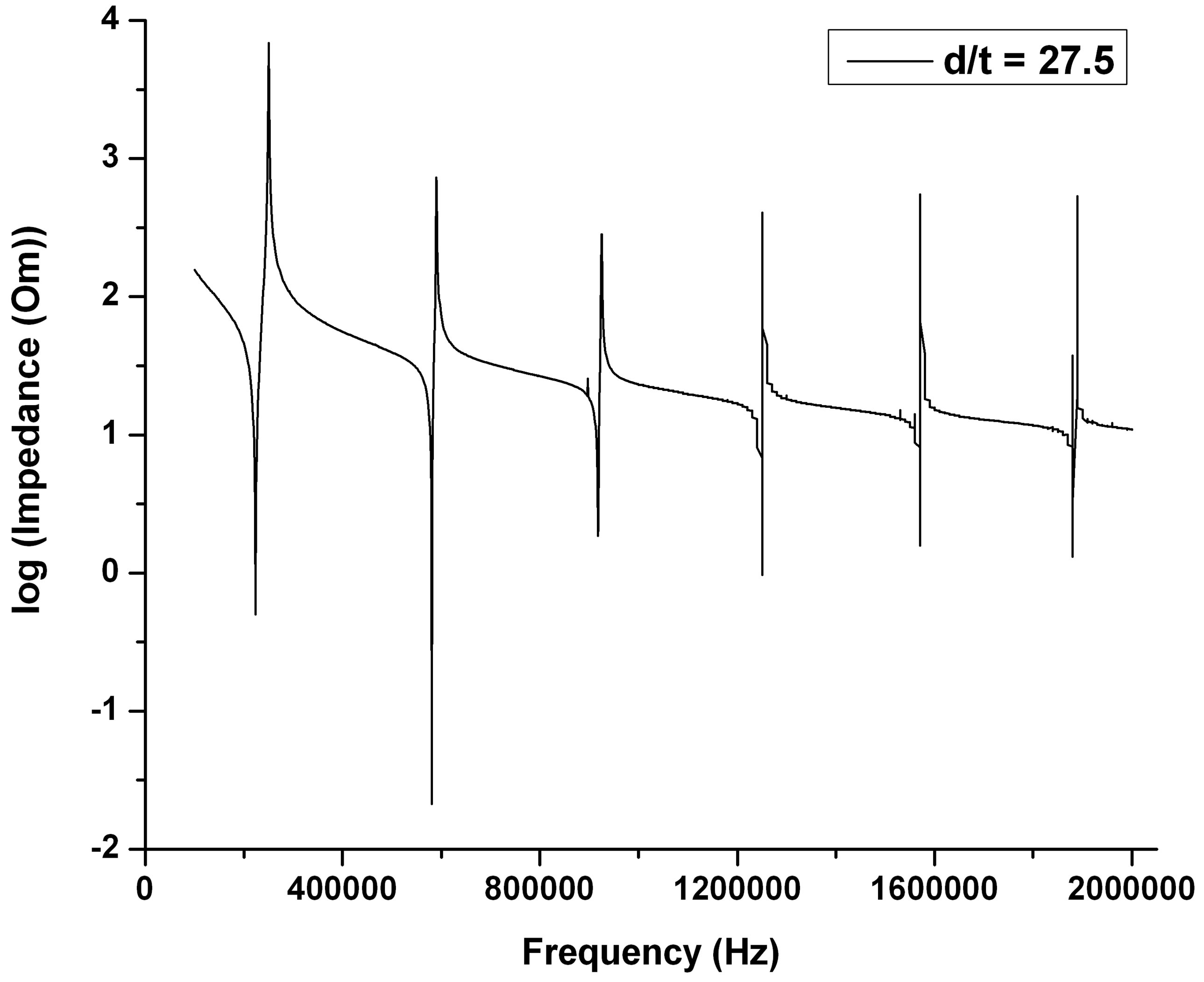 (f)
(f)
Figure 3. The frequency spectrums of piezoelectric ceramic disk with the change of the (d/t) ratio (a)-(c) PZT; (d)-(f) BZT-50BCT.
vibration overtone modes exist in the measured frequency range. When the (d/t) ratio was to 10, more than 7 radial vibration modes are existed in the measured frequency range. However, at this ratio ((d/t) = 10), for the measured frequencies higher than 700 kHz, the disturb vibration signals appear in the spectrum. These signals are called the spurious vibration signals that may be caused by other vibration mode; such as twist mode, bending mode or thickness mode. The similar results are taken out in the vibration modes for BZT-50BCT samples.
The analysis results of the effects of the change of thickness on the ratio of impedance (with a constant diameter t = 5.5 mm) between the fundamental series resonant frequency and the parallel resonant frequency (the Zmax/Zmin ratio) of piezoceramic samples are shown in Figure 4. The maximum values of Zmax/Zmin ratio are observed for BaTiO3 and BZT-50BCT samples (corresponding to thickness t = 0.9 mm and t = 0.7 mm) and on the contrary, the minimum value of this ratio is found for PZT sample (t = 0.8 mm). This further supports the conclusions that not only the variation of thickness (with a constant diameter) has an effect on the change of Zmax/ Zmin ratio but this ratio is affected by material properties of samples. There is no enough evidence to affirm that these results are caused by the Pb and Pb-free component in materials. However, we predict that the Pb component in materials maybe is a factor for this affect.
Figure 5 shows a comparison of the influence of the change of the diameter on the resonant characteristics with the above optimum thicknesses for PZT (corresponding to thickness t = 0.8 mm) and BZT-50BCT (t = 0.7 mm) samples. It can be observed that for the BZTBCT sample, the Zmax/Zmin ratio achieves stable with the d/t ratio in range from 13.1 to 13.6 and have the minimum tendency, but for the PZT sample, there are the opposite results. These results, as explained before, strongly are affected by the component of material on the impedance measurement.
4. Conclusions
For piezoelectric ceramic disk, the change of thickness does not affect the planar effective electromechanical coupling factor because the resonant spectrum doesn’t shift. With the change of the (diameter/thick) ratio, the vibration modes are affected. Besides the fundamental mode in the radial vibration, there are some different overtone modes in the high frequency range. Furthermore, the numbers of overtones modes are increased with the decreasing of (d/t) ratio.
The impedance ratio (the Zmax/Zmin ratio) at the fundamental resonant frequency is affected by the change of (diameter/thickness) ratio.
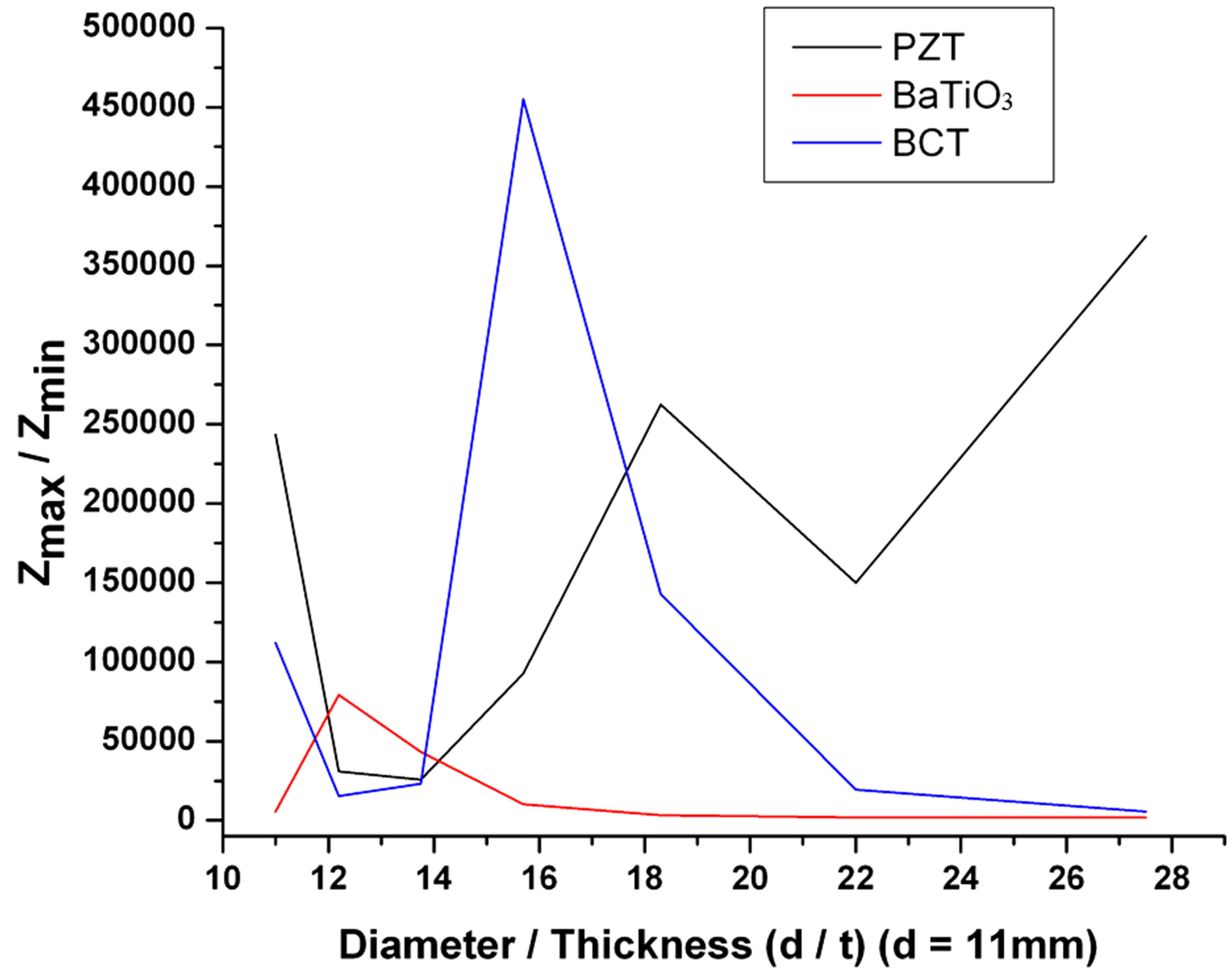
Figure 4. Th dependence of the ratio of impedance (the Zmax/Zmin ratio) on the change of the thickness.

Figure 5. Relation between the ratio of impedance (the Zmax/Zmin ratio) and the change of the diameter/thickness.
In addition, the results are found that the FEM model connected the simulation program has excellent agreement to the experimental data in studying the properties of the new material groups.
5. Acknowledgements
This work is supported by the National Foundation for Science and Technology Development (NAFOSTED) (No.103.02.06.09).
REFERENCES
- B. Sahoo, V. A. Jaleel and Panda, Actuators, Materials Science and Engineering, Vol. 126, 2006, pp. 80-85.
- L. F. Hong, Y. P. Chen, X. J. Wu, Q. L. Huang and X. T. Luo, Journal of Materials Science, Vol. 39, 2004, pp. 2997-3001. http://dx.doi.org/10.1023/B:JMSC.0000025825.04281.89
- B. Jaffe, R. S. Roth and S. Marzullo, Journal of Applied Physics, Vol. 25, 1954, p. 809. http://dx.doi.org/10.1063/1.1721741
- N. Setter, D. Damjanovic, L. Eng, G. Fox, S. Gevorgian, S. Hong, A. Kingon, H. Kohlstedt, N. Y. Park, G. B. Stephenson, I. Stolitchnov, A. K. Taganstev, D. V. Taylor, T. Yamada and S. Streiffer, Journal of Applied Physics, Vol. 100, 2006, Article ID: 051606. http://dx.doi.org/10.1063/1.2336999
- R. E. Newnham, “Functional Composites for Sensors and Actuators: Smart Materials,” In: S. K. Majumdar, R. E. Tressler and E. W. Miller, Eds., Pennsylvania Academy of Science, Pennsylvania, 1998, pp. 259-275.
- W. Liu and X. Ren, Physical Review Letters, Vol. 103, 2009, Article ID: 257602. http://dx.doi.org/10.1103/PhysRevLett.103.257602
- N. Guo and P. Cawley, The Journal of the Acoustical Society of America, Vol. 92, 1992, pp. 3379-3388. http://dx.doi.org/10.1121/1.404188
- C. H. Huang, Y. C. Lin and C. C. Ma, IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, Vol. 51, 2004, pp. 12-24. http://dx.doi.org/10.1109/TUFFC.2004.1268463
- H. A. Kunkel, S. Locke and B. Pikeroen, IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Controll, Vol. 37, 1990, pp. 316-328. http://dx.doi.org/10.1109/58.56492
- E. A. G. Shaw, The Journal of the Acoustical Society of America, Vol. 28, 1956, pp. 38-50.
- N. Guo, P. Cawley and D. Hitchings, Journal of Sound and Vibration, Vol. 159, 1992, pp. 115-138. http://dx.doi.org/10.1016/0022-460X(92)90454-6
- N. F. Ivina, Acoustical Physics, Vol. 47, 2001, pp. 714- 720. http://dx.doi.org/10.1134/1.1418899
- M. Masaki, H. Hashimoto, W. Masahiko and I. Suzuki, Journal of the European Ceramic Society, Vol. 28, 2008, pp.133-138. http://dx.doi.org/10.1016/j.jeurceramsoc.2007.05.021
- C. H. Huang, Y. C. Lin and C. C. Ma, IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, Vol. 51, 2004, pp. 12-24. http://dx.doi.org/10.1109/TUFFC.2004.1268463
- D. Kybartas and A. Lukosevicius, Ultragarsas, Vol. 4, 2004, pp. 31-36.
- V. T. Tung, N. T. Tinh, N. H. Yen, L. T. N. Bao and D. A. Tuan, Journal of Materials Science and Engineering A, Vol. 3, 2013, pp. 283-289.
- V. T. Tung, N. T. Tinh, N. H. Yen and D. A. Tuan, International Journal of Materials and Chemistry, Vol. 3, 2013, pp. 59-63.
- D. Z. Xue, Y. M. Zhou, H. X. Bao, C. Zhou, J. H. Gao and X. B. Ren, Journal of Applied Physics, Vol. 109, 2011, Article ID: 054110. http://dx.doi.org/10.1063/1.3549173

