Journal of Modern Physics
Vol. 4 No. 8A (2013) , Article ID: 36098 , 7 pages DOI:10.4236/jmp.2013.48A012
On the Modern Status of the Universe Rotation Problem
V. G. Fessenkov Astrophysical Institute, National Centre for Cosmic Researches and Technologies, National Space Agency, Almaty, Kazakhstan
Email: chechin-lm@mail.ru, leonid.chechin@gmail.com
Copyright © 2013 L. M. Chechin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 15, 2013; revised July 17, 2013; accepted August 12, 2013
Keywords: Universe Rotation; Cosmic Vacuum; Anisotropy of Deceleration Parameter
ABSTRACT
The brief modern review of the Universe rotation problem is given. Also it was argued the vacuum concept of the Universe rotation, found the galactic coordinates of the Universe rotation axis, based theoretically the concept of the decaleration parameter anisotropy.
1. Introduction
One of the most important global characteristics of the Universe is its rotation. In fact, in article [1] it was emphasized that in contrast to most astronomical objects (such as planets, stars, and galaxies), the Universe as a whole is usually considered to be non-rotational. However, the possibility that the Universe rotates should not be ignored. In fact, the solutions of general relativity corresponding to a rotating Universe have been found in [2-5], directly indicating that a global rotation is physically allowed.
There are many other approaches to constrain the global rotation.
Based on the idea that a global rotation induces a total net spin of galaxies, the global rotation can be limited [6]. Moreover, empirical relations between angular momentum and mass of galaxies/clusters, such as  for spiral galaxies and
for spiral galaxies and 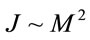 for clusters can be explained by the global rotation [7]. The acceleration caused by the global rotation may be used to explain parts of the accelerating expansion of our Universe, and thus the global rotation can be constrained by Supernova type Ia data.
for clusters can be explained by the global rotation [7]. The acceleration caused by the global rotation may be used to explain parts of the accelerating expansion of our Universe, and thus the global rotation can be constrained by Supernova type Ia data.
Beside, authors quoted number of previous articles devoted to clarifying this problem and conclude that study of global rotation is of interest in many different aspects of cosmology, and constraint of the rotation speed of the Universe is important.
To develop a model that preserves the homogeneity and isotropy of the mean CMB, they studied the rotation of the Universe as a perturbation in the RobertsonWalker framework with a cosmological constant. Unlike the Bianchi models, such an approach allows to have non-zero rotation but trivial shear. Since the global rotation does not have any influences on the first-order SachsWolfe effect (SW effect), we need to calculate the metric up to second-order perturbations and find the secondorder SW effect. Then, they constrained the angular speed of the rotation using recent data on CMBA. As the result their model is inhomogeneous with an axial symmetry in general. Moreover, the global rotation in this model is not only radial-dependent, but also time-dependent.
In fact, the angular velocity describes by expression
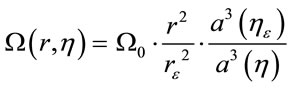 , where
, where 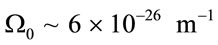
in SI unit. The subscripts “0” and “e” at radius 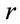 and conformal time
and conformal time 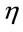 are denoting the hypersurfaces at origin and last photons scattering in SW effect respectively. In doing this the angular velocity of matter can be negative while the rotation speed of the Universe is always positive and is less than
are denoting the hypersurfaces at origin and last photons scattering in SW effect respectively. In doing this the angular velocity of matter can be negative while the rotation speed of the Universe is always positive and is less than 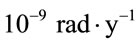 at the last scattering surface.
at the last scattering surface.
The first experimental evidence of the Universe rotation was done by Birch [8], evidently. In this article he results of a study of the position angles and polarization of high luminosity classical-double radio sources are discussed, taking into account a sample of 94 radio sources. There appears to be strong evidence that the Universe is anisotropic on a large scale, producing position angle offsets in the polarization and brightness distributions of radio sources. These can probably be explained on the basis of a rotation of the Universe with an angular velocity of approximately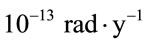 . Such a rotation would have drastic cosmological consequences, since it would violate Mach’s principle and the widely held assumption of large-scale isotropy.
. Such a rotation would have drastic cosmological consequences, since it would violate Mach’s principle and the widely held assumption of large-scale isotropy.
Contrary to this in article [9] it was concluded, from an independent analysis of a new, enhanced sample of radio sources, that there is no evidence for a large-scale anisotropy of this type, or for universal rotation.
Nevertheless, the observational proofing of Universe rotation phenomenon is still important up to the present days. Really, in [10] a preference for spiral galaxies in one sector of the sky to be left-handed or right-handed spirals would indicate a parity violating asymmetry in the overall Universe and a preferred axis was considered. This study uses 15158 spiral galaxies with redshifts 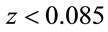 from the Sloan Digital Sky Survey. An unbinned analysis for a dipole component that made no prior assumptions for the dipole axis gives a dipole asymmetry of
from the Sloan Digital Sky Survey. An unbinned analysis for a dipole component that made no prior assumptions for the dipole axis gives a dipole asymmetry of  with a probability of occurring by chance of
with a probability of occurring by chance of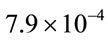 . A similar asymmetry is seen in the Southern Galaxy spin catalog of Iye and Sugai. The axis of the dipole asymmetry lies at approx.
. A similar asymmetry is seen in the Southern Galaxy spin catalog of Iye and Sugai. The axis of the dipole asymmetry lies at approx. , roughly along that of our Galaxy and close to alignments observed in the WMAP cosmic microwave background distributions. The observed spin correlation extends out to separations
, roughly along that of our Galaxy and close to alignments observed in the WMAP cosmic microwave background distributions. The observed spin correlation extends out to separations , while spirals with separations <20 Mpc/h have smaller spin correlations.
, while spirals with separations <20 Mpc/h have smaller spin correlations.
Moreover, in [11] a statistically significant anisotropy of the Hubble diagram at redshifts  is discovered with the confidence level
is discovered with the confidence level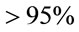 . While data from the North Galactic hemisphere favor the accelerated expansion of the Universe, data from the South Galactic hemisphere are not conclusive. The hemispheric asymmetry is maximal toward a direction close to the equatorial poles. The discrepancy between the equatorial North and South hemispheres shows up in the SN calibration. For the ΛCDM model fitted to all available SNe, authors found the same asymmetry. This asymmetry may be the evidence of the Universe rotation axis existence.
. While data from the North Galactic hemisphere favor the accelerated expansion of the Universe, data from the South Galactic hemisphere are not conclusive. The hemispheric asymmetry is maximal toward a direction close to the equatorial poles. The discrepancy between the equatorial North and South hemispheres shows up in the SN calibration. For the ΛCDM model fitted to all available SNe, authors found the same asymmetry. This asymmetry may be the evidence of the Universe rotation axis existence.
It is very important to mark that in article [12] was put forward he question—does the Universe accelerate equally in all directions? Authors employed the union compilation of Type Ia supernovae with a maximum likelihood analysis to search for a dark energy dipole. To approach this problem, authors presented a simple, computationally efficient, and largely model independent method. They opted to weight each SN by its observed error estimate, so poorly measured SNe that deviate substantially from the Hubble law do not produce spurious results. As the result they found, with very low significance, a dipole in the cosmic acceleration directed roughly towards the cosmic microwave background dipole, but this is almost certainly coincidental. Such dipole indicates the Universe anisotropy and may coincide with the direction of its rotation axis.
Another variant of confirmation the Universe rotation axis existence have been done in article [13].
The novel aspects of the Universe rotation problem were considered in [14]. In this paper author discussed the observational aspects of rotation in the Universe on different scales. He shows dependence between the angular momentum of the structures and their size. The presented observational situation is that the galaxies, their pairs and compact groups have a non-vanishing angular momentum. In the structures of mass corresponding to groups of galaxies, this feature has not been found, while in the clusters and superclusters alignment of galaxy orientation has been actually found. Also it’s known that galaxies have net angular momentum due to the fact that we actually measure the rotation curves of galaxies. These facts lead to the conclusion that theories which connect galaxy angular momentum with its surrounding structure are at some extend favored by data. Author shows that in the light of scenarios of galaxy formations this result could be interpreted as an effect of tidal forces mechanism, but it is also consistent with Li’s model, in which galaxies form in the rotating Universe.
The article organizes as follows. In second section we argued the vacuum conception of the Universe rotation. In third section we calculate the galactic coordinates of the Universe rotational axis. Forth section devoted to the theoretical basing picked axis in the Universe existence. In conclusion we briefly summarize the results of article.
2. Vacuum Conception of the Universe Rotation
But now question arises—if the Universe rotates what is the physical reason of this phenomenon? Such question is very important because in all of previous article the cosmological rotation has been introduced “by hands”. One of the first articles was done by Ellis and Olive [15]. They pointed out that an inflationary episode in the very early Universe could solve the rotation problem and thus make the Mach principle redundant as an explanation. The difficulties posed by the rotation-induced shear for the inflationary explanation are avoided if the inflation occurred at the Planck epoch. The problem of the slow rotation of the Universe is addressed by introducing a dimensionless measure of the angular velocity in the early Universe, which must have been less than 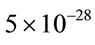 in order to be compatible with present-day upper limits on rotation.
in order to be compatible with present-day upper limits on rotation.
Note that article [16] has been prepared in this trend recently. Its aim is the searching of rotational movement of galaxies, caused by the cosmic vacuum or antigravitational vacuum force and its application to the Universe rotation problem.
So, considering a galaxy as the rigid body we’ll examine its rotation under acting of vacuum antigravitational force with respect to the center-of-mass point.
In [16] it was argued that elementary vacuum force acted on any volume of a galaxy  is
is
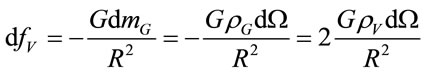 . (2.1)
. (2.1)
At basing (2.1) it was took into account the vacuum equation of state 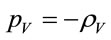 and fact that according to the Friedmann cosmological model the gravitation produces by generalized mass density
and fact that according to the Friedmann cosmological model the gravitation produces by generalized mass density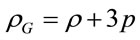 , where
, where 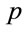 is the substrate pressure. Let
is the substrate pressure. Let 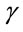 is the angle between vectors
is the angle between vectors  and
and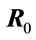 . Then under the condition
. Then under the condition 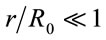 we find the element of gravitational repelling force
we find the element of gravitational repelling force
 (2.2)
(2.2)
and its total expression

 , (2.3)
, (2.3)
where integral must be taken over the volume of galaxy and  is the vacuum potential.
is the vacuum potential.
Introducing the vacuum moments 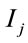 of the galaxy along axes
of the galaxy along axes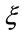 ,
,  ,
,  and cross-section areas
and cross-section areas
 , corresponding them, it’s possible write down the vacuum perturb force and the vacuum potential as follows
, corresponding them, it’s possible write down the vacuum perturb force and the vacuum potential as follows
 . (2.4)
. (2.4)
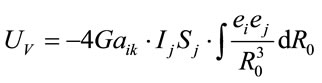 , (2.5)
, (2.5)
accordingly.
Later on we choose the elliptical galaxy as the model of examining type of galaxies. This lead not only to simplify the process of the analytical solving our problem, but allowed to compare results with the real astronomical database. Consider an elliptical galaxy that have two equal main moments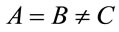 . Than the potential will not depends on angle
. Than the potential will not depends on angle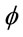 . Hence, it may be equals to zero, i.e.
. Hence, it may be equals to zero, i.e.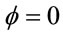 .
.
For the chosen shape of galaxy its equations of rotational motion are
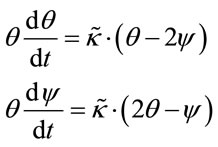 , (2.6)
, (2.6)
where coefficient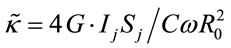 . The system (2.6) is easy transforms to the differential equation of the first order
. The system (2.6) is easy transforms to the differential equation of the first order
 , (2.7)
, (2.7)
The solution of this equation describes by standard quadrature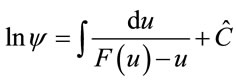 , with variable
, with variable  , and
, and  [17]. In [16] it was shown that
[17]. In [16] it was shown that
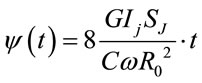 . (2.8)
. (2.8)
Basing on this result it is easy to calculate the angular velocity of the elliptical galaxy around  axis. In fact, as for this case
axis. In fact, as for this case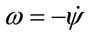 , than its module equals
, than its module equals
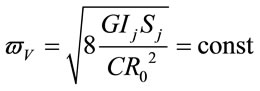 . (2.9)
. (2.9)
This expression describes the angular velocity that galaxy acquires due to the vacuum antigravitation.
Consider, for example, the giant elliptical galaxy NGC 4486 (М 87), that locates from us at distance R0 = 15 MPc, while its proper sizes  equals
equals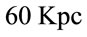 . With account of above cited vacuum density we estimate the magnitude of Expression (18) now. Putting
. With account of above cited vacuum density we estimate the magnitude of Expression (18) now. Putting
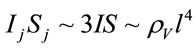 and assuming that
and assuming that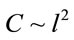 , we find
, we find
 . Substitution the needed values into this expression give the following estimation
. Substitution the needed values into this expression give the following estimation .
.
At the same time analyses of (2.9) shows that its maximal magnitude will be under the condition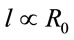 . Then expression for the vacuum angular velocity simplifies and takes on the form
. Then expression for the vacuum angular velocity simplifies and takes on the form
 . (2.10)
. (2.10)
This expression is possible to interpret as the minimal angular velocity in the Universe that vacuum can create at arbitrary object its numerical value is about 10−19 sec−1. Hence, the vacuum itself create the identical initial angular velocity at all of cosmic objects. Thus it is possible to say that cosmic vacuum not only creates the microscopic baryonic substance, but pre-determines its global characteristics.
As the condition  indicates the passing to the entire Universe it results about its total rotation. As it seems Expression (2.10) is invariant and don’t depend nether the frame of reference nor choosing the geometrical sizes of the Universe at given cosmological epoch. Hence, at the earliest stages of Universe evolution, for example at baryonic asymmetry stage, when vacuum density was about
indicates the passing to the entire Universe it results about its total rotation. As it seems Expression (2.10) is invariant and don’t depend nether the frame of reference nor choosing the geometrical sizes of the Universe at given cosmological epoch. Hence, at the earliest stages of Universe evolution, for example at baryonic asymmetry stage, when vacuum density was about  its angular velocity was essentially larger and was equal
its angular velocity was essentially larger and was equal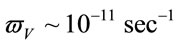 . For the very early Universe vacuum density was about
. For the very early Universe vacuum density was about  in order and its angular velocity was drastically larger
in order and its angular velocity was drastically larger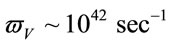 .
.
Mark, at such angular velocity the border of Universe moved with linear velocity not larger the speed of light. In fact, as the sizes of Universe at born time were Planckian type, i.e. , than linear velocity of the Universe border will be
, than linear velocity of the Universe border will be 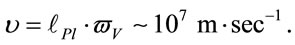 This velocity is smaller that speed of light truly, that is must be in realty.
This velocity is smaller that speed of light truly, that is must be in realty.
What about the observable angular velocity of the Universe at the present epoch? In papers [6,7] there were given following estimations of its angular velocity . In article [1], that was done on the base of novel experimental data on the relic radiation distribution divergence from Gaussian, was shown that the Universe angular velocity must be smaller than
. In article [1], that was done on the base of novel experimental data on the relic radiation distribution divergence from Gaussian, was shown that the Universe angular velocity must be smaller than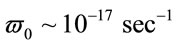 .
.
From these estimations it result that Universe angular velocity must be in the following range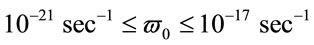 . Our previous estimate of the Universe rotation
. Our previous estimate of the Universe rotation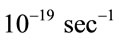 , as it seems, is in good correlation with the specified interval.
, as it seems, is in good correlation with the specified interval.
At the same time the peculiarity of quoted articles is the Universe rotation searching in the framework of relativistic cosmology and its determination by a baryonic substrate. In contrary, in our case the Universe rotation determines by Newtonian’s mechanics and is the consequence of vacuum presence. That is why the ratio of Universe angular velocity to the Hubble parameter is about unit, i.e.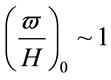 . From this follows the correctness of Gamov’s remark [18] that the unique reason for Universe expansion and its rotation must be. If take into account that vacuum creates all baryonic substance, it is the moving force of the total Universe evolution, hence.
. From this follows the correctness of Gamov’s remark [18] that the unique reason for Universe expansion and its rotation must be. If take into account that vacuum creates all baryonic substance, it is the moving force of the total Universe evolution, hence.
3. Galactic Coordinates of the Universe Rotational Axis
Talking about the Universe rotation it is not ignore the difficulty connected with the determination of the Universe rotational axis and its orientation in the space. Such question was considered by number authors, but from observational point of view preferentially. We’ll examine it from the theoretical positions basing on the coordinate transformation that expressed by Euler angles and galactic coordinates.
Remind that galactic coordinates system this is the system with origin placed on the Sun and extended through the center of Galaxy. Its plane coincides with the plane of Galaxy dick. In doing this, its latitude 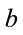 is measured from galaxies plane to an object and takes magnitudes from −90˚ up to +90˚. Galactic longitude
is measured from galaxies plane to an object and takes magnitudes from −90˚ up to +90˚. Galactic longitude  is measured at the Galaxy plane from the baseline connected the Sun and galactic center up to the baseline connected the Sun and object. Counting directs to the same way that the right ascension in the second equatorial coordinates. Therefore the galactic longitude puts in limits from 0 ˚ up to 360˚.
is measured at the Galaxy plane from the baseline connected the Sun and galactic center up to the baseline connected the Sun and object. Counting directs to the same way that the right ascension in the second equatorial coordinates. Therefore the galactic longitude puts in limits from 0 ˚ up to 360˚.
The position of object in galactic coordinates describes by matrix expression
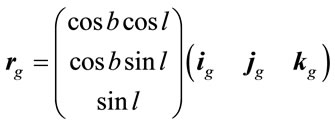 , (3.1)
, (3.1)
where 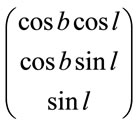 is the matrix of galactic coordinates while
is the matrix of galactic coordinates while —its basis vectors.
—its basis vectors.
The radius-vector  of a celestial object that is expressed by equatorial coordinates
of a celestial object that is expressed by equatorial coordinates 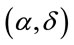 may be decomposed by basis vectors of other coordinates of galactic coordinates
may be decomposed by basis vectors of other coordinates of galactic coordinates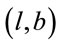 , in particular. As equatorial coordinates
, in particular. As equatorial coordinates  is connected with the Euler coordinates
is connected with the Euler coordinates 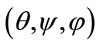 taken under the condition
taken under the condition 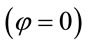 by the equalities
by the equalities  and
and , we have the following relationship
, we have the following relationship
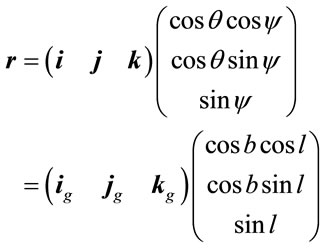 (3.2)
(3.2)
To find the explicit form of transformation between two coordinate systems it is necessary to calculate the rotation matrix from first basis unit vectors to second one. For example, as it follows from above the matrix of galactic coordinates is
 . (3.3)
. (3.3)
Also remind that ort 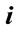 is directed to the point of spring equinox; ort
is directed to the point of spring equinox; ort —to the point of right ascension that equals
—to the point of right ascension that equals ; ort
; ort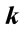 —to the North celestial pole.
—to the North celestial pole.
Finally, we have to calculate the matrix
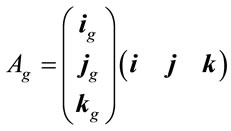 . Basing on the magnitudes of angles for right ascension and declination, defined for the B1950 epoch1, it possible to show that [19]
. Basing on the magnitudes of angles for right ascension and declination, defined for the B1950 epoch1, it possible to show that [19]
 (3.4)
(3.4)
For next calculations find the concrete magnitudes of Euler angles whose general expression was found in Section 2.
From its results we get
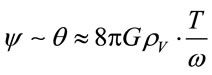 , (3.5)
, (3.5)
where 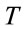 is the timelife of our Universe. Setting
is the timelife of our Universe. Setting 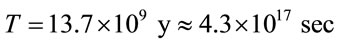 , angular velocity
, angular velocity 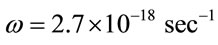 and having in mind that
and having in mind that  ,
, 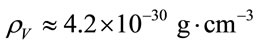 ,
,  , we get following estimations
, we get following estimations
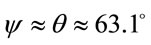 . (3.6)
. (3.6)
As 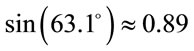 and
and 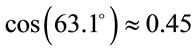 the explicit form of the galactic coordinates matrix will be
the explicit form of the galactic coordinates matrix will be
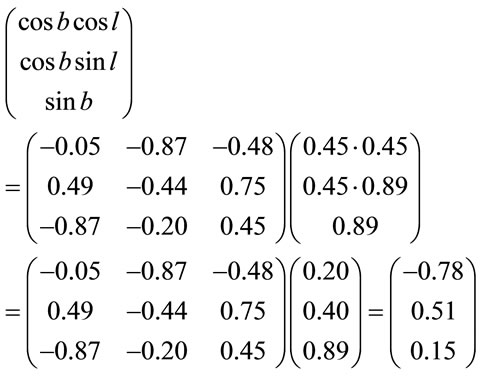 (3.7)
(3.7)
From this we get the system of three equations for two variables 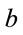 and
and 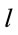
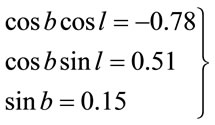 . (3.8)
. (3.8)
From two last of them we find ,
,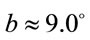 . Compare these magnitudes with results of article [20,21], where the galactic coordinates of the Universe rotation axis were determined as
. Compare these magnitudes with results of article [20,21], where the galactic coordinates of the Universe rotation axis were determined as . It’s easy to see that the axis passes through the Sun and point O with angular coordinates
. It’s easy to see that the axis passes through the Sun and point O with angular coordinates 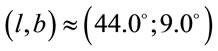 will coincide with the axis passes through the Sun and point with angular coordinates
will coincide with the axis passes through the Sun and point with angular coordinates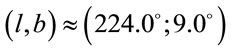 . That is why it possible concludes that Universe rotation axis has this coordinates namely2.
. That is why it possible concludes that Universe rotation axis has this coordinates namely2.
The divergence between observational angular coordinates  and our theoretically predicted coordinates
and our theoretically predicted coordinates  explains by accounting the vacuum density only at the calculation of Euler coordinates. Hence, except vacuum density it is necessary take into account densities of dark matter and baryonic matter that are the integral components of any galaxies structure. Nevertheless, our approach demonstrates the possible way of theoretical deducing the space orientation of the Universe rotational axis.
explains by accounting the vacuum density only at the calculation of Euler coordinates. Hence, except vacuum density it is necessary take into account densities of dark matter and baryonic matter that are the integral components of any galaxies structure. Nevertheless, our approach demonstrates the possible way of theoretical deducing the space orientation of the Universe rotational axis.
Its fruitfulness seems through the prism of Universe evolution, already. In fact, as the magnitude of vacuum density is different at different epochs of its evolution, the space orientation of the rotational axis changes, also. For instance, at the baryonic asymmetry epoch when vacuum density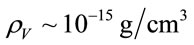 , angular velocity
, angular velocity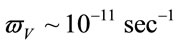 , timelife
, timelife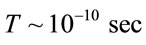 , than Euler angle
, than Euler angle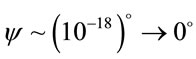 . So, the angular coordinates of the rotational axis where
. So, the angular coordinates of the rotational axis where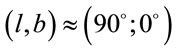 .
.
4. Basing the Picked Axis in the Universe
Now we mention the fundamental article [11], once again, where the asymmetry of Hubble’s diagrams for the North and the South sky hemispheres was searched. This asymmetry cannot be explains by peculiar motion of the observer, but most apparently due to the any bulk flow along the direction 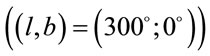 in the Universe existence that earlier was argued in article [22]. Recently R.-G. Cai and Z.-L. Tuo [21] determined more precisely this direction
in the Universe existence that earlier was argued in article [22]. Recently R.-G. Cai and Z.-L. Tuo [21] determined more precisely this direction 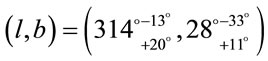 and found the maximum anisotropy of the deceleration parameter
and found the maximum anisotropy of the deceleration parameter
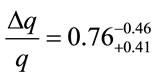 .
.
Evidently, these results are possible to summaries as follows, our Universe is anisotropic in realty and possesses by any principal space axis. That is why the cosmological deceleration parameter will be anisotropic, also and must be depend on the principal space direction in definite way. These statements require theoretical basing the direction dependence of the cosmological deceleration parameter phenomenon.
Our searching we start from the well-known results. For the uniform isotropic metric of the space-flat Universe 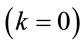 the Einstein’s equations for the scale factor
the Einstein’s equations for the scale factor 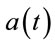 are [23]
are [23]
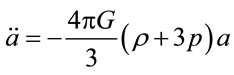 , (4.1)
, (4.1)
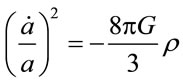 , (4.2)
, (4.2)
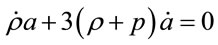 . (4.3)
. (4.3)
Put that scale factor expresses as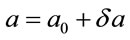 , where
, where  is the distance in uniform space, while
is the distance in uniform space, while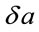 —small addition (perturb term) for describing the possible space anisotropy. Putting it into the Newtonian Equation (4.1) we get two equations—basic one
—small addition (perturb term) for describing the possible space anisotropy. Putting it into the Newtonian Equation (4.1) we get two equations—basic one
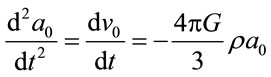 (4.4)
(4.4)
and perturb one
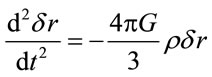 . (4.5)
. (4.5)
Later on these equations will be considered independently each other.
Performing the above mentioned Tolman transformation  [23] and substituting it into (4.1) for the case of vacuum (
[23] and substituting it into (4.1) for the case of vacuum (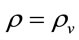 ,
,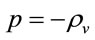 ) we find equation that get the inflationary regime of the Universe expanding
) we find equation that get the inflationary regime of the Universe expanding
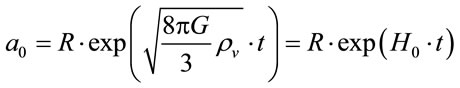 . (4.6)
. (4.6)
It leads to the Hubble expansion law
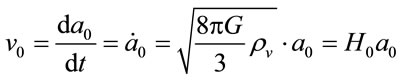 (4.7)
(4.7)
and to the corresponding acceleration
 . (4.8)
. (4.8)
Now consider the Equation (4.5). Suppose that in this equation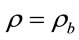 , where
, where  is the baryonic substance density. The baryonic substance pressure
is the baryonic substance density. The baryonic substance pressure 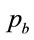 let equals zero, for simplicity.
let equals zero, for simplicity.
Last requirement means considering the presence of two-component substance—cosmic vacuum and baryonic dust—in the Universe, that are not interact each other in the basic approximation.
By introducing the designation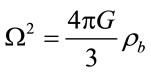 , from (4.5) it follows
, from (4.5) it follows
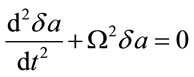 (4.9)
(4.9)
This oscillatory-type equation possesses by two roots
 . (4.10)
. (4.10)
They lead to the presence of two perturb (with respect to (4.7)) velocities
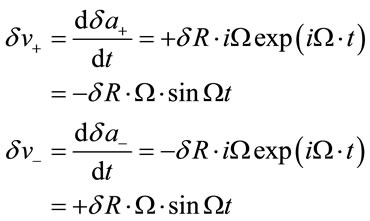 (4.11)
(4.11)
and two corresponding accelerations
 . (4.12)
. (4.12)
From physical viewpoint expressions (4.10)-(4.12) mean that presence of baryonic dust matter creates two space-opposite fluxes that are propagate on the background of expanding and accelerating “Hubble vacuum flux” along the Universe rotation axis. That is why it possible writes down the expressions for total distance, velocity and acceleration of any probe particle (galaxy)
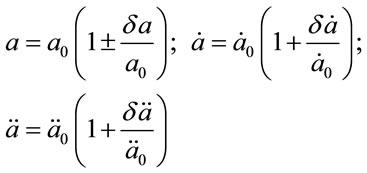 (4.13)
(4.13)
Thus the cosmological deceleration parameter q with the accuracy no higher than  is
is
 . (4.14)
. (4.14)
Basing on the definitions of  and
and  we introduce the new coefficient
we introduce the new coefficient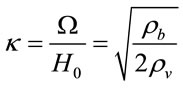 . As in unit of the critical density
. As in unit of the critical density 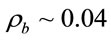 and vacuum density
and vacuum density 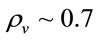 , coefficient
, coefficient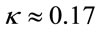 , henceforth.
, henceforth.
From (4.14) it is possible find the relative acceleration difference between two baryonic fluxes with respect to the “Hubble vacuum flux”,
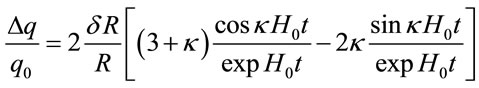 . (4.15)
. (4.15)
Assuming that for modern epoch 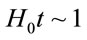 we approximately get
we approximately get . Hence, the first term in right side of (4.15) tends to 1.2, while the second term tends to zero. So,
. Hence, the first term in right side of (4.15) tends to 1.2, while the second term tends to zero. So,
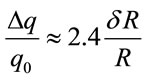 . (4.16)
. (4.16)
Basing on our assumption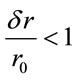 , that was argued earlier, we may put that it will satisfy if the ratio
, that was argued earlier, we may put that it will satisfy if the ratio
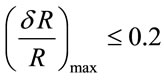 . This leads to the estimation
. This leads to the estimation
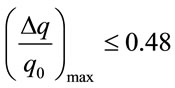 that is in good correlation (case of the upper magnitude index) with the value
that is in good correlation (case of the upper magnitude index) with the value
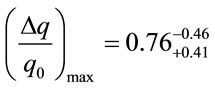 in [22].
in [22].
5. Conclusions
So, we briefly reviewed the modern status of the Universe rotation problem. In numbers of examined articles, this problem was considered from different viewpoints and done the following common result—our Universe rotate, most probably. On the this statement grounding it was considered the vacuum concept of the Universe rotation, found the galactic coordinates of the Universe axis rotation and based the concept of the deceleration parameter anisotropy along this axis.
It also was shown that all of our theoretical results have the real observational confirmation.
6. Acknowledgements
I would like to express my gratitude to Professor G. F. Smoot III for discussion the Universe rotation problem during his visit the VI Astana world economical forum, 22-24 May 2013, Kazakhstan.
REFERENCES
- S. C. Su and M. C. Chu, The Astrophysical Journal, Vol. 703, 2009, pp. 354-361. doi:10.1088/0004-637X/703/1/354
- K. Gödel, Reviews of Modern Physics, Vol. 21, 1949, pp. 447-450. doi:10.1103/RevModPhys.21.447
- S. Hawking, MNRAS, Vol. 142, 1969, pp. 129-141.
- J. D. Barrow, R. Juszkiewicz and D. N. Sonoda, MNRAS, Vol. 213, 1985, pp. 917-943.
- J. D. Barrow and C. G. Tsagas, Classical and Quantum Gravity, Vol. 21, 2004, pp. 1773-1790. doi:10.1088/0264-9381/21/7/005
- L. X. Li, General Relativity and Gravitation, Vol. 30, 1998, pp. 497-507. doi:10.1023/A:1018867011142
- W. Godlowski and M. Szydlowski, General Relativity and Gravitation, Vol. 35, 2003, pp. 2171-2187. doi:10.1023/A:1027301723533
- P. Birch, Nature, Vol. 298, 1982, pp. 451-454. doi:10.1038/298451a0
- M. F. Bietenholtz and P. P. Kronberg, The Astrophysical Journal, Part 2, Vol. 287, 1984, pp. L1-L2. doi:10.1086/184383
- M. J. Longo, Physics Letters B, Vol. 699, 2011, pp. 224-229.
- D. J. Schwarz and B. Weinhorst, Astronomy & Astrophysics, Vol. 474, 2007, pp. 717-729. doi:10.1051/0004-6361:20077998
- R. Cooke and D. Lynden-Bell, MNRAS, Vol. 401, 2010, pp. 1409-1414. doi:10.1111/j.1365-2966.2009.15755.x
- L. M. Chechin, International Journal of Astronomy and Astrophysics, Vol. 2, 2012, pp. 195-198. doi:10.4236/ijaa.2012.24024
- W. Godlowski, IJMPD, Vol. 20, 2011, pp. 1643-1674. doi:10.1142/S0218271811019475
- J. Ellis and K. A. Olive, Nature, Vol. 303, 1983, pp. 679- 681. doi:10.1038/303679a0
- L. M. Chechin, Astron. Rep., Vol. 87, 2010, pp. 784-788. doi:10.1134/S1063772910080044
- V. V. Stepanov, “Course of the Differential Equations,” GIFML, Moscow, 1958.
- G. Gamov, Nature, Vol. 158, 1946, p. 549. doi:10.1038/158549a0
- V. Ye. Zharov, “The Spherical Astronomy,” Vek 2, Moscow, 2006.
- M. J. Hudson, R. J. Smith, J. R. Lucey and E. Branchini, MNRAS, Vol. 352, 2004, pp. 61-75. doi:10.1111/j.1365-2966.2004.07893.x
- R.-G. Cai and Z.-L. Tuo, arXiv:1109.0941v4 [astro-ph. CO], 2011.
- Y. Itoh, K. Yahata and M. Takada, arXiv:astro-ph/0912. 1460v2.
- Ya. B. Zel’dovich and I. D. Novikov, “Relativistic Astrophysics, 2. The Structure and Evolution of the Universe,” University of Chicago Press, Chicago, 1983.
NOTES
1Passage to coordinates defined for the current epoch J2000.0 don’t change our subsequent result.
2Usage of the first equation in (3.8) leads to the approximately same result.

