Journal of Modern Physics
Vol.4 No.11(2013), Article ID:40187,6 pages DOI:10.4236/jmp.2013.411187
Ion-Acoustic Higher Order Non-Linear Structures in Quantum Dusty Plasma
1Department of Electrical and Electronic Engineering, Bangladesh University of Business and Technology, Dhaka, Bangladesh
2Institute of Natural Science, United International University, Dhaka, Bangladesh
Email: monirul.h@bubt.edu.bd
Copyright © 2013 Md Manir Hossain et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 3, 2013; revised July 5, 2013; accepted August 1, 2013
Keywords: Negative Dust; Quantum Plasma; Fermi Electron; Modified K-dV Equation; Gardner Solitons; RPM
ABSTRACT
The prominent features of higher order nonlinear ion-acoustic waves involving quantum corrections in an unmagnetized quantum dusty plasma are revisited with the theoretical framework of Hossain et al. [1]. The fluid model is demonstrated here by its constituent inertial ions, Fermi electrons with quantum effect, and immovable dust grain with negative charge. We have used the ideology of Gardner equation. The well-known RPM method is employed to derive the equation. Indeed, the basic features of quantum dust ion-acoustic Gardner solitons (GSs) are pronounced here. GSs are shown to exist for the value of dust to ion ratio around 2/3 which is valid for space plasma [2], and are different from those of K-dV (Korteweg-de Vries) solitons, which do not exist for the value around 2/3. The implications of our results are suitable for cosmological and astrophysical environments.
1. Introduction
Quantum plasmas have attracted a great deal of attention because of their potential applications in dense plasma particularly in different astrophysical and cosmological systems [3-5] (e.g. interstellar or molecular clouds, planetary rings, comets, interior of white dwarf stars, etc.), in nanostructures [6], in microelectronic device [7] as well as in the next-generation intense laser [8]. Many authors have proposed some theories including the quantum corrections to the quantum plasma echoes [9], the self-consistent dynamics of Fermi gases [10], quantum beam instabilities [11], wave interactions in quantum magnetoplasmas [12], classical and quantum kinetics of the Zakharov system [13], quantum corrections to the Zakharov equations [14], expansion of quantum electron gas into vacuum [15], quantum ion acoustic waves [16], quantum Landau damping [17], magnetohydrodynamics of quantum plasmas [18], etc. Quantum plasmas have extremely high plasma number densities and low temperatures. At extremely low temperatures, the thermal de Broglie wavelength becomes comparable to the interelectron distance and the electron temperature becomes comparable to the electron Fermi temperature 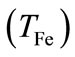 and the electrons follow Fermi Dirac distribution law. In this condition, quantum mechanical effects are expected to play a significant role in the behavior of charged particles [19-21]. As electrons are lighter than ions, the quantum behavior of electron is reached faster than ions. The dust particles are quite common in various plasma systems. The inclusion of immobile charged dust in electron-ion plasmas leads to introduce a new mode. Shukla and Silin [22] have first theoretically shown the existence of low-frequency dust ion-acoustic (DIA) waves in a dusty plasma, which was latter observed in laboratory experiments [23,24]. The phase speed of the DIA waves is much smaller (larger) than electron (ion) thermal speed. The inertia is provided by the ion mass while the restoring force comes from the electron thermal pressure. These waves differ from usual ion-acoustic waves [25] due to the conservation of equilibrium charge density
and the electrons follow Fermi Dirac distribution law. In this condition, quantum mechanical effects are expected to play a significant role in the behavior of charged particles [19-21]. As electrons are lighter than ions, the quantum behavior of electron is reached faster than ions. The dust particles are quite common in various plasma systems. The inclusion of immobile charged dust in electron-ion plasmas leads to introduce a new mode. Shukla and Silin [22] have first theoretically shown the existence of low-frequency dust ion-acoustic (DIA) waves in a dusty plasma, which was latter observed in laboratory experiments [23,24]. The phase speed of the DIA waves is much smaller (larger) than electron (ion) thermal speed. The inertia is provided by the ion mass while the restoring force comes from the electron thermal pressure. These waves differ from usual ion-acoustic waves [25] due to the conservation of equilibrium charge density 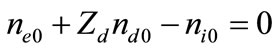 and the strong inequality
and the strong inequality , where
, where  is the particle number density of the species
is the particle number density of the species  with
with  for electrons,
for electrons,  for ions and
for ions and 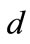 for dust,
for dust, 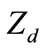 is the number of electrons residing onto the dust grain surface, and
is the number of electrons residing onto the dust grain surface, and 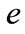 is the magnitude of an electronic charge. Therefore, a dusty plasma can not support the usual ion-acoustic waves, but can do the DIA waves of Shukla and Silin [22]. The nonlinear waves associated with the DIA and QDIA waves particularly solitary waves (SWs) [26,27] and shock waves [28] have received a great deal of interest in understanding the basic properties of localized electrostatic perturbation in space [29,30] and laboratory dusty plasmas [31-34]. A number of investigations have been made on QDIA SWs [35] and shocks [28] by using K-dV equation. For plasmas with more than two species, it can arise cases where the K-dV equation is not valid near a critical value of a certain parameter (say
is the magnitude of an electronic charge. Therefore, a dusty plasma can not support the usual ion-acoustic waves, but can do the DIA waves of Shukla and Silin [22]. The nonlinear waves associated with the DIA and QDIA waves particularly solitary waves (SWs) [26,27] and shock waves [28] have received a great deal of interest in understanding the basic properties of localized electrostatic perturbation in space [29,30] and laboratory dusty plasmas [31-34]. A number of investigations have been made on QDIA SWs [35] and shocks [28] by using K-dV equation. For plasmas with more than two species, it can arise cases where the K-dV equation is not valid near a critical value of a certain parameter (say ). The nonlinear term vanishes at this critical value (at
). The nonlinear term vanishes at this critical value (at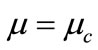 ) [36] which makes soliton amplitude large enough to break down the validity of K-dV equation. The mmK-dV (mixed modified K-dV) equation, also known as Gardner equation, can give soliton solution around this critical value [37]. The technique of analyzing SWs is Gardner approach which leads to a standard Gardner equation. From the analysis of standard Gardner equation, SW of permanent profile is found, which is known as Gardner soliton (GS) [1,38,39]. In our present manuscript, we attempt to study the basic features of QDIA GSs by deriving modified Gardner equation, which is valid around
) [36] which makes soliton amplitude large enough to break down the validity of K-dV equation. The mmK-dV (mixed modified K-dV) equation, also known as Gardner equation, can give soliton solution around this critical value [37]. The technique of analyzing SWs is Gardner approach which leads to a standard Gardner equation. From the analysis of standard Gardner equation, SW of permanent profile is found, which is known as Gardner soliton (GS) [1,38,39]. In our present manuscript, we attempt to study the basic features of QDIA GSs by deriving modified Gardner equation, which is valid around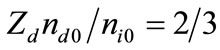 , in a quantum dusty plasma containing inertial ions, Fermi electrons with quantum effect, and negatively charged immobile dust. The manuscript is organized as follows. The model equations are provided in Section 2. The Gardner equation is derived by using the reductive perturbation method in Section 3. The analytical solutions are presented in Section 4. A brief discussion is finally given in Section 5.
, in a quantum dusty plasma containing inertial ions, Fermi electrons with quantum effect, and negatively charged immobile dust. The manuscript is organized as follows. The model equations are provided in Section 2. The Gardner equation is derived by using the reductive perturbation method in Section 3. The analytical solutions are presented in Section 4. A brief discussion is finally given in Section 5.
2. Model Equations
We consider a one-dimensional, collisionless, unmagnetized quantum dusty plasma system composed of inertial ions, massless Fermi electrons with quantum effect, and negatively charged immobile dust. Thus, at equilibrium we have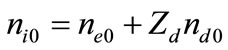 . The nonlinear dynamics of these low-frequency (purely electrostatic) QDIA waves in such a plasma system is described by the normalized equations of the form
. The nonlinear dynamics of these low-frequency (purely electrostatic) QDIA waves in such a plasma system is described by the normalized equations of the form
 (1)
(1)
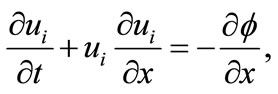 (2)
(2)
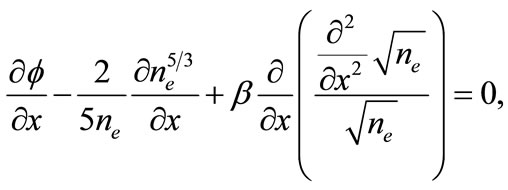 (3)
(3)
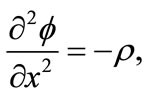 (4)
(4)
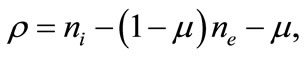 (5)
(5)
where 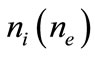 is the ion (electron) number density normalized by its equilibrium value
is the ion (electron) number density normalized by its equilibrium value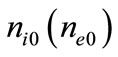 ,
, 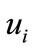 is the ion fluid speed normalized by quantum ion-acoustic speed
is the ion fluid speed normalized by quantum ion-acoustic speed  with
with 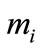 being the ion rest mass,
being the ion rest mass, 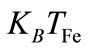 is the electron Fermi energy,
is the electron Fermi energy, 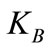 is the Boltzmann constant, and TFe is the Fermi temperature of electron,
is the Boltzmann constant, and TFe is the Fermi temperature of electron, 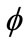 is the electrostatic wave potential normalized by
is the electrostatic wave potential normalized by 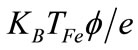 with e being the magnitude of the charge of an electron, ρ is the normalized surface charge density, and
with e being the magnitude of the charge of an electron, ρ is the normalized surface charge density, and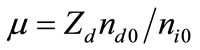 . The time variable
. The time variable  is normalized by
is normalized by  and the space variable is normalized by
and the space variable is normalized by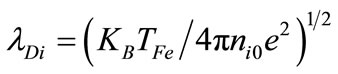 . In Equation (3) we have used the following Fermi pressure law for the electron species [40,41]
. In Equation (3) we have used the following Fermi pressure law for the electron species [40,41]
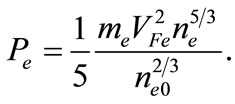 (6)
(6)
Also 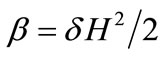 with
with 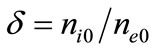 and
and  is the ratio between the plasmon energy and the electron Fermi energy where
is the ratio between the plasmon energy and the electron Fermi energy where 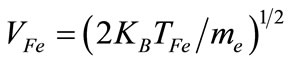 is the electron Fermi speed at temperature
is the electron Fermi speed at temperature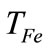 .
.
3. Gardner Equation
We first obtain the well known K-dV equation and see why Gardner equation is needed to find SW solution.
3.1. Derivation of the K-dV Equation
To obtain the QDIA K-dV equation, we introduce the stretched coordinates
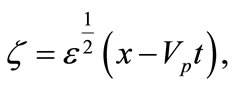 (7)
(7)
 (8)
(8)
where  is the QDIA wave phase speed
is the QDIA wave phase speed 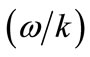 and
and  is a smallness parameter measuring the weakness of the dispersion
is a smallness parameter measuring the weakness of the dispersion . We then expand
. We then expand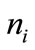 ,
, 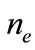 ,
, 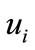 ,
, 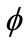 , and
, and 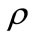 in power series of
in power series of 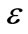
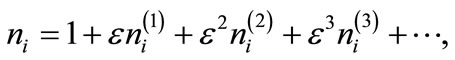 (9)
(9)
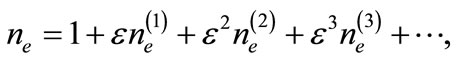 (10)
(10)
 (11)
(11)
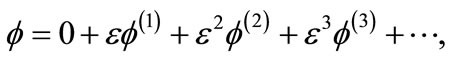 (12)
(12)
 (13)
(13)
and develop equations in various powers of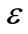 . To the lowest order in
. To the lowest order in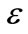 , Equations (1)-(13) give
, Equations (1)-(13) give
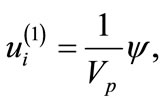 (14)
(14)
 (15)
(15)
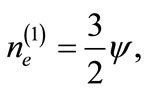 (16)
(16)
 (17)
(17)
where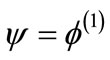 . Equation (17) represents the linear dispersion relation for the QDIA waves. This clearly indicates that the QDIA wave phase speed
. Equation (17) represents the linear dispersion relation for the QDIA waves. This clearly indicates that the QDIA wave phase speed 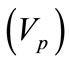 increases with the increase of the dust charge density
increases with the increase of the dust charge density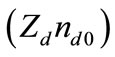 .
.
To the next higher order of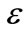 , one can obtain another set of coupled equations for
, one can obtain another set of coupled equations for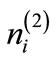 ,
, 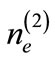 , and
, and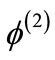 , which -along with the first set of coupled linear equations for
, which -along with the first set of coupled linear equations for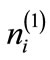 ,
, 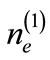 , and
, and 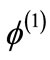 -reduce to a nonlinear dynamical equation of the form
-reduce to a nonlinear dynamical equation of the form
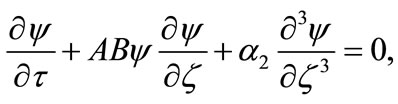 (18)
(18)
where
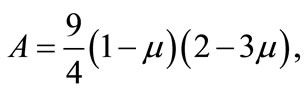 (19)
(19)
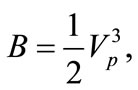 (20)
(20)
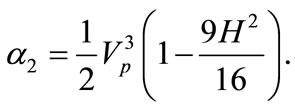 (21)
(21)
Equation (18) is known as K-dV equation. The stationary localized solution of Equation (18) is given by
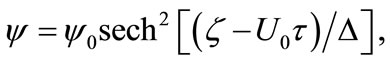 (22)
(22)
where the amplitude 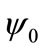 and the width
and the width 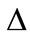 are given by
are given by 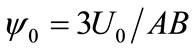 and
and , respectively.
, respectively.  is the mach number. As
is the mach number. As 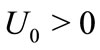 and
and
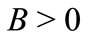 , (22) clearly indicates that 1) small amplitude solitary waves with
, (22) clearly indicates that 1) small amplitude solitary waves with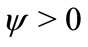 , i.e. positive soliton exists if
, i.e. positive soliton exists if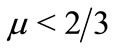 , 2) small amplitude solitary waves with
, 2) small amplitude solitary waves with , i.e. negative soliton exists if
, i.e. negative soliton exists if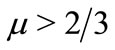 , and 3)
, and 3)  for
for  i.e. the nonlinear term vanishes at μ = μc and is not valid near μ = μc which makes soliton amplitude large enough to break down its validity. To find soliton solution around
i.e. the nonlinear term vanishes at μ = μc and is not valid near μ = μc which makes soliton amplitude large enough to break down its validity. To find soliton solution around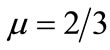 , we now obtain gardner equation.
, we now obtain gardner equation.
3.2. Derivation of the Gardner Equation
To study QDIA GSs by analyzing the ingoing solutions of Equations (1)-(5), we first introduce the stretched coordinates [37]
 (23)
(23)
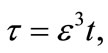 (24)
(24)
By using Equations (23) and (24) in Equations (1)-(6), and Equations (9)-(13) and to the lowest order in ε, we find the same values of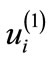 ,
, 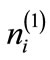 ,
, 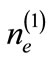 , and
, and  as like as that of the K-dV. To the next higher order in
as like as that of the K-dV. To the next higher order in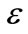 , we obtain a set of equations, which, after using Equations (14)-(17), can be simplified as
, we obtain a set of equations, which, after using Equations (14)-(17), can be simplified as
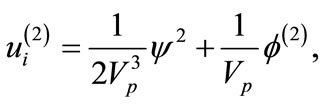 (25)
(25)
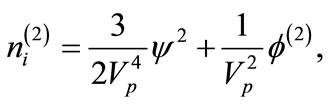 (26)
(26)
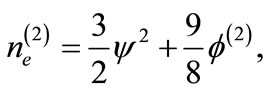 (27)
(27)
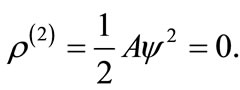 (28)
(28)
It is obvious from Equation (28) that 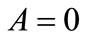 since
since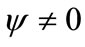 . One can find that
. One can find that 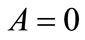 at its critical value
at its critical value 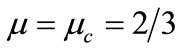 (which is a solution of
(which is a solution of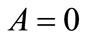 ). So, for
). So, for 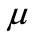 around its critical value
around its critical value ,
, 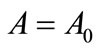 can be expressed as
can be expressed as
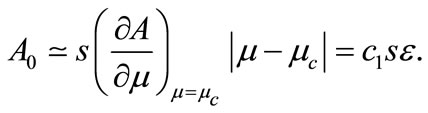 (29)
(29)
where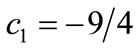 ,
, 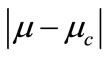 is a small and dimensionless parameter, and can be taken as the expansion parameter
is a small and dimensionless parameter, and can be taken as the expansion parameter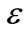 , i.e.
, i.e.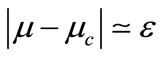 , and
, and 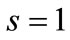 for
for 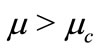 and
and 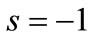 for
for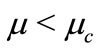 . So,
. So, 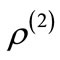 can be expressed as
can be expressed as
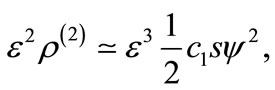 (30)
(30)
which, therefore, must be included in the third order Poissons equation. To the next higher order in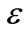 , and after some mathematical calculations we obtain a set of equations
, and after some mathematical calculations we obtain a set of equations
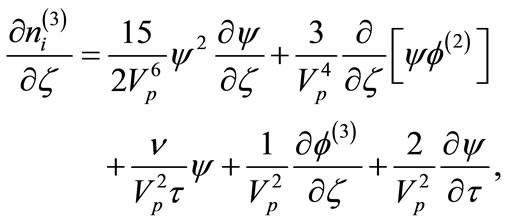 (31)
(31)
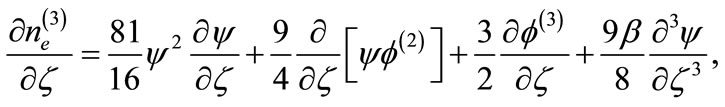 (32)
(32)
 (33)
(33)
Now, combining Equations (31)-(33), we obtain a equation of the form
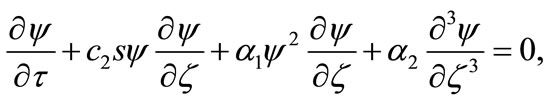 (34)
(34)
where
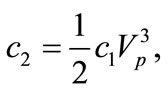 (35)
(35)
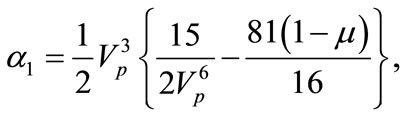 (36)
(36)
And  is given in Equation (21). Equation (34) is known as Gardner equation. It is important to note that if we neglect
is given in Equation (21). Equation (34) is known as Gardner equation. It is important to note that if we neglect 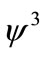 term and put
term and put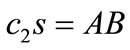 , the Gardner equation reduces to K-dV equation which has derived in Equation (18). However, in this K-dV equation the nonlinear term vanishes at
, the Gardner equation reduces to K-dV equation which has derived in Equation (18). However, in this K-dV equation the nonlinear term vanishes at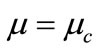 , and is not valid near
, and is not valid near  which makes soliton amplitude large enough to break down its validity. But the Gardner equation derived here is valid for
which makes soliton amplitude large enough to break down its validity. But the Gardner equation derived here is valid for 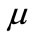 near its critical value.
near its critical value.
4. SW Solution of the Gardner Equation
To analyze stationary GSs, we first introduce a transformation 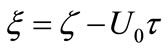 which allows us to write Equation (34), under the steady state condition, as
which allows us to write Equation (34), under the steady state condition, as
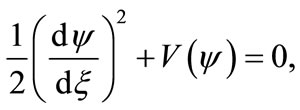 (37)
(37)
where the pseudo-potential  is
is
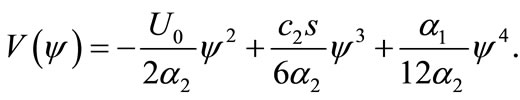 (38)
(38)
It is obvious from Equation (38) that
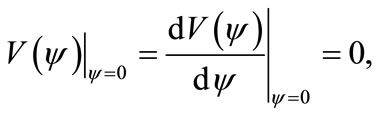 (39)
(39)
 (40)
(40)
The conditions of Equations (39) and (40) imply that SW solutions of (37) exist if
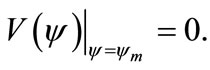 (41)
(41)
The latter can be solved as
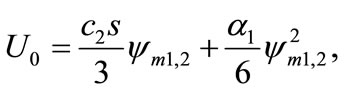 (42)
(42)
 (43)
(43)
where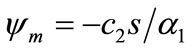 , and
, and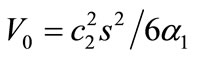 . Now, using Equations (38) and (43) in Equation (37) we have
. Now, using Equations (38) and (43) in Equation (37) we have
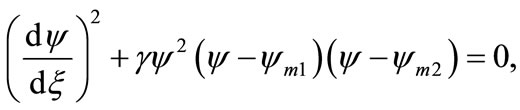 (44)
(44)
where . The SW solution of Equations (37) or (44) is, therefore, directly given by
. The SW solution of Equations (37) or (44) is, therefore, directly given by
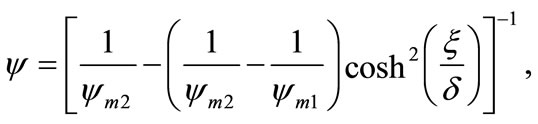 (45)
(45)
where  are given in Equation (43) and SWs width
are given in Equation (43) and SWs width 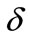 is
is
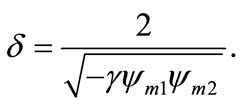 (46)
(46)
Figures 1-4 show the variation of amplitude of positive (negative) GSs with μ for U0 = 0.5 and H = 0.3. These figures clearly indicate that both positive and negative GSs exist around the crical value,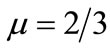 . It has been found that the amplitude (magnitude of the amplitude) of both positive and negative GSs decrease with the increase of μ. Figures 2-5 represent the variation of amplitude of positive (negative) GSs with U0 for μ = 0.66 (μ = 0.67) and H = 0.3. These figures indicate that the amplitude of both positive and negative GSs increase with the increase of U0. We have found that the amplitude of positive and negative GSs does not vary with the quantum diffraction parameter, H but the width of the both positive and negative GSs vary with it. Figures 3-6 imply that the width of both positive and negative GSs decrease with the increase of H and increase with the increase of μ. We have also noticed that in our present system the GSs exist when the quantum effect of electron is neglected.
. It has been found that the amplitude (magnitude of the amplitude) of both positive and negative GSs decrease with the increase of μ. Figures 2-5 represent the variation of amplitude of positive (negative) GSs with U0 for μ = 0.66 (μ = 0.67) and H = 0.3. These figures indicate that the amplitude of both positive and negative GSs increase with the increase of U0. We have found that the amplitude of positive and negative GSs does not vary with the quantum diffraction parameter, H but the width of the both positive and negative GSs vary with it. Figures 3-6 imply that the width of both positive and negative GSs decrease with the increase of H and increase with the increase of μ. We have also noticed that in our present system the GSs exist when the quantum effect of electron is neglected.
5. Discussion
We have investigated QDIA GSs in quantum dusty plasma by deriving Gardner equation. The K-dV solitons are not valid for 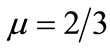 and
and , which vanish
, which vanish
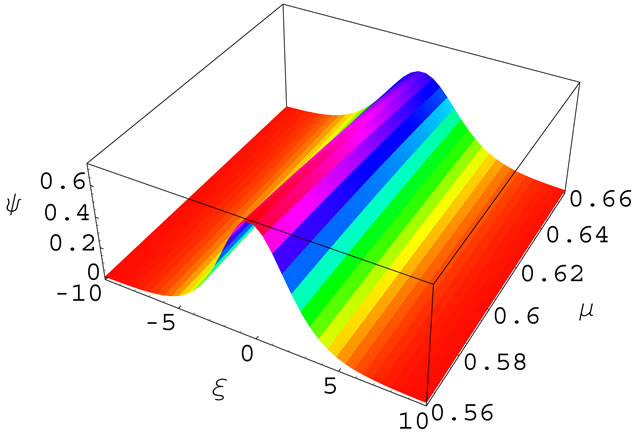
Figure 1. (Color online) Showing the variation of amplitude of the QDIA positive GSs with μ for U0 = 0.5 and H = 0.3.

Figure 2. (Color online) Showing the variation of amplitude of the QDIA positive GSs with U0 for μ = 0.66 and H = 0.3.

Figure 3. (Color online) Showing the variation of width of the QDIA positive GSs with H and μ for U0 = 0.1.

Figure 4. (Color online) Showing the variation of amplitude of the QDIA negative GSs with μ for U0 = 0.5 and H = 0.3.
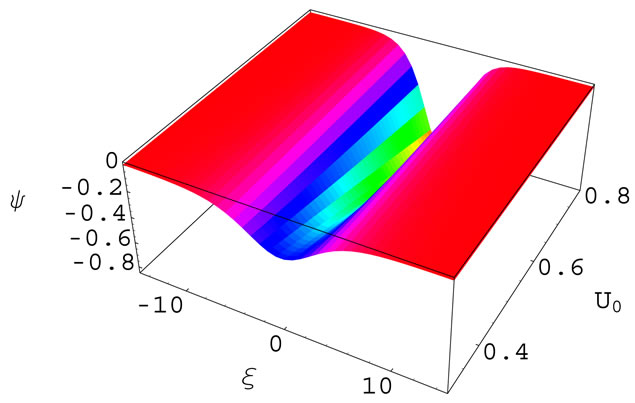
Figure 5. (Color online) Showing the variation of amplitude of the QDIA negative GSs with U0 for μ = 0.67 and H = 0.3.
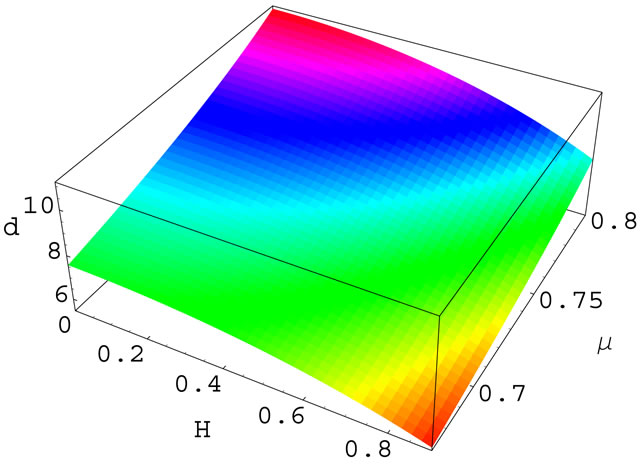
Figure 6. (Color online) Showing the variation of width of the QDIA negative GSs with H and μ for U0 = 0.1.
at the nonlinear coefficients of the K-dV equation. However, the QDIA GSs investigated in our present work are valid for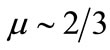 . The results, which have been obtained from this investigation, can be summarized as follows:
. The results, which have been obtained from this investigation, can be summarized as follows:
1) The quantum dusty plasma system under consideration supports finite amplitude GSs, whose basic features (polarity, amplitude, width, etc.) depend on the ion and dust number densities and quantum diffraction (tunneling) parameter, H.
2) GSs are shown to exist for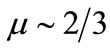 , and are found to be different from K-dV solitons, which do not exist for
, and are found to be different from K-dV solitons, which do not exist for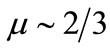 .
.
3) It has been found that at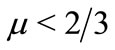 , positive GSs exist, whereas at
, positive GSs exist, whereas at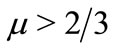 , negative GSs exist.
, negative GSs exist.
4) We have seen that the amplitude of positive and negative GSs decreases with μ, increases with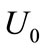 , and does not depend on H.
, and does not depend on H.
5) We have also observed that the width of the GSs increases with μ but decreases with the increase of H.
It should be mentioned here that in our present investigation, we have neglected the quantum effect of ions since ions are heavier than electrons. However, QDIA solitary waves in quantum dusty plasma with or without the effects of obliqueness and external magnetic field are also problems of recent interest for many space and laboratory dusty plasma situations, but beyond the scope of our present investigation. In conclusion, we propose that a new experiment may be designed based on our results to observe such waves in both laboratory and space quantum dusty plasma system.
6. Acknowledgements
The Third World Academy of Science (TWAS) Research Grant for research equipment is gratefully acknowledged.
REFERENCES
- M. M. Hossain, A. A. Mamun and K. S. Ashrafi, Physics of Plasmas, Vol. 18, 2011, Article ID: 103704. http://dx.doi.org/10.1063/1.3646738
- A. A. Mamun and P. K. Shukla, Physics Letters A, Vol. 290, 2001, pp. 173-175. http://dx.doi.org/10.1016/S0375-9601(01)00669-7
- Y. D. Jung, Physics of Plasmas, Vol. 8, 2001, p. 3842. http://dx.doi.org/10.1063/1.1386430
- G. Chabier, F. Dquchin and Y. Potekhin, Journal of Physics: Condensed Matter, Vol. 14, 2002, p. 133.
- M. Opher, L. O. Silvia, D. E. Danger, V. K. Decyk and J. M. Dawson, Physics of Plasmas, Vol. 8, 2001, p. 2454. http://dx.doi.org/10.1063/1.1362533
- G. Manfredi, Fields Institute Communications, Plasmas, Vol. 46, 2005, pp. 263-287.
- A. Markowich, C. Ringhofer and C. Schmeiser, “Semiconductor Equations,” Springer, Vienna, 1990. http://dx.doi.org/10.1007/978-3-7091-6961-2
- D. Kremp, Th. Bornath, M. Bonitz and M. Shlanges, Physical Review E, Vol. 60, 1999, pp. 4725-4732. http://dx.doi.org/10.1103/PhysRevE.60.4725
- G. Manfredi and M. Feix, Physical Review E, Vol. 53, 1996, pp. 6460-6470. http://dx.doi.org/10.1103/PhysRevE.53.6460
- G. Manfredi and F. Haas, Physical Review B, Vol. 64, 2001, Article ID: 075316. http://dx.doi.org/10.1103/PhysRevB.64.075316
- D. Anderson, B. Hall, M. Lisak and M. Marklund, Physical Review E, Vol. 65, 2002, Article ID: 046417. http://dx.doi.org/10.1103/PhysRevE.65.046417
- P. K. Shukla and S. Ali, Physics of Plasmas, Vol. 13, 2006, Article ID: 112111. http://dx.doi.org/10.1063/1.2390688
- M. Marklund, Physics of Plasmas, Vol. 12, 2005, Article ID: 082110. http://dx.doi.org/10.1063/1.2012147
- L. G. Garcia, F. Haas, L. P. L. de Oliveira and J. Goedert, Physics of Plasmas, Vol. 12, 2005, Article ID: 012302. http://dx.doi.org/10.1063/1.1819935
- S. Mola, G. Manfredi and M. R. Feix, Journal of Physics of Plasmas, Vol. 50, 1993, pp. 145-162. http://dx.doi.org/10.1017/S0022377800026969
- F. Haas, L. G. Garcia, J. Goedert and G. Manfredi, Physics of Plasmas, Vol. 10, 2003, p. 3858. http://dx.doi.org/10.1063/1.1609446
- N. Suh, M. R. Feix and P. Bertrand, Journal of Computational Physics, Vol. 94, 1991, pp. 403-418. http://dx.doi.org/10.1016/0021-9991(91)90227-C
- F. Haas, Physics of Plasmas, Vol. 12, 1993, Article ID: 062117. http://dx.doi.org/10.1063/1.1939947
- P. K. Shukla and S. Ali, Physics of Plasmas, Vol. 12, 2005, Article ID: 114502. http://dx.doi.org/10.1063/1.2136376
- P. K. Shukla, Physics Letters A, Vol. 352, 2006, pp. 242- 243. http://dx.doi.org/10.1016/j.physleta.2005.11.065
- L. Stenflo, P. K. Shukla and M. Marklund, Europhysics Letters, Vol. 74, 2006, p. 844. http://dx.doi.org/10.1209/epl/i2006-10032-x
- P. K. Shukla and V. P. Silin, Physica Scripta, Vol. 45, 2002, p. 508. http://dx.doi.org/10.1088/0031-8949/45/5/015
- A. Barkan, N. D’Angelo and R. L. Merlino, Planetary and Space Science, Vol. 44, 1996, pp. 239-242. http://dx.doi.org/10.1016/0032-0633(95)00109-3
- R. L. Merlino, A. Barkan, C. Thompson and N. D’Angelo, Physics of Plasmas, Vol. 5, 1998, p. 1607. http://dx.doi.org/10.1063/1.872828
- K. E. Lonngren, Physics of Plasmas, Vol. 25, 1983, p. 943. http://dx.doi.org/10.1088/0032-1028/25/9/001
- W. Masood, A. Mushtaq and R. Khan, Physics of Plasmas, Vol. 14, 2007, Article ID: 123702. http://dx.doi.org/10.1063/1.2803775
- S. A. Khan and A. Mushtaq, Physics of Plasmas, Vol. 14, 2007, Article ID: 083703. http://dx.doi.org/10.1063/1.2756752
- W. Masood, M. Siddiq, S. Nargis and A. M. Mirza, Physics of Plasmas, Vol. 16, 2009, Article ID: 013705. http://dx.doi.org/10.1063/1.3068171
- C. K. Goertz, Reviews of Geophysics, Vol. 27, 1989, pp. 271-292. http://dx.doi.org/10.1029/RG027i002p00271
- G. E. Morfill and A. V. Ivlev, Reviews of Modern Physics, Vol. 81, 2009, pp. 1353-1404. http://dx.doi.org/10.1103/RevModPhys.81.1353
- R. L. Merlino and J. Goree, Physics Today, Vol. 57, 2004, p. 32. http://dx.doi.org/10.1063/1.1784300
- P. K. Shukla and A. A. Mamun, Introduction to Dusty Plasma Physics, IoP Publishing Ltd., Bristol, 2002, 8-27. http://dx.doi.org/10.1887/075030653X
- M. Asaduzzaman, “Electro-Acoustic Waves in Presence of Polarization Force,” LAP LAMBERT Academic Publishing, Saarbrücken, 2012.
- M. Asaduzzaman and A. A. Mamun, Physical Review E, Vol. 86, 2012, Article ID: 016409. http://dx.doi.org/10.1103/PhysRevE.86.016409
- S. A. Khan, S. Mahmood and A. M. Mirza, Physics Letters A, Vol. 372, 2009, pp. 148-153. http://dx.doi.org/10.1016/j.physleta.2007.10.062
- M. Asaduzzaman and A. A. Mamun, Astrophysics and Space Science, Vol. 341, 2012, pp. 535-542. http://dx.doi.org/10.1007/s10509-012-1102-x
- N. C. Lee, Physics of Plasmas, Vol. 16, 2009, Article ID: 042316. http://dx.doi.org/10.1063/1.3121242
- M. M. Hossain and A. A. Mamun, Journal of Physics A: Mathematical and Theoretical, Vol. 45, 2012, Article ID: 125501. http://dx.doi.org/10.1088/1751-8113/45/12/125501
- M. Hasan, M. M. Hossain and A. A. Mamun, Astrophysics and Space Science, Vol. 345, 2013, pp. 113-118. http://dx.doi.org/10.1007/s10509-013-1384-7
- A. Mushtaq and S. A. Khan, Physics of Plasmas, Vol. 14, 2007, Article ID: 052307. http://dx.doi.org/10.1063/1.2727474
- L. D. Landau and E. M. Lifshitz, “Statistical Physics, Pt. 1,” Butterworth-Heinemann, Oxford, 1980.

