Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33083,7 pages DOI:10.4236/jmp.2013.46108
Out-of-Equilibrium Dissipative ac—Susceptibility in Quantum Ising Spin Glass
1Dipartimento di Fisica “E.R.Caianiello”, Università di Salerno, Fisciano-Salerno, Italy 2CNISM-Consorzio Nazionale Interuniversitario per le Scienze Fisiche della Materia, Unità di Salerno, Salerno, Italy
Email: busiello@sa.infn.it
Copyright © 2013 Gaetano Busiello. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 13, 2013; revised March 22, 2013; accepted April 23, 2013
Keywords: Spin Glasses; Non-Equilibrium Dynamics; Droplet Theory
ABSTRACT
The imaginary part of the non-equilibrium magnetic susceptibility of Ising spin glass in a transverse field under timedependent longitudinal external magnetic field has been calculated at very low temperature on the basis of quantum droplet model and quantum linear response theory. Quantum and aging effects on the low temperature dynamics of the model are discussed. A comparison with recent theoretical and experimental data in spin glass is made.
1. Introduction
Over the last two decades there is a great deal of research on the experimental and theoretical description of disordered magnetic materials. The understanding of the interplay between disorder, quantum and thermal fluctuations remains among the most relevant problem of condensed matter physics. In strongly disordered systems the dynamics becomes very slow which is characteristic of glassy state and aging scenario [1-8]. Aging phenomena and non-equilibrium slow dynamics have been investigated during last years in many materials with glassy properties such as spin glasses [1-8], polymer glasses [9,10], gels [11] and other areas like neural networks, information processing, optimization problems [12]. Despite a great progress towards the understanding of nonequilibrium dynamics, some problems remain open. One of them is an investigation of a very low temperature nonequilibrium dynamics in quantum spin glasses, namely the nature of quantum channels of relaxation, the behavior of quantum glassy system subjected to periodic driving force, aging at very low temperatures. The natural basis for the interpretation of aging is based on coarsening ideas of a slow domain growth of a spin-glass type ordered phase [8,13,14]. A large attention in the last decade was paid to the spin glasses representing a model systems for study of non-equilibrium dynamics providing a measure of processes causing the aging: the magnetic susceptibility [15-22].
In classical spin glasses in the ac susceptibility measurements the magnetic response of the system to a small oscillating magnetic field applied after quenching exhibits aging effects. This response depends on its thermal history and the time interval the system has been kept at a constant temperature in the glass phase [1-8,15-17].
It is assumed that isothermal aging of a d-dimensional spin glass is a coarsening process of domain walls, and the temporal ac susceptibility (real part 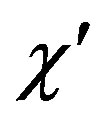 andimaginary part
andimaginary part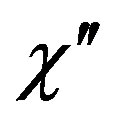 ) at a given frequency of ac magnetic field ω at time t after the quenching scales as [23-25]
) at a given frequency of ac magnetic field ω at time t after the quenching scales as [23-25]
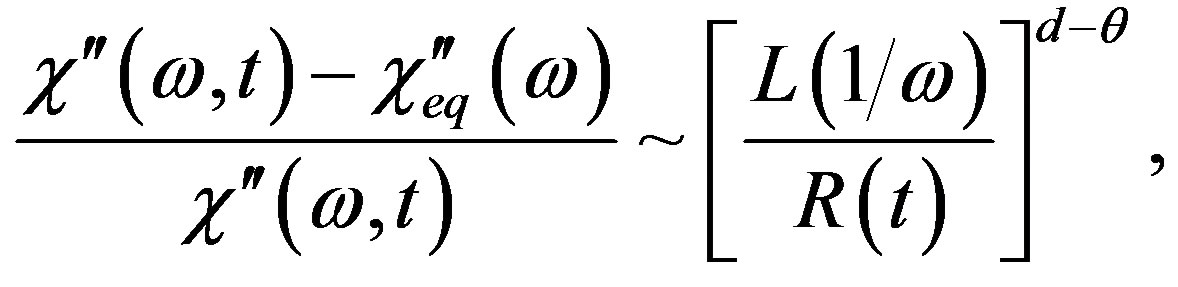 (1)
(1)
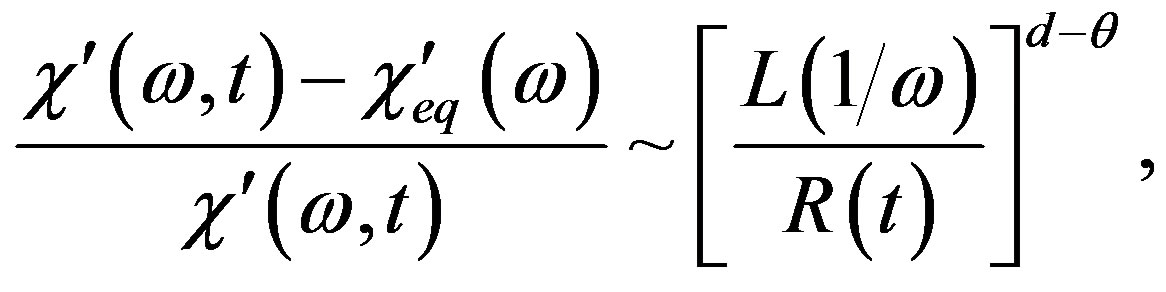 (2)
(2)
for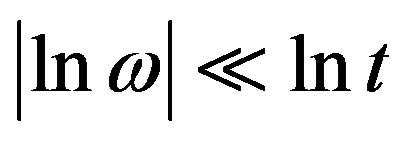 , if
, if 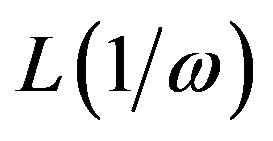 is proportional to
is proportional to 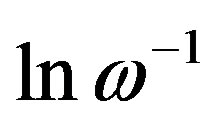 and
and 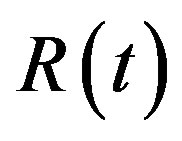 is proportional to
is proportional to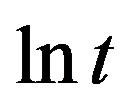 ;
;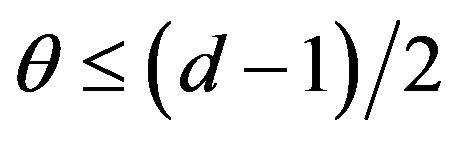 . Here
. Here 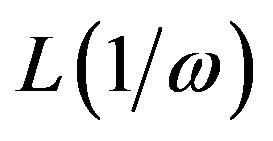 is size of the droplet being polarized by oscillating field and
is size of the droplet being polarized by oscillating field and 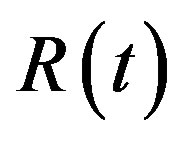 is the typical domain size,
is the typical domain size, 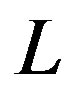 and
and 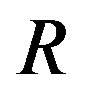 may scale according logarithmic growth law or algebraic one [23-25].
may scale according logarithmic growth law or algebraic one [23-25]. 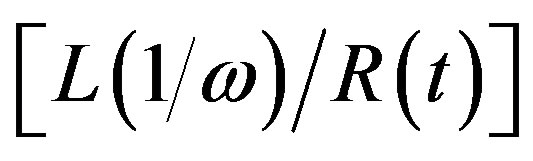 is proportional to
is proportional to 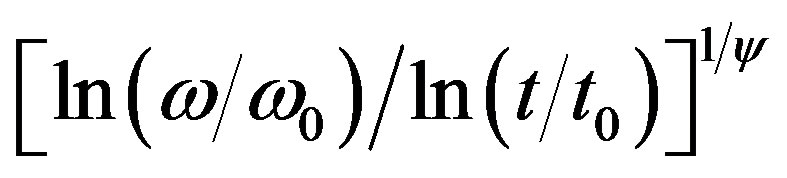 if droplet theory is used,
if droplet theory is used, 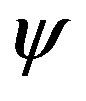
is some exponent,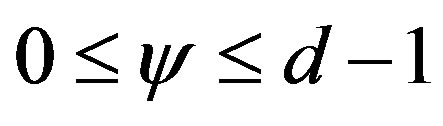 , and
, and  is a certainmicroscopic characteristic time [26]. The logarithmic growth law (like the algebraic one) is supported by recent experiments [23-25]. The expressions (1) and (2) are found when relaxation is governed by thermal activation over a free energy barrier
is a certainmicroscopic characteristic time [26]. The logarithmic growth law (like the algebraic one) is supported by recent experiments [23-25]. The expressions (1) and (2) are found when relaxation is governed by thermal activation over a free energy barrier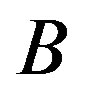 . It is supposed that barriers for annihilation and creation of the droplet excitations scale as
. It is supposed that barriers for annihilation and creation of the droplet excitations scale as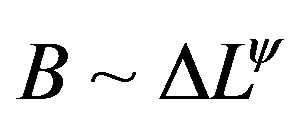 , where
, where  is a barrier energy at temperature
is a barrier energy at temperature  (
(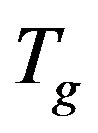 is the spin glass transition temperature). The barriers have a broad distribution of energies. A droplet with barrier
is the spin glass transition temperature). The barriers have a broad distribution of energies. A droplet with barrier 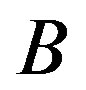 lasts for a time
lasts for a time 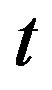 of order of
of order of  where
where 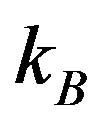 is Boltzmann’s constant; here
is Boltzmann’s constant; here  is a rate of classic activation over energy barrier
is a rate of classic activation over energy barrier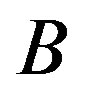 . After a time
. After a time 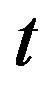 after quenching the domain size in the system grows as
after quenching the domain size in the system grows as
 .
.
In the ac susceptibility measurements, the ac field excites droplets of length scales  up to
up to
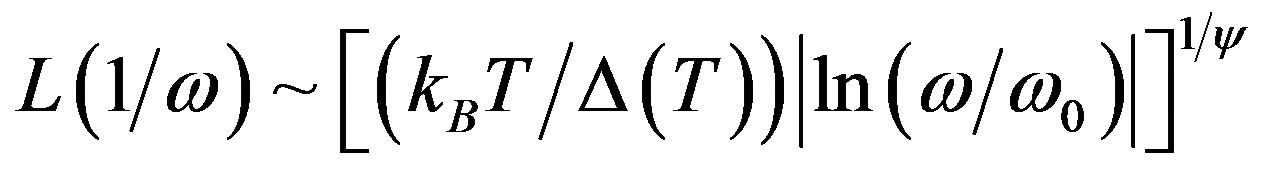 .
.
Because in aging experiments the time 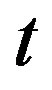 spent after quench is
spent after quench is 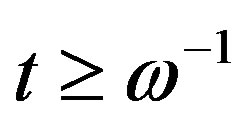 [23-26] one has
[23-26] one has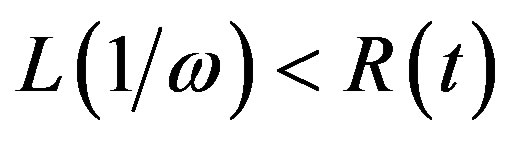 . These droplets have walls which partly coincide with walls of the domain of size
. These droplets have walls which partly coincide with walls of the domain of size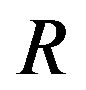 .
.
In this paper we investigate the real time non-equilibrium dynamics in d-dimensional Ising spin glass in a transverse field in terms of droplet model at very low temperatures [26]. We calculate the dissipative component of the ac susceptibility as a function of the time elapsedsince a thermal quench and frequency of driven field.
2. Model Hamiltonian
The droplet model describing the low-dimensional shortrange Ising spin glass is based on renormalization group arguments [26,28]. In dimensions above the lower critical dimension 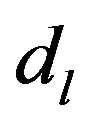 (usually in spin glass
(usually in spin glass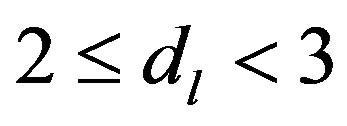 ) the droplet model finds a low temperature spin-glass phase in zero magnetic field. This phase differs essentially from the spin-glass phase in the mean-field approximation of the Sherrington-Kirkpatrick infinite-range spin-glass model [13]. In the droplet model there are only two pure thermodynamical states related to each other by a global spin flip. In magnetic field there is no phase transition. A droplet is an excited cluster in an ordered state where all the spins are inverted. The natural scaling ansatz for droplet free energy
) the droplet model finds a low temperature spin-glass phase in zero magnetic field. This phase differs essentially from the spin-glass phase in the mean-field approximation of the Sherrington-Kirkpatrick infinite-range spin-glass model [13]. In the droplet model there are only two pure thermodynamical states related to each other by a global spin flip. In magnetic field there is no phase transition. A droplet is an excited cluster in an ordered state where all the spins are inverted. The natural scaling ansatz for droplet free energy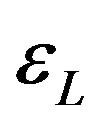 , which are considered to be independent random variables, is
, which are considered to be independent random variables, is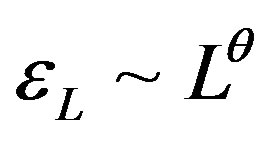 ,
,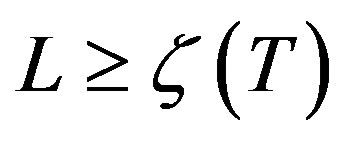 ;
;  is the correlation length,
is the correlation length,  is the length scale of droplet and
is the length scale of droplet and  is the zero temperature thermal exponent. The droplet excitations have a broad distribution of their free energies at scale
is the zero temperature thermal exponent. The droplet excitations have a broad distribution of their free energies at scale 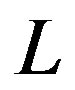 for large
for large 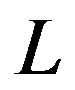 in a scaling form [4]
in a scaling form [4]
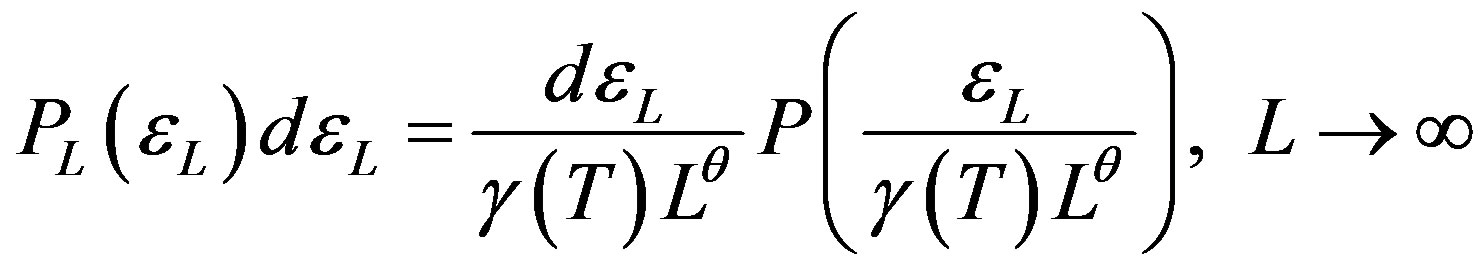 (3)
(3)
It is assumed that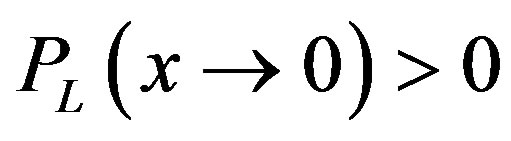 ,
, 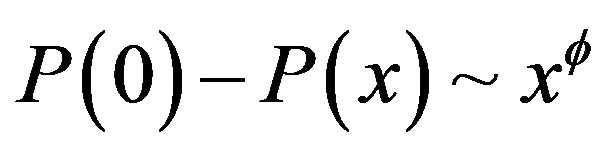 ,
,
 ,
,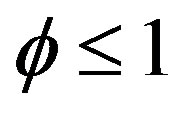 .
. is a generalized temperature dependent stiffness modulus which is of order of characteristic exchange
is a generalized temperature dependent stiffness modulus which is of order of characteristic exchange 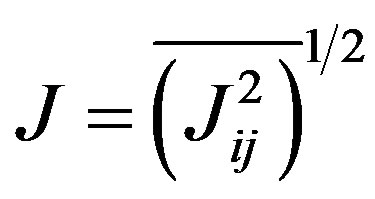 at
at 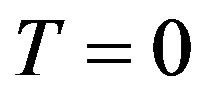 and vanishes for
and vanishes for
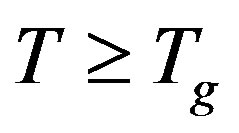 . One droplet consists of order
. One droplet consists of order 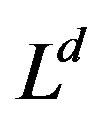 spins. Below
spins. Below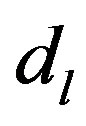 ,
,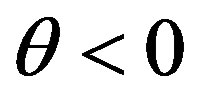 ; above
; above 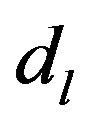 one has
one has . The droplet model of classical Ising spin glass was considered by D.S. Fisher and D.A. Huse [26,27].
. The droplet model of classical Ising spin glass was considered by D.S. Fisher and D.A. Huse [26,27].
In this paper we use a phenomenological quantum droplet model of spin glass theory [26-29] (which does not use the mean-field approximation) in order to describe the non equilibrium behavior of the magnetic dynamical susceptibility at very low (but finite) temperatures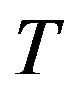 .
.
We consider the following model hamiltonian of ddimensional Ising spin glass in a transverse field,
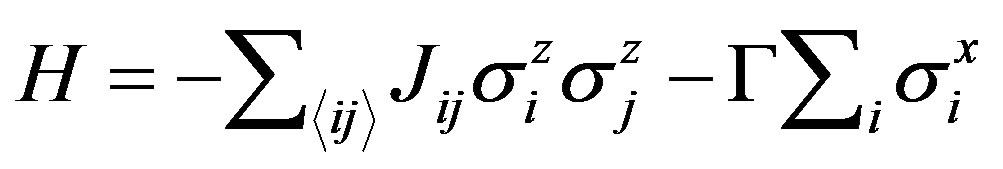 (4)
(4)
where  and
and 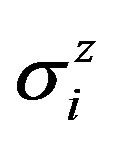 are the Pauli matrices,
are the Pauli matrices, 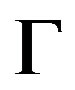 is the strength of the transverse field and the nearest neighbor interactions
is the strength of the transverse field and the nearest neighbor interactions  are independent random variables of mean zero and the sum in Equation (4) is performed over nearest neighbors.
are independent random variables of mean zero and the sum in Equation (4) is performed over nearest neighbors.
The quantum spin glass transition in a dilute dipole coupled magnet 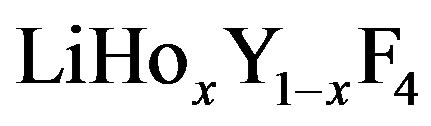 is described by this model hamiltonian [4,13,20]. It is supposed that this model may also represent, for example, the physics of deuteron glass such as
is described by this model hamiltonian [4,13,20]. It is supposed that this model may also represent, for example, the physics of deuteron glass such as  and mixed betaine phosphate-phosphite [28]. The transverse field in [28] is interpreted as the frequency of the proton tunneling.
and mixed betaine phosphate-phosphite [28]. The transverse field in [28] is interpreted as the frequency of the proton tunneling.
In ref. [26,27], M. J. Thill and D. A. Huse have shown that for enough low T the quantum hamiltonian Equation (4) can be represented as independent quantum two-level systems (low energy droplets) with the hamiltonian,
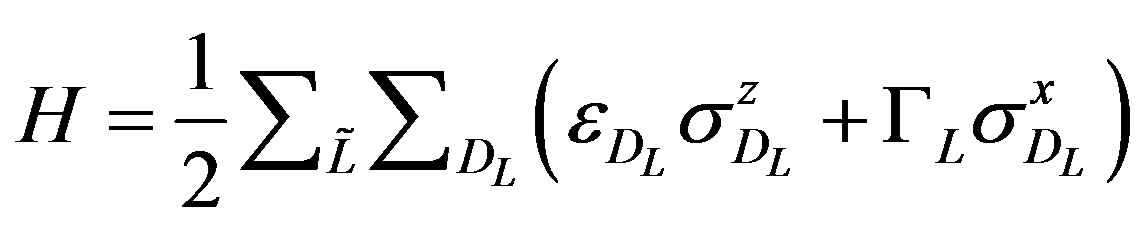 (5)
(5)
where 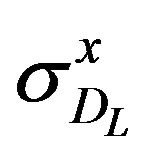 and
and 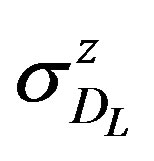 are the Pauli matrices representing the two states of the droplet
are the Pauli matrices representing the two states of the droplet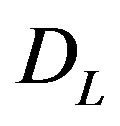 ; the sum is over all droplets
; the sum is over all droplets 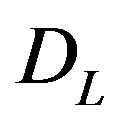 at length scale
at length scale 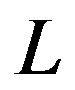 and over all length scales
and over all length scales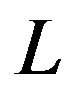 , and
, and
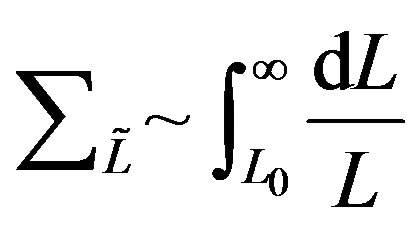
where 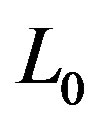 is a short-distance cutoff;
is a short-distance cutoff; 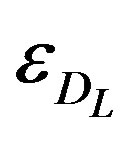 is the droplet energy which is independent random variable with scaling ansatz
is the droplet energy which is independent random variable with scaling ansatz 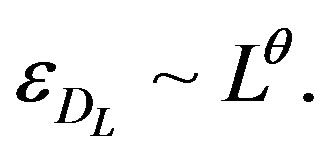 The droplet length scale
The droplet length scale 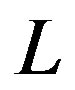 is more or of order of the correlation length.The value
is more or of order of the correlation length.The value 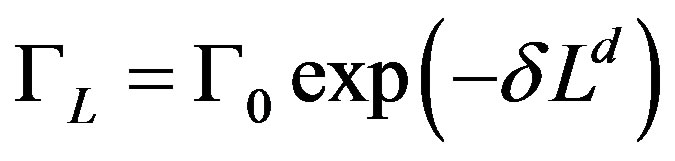 which regulates the strength of quantum fluctuations (
which regulates the strength of quantum fluctuations (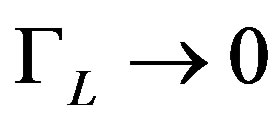 corresponds to the classical limit) is the tunneling rate for a droplet of linear size
corresponds to the classical limit) is the tunneling rate for a droplet of linear size 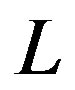 and
and 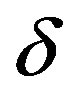 is a coefficient which is approximately the same for all droplets.
is a coefficient which is approximately the same for all droplets. 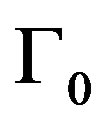 is a microscopic tunneling rate and, finally, we assume
is a microscopic tunneling rate and, finally, we assume 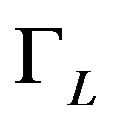 is the same for all droplets of scale
is the same for all droplets of scale 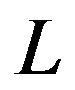 [26,27].
[26,27].
In the quantum droplet model of Thill and Huse [26,27] the relative reduction of the Edwards-Anderson order parameter 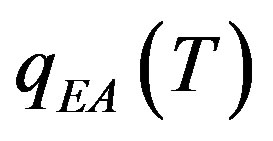 from its zero temperature value
from its zero temperature value 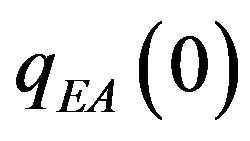 for
for 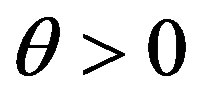 is given by,
is given by,
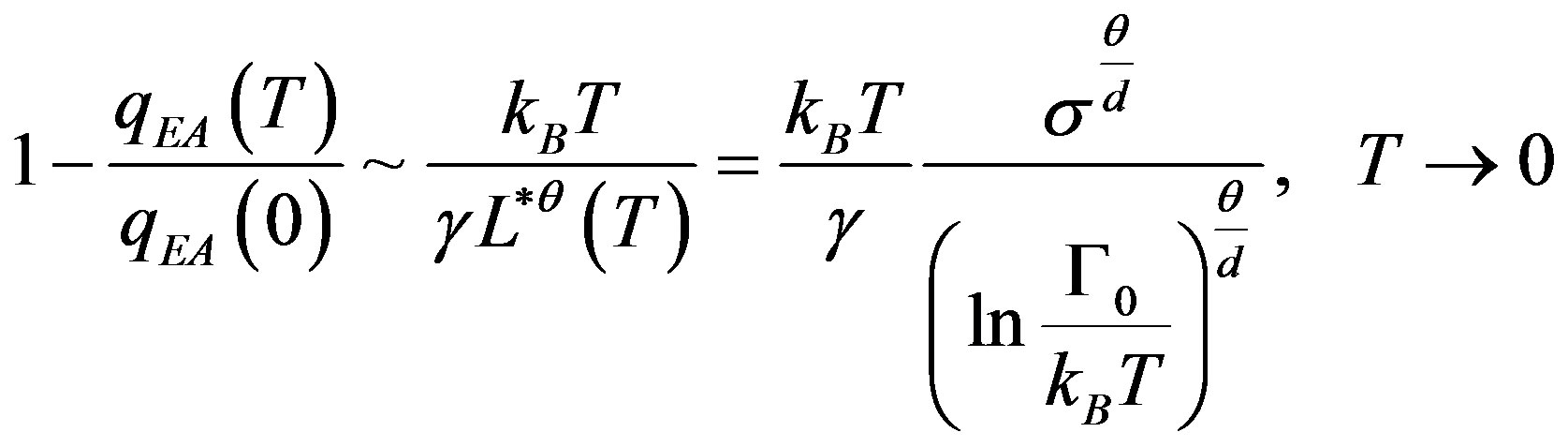
Here 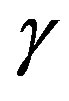 is the stiffness modulus, and
is the stiffness modulus, and
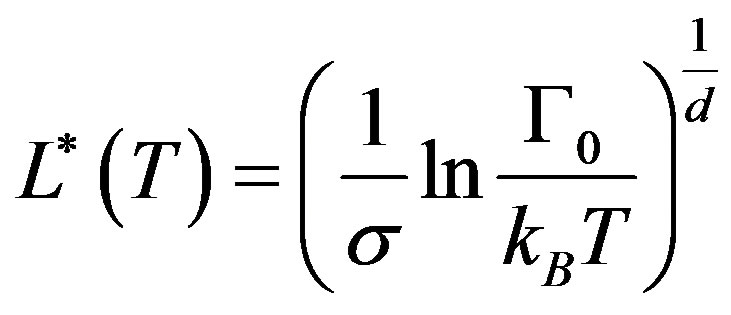
is the classical-to-quantum crossover length scale defined by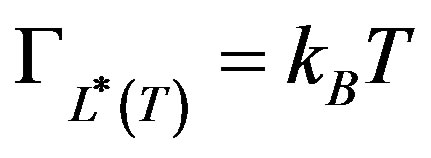 . For droplets with
. For droplets with  and
and
 (quantum regime [26-28]), the excitation energy
(quantum regime [26-28]), the excitation energy 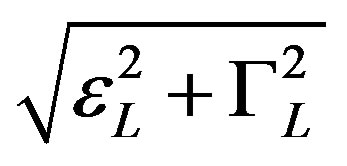 is always greater than
is always greater than 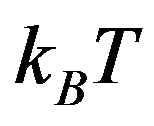 and thermal fluctuations are irrelevant. These droplets behave quantum mechanically. The larger droplets
and thermal fluctuations are irrelevant. These droplets behave quantum mechanically. The larger droplets 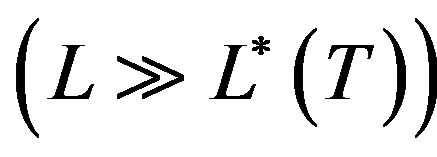 have
have 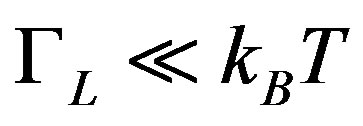 and behave classically. In quantum regime the length growth is due to quantum fluctuations connected with droplet are quantum-mechanically active for
and behave classically. In quantum regime the length growth is due to quantum fluctuations connected with droplet are quantum-mechanically active for  is proportional to
is proportional to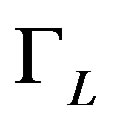 .
.
3. Dynamic Nonequilibrium Magnetic Susceptibility
We consider the time dependent Hamiltonian  of the quantum system in the form [34]
of the quantum system in the form [34]
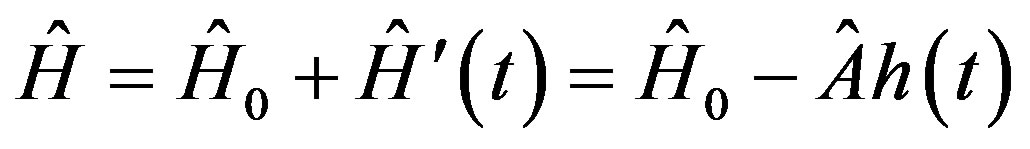 (6)
(6)
where 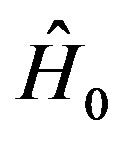 is the Hamiltonian of the unperturbed system and describes the equilibrium system.We suppose that the external perturbation
is the Hamiltonian of the unperturbed system and describes the equilibrium system.We suppose that the external perturbation 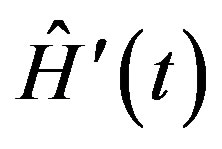 is in some sense small.
is in some sense small.  is a linear operator which connects external timedependent force
is a linear operator which connects external timedependent force  with the system. We shall use the quantum-mechanical equations for the system dynamical response
with the system. We shall use the quantum-mechanical equations for the system dynamical response  to the force
to the force 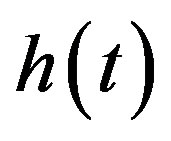 in terms of the time-evolution operator
in terms of the time-evolution operator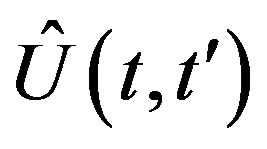 ;
; is an Heisenberg operator,
is an Heisenberg operator, 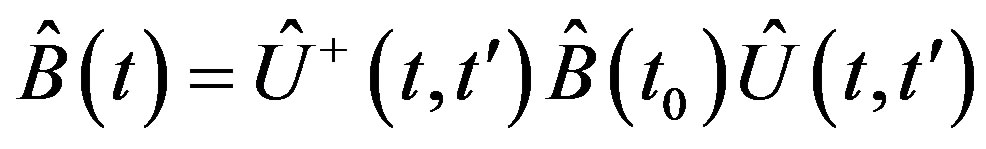 ,
,
 is the average value of
is the average value of 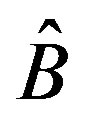 in equilibrium; the sign + means conjugate value. It is necessary to approximate
in equilibrium; the sign + means conjugate value. It is necessary to approximate  using the well-known perturbation expansion through first order in
using the well-known perturbation expansion through first order in . We have
. We have
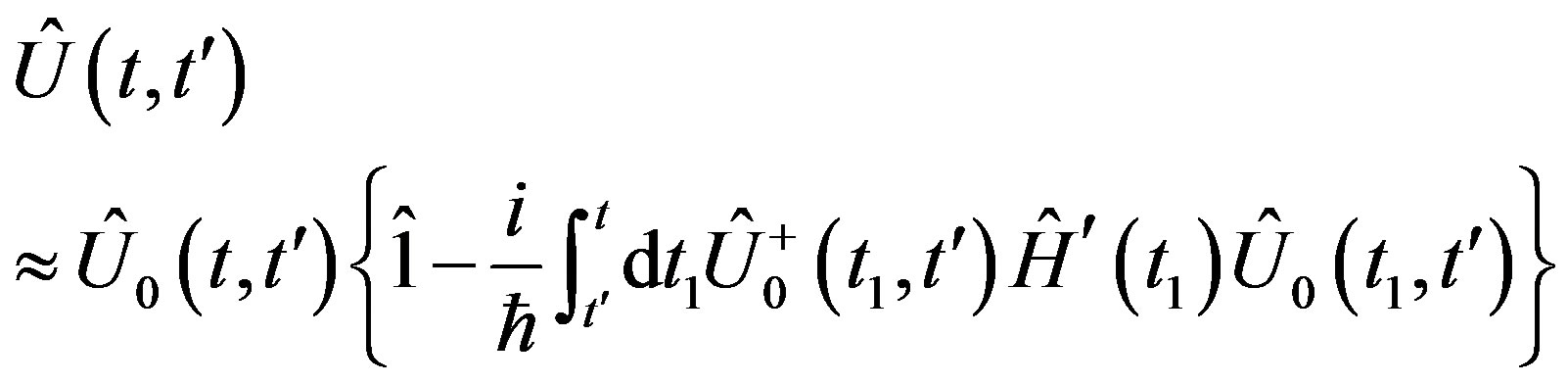 (7)
(7)
where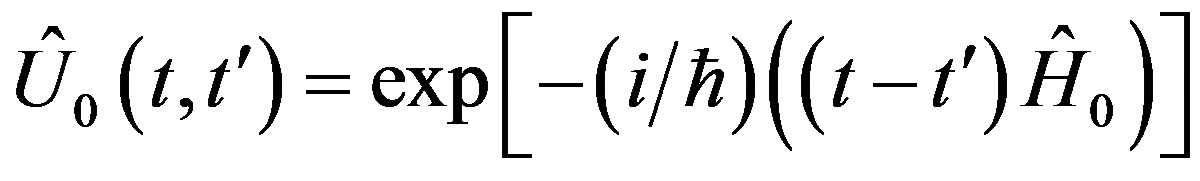 .
.
We consider the functional of the dynamic response of the form [34]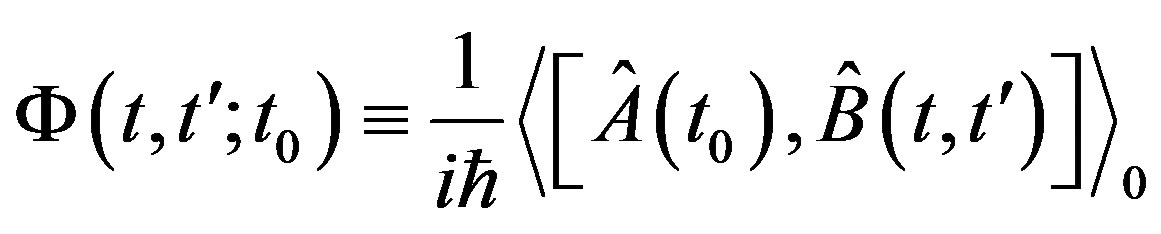 , where
, where
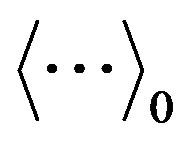 means thermal average with a density matrix
means thermal average with a density matrix
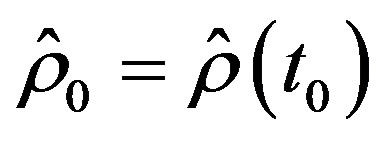 ,
,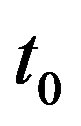 is the time moment when the perturbating field is turned on,
is the time moment when the perturbating field is turned on,
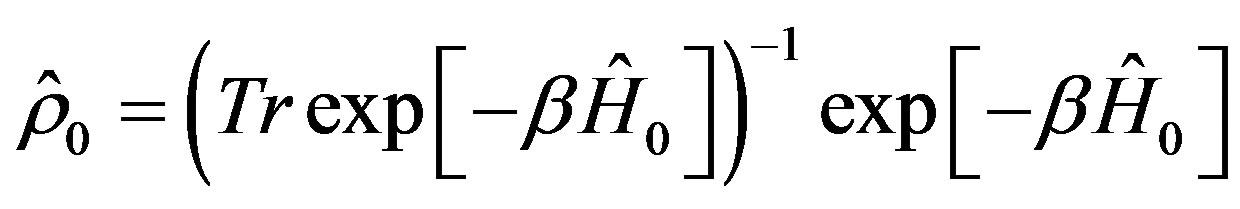 .
.
Now we apply the aforementioned expressions for dynamic response to a magnetic droplet system. The response 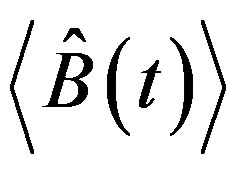 is then the induced magnetization
is then the induced magnetization 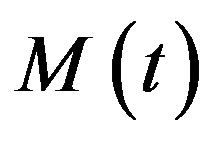
of the system. 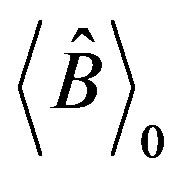 is the equilibrium magnetization
is the equilibrium magnetization
 . Let a small magnetic oscillating field
. Let a small magnetic oscillating field 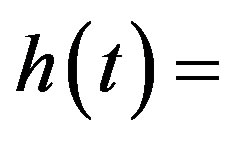
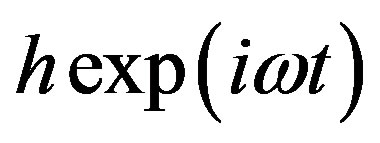 be applied in z-direction. Here
be applied in z-direction. Here 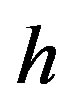 and
and  are the amplitude and frequency of the ac field.
are the amplitude and frequency of the ac field.
When one measures the ac susceptibility in spin glasses in the external magnetic oscillating field it is observed an aging effect: magnetic response of the system to the weak external field depends on the thermal history of the sample, on the time during which the system was kept in a spin glass phase. The sample is quenched in zero magnetic field from temperature 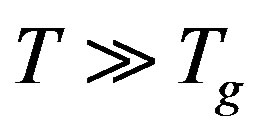 to the temperature
to the temperature 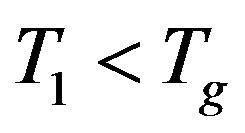 which is reached at time
which is reached at time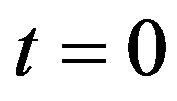 . At this moment a very small external magnetic oscillating field
. At this moment a very small external magnetic oscillating field 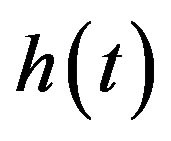 is applied to measure the ac susceptibility of the sample. The evolution continues in isothermal conditions,
is applied to measure the ac susceptibility of the sample. The evolution continues in isothermal conditions, 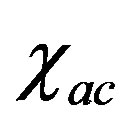 is measured as a function of the time
is measured as a function of the time 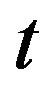 elapsed since the sample reached the temperature
elapsed since the sample reached the temperature  at fixed frequency
at fixed frequency .
.
The system is probed at the time 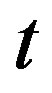 after quench end (“the age”). Using the linear response theory the magnetization of magnetic system is [35]
after quench end (“the age”). Using the linear response theory the magnetization of magnetic system is [35]
 (8)
(8)
where 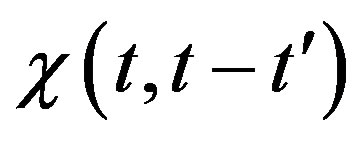 is the magnetic dynamic susceptibility and defines the magnetic response at moment
is the magnetic dynamic susceptibility and defines the magnetic response at moment 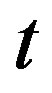 to a unit pulse of magnetic field at moment
to a unit pulse of magnetic field at moment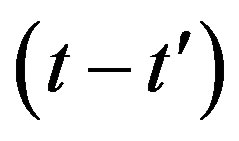 . The nonequilibrium processes are investigated by means of low-frequency susceptibility measurements. The frequency dependent ac susceptibility is measured by means of applied ac magnetic field
. The nonequilibrium processes are investigated by means of low-frequency susceptibility measurements. The frequency dependent ac susceptibility is measured by means of applied ac magnetic field 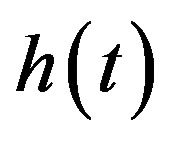 at time
at time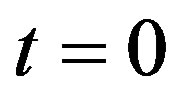 . Then one can find
. Then one can find 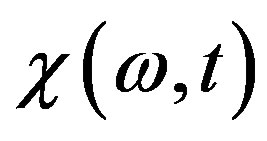 by the Fourier-transform of the magnetization over the time interval
by the Fourier-transform of the magnetization over the time interval  centered on
centered on 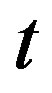 [15,35],
[15,35],
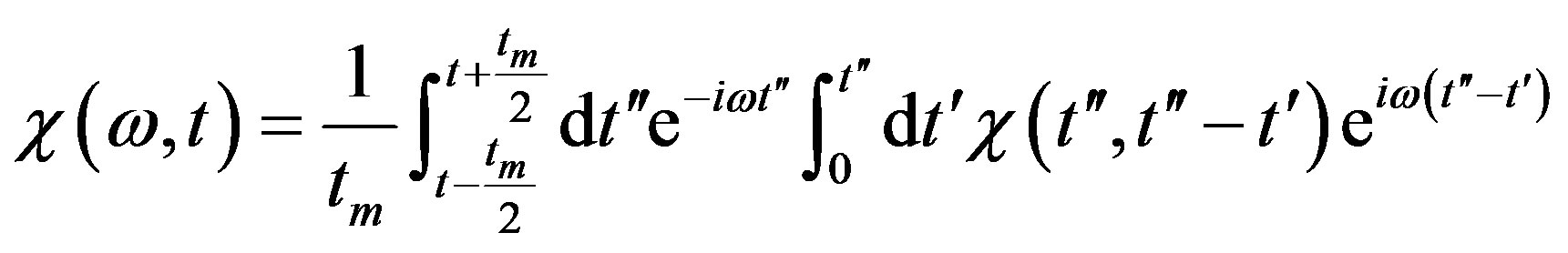 (9)
(9)
If magnetic response function slightly changes over the time segment 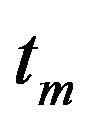 then the susceptibility
then the susceptibility 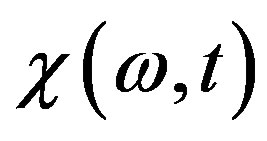 will be equal to [15,35]
will be equal to [15,35]
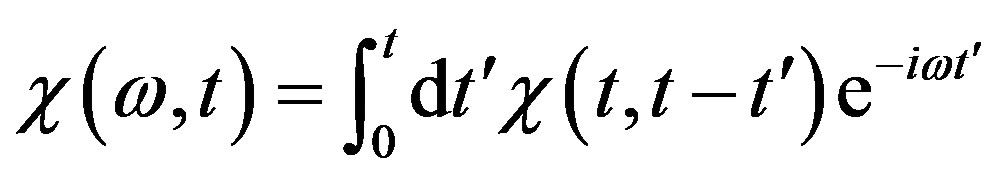 (10)
(10)
We consider the behavior of the magnetic droplet system described by the Hamiltonian  and under ac field
and under ac field 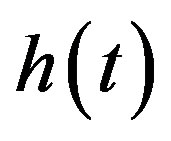 in quantum regime
in quantum regime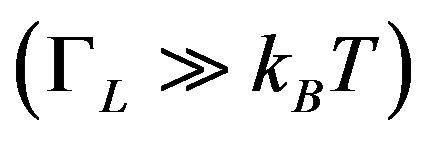 . In our calculations, we suppose that
. In our calculations, we suppose that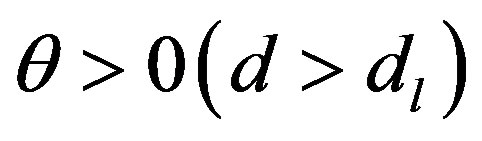 . There is a complicated crossover between classic and quantum behaviors of the droplets which depends on temperature, ac field frequency and length scale
. There is a complicated crossover between classic and quantum behaviors of the droplets which depends on temperature, ac field frequency and length scale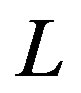 . According to [26,27] the dynamical crossover length is determined from the condition
. According to [26,27] the dynamical crossover length is determined from the condition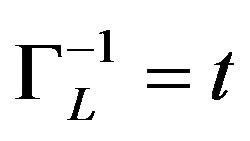 , i.e.
, i.e. . The system behaves presumably classically or quantum mechanically when the dominant length scale
. The system behaves presumably classically or quantum mechanically when the dominant length scale  is above or below
is above or below 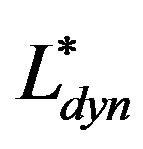 for fixed frequency
for fixed frequency .
.
Following to aforementioned quantum droplet theory with model Hamiltonian (4) and domain growth ideas, we calculate the magnetic dynamic susceptibility using the dynamical response functional which includes first and second order linear response functions. The contribution of a single droplet to the ac susceptibility up to some factor 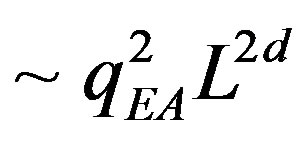 is,
is,
 (11)
(11)
where 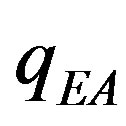 is the Edwards-Anderson order parameter,
is the Edwards-Anderson order parameter,
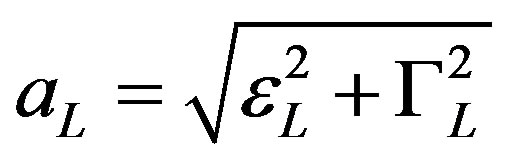 ,
, 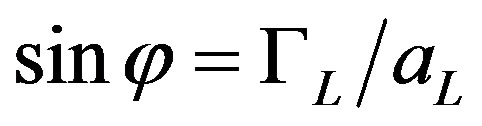 ,
, 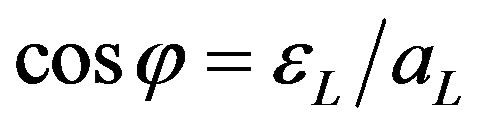 ,
,
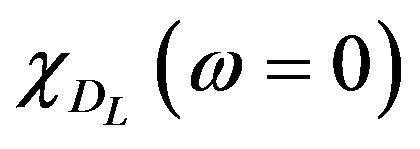 is the static susceptibility of the droplet
is the static susceptibility of the droplet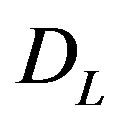 . The expression (11) is obtained for low frequencies under the condition
. The expression (11) is obtained for low frequencies under the condition (and
(and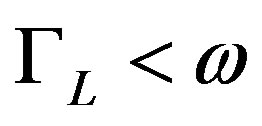 ), because this condition is used to observe non-stationary dynamics in susceptibility measurements [5]. Now we have to average the susceptibility (11) over droplet energies
), because this condition is used to observe non-stationary dynamics in susceptibility measurements [5]. Now we have to average the susceptibility (11) over droplet energies 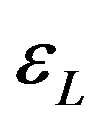 and over droplet length scales
and over droplet length scales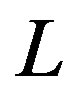 . We use the droplet energy distribution
. We use the droplet energy distribution 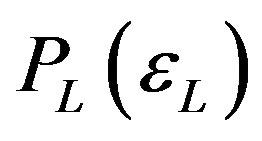 given by Equation (3). Here we assume
given by Equation (3). Here we assume . While integrating over
. While integrating over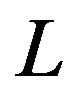 , we note that the susceptibility is dominated by droplets of length scale
, we note that the susceptibility is dominated by droplets of length scale
 ;
; 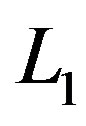 is the natural length scale of the problem when
is the natural length scale of the problem when 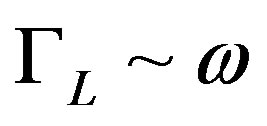 and it is the low limit ofthe integration over
and it is the low limit ofthe integration over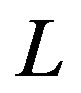 . The upper limit is
. The upper limit is
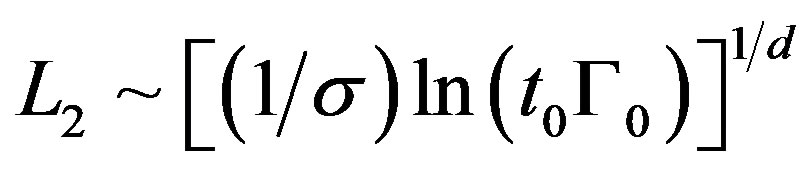 . After integration over droplet energies and length scales we obtain the following expression for imaginary part of susceptibility of the droplet system:
. After integration over droplet energies and length scales we obtain the following expression for imaginary part of susceptibility of the droplet system:
 (12)
(12)
where 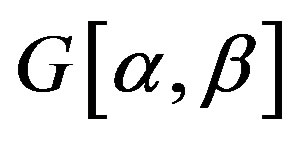 is the incomplete gamma-function,
is the incomplete gamma-function, 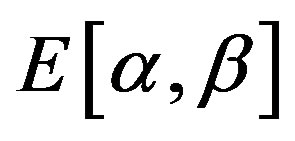 is the exponential integral function,
is the exponential integral function,
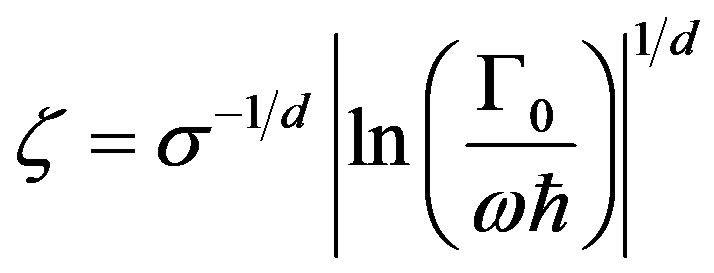 ,
,  ,
, 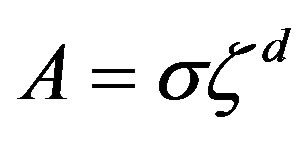 ,
, 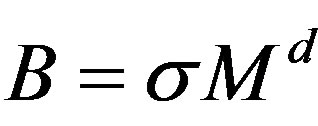 ,
,  ,
, 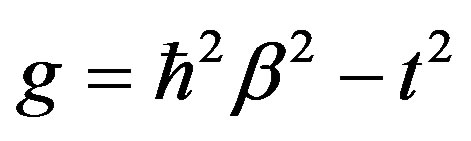 ,
, 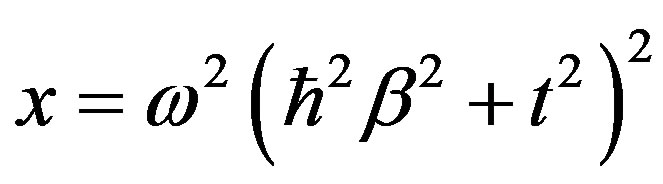 ,
,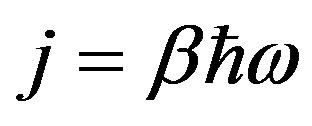 .
.
During the calculations we have used the following approximations: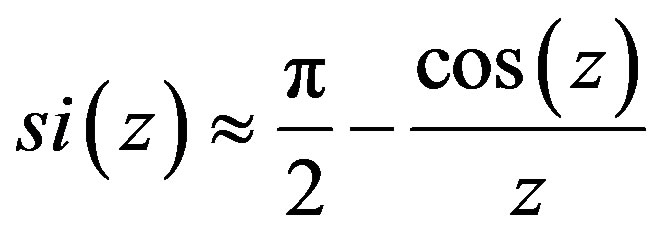 ,
,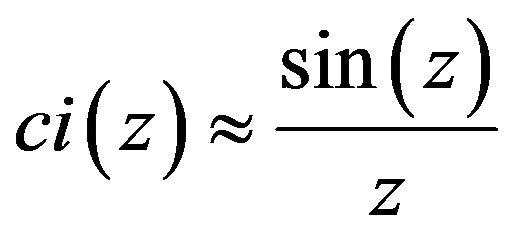 .
.
The Equation (12) is the main result of this paper.
As we see, the susceptibility 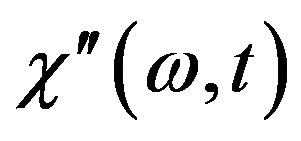 depends on many parameters of the droplet system and the external ac magnetic field: on the form of droplet energies distribution
depends on many parameters of the droplet system and the external ac magnetic field: on the form of droplet energies distribution , on the droplet microscopic tunneling rate
, on the droplet microscopic tunneling rate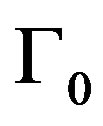 , on the temperature, on the system “age”
, on the temperature, on the system “age”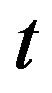 , on the ac field frequency and amplitude. Furthermore, we note that the expression (12) consists of terms which are time independent which describe oscillations with frequency, and terms which depend on
, on the ac field frequency and amplitude. Furthermore, we note that the expression (12) consists of terms which are time independent which describe oscillations with frequency, and terms which depend on 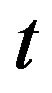 and define nonstationary non-equilibrium dynamics of the droplet system. Thus the imaginary part of susceptibility can be represented as a sum of stationary part
and define nonstationary non-equilibrium dynamics of the droplet system. Thus the imaginary part of susceptibility can be represented as a sum of stationary part 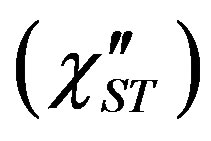 and non-stationary part
and non-stationary part :
:
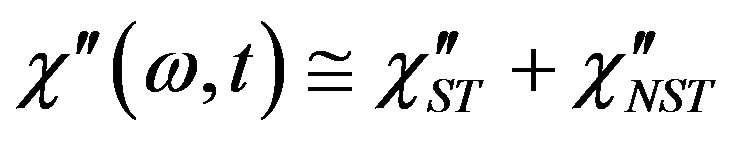 (13)
(13)
For a numerical calculations of the expression (12), we take the following values of the parameters: ,
, 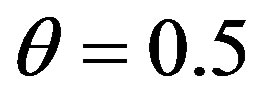 ,
, 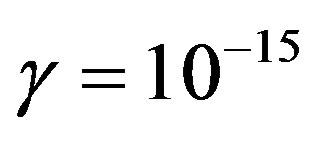 ,
, 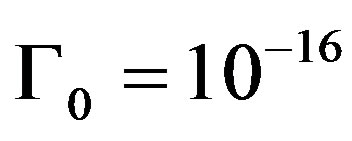 ,
, 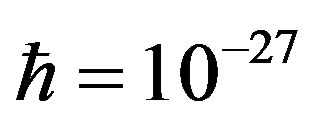 ,
,  ,
, 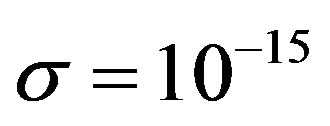 ,
, 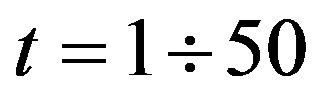 ,
, .
.
In Figures 1-3 it is shown the 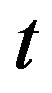 -dependence of the imaginary part
-dependence of the imaginary part at different fixed Т (Figure 1),
at different fixed Т (Figure 1),  (Figure 2) and
(Figure 2) and  (Figure 3). The susceptibility quickly goes down and then slowly decays to some value with oscillations. Then we observe the stationary behavior of susceptibility. In particular, in Figure 2 we observe as, on longer times, the quantum fluctuations (
(Figure 3). The susceptibility quickly goes down and then slowly decays to some value with oscillations. Then we observe the stationary behavior of susceptibility. In particular, in Figure 2 we observe as, on longer times, the quantum fluctuations (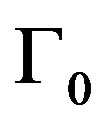 dependence) becomes irrelevant.
dependence) becomes irrelevant.

Figure 1. Imaginary part 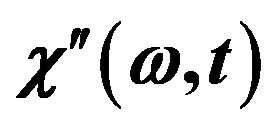 as function of time
as function of time  at
at 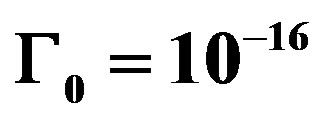 and
and 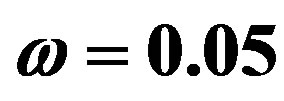 for different temperatures
for different temperatures  and
and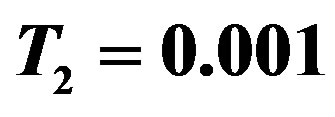 .
.
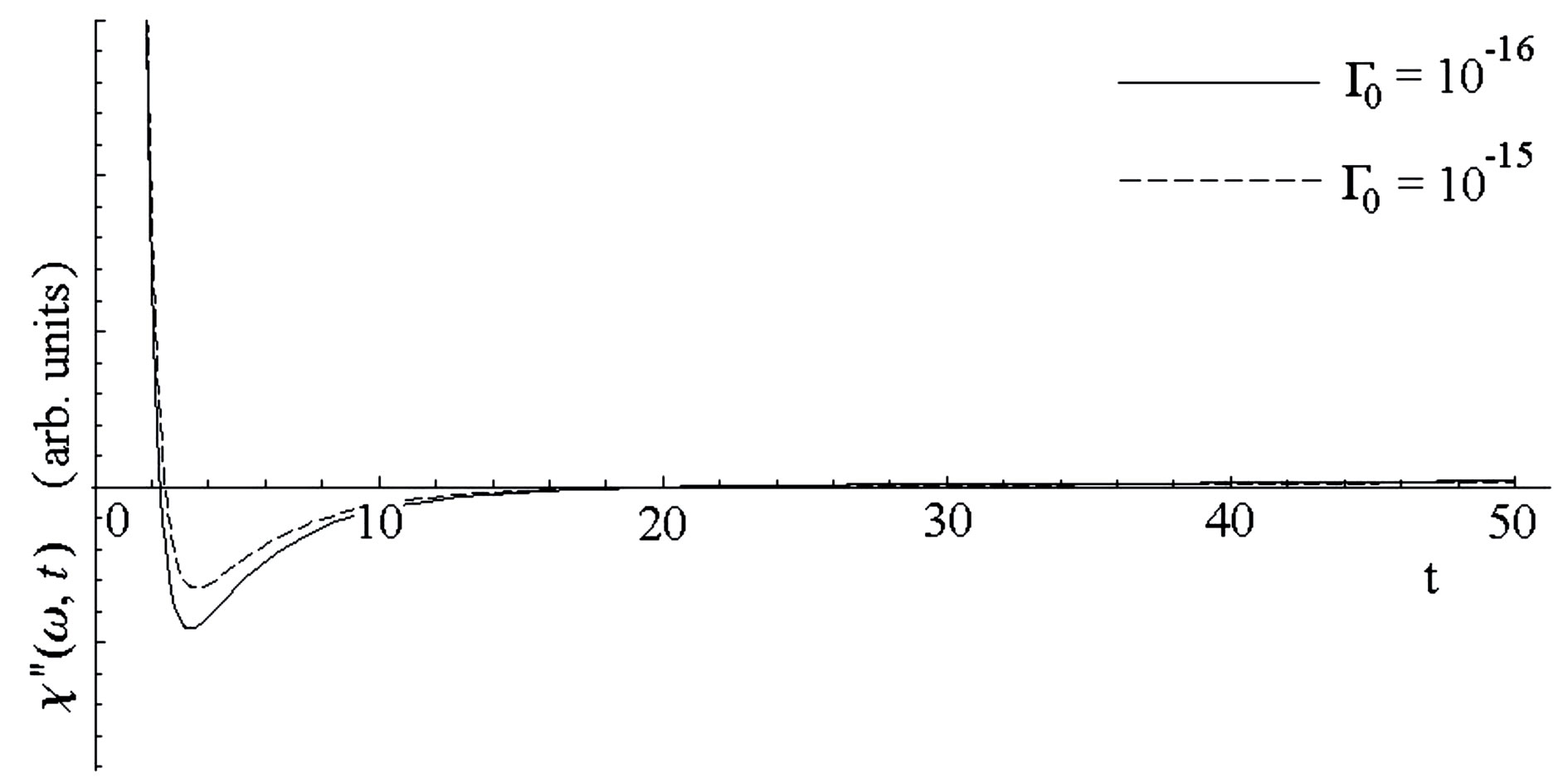
Figure 2. Imaginary part 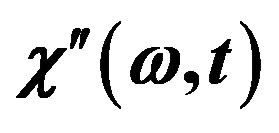 as function of time
as function of time 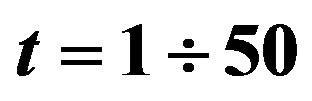 at
at 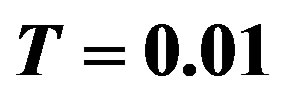 and
and 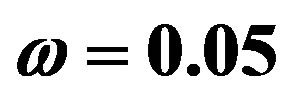 for different values of quantum parameter
for different values of quantum parameter 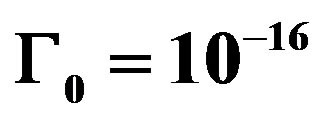 and
and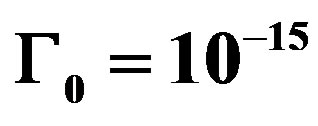 .
.
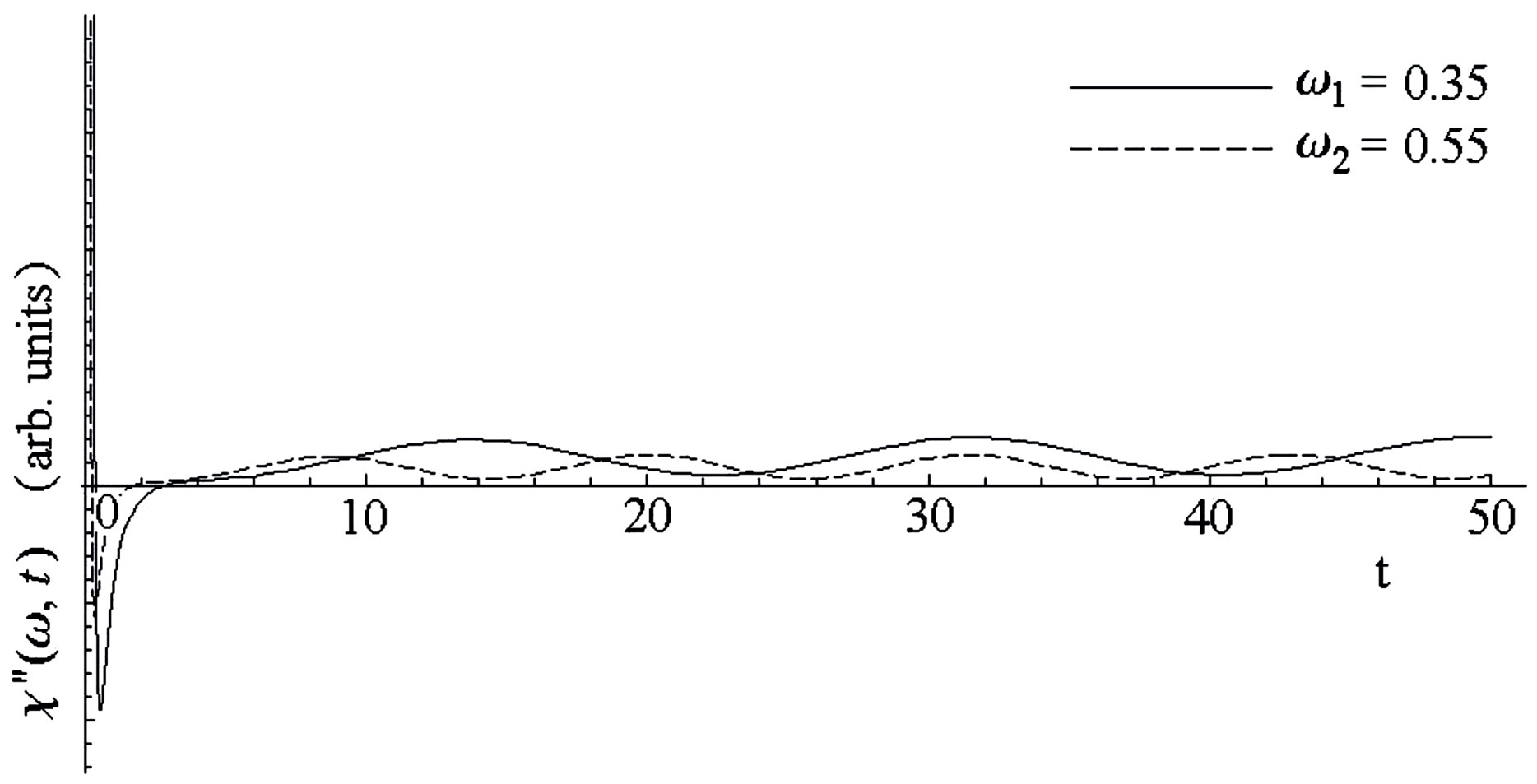
Figure 3. Imaginary part 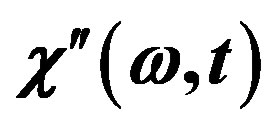 as function of time
as function of time 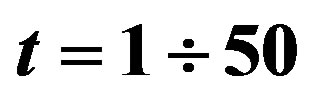 at
at 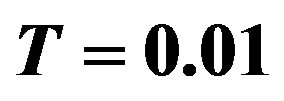 and
and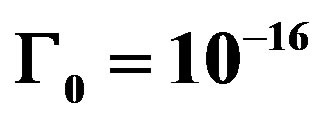 for different frequencies
for different frequencies 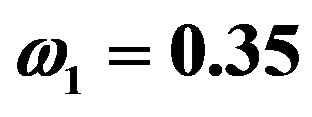 and
and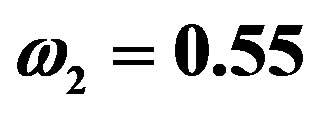 .
.
4. Discussion and Conclusions
In this paper we have investigated the low temperature non-equilibrium dynamic behavior of magnetic susceptibility in d-dimensional short-range Ising spin glass in a transverse field in terms of phenomenological droplet model taking into account quantum fluctuations. In particular we calculated the imaginary part of low-frequency susceptibility 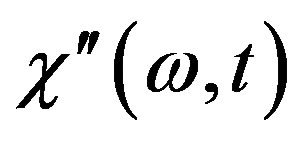 as function of time
as function of time 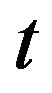 (elapsed from the quench to measurement moment) and frequency
(elapsed from the quench to measurement moment) and frequency  of the ac magnetic field. It has been shown that the imaginary part of
of the ac magnetic field. It has been shown that the imaginary part of 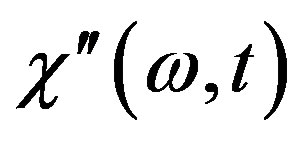 of the droplet system at low temperatures (quantum regime) has two time regions where its time behavior has different nature. On short times
of the droplet system at low temperatures (quantum regime) has two time regions where its time behavior has different nature. On short times  we observe quickly non-equilibrium dynamic decay of
we observe quickly non-equilibrium dynamic decay of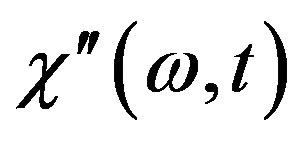 . On long times the susceptibility curve is a periodical function oscillating near some constant value (stationary process). We find temperature dependence of imaginary part of susceptibility and show how the quantum fluctuations influence the dynamic susceptibility of the droplet system at very low temperatures. If the ac field frequency increases then the nonequilibrium dynamics is suppressed. Thus the droplet system response to an external perturbing field depends on its thermal history.
. On long times the susceptibility curve is a periodical function oscillating near some constant value (stationary process). We find temperature dependence of imaginary part of susceptibility and show how the quantum fluctuations influence the dynamic susceptibility of the droplet system at very low temperatures. If the ac field frequency increases then the nonequilibrium dynamics is suppressed. Thus the droplet system response to an external perturbing field depends on its thermal history.
In [17] it is shown that the behavior of response function 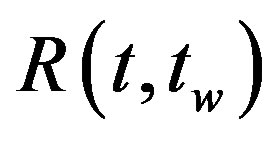 confirms the existence of two time regimes in spin glass: stationary and aging regimes in quantum systems. The theoretical curve (Figure 2 in [17]) of
confirms the existence of two time regimes in spin glass: stationary and aging regimes in quantum systems. The theoretical curve (Figure 2 in [17]) of 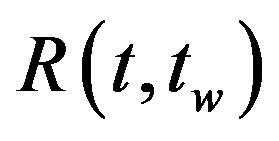 was given as function of
was given as function of 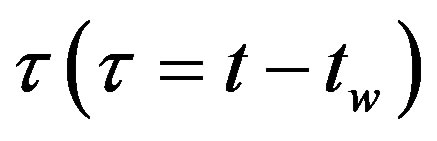 for
for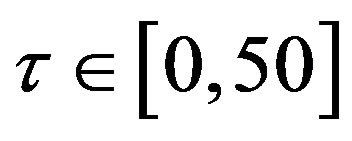 , and
, and 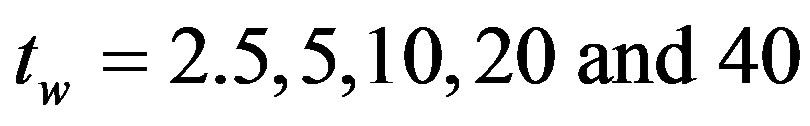 (
(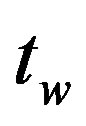 —waiting time). For
—waiting time). For  (
( is some characteristic time) a stationary regime was found, whereas for
is some characteristic time) a stationary regime was found, whereas for 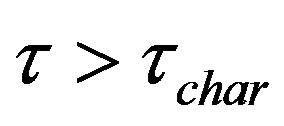 the dynamics is non-stationary. In [17] it is shown that quantum fluctuations in quantum glassy systems depress the phase transition temperature, in a glassy phase the aging effect survives the quantum fluctuations, and because of quantum fluctuations, the fluctuation-dissipation theorem is modified. In reference [19-21] it is shown that all terms in the dynamical equations governing the timeevolution of spin response and correlation function which are due to quantum effects, are irrelevant at long times. Quantum effects enter only through the renormalization of parameters in dynamical equations [19-21]. The behavior of spin response as function of τ in [36] is similar to behavior of dynamical susceptibility in our paper. In [36] it is shown that quantum fluctuation slightly influences the aging regime and the quantum system behavior is approximately classic.
the dynamics is non-stationary. In [17] it is shown that quantum fluctuations in quantum glassy systems depress the phase transition temperature, in a glassy phase the aging effect survives the quantum fluctuations, and because of quantum fluctuations, the fluctuation-dissipation theorem is modified. In reference [19-21] it is shown that all terms in the dynamical equations governing the timeevolution of spin response and correlation function which are due to quantum effects, are irrelevant at long times. Quantum effects enter only through the renormalization of parameters in dynamical equations [19-21]. The behavior of spin response as function of τ in [36] is similar to behavior of dynamical susceptibility in our paper. In [36] it is shown that quantum fluctuation slightly influences the aging regime and the quantum system behavior is approximately classic.
As far as we know there are no experiments on quantum spin glasses. In papers [17,23] there are experimental data for dynamic susceptibility in classic spin glasses. P. Svedlindh et al. [35] have investigated the behavior of  and have found that decay is close to a logarithmic one. Shins et al. [22] also show that susceptibility decays with time in a nearly logarithmic way.
and have found that decay is close to a logarithmic one. Shins et al. [22] also show that susceptibility decays with time in a nearly logarithmic way.
In our quantum system at very low temperature, we cannot find agreement with these data because classical and quantum spin glass has, in general, different behavior. We may compare our results with experimental data only approximately because these experimental data are on classical spin glasses and we consider here low-temperature dynamics of quantum spin glass. We observe a qualitatively similar behavior in the range of the small times elapsed since the quench.
REFERENCES
- A. J. Bray and M. A. Moore, “Heidelberg Colloquium on Glassy Dynamics,” J. L. van Hemmen and I. Morgenstern, Eds., Springer, Berlin, 1986.
- K. H. Fisher and J. A. Hertz, “Spin Glass,” Cambridge University Press, England, 1991. doi:10.1017/CBO9780511628771
- H. Rieger, Annual Reviews of Computational Physics, Vol. 2, 1995, p. 295.
- A. P. Young, “Spin Glass and Random Field,” World Scientific, Singapore, 1988.
- J.-L. Barrat, M. Feidelman, J. Kurchan and J. Dalibard. “Slow Relaxations and Nonequilibrium Dynamics in Condensed Matter,” Springer, Berlin, 2003.
- L. Berthier and J.-P. Bouchaud, Physical Review B, Vol. B66, 2002, Article ID: 054404. doi:10.1103/PhysRevB.66.054404
- D. Herrison and M. Ocio, The European Physical Journal B, Vol. 40, 2004, pp. 283-294. doi:10.1140/epjb/e2004-00278-6
- M. Suzuki and I. S. Suzuki, The European Physical Journal B, Vol. 41, 2004, pp. 457-470. doi:10.1140/epjb/e2004-00339-x
- L. C. E. Struik, “Physical Aging in Amorphous Polimers and Other Materials,” Elsevier, Houston, 1978.
- L. Bellon, S. Ciliberto and C. Laroche, Europhysics Letters, Vol. 51, 2000, p. 551. doi:10.1209/epl/i2000-00368-1
- V. Norman, S. Muller, J.-C. Ravey and A. Parker, Macromolecules, Vol. 33, 2000, pp. 1063-1071. doi:10.1021/ma9909455
- H. Nishimori, “Statistical Physics of Spin Glasses and Information Processing,” Oxford University Press, 2001. doi:10.1093/acprof:oso/9780198509417.001.0001
- J. A. Mydosh, “Spin Glasses: An Experimental Introduction,” Taylor & Francis, London, 1993.
- D. A. Huse, Physical Review, Vol. B43, 1991, pp. 8673- 8675. doi:10.1103/PhysRevB.43.8673
- T. Komori, H. Yoshino and H. Takayama, Journal of the Physical Society of Japan, Vol. 68, 1999, p. 3387.
- V. S. Zotev, G. G. Kenning and R. Orbach, Physical Review B, Vol. 66, 2002, Article ID: 014412. doi:10.1103/PhysRevB.66.014412
- L. F. Cugliandolo and G. Lozano, Physical Review B, Vol. 59, 1999, pp. 915-942. doi:10.1103/PhysRevB.59.915
- F. Krzakala and O. C. Martin, Physical Review Letters, Vol. 85, 2000, pp. 3013-3016. doi:10.1103/PhysRevLett.85.3013
- M. P. Kennett, C. Chamon and J. Ye, Physical Review B, Vol. 64, 2001, Article ID: 224408. doi:10.1103/PhysRevB.64.224408
- H. Yoshino, K. Hukushima and H. Takayama, Physical Review B, Vol. 66, 2002, Article ID: 064431. doi:10.1103/PhysRevB.66.064431
- H. E. Castillo, C. Chamon, L. F. Cugliandolo and M. P. Kennett, Physical Review Letters, Vol. 88, 2002, Article ID: 237201. doi:10.1103/PhysRevLett.88.237201
- G. Busiello, R. V. Saburova and V. G. Sushkova, The European Physical Journal B, Vol. 39, 2004, pp. 69-76. doi:10.1140/epjb/e2004-00172-3
- A. G. Shins, A. F. Arts and H. W. de Wijn, Physical Review Letters, Vol. 70, 1993, p. 2340.
- V. Dupuis, V. Vincent, J.-Ph. Bouchaud, J. Hammann, A. Ito and H. A. Katori, Physical Review B, Vol. 64, 2001, Article ID: 174204. doi:10.1103/PhysRevB.64.174204
- P. E. Jonsson, H. Yoshima, P. Nordblad, A. H. Katori and A. Ito, Physical Review Letters, Vol. 88, 2002, Article ID: 257204. doi:10.1103/PhysRevLett.88.257204
- D. S. Fisher and D. A. Huse, Physical Review Letters, Vol. 56, 1986, pp. 1601-1604. doi:10.1103/PhysRevLett.56.1601
- M. J. Thill and D. A. Huse, Physica A: Statistical Mechanics and Its Applications, Vol. 241, 1995, pp. 321-365. doi:10.1016/0378-4371(94)00247-Q
- G. Busiello and R. V. Saburova, International Journal of Modern Physics B, Vol. 14, 2000, p. 1843. doi:10.1142/S0217979200002168
- G. Busiello, R. V. Saburova and V. G. Sushkova, Solid State Communications, Vol. 119, 2001, pp. 545-548. doi:10.1016/S0038-1098(01)00267-8
- M. J. P. Gingras and P. Henelius, Proceedings of International Conference on Frustration in Condensed Matter (ICFCM), Sendai, 11-14 January 2011.
- Z. Kutnjak, R. Pirc, A. Levstik, C. Filipic, R. Blinc and R. Kind, Physical Review B, Vol. 50, 1984, pp. 12421-12428. doi:10.1103/PhysRevB.50.12421
- S. L. Hutton, I. Fehst, R. Bohmer, M. Braune, B. Mertz, P. Lunkenheimer and A. Loidl, Physical Review Letters, Vol. 66, 1991, pp. 1990-1993. doi:10.1103/PhysRevLett.66.1990
- W. Wu, D. Bitko, T. F. Rosenbaum and G. Aeppli, Physical Review Letters, Vol. 71, 1993, pp. 1919-1922. doi:10.1103/PhysRevLett.71.1919
- W. T. Grandy, “Foundation of Statistical Mechanics,” D. Reidel Publishing Company, Dordrecht, 1988. doi:10.1007/978-94-009-2881-7
- P. Svedlindh, K. Gunnarsson and J.-O. Andersson, Physical Review B, Vol. 46, 1992, pp. 13867-13873. doi:10.1103/PhysRevB.46.13867
- G. Biroli and O. Parcollet, Physical Review B, Vol. 65, 2002, Article ID: 094414. doi:10.1103/PhysRevB.65.094414

